mn 122
谐振峰值
Am(m) 2
1
12
振荡环节的对数频率特性
L ()2l0 oG g (j) 2l0 o(g 1 n 2 2)24 2 n 2 2
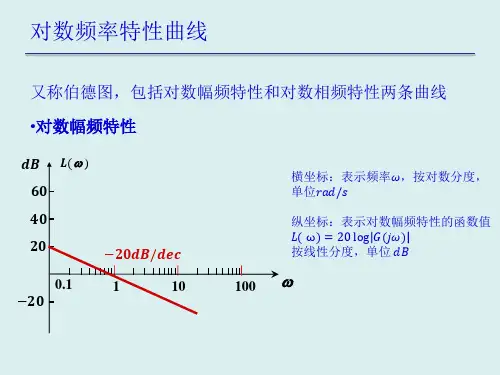
n L()0低频渐近线是零分贝线。
n L ( ) 4 0lo g (/ n) 4 0lo g (T ) n 1 /T
高频段是一条斜率为- 40/dB的直线,和零分
幅频特性的谐振峰值和谐振角频率:
G(ju)
1
(1u2)242u2
d G d (j) u u 0 ,u r 1 22 ( 1 /2 0 .7)0
r n12 2 ( 1/ 20 .7) 0
幅频特性的谐振角频率和谐振峰值:
rn1 22, M r G (jr) 1 /21 2
谐振频率
1 / T , L () 2l0 o1 g2 T 2 2l0 o 1 0 g ( d)B
在频率很低时,对数幅频曲线可用0分贝线近似。
1 / T , L ( ) 2l0 o1 g 2 T 2 2l0 o T g
当频率很高时,对数幅频曲线可用一条直线近似,直
线斜率为-20dB/dec,与零分贝线相交的角频率为 1/T 。
( )
0 0.1 1 10
0 o 0.1 1 10
45o
20
90o
对数坐标刻度图
注意:
➢纵坐标是以幅值对数分贝数刻度的,是均匀的;横 ➢ 坐标按频率对数标尺刻度,但标出的是实际的值, ➢ 是不均匀的。 ——这种坐标系称为半对数坐标系。 ➢在横轴上,对应于频率每增大10倍的范围,称为十 ➢ 倍频程(dec),如1-10,5-50,而轴上所有十倍频 程 ➢ 的长度都是相等的。 ➢为了说明对数幅频特性的特点,引进斜率的概念, ➢ 即横坐标每变化十倍频程〔即变化〕所对应的纵 坐