第四章流体通过颗粒层(含小结)

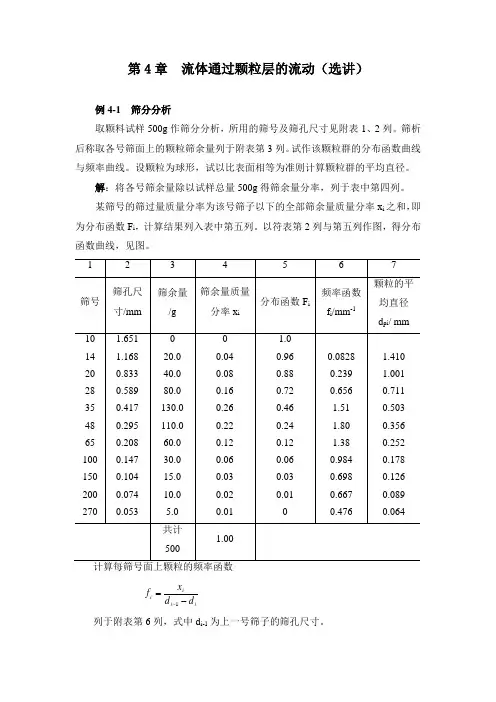
第4章 流体通过颗粒层的流动（选讲）例4-1 筛分分析取颗料试样500g 作筛分分析，所用的筛号及筛孔尺寸见附表1、2列。

筛析后称取各号筛面上的颗粒筛余量列于附表第3列。

试作该颗粒群的分布函数曲线与频率曲线。

设颗粒为球形，试以比表面相等为准则计算颗粒群的平均直径。

解：将各号筛余量除以试样总量500g 得筛余量分率，列于表中第四列。

某筛号的筛过量质量分率为该号筛子以下的全部筛余量质量分率x i 之和，即为分布函数F i ，计算结果列入表中第五列。

以符表第2列与第五列作图，得分布函数曲线，见图。

ii ii d d x f -=-1列于附表第6列，式中d i-1为上一号筛子的筛孔尺寸。

每号筛面上颗粒的平均直径取该号与上一号筛孔尺寸的算术平均值，列于附表第7列。

以第6、7两列数据作图得频率函数曲线。

以比表面相等为准则求取该批颗粒的平均直径d m 。

∑=pii m dx d 1例4-2 空隙率及比表面的测定如图所示，空气通过待测粉体组成的床层，其流量用毛细管流量计测得，床层压降用U 形压差计测得。

今用12.2g 水泥充填成截面5.0cm 2、厚度为1.5cm 的床层。

在常压下，20℃的空气以4.0×10-6m3/s 的流量通过床层，测得床层压降Δp 为1500Pa 。

已知水泥粉末的密度ρp 为3120kg/m 3，试计算水泥的比表面。

解：充填密度 3243/1627015.0105102.12m kg =⨯⨯⨯='--ρ 床层填充密度与颗粒密度间的关系为 )1(ερρ-='p 床层空隙率 48.03120162711=-='-=d ρρε 床层的表观气速 s m A q u V /008.0100.5100.446=⨯⨯==-- 空气的粘度为 μ=1.81×10-5Pa·s而 u a L p μεε322)1(0.5-=∆ 则 008.01081.148.0)48.01(0.5015.015005322⨯⨯⨯-⨯=-a 求出 α= 2.38×105 m 2/m 3 检证雷诺数 μερa u )1(e R -=' 3551029.4108.11038.2)48.01(008.02.1--⨯=⨯⨯⨯⨯-⨯=例4-3 悬浮液及滤饼参数的测定实验室中过滤质量分率为0.1的二氧化钛水悬浮液，取湿滤饼100g 经烘干后称重得固体质量为55g 。

第四章 流体通过颗粒层的流动典型例题1. 有一板框过滤机，恒压下过滤某种悬浮液，过滤1h 后，得到滤液60m 3,然后用5m 3的清水（物性与滤液相近）进行洗涤，拆装时间为20min ，已测得V e =4m 3,试求：(1) 过滤末速率为多少m 3滤液/h ?(2) 洗涤时间为多少h ?(3) 该机生产能力为多少m 3滤液/h ?解：（1）已知33360m ,20min,4m ,5m e W V V V τ====2222622322602604m 4080h 14080m ()31.875h 2()2(604)e eE e V VV KA V VV KA dV KA d V V τττ+=++⨯⨯∴===∴===+⨯+ (2) 315m ()()7.970.63h h 47.97()W W E W W V dV dV dV d d d ττττ==∴=== (3) 360m 30.6h 2010.6360W D V Q τττ===++++滤液2. 某板框过滤机在恒压下操作，过滤阶段的时间为2h ，已知第1h 过滤得8m 3滤液，滤饼不可压缩，滤布阻力可忽略，试求：（1） 第2h 可得多少滤液？（2） 过滤2h 后用2m 3清水（粘度与滤液相近），在同样压力下对滤饼进行横穿洗涤，求洗涤时间；（3） 若滤液量不变，仅将过滤压差提高1倍，问过滤时间为多少？（4） 若过滤时间不变，仅将过滤压差提高1倍，问滤液量为多少？解：（1）22V KA τ=将318m V = 11h τ=代入上式，得 642=KA 所以32188 3.31m V V V ∆=-===(2) 由过滤基本方程22()e dV KA d V V τ=+ 由题知0e V = 328 3.3111.31m V =+= 代入得232364() 2.83m /h 2211.311 2.83()()0.71m /h 442 2.83h 0.71()E W E W W W dV KA d V dV dV d d V dV d τττττ===⨯====== （3）s =0 212=∆∆p p ∵K p ∝∆ ∴ 21212=∆∆=p p K K ∵222211K A K A ττ= ∴121221h 2（）ττ===K K （4）2)(12212==K K V V ，32111.3115.99m V ===3. 用一板框过滤机，对某种悬浮液进行恒压过滤，过滤时间为20min,得到滤液20m 3,滤饼不洗涤，拆装时间为15min,滤饼不可压缩，介质阻力可忽略不计。

第4章流体通过颗粒层的流动概述由众多固体堆积而成的静止颗粒层称为固定床。

工业生产中流体通过固定床流动的典型例子：1. 固定床反应器----催化剂颗粒堆积成的固定床。

2. 悬浮液的过滤----悬浮液中颗粒沉积形成的滤饼可看成固定床．本章重点考查流体通过固定床的基本流动规律和过滤操作规律。

４.2 颗粒床层的特性颗粒床层由不同大小和形状的颗粒组成，流体在其中的流动与管内流动类似。

但颗粒床层内的流道尺寸不同，形状各异，具有复杂的网状结构。

对其特性的了解应从组成通道的颗粒着手。

4.2.1 单颗粒的特性 ()球形颗粒的几何特性可用单一参数d p全面表示，如：体积：（４－１）面积：（４－２）球形颗粒比表面积：（４－３）非球形颗粒：非球形颗粒的几何特征不能用单一参数全面表示，通常以某种等当的球形颗粒近似表示，以使所考查领域内非球形颗粒的特征与球形颗粒等效。

此球的直径称d e。

当量直径可用不同方式定义。

(1). 体积当量直径：使当量球形颗粒的体积等于实际颗粒的体积V。

（４－４）(2). 面积当量直径：使当量球形颗粒的表面积πd es2等于实际颗粒的表面积S。

（４－５）(3). 比表面当量直径：使当量球形颗粒的6/d ea等于实际颗粒的比表面积a（４－６）非球形颗粒的形状系数：对非球形颗粒，只以一个当量直径不能确定其几何特征，因此定义形状系数。

（４－７）4．2．2 颗粒群特性由不同大小、形状颗粒组成的颗粒群，各单个颗粒的尺寸不会完全一样。

颗粒群的大小分布用筛分分析得出。

筛分分析——用一组具有不同大小筛孔的利用筛孔的机械阻挡，将颗粒群按其粒度范围分为若干子群即对其分布进行测定（为促使颗粒通过筛孔，筛面应作某种运动）。

通过筛孔的颗粒量称为筛过量，截留于筛面的颗粒量称为筛余量。

称取各筛面上的颗粒筛余量，即得筛分分析基本数据，筛分分析适用于>70μm的颗粒 ()标准筛--不同国家采用不同的标准筛制，其筛孔为正方形时，其尺寸可直接用边长（mm）表示；也可用筛号或筛目（筛网单位长度上的孔数）表示。

第一章流体流动质点含有大量分子的流体微团，其尺寸远小于设备尺寸，但比起分子自由程却要大得多。

连续性假定假定流体是由大量质点组成的、彼此间没有间隙、完全充满所占空间的连续介质。

拉格朗日法选定一个流体质点,对其跟踪观察，描述其运动参数(如位移、速度等)与时间的关系。

欧拉法在固定空间位置上观察流体质点的运动情况，如空间各点的速度、压强、密度等，即直接描述各有关运动参数在空间各点的分布情况和随时间的变化。

定态流动流场中各点流体的速度u 、压强p不随时间而变化。

轨线与流线轨线是同一流体质点在不同时间的位置连线，是拉格朗日法考察的结果。

流线是同一瞬间不同质点在速度方向上的连线，是欧拉法考察的结果。

系统与控制体系统是采用拉格朗日法考察流体的。

控制体是采用欧拉法考察流体的。

理想流体与实际流体的区别理想流体粘度为零，而实际流体粘度不为零。

粘性的物理本质分子间的引力和分子的热运动。

通常液体的粘度随温度增加而减小，因为液体分子间距离较小，以分子间的引力为主。

气体的粘度随温度上升而增大，因为气体分子间距离较大，以分子的热运动为主。

总势能流体的压强能与位能之和。

可压缩流体与不可压缩流体的区别流体的密度是否与压强有关。

有关的称为可压缩流体，无关的称为不可压缩流体。

伯努利方程的物理意义流体流动中的位能、压强能、动能之和保持不变。

平均流速流体的平均流速是以体积流量相同为原则的。

动能校正因子实际动能之平均值与平均速度之动能的比值。

均匀分布同一横截面上流体速度相同。

均匀流段各流线都是平行的直线并与截面垂直,在定态流动条件下该截面上的流体没有加速度, 故沿该截面势能分布应服从静力学原理。

层流与湍流的本质区别是否存在流体速度u、压强p的脉动性，即是否存在流体质点的脉动性。

稳定性与定态性稳定性是指系统对外界扰动的反应。

定态性是指有关运动参数随时间的变化情况。

边界层流动流体受固体壁面阻滞而造成速度梯度的区域。

边界层分离现象在逆压强梯度下，因外层流体的动量来不及传给边界层，而形成边界层脱体的现象。

第四章 流体通过颗粒层的压降固定床压降4-1．某种圆柱形颗粒催化剂其直径为d p ，高为h ，试求等体积的当量直径d e 及球形度ψ。

现有h =d p =4mm 的颗粒，填充在内径为1m 的圆筒形容器内，填充高度为1.5m ，床层空隙率为0.43。

若在20℃、101.3kPa 下使360m 3/h 的空气通过床层，试估算床层压降为多少？解：3232323466hd h d Vd p pev===πππ2222pppp es d h d d h d Sd +=+==ππππpp pppp p esevd h h d d h hd dh d hd d d +=+=+==2182182433232313123132343222ψ()()32333333232/m m 105.11041043104104263262321866⨯=⨯⨯⨯⨯⨯+⨯⨯⨯=+=+==----h d d h hd d h h d d p p p pp ev ψα m/s 127.03600114.33604422=⨯⨯⨯==D q u v π 查20℃、101.3kPa 下空气的3kg/m 205.1=ρ，s Pa 1081.15⋅⨯=-μ()()89.91081.143.01105.1127.0205.1153=⨯⨯-⨯⨯⨯=-='-μεαρu R e使用欧根方程()()()()()Pa12.223127.0205.143.043.01105.129.0127.01081.143.043.01105.117.45.1129.0117.42335322323322=⎥⎥⎦⎤⎢⎢⎣⎡⨯⨯-⨯⨯⨯+⨯⨯⨯-⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛-+-=∆-u a u a L P ρεεμεε *4-2．用20℃、101.3kPa 空气通过某固定床脱硫器，测得如下数据：空塔气速 0.3m/s, 单位床层高度的压降 220 Pa/m ； 0.8m/s, 1270 Pa/m 。

4.1.1 工业背景固定床是由许多固体颗粒堆积成的静止颗粒层。

①流体物性：ρ,μ②操作因素：u③设备因素：颗粒直径，22eS eVd d =ψψ≤1 与球形差异度4.2.3 床层特性①床层空隙率ε受充填方式的影响均匀颗粒0.26—0.48与dp 分布有关乱堆床层0.47—0.7床床床空V V V V V p −==ε床V V p )1(ε−=ε对反映床层紧密程度，对流体流动的阻力有极大影响非球形乱堆的ε大于球形颗粒，非均匀颗粒ε小于均与颗粒。

,1f h εε↓↑<∑。

几何边界复杂，无法解析解，要靠实验需要用数学模型法来考虑②空隙中实际速度与空隙大小有关。

4.4 过滤过程 4.4.1基本原理 最简单的过滤操作： 布氏漏斗 悬浮液中固体颗粒被 过滤介质截留，清液在 压差下通过多孔过滤介 质，使固液分离。

过滤介质缝隙并不需要比颗粒小---架桥现象5%以上颗粒大 于过滤介质孔径 “穿滤”⎧深层过滤 两种过滤方式 ⎨ ⎩滤饼过滤 推动力：重力、压力、离心力滤浆 滤饼 过滤介质 滤液深层过滤滤饼过滤过滤介质： 多孔性介质、耐腐蚀、耐热并具有 足够的机械强度。

工业用过滤介质主要有：滤浆 滤饼织物介质，如棉、麻、丝、毛、合过滤介质 成纤维、金属丝等编织 滤液 成的滤布； 多孔性固体介质，如素瓷板或管、 烧结金属等。

滤饼过滤滤饼的压缩性：空隙结构易变形的滤饼为可压缩滤饼。

助滤剂： 是不可压缩的粉状或纤维状固体， 如硅藻土、纤维粉末、活性炭、石棉。

使用时，可预涂，也可以混入待滤 的滤浆中一起过滤。

滤浆 滤饼过滤介质 滤液方式1.预涂滤饼过滤方式2.混入悬浮液4.4.2 过滤过程的数学描述 4.4.2.1 物料衡算 过滤过程的数学描述 物料衡算滤浆 滤饼 过滤介质 滤液滤饼过滤定 义w ：质量分数（kg固/kg悬） φ ：体积分数（m3固/m3悬） ε：滤饼空隙率 V悬 ：悬浮液总量 L： 滤饼厚度 A：过滤面积 LA：滤饼体积（包括ε）悬浮液含固量表示方法： 质量分数w, kg固体/kg悬浮液 3 3 φ , m /m 体积分数 固体 悬浮液滤浆 滤饼 过滤介质 滤液滤饼过滤取1m3悬浮液w=φρ p φρ p + (1 − φ ) ρw ：质量分数（kg固/kg悬） 3固/m3悬） ：体积分数（ m φ注意：①滤液、滤饼、清液方向要清楚 ②基准要选好 滤饼空隙率ε与含清液质量分率w’关系 取1kg滤饼 取1m3滤饼 ερ w' / ρ w' = ε= ερ + (1 − ε ) ρ p w' / ρ + ( 1 − w' ) / ρ p物料恒算基本关系式• • • • • 悬浮液中固体质量=滤饼中颗粒质量 悬浮液中清液量=滤液量+滤饼中清液量 悬浮液的总量=颗粒量+全部清液 =滤饼的量+滤液 滤饼的量=固体颗粒的量+滤饼中滤液的量颗粒在液体中不发生溶胀V ⎧V悬 = V + LA q = ，单位面积滤液量 ⎨ A φ = − ε V LA 1 （ ） ⎩ 悬φ V φ = L= q 1−ε −φ A 1−ε −φL为滤饼厚度φ=w/ρp w / ρ p + (1 − w ) / ρw ：质量分数（kg固/kg悬） φ ：体积分数（m3固/m3悬）。