流体通过颗粒层的流动
- 格式:doc
- 大小:2.91 MB
- 文档页数:18


第4章流体通过颗粒层的流动概述由众多固体堆积而成的静止颗粒层称为固定床。
工业生产中流体通过固定床流动的典型例子:1. 固定床反应器----催化剂颗粒堆积成的固定床。
2. 悬浮液的过滤----悬浮液中颗粒沉积形成的滤饼可看成固定床.本章重点考查流体通过固定床的基本流动规律和过滤操作规律。
4.2 颗粒床层的特性颗粒床层由不同大小和形状的颗粒组成,流体在其中的流动与管内流动类似。
但颗粒床层内的流道尺寸不同,形状各异,具有复杂的网状结构。
对其特性的了解应从组成通道的颗粒着手。
4.2.1 单颗粒的特性 ()球形颗粒的几何特性可用单一参数d p全面表示,如:体积:(4-1)面积:(4-2)球形颗粒比表面积:(4-3)非球形颗粒:非球形颗粒的几何特征不能用单一参数全面表示,通常以某种等当的球形颗粒近似表示,以使所考查领域内非球形颗粒的特征与球形颗粒等效。
此球的直径称d e。
当量直径可用不同方式定义。
(1). 体积当量直径:使当量球形颗粒的体积等于实际颗粒的体积V。
(4-4)(2). 面积当量直径:使当量球形颗粒的表面积πd es2等于实际颗粒的表面积S。
(4-5)(3). 比表面当量直径:使当量球形颗粒的6/d ea等于实际颗粒的比表面积a(4-6)非球形颗粒的形状系数:对非球形颗粒,只以一个当量直径不能确定其几何特征,因此定义形状系数。
(4-7)4.2.2 颗粒群特性由不同大小、形状颗粒组成的颗粒群,各单个颗粒的尺寸不会完全一样。
颗粒群的大小分布用筛分分析得出。
筛分分析——用一组具有不同大小筛孔的利用筛孔的机械阻挡,将颗粒群按其粒度范围分为若干子群即对其分布进行测定(为促使颗粒通过筛孔,筛面应作某种运动)。
通过筛孔的颗粒量称为筛过量,截留于筛面的颗粒量称为筛余量。
称取各筛面上的颗粒筛余量,即得筛分分析基本数据,筛分分析适用于>70μm的颗粒 ()标准筛--不同国家采用不同的标准筛制,其筛孔为正方形时,其尺寸可直接用边长(mm)表示;也可用筛号或筛目(筛网单位长度上的孔数)表示。







第4章 流体通过颗粒层的流动典型例题例1:过滤机的最大生产能力用一板框压滤机对悬浮液进行恒压过滤,过滤20分钟得滤液 20m 3 ,过滤饼不洗涤,拆装时间为15分钟,滤饼不可压缩,介质阻力可略。
试求: (1) 该机的生产能力,以 m 3 (滤液)/h 表示(2)如果该机的过滤压力增加 20℅,该机的最大生产能力为多少 m 3(滤液)/h ? 解:(1)h m V Q D /3.34601520203=⨯+=+=θθ (2)根据恒压过滤方程V 2=KA 2θ202020222===θV KA为了得到最大生产能力,则应 min 15==D f θθ在原压力下对应的滤液量为 300152022=⨯==f opt KA V θ33.17m V opt = ΔP ’=1.2ΔPV ∝ΔP 1/2395.183.172.1m V opt =⨯=h m V Q Df opt/9.3760151595.183max =⨯+=+=θθ例2:滤饼的洗涤问题采用板框压过滤机进行恒压过滤,操作1小时后,得滤液 15m 3 ,然后用2m 3的清水在相同的压力下对滤饼进行横穿洗涤。
假设清水的粘度与滤液的粘度相同。
滤布阻力可略,试求: (1) 洗涤时间(2) 若不进行洗涤,继续恒压过滤1小时,可另得滤液多少 m 3 ? 解:V 2=KA 2θKA 2=152采用横穿洗涤法,则有:Ew d dV d dV ⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛θθ41 hr V KA V f w w 07.11521541224122=⨯⨯=⨯=θ 或者 hr Jf w 07.114115222=⨯⨯==θδθ''22θKA V = , 322.21215''m KA V =⨯==θ 32.6152.21m V =-=∆例3:操作压强对过滤机生产能力的影响用板框过滤机过滤某悬浮液,一个操作周期内过滤 20分钟后共得滤液 4m 3 (滤饼不可压缩,介质阻力可略)。

第三章流体通过颗粒层的流动一、基本知识1.下列关于非均相物系的举例及说明中错误的是。
甲:泡沫液,是液气组成的非均相物质,其中分散相是液体,分散介质是气体。
乙:乳浊液,是液固组成的非均相物质,其中连续相是液体,分散介质是固体。
丙:烟尘气,是气固组成的非均相物质,其中连续相是气体,分散介质是固体。
丁:雾沫气,是气液组成的非均相物质,其中分散相是液体,分散介质是气体。
①甲、乙②乙、丙③丙、丁④丁、甲2.下面论断中正确的有。
①单位体积固体颗粒所具有的表面积称为该固体颗粒的比表面积②根据不同方面的等效性(质量等效、体积等效、比表面积等效等),可以定义不同的当量直径③形状系数是与非球形颗粒体积相等的球的表面积除以非球形颗粒的表面积的商④对于球形颗粒,只要一个参数,即颗粒直径便可惟一地确定其体积、表面积和比表面积⑤对于非球形颗粒,必须定义两个参数(通常定义体积当量直径和形状系数)才能确定其体积、表面积和比表面积3.下面有关颗粒群论断中正确的是。
①在任何颗粒群中,都存在一定的尺寸(粒度)分布②颗粒粒度的测量方法有筛分法、显微镜法、沉降法、电阻变化法、光散射与衍射法、表面积法等③对于大于70μm的颗粒,也就是工业固定床经常遇到的情况,常采用一套标准筛进行测量(筛分分析)④筛分使用的标准筛系金属丝网编织而成,各国习用筛的开孔规格各异,常用的泰勒制是以每英寸边长上的孔数为筛号或称目数4.下面有关颗粒群筛分结果论断中正确的有。
①筛分结果可用分布函数和频率函数图示②分布函数曲线上对应于某一尺寸dpi的分布函数Fi值表示直径小于dpi的颗粒占全部试样的质量分率,而该批颗粒的最大直径dp,max。
处,其分布函数Fi的值为1③频率分布曲线上在一定粒度范围内的颗粒占全部颗粒的质量分率等于该粒度范围内频率函数曲线下的面积,而频率分布函数曲线下的全部面积等于l④颗粒群的任何一个平均直径都不能全面代替一个分布函数5.颗粒的比表面积α和床层的比表面αB及床层的空隙率ε之间的关系式为。
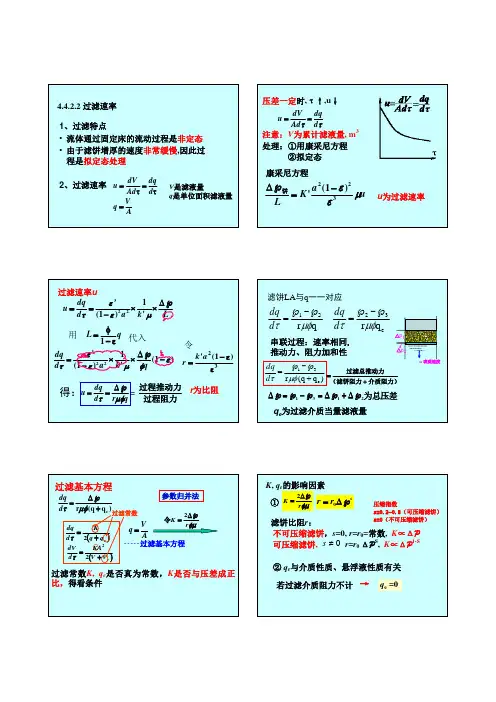
第4章流体通过颗粒层的流动一、选择题1.推导液体流过滤饼(固定床)的过滤基本方程式的基本假设是:液体在多孔介质中流型属(),依据的公式是()公式。
[南京理工大学2010年研]A.层流,欧根B.湍流,欧根C.层流,柯士尼D.湍流,柯士尼【答案】C【解析】滤液通过滤饼层流动的特点:①滤液穿过滤饼中不规则的孔道;②滤液在孔道中的大部分流动为层流;③过滤属非定态操作。
依据的是柯士尼(康采尼,音译过来的)公式()22251c p u L a εμε∆⎛⎫=⎪-⎝⎭2.恒压过滤时,如介质阻力不计,滤饼不可压缩,滤饼压差增大一倍时同一过滤时刻所得滤液量()。
[浙江大学2011年研]A.增大至原来的2倍B.增大至原来的4倍C.增大至原来的倍D.增大至原来的1.5倍【答案】C【解析】介质阻力忽略不计,则V 2=KA 2τ,滤饼不可压缩,则2pK r φμ∆=,ΔP 增加一倍,则V 增加为原来的2倍。
二、填空题1.气体通过颗粒床层的流动,当床层表观气速大于起始流化速度且小于带出速度时,随气速增加,床层空隙率______,床层降压______。
[北京化工大学2012年研]【答案】增大;不变【解析】固定床阶段压降增大;而当为流化床阶段,表观气速大于等于起始流化速度,床层空隙率增大,但压降不变。
2.用转筒真空过滤机过滤某种悬浮液,已知在转速为1rpm 时的生产能力为4.8m 3/h,现要将生产能力提高20%,若过滤介质阻力可忽略不计,则转速应改为______,或将转筒的浸没角增为原来的______倍。
[华南理工大学2011年研]【答案】1.44rpm;1.44倍【解析】转筒真空过滤机的生产能力Q=465n K ψ,n Q ψ∝∝。
三、计算题用一板框压滤机在恒压下过滤某一悬浮液,过滤面积为0.4m 2,过滤操作4小时后得滤液80m 3,过滤介质阻力可忽略不计。
试求:(1)若其它情况不变,但过滤面积加倍,可得多少滤液?(2)若其它情况不变,但过滤时间缩短为2小时,可得多少滤液?(3)若在原表压下过滤4小时后,再用5m 3水洗涤滤饼,洗涤时间(h)又为多少?假设滤液与水性质相近。
4.1.1 工业背景固定床是由许多固体颗粒堆积成的静止颗粒层。
①流体物性:ρ,μ②操作因素:u③设备因素:颗粒直径,22eS eVd d =ψψ≤1 与球形差异度4.2.3 床层特性①床层空隙率ε受充填方式的影响均匀颗粒0.26—0.48与dp 分布有关乱堆床层0.47—0.7床床床空V V V V V p −==ε床V V p )1(ε−=ε对反映床层紧密程度,对流体流动的阻力有极大影响非球形乱堆的ε大于球形颗粒,非均匀颗粒ε小于均与颗粒。
,1f h εε↓↑<∑。
几何边界复杂,无法解析解,要靠实验需要用数学模型法来考虑②空隙中实际速度与空隙大小有关。
4.4 过滤过程 4.4.1基本原理 最简单的过滤操作: 布氏漏斗 悬浮液中固体颗粒被 过滤介质截留,清液在 压差下通过多孔过滤介 质,使固液分离。
过滤介质缝隙并不需要比颗粒小---架桥现象5%以上颗粒大 于过滤介质孔径 “穿滤”⎧深层过滤 两种过滤方式 ⎨ ⎩滤饼过滤 推动力:重力、压力、离心力滤浆 滤饼 过滤介质 滤液深层过滤滤饼过滤过滤介质: 多孔性介质、耐腐蚀、耐热并具有 足够的机械强度。
工业用过滤介质主要有:滤浆 滤饼织物介质,如棉、麻、丝、毛、合过滤介质 成纤维、金属丝等编织 滤液 成的滤布; 多孔性固体介质,如素瓷板或管、 烧结金属等。
滤饼过滤滤饼的压缩性:空隙结构易变形的滤饼为可压缩滤饼。
助滤剂: 是不可压缩的粉状或纤维状固体, 如硅藻土、纤维粉末、活性炭、石棉。
使用时,可预涂,也可以混入待滤 的滤浆中一起过滤。
滤浆 滤饼过滤介质 滤液方式1.预涂滤饼过滤方式2.混入悬浮液4.4.2 过滤过程的数学描述 4.4.2.1 物料衡算 过滤过程的数学描述 物料衡算滤浆 滤饼 过滤介质 滤液滤饼过滤定 义w :质量分数(kg固/kg悬) φ :体积分数(m3固/m3悬) ε:滤饼空隙率 V悬 :悬浮液总量 L: 滤饼厚度 A:过滤面积 LA:滤饼体积(包括ε)悬浮液含固量表示方法: 质量分数w, kg固体/kg悬浮液 3 3 φ , m /m 体积分数 固体 悬浮液滤浆 滤饼 过滤介质 滤液滤饼过滤取1m3悬浮液w=φρ p φρ p + (1 − φ ) ρw :质量分数(kg固/kg悬) 3固/m3悬) :体积分数( m φ注意:①滤液、滤饼、清液方向要清楚 ②基准要选好 滤饼空隙率ε与含清液质量分率w’关系 取1kg滤饼 取1m3滤饼 ερ w' / ρ w' = ε= ερ + (1 − ε ) ρ p w' / ρ + ( 1 − w' ) / ρ p物料恒算基本关系式• • • • • 悬浮液中固体质量=滤饼中颗粒质量 悬浮液中清液量=滤液量+滤饼中清液量 悬浮液的总量=颗粒量+全部清液 =滤饼的量+滤液 滤饼的量=固体颗粒的量+滤饼中滤液的量颗粒在液体中不发生溶胀V ⎧V悬 = V + LA q = ,单位面积滤液量 ⎨ A φ = − ε V LA 1 ( ) ⎩ 悬φ V φ = L= q 1−ε −φ A 1−ε −φL为滤饼厚度φ=w/ρp w / ρ p + (1 − w ) / ρw :质量分数(kg固/kg悬) φ :体积分数(m3固/m3悬)。
4. 流体通过颗粒层的流动4.1 概述由众多固体颗粒堆积而成的静止的颗粒床层称为固定床。
许多化工操作都与流体通过固定床的流动有关,其中最常见的有:(1)固定床反应器(组成固定床的是粒状或片状催化剂)(2)悬浮液的过滤(组成固定床的是悬浮液中的固定颗粒堆积而成的滤饼看作是固定床)4.2颗粒床层的特性(1)床层空隙率ε固定床层中颗粒堆积的疏密程度可用空隙率来表示,其定义如下:ε=空隙体积床层体积=V v -床层体积颗粒所占体积床层体积V =1-v Vε的大小反映了床层颗粒的紧密程度,ε对流体流动的阻力有极大的影响。
ε↑,f h ↑∑。
ε<1 (2)床层自由截面积分率A 。
A 0 =流动截面积床层截面积=P A 床层截面积A-颗粒所占的平均截面积A 床层截面积=1-P A A现在我们来分析一下空降率ε与床层自由截面积分率0A 之间有何关系。
假设床层颗粒是均匀堆积(即认为床层是各向同性的)。
想象用力从床层四周往中间均匀压紧,把颗粒都压到中间直径为1D 长为L 的圆柱中(圆柱内设有空隙)。
ε=1-v V0A =1-P A A =1-21244D LD L ππ=1-21244D D ππ =1-21D D ⎛⎫ ⎪⎝⎭ =1-21D D ⎛⎫ ⎪⎝⎭所以对颗粒均匀堆积的床层(各向同性床层),在数值上ε=A 。
(3)床层比表面B aB a =V颗粒表面积S 床层体积 , 颗粒比表面a =S V 颗粒表面积颗粒体积 取V =13m 床层考虑,B a =1S ,a =S v =1S ε- 所以 B a =a (1-ε) 此式是近似的,在忽略床层中固颗粒相互接触而彼此覆盖使裸露的颗粒表面积减少时成立。
4.3流体通过固定床的压降固定床中颗粒间存在着网络状的空隙形成许多可供流体通过的细小通道。
这些通道是曲折而且互相交联,其截面大小和形状又是很不规则的。
流体通过如此复杂的通道时的阻力(压降)自然难以进行理论计算,必须依靠实验来解决问题。
现在介绍一种实验规划方法——数学模型法。
4.3.1颗粒床层的简化模型(1)床层的简化物理模型在固定床内大量细小而密集的固体颗粒对流体的运动形成了很大的阻力。
此阻力一方面可使流体沿床截面的速度分布变的相当均匀,另一方面却在床层两端造成很大压降。
工程上感兴趣的主要是床层的压降。
为解决流体流过固定床层的压降计算问题,我们必须把图(a)所示的难以用数学方程描述的颗粒层内的实际流动过程进行大幅度的简化,使之可以用数学方程式加以描述。
经简化而得到的等效流动过程称之为原真实流动过程的物理模型。
那么如何进行简化可以得到等效流动过程呢?经过分析我们知道,单位体积床层所具有的颗粒表面积(即床层比表面积Ba)和床层空隙率ε对流动阻力有决定性的作用。
为得到等效流动过程,简化后的物理模型中的Ba和ε应与真空模型的Ba和ε相等,为此许多研究者将床层中的不规则通道简化成长度为eL的一组平行细管(图(b)),并规定:①细管的内表面积等于床层颗粒的全部表面;②细管的全部流动空间等于颗粒床层的空隙体积。
根据上述假定,可求得这些虚拟细管的当量直径eded=4⨯通道的截面积湿润周边=4⨯ee/L VL V⨯⨯(通道截面积)(湿润周边)/=4//VV⨯空隙体积颗粒表面积=4⨯Baε=41aεε-()按此简化模型,流体通过固定床的压降等同于流体通过一组当量直径为ed、长度为eL的细管的压降。
(2)流体压降的数学模型上述简化的物理模型,已将流体通过具有复杂几何边界(网络状孔道)的床层的压降简化为通过均匀圆管的压降,故可用第一章流体流过圆管的阻力损失作出如下的数学描述e1fe2L uhdλρ==V p式中1u为流体在细管内的流速,由于细管内的流动过程等效与原真实流动过程,故1u可取为实际填充床中颗粒空隙间的流速。
它与表现流速u的关系为:体积流量=1u101A u AA u A Auε===流动所以1uuε=单位床层高度的虚拟压强降2e()(1)()42uL aL Lρεελε∆-=p=2e3(1)()8L auLελρε-细管长度e e e L L L L L L ≠∝=实际床层高度,但,即常数 将其并入λ中得(e8L L λλ'=)23(1)a u Lελρε∆-'=p(4-22) 式中p L∆为单位床层高度的虚拟压强差,当床层不高,重力的影响可以忽略时, p L L∆∆≈p 为简化起见,以后在本章中∆p 均称为压降,或以后出现的公式p ∆=∆p 或干脆用p ∆表示。
式(4-22)即为流体通过固定床压降的数学模型,其中包括一个未知的待定系数λ'。
λ'称为模型参数,就其物理意义而言,也可称为固定床的流动摩擦系数。
(3)模型的检验和模型参数的估值上述床层的简化处理只是一种假定,模型正确与否必须经过实验检验,其中的模型参数λ'亦必须由实验测定。
康采尼(Kozeny )对此进行了实验研究,发现在流速教低,床层雷诺数e 1Re 24(1)d u u a ρρμεμ'==<-时,实验数据能较好地符合下式 (1)Re K K a εμλρμ''-'==' (4-23) 式中K '称为康采尼常数,其值为5.0。
对于不同的床层,K '的可能误差不超过10%,这表明上述的简化模型确实是实际过程的合理简化。
把式(4-23)代入式(4-22)得223(1)a K u L εμε∆-'=p (4-25) 上式称为康采尼方程,它仅适用于低累诺数(Re 2'<)范围,对于本章后面要重点讨论的过滤操作此式成立。
而对于较宽的Re '范围,可用教材p164式(4-26)~式(4-28)的欧根(Ergun )方程描述。
(对非球型颗粒,以ev d ψ代替欧根公式中的p d ,ψ称为形状系数,其意义见p157,ev d 称为体积当量直径,其定义为p156(4-4)。
还有es ea ,d d 定义请自学。
)从康采尼方程或欧根方程可看出,影响床层压降∆p 的变量有三类:① 操作变量u ;② 流体物性μρ和;③ 床层特性ε和a在上述因素中,影响最大的是空隙率ε,在其他条件不变时,若ε从0.5降至0.4,从式(4-25)中不难算出L ∆p 将增加2.8倍!另一方面ε又随装填料情况而变,同一种物料用同样方式装填,其ε也未必能够重复。
因此,在设计计算时,ε的选取应当十分慎重。
(4)因次分析法和数学模型法的比较由于化工过程的复杂性,在大多数情况下均难以采用数学解析法求解,而必须依靠实验。
为了以尽量少的实验得到可靠和明确的结果,任何实验都必须在理论的指导下进行。
指导实验的理论包括两个方面,一是化学工程学科本身的基本规律和基本观点,二是正确的实验方法论。
到目前为止,我们已学过的指导实验的理论有两个,一个是因次分析法,另一个就是前面介绍的数学模型法。
这两个理论的主要特点我们要简要回顾总结一下。
因次分析法的步骤:①找出过程的影响因素(此步是因次分析法成败的关键,若遗漏某个重要的影响因素将得不到可靠的结果,若引进无关的物理量则可能得到没有意义的数群。
找影响因素一般是靠经验及若干实验结果分析);②将影响过程的各个物理量的因次抽出进行分析,整理成若干个无因次数群(数群的数目少于自变量的数目,使实验工作量减少);③通过实验确定各数群之间的定量关系(因次分析只考虑物理量的因次,没有考虑物理量的数值部分,故各数群的指数及数群前的系数仍需通过实验确定。
这样得到的各数群之间的关系式只能反映过程的外部联系,而对过程的内部规律不甚了解,如同“黑箱”。
然而,这正是因次分析法的一大特点,它使用因次分析法成为对各种研究对象原则上皆适用的一般方法。
对某些复杂过程,哪怕研究者对其内部规律不甚了解,照样可以进行研究);数学模型法的步骤(与因次分析法相反,数学模型立足于对所有研究过程的深刻理解):①将复杂的真实过程简化成易于用数学方程式描述的物理模型(对过程的合理简化是数学模型法成败的关键);②对所得的物理模型进行数学描述即建立数学模型(要简话得到一个足够简单又可用数学方程式表示且不失真的物理模型,必须对过程的内在规律特别是过程的特殊性有着深刻的理解。
这一点通过前面导出颗粒床层的数学模型,同学们应该有深刻的体会);③通过实验对数学模型的合理性进行检验并测定模型参数(数学模型法不能摆脱实验,最后还要通过实验解决问题。
但是,在因次分析法中实验的目的是为了搜索寻找各数群之间的函数关系;而在数学模型法中。
实验的目的是为了检验模型的合理性并测定为数较少的模型参数。
显然,检验性的实验要比搜索性的实验简易得多)。
有以上所述不难看出,在两种实验规划方法中,数学模型法更具有科学性。
但是数学模型法立足于对所研究过程的深刻理解,没有深刻的理解就不能作出恰如其分的简化,此法便不能使用。
因此,数学模型法的发展并不意味着因次分析法可以完全抛弃;相反两种方法应同时并存,各有所用,相辅相成。
4.4过滤原理及设备4.4.1过滤原理(1)过滤是利用可以让液体通过而不能让固体通过的多孔介质,将悬浮液中的固、液两相加以分离的操作。
(2)过滤方式①滤饼过滤(见图4-7a)过滤时悬浮液置于过滤介质的一侧。
过滤介质常用多孔织物,其网孔尺寸未必一定须小于被截留的颗粒直径。
在过滤操作开始阶段,会有部分颗粒进入过滤介质网孔中发生架桥现象(图4-7b),也有少量颗粒穿过介质而混与滤液中。
随着滤渣的逐步堆积,在介质上形成一个滤渣层,称为滤饼。
不断增厚的滤饼才是真正有效的过滤介质,而穿过滤饼的液体则变为清净的滤液。
通常,在操作开始阶段所得到滤液是浑浊的,须经过滤饼形成之后返回重滤。
②深层过滤颗粒尺寸比介质孔道小的多,孔道弯曲细长,颗粒进入孔道后容易被截留。
同时由于流体流过时所引起的挤压和冲撞作用。
颗粒紧附在孔道的壁面上。
介质表面无滤饼形成,过滤是在介质内部进行的。
(3)过滤介质①织物介质:即棉、毛、麻或各种合成材料制成的织物,也称为滤布。
②粒状介质:细纱、木炭、碎石等。
③多孔固体介质(一般要能够再生的才行):多孔陶瓷、多孔塑料、多孔玻璃等。
(4)助滤剂若悬浮液中颗粒过于细小将会使通道堵塞,或颗粒受压后变形较大,滤饼的孔隙率大为减小。
造成过滤困难,往往加助滤剂以增加过滤速率。
助滤剂的加法有两种:①直接以一定比例加到滤浆中一起过滤。
若过滤的目的是回收固体物此法便不适用。
②将助滤剂预先涂在滤布上,然后再进行过滤。
此法称为预涂。
助滤剂是一种坚硬而形状不规则的小颗粒,能形成结构疏松而且几乎是不可压缩的滤饼。
常用作助滤剂的物质有:硅藻土、珍珠岩、炭粉、石棉粉等。
4.4.2过滤设备4.2.2.1板框过滤机(1)结构与工作原理由多块带凸凹纹路的滤板和滤框交替排列于机架而构成。