典型信号的傅里叶级数

coswt傅里叶级数
（最新版）
目录
1.傅里叶级数的概念
2.coswt 傅里叶级数的意义
3.coswt 傅里叶级数的求解方法
4.coswt 傅里叶级数的应用
正文
傅里叶级数是一种将周期函数分解为一系列正弦和余弦函数的方法。

在数学和物理学中，这种方法被广泛应用。

coswt 傅里叶级数就是其中一个典型的例子。

coswt 傅里叶级数，指的是将函数 cos(wt) 分解为一系列正弦和余
弦函数的级数。

其中，w 是角频率，t 是时间。

这个级数的求解，可以帮助我们更好地理解余弦函数的周期性，以及它在不同频率下的振幅和相位。

求解 coswt 傅里叶级数的方法，一般采用傅里叶变换。

首先，我们
需要将时间域的信号转换到频率域，然后，通过查看频率域的信号，我们可以得到每个频率的振幅和相位。

最后，我们将这些信息带回时间域，就可以得到 coswt 傅里叶级数。

coswt 傅里叶级数在许多领域都有应用，包括信号处理、图像处理、通信系统等。

例如，在信号处理中，我们可以通过求解 coswt 傅里叶级数，来去除信号中的噪声，或者增强信号的某些频率成分。

在图像处理中，我们可以通过求解 coswt 傅里叶级数，来实现图像的频域滤波，从而改
善图像的质量。

在通信系统中，我们可以通过求解 coswt 傅里叶级数，
来分析信号的频谱，从而更好地进行信号的调制和解调。

总的来说，coswt 傅里叶级数是一种重要的数学工具，它在许多领域
都有广泛的应用。

傅里叶级数公式傅里叶级数是一种数学工具，用于将一个周期性函数表示为无限多个简单的正弦和余弦函数的和。

它由法国数学家傅里叶在19世纪中叶发现，并在物理学、工程学和其他领域中得到广泛应用。

本文将介绍傅里叶级数的定义、数学表达式和一些应用示例。

定义给定一个周期为T的函数f(t)，其傅里叶级数表示为：傅里叶级数公式傅里叶级数公式其中a0、an和bn是傅里叶系数，可以通过以下公式计算：傅里叶系数公式傅里叶系数公式傅里叶系数公式傅里叶系数公式傅里叶系数公式傅里叶系数公式数学表达式傅里叶级数公式可以进一步简化为以下形式：傅里叶级数公式简化形式傅里叶级数公式简化形式其中cn是复傅里叶系数，可以通过以下公式计算：复傅里叶系数公式复傅里叶系数公式应用示例傅里叶级数在信号处理、图像处理和音频处理等领域中有广泛的应用。

以下是一些傅里叶级数的应用示例：1. 信号分析傅里叶级数可以将任意周期性信号分解为不同频率的正弦和余弦函数的和，从而帮助我们理解信号的频谱特征。

通过计算傅里叶系数，我们可以得到信号在不同频率上的幅度和相位信息。

2. 图像压缩傅里叶级数被广泛用于图像压缩算法中，例如JPEG压缩。

通过将图像转换为频域表示，可以将高频部分压缩或丢弃，从而实现图像的压缩和存储。

3. 音频合成傅里叶级数可以用于合成音频信号。

通过给定一些具有不同频率和幅度的正弦和余弦函数的傅里叶系数，我们可以通过求和运算生成一个新的音频信号。

4. 信号滤波傅里叶级数在信号滤波中也有广泛应用。

通过将信号转换到频域，并在频域对信号进行滤波操作，可以实现去除噪声、降低干扰等效果。

总结傅里叶级数是一种将周期性函数表示为正弦和余弦函数的和的数学工具。

它帮助我们理解信号的频谱特征，进行信号分析、图像压缩、音频合成和信号滤波等应用。

通过计算傅里叶系数，我们可以获得信号在不同频率上的幅度和相位信息。

傅里叶级数在现代科学和工程中具有重要的地位，对于理解和处理周期性信号至关重要。

常用傅里叶级数展开公式傅里叶级数展开是指将一个周期函数表示成一组正弦和余弦函数的和的形式，从而方便研究周期函数的性质。

傅里叶级数理论建立于 1822 年由法国数学家约瑟夫·傅里叶发现。

在数学、物理、工程等领域均有广泛应用。

下面我们来看一下常用的傅里叶级数展开公式。

1. 周期函数的傅里叶级数展开设 $f(x)$ 为周期为 $2l$ 的周期函数，则对于$x\in(-l,l)$ 函数 $f(x)$ 可以表示为以下形式：$$ f(x) =\frac{a_0}{2}+\sum_{n=1}^{+\infty}(a_n \cos\frac{n\pi x}{l}+b_n \sin \frac{n\pi x}{l}) $$其中，$a_0,a_n,b_n$ 称为傅里叶系数，具体计算方法如下：$$ a_0=\frac{1}{l}\int_{-l}^{l}f(x)dx $$$$ a_n=\frac{1}{l}\int_{-l}^{l}f(x)\cos\frac{n\pi x}{l}dx $$$$ b_n=\frac{1}{l}\int_{-l}^{l}f(x)\sin\frac{n\pi x}{l}dx $$2. 正弦级数和余弦级数上面提到的傅里叶级数展开可以分为正弦级数和余弦级数。

当 $f(x)$ 为偶函数时，我们就可以展开成余弦级数形式：$$ f(x) = \frac{a_0}{2}+\sum_{n=1}^{+\infty}a_n \cos \frac{n\pi x}{l} $$其中，$a_0,a_n$ 的计算方法与上述相同。

当 $f(x)$ 为奇函数时，我们就可以展开成正弦级数形式：$$ f(x) = \sum_{n=1}^{+\infty}b_n \sin\frac{n\pi x}{l} $$其中，$b_n$ 的计算方法也与上述相同。

3. 周期不为 $2l$ 的函数的傅里叶级数展开对于周期不为 $2l$ 的函数，我们需要将其转化为一个周期为 $2l$ 的函数，并称其为 $F(x)$，然后再做傅里叶级数展开。

傅里叶级数与傅里叶变换傅里叶级数和傅里叶变换是数学中重要的概念，广泛应用于信号处理、图像处理、通信系统等领域。

它们为我们理解和分析周期信号以及非周期信号提供了有效的数学工具。

本文将分别介绍傅里叶级数和傅里叶变换的基本概念、性质和应用。

一、傅里叶级数傅里叶级数是指将一个周期函数表示成一系列正弦和余弦函数的和。

它的基本思想是利用正弦和余弦函数的基本频率，将一个周期函数分解成多个不同频率的谐波分量，从而得到函数的频谱内容。

在数学上，傅里叶级数表示为：\[f(t) = \sum_{n=-\infty}^{\infty}c_ne^{i \omega_n t}\]其中，$c_n$代表系数，$e^{i \omega_n t}$是正弦和余弦函数的复数形式，$\omega_n$是频率。

将周期函数用傅里叶级数表示的好处是，可以通过调整系数来控制频谱内容，进而实现信号的滤波、合成等操作。

傅里叶级数的性质包括线性性、对称性、频谱零点等。

线性性意味着可以将不同的周期函数的傅里叶级数叠加在一起，得到它们的叠加函数的傅里叶级数。

对称性则表示实函数的傅里叶级数中系数满足一定的对称关系。

频谱零点表示在某些特殊条件下，函数的傅里叶级数中某些频率的系数为零。

傅里叶级数的应用广泛，例如在音频信号处理中，利用它可以进行音乐合成、乐音分析和音频压缩等操作。

此外，在图像处理领域，傅里叶级数被广泛应用于图像滤波、增强、噪声消除等方面。

二、傅里叶变换傅里叶变换是傅里叶级数的推广，用于处理非周期信号。

它将时域的信号转换为频域的信号，从而可以对信号进行频谱分析和处理。

傅里叶变换的定义为：\[F(\omega) = \int_{-\infty}^{\infty}f(t)e^{-i \omega t}dt\]其中，$F(\omega)$表示信号的频域表示，$f(t)$为时域信号，$\omega$为连续的角频率。

傅里叶变换可以将时域的信号分解成不同频率的复指数函数，并用复数表示频谱信息。

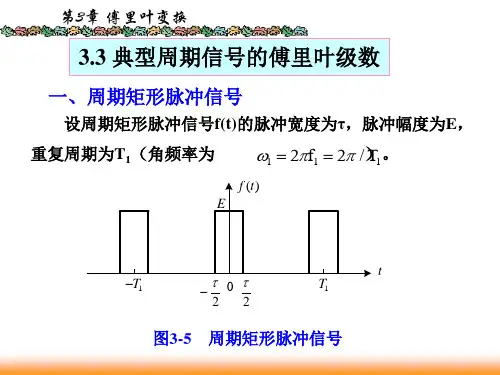
基本函数的傅里叶级数展开公式
傅里叶级数展开是一种将周期函数表示为无限三角函数序列的方法。

在此基础上，我们可以将各种复杂的信号分解为简单的周期函数，从而更好地理解和处理信号。

基本函数的傅里叶级数展开公式如下：
1. 正弦函数的展开公式
对于周期为T的正弦函数f(x)=sin(2πx/T)，它的傅里叶级数展开式为：
f(x)=a0+∑(n=1)∞(an*sin(2πnx/T)+bn*cos(2πnx/T)) 其中，
a0=1/T∫(0~T)f(x)dx
an=2/T∫(0~T)f(x)sin(2πnx/T)dx
bn=2/T∫(0~T)f(x)cos(2πnx/T)dx
2. 余弦函数的展开公式
对于周期为T的余弦函数f(x)=cos(2πx/T)，它的傅里叶级数展开式为：
f(x)=a0+∑(n=1)∞(an*cos(2πnx/T)+bn*sin(2πnx/T)) 其中，
a0=1/T∫(0~T)f(x)dx
an=2/T∫(0~T)f(x)cos(2πnx/T)dx
bn=2/T∫(0~T)f(x)sin(2πnx/T)dx
以上就是基本函数的傅里叶级数展开公式。

需要注意的是，这些
公式仅适用于周期为T的函数，而且函数必须满足一定的条件才能进行傅里叶级数展开。

同时，傅里叶级数方法也有其局限性，不能用来处理所有类型的信号。

傅里叶级数概念
傅里叶级数概念
傅里叶级数是一种用正弦和余弦函数来表示周期函数的方法。

具体地说，对于一个周期为T的函数f(x)，傅里叶级数可以表示为：
f(x) = a0 + Σan cos(nωx) + Σbn sin(nωx)
其中，a0、an和bn都是系数，ω为角频率，n为正整数。

不同于其他方法，傅里叶级数的系数只依赖于函数在一个周期内的取值。

使用傅里叶级数的好处是可以将任意周期函数用少数几个正弦和余弦函数的和来表示。

这种表示方式不仅简单，还能提供有用的信息，例如：
1. 特定的系数an和bn可以用来计算函数的傅里叶变换，进而确定函数的频谱（函数在频率域的表示）。

2. 傅里叶级数的收敛性定理可以帮助我们理解周期函数在各个点的行为和性质。

3. 傅里叶级数在信号处理、图像处理、量子力学和泛函分析等领域有广泛的应用。

总之，傅里叶级数是一种非常有用的理论工具，可以帮助我们更好地理解周期函数的性质和行为，并在实际应用中提供便利。

信号与系统傅里叶级数表示信号与系统是电子信息类专业中的重要基础课程，是学习和理解信号的产生、传输和处理的基础。

傅里叶级数是信号与系统中非常重要的数学工具，能够将一个周期信号分解成若干个简单的正弦函数的叠加，从而对信号进行分析和处理。

傅里叶级数是由法国数学家傅里叶在19世纪初提出的。

他认为任何一个周期信号都可以表示成若干个正弦函数的叠加，这些正弦函数的频率是原信号频率的整数倍。

傅里叶级数的表达式是一个无穷级数，其中包含了信号的频率、振幅和相位等信息。

在信号与系统中，傅里叶级数的应用非常广泛。

首先，傅里叶级数可以用来分析和处理周期信号。

周期信号是指在某个时间段内重复出现的信号，比如正弦信号和方波信号等。

通过将周期信号展开成傅里叶级数的形式，可以得到信号的频谱信息，即信号中各个频率分量的振幅和相位。

傅里叶级数还可以用来分析和处理非周期信号。

非周期信号是指在无限时间内不重复出现的信号，比如脉冲信号和矩形信号等。

虽然非周期信号不能直接使用傅里叶级数展开，但可以通过对信号进行周期延拓，将其转化为周期信号，然后再利用傅里叶级数进行分析和处理。

除了信号的分析，傅里叶级数还可以用来实现信号的合成。

通过给定一组正弦函数的振幅和相位，可以将它们叠加起来，得到一个新的信号。

这种信号的合成在通信系统中非常重要，可以用来调制信号、生成频谱等。

傅里叶级数的应用不仅局限于信号与系统领域，还广泛应用于其他领域。

在图像处理中，可以将图像视为一个二维信号，利用二维傅里叶级数对图像进行分析和处理。

在音频处理中，可以将音频信号视为一个一维信号，利用一维傅里叶级数对音频进行分析和处理。

在视频处理中，可以将视频视为一个三维信号，利用三维傅里叶级数对视频进行分析和处理。

傅里叶级数是信号与系统中非常重要的数学工具，能够将一个周期信号分解成若干个简单的正弦函数的叠加。

通过傅里叶级数的分析和合成，可以对信号进行详细的频谱分析和处理。

傅里叶级数的应用不仅局限于信号与系统领域，还广泛应用于其他领域，如图像处理、音频处理和视频处理等。

傅里叶级数公式傅里叶级数是数学中的一个重要概念，它可以将任意周期函数表示为一组正弦和余弦函数的线性组合。

这个公式的应用非常广泛，涵盖了信号处理、波动理论、热传导等领域。

我们来介绍一下傅里叶级数的定义。

对于一个周期为T的函数f(t)，傅里叶级数可以表示为以下形式：f(t) = a0 + Σ(an*cos(nωt) + bn*sin(nωt))其中，a0是f(t)的直流成分，an和bn是f(t)的交流成分，ω是圆频率，n是一个正整数。

傅里叶级数的重要性在于它可以将一个复杂的周期函数分解成无穷多个简单的正弦和余弦函数的叠加。

傅里叶级数的计算方法是通过求解函数f(t)与正弦余弦函数的内积来确定系数an和bn。

这里的内积是指两个函数在一个周期内的乘积再求平均。

具体来说，an和bn可以通过以下公式计算得到：an = (2/T) * ∫[0,T] f(t)*cos(nωt) dtbn = (2/T) * ∫[0,T] f(t)*sin(nωt) dt这里，∫[0,T]是对一个周期内的积分，dt表示微元。

通过计算这两个积分，我们可以得到函数f(t)的傅里叶系数an和bn。

傅里叶级数的应用非常广泛。

在信号处理中，我们可以利用傅里叶级数将一个复杂的信号分解成频谱，以便进一步分析和处理。

在波动理论中，傅里叶级数可以帮助我们理解波的传播和干涉现象。

在热传导问题中，傅里叶级数可以用来解决非稳态热传导方程。

除了傅里叶级数的定义和计算方法，还有一些重要的性质值得我们关注。

首先是傅里叶级数的收敛性。

对于一个连续函数f(t)，如果它在一个周期内满足一定的条件，那么它的傅里叶级数就会收敛于f(t)。

这个条件就是函数f(t)在一个周期内是有界的，并且具有有限个有限间断点。

另外一个重要的性质是傅里叶级数的线性性。

这意味着如果我们有两个函数f(t)和g(t)，它们的傅里叶级数分别为：f(t) = Σ(an*cos(nωt) + bn*sin(nωt))g(t) = Σ(cn*cos(nωt) + dn*sin(nωt))那么它们的线性组合h(t) = af(t) + bg(t)的傅里叶级数就是：h(t) = Σ[(a*an + b*cn)*cos(nωt) + (a*bn + b*dn)*sin(nωt)]这个性质对于我们进行信号处理和波动分析非常有帮助，可以将不同的信号叠加在一起进行处理。