高二数学下册期末联考检测试题10

格式：doc
大小：1.11 MB
文档页数：7

下载文档原格式

浙江省宁波市九校高二下学期期末联考数学试卷-含答案

宁波市九校联考高二数学试题一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合2{|13}{|320}A x x B x x x =-≤≤=-+<,,则=)(B C A R I（）A.[1,1)(2,3)-UB.]3,2[]1,1[Y -C. )2,1(D.R2.已知i 是虚数单位，则ii-+11= （） A.1 B.1- C. i - D.i3.已知曲线x x f ln )(=在点))2(,2(f 处的切线与直线01=++y ax 垂直，则实数a 的值为 ( )A.21 B.2- C. 2 D.21-4.下面四个条件中，使a b >成立的必要而不充分的条件是（）A.1a b ->B.1a b +>C.a b >D.33a b > 5.已知函数1ln 1)(--=x x x f ，则)(x f y =的图像大致为（）A. B. C. D.6.从1,2,3,,9L 这九个整数中同时取四个不同的数，其和为偶数，则不同取法共有（） A.62 B.64 C.65 D.667.已知n m b n am b a a b ,,,,111则--==<<的大小关系为（）A. n m <B. n m =C. n m >D. n m ,的大小关系不确定，与b a ,的取值有关 8.已知下列各式：①1)1|(|2+=+x x f ；②x x f =+)11(2；③||)2(2x x x f =-； ④x x x f -+=33|)(|.其中存在函数)(x f 对任意的R x ∈都成立的是（）A.①④B.③④C.①②D.①③9.设函数)0(log )(2>++=a b ax x x f ,若存在实数b ,使得对任意的[])0(2,>+∈t t t x第二学期学年2016都有a x f +≤1|)(|，则t 的最小值是（） A.2 B.1 C.43 D.3210.定义在R 上的可导函数)(x f 满足32)()(x x f x f =--,当(]0,∞-∈x 时,3)(2x x f <'实数a 满足1332)()1(23+-+-≥--a a a a f a f ,则a 的取值范围是（） A.⎪⎭⎫⎢⎣⎡∞+，23 B.⎥⎦⎤⎝⎛∞-23, C. ⎪⎭⎫⎢⎣⎡∞+，21 D.⎥⎦⎤⎝⎛∞-21, 二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分. 11.若,3log ,2log n m a a ==则=+n m a 2 ,用n m ,表示6log 4为 . 12.已知nxx )212(-的展开式中二项式系数和为64，则=n ,该展开式中常数项为 .13.已知函数10,2,122,4)(≠>⎩⎨⎧>++≤+-=a a x a a x x x f x 且其中.若21=a 时方程b x f =)(有两个不同的实根，则实数b 的取值范围是；若)(x f 的值域为[)∞+，2，则实数a 的取值范围是 . 14.函数xxee x x xf --+-=2)(3的奇偶性为 ,在R 上的增减性为 (填“单调递增”、“单调递减”或“有增有减”）.15.小明和爸爸妈妈、爷爷奶奶一同参加《中国诗词大会》的现场录制，5人坐成一排.若小明的父母至少有一人与小明相邻，则不同的坐法总数为 . 16.已知ax a x x a x x x f 22|1||1|)(-+--+-+=）（0>x 的最小值为23，则实数=a . 17.已知函数）R b a b ax x x f ∈++=,()(2在区间(]1,0上有零点0x ，则)31914(00-+x x ab 的最大值是 .三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.18.已知*∈N n ，(1)(2)(),n S n n n n =+++L 213(21)nn T n =⨯⨯⨯⨯-L .(Ⅰ)求 321321,,,,,T T T S S S ；(Ⅱ)猜想n S 与n T 的关系，并用数学归纳法证明.19.(Ⅰ)已知1021001210(21)(1)(1(1)x a a x a x a x -=+-+-++-L ），其中,1,2,10i a R i ∈=L .（i ）求01210a a a a ++++L ；（ii ）求7a .(Ⅱ)2017年5月,北京召开“一带一路”国际合作高峰论坛.组委会将甲、乙、丙、丁、戊五名志愿者分配到翻译、导游、礼仪、司机四个不同的岗位，每个岗位至少有一人参加，且五人均能胜任这四个岗位.（i ）若每人不准兼职，则不同的分配方案有几种？（ii)若甲乙被抽调去别的地方，剩下三人要求每人必兼两职，则不同的分配方案有几种？ 20.已知R a ∈,函数)(x f 满足.12)2(22-+-=a ax x f x(Ⅰ)求)(x f 的解析式,并写出)(x f 的定义域； (Ⅱ)若)(x f 在]2,2[2212+--a aa 上的值域为[]0,1-，求实数a 的取值范围.21.已知函数()1e1xf x x-=-+. (Ⅰ)证明当[]0,3x ∈时,xe x 911+≥-. (Ⅱ)证明当[]2,3x ∈时, 0)(72<<-x f .22.已知1-<a ，函数)(|1|)(33R x ax x x x f ∈++-=. (Ⅰ)求函数)(x f 的最小值；(Ⅱ)已知存在实数),1(,≤<n m n m 对任意),,(0n m t ∈总存在两个不同的),,1(,21+∞∈t t 使得)()(2)(210t f t f t f ==-，求证：274≤-m n .2016学年第二学期宁波市九校联考高二数学参考答案一、选择题（本大题共10小题，每小题4分，共40分）BDCBA DCADD二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分.11.12 ，2m n m + 12.6，60 13.）（49,2 ,),1()1,21[+∞⋃ 14.奇，单调递增 15.84 16.45 17.14410)31914()(,170002≥-+=--=x x x g ax x b 题：20000()()()ab g x a x ax g x ⋅=--[])()(000x g a x a x --≤343200000()1()44439x g x x x x ⋅≤=-+求导知其在11220,,,,,13333⎛⎤⎡⎤⎡⎤⎥⎢⎥⎢⎥⎝⎦⎣⎦⎣⎦上分别递增、递减、递增，故 1441)}1(),31(max{=⋅⋅≤g ab g ab 其.)21,21,1(0时等号成立-=-==b a x方法2：三、解答题：本大题共5小题，共74分 18.（本小题满分14分）解：(Ⅰ)120,12,2332211======T S T S T S ； ……（3分）(Ⅱ)猜想：n n S T =（*n N ∈） ……（4分）证明：(1)当1n =时，11S T =； ……（6分）（2）假设当()*1n k k k N=≥∈且时，kk ST =，即(1)(2)()213(21)kk k k k k +++=⨯⨯⨯-L L ，……（8分）则当1n k =+时200002002222200000011()493113=92()11313131(1)(1)942362362144ax b x x ab x ax b x ax b x x x x x +=-+-+⎡⎤≤=-=-≤⎢⎥⎣⎦g 可得则（-）（-）111)(12)(11)(1)(11)k S k k k k k k k k +=++++++-+++++L （ =(2)(3)(2)(21)(22)k k k k k ++++L=213(21)(21)(22)1k k k k k ⨯⨯⨯-⨯+++L =11213(21)(21)k k k k T ++⨯⨯⨯-+=L . ……（13分）即1+=k n 时也成立,由（1）（2）可知*n N ∈，n n S T =成立 ……（14分） 19.（本小题满分15分）解：(Ⅰ)（i ）令,2=x 则10012103(59049)a a a a ++++=L 即.……（3分) (ii)令10210012101,(12),x y y a a y a y a y -=+=+++L 则得77710215360.a C == …… （7分）(Ⅱ)（i ）.2404425=⋅A C……（11分）(ii) ()114)))(((233233424324=-+-C C C CC ……（15分）20.（本小题满分15分）解：(Ⅰ)令20,xt =>则,log 2t x =则,1log 2)(log )(2222-+-=a t a t t f 即.1log 2)(log )(2222-+-=a x a x x f ……（5分）定义域为()+∞,0 ……（7分） (Ⅱ))(x f 在]2,2[2212+--a aa 上的值域为[]0,1-等价于12)(22-+-=a ax x x g在区间]22,1[2+--a a a 上的值域为].0,1[- ……（9分）101+1y x ay x a x a =-⇒==⇒=-=令或由图可得2221a a a a ≤-+≤+ ……（13分）12a a ≤≤≤≤或 ……（15分）21.（本小题满分15分）解(Ⅰ)证明要证1e19xx-≥+, 也即证e 19xx ≤+. ……（2分）令()e 91xF x x =--, 则()'e 9xF x =-. 令()'0F x >, 则2ln3x >. 因此, 当02ln3x ≤<时, 有()'0F x <, 故()F x 在[]0,2ln3上单调递减; 当2ln33x <≤时, 有()'0F x >, 故()F x 在[]2ln3,3上单调递增. ……（5分）所以, ()F x 在[]0,3上的最大值为()(){}max 0,3F F .又()00F =,()33e 280F =-<. 故()[]0, 0,3F x x ≤∈成立, 即[]e 19, 0,3xx x ≤+∈成立. 原命题得证. ……（7分） (Ⅱ) 证明由 (I) 得当[]2,3x ∈时, ()111e1191xf x x x x -=-≥-+++令()11191t x x x=-++, 则 ()()()()()()()()()()()[]22222222222199119'19911191917280, 2,3.191x x t x x x x x x x x x x x --+-+=-+⋅++=-=++++-=≥∈++（9分）所以, ()t x 在[]2,3上单调递增，即()()[]161622, 2,357567t x t x ≥=->-=-∈所以()f x 72->得证. ……（12分）下证0)(<x f . 即证1+>x e x令),1()(+-=x e x h x则01)(>-='xe x h ，所以)(x h 在[]32，上单调递增, 所以，03)1()(2>-≥+-=e x e x h x ，得证. ……（15分）另证：要证7211911->+-+x x ，即证011892>+-x x ，令8)19(1189)(22--=+-=x x x x m 在[]32，上递增，所以01)2()(>=≥m x m 得证.22.（本小题满分15分）解：（1）⎩⎨⎧≥-+<+=++-=1,121,1|1|)(333x ax x x ax ax x x x f记)1(12)(),1(1)(321≥-+=<+=x ax x x f x ax x f则a x x f +=2'26)( , 因为 1-<a 则由6,0)('2ax x f -±==得 ……（2分）（i ）时，即1616-<≤-≤-a a，上递增，在上递减，在),1[)()1,()(21+∞-∞x f x f 所以1)1()]([min +==a f x f ……（4分）（ii ）时，即616-<>-a a,上递减，在)1,()(1-∞x f 递增，上递减，在在)6[)6,1[)(2∞+--a a x f , 所以1632)6()(2min --=-=aa a f x f综上，⎪⎩⎪⎨⎧-<≤-+-<--=16,16,1632)(mina a a aa x f……（6分）（2）不妨设,21t t <则由（1）知，若,16-<≤-a 则)(2x f 在),1(+∞上递增，不满足题意，所以6-<a . ……（7分）所以),6(),6,1(21+∞-∈-∈a t a t ，且 1632)6()(2min --=-=a a a f x f （i ）>-+21a 1632--a a ，即⎩⎨⎧<<--<1)1(2)(22721x f x f a 时，由即 ⎩⎨⎧<+<-+1121x a ax ，解得121<<+x a ，即)1,21(0a t +∈ 所以)1,21(),(a n m +⊆，所以1,21≤+≥n a m ，所以2742<-≤-a m n ……（11分）（ii ）≤-+21a 1632--a a ，即⎪⎩⎪⎨⎧->-<--<≤-)6(2)()1(2)(62272121a f x f f x f a 时，由即⎪⎩⎪⎨⎧-->-++<-+163221121aa ax a ax ，解得63221a x a -<<+，所以)632,21(),(a a n m -+⊆，所以632,21a n a m -≤+≥ 所以aa m n 21632---≤- 令]23,1(6∈=-u a ，则23113221632uu a a +-=--- 令231132)(u u u +-=ϕ，则0)11(32)(3'>-=u u ϕ 所以 231132)(u u u +-=ϕ在]23,1(∈u 递增，所以 274)23()(=≤ϕϕu ，所以 274)(≤≤-u m n ϕ. ……（15分）。

2024河南省新未来高二下学期7月期末联考数学试题及答案

绝密★启用前金科·新未来2023~2024学年度下学期期末质量检测高二数学全卷满分150分，考试时间120分钟。

注意事项：1、答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将条形码粘贴在答题卡上的指定位置。

2、请按题号顺序在答题卡上各题目的答题区域内作答，写在试卷、草稿纸和答题卡上的非答题区域均无效。

3、选择题用2B 铅笔在答题卡上把所选答案的标号涂黑；非选择题用黑色签字笔在答题卡上作答；字体工整，笔迹清楚。

4．考试结束后，请将试卷和答题卡一并上交。

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知等差数列{}n a 满足3616a a +=，且534a a −=，则首项1a =（） A ．1−B ．0C ．1D ．32．已知曲线()ln 2f x ax x =+−在点()()1,1f 处的切线方程是2y x b =+，则b =（） A ．3−B ．2−C ．1D ．-13．在各项为正的等比数列{}n a 中，8a 与10a 的等比中项为2，则26212log log a a +=（） A ．4 B ．3C ．1D ．24．函数()()321303f x x x x x =−−≤的最大值是（） A ．53B ．0C ．2D ．35．已知双曲线2222:1x y C a b−=的一条渐近线与圆22:(25E x y −+=相交于,A B 两点，且8AB =，则双曲线C 的离心率为（）A BC D6．若函数()22e xf x ax =−在区间()2,1−−上单调递减，则a 的取值范围是（） A ．[)2e,+∞B ．41,2e−+∞C ．21,e−∞−D ．21,0e−7．已知*211,,212nn n a b n n n∈==−+N ，数列{}n a 与数列{}n b 的公共项按从大到小的顺序排列组成一个新数列{}n c ，则数列{}n c 的前99项和为（） A ．12B ．99199C ．99197D ．1981998．在平面坐标系xOy 中，一个质点从原点出发，每次移动一个单位长度，且上下左右四个方向移动的概率相等，若该质点移动6次后所在坐标为()2,0，则该质点移动的方法总数为（） A ．120B ．135C ．210D ．225二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9．已知等差数列{}n a 的前n 项和为n S ，等比数列{}n b 的前n 项积为n T ，则（） A ．{}n n a b +不可能为等比数列 B ．{}n n a b 可能为等差数列 C ．n S n是等差数列D ．2n n T是等比数列 10．已知抛物线2:4C y x =的焦点为F ，准线为l ，点P 是C 上位于第一象限的动点，点M 为l 与x 轴的交点，则下列说法正确的是（） A ．F 到直线l 的距离为2B ．以P 为圆心PF 为半径的圆与l 相切C ．直线MP 斜率的最大值为2D ．若FM FP =，则FMP △的面积为211．已知函数()()e ,ln xf x xg x x x =−=−，则下列说法正确的是（） A ．()exg 在()0,+∞上是增函数B ．1x ∀>，不等式()()2ln f ax f x≥恒成立，则正实数a 的最小值为2eC ．若()f x t =有两个零点12,x x ，则120x x +>D ．若()()12(2)f x g x t t ==>，且210x x >>，则21ln tx x −的最大值为1e三、填空题：本题共3小题，每小题5分，共15分．12．已知变量x 和y 的统计数据如下表：x 1 2 3 4 5 y 1.5 2 m 4 4.5若由表中数据得到经验回归直线方程为 0.80.6x y =+，则m =_________．13．已知函数()2e xf x ax =−，若()f x 的图象经过第一象限，则实数a 的取值范围是_________．14．不透明的袋子中装有2个白球，3个黑球（除颜色外，质地大小均相同），学生甲先取出2个球（不放回），学生乙在剩下的3个球中随机取一个，已知甲至少取走了1个黑球，则乙取出白球的概率为_________．四、解答题：本题共5小题，共77分．解答应写出必要的文字说明、证明过程及演算步骤．15．（本小题满分13分）已知数列{}n a 是公差不为零的等差数列，111a =−，且256,,a a a 成等比数列．（1）求{}n a 的通项公式；（2）设n S 为{}n a 的前n 项和，求n S 的最小值． 16．（本小题满分15分）如图，在三棱锥P ABC −中，AB ⊥平面,,PAC E F 分别为,BC PC 的中点，且22PA AC AB ===．（1）证明：PC ⊥平面ABF ；（2）若AC PA ⊥，求平面AEF 与平面PAC 的夹角的余弦值． 17．（本小题满分15分）某学校食堂提供甲、乙、丙三种套餐，每日随机供应一种，且相邻两天不重复．已知食堂今天供应套餐甲，（1）求接下来的三天中食堂均未供应套餐甲的概率；（2）用随机变量X 表示接下来的三天中食堂供应套餐乙的天数，求X 的分布列与期望． 18．（本小题满分17分）已知椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ，，过F 的直线交C 于,A B 两点，O 为坐标原点，当AB OF ⊥时，AB =．（1）求C 的方程；（2）过F 的另一条直线交C 于,D E 两点，设直线AB 的斜率为()110k k ≠，直线DE 的斜率为2k ，若122k k =，求AB DE −的最大值．19．（本小题满分17分）已知函数()()()e 1,ln 1xf xg x x =−=+．（1）若()()f x kg x ≥在()0,+∞上恒成立，求k 的取值范围；（2）设()()111,0A x y x >为()y f x =图象上一点，()()222,0B x y x >为()y g x =−图象上一点，O 为坐标原点，若AOB ∠为锐角，证明：221x x >．金科·新未来2023~2024学年度下学期期末质量检·高二数学参考答案、提示及评分细则题号 1 2 3 45 6 7 891011答案 C A D A D B B D BC ABD ABD一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．【答案】C【解析】设等差数列{}n a 的公差为d ，因为3616a a +=，且534a a −=，所以36153271624a a a d a a d +=+= −== ，所以112a d ==．故选C ． 2．【答案】A【解析】函数()ln 2f x ax x =+−，求导得()1f x a x′=+，依题意，()112f a +′==，得()1,ln a f x x x ==+−2，显然()11f =−，因此12b −=+，所以3b =−．故选A ．3．【答案】D【解析】因为8a 与10a 的等比中项为2，所以281024a a ==，所以()()26212261228102log log log log log 42a a a a a a +=⋅=⋅==．故选D ．4．【答案】A 【解析】因为()()321303f x x x x x =−−≤，所以()223f x x x =−−′，令()0f x ′>，得1x <−，令()0f x ′<，得10x −<<，所以函数()f x 在(),1−∞−上单调递增，在()1,0−上单调递减，所以()f x 的最大值是()513f −=．故选A ． 5．【答案】D【解析】根据题意得，圆心E 到C的渐近线的距离为3,=∴设渐近线方程为by x a=，则223,9,b e a =∴=，故选D ． 6．【答案】B【解析】依题意，()222e0xf x ax =−≤′在()2,1−−恒成立，即2e x a x ≥恒成立，设()2e xg x x=，则()()22e 21x x g x x′−=，所以()0g x ′≤，所以()g x 在()2,1−−单调递减，所以()4122e a g ≥−=−，故选B ． 7．【答案】B【解析】因为数列{}21n −是正奇数数列，对于数列{}22n n +等价于{}2(1)1n +−，当n 为奇数时，设()*21n k k =−∈N ，则22(1)141n k +−=−为奇数；当n 为偶数时，设()*2n k k =∈N ，则()22(1)1(21)141n k k k +−=+−=+为偶数，所以()()22111111,4141212122121n nc c n n n n n n====−−−−+−+，所以129911111111991123351971992199199c c c +++=×−+−++−=×−=，故选B ． 8．【答案】D【解析】情形一，质点往右移动4次，往左移动2次，26C 15=，情形二，质点往右移动3次，往左移动1次，往上移动一次，往下移动一次，3363C A 120=，情形三，质点往右移动2次，往上移动2次，往下移动2次，2264C C 90=，所以质点移动的方法总数为225，故选D ．二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9．【答案】BC （全部选对得6分，选对1个得3分，有选错的得0分）【解析】对于A ，当{}n a 为常数列，且0n a =时，因为{}n b 是等比数列，所以{}n n a b +为等比数列，所以A 错误．对于B ，当{}n b 为常数列时，因为{}n a 为等差数列，所以{}n n a b 为等差数列，所以B 正确．对于C ，设{}n a 的公差为d ，则()112n n n S na d +=+，得()112nn Sa d n +=+，因为1112n n S S d n n +−=+，所以数列n S n是等差数列，所以C 正确．对于D ，设{}n b 的公比为q ，则1111112122222n n n n n n n n n nT T b b q T T +++++⋅，当1q ≠时，112n b q 不是常数，所以2n n T 不是等比数列，所以D 错误．故选BC ．10．【答案】ABD （全部选对得6分，选对1个得2分，选对2个得4分，有选错的得0分）【解析】易知()1,0F ，准线:1l x =−，所以F 到直线l 的距离为2，A 选项正确；由抛物线的定义，点P 到准线的距离等于PF ，所以以P 为圆心PF 为半径的圆与l 相切，B 选项正确；当直线MP 与抛物线相切时，MP 的斜率取得最大值．设直线:1MP x my =−，与抛物线24y x =联立可得：2440y my −+=，令2Δ16160m =−=得：1m =±，所以直线MP 斜率的最大值为1，C 选项错误；若2FM FP ==，设200,4y P y，则2124y +=，解得02y =，所以FMP △的面积为01222y ××=，D 选项正确，故选ABD ． 11．【答案】ABD （全部选对得6分，选对1个得2分，选对2个得4分，有选错的得0分）【解析】A 项中，令e xt =，则ln x t =，由()0,x ∈+∞知1t >，此时函数为1ln ,10y t t y t′=−=−>，所以函数ln y t t =−在()1,+∞上是单调增函数，即()exg 在()0,+∞上是增函数，所以A 项正确；B 项中，1x >时，2ln 0x >，又a 为正实数，所以0ax >，又()e 10x f x =′−>，所以()f x 单调递增，所以不等式等价于2ln ax x ≥对1x ∀>恒成立，即max2ln x a x ≥，令()2ln x x x ϕ=，知()222ln x x x ϕ−′=，所以()x ϕ在()1,e 上递增，在()e,+∞上递减，所以()()max 2()e ex ϕϕ==，所以B 项正确；C 项中，易知()e x f x x =−在(),0−∞上递减，在()0,+∞上递增，()min ()01f x f ==，所以1t >，不妨设12x x <，则必有120x x <<，若12x x +> 0，则等价于210x x >−>，等价于()()21f x f x >−，等价于()()11f x f x >−，令()()()F x f x f x =−−，()()()(),0,e e 20x x x F x f x f x −′′′∈−∞=+−=+−>，即()F x 在(),0−∞上递增，所以()()00F x F <=，则()1,0x ∈−∞时，()()11f x f x <−，所以120x x +>不成立，即C 错误；D 项中，由()e xf x x =−在(),0−∞上递减，在()0,+∞上递增，()g x 在()0,1上递减，在()1,+∞上递增，易知()()f x g x =有唯一的解()00,1x ∈，又()1e 12f =−<，所以211x x >>，由()()12f x g x =，即12ln 1222e ln e ln x x x x x x −=−=−，即有()()12ln f x f x =，所以12ln x x =，即12e x x =，所以1211ln ln ln e x t t tx x x t ==−−，又2t >，所以21min ln 1e t x x =− ，所以D 正确．三、填空题：本题共3小题，每小题5分，共15分．12．【答案】3【解析】易知3x =，经验回归直线 0.80.6x y =+过样本点的中心(),x y ，所以0.830.63y =×+=，所以524 4.3.515m ++++=×，解得3m =．13．【答案】e ,2+∞【解析】由()f x 的图象经过第一象限，得0x ∃>，使得()0f x >，即e 2xa x >，设()e (0)x g x x x=>，求导得()()2e 1x x g x x =′−，当01x <<时，()0g x ′<，当1x >时，()0g x ′>，函数()g x 在()0,1上单调递减，在()1,+∞上单调递增，则()min ()1e g x g ==，有2e a >，所以实数a 的取值范围是e ,2+∞．14．【答案】49【解析】甲取走1个黑球1个白球的方法数为1123C C 6=，取走2个黑球的方法数为23C 3=，所以乙取出白球的概率为613246336339P=×+×=++．四、解答题：本题共5小题，共77分．解答应写出必要的文字说明、证明过程及演算步骤．15．【答案】（1）213na n =−（2）36− 【解析】（1）设{}n a 的公差为d ，则25611,114,115a d a d a d =−+=−+=−+，依题意，2526a a a =，即()()2(114)11115d d d −+=−+−+，整理得，()1120d d −=，解得，2d =或0d =（舍），所以()1121213n a n n =−+−=−；（2）21112131222n n a a n S n n n n +−+−=×=×=−，因为2212(6)3636n S n nn =−=−−≥−，当且仅当6n =时，等号成立，所以n S 的最小值为36−．16．【答案】（1）略（2【解析】（1）因为F 为PC 的中点，PA AC =，所以PC AF ⊥，因为AB ⊥平面,PAC PC ⊂平面PAC ，所以AB PC ⊥，又,,AF AB A AF AB =⊂ 平面ABF ；所以PC ⊥平面ABF ；（2）若AC PA ⊥，则,,AB AC AP 两两垂直，建立如图所示分别以,,AB AC AP 为,,x y z 轴的空间直角坐标系，()()()()0,0,0,,0,1,1,1,0,0,0,2,0A E F B C，()()()10,2,0,,1,0,0,1,1,1,0,02ACAE AF AB ====，设平面AEF 的法向量为()111,,n x y z = ，则有0,0,AE n AF n ⋅=⋅=即111110,20,x y y z +=+=令11y =，则112,1x z =−=−，所以平面AEF 的一个法向量为()2,1,1n =−−，易知AB ⊥平面,PAC ∴平面PAC 的法向量为()1,0,0AB =，设平面AEF 与平面PAC 夹角为θ，则cos AB n AB nθ⋅==⋅，所以平面AEF 与平面PAC ． 17．【答案】（1）14 （2）98【解析】（1）记事件A =“接下来的三天中食堂都未供应套餐甲”，则()1111224P A =××=，所以接下来的三天中食堂均未供应套餐甲的概率为14；（2）X 的所有可能取值分别为0，1，2，则()111102228P X ==××=， ()11121224P X ==××=()11511488P X ==−−=X 的分布列为X 0 1 2P18 58 14所以X 的期望为()151********E X =×+×+×=． 18．【答案】（1）2212x y += （2【解析】（1）设焦距为2c ，当AB OF ⊥时，将x c =代入椭圆方程可得，22221c y a b +=，解得2b y a =±，所以22b AB a==ca=，解得1a b ，所以C 的方程为2212x y +=；（2）设直线()()11112211:1,,,,AB x m y m A x y B x y k=+=，与椭圆线方程联立1221220x m y x y =+ +−=可得，()22112210m y m y ++−=，由韦达定理，11212221121,22m y y y y m m −−+==++，所以2AB y =−=21112m − +，同理可得，22112CD m =− +，2212AB DE m −=−+，因为122k k =，所以212m m =，故21142AB DE m −=−=+1≤，当且仅当11k =±时，等号成立，所以||AB DE −的最大值为． 19．【答案】（1）1k ≤（2）略【解析】（1）先证明()f x x >，构造函数()()e 1x F x f x x x =−=−−，则()e 10xF x =′−>，故()F x 单调递增，从而()()00F x F >=，即e 1xx >+，因此()ln 1x x >+，当1k ≤时，()()ln 1ln 1e 1x k x x x +≤+<<−，符合题意；当1k >时，构造函数()()()()e 1ln 1x G x f x kg x k x −−−+，则()()e ,1x k G x G x x ′=−+′单调递增，且()()010,ln 01ln k G k G k k k =′′−<=−>+，故存在()00,ln x k ∈，使得()00G x ′=，且()00,x x ∈时，()0G x ′<，即()G x 单调递减，则当()00,x x ∈时，()()00G x G <=，与题意矛盾．综上所述，1k ≤；（2）依题意可知，cos 0AOB ∠>，则0OA OB ⋅> ，即12120x x y y +>，即()()1122e 1ln 1x x x x >−+．因为12,0x x >，则不等式为()1212ln 1e 1x x x x +>−，设11e 1x x =′−，则不等式为()()22ln 1ln 11x x x x +++′>′，设()()ln 1x h x x+=，则()()2ln 11x x x h x x −+′+=，设()()ln 1H x x =−+，则()22110(1)1(1)x H x x x x ′−=−=<+++，因此()()00H x H <=，即()0h x ′<，即()h x 单调递减，因此()()12h x h x ′>，可得12x x ′<，即12e 1xx <+．首先证明：2e 1(0)x x x >+>，设()2e 1x t x x =−−，则()e 2x t x x =′−，由（1）可知1e 1,e x x x x −>+∴>，从而e e 2x x x >>，故()()0,t x t x ′>单调递增，因此()()00t x t >=，从而2e 1x x >+，因而12211e 1x x x +>>+，故221x x >．。

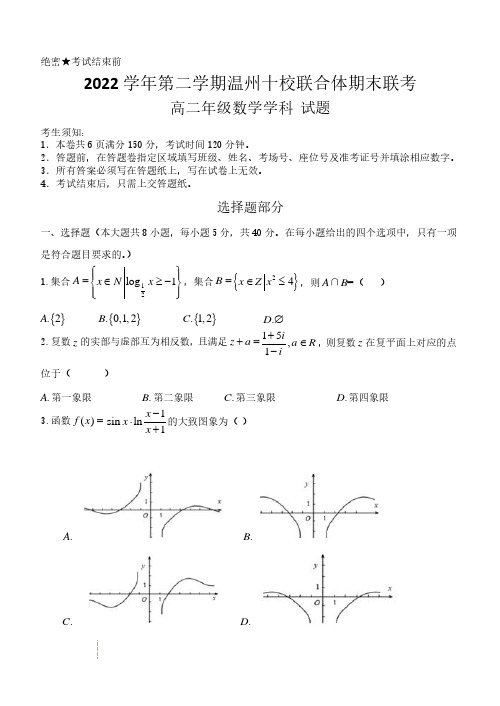
浙江省温州市十校联合体2022-2023学年高二下学期期末联考数学试题高二数学试题

绝密★考试结束前2022 学年第二学期温州十校联合体期末联考高二年级数学学科试题考生须知： 1．本卷共 6 页满分 150 分，考试时间 120 分钟。

2．答题前，在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字。

3．所有答案必须写在答题纸上，写在试卷上无效。

4．考试结束后，只需上交答题纸。

选择题部分一、选择题（本大题共 8 小题，每小题 5 分，共 40 分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1.集合 A =12log 1x N x ∈≥− ，集合 B ={}24x Z x ∈≤，则 A ∩B =（）A .{2}B .{0,1, 2}C .{1, 2}D .∅2.复数 z 的实部与虚部互为相反数，且满足z + a =151i i+−, a ∈ R ，则复数 z 在复平面上对应的点位于（） A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限3.函数 f ( x ) = 1sin ln 1x x x −⋅+的大致图象为（）A .B .C .D .4. 52()()ax x x x+−的展开式中各项系数的和为 − 2 ，则该展开式中常数项为（）A . − 40B . − 20C .20D .40 5.冯老师教高二 4 班和 5 班两个班的数学，这两个班的人数相等．某次联考中，这两个班的数学成绩均近似服从正态分布，其正态密度函数 f ( x )22()2x µσ−−的图象如图所示，其中 µ是正态分布的期望， σ 是正态分布的标准差，且P (X µ−≤ σ) = 0.6827 ， P ( X µ−≤ 2σ) = 0.9545 ， P ( X µ− ≤ 3σ)= 0.9973, 关于这次数学考试成绩，下列结论正确的是（）A . 4 班的平均分比 5 班的平均分高B . 相对于 5 班，4 班学生的数学成绩更分散C . 4 班 108 分以上的人数约占该班总人数的 4.55%D . 5 班 112 分以上的人数与 4 班 108 分以上的人数大致相等6.冬季两项是冬奥会的项目之一，是把越野滑雪和射击两种不同特点的竞赛项目结合在一起进行的运动，其中冬季两项男子个人赛，选手需要携带枪支和 20 发子弹，每滑行 4 千米射击一轮，共射击 4 轮，每轮射击 5 次，若每有 1 发子弹没命中，则被罚时 1 分钟，总用时最少者获胜.已知某男选手在一次比赛中共被罚时3 分钟，假设其射击时每发子弹命中的概率都相同，且每发子弹是否命中相互独立，记事件 A 为其在前两轮射击中没有被罚时，事件 B 为其在第 4 轮射击中被罚时 2 分钟，那么()P A B =（）A.12 B. 14C. 13D. 38 7.我们知道：y = f ( x ) 的图象关于原点成中心对称图形的充要条件是 y = f ( x ) 为奇函数，有同学发现可以将其推广为：y = f ( x ) 的图象关于 (a , b ) 成中心对称图形的充要条件是 y = f ( x + a ) − b 为奇函数.若 f ( x ) = x 3 − 3 x 2 的对称中心为 (m , n) ，则f (2023) + f (2021) + + f (3) + f (−1) + f (−3) + f (−5) + f (−2019) + f (−2021) =（）A . 8088B . 4044C . − 4044D . − 20228.设 a =9109, b = ln1.09, c = e 0.09 − 1 ，则下列关系正确的是（） A . a > b > c B . b > a > c C . c > a > b D . c > b > a 二、选择题（本大题共 4 小题，每小题 5 分，共 20 分。

广东省四校(华附、省实、广雅、深中)2023-2024学年高二下学期期末联考数学试题(解析版)

华附､省实､广雅､深中2022级高二下学期四校联考数学注意事项：1.答卷前，考生务必用黑色字迹的钢笔或签字笔将自己的校名､姓名､考号､座位号等相关信息填写在答题卡指定区域内，并用2B 铅笔填涂相关信息.2.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后.再选涂其它答案；不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的本试卷共4页，19小题，满分150分.考试用时120分钟..1.若()i 11z +=（i为虚数单位），则z z −=（）A.2−B.2i− C.2D.2i【答案】D 【解析】【分析】根据复数代数形式的除法运算化简z ，即可求出其共轭复数，再由复数的减法计算可得.【详解】因为()i 11z +=，所以11i iz +==−，所以1i z =−−，则1i z =−+，所以()()1i 1i 2i z z −=−+−−−=.故选：D2.已知等比数列{}n a 中，1241,9a a a ==，则7a =（） A.3 B.3或-3C.27D.27或-27【答案】C【解析】【分析】根据等比数列的通项公式，计算得到等比数列的等比，结合通项公式计算得出答案；【详解】设等比数列{}n a 的公比为1212134,1,9,93q a a a qa a q q ==∴=⇒= ，则6371327a a q ===，故选：C.3. 已知圆22:2O x y +=与抛物线2:2(0)C x py p =>的准线相切，则p 的值为（）A. B.C. 4D. 2【答案】A 【解析】【分析】写出抛物线C 的准线方程，根据该准线与圆O 相切求出实数p 的值.【详解】由题意可知，圆O 的圆，抛物线C 的准线方程为2py =−，由于抛物线C 的准线方程与圆O 相切，则2p=，解得p =. 故选：A.4. 如图所示，在正方形铁皮上剪下一个扇形和一个直径为2的圆，使之恰好围成一个圆锥，则圆锥的高为（）A. B.C.D.【答案】C 【解析】【分析】由扇形的弧长等于圆锥底面圆的周长得2π2π2R r =，求得4R =，进而由h =可求得圆锥的高.【详解】由图可知，扇形的弧长等于圆锥底面圆的周长，圆锥底面圆的半径为1r =，设扇形半径为R ，则有π2π2R r =，解得4R =，所以圆锥的母线长为4R =，故圆锥的高h =故选：C.5. 某校高二年级下学期期中考试数学试卷满分为150分，90分以上（含90分）为及格.阅卷结果显示，全年级800名学生的数学成绩近似服从正态分布，试卷的难度系数（=平均分/150）为0.49，标准差为22，则该次数学考试及格的人数约为（）附：若()2,X N µσ ，记()()p k P k X k µσµσ=−≤≤+，则()()0.750.547,10.683p p ≈≈. A. 127人 B. 181人 C. 254人 D. 362人【答案】B 【解析】【分析】首先求出平均数，即可得到学生的数学成绩()273.5,22X N ，再根据所给条件求出()5790P X ≤≤，即可求出()90P X ≥，即可估计人数.【详解】依题意可知平均分为1500.4973.5×=，又标准差为22，所以学生的数学成绩()273.5,22X N ，即73.5µ=，22σ=，又9073.50.7522−=，所以()()()00.57900.75.750.54775P X P X p µσµσ≤≤=−≤≤+=≈，所以()10.547900.22652P X −≥=≈=，又8000.2265181.2×=，所以该次数学考试及格的人数约为181人. 故选：B6. 已知双曲线2213y x −=的左、右焦点分别为12,F F ，直线y x =与双曲线的右支交于点P ，则12PF PF ⋅=（）A. 1−B. 0C. 1D. 2【答案】A 【解析】【分析】首先求出焦点坐标，再联立直线与双曲线方程，求出交点P 的坐标，再由数量积的坐标表示计算可得.【详解】双曲线2213y x −=的左、右焦点分别为()12,0F −，()22,0F ，由2213y x y x −= =，解得x y= =x y = =P ，则12PF =−，22PF =− ，所以212221PF PF ⋅=−×+=− . 故选：A7. 现有一组数据0,1,2,3,4,5，若将这组数据随机删去两个数，则剩下数据的平均数小于3的概率为（） A.23B.1115C.45D.1315【答案】B 【解析】【分析】设删去的两数之和为x ，依题意可得15362x−<−，求出x 的范围，再列出所有可能结果，最后利用古典概型的概率公式计算可得.【详解】依题意得这组数据各数之和为01234515+++++=，设删去的两数之和为x ，若剩下数据的平均数小于3，则15362x−<−，解得3x >，则删去的两个数可以为()0,4，()0,5，()1,3，()1,4，()1,5，()2,3，()2,4，()2,5，()3,4，()3,5，()4,5共11种情况，从0,1,2,3,4,5中任意取两个数有：()0,1，()0,2，()0,3，()0,4，()0,5，()1,2，()1,3，()1,4，()1,5，()2,3，()2,4，()2,5，()3,4，()3,5，()4,5，共15种情况，故所求概率1115P=. 故选：B8. 若函数()()21e 12xg x x b x =−+−存在单调递减区间，则实数b 的取值范围是（） A. [0,)+∞ B. ()0,∞+C. (],0−∞D. (),0∞−【答案】D【解析】【分析】根据题意转化为导函数e 10x x b −+−<有解，参变分离e 1x b x <−++有解,设()e 1x f x x =−++，则实数max ()b f x <，求导计算可得解；【详解】函数()()21e 12xg x x b x =−+−的定义域为R , 求导得()e 1xg x x b ′=−+−，函数存在单调递减区间，所以e 10x x b −+−<有解，即e 1x b x <−++有解，设()e 1x f x x =−++，则实数max ()b f x <，则()e 1x f x ′−+=，令()0f x ′=，得0x =，当0x <时，()0,()′>f x f x 在(),0∞−上递增；当0x >时，()0,()′<f x f x 在(),0∞−上递减；所以函数()f x 有最大值(0)0f =，因此0b <. 故选：D.二､多选题：本题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分.9. 若“2x k <−或x k >”是“23x −<<”的必要不充分条件，则实数k 的值可以是（） A. 3B. 3−C. 5D. 5−【答案】BCD 【解析】【分析】令{|2A x x k =<−或}x k >，{}|23B x x =−<<，依题意可得B 真包含于A ，即可求出参数的取值范围.【详解】令{|2A x x k =<−或}x k >，{}|23B x x =−<<，因为“2x k <−或x k >”是“23x −<<”的必要不充分条件，所以B 真包含于A ，所以2k ≤−或23k −≥，解得2k ≤−或5k ≥，结合选项可知符合题意的有B 、C 、D. 故选：BCD10. 下列关于成对数据统计的表述中，正确的是（） A. 成对样本数据的经验回归直线一定经过点(),x yB. 依据小概率事件0.1α=的2χ独立性检验对零假设0H 进行检验，根据22×列联表中的数据计算发现20.10.837 2.706x χ≈<=，由()2 2.7060.1P χ≥=可推断0H 不成立，即认为X 和Y 不独立，该推断犯错误的概率不超过0.1C. 在残差图中，残差点的分布随解释变量增大呈现扩散的趋势，说明残差的方差不是一个常数，不满足一元线性回归模型对随机误差的假设D. 决定系数2R 越大，表示残差平方和越大，即模型的拟合效果越差【答案】AC 【解析】【分析】根据经验回归方程的性质判断A ，根据独立性检验的基本思想判断B ，根据回归分析的相关知识判断C 、D.【详解】对于A ：成对样本数据的经验回归直线一定经过点(),x y ，故A 正确；对于B ：因为20.10.837 2.706x χ≈<=，由()22.7060.1P χ≥=可推断0H 成立，即认为X 和Y 独立，故B 错误；对于C说明残差的方差不是一个常数，不满足一元线性回归模型对随机误差的假设，故C 正确；对于D ：决定系数2R 越大，表示残差平方和越小，即模型的拟合效果越好，故D 错误. 故选：AC11. 如图，心形曲线22:()1L x y x +−=与y 轴交于,A B 两点，点P 是L 上的一个动点，则（）A. 点和()1,1−均在L 上B. 点PC. OP 的最大值与最小值之和为3D. PA PB +≤ 【答案】ABD 【解析】【分析】点代入曲线判断A ，根据曲线分段得出函数取得最大值判断B ，应用三角换元再结合三角恒等变换求最值判断C ，应用三角换元结合椭圆的方程得出恒成立判断D. 【详解】令0x =，得出1y =±，则()()1,0,1,0,A B −对于A ：x =时，2112y += 得0y =或y =，=1x −时，()2111y +−=得1y =，所以和()1,1−均在L 上，A 选项正确；对于B ：因为曲线关于y 轴对称，当0x ≥时，()221x y x+−=，所以y x =+()()222221112y y x x x x ==+−+≤++−=，所以x =y B 选项正确；对于C ：OP =，因为曲线关于y 轴对称，当0x ≥时，设cos ,sin x y x θθ=−=，所以()2222222cos cos sin 2cos sin 2sin cos OP x y θθθθθθθ=+=++=++()1cos23131sin2cos2sin222222θθθθθϕ+=++=++=++，因为θ可取任意角，所以OP 取最小值=，OP 取最大值=，C 选项错误；对于D ：PA PB +≤等价为点P 在椭圆22132y x +=内，即满足()222cos sin 3cos 6θθθ++≤，即()()31+cos221sin 262θθ++≤，整理得4sin23cos25θθ+≤，即()sin 21θβ≤+恒成立，故D 选项正确. 故选：ABD.【点睛】方法点睛：应用三角换元，再结合三角恒等变换化简，最后应用三角函数值域求最值即可.三､填空题：本题共3小题，每小题5分，共15分.12. 6(21)x y +−的展开式中，所有项的系数和为__________. 【答案】64 【解析】【分析】令1xy ==计算可得. 【详解】令1xy ==，可得所有项的系数和为()642611+−=. 故答案为：6413. 如图，正八面体ABCDEF 的12条棱长相等，则二面角E AB F −−的余弦值为__________.【答案】13−.【解析】【分析】AB 的中点为G ，EGF ∠为二面角E AB F −−的平面角，结合正八面体的几何特征，利用余弦定理求值即可.【详解】连接,AC BD 交于点O ，连接EF ，取AB 的中点G ，连接,EG FG ，根据正八面体的几何特征，有EF 过点O ，EG AB ⊥，FG AB ⊥，又EG ⊂平面ABE ，FG ⊂平面ABF ，平面ABE ∩平面ABF AB =，所以EGF ∠为二面角E AB F −−的平面角.正八面体中， EF ⊥平面ABCD ，AC ⊂平面ABCD ，则EF AC ⊥，所以AOE △是直角三角形，设正八面体棱长为2，则AO =，2AE =，所以OE =，得EF =在AEB △中，EGAB =，同理GF =在EGF △中，由余弦定理，可得2221cos 23EG FG EF EGF EG FG +−∠==−⋅⋅ 故答案为：13−.14. 数列{}n a 前n 项和为n S ，且111,22n n a a a n +=−=，则满足2024n S >的最小正整数n 为__________. 【答案】9 【解析】【分析】先构造等比数列，再应用等比等差数列前n 项和公式计算，最后判断最小值n 即可.【详解】因为122n n a a n +−=，所以()124244n n a n a n +++++，所以()()124222n n a n a n +++=++,所以{}22n a n ++是公比为2首项为1225a ++=的等比数列，所以112252,5222n n n n a n a n −−++=×=×−−.则()()()()()0112512422522246225213122n n n n n n S n n n −−++=+++−++++=−=−−−− ,因为152220,n n a n −=×−−>则n S 单调递增，又因为()8285218385255642411872024S =−−−×=×−−=<,()9295219395511812724472024S =−−−×=×−−=>.则2024n S >的最小正整数n 为9. 故答案为：9.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15. 已知ABC 的内角,,A B C 的对边分别为,,a b c ，且sin sin sin A B Cb c a b+=+−. 的（1）求A ；（2）如图，若点D 是BC 边上一点，且,2AB AD BD CD ⊥=，求ADB ∠. 【答案】（1）2π3A =（2）π3ADB ∠= 【解析】【分析】（1）利用正弦定理将已知等式统一成边的形式，化简后利用余弦定理可求出角A ；（2）由AB AD ⊥结合2π3A =可得π6DAC ∠=，然后在ABD △和ACD 分别利用正弦定理结合已知条件可得b c =，进而可求出ADB ∠. 【小问1详解】因sin sin sin A B Cb c a b+=+−，所以由正弦定理得a b b c bca +=+−，所以222ab bc c −=+，所以222b c a bc +−=−所以由余弦定理得2221cos 222b c a bc A bc bc +−−===−，因为()0,πA ∈，所以2π3A =；【小问2详解】因为AB AD ⊥，所以π2BAD ∠=，所以2πππ326DAC BAC BAD ∠=∠−∠=−=，在ABD △中，由正弦定理得πsin sin sin 2AB BD BD BDADB BAD ===∠∠，在ACD 中，由正弦定理得2πsin sin sin 6AC CD CD CDADC DAC===∠∠，因为πADB ADC ∠+∠=，所以sin sin ADB ADC ∠=∠为因为2BD CD =，所以AB AC =，即b c =，所以π6BC ==, 所以πππππ263ADB BAD B ∠=−∠−=−−=. 16. 如图，四棱锥P ABCD −的侧面PCD 为正三角形，底面ABCD 为梯形，//AB CD ，平面PCD ⊥平面ABCD ，已知44CD AB ==，13PM MD =.（1）证明：AM //平面PBC ；（2）若,AC AD PA ==，求直线AM 与平面PAB 所成角的正弦值. 【答案】（1）证明见解析（2 【解析】【分析】（1）取PC 上的点N ，使14PN PC = ，可得MN AB =，则由线线平行可证线面平行；（2）取CD 中点O ，连,AO PO ，根据题意可证AO CD ⊥，PO ⊥平面ABCD ，所以以O 为坐标原点，,,OA OC OP分别为,,x y z 轴正方向，建立如图所示空间直角坐标系A xyz −，利用线面角的空间向量法求解. 【小问1详解】取PC 上的点N ，使14PN PC =，则()1144MN PN PM PC PD DC AB =−=−== ，所以四边形ABNM 为平行四边形，所以//AM BN ，又BN ⊂平面PBC ，AM ⊄平面PBC ，所以AM //平面PBC ；【小问2详解】取CD 中点O ，连,AO PO ，因AC AD =，所以AO CD ⊥，因为PCD为正三角形，所以,PO CD PO ⊥，又平面PCD ⊥平面ABCD ，平面PCD 平面ABCD CD =，PO ⊂平面PCD ，所以PO ⊥平面ABCD ，因为AO ⊂平面ABCD ，所以PO AO ⊥，AO ==以O 为坐标原点，,,OA OC OP分别为,,x y z 轴正方向，建立如图所示空间直角坐标系A xyz −，则A ，(0,2,0)C ，(0,2,0)D −，)B，(0,0,P ，则(0,1,0)AB =，PA =−，1142AM AP PD =+=−，设(,,)n x y z =为平面PAB 的法向量，则0000y n AB n PA = ⋅=⇒ −=⋅=，可取)n = ，cos ,n AM n AM n AM⋅===⋅，故直线AM 与平面PAB. 17. 一个袋子中有30个大小相同球，其中有10个红球､20个白球，从中随机有放回地逐次摸球作为样为的本，摸到红球或者第5次摸球之后停止.用X 表示停止时摸球的次数. （1）求X 的分布列和期望；（2）用样本中红球的比例估计总体中红球的比例，求误差的绝对值不超过0.1的概率. 【答案】（1）分布列见解析，()21181E X = （2）2081【解析】【分析】（1）对于有放回的摸球，()()112,33P A P A ==，且i A ()1,2,3,4,5i =相互独立的，X 的可能取值为1,2,3,4,5，依次求出概率，可得分布列，再由期望公式求解；（2）设样本中红球的比例为f ，B =“样本中有红球”，且7133030C f =≤≤ ，分B 不发生，和B 发生求概率，从而得解. 【小问1详解】设=i A “第i 次摸出红球”，1,2,3,4,5i =，对于有放回的摸球，()()1101202,303303P A P A ====，且i A ()1,2,3,4,5i =相互独立的， X 的可能取值为1,2,3,4,5，则由题意可知，()(()()11212121,23339P X P A P X P A A ======⋅=， ()()212321433327P X P A A A ===⋅= ，()()3123421843381P X P A A A A ===⋅=，()()412342165381P X P A A A A ====，期望()124816211123453927818181E X =×+×+×+×+×=. 【小问2详解】总体中的红球比例13，设样本中红球的比例为f ，设B =“样本中有红球”，且17130.133030C f f =−≤=≤≤ ，若B 不发生，则0f =，此时C =∅，所以()0P BC =，若B 发生，则1f X =，此时711330303030137BC X X =≤≤=≤≤，所以()()()482034278181P BC P X P X =+===+=，所以，()()()2081P C P BC P BC =+=. 18. 已知椭圆2222:1(0)x y E a b a b+=>>的长轴长为()()1,2,0,2,02M N −.（1）求椭圆E 的方程；（2）过()4,0P 作一条斜率存在且不为0的直线l 交E 于,A B 两点. （i ）证明：直线AM 和直线BM 的斜率均存在且互为相反数；（ii ）若直线AM 与直线BN 交于点Q ，求Q 的轨迹方程. 【答案】（1）22186x y +（2）（i ）证明见解析；（ii）()212,02x x y −=≠≠【解析】【分析】（1）根据已知条件直接计算出椭圆相关基本量即可；（2）（i ）设()11,A x y ，()22,B x y ，直线l 的方程为()()40y k x k =−≠，联立方程组，利用韦达定理证明；（ii ）设直线，直线()()22:22BM x y y x +=+，联立方程组得204x x =，0202y y x =，采用代入法可得Q 的轨迹方程. 【小问1详解】根据题意，2a =，因为椭圆离心率为12，所以12c ea ==，所以c =6b =，所以椭圆的方程为22186x y +；【小问2详解】（i ）设()11,A x y ，()22,B x y ，直线l 的方程为()()40y k x k =−≠，联立方程()224186y k x x y =− += ，消去y 得：()2222343264240k x k x k +−+−=，则()2Δ96340k=−>，即k <由韦达定理得，212232=34k x x k++，2122642434k x x k −⋅=+，当k =Δ0=，122x x ==，不合题意，故122,2x x ≠≠，所以直线AM 和直线BM 的斜率均存在，1212,22B A M M y y k k x x =−−=，所以()()()()()()122112121242422222AM BM k x x k x x y yk k x x x x −−+−−+=+=−−−− ()()222121212122616024k x x x x x x x x ⋅−++ =⋅−++，即直线AM 和直线BM 的斜率均存在且互为相反数；（ii ）由（i ）知22x ≠，且222BM AM y k k x ==−−，可设直线()()22:22AM x y y x −=−，直线()()22:22BM x y y x +=+，设()00,Q x y ，则()()()()202020202222x y y x x y y x −=−− +=+ ，整理得20202022x y y y y x = = ①，由题意知20y ≠，由①知000,0y x ≠≠，所以由①知，204x x =，0202y y x =②，将②代入2222186x y +=得2022002213y x x +=，化简得0022123x y −=，又因为22x ≠，所以02x ≠，所以Q 的轨迹方程为()2212,023x y x y −=≠≠..【点睛】方法点睛：利用韦达定理法解决直线与圆锥曲线相交问题的基本步骤如下：（1）设直线方程，设交点坐标为()11,x y ，()22,x y ；（2）联立直线与圆锥曲线的方程，得到关于x （或y ）的一元二次方程，必要时计算∆；（3）列出韦达定理；（4）将所求问题或题中的关系转化为1212,x x x x +的形式；（5）代入韦达定理求解.19. 拟合（Fittiong ）和插值（Imorterpolation ）都是利用已知的离散数据点来构造一个能够反映数据变化规律的近似函数，并以此预测或估计未知数据的方法.拟合方法在整体上寻求最好地逼近数据，适用于给定数点.适用于需要高精度模型的场景，实际应用中常用多项式函数来逼近原函数，我们称之为移项式插值.例如，为了得到1cos 2的近似值，我们对函数()πcos 2f x x=进行多项式插值.设一次函数()1L x ax b =+满足()()()()11001110L f L f == == ，可得()f x 在[]0,1上的一次插值多项式()11L x x =−+，由此可计算出1cos 2的“近似值”11111cos10.6822πππf L=≈=−≈，显然这个“近似值”与真实值的误差较大.为了减小插值估计的误差，除了要求插值函数与原函数在给定节点处的函数值相等，还可要求在部分节点处的导数值也相等，甚至要求高阶导数也相等.满足这种要求的插值多项式称为埃尔米特（Hermite ）插值多项式.已知函数()πcos 2f x x = 在[]0,1上的二次埃尔米特插值多项式()2H x ax bx c ++满足()()()()()()001100H f H f H f =′=′ =（1）求()H x ，并证明当[]0,1x ∈时，()()f x H x ；（2）若当[]0,1x ∈时，()()2f x H x x λ− ，求实数λ的取值范围；（3）利用()H x 计算1cos 2的近似值，并证明其误差不超过140. （参考数据：2110.318,0.101ππ≈≈；结果精确到0.001）【答案】（1）()21H x x =−+，证明见解析；（2）2π1,8−+∞（3）1cos 0.8992≈，证明见解析【解析】【分析】（1）由题意列方程组求出,,a b c ，得()H x ；通过构造函数，利用导数求最值证明()()f x H x ≤；（2）令()()()()22π1cos 12G x H x f x x x x λλ=−−=−+−+，问题转化为()0G x ≤在[]0,1x ∈时恒成立，利用导数求函数单调性和最值，得条件满足时实数λ的取值范围；（3）由111cos 2ππf H =≈，代入求值即可，由误差2211π11ππ8πe f H =−≤− ，可证得结论.【小问1详解】()πcos 2f x x = ，()10f =，()01f =，()ππsin 22f x x′=−，()0 0f ′=，()2H x ax bx c ++，()2H x ax b ′=+，由()()()()()()001100H f H f H f =′=′=得100c a b c b = ++== ，解得101a b c =− = = ，因此()21H x x =−+. 设()()()2πcos 12F x f x H x x x =−=+−，[]0,1x ∈，()ππsin 222F x x x ′=−+ ，令()()1F x F x ′=，则()21ππcos 242F x x′=−+ ，因为()1F x ′在[0,1]上单调递增，且()21π0204F ′=−+<，()1120F ′=>，故存在()10,1x ∈使()110F x ′=，且()F x ′在()10,x 上单调递减，在()1,1x 上单调递增，又()00F ′=，()()100F x F ′′<=，()π120 2F ′=−+>，所以()F x ′在()0,1上存在唯一的零点()21,1x x ∈，使得()20F x ′=，且()F x 在()20,x 上单调递减，在()2,1x 上单调递增，又()()010F F ==，所以()0F x ≤，即()()f x H x ≤.【小问2详解】由（1）知()()2f x H x x λ−≤等价于()()2H x f x x λ−≤，且0λ≥，设()()()()22π1cos 12G x H x f x x x x λλ=−−=−+−+，[]0,1x ∈，则()0G x ≤， ()()ππ21sin 22G x x x λ′=−++，令()()1G x G x ′=，则())21ππ21cos 42G x x λ′=−++，令()()21G x G x ′=，则()32ππsin 082G x x′=−≤，所以1()G x ′在[]0,1上单调递减，若2π18λ≥−，则()()()211π02104G x G λ′′≤=−++≤，所以()G x ′在[]0,1上单调递减，所以()()00G x G ′′≤=，所以()G x 在[]0,1上单调递减，所以()(0)0G x G ≤=；若2π018λ≤<−，则()21π(0)2104G λ′=−++>，而1(1)2(1)0G λ′=−+<，故存在()00,1x ∈，使10()0G x ′=，从而()00,x 上，1()0G x ′>，()G x ′单调递增，()()00G x G ′′>=，在于是()G x 单调递增，()()00G x G >=不符合题意. 综上所述，λ的取值范围为2π1,8 −+∞. 【小问3详解】21111cos10.8992πππf H=≈=−+≈. 由（2）知，()()22π18f x H x x −≤−，所以，误差22211π1111111ππ8π8π81040e f H =−≤−=−<−=. 【点睛】方法点睛：在实际解决“新定义”问题时，关键是正确提取新定义中的新概念、新公式、新性质、新模式等信息，确定新定义的名称或符号、概念、法则等，并进行信息再加工，寻求相近知识点，明确它们的共同点和不同点，探求解决方法，在此基础上进行知识转换，合理归纳，结合相关的数学技巧与方法来分析与解决. 不等式证明或不等式恒成立问题常转化为函数的单调性、极(最)值问题处理，构造一个适当的函数，利用它的单调性进行解题，是一种常用技巧.。

青海省部分名校2023-2024学年高二下学期期末联考数学试题(含答案)

高二数学试卷注意事项：1.答题前，考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

4.本试卷主要考试内容：人教A 版选择性必修第一册至选择性必修第三册。

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.在填写高考志愿表时，一名高中毕业生了解到A ，B 两所大学分别有7，8个自己感兴趣的专业，若这名同学只能从这些专业中选择1个，则他不同的选择种数为A.56B.15C.28D.302.曲线在点处的切线的方程为A. B.C. D.3.已知变量x 和y 的统计数据如下表：x 12345y0.91.31.82.43.1若x ，y 线性相关，经验回归方程为，据此可以预测当时，y =A.5.75 B.7.5 C.7.55 D.84.已知F 为抛物线的焦点，点M 在C 上，且，则点M 到y 轴的距离为A.6B.5C.4D.5.两批同种规格的产品，第一批占70%，次品率为6%；第二批占30%，次品率为5%.将这两批产品混合，从混合产品中任取1件，则这件产品是次品的概率为A.5.5%B.5.6%C.5.7%D.5.8%6.在等比数列中，，，则A.64 B.128 C. D.7.已知一组数据1，2，2，5，5，6的第60百分位数为m ，随机变量X 的分布列为X 2m 14P0.30.60.1A.5B.6C.9.8D.10.88.10人（含甲、乙、丙）随机站成一排，则甲、乙、丙3人站在一起的概率为31()3f x x x=-(1,(1))f 1080x y +-=1080x y --=860x y --=860x y +-=ˆˆ0.55yx a =+10x =2:8C y x =||6MF={}n a 4148a a =231a a =13a =()D X =A.B.C.D.二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.已知，，则A.A 与B 相互独立 B.A 与B 相互对立C. D.10.已知函数有2个极值点，则的解析式可能为A. B.C. D.11.若函数在上单调递减，则a 的取值可以是A.0.39C.0.42三、填空题：本题共3小题，每小题5分，共15分.12.在的展开式中，的系数为.13.已知等差数列的前n 项和为，且，则.14.将0，1，2，3，4，6六个数字填入如图所示的2×3方格中，要求每个方格填一个数字，且每个数字不重复，则在这三列数字中，第一列的数字之和最小的概率为.四、解答题：本题共5小题，共77分.解答应写出文字说明、证明过程或演算步骤.15.（13分）某学校随机调查了1000名学生，将所得数学和语文期末考试成绩的样本观测数据整理得到如下列联表：语文成绩数学成绩优秀不优秀合计优秀400200600不优秀200200400合计6004001000（1）依据的独立性检验，能否认为数学成绩与语文成绩有关联？（2）按数学成绩是否优秀用分层随机抽样的方法从1000名学生中选取5人，再从这5人中任选3人，求118115130190(|)()0.3P B A P B ==(|)0.6P C B =()0.18P BC =()0.5P BC =()f x ()f x ()sin 3f x x x =+3()31f x x x =-+2()()e xf x x x =-()ln f x x x=2()log (1)log (1)(01)a a f x x x a +=-++<<(1,)+∞1-6212x x ⎛⎫- ⎪⎝⎭61x {}n a n S 921S =5a =0.01α=恰有2名数学成绩优秀的学生被选中的概率.附：，其中.0.10.050.012.7063.8416.63516.（15分）已知某地生产的白砂糖是按袋装销售的，每袋白砂糖的质量M （单位：g ）服从正态分布，且.（1）求，；（2）若甲从该地生产的白砂糖中随机购买3袋，如果每袋质量都小于248g ，那么甲得100积分，如果有2袋质量小于248g ，那么甲得50积分，如果至少有2袋质量不小于248g ，那么甲扣5积分，记甲获得X 积分，求X 的数学期望.17.（15分）如图，在四棱锥P -ABCD 中，PA ⊥底面ABCD ，BC //平面PAD ，BC ⊥AB .（1）证明：AD ⊥平面PAB .（2）若AD =AB ，PA =BC ，且直线PD 与直线BC 所成角的正切值为，求二面角A -CD -P 的余弦值.18.（17分）已知椭圆的左、右焦点分别为，，A ，B 两点均在C 上，且，.（1）若，求C 的方程；（2）若，直线AB 与y 轴交于点P ，且，求四边形AF 1BF 2的周长.19.（17分）若函数满足对于任意的，恒成立，则称为“反转函数”.已22()()()()()n ad bc a b c d a c b d χ-=++++n a b c d =+++αx α2(250,)N σ(252)0.8P M =...(248)P M <(248252)P M (3)22222:1(1)1x y C a a a +=>-1F 2F 120AF AF ⋅= 12F AB BAF ∠=∠12||||AF AF =12||||AF AF ≠ 3AP BP =()f x (0,1)(1,)x ∈+∞ 1(1)()0x f x f x ⎡⎤⎛⎫--< ⎪⎢⎥⎝⎭⎣⎦()f x知函数，.（1）当时，证明：为“反转函数”.（2）已知有三个零点，，，且.①求a 的取值范围；②证明：.1()ln f x a x x=+1()()g x f x f x ⎛⎫=- ⎪⎝⎭1a =()f x ()g x 1x 2x 3x 123x x x <<12364a x x x >++高二数学试卷参考答案1.B 不同的选择种数为7+8=15.2.B 由题可知，所以，又，所以切线的方程为，即.3.A ，.所以，即.令，解得.4.C 由题意得点M 到C 的准线的距离为6，所以点M 到y 轴的距离为.5.C 用事件，分别表示取到的产品来自第一批、第二批，B 表示取到次品.由题意得，，，，所以由全概率公式得.6.B 由题意得，得.则.由，得.所以.7.D ∵6×60%=3.6，∴m =5，∴，∴.8.B 由捆绑法可得，甲、乙、丙站在一起的概率为.9.AC 由，得A 与B 相互独立，A 正确，B 错误.由，得，C 正确，D 错误.10.BC 由题意得的导函数有两个异号零点.由，得恒成立，A 错误.由，得，令，得，B 正确.由，得，令，得，因为，所以有两个异号零点，C 正确.由，得，令，得，D 错误.221()9f x x x '=+(1)10f '=(1)312f =-=)2101(y x -=-1080x y --=1(12345)35x =⨯++++=1(0.9 1.3 1.8 2.4 3.1) 1.95y =⨯++++=ˆ 1.90.5530.25a=-⨯=ˆ0.550.25y x =+10x =ˆ0.55100.25 5.75y =⨯+=2x =-624-=1A 2A 1%)(70P A =2%)(30P A =1(|6%)P B A =2(|5%)P B A =1122(()(|)()(|))P B P A P B A P A P B A +=5.7%=4331423448a a a a a a ===42a =144812a a ==3341122a a q q ===34q =9313424128a a q ==⨯=()20.350.6140.15E X =⨯+⨯+⨯=22()(25)0.3(55)0.6D X =-⨯+-⨯+2(145)0.110.8-⨯=3833831010A A A 1A 10915==⨯(|)()P B A P B =()(|)0.6()P BC P C B P B ==()0.60.30.18P BC =⨯=()f x ()f x '()sin 3f x x x =+()cos 30f x x '=+>3()31f x x x =-+2()33f x x '=-()0f x '=1x =±2()()e x f x x x =-2()(1)e x f x x x '=+-()0f x '=210x x +-=24(1)501-⨯-==>∆()f x '()ln f x x x =()ln 1f x x '=+()0f x '=1ex =11.BCD .当，时，，所以对恒成立，设，则且，则解得.12.60 由题意得.所以的系数为60.13.由题意得，得.14. 因为，所以第一列的数字之和必然小于6.当第一列的数字之和小于4，即第一列的数字为0，1或0，2或0，3或1，2时，均有种不同的排法.当第一列的数字之和等于4，即第一列的数字为0，4或1，3时，均有种不同的排法.当第一列的数字之和等于5，即第一列的数字为2，3或1，4时，均有种不同的排法.故第一列的数字之和最小的概率为.15.解：（1）零假设为：数学成绩与语文成绩无关联.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1分根据列联表中的数据，计算得到.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分根据的独立性检验，我们推断不成立，即数学成绩与语文成绩有关联.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分（2）由题意得选取的5人中数学成绩优秀的学生人数为，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分不优秀的学生人数为，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分则恰有2名数学成绩优秀的学生被选中的概率为.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙13分16.解：（1）因为M 服从正态分布，且，，所以，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分所以.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分（2）甲从该地生产的白砂糖中随机购买3袋，设质量小于248g 的袋数为Y ，依题意可得，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分211[ln ln(2)]ln(2)ln ()(1)ln (1)ln(2)(1)ln ln(2)x a a a af x x a x a x a a ++++-'=+=-++-⋅+01a <<1x >2(1)ln ln(2)0x a a -⋅+<[ln ln(2)]ln(2)ln 0x a a a a ++++-…(1,)x ∈+∞()[ln ln(2)]ln(2)ln g x x a a a a =++++-2ln ln(2)ln(2)0a a a a ++=+…(1)2ln(2)0g a =+…221,01,a a a ⎧+⎨<<⎩…1,1)a ∈422626160C (2)x x x ⎛⎫⋅⋅-= ⎪⎝⎭61x 7319959()9212a a S a +===573a =2501234616633+++++=<2424A A 2422224222()A A A A A -22222222A A A A 24242222222242422222226642()225A A A A A A A A A A A A +-+=0H 221000(400200200200)25027.8 6.6356004006004009χ⨯⨯-⨯==≈>⨯⨯⨯0.01α=0H 600531000⨯=532-=21323535C C C =2(250,)N σ(252)0.8P M = (248252)2502+=(248)(252)1(252)0.2P M P M P M <=>=-=…(248252)10.220.6P M =-⨯=……~(3,0.2)Y BX 的可能取值为100，50，，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙13分所以.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙15分17.（1）证明：∵PA ⊥底面ABCD ，∴PA ⊥BC .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1分∵BC ⊥AB ，PA ∩AB =A ，∴BC ⊥平面PAB .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分∵BC //平面PAD ，平面PAD ∩平面ABCD =AD .∴BC //AD ，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分∴AD ⊥平面PAB .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分（2）解：∵BC //AD ，∴直线PD 与直线BC 所成的角为∠PDA .∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分∵PA ⊥底面ABCD .∴PA ⊥AD ，∴，即.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分设AD 为2个单位长度，以A 为原点，AB ，AD ，AP 所在的直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系，则，，，，.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分设平面PDC 的法向量为，则取，则，，得.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分易得平面ABCD 的一个法向量为，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙13分由图可知二面角A -CD -P 为锐角，则二面角A -CD -P 的余弦值为.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙15分18.解：由椭圆定义可知，，.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分（1）由，可知，若，则△F 1AF 2为等腰直角三角形，，45-3(100)(3)0.20.008P X P Y =====223(50)(2)C 0.2(10.2)0.096P X P Y ====⨯⨯-=1233(5)(2)C 0.2(10.2)(10.2)0.3840.5120.896P X P Y =-=<=⨯⨯-+-=+=()1000.008500.09650.896 1.12E X =⨯+⨯-⨯=3tan 2PA PDA AD ∠==32PA AD =(2,3,0)C (0,2,0)D (0,0,3)P (2,1,0)CD =-- (0,2,3)DP =-(,,)x y z =n 20,230,CD x y DP y z ⎧⋅=--=⎪⎨⋅=-+=⎪⎩n n1x =-2y =43z =41,2,3⎛⎫=- ⎪⎝⎭n (0,0,1)=m||||⋅=m n m n 12||||2AF AF a +=2221)1(c a a =--=120AF AF ⋅= 12AF AF ⊥ 12||||AF AF =222(2)a a c +=分解得，故C的方程为.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分（2）若，不妨设，，则，且，，.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分因为∠F 1AB =∠BAF 2，点P 在y 轴上，且，所以，且.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分由余弦定理可得，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分整理得，因为，所以.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分同理可得，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙13分整理得.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙14分由韦达定理得，，可知，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙15分则，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙16分解得，故四边形AF 1BF 2的周长为∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙17分19.（1）证明：当时，，，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙1分得，则在上单调减.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙2分当时，，当时，，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3分22a =2212x y +=12||||AF AF ≠ 1||AF x = ||BP y = 2||2AF a x =-a x ≠|2|AB y = |3|AP y =12AF AF ⊥124F AB BAF π∠=∠=12||||PF PF =2222(3)23(2)(3)2)3x y x y a x y a x y +-⨯=-+--⨯)4()a x y a a x -=-a x ≠y =12||||2BF BF a +==2a =22240x ax a -+=122x x a +=2122a x x =1212||||AF AF x x ⋅= 22222121212||||()23(2)AF AF x x x x a c ⋅=+-==a =4a =1a =1()ln f x x x=+11()()2ln (0)g x f x f x x x x x ⎛⎫=-=+-> ⎪⎝⎭22221(1)()10x g x x x x -'=--=-<()g x (0,)+∞01x <<()(1)0g x g >=1x >()(1)0g x g <=所以对于任意的，，即恒成立.故为“反转函数”.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙4分（2）①解：由题意得，.令，.当时，，，则在上单调递减，不符合题意；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙5分当时，，则在上单调递减，不符合题意；∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙6分当时，则在，上单调递减，在上单调递增.因为，所以，.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙7分设函数，得，则是增函数，得，即.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙8分由，得，所以，.设函数，得，，则是增函数，因为，所以是增函数，则，即.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙9分综上，，得，由零点存在定理可知，当时，有3个零点.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙10分②证明：（方法一）由①可知，由题意得，在上存在唯一零点，(0,1)(1,)x ∈+∞ (1)()0x g x -<1(1)()0x f x f x ⎡⎤⎛⎫--< ⎪⎢⎥⎝⎭⎣⎦()f x 1()2ln g x a x x x =+-2221()(0)x ax g x x x -+'=->2()21t x x ax =-+244a ∆=-11a -……0∆…()0g x '…()g x (0,)+∞1a <-()0g x '<()g x (0,)+∞1a >()g x (0,a ()a +∞(a a -+1a a -<<+(1)0g =(0g a <(0g a +>()e (1)x F x x x =->()e 10x F x '=->()F x 2(2)e 2(1)e 10a F a a F =->=->2e 2a a >a >2a a >+2e 21a a a >>>211e 2a a a <<=-222()e e (1)x G x x x =->22()2e 2e x G x x '=-22()4e 2e 0x G x ''=->()G x '22()(1)2e 2e 0G x G ''>=-=()G x 22222()e e (1)e e 0a G a a G =->=-=222e e a a >22222222111e 4e 40e e e a aa a g a a a ⎛⎫=-->--> ⎪⎝⎭22221(e )4e 0e a aa g a =+-<1a >()g x 23011x x <<=<112ln ()g a x x g x x x ⎛⎫=-+-=- ⎪⎝⎭()g x (1,)+∞且，，所以.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分易得则，即.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分要证，即证，即，得，，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙13分即证.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙14分设函数，得，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙15分令，则，所以在上是减函数，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙16分所以，故不等式得证.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙17分（方法二）由①可知，由题意得，在上存在唯一零点，且，，所以.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙11分111x >1311()()0g x g g x x ⎛⎫=== ⎪⎝⎭131x x =11133312ln ,12ln ,a x x x a x x x ⎧=-⎪⎪⎨⎪=-⎪⎩3131(ln ln )a x x x x -=-3131ln ln x x a x x -=-12346x x x a ++>1364x x a +>-3131316()4ln ln x x x x x x -+>--3131316()ln ln 4x x x x x x -->++3113313166ln ln 44x x x x x x x x ->-++++33333333316)61ln ln 1114(4x x x x x x x x x ⨯->->++++2266()ln ln 1414x x P x x x x x x x=-=-++++2226116ln ln 14141x P x x x x x x x⎛⎫=-=+ ⎪++⎝⎭++2216(1)()()2ln 41x h x P x P x x x x -⎛⎫=-=- ⎪++⎝⎭24324222222121212146412(1)()220(41)(41)(41)x x x x x x x h x x x x x x x x x x ⎡⎤++-+-+-'=-=-⨯=-⎢⎥++++++⎣⎦…()h x (0,)+∞33333333333()16611ln ()ln 11144x x P P x x x x x x x x x ⨯⎛⎫=->=-> ⎪⎝⎭++++12301x x x <<=<112ln ()g a x x g x x x ⎛⎫=-+-=- ⎪⎝⎭()g x (1,)+∞111x >1311()()0g x g g x x ⎛⎫=== ⎪⎝⎭131x x =易得则，即.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙12分要证，即证，即.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙13分得，即证.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙14分令.则，∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙16分所以在上单调递增，，故不等式得证.∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙17分11133312ln ,12ln ,a x x x a x x x ⎧=-⎪⎪⎨⎪=-⎪⎩3131(ln ln )a x x x x -=-3131ln ln x x a x x -=-12346x x x a ++>1364x x a +>-31313164l (n ln )x x x x x x -+>--3333311642ln x x x x x -+>⨯-23332333(1)ln (1)41x x x x x ->>++223(1)()ln (1)41t h t t t t t -=->++2432422222211212124641(1)()0(41)(41)(41)t t t t t t t h t t t t t t t t t t ++-+-+-'=-==>++++++()h t (1,)+∞()(1)0h t h >=。

高二数学下学期期末考试试题理含解析试题 10

智才艺州攀枝花市创界学校一中、安师大附中、一中二零二零—二零二壹高二数学下学期期末考试试题理〔含解析〕一、选择题：本大题一一共12个小题，每一小题5分，一共60分.在每一小题给出的四个选项里面，只有一项为哪一项哪一项符合题目要求的.{|1}A x x =>，{}3|log 1B x x =<，那么〔〕A.{|1}A B x x ⋂=≤RB.{|03}A B x x ⋃=<<C.{|13}A B x x ⋂=<<D.{|1}A B x x ⋃=≤R【答案】C 【解析】【分析】分别求出集合A 和B ，由交、并、补的概念即可得到结果．【详解】∵集合{|1}A x x =>，3log 1{|}{|03}B x x x x =<=<<，∴{|1}RA x x =≤，|1{}0RA B x x ⋂=<≤，故A 错误；{|3}A B x x =<，故B 错误；{|13}A B x x ⋂=<<，故C 正确；{|3}R A B x x =<，故D 错误．应选C ．232iz i-=+，那么z 的虚部是〔〕A.713-B.713C.713i -D.713i 【答案】B 【解析】【分析】直接利用复数代数形式的乘除运算化简得z ，进而可得z 的虚部.【详解】∵()()()()2322473232321313i i i z i i i i ---===-++-， ∴413713z i =+， ∴z 的虚部是713，应选B ．【点睛】此题考察复数代数形式的乘除运算，考察复数的根本概念，一共轭复数的概念，属于根底题．n S 为等比数列{}n a 的前n 2342S S S =+，12a =，那么2a =〔〕A.2B.-4C.2或者-4D.4【答案】B 【解析】【分析】利用等比数列的前n 项和公式求出公比，由此能求出结果．【详解】∵n S 为等比数列{}n a 的前n 项和，2342S S S =+，12a =，∴()()()34212122211q q q qq--+=+--，解得2q =-，∴214a a q ==-，应选B ．【点睛】此题主要考察等比数列的性质以及其的前n 项和等根底知识，考察运算求解才能，是根底题． 4.假设某几何体的三视图如下列图，那么这个几何体的外表积是〔〕A.16+B.15+C.19D.【答案】B 【解析】【分析】判断几何体的形状几何体是正方体与一个四棱柱的组合体，利用三视图的数据求解几何体的外表积即可．【详解】由题意可知几何体是正方体与一个四棱柱的组合体，如图：几何体的外表积为：1261222221152++⨯+⨯+⨯⨯=+ 应选B ．【点睛】此题考察三视图求解几何体的外表积，判断几何体的形状是解题的关键，属于中档题.1C ：sin y x =，2C ：cos 23y x π⎛⎫=- ⎪⎝⎭，那么下面结论正确的选项是〔〕A.把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移3π个单位长度，得到曲线2CB.把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移23π个单位长度，得到曲线2CC.把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移12π个单位长度，得到曲线2CD.把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移12π个单位长度，得到曲线2C 【答案】C 【解析】【分析】由题意利用诱导公式得1sin cos :2C y x x π⎛⎫==- ⎪⎝⎭，根据函数()cos y A x ωϕ=+的图象变换规律，得出结论．【详解】曲线1sin cos :2C y x x π⎛⎫==- ⎪⎝⎭，2cos 23:C y x π⎛⎫=- ⎪⎝⎭，∴把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，可得cos 22y x π⎛⎫=- ⎪⎝⎭的图象，再把得到的曲线向左平移 12π个单位长度，得到曲线2cos 2cos 263:2C x x πππ⎛⎫⎛⎫+-=- ⎪ ⎪⎝⎭⎝⎭的图象，应选C ．【点睛】此题主要考察函数()cos y A x ωϕ=+的图象变换规律，属于根底题．6.为理解某社区居民的家庭年收入和年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：根据上表可得回归直线方程ˆˆˆybx a =+，其中0.78b ∧=，a y b x ∧∧=-元，据此估计，该社区一户收入为16万元家庭年支出为〔〕【答案】A 【解析】【分析】由求得 x ， y ，进一步求得 a ，得到线性回归方程，取16x =求得y 值即可．【详解】8.38.69.911.1512.1 10x +++=+=， 5.97.88.18.49.858y ++++==．又 0.78b =，∴80.78100.2a y bx --⨯===． ∴ 0.780.2y x =+．取16x =，得 0.78160.212.68y ⨯+==万元，应选A ．【点睛】此题主要考察线性回归方程的求法，考察了学生的计算才能，属于中档题． 7.α，β是相异两个平面，m ，n 〕 A.假设mn ，m α⊂，那么n αB.假设m α⊥，m β⊥，那么αβ∥C.假设m n ⊥，m α⊂，n β⊂，那么αβ⊥D.假设m αβ=，n m ∥，那么n β【答案】B 【解析】【分析】在A 中，根据线面平行的断定判断正误；在B 中，由平面与平面平行的断定定理得//αβ；在C 中，当l αβ=时，不妨令//m l ，//n l ，那么n m ∥，在D 中，据线面平行的断定判断正误；【详解】对于A ，假设//m n ，m α⊂，那么//n α或者n⊂α，故A 错；对于B ，假设m α⊥，m β⊥，那么由平面与平面平行的断定定理得//αβ，故B 正确；对于C ，当l αβ=时，不妨令//m l ，//n l ，那么n m ∥，故C 错误；对于D ，假设B m α⋂=，//n m ，那么//n β或者n β⊂，故D 错，应选B ．.()3,1P 的直线l 与函数21()26x f x x -=-的图象交于A ，B 两点，O 为坐标原点，那么()OA OB OP +⋅=〔〕B.C.10D.20【答案】D 【解析】【分析】判断函数()f x 的图象关于点P 对称，得出过点()3,1P 的直线l 与函数()f x 的图象交于A ，B 两点时，得出A ，B 两点关于点P 对称，那么有 2OA OBOP +=，再计算()OA OB OP +⋅的值．【详解】()52121263x f x x x -==+--，∴函数21()26x f x x -=-的图象关于点()3,1P 对称， ∴过点()3,1P 的直线l 与函数()2126x f x x -=-的图象交于A ，B 两点，且A ，B 两点关于点()3,1P 对称， ∴ 2OA OB OP +=，那么()()222223120OA OB OP OP +⋅==⨯+=．应选D ．【点睛】此题主要考察了函数的对称性，以及平面向量的数量积运算问题，是中档题．2222:1(0)x y C a b a b+=>>的左焦点为F ，假设F 关于直线0x y +=的对称点A 是椭圆C 上的点，那么椭圆的离心率为〔〕A.2B.21-1【答案】A 【解析】【分析】利用点()0F c -，关于直线0x y +=的对称点()0,A c ，且A 在椭圆上，得b c =，即得椭圆C 的离心率；【详解】∵点()0F c -，关于直线0x y +=的对称点A 为()0,A c ，且A 在椭圆上，即22b c =，∴c b =，∴椭圆C 的离心率2e ===．应选A ．【点睛】此题主要考察椭圆的离心率，属于根底题．10.225sin )ax dx -=⎰，且2am π=.那么展开式212(1)mx x ⎛⎫-- ⎪⎝⎭中x 的系数为〔〕 A.12 B.-12 C.4D.-4【答案】D 【解析】【分析】求定积分得到a 的值，可得m 的值，再把()1mx -按照二项式定理展开式，可得212(1)mx x ⎛⎫-- ⎪⎝⎭中x 的系数．【详解】∵2222215sin )2522ax dx cosxππ--==⋅⋅-=⎰，且24am π==，那么展开式()()422112121m x x x x ⎛⎫⎛⎫--=-- ⎪ ⎪⎝⎭⎝⎭()2342121464x x x x x ⎛⎫=-⋅-+-+ ⎪⎝⎭，故含x 的系数为844-+=-，应选D ．【点睛】此题主要考察求定积分，二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于根底题．P ABC -中，点E ，F 分别在棱PB ，PC 上，假设PE PF ≠且2AE AF ==，EF =么四面体P AEF -的体积为〔〕A.112B.19C.18D.16【答案】C 【解析】【分析】由题意画出图形，设PA x =，PE y =，PF z =，由余弦定理得到关于x ，y ，z 的方程组，求解可得x ，yz 的值，然后分别求出三角形PEF 的面积及A 到平面PEF 的高，代入棱锥体积公式得答案．【详解】如图，设PA x =，PE y =，PF z =，∵2AE AF ==，EF =∴由余弦定理得，221242xy xy +-⋅=① 221232y z yz +-⋅=②221242z x zx +-⋅=③③-①得，22z y xz xy -=-，即()()()z y z y x z y +-=-，∵z y ≠，那么x z y =+，代入③，得224z y zy ++=，又223zy zy +-=，得12yz =，2272y z +=，∴2x y z =+====．∴A 到平面PEF 的间隔332d x ===∴1122813P AEFV yz -⨯⨯⨯==，应选C ．【点睛】此题考察棱柱、棱锥、棱台体积的求法，考察数形结合的解题思想方法，考察计算才能，是中档题．12.：2ln ()2ln (2)x f x m x m x=-+，方程()f x x =有1个根，那么m 不可能是〔〕A.-3B.-2C.-1D.0【答案】D 【解析】【分析】由题意可得()2ln ln 221x x m m x x ⎛⎫⋅-+⋅= ⎪⎝⎭，可令ln x t x =，求得导数和单调性、最值，运用排除法即可得到所求结论．【详解】()()2ln 2ln 2xf x m x m x=-+，方程()f x x =有1个根，可得()2ln ln 221x x m m x x ⎛⎫⋅-+⋅= ⎪⎝⎭，可令ln x tx =，21ln x t x-'=，可得0x e <<时，0t '>，t 递增；x e >时，0t '<，t 递减，可得xe =时，获得最大值 1e ，且x e >时，10e e<<，假设3m =-时，261t t -+=，可得30,t=<13e+>舍去，方程()f x x =有1个根；假设2m =-时，41t-=，可得104t =-<，方程()f x x =有1个根；假设1m =-时，221t t --=，可得10t =-<，方程()f x x =有1个根；假设0m =时，221t -=，无解方程()f x x =没有实根．应选D ．【点睛】此题考察函数方程的转化思想，以及换元法和导数的运用：求单调性和极值、最值，考察化简运算才能，属于中档题．二、填空题〔每一小题5分，总分值是20分，将答案填在答题纸上〕x ，y ，z 满足约束条件4802400x y x y y --≤⎧⎪-+≥⎨⎪≤⎩，那么z =__________．【解析】【分析】画出满足条件的平面区域，结合z =z 的最小值即可．【详解】画出x ，y ，z 满足约束条件4802400x y x y y --≤⎧⎪-+≥⎨⎪≤⎩，的平面区域，如下列图：而z =()40-，的间隔，显然()40-，到直线240x y -+=的间隔是最小值，由d ==，．【点睛】此题主要考察了简单的线性规划问题，考察数形结合思想，属于中档题． 14.以下列图所示的算法流程图中，输出的S 表达式为__________．【答案】112399++++【解析】【分析】根据流程图知当1i=，满足条件100i <，执行循环体，1S =，依此类推，当100i =，不满足条件100i <，退出循环体，从而得到结论．【详解】1i=，满足条件100i <，执行循环体，1S =2i =，满足条件100i <，执行循环体，12S =+ 3i =，满足条件100i <，执行循环体，123S =++…依此类推99i=，满足条件100i <，执行循环体，1299S =++⋯+，100i =，不满足条件100i <，退出循环体，输出1112399S S ==+++⋯+，故答案为112399++++．【点睛】此题主要考察了循环构造应用问题，此循环是先判断后循环，属于中档题．{}22221,2,3,,A n =中所有3个元素的子集的元素和为__________．【答案】(2)(1)(1)(21)12n n n n n --++【解析】【分析】集合A 中所有元素被选取了21n C -次，可得集合{}22221,2,3,,A n =中所有3个元素的子集的元素和为()222122123n n C -+++⋯+即可得结果.【详解】集合{}22221,2,3,,A n =中所有元素被选取了21n C-次，∴集合{}22221,2,3,,A n =中所有3个元素的子集的元素和为()()()()2112112n n n n n --++=，故答案为(2)(1)(1)(21)12n n n n n --++．【点睛】此题考察了集合的子集、正整数平方和计算公式，属于中档题．21yax 上存在关于直线112y x =+成轴对称的两点，那么a 的取值范围是__________．【答案】34a >【解析】【分析】假设存在对称的两个点P ，Q ，利用两点关于直线112y x =+成轴对称，可以设直线PQ 的方程为2y x b =-+，由于P 、Q 两点存在，所以方程组22 1y x by ax =-+⎧⎨=-⎩有两组不同的实数解，利用中点在直线上消去参数b ，建立关于a 的函数关系，求出变量a 的范围．【详解】设抛物线上关于直线1:12l y x =+对称的两相异点为()11,P x y 、()22,Q x y ，线段PQ 的中点为()00,M x y ，设直线PQ 的方程为2y x b =-+，由于P 、Q 两点存在，所以方程组22 1y x by ax =-+⎧⎨=-⎩有两组不同的实数解，即得方程()2210ax x b +-+=①判别式()4410a b =++>②．可得01x a =-，02y b a=+， ∵M l ∈，∴00112y x =+⇒512b a =-…③由②③可得34a >，故答案为34a >.【点睛】此题考察了直线与抛物线的位置关系，以及对称问题，属于中档题．三、解答题：一共70分.解容许写出文字说明、证明过程或者演算步骤.ABCD 中，90ADC ∠=︒，45A ∠=︒，4AB =，=AD〔1〕求sin ADB ∠；〔2〕假设DC=ABCD 的面积.【答案】〔1〕sin ADB∠=〔2〕9【解析】【分析】〔1〕在ABD△中由余弦定理得BD，再由正弦定理能求出sin ADB∠；〔2〕cos sin 5BDC ADB ∠=∠=，四边形ABCD 的面积ADBBDCS SS=+，由此能求出结果．【详解】〔1〕在平面四边形ABCD 中，90ADC ∠=︒，45A ∠=︒，4AB =，=ADABD △中，由余弦定理可得：BD===，∵sin sinAB BDADB BAD=∠∠，∴4AB sin BADsin ADBBD⋅∠∠===〔2〕BCD中，cos sinBDC ADB∠=∠=，【点睛】此题考察角的正弦值、四边形面积的求法，考察正弦定理、余弦定理等根底知识，考察运算求解才能，是中档题．{}na满足13a=，21143nn na a-+-=⨯，*n∈N.〔1〕求数列{}n a的通项公式；〔2〕令23n nb na=，求数列{}n b的前n项和n S.【答案】〔1〕()()1*3912nna n-+=∈N〔2〕()*9(81)1(1)64642nnn n nS n-+=++∈N【解析】【分析】〔1〕由数列恒等式()()()112211n n n n na a a a a a a a---=-+-+⋯+-+，结合等比数列的求和公式，可得所求；〔2〕求得()11923nn nb na n-==+，运用数列的分组求和和错位相减法求和，结合等比数列的求和公式，可得所求和．【详解】〔1〕13a=，21143nn na a-+-=⨯当2n≥时，()()()()11223211n n n n n n na a a a a a a a a a-----=-+-+-++-+而13a=，符合上式，所以数列{}n a的通项公式为()()1*3912nna n-+=∈N〔2〕()11923n n n b na n -==+，设211129399n nT n -=⋅+⋅+⋅++⋅，2391929399n n T n =⋅+⋅+⋅+⋯+⋅，相减可得21819999n nnT n --=+++⋯+-⋅19919nn n -=-⋅-，化简可得18)19(64nn n T +-⋅=，可求和得：()*9(81)1(1)64642n n n n n S n -+=++∈N【点睛】此题考察等比数列的通项公式和求和公式的运用，考察数列的分组求和和裂项相消求和，考察化简运算才能，属于中档题．〔1〕取出的3个小球颜色互不一样的概率；〔2〕随机变量ξ的概率分布和数学期望；〔3〕求某人抽奖一次，中奖的概率. 【答案】〔1〕811〔2〕分布列见解析，数学期望为5611〔3〕1355【解析】【分析】〔1〕设事件A 表示“取出的3个小球上的颜色互不一样〞，利用古典概型、排列组合能求出取出的3个小球颜色互不一样的概率；〔2〕由题意得ξ有可能的取值为：2，3，4，5，6，分别求出相应的概率，由此能求出随机变量的概率分布列和数学期望；〔3〕设事件C 表示“某人抽奖一次，中奖〞，那么()( 3 4)(3)(4)P C P P P ξξξξ=====+=或，由此能求出结果.【详解】〔1〕“一次取出的3个小球上的颜色互不一样〞的事件记为A ，那么311162223128()11C C C C P A C ⋅⋅⋅==〔2〕由题意ξ有可能的取值为：2，3，4，5，6211222223121(2)55C C C C P C ξ⋅+⋅===； 211242423124(3)55C C C C P C ξ⋅+⋅===； 211262623129(4)55C C C C P C ξ⋅+⋅===； 2112828231216(5)55C C C C P C ξ⋅+⋅===；所以随机变量ξ的概率分布为因此ξ的数学期望为14916556()23456555555551111E ξ=⨯+⨯+⨯+⨯+⨯= 〔3〕“某人抽奖一次，中奖〞的事件为C ，那么【点睛】此题考察概率、离散型随机变量的分布列、数学期望的求法，考察古典概型、排列组合等根底知识，考察运算求解才能，是中档题. 20.如图，直三棱柱111ABC A B C -中，AB AC =且AB AC ⊥，D ，E 分别为1AA ，1B C 的中点.〔1〕证明：DE ⊥平面1BCC ；〔2〕假设直线1B C 与平面BCD 所成的角的大小为30，求锐二面角A BD C --的正切值.【答案】〔1〕详见解析〔2【解析】【分析】〔1〕由条件可得DAFE 是平行四边形，从而//AF DE ，由条件能证明AF ⊥平面1BCC ，由此能证明DE ⊥平面1BCC ；〔2〕以A 为坐标原点，AB ，AC ，1AA 分别为x ，y ，z 轴建立空间直角坐标系，不妨设2AB AC ==，12AA m =，求出面BDC 的一个法向量为21,1,n m ⎛⎫= ⎪⎝⎭，根据线面角可求出12AA m ==ADB △中求出AG =AGC 即可求出结果. 【详解】〔1〕取BC 中点F ，连接EF ，那么11//2E BF B ，从而//EF DA ，连接AF ，那么ADEF 为平行四边形，从而AF DE ∥.∵直三棱柱中，1CC ⊥平面ABC ，AF ⊂面ABC ，∴1AF CC ⊥,∵AB AC =，F 是BC 的中点，∴AF BC ⊥,∵1BCCC C =，∴AF ⊥面1BCC故DE ⊥平面1BCC 〔2〕以A 为坐标原点，AB ，AC ，1AA 分别为x ，y ，z 轴建立空间直角坐标系，由条件：不妨设2AB AC ==，12AA m =，()0,0,0A ，()2,0,0B ，()0,2,0C ，()10,0,2A m ，()0,0,D m ，()12,0,2B m(2,2,0)BC =-，(2,0,)BD m =-，1(2,2,2)B C m =--设平面BDC 的一个法向量为(,,)nx y z =，2002200x mz n BD x y n BC ⎧-+=⎧⋅=⇒⎨⎨-+=⋅=⎩⎩，可取21,1,n m ⎛⎫= ⎪⎝⎭为一个法向量211|cos ,|sin3022BC n m AA m <>=︒⇒=⇒==，过A 作AG BD ⊥，连CG ，那么AGC ∠为二面角A BD C --的平面角，在ADB △中，BD AGAD AB AG ⋅=⋅⇒=，在AGC 中，2AC =，AG =tan AC AGC AG∠==【点睛】此题主要考察直线与平面垂直的证明，考察二面角的求法，解题时要认真审题，注意向量法的合理运用，属于中档题.2(:0)y ax a >Γ=的焦点为F ，假设过F 且倾斜角为4π的直线交Γ于M ，N 两点，满足||4MN =.〔1〕求抛物线Γ的方程；〔2〕假设P 为Γ上动点，B ，C 在y 轴上，圆22(1)1x y -+=内切于PBC ，求PBC 面积的最小值. 【答案】〔1〕22y x =〔2〕8【解析】【分析】〔1〕求出抛物线的焦点，设出直线MN 的方程，代入抛物线方程，运用韦达定理和抛物线的定义，可得2a =，进而得到抛物线方程；〔2〕设()00,P x y ，()0,B b ，()0,C c ，不妨设b c >，直线PB 的方程为00y by b x x --=，由直线与圆相切的条件：d r =，化简整理，结合韦达定理以及三角形的面积公式，运用根本不等式即可求得最小值.【详解】〔1〕抛物线2(:0)y ax a >Γ=的焦点为,04a F ⎛⎫⎪⎝⎭，那么过点F 且斜率为1的直线方程为4a y x =-，联立抛物线方程2y ax =，消去y 得：2230216a ax x -+=，设()()1122,,,Mx y N x y ，那么1232ax x +=，由抛物线的定义可得12||242aMN x x a =++==，解得2a =，所以抛物线的方程为2:2y x Γ=〔2〕设()00,Px y ，()0,B b ，()0,C c ，不妨设b c >，00:PB y bl y b x x --=化简得：()0000y b x x y x b --+=，圆心()1,0到直线PB 的间隔为1，1=，即()()()222220000002y b x y b x b y b x b -+=-+-+，不难发现02x >，上式又可化为()2000220x b y b x -+-=，同理有()2000220x c y c x -+-=，所以,b c 可以看做关于t 的一元二次方程()2000220x t y t x -+-=的两个实数根，0022y b c x -⇒+=-，()()220002020042()22x y x x bc b c x x +--=⇒-=--，由条件：2002y x =()2220042()22x x b c b c x x ⇒-=⇒-=-- ()()20000014()248222PBCx S b c x x x x ∆=-==-++≥--，当且仅当04x =时取等号.∴PBC 面积的最小值为8.【点睛】此题主要考察了抛物线的定义、方程和性质，主要考察定义法和方程的运用，同时考察直线和抛物线方程联立，运用韦达定理，直线和圆相切的条件：dr =，以及根本不等式的运用，属于中档题.ln ()()xf x a x a=∈+R ，曲线()y f x =在点(1,(1))f 处切线与直线80x y ++=垂直.〔1〕试比较20192018与2018 2019的大小，并说明理由；〔2〕假设函数()()=-g x f x k 有两个不同的零点1x ，2x ，证明：212x x e ⋅>. 【答案】〔1〕2019201820182019>，理由见解析〔2〕详见解析【解析】【分析】〔1〕求出()f x 的导数，由两直线垂直的条件，即可得切线的斜率和切点坐标，进而可知()f x 的解析式和导数，求解单调区间，可得()()20182019f f >，即可得到20192018与2018 2019的大小；〔2〕运用分析法证明，不妨设210x x >>，由根的定义化简可得()1212ln ln x x k x x +=+，()1212ln ln x x k x x -=-，要证：212x x e ⋅>只需要证：()122k x x +>，求出k，即证212112ln ln 2x x x x x x ->-+，令211x t x =>，即证2(1)ln 1t t t ->+，令2(1)()ln (1)1t h t t t t -=->+，求出导数，判断单调性，即可得证.【详解】〔1〕函数ln ()()xf x a x a =∈+R ，21ln ()()ax xf x x a +-'=+，所以21(1)(1)a f a +'=+，又由切线与直线80x y ++=垂直，可得()11f '=，即111a=+，解得0a =，此时2ln 1ln ()()x xf x f x x x-'=⇒=，令()0f x '>，即1ln 0x ->，解得0x e <<，令()0f x '<，即1ln 0x -<，解得x e >，即有()f x 在()0,e 上单调递增，在(),e +∞单调递减所以ln 2018ln 2019(2018)(2019)2019ln 20182018ln 201920182019f f ⇒>⇒>⇒>即2019201820182019>〔2〕不妨设210x x >>，由条件：()()2122110ln ln 0gx g x x kx x kx ==⇒-=-=()1212ln ln x x k x x +=+，()1212ln ln x x k x x -=-要证：212x x e ⋅>只需要证：12ln ln 2x x +>，也即为()122kx x +>，由2121ln ln x x k x x -=-只需要证：()2121221121212ln ln 2ln x x x x x x x x x x x x -->⇒>-++，设211x t x =>即证：2(1)ln (1)1t t t t ->>+，设2(1)()ln (1)1t h t t t t -=->+，那么22214(1)()0(1)(1)t h t t t t t '-=-=>++ ()h t 在()1,+∞上是增函数，故()(1)0h h ι>=，即()21ln 1t tt ->+得证，所以212x x e ⋅>.【点睛】此题主要考察了导数的运用，求切线的斜率和单调区间，构造函数，运用单调性解题是解题的关键，考察了化简运算整理的才能，属于难题.。

福建省福州市八县(市)协作校2023-2024学年高二下学期期末联考试题数学含答案

福州市八县（市）协作校2023—2024学年第二学期期末联考高二数学试卷（答案在最后）【完卷时间：120分钟；满分：150分】命题：连江县教师进修学校附属中学一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.命题“x x x ∃∈+R ，＜”的否定是（）A.0x x x ∃∈+R ，≤B.0x x x ∃∈+R ，≥C.0x x x ∀∈+R ，＜ D.0x x x ∀∈+R ，≥2.在以下4幅散点图中，y 和x 成正线性相关关系的是（）A. B.C. D.3.假如女儿身高y （单位：cm ）关于父亲身高x （单位：cm ）的经验回归方程为 0.8125.82y x =+，已知父亲身高为170cm ，则（）A.女儿的身高必为164 cmB.女儿的身高估计为164 cmC.女儿的身高必为178 cmD.女儿的身高估计为178 cm4.X 是离散型随机变量，()()16,0.5,25E X D X X X ===-，那么()1E X 和()1D X 分别是()A .()()1112,1E X D X == B.()()117,1E X D X ==C.()()1112,2E X D X == D.()()117,2E X D X ==5.已知随机变量()2~X N μσ，，随机变量()2~2Y N μσ+，，若()0P X =≤()2P X ≥，()20.3P Y =≤，则()34P Y =≤≤（）A .0.2B.0.3C.0.5D.0.76.函数ln 1xy ex =--的图象大致是（）A. B.C. D.7.已知,x y 为正实数，1ln ln x y x y+=-，则（）A.x y＞ B.x y＜ C.1x y +＞ D.1x y +＜8.已知函数()f x 的定义域为R ，且()()2f x f x =-．若函数()()22g x f x x x =+-有唯一零点，则()1f =（）A.1- B.0C.1D.2二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9.已知0a b c ∈R ＜＜，，则下列不等式成立的是（）A.11b a< B.33ac bc ＜ C.22a b > D.11a b b a++＜10.高斯取整函数[]y x =又称“下取整函数”，其中[]x 表示不大于x 的最大整数，如32,2⎡⎤-=-⎢⎥⎣⎦[]533,22⎡⎤-=-=⎢⎥⎣⎦．若函数()[],R f x x x x =-∈，则()f x 的值可能是（）A.0B.0.5C.1D.211.若()()()()()12211120121112231111x a a x a x a x a x -=+-+-++-+- ，则（）A.01a =- B.()121213ii i a =-=∑C.12124ii ia==∑ D.12112iii a ==-∑三、填空题：本题共3小题，每小题5分，共15分．12.已知函数2log ,0()3,0xx x f x x >⎧=⎨≤⎩，则14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值为____．13.如图，曲线①②③④中有3条分别是函数2xy =，3xy =，13xy ⎛⎫= ⎪⎝⎭的图象，其中曲线①与④关于y 轴对称，曲线②与③关于y 轴对称，则13xy ⎛⎫= ⎪⎝⎭的图象是曲线____．（填曲线序号）14.某班安排甲、乙、丙、丁4位同学参加3项不同的社会公益活动，要求每项活动至少有1人参加，且甲、乙不能参加同一项活动，则共有____种不同的安排方案．（用数字作答）四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15.已知集合{}{}23100221A x x x B x m x m =--=-≤≤+＜，．（1）当1m =时，求()A B A B R ，ð；（2）若B A ⊆，求实数m 的取值范围．16.当药品A 注射到人体内，它在血液中的残余量会以每小时25%的速度减少.（1）按照医嘱，护士给患者甲注射了mg a 药品A 两小时后，患者甲血液中药品A 的残存量为225mg ，求a 的值；（2）另一种药物B 注射到人体内，它在血液中的残余量会以每小时10%的速度减少.如果同时给两位患者分别注射800mg 药品A 和500mg 药品B ，请你计算注射后几个小时两位患者体内两种药品的残余量恰好相等.（第（2）问计算结果保留2位小数）参考值：lg 20.301=，lg 30.477=.17.节日在即，某店家为此购入一批袋装糖果（每袋1kg ），现从中随机抽取100袋，将它们进行分级，统计结果如下：等级一等品二等品三等品袋数404020（1）若将频率视为概率，从这100袋糖果中有放回地随机抽取4袋，求恰好有2袋是三等品的概率；（2）用样本估计总体，该店家制定了两种销售方案：方案一：将糖果混合后不分类售出，售价为20元/kg；方案二：按品级出售，售价如下：等级一等品二等品三等品售价（元/kg）242217为追求更高利润，该店家应采用哪种方案？（3）用分层抽样的方法从这100袋糖果中抽取10袋，再从抽取的10袋糖果中随机抽取3袋，记抽到一等品的袋数为X，求X的分布列与数学期望．18.2023年5月13日，榕江和美乡村足球超级联赛（简称“村超”）盛大开幕，迅速在全国范围内乃至国际舞台上引起了热烈反响，激发了全民的运动热情．今年，更是迎来了足球传奇人物卡卡的亲临访问．现有一支“村超”球队，其中甲球员是其主力队员，且是一位多面手，胜任多个位置．经统计，该球队在已进行的42场“村超”比赛中，甲球员是否上场时该球队的胜负情况如下表所示：上场球队的胜负情况合计胜负甲球员上场535甲球员未上场7合计3242（1）完成22⨯列联表，依据小概率值0.01α=的独立性检验，分析球队的胜负是否与甲球员上场有关；（2）由于教练布阵的不同，甲球员在场上的位置会进行调整，根据以往的数据统计，甲球员上场时，打前锋、中场、后卫的概率分别为0.6，0.2，0.2，相应球队赢球的概率分别为0.9，0.5，0.8．当甲球员上场参加比赛时，（ⅰ）求球队赢球的概率；（ⅱ）如果球队已获胜，计算该场比赛甲球员打前锋的概率．附：22()()()()()n ad bc a b c d a c b d χ-=++++，n a b c d =+++．α0.150.100.050.0250.0100.001x α2.0722.7063.8415.0246.63510.82819.已知函数()2121x x f x -=+．（1）我们知道要研究一个函数的性质，通常会从函数的定义域、值域（最值）、奇偶性（对称性）、单调性（极值）、周期性、特殊的点与线（如渐近线）等方面着手．据此，请回答以下问题：（ⅰ）试探究函数()f x 的性质并说明理由；（ⅱ）根据（ⅰ）中结论作出()f x 的草图；（2）若1,3x ∞⎡⎫∀∈+⎪⎢⎣⎭，都有()()2332log log 0mf x fx ++＞，求实数m 的取值范围．福州市八县（市）协作校2023—2024学年第二学期期末联考高二数学试卷【完卷时间：120分钟；满分：150分】命题：连江县教师进修学校附属中学一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.命题“x x x ∃∈+R ，＜”的否定是（）A.0x x x ∃∈+R ，≤B.0x x x ∃∈+R ，≥C.0x x x ∀∈+R ，＜ D.0x x x ∀∈+R ，≥【答案】D 【解析】【分析】将特称命题否定为全称命题即可.【详解】命题“0x x x ∃∈+R ，＜”的否定是“0x x x ∀∈+R ，≥”.故选：D2.在以下4幅散点图中，y 和x 成正线性相关关系的是（）A. B.C. D.【答案】B 【解析】【分析】利用散点图可直观看出是否线性相关和正相关．【详解】对于A ，由于散点图分散，估计没有线性相关关系，故A 错误；对于B ，根据散点图集中在一条递增的直线附近，说明它们线性相关且是正相关，故B 正确；对于C ，根据散点图集中在一条递减的直线附近，说明它们线性相关且是负相关，故C 错误；对于D ，根据散点图集中在一条曲线附近，说明它们非线性相关，故D 错误；故选：B ．3.假如女儿身高y （单位：cm ）关于父亲身高x （单位：cm ）的经验回归方程为 0.8125.82y x =+，已知父亲身高为170cm ，则（）A.女儿的身高必为164 cmB.女儿的身高估计为164 cmC.女儿的身高必为178 cmD.女儿的身高估计为178 cm【答案】B 【解析】【分析】根据经验回归方程求解即可.【详解】由 0.8125.82y x =+，170x =，代入得ˆ0.8117025.82163.52164y=⨯+=≈cm ，故选：B4.X 是离散型随机变量，()()16,0.5,25E X D X X X ===-，那么()1E X 和()1D X 分别是()A.()()1112,1E X D X ==B.()()117,1E X D X ==C.()()1112,2E X D X ==D.()()117,2E X D X ==【答案】D 【解析】【分析】由期望和方差的运算性质求解即可【详解】由期望和方差的运算性质知E(X 1)=E(2X－5)=2E(X)-5=7D(X 1)=D(2X－5)=22D(X)＝2故选D【点睛】本题考查期望和方差的运算性质，熟记公式，准确计算是关键，是基础题5.已知随机变量()2~X N μσ，，随机变量()2~2Y N μσ+，，若()0P X =≤()2P X ≥，()20.3P Y =≤，则()34P Y =≤≤（）A.0.2 B.0.3C.0.5D.0.7【答案】A 【解析】【分析】由()0P X =≤()2P X ≥结合对称性得出μ，再由对称性得出()34P Y ≤≤.【详解】因为()0P X =≤()2P X ≥，所以0212μ+==，因为()20.3P Y =≤，所以()230.50.30.2P Y =-=≤≤，又()34P Y =≤≤()230.2P Y =≤≤，所以A 正确；故选：A 6.函数ln 1xy ex =--的图象大致是（）A. B.C. D.【答案】D 【解析】【分析】去掉绝对值，得到具体的函数表达式，即可作出判断.【详解】当1x ≥时，()ln 111xy e x x x =--=--=，排除C ；当01x <<时，()ln 111111xy e x x x x x=--=--=+->，排除AB 选项.故选：D.7.已知,x y 为正实数，1ln ln x y x y+=-，则（）A.x y ＞B.x y＜ C.1x y +＞ D.1x y +＜【答案】C 【解析】【分析】利用构造一个函数，结合求导思想分析单调性，从而可得出选项.【详解】由1ln ln x y x y +=-得：111ln ln ln x x y y y y+=-+=+，构造函数()ln f x x x =+，则()110f x x+'=>，可知()ln f x x x =+在()0,∞+上递增，结合11ln lnx x y y+=+，得1x y =，即1xy =由基本不等式可知：2x y +≥=，当且仅当1x y ==时等号成立，所以1x y +>.故选：C.8.已知函数()f x 的定义域为R ，且()()2f x f x =-．若函数()()22g x f x x x =+-有唯一零点，则()1f =（）A.1-B.0C.1D.2【答案】A 【解析】【分析】转化为两函数图象交点问题，函数图象对称轴都为1x =且两函数图象只有唯一交点即可知交点横坐标为1得解.【详解】因为函数()f x 的定义域为R ，且()()2f x f x =-，所以函数()f x 的图象关于1x =轴对称，由()()22g x f x x x =+-有唯一零点知，2()2f x x x =--有唯一根，即()y f x =与2()2h x x x =--的图象有唯一交点，而2()2h x x x =--图象关于1x =对称，所以(1)(1)1f h ==-.故选：A二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9.已知0a b c ∈R ＜＜，，则下列不等式成立的是（）A.11b a< B.33ac bc ＜ C.22a b > D.11a b b a++＜【答案】ACD 【解析】【分析】利用作差法，结合不等式的性质，即可由选项逐一求解.【详解】对于A ，由于0a b <<，则0,0ab a b >-<，所以110a bb a ab -<-=，故11b a<，A 正确，对于B ，若0c =时，33ac bc =，故B 错误，对于C ，由于0,0a b a b +<-<，所以()()220a b a b a b -=+->，故22a b >，C 正确，对于D,由于0,0ab a b >-<⇒()11110a b a b b a ab ⎛⎫⎛⎫+-+=-+< ⎪ ⎪⎝⎭⎝⎭，故11a b b a ++＜，D 正确，故选：ACD10.高斯取整函数[]y x =又称“下取整函数”，其中[]x 表示不大于x 的最大整数，如32,2⎡⎤-=-⎢⎥⎣⎦[]533,22⎡⎤-=-=⎢⎥⎣⎦．若函数()[],R f x x x x =-∈，则()f x 的值可能是（）A.0B.0.5C.1D.2【答案】AB 【解析】【分析】根据定义可得()[],R f x x x x =-∈的表达式，通过图象可得函数的值域，即可求解.【详解】由题意可得2,211,10[],011,12...,x x x x y x x x x x x +-≤<-⎧⎪+-≤<⎪⎪=-=≤<⎨⎪-≤<⎪⎪⎩，则对应的图象为：由图象可知()[)0,1f x ∈.故选：AB11.若()()()()()12211120121112231111x a a x a x a x a x -=+-+-++-+- ，则（）A.01a =-B.()1212013iii a=-=∑C.12124i i ia ==∑ D.12112ii i a ==-∑【答案】BCD 【解析】【分析】对于A ，令1x =可求出0a ，对于B ，令0x =可求得答案，对于C ，对等式两边求导后，令2x =可求得答案，对于D ，令32x =结合01a =可求得答案.【详解】对于A ，令1x =，则()12023a -=，得01a =，所以A 错误，对于B ，令0x =，则()1201211123a a a a a -=-+--+ ，所以()1212013ii i a =-=∑，所以B 正确，对于C ，由()()()()()12211120121112231111x a a x a x a x a x -=+-+-++-+- ，得()()()()111011121112242321111121x a a x a x a x -=+-++-+- ，令2x =，则()11121112244321112a a a a ⨯-=++++ ，所以12124i i ia ==∑，所以C 正确，对于D ，令32x =，则211120121112111102222a a a a a ⎛⎫⎛⎫⎛⎫=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以211121211120111112222a a a a a ⎛⎫⎛⎫⎛⎫++++=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以12112ii i a ==-∑，所以D 正确，故选：BCD三、填空题：本题共3小题，每小题5分，共15分．12.已知函数2log ,0()3,0x x x f x x >⎧=⎨≤⎩，则14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值为____．【答案】19【解析】【分析】先求14f ⎛⎫⎪⎝⎭，再求14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭即可.【详解】由题意得22211log log 2244f -⎛⎫===-⎪⎝⎭，所以211(2)349f f f -⎛⎫⎛⎫=-== ⎪ ⎪⎝⎭⎝⎭.故答案为：1913.如图，曲线①②③④中有3条分别是函数2xy =，3xy =，13xy ⎛⎫= ⎪⎝⎭的图象，其中曲线①与④关于y 轴对称，曲线②与③关于y 轴对称，则13xy ⎛⎫= ⎪⎝⎭的图象是曲线____．（填曲线序号）【答案】②【解析】【分析】由指数函数的性质先确定曲线③是函数3x y =的图象，由对称性得13xy ⎛⎫= ⎪⎝⎭的图象.【详解】由指数函数的单调性可知，函数2x y =和3x y =的图象分别是曲线③④中的一条，当1x =时，1132>，所以曲线③是函数3x y =的图象，函数13xy ⎛⎫= ⎪⎝⎭的图象与函数3x y =的图象关于y 轴对称，所以13xy ⎛⎫= ⎪⎝⎭的图象是曲线②.故答案为：②.14.某班安排甲、乙、丙、丁4位同学参加3项不同的社会公益活动，要求每项活动至少有1人参加，且甲、乙不能参加同一项活动，则共有____种不同的安排方案．（用数字作答）【答案】30【解析】【分析】以丙、丁参加同一项活动和丙、丁不参加同一项活动分类讨论，结合排列组合知识求解即可.【详解】当丙、丁参加同一项活动时，共有33A 3216=⨯⨯=种；当丙、丁不参加同一项活动时，共有211322A C C 24⋅⋅=种；综上，共有30种不同的安排方案．故答案为：30四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15.已知集合{}{}23100221A x x x B x m x m =--=-≤≤+＜，．（1）当1m =时，求()A B A B R ，ð；（2）若B A ⊆，求实数m 的取值范围．【答案】（1）()2,5A B ⋃=-，()()()2,13,5A B ⋂=-⋃R ð（2）(,2)-∞【解析】【分析】（1）解一元二次不等式可得集合A ,再由集合交并补混合运算可得结果.（2）由B A ⊆可知B 是A 的子集，对B 是否为空集分析讨论，解不等式可得结果.【小问1详解】由23100x x --＜,得()()520x x -+＜，解得25x -＜＜，所以()2,5A =-．当1m =时，[]1,3B =，所以()2,5A B ⋃=-，B R ð()(),13,∞=-∞⋃+，所以()()()2,13,5A B ⋂=-⋃R ð．【小问2详解】①若B =∅，则221m m -+＞，即13m ＜．此时满足B A ⊆．②若B ≠∅，则13m ≥，要使B A ⊆，当且仅当1322215m m m ⎧≥⎪⎪--⎨⎪+⎪⎩＞＜，解得123m ≤＜．综上，m 的取值范围为(,2)-∞．16.当药品A 注射到人体内，它在血液中的残余量会以每小时25%的速度减少.（1）按照医嘱，护士给患者甲注射了mg a 药品A 两小时后，患者甲血液中药品A 的残存量为225mg ，求a 的值；（2）另一种药物B 注射到人体内，它在血液中的残余量会以每小时10%的速度减少.如果同时给两位患者分别注射800mg 药品A 和500mg 药品B ，请你计算注射后几个小时两位患者体内两种药品的残余量恰好相等.（第（2）问计算结果保留2位小数）参考值：lg 20.301=，lg 30.477=.【答案】（1）400（2）15.24【解析】【分析】（1）根据题意，列出方程代入计算，即可得到结果；（2）根据题意，列出方程，结合对数的运算代入计算，即可得到结果.【小问1详解】由题意可得，注射药品A 两小时后药品A 的残存量为()20000125g 56.25m a a -=，所以0056.25225a =，解得400a =，即注射了400mg 药品A ，a 的值为400.【小问2详解】设药物B 注射量为m ，则n 小时后残余量为()00110nm -，设药物A 注射量为t ，则n 小时后残余量为()00125n t -，又题可知，药物A 注射量为800mg ，药物B 注射量为500mg ，设n 小时后残余量相同，则()()0000800125500110nn-=-，即0.91.60.75n⎛⎫= ⎪⎝⎭，两边取对数可得lg1.6lg1.2n=，即86lg lg 55n =，即1010lg8lglg 6lg 22n ⎛⎫-=- ⎪⎝⎭，即()4lg 21lg121n -=-，即()4lg 21lg 3lg 41n -=+-，即()40.30110.47720.3011n ⨯-=+⨯-，解得15.24n ≈，所以注射15.24小时后两位患者体内两种药品的残余量恰好相等.17.节日在即，某店家为此购入一批袋装糖果（每袋1kg ），现从中随机抽取100袋，将它们进行分级，统计结果如下：等级一等品二等品三等品袋数404020（1）若将频率视为概率，从这100袋糖果中有放回地随机抽取4袋，求恰好有2袋是三等品的概率；（2）用样本估计总体，该店家制定了两种销售方案：方案一：将糖果混合后不分类售出，售价为20元/kg ；方案二：按品级出售，售价如下：等级一等品二等品三等品售价（元/kg ）242217为追求更高利润，该店家应采用哪种方案？（3）用分层抽样的方法从这100袋糖果中抽取10袋，再从抽取的10袋糖果中随机抽取3袋，记抽到一等品的袋数为X ，求X 的分布列与数学期望．【答案】（1）96625（2）方案二（3）分布列见解析，数学期望为65【解析】【分析】（1）根据二项分布的概率公式即可求解，（2）求解方案二中1kg 糖果的售价为Y ，即可比较求解，（3）由抽样比求解个数，即可利用超几何分布的概率公式求解分布列，进而可求解期望.【小问1详解】设事件A =“从这100袋糖果中随机抽取1个，抽到三等品”，则()2011005P A ==．现有放回地随机抽取4个，设抽到三等品的袋数为Z ，则1(4,)5B Z ，所以恰好有2袋是三等品的概率()222414962C 55625P Z ⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭【小问2详解】设方案二中1kg 糖果的售价为Y ，则()40402024221721.8100100100E Y =⨯+⨯+⨯=（元），因为()20E Y >，从追求更高利润考虑，该店家应采用方案二．【小问3详解】用分层抽样的方法从这100袋糖果中抽取10袋，则其中一等品有4袋，非一等品有6袋．依题意，X 服从超几何分布，其可能的取值为0，1，2，3．()36310C 10C 6P X ===，()2164310C C 11C 2P X ===，()1264310C C 32C 10P X ===，()34310C 13C 30P X ===所以X 的分布列为X0123P1612310130所以()1131601236210305E X =⨯+⨯+⨯+⨯=．18.2023年5月13日，榕江和美乡村足球超级联赛（简称“村超”）盛大开幕，迅速在全国范围内乃至国际舞台上引起了热烈反响，激发了全民的运动热情．今年，更是迎来了足球传奇人物卡卡的亲临访问．现有一支“村超”球队，其中甲球员是其主力队员，且是一位多面手，胜任多个位置．经统计，该球队在已进行的42场“村超”比赛中，甲球员是否上场时该球队的胜负情况如下表所示：上场球队的胜负情况合计胜负甲球员上场535甲球员未上场7合计3242（1）完成22⨯列联表，依据小概率值0.01α=的独立性检验，分析球队的胜负是否与甲球员上场有关；（2）由于教练布阵的不同，甲球员在场上的位置会进行调整，根据以往的数据统计，甲球员上场时，打前锋、中场、后卫的概率分别为0.6，0.2，0.2，相应球队赢球的概率分别为0.9，0.5，0.8．当甲球员上场参加比赛时，（ⅰ）求球队赢球的概率；（ⅱ）如果球队已获胜，计算该场比赛甲球员打前锋的概率．附：22()()()()()n ad bca b c d a c b dχ-=++++，n a b c d=+++．α0.150.100.050.0250.0100.001xα 2.072 2.706 3.841 5.024 6.63510.828【答案】（1）列联表见解析，认为球队的胜负与甲球员是否上场有关（2）（ⅰ）0.8；（ⅱ）0.675【解析】【分析】（1）根据题中数据完成列联表即可，根据公式求出2χ，再对照临界值表即可得出结论；（2）（ⅰ）根据条件概率和全概率公式求解即可；（ⅱ）利用条件概率公式和乘法公式就算即可.【小问1详解】根据题意，可得22⨯的列联表：上场球队的胜负情况合计胜负甲球员上场30535甲球员未上场257合计321042零假设为0H ：球队的胜负与甲球员是否上场无关，根据列联表中的数据，经计算得到()()()()()()2220.01423055210.5 6.6353210357n ad bc x a b c d a c b d χ-⨯⨯-⨯===++++⨯⨯⨯＞，根据小概率值0.01α=的独立性检验，我们推断0H 不成立，即认为球队的胜负与甲球员是否上场有关，此推断犯错误的概率不大于0.01；【小问2详解】设A =“甲球员上场打前锋”，B =“甲球员上场打中场”，C =“甲球员上场打后卫”，D =“球队获得胜利”．则A B C Ω=⋃⋃，且,,A B C 两两互斥，依题意得，()()()0.6,0.2P A P B P C ===()()()0.9,0.5,0.8P D A P D B P D C ===；（ⅰ）由全概率公式得()()()()()()()P D P A P D A P B P D B P C P D C=++0.60.90.20.50.20.8=⨯+⨯+⨯0.8=；（ⅱ）“如果球队已获胜，计算该场比赛甲球员打前锋的概率”，就是计算在D 发生的条件下，事件C 发生的概率，则所求概率()()()()()()0.6090.6750.8P A P D A P AD P A D P D P D ⨯====.【点睛】思路点睛：用定义法求条件概率()P B A 的步骤：（1）分析题意，弄清概率模型；（2）计算()P A 、()P AB ；（3）代入公式求()()()P AB P B A P A =.19.已知函数()2121x x f x -=+．（1）我们知道要研究一个函数的性质，通常会从函数的定义域、值域（最值）、奇偶性（对称性）、单调性（极值）、周期性、特殊的点与线（如渐近线）等方面着手．据此，请回答以下问题：（ⅰ）试探究函数()f x 的性质并说明理由；（ⅱ）根据（ⅰ）中结论作出()f x 的草图；（2）若1,3x ∞⎡⎫∀∈+⎪⎢⎣⎭，都有()()2332log log 0mf x fx ++＞，求实数m 的取值范围．【答案】（1）（ⅰ）答案见解析；（ⅱ）作图见解析（2）193,3⎡⎫-⎪⎢⎣⎭【解析】【分析】（1）利用定义法来研究函数的各个性质，最后可作出草图；（2）利用复合函数思想由内到外研究函数值域，最后化归到含参二次不等式恒成立，即可求解.【小问1详解】①定义域：()f x 的定义域为R ．②值域：因为()2121x f x =-+，20x>，12+11012+1x x ><<，，所以()11f x -<<，故()f x 的值域为()1,1-．③奇偶性：x ∀∈R ，x -∈R ，()()21122112x xx xf x f x -----===-++，所以()f x 为奇函数．④单调性：12x x ∀∈R ，，且12x x <，则1222x x<，所以()()()()()1212121222222021212121x x x x x x f x f x --=-+=<++++，即()()12f x f x <，所以()f x 为增函数．⑤当x →+∞时，2x →+∞，()21121xf x =-→+；当x →-∞时，20x →，()21101f x →-=-+．所以直线1y =±为()f x 图象的渐近线．综合上述讨论，可作出()f x的草图如下：【小问2详解】当13x ≥时，331log log 13x =-≥，由（1）知，()f x 为增函数，所以()()131211log 1213t f x f ---=≥-==-+，由（1）知()f x 的值域为()1,1-，故t 的取值范围为1,13⎡⎫-⎪⎢⎣⎭所以1,3x ∞⎡⎫∀∈+⎪⎢⎣⎭，都有()()2332log log 0mf x f x ++>，等价于220t mt ++>对于1,13t ⎡⎫∀∈-⎪⎢⎣⎭都成立，记()22t t mt ϕ=++，则()2Δ8011,232111203931120m m m m m ϕϕ⎧=-≥⎪⎪-≤--≥⎪⎨⎛⎫⎪-=-+> ⎪⎪⎝⎭⎪=++≥⎩，，，或280.m ∆=-<解得1933m m m ≤<-≤≤--<<或，综上，m 的取值范围是193,3⎡⎫-⎪⎢⎣⎭．。

浙江省宁波市九校2022-2023学年高二下学期期末联考数学试题(解析版)

2022学年第二学期宁波市九校联考高二数学试题一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知复数z 满足i 1i z ⋅=+，则z 对应的点位于（） A. 第一象限 B. 第二象限C. 第三象限D. 第四象限【答案】A 【解析】【分析】根据复数的除法运算法则，求出复数z ，即可求解. 【详解】由i 1i z ⋅=+，得21i (1i)(i)=1i ii z ++−==−−，所以1i z =+，在复平面内对应的点为(1,1) 所以对应点位于第一象限. 故选：A.2. 设集合(){},21x Mx y y ==−，()π,cos ,442N x y y x x==−≤≤，则M N ∩中元素的个数为（） A. 2 B. 3 C. 4 D. 5【答案】B 【解析】【分析】在同一坐标系下画出两集合对应函数图象，交点个数即为交集元素个数【详解】对于函数21x y =−，当0x <时，01y <<；当0x ≥时，0y ≥.对于函数πcos,442yx x −≤≤，222ππ,πx ∈− ，则11y −≤≤且端点处取最大值两函数图象在同一坐标系下大致如下，则两函数图象有3个交点，即M N ∩中元素的个数为3个. 故选：B3. 已知随机变量()211~,X N µσ，()222~,Y N µσ，它们的分布密度曲线如下图所示，则下列说法中正确.的是（）A. 12µµ<，2212σσ< B. 12µµ<，2212σσ> C 12µµ>，2212σσ<D. 12µµ>，2212σσ>【答案】B 【解析】【分析】由图结合正态分布曲线特点可得答案.【详解】由图可得随机变量X 的均值比随机变量Y 的均值小，则12µµ<.又由图得，随机变量X 的分布比随机变量Y 的分布更加分散，则2212σσ>. 故选：B4. 已知平面向量a ，b满足a b a b +=− ，则b a − 在a 上的投影向量为（） A. a −B. aC. b −D. b【答案】A 【解析】【分析】由已知可得0a b ⋅=，根据投影向量的定义及数量积的运算律求投影向量即可.【详解】由a b a b +=− 知：222222a a a b b a b b−=+⋅+⋅+ ，可得0a b ⋅= ，所以b a − 在a上的投影向量为22()a b a a a b a a a aa a⋅−⋅−⋅=⋅=−. 故选：A 5. 若1sin()43πα+=，(0,)απ∈，则cos 2=α（） A. 79−B.C.D. 【答案】D 【解析】.【分析】根据同角三角函数的关系结合角度范围可得cos()4πα+，再根据二倍角公式可得sin[2()]4πα+，结合诱导公式可得cos 2α.【详解】因为(0,)απ∈，所以5(,)444πππα+∈，又13sin()sin 434ππα+=<，所以3(,)44ππαπ+∈，所以cos()4πα+，所以cos 2sin(2)sin[2()]2sin()cos()2444ππππααααα=+=+=++＝故选：D6. 在ABC 中，点O 满足2CO OB = ，过点O 的直线分别交射线AB ，AC 于点M ，N ，且AM mAB =，AN nAC =，则2m n +的最小值为（） A.83B.103C. 3D. 4【答案】A 【解析】【分析】利用共线定理的推论可得21133m n+=，然后妙用“1”可得. 【详解】由题可知，0,0m n >>，因为AM mAB = ，AN nAC =，所以1AB AM m= ，1AC AN n = ，又2CO OB = ，所以22AO AC AB AO −=−，所以21213333AO AB AC AM AN m n=+=+，因为,,M O N 三点共线，所以21133m n+=，所以2144482(2)()3333333m n m n m n m n n m +=++=++≥+=，当且仅当43321133m nn mm n = +=，即42,33m n ==时，等号成立.所以2m n +的最小值为83.故选：A7. 已知()f x 是定义在R 上的奇函数，且()22f =，若对任意的1x ，()20,x ∈+∞，均有()()12121f x f x x x −>−成立，则不等式()11f x x −+>的解集为（）A. ()()2,02,−+∞B. ()(),20,2−∞−C. ()(),11,3−∞−D. ()()1,13,−+∞【答案】D 【解析】【分析】构造函数()()gx f x x =−，则()()g x f x x =−在()0,∞+上递增，判断()()g x f x x =−也是是定义在R 上的奇函数，可得()()gx f x x =−在(),0∞−上递增，分类讨论列不等式求解即可. 【详解】因为对任意的1x ，()20,x ∈+∞，均有()()12121f x f x x x −>−成立，不妨设2x >1>0x ，则−1x 20x <，所以()()()()12121122f x f x x x f x x f x x ⇒−<−−<−，构造函数()()gx f x x =−，则()()g x f x x =−在()0,∞+上递增，因为()f x 是定义在R 上的奇函数，所以()()g x f x x =−也是是定义在R 上的奇函数，所以()()gx f x x =−在(),0∞−上递增，不等式()11f x x −+>化为()()()11010f x x g x −−−>⇒−>，因为()()()()()2222020220f f g g g =⇒−=⇒=⇒−=−=，则()()121231010x g x g x x x −> −> ⇒⇒>−>−> ，或()()1212111010x g x g x x x −>− −>− ⇒⇒−<<−<−<； 10x −=时，()00g =，不合题意；综上不等式()11f x x −+>的解集为()()1,13,−+∞ ，故选：D.8. 三面角是立体几何的重要概念之一.三面角−P ABC 是指由有公共端点P 且不共面的三条射线PA ，PB ，PC 以及相邻两射线之间的平面部分所组成的空间图形.三面角余弦定理告诉我们，若APC α∠=，BPC β∠=，APB γ∠=，平面APC 与平面BPC 所成夹角为θ，则cos cos cos cos sin sin γαβθαβ−=.现已知三棱锥−P ABC ，PA =，3BC =，45APC ∠=°，60BPC ∠=°，90APB ∠=°，则当三棱锥−P ABC 的体积最大时，它的外接球的表面积为（）A. 18πB. 36πC.87π2D.117π2【答案】B 【解析】【分析】作出图形，作BD PC ⊥，BM ⊥平面APC ，则θ∠=BDM ，先表示出13P ABCAPC V S BM −=⋅ ，接着用条件表示成P ABC V −=−P ABC 的体积最大，则PB PC ⋅最大，利用基本不等式得出3PB PC ==时，其体积最大，然后补全三棱锥成棱柱，根据棱柱外接球半径即可求解.【详解】由题知，45APC ∠=°，60BPC ∠=°，90APB ∠=°，平面APC 与平面BPC 所成夹角为θ，作BD PC ⊥，BM ⊥平面APC ，则θ∠=BDM ，由题意得13P ABCAPC V S BM −=⋅ ，cos cos cos cos sin sin γαβθαβ−===()0,πθ∈，sin θ=，sin BM BD θβ=⋅ 13sin 22APC S PA PC PC α=⋅⋅=⋅ ，所以13P ABC APC V S BM −=⋅= 要使三棱锥−P ABC 的体积最大，则PB PC ⋅最大，在PBC 中，由余弦定理得， 2221cos 22PB PC BC BPC PB PC+−∠==⋅⋅，整理得，229PB PC PB PC +−=⋅，2292PB PC PB PC PB PC +=⋅+≥⋅，即9PB PC ⋅≤，当且仅当3PB PC ==时，等号成立，则PA =，3PB PC BC ===，AB =因为222cos 2PA PC AC APC PA PC+−∠=⋅⋅，解得3AC =，所以222PC AC PA +=，222AC BC AB +=，即AC PC ⊥，ACBC ⊥，60BCP ∠=°，所以补全三棱锥成棱柱，如下图，则四边形BCPD 是菱形，点O 为其外接球的球心，即AD 中点，所以3BP =，2cos30CD PC =⋅⋅°=6AD =，所以外接球半径为3，即三棱锥−P ABC 外接球的表面积为24π336π×=. 故选：B【点睛】三棱锥外接球表面积问题，从以下几个角度分析：（1）面面角的定义以及辨析；（2）求解最值时，基本不等式的利用；（3）几何体割补法的应用；（4）数形结合思想的应用.二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9. 下列等式成立的是（） A. 0!0=B. 11A A m m n n n −−=C. 11(1)C (1)C mm n n n m +++=+ D. 111C C C m m m n n n −+++=【答案】BC 【解析】【分析】利用排列数、组合数公式对各选项逐一计算判断作答. 【详解】根据阶乘的概念可知，0!1=，故A 错误；()()()111!!!!A A m m n n n n n n n m n m −−−===−−，故B 正确；因为11(1)!1!1C C (1)!()!1!()!1m m n n n n n n m n m m m n m m +++++===+−+−+，所以11(1)C (1)C m m n n n m +++=+，故C 正确；根据组合数的性质可知11C C C mm m n n n −++=，故D 错误；故选：BC10. 以下四个正方体中，满足AB ⊥平面CDE 的有（）A. B.C. D.【答案】BD 【解析】AC ，根据直线与平面垂直的判定定理判断BD. 【详解】对A ，CE AD ∥，π4DAB ∠=，AB ∴与CE 所成角为π4，故AB 与平面CDE 不垂直，故A 错误；对B ，在正方体中，ED ⊥平面ABD ，AB ⊂平面ABD ，所以AB ED ⊥，又AB CE ，DE CE E ∩=，,DE CE ⊂平面CDE ，所以AB ⊥平面CDE ，故B 正确；对C ，连接,AF BF ，如图，在正方体中，由正方体面上的对角线相等可知，ABF △为正三角形，所以π3BAF ∠=，又CE AF ∥，AB 与CE 所成的角为π3，所以AB 与平面CDE 不垂直，故C 不正确；对D ，连接,MB BN ，如图，因为AM ⊥平面CMEB ，EC ⊂平面CMEB ，所以AM EC ⊥，又BM EC ⊥，,BM AM M BM AM =⊂ ，平面AMB ，所以EC ⊥平面AMB ，又AB ⊂平面AMB ，所以EC AB ⊥，同理可得ED AB ⊥，再由,,EC ED E EC ED =⊂ 平面ECD ，所以AB ⊥平面CDE ，故D 正确. 故选：BD11. 已知函数()f x 的定义域为R ，()21f x +是偶函数，()1f x −的图象关于点()3,3中心对称，则下列说法正确的是（）A. ()()2f x f x =+ B. ()203f =C. ()()24f x f k x +=−，Z k ∈D.411()123k i f i k −==−∑，Z k ∈【答案】BCD 【解析】【分析】根据()21f x +是偶函数可得函数()f x 关于直线1x =对称，由()1f x −的图象关于点()3,3中心对称可得()f x 关于点(2,3)成中心对称，据此可推导出函数为周期函数，判断A ，再由函数的周期求出()20f 判断B ，由周期性及对称性可判断C ，由以上分析利用()()41411()4k ki i f i f i f k −===−∑∑求解可判断D.【详解】因为()21f x +是偶函数，所以(21)(21)f x f x −+=+，可得(1)(1)−+=+f x f x ，故()f x 关于直线1x =对称，因为()1f x −的图象关于点()3,3中心对称，所以()f x 关于点(2,3)成中心对称，所以(2)(2)6f x f x −++=，又由(1)(1)−+=+f x f x 可得()(2)f x f x −=+，所以(2)()6f x f x −+−=，即(2)()6f x f x ++=，所以(4)(2)6f x f x +++=，两式相减可得(4)()0f x f x +−=，即(4)()f x f x +=，所以4T =，故A 错误；由周期4T =，()20(4)(0)f f f ∴==，又(0)(4)6f f +=，所以(0)(4)3f f ==，即()203f =，故B 正确；由周期4T =，()4()f k x f x ∴−=−，Z k ∈，由()(2)f x f x −=+可得，()()24f x f k x +=−，Z k ∈，故C 正确；由上述分析可知(2)(4)3f f ==，又因为(1)(3)6f f +=，所以(1)(2)(3)(4)12f f f f +++=，所以()()41411()4123k ki i f i f i f k k −===−=−∑∑，故D 正确. 故选：BCD【点睛】关键点点睛：当函数满足()()f a x f b x +=−时，函数()f x 关于直线2a bx +=对称，当函数满足()()2f a x f b x c ++−=时，函数关于点,2a b c +成中心对称.12. 摸出一个小球，记录颜色后放回，当三种颜色的小球均被摸出过时就停止摸球.设=i A “第i 次摸到红球”，i B =“第i 次摸到黄球”，i C =“第i 次摸到蓝球”，i D =“摸完第i 次球后就停止摸球”，则（）A. ()329P D =B. ()41227P D A =C. ()11223n n n P D −−−=，3n ≥ D. ()312223n n n n n P D B C −−−−=，3n ≥【答案】ACD 【解析】【分析】AC 选项，求出n D 包含的事件数为()12322C n −−，从而得到()n P D ，并计算出()3P D ；B 选项，计算出()41227P D A =，()113P A =，利用条件概率公式计算出答案，D 选项，表达出()31223n n n n n P D B C −−−=，3n ≥，和()21233n n n n P B C −−−=，3n ≥，利用条件概率公式得到答案.【详解】AC 选项，n D =“摸完第n 次球后就停止摸球”，有放回的摸n 次，有3n 种可能，若恰好摸球n 次就停止摸球，则恰好第n 次三种颜色都被摸到，即前()1n −次摸到2种颜色，第n 次摸到第三种颜色，共()12322C n −−种情况，则()()1311222322C 3nn n nn P D −−−−==−，3n ≥，()23222239P D −==，AC 正确； B 选项，事件41D A 表示第一次摸到红球，摸到第4次，摸球结束，若第2次或第3次摸到的球为红球，此时有12A 种情况，不妨设第2次摸到的球为红球，则第3次和第4次摸到的球为蓝球或黄球，有2种可能，故有122A 4=种情况，若第2次和第3次都没有摸到红球，则第2次和第3次摸到的球颜色相同，第4次摸到的球和第2,3次摸到的球颜色不同，故有22A 2=种情况，故()41426n D A =+=，其中摸4次球可能得情况有4381=种情况，故()41761228P D A ==，其中()113P A =，故()4129P D A =，B 错误； D 选项，12n n n D B C −−表示“第()2n −次摸到蓝球，第()1n −次摸到黄球，第n 次摸到红球，停止摸球”，则前()3n −次摸到的球时蓝球或红球，故有32n −种可能，故()31223n n n n n P D B C −−−=，3n ≥，12n n B C −−表示“在前n 次摸球中，第()2n −次摸到蓝球，第()1n −次摸到黄球”，故有23n −种可能，故()21233n n n n P B C −−−=，3n ≥，则()312223n n n n n P D B C −−−−=，3n ≥，D 正确.故选：ACD【点睛】常见的条件概率处理方法，其一是用样本点数的比值处理，需要弄情况事件包含的样本点数，其二是用概率的比值处理，也可以缩小样本空间，从而确定概率，解决实际问题的关键在于分析情况基本事件.三、填空题：本题共4小题，每小题5分，共20分.13. 已知实数a ，b 满足25a bm ==且1112a b +=，则m ＝______. 【答案】100 【解析】【分析】根据指数与对数的互化公式，表示出,a b ，再结合换底公式表示出1112a b +=，最后结合对数运算即可求解【详解】由25a bm ==可得2511log ,log log 2,log 5m m a m b m a b==⇒==，又1112a b +=，即1log 2log 5log 102m m m +==，所以1210m =，即100m = 故答案为：10014. 现有一枚质地不均匀的硬币，若随机抛掷它两次均正面朝上的概率为12，则随机抛掷它两次得到正面、反面朝上各一次的概率为______；若随机抛掷它10次得到正面朝上的次数为ξ，则()E ξ=______.（第一空2分，第二空3分）【答案】 ①1##1−②. 【解析】【分析】p ，再由独立重复试验求出正面、反面朝上各一次的概率为，由二项分布的期望公式求期望.【详解】设这枚硬币正面朝上的概率为p ，反面朝上的概率为1p −，则两次正面朝上的概率为212p =，解得p = ，所以随机抛掷两次得到正面，反面朝上各一次的概率为()12C 1211P p p =−=− . 由题易知随机变量ξ服从二项分布ξ~10B ，则()10E ξ=.1−；15. 已知函数()()ln 2e ,0234,0x a x f x x ax a x − −<= −++−≥ ，若()f x 有4个零点，则实数a 的范围是______..【答案】41,3【解析】【分析】由题可得方程()ln e x a −=与方程22340,0x ax a x −++−=≥各有两个根，对于前者转化为函数()()ln ex g x −=图象与直线y a =有两个交点，后者由判别式结合韦达定理可得a 范围，综合后可得答案.【详解】当0x <时，()()()ln ,1ln ln ,10x x x x x −≤− −= −−−<<，则函数()()()()ln ln ln e ,1e 1e,10x x x x x g x x x −−−− =−<− == =−−≤<在(),1−∞−上单调递减，在[)10−，上单调递增，据此可得()g x 大致图象如下，又()ln e x a −=方程的解的个数相当于函数()g x 图象与直线y a =交点个数，方程22340,0x ax a x −++−=≥最多2个根，()f x 有4个零点，则方程()ln e x a −=与方程22340,0x ax a x −++−=≥各有两个根.设方程22340,0x ax a x −++−=≥两根为12,x x ，则212121Δ41216041203430a a a a x x a x x a > +−>⇒<≤+=> =−≥ . 故答案为：41,3.【点睛】16. 已知平面向量a ，b ，()1,2i c i =满足22a b b ==⋅=，1i c a −= ，则()1222R c b c b λλλ−+−∈的最小值为______.【答案】3−##3−+【解析】【分析】求出向量,a b的模及夹角，记1122,,2,,2OA a OB b OB b OC c OC c λ=====′ ，得出对应点的轨迹，利用数形结合求最值.【详解】由||2||2a b b==⋅=，即21cos ,a b ×× ，所以π,4a b = ，记1122,,2,,2OA a OB b OB b OC c OC c λ′=====，因为1i c a −=，所以1C 在以A 为圆心，1为半径的圆上，2C 在以A ′为圆心，2为半径的圆上，其中(2,0),(4,0)A A ′，所以11222122222||||c B b c b c b c b C B C λλλλ−+−=−′+=′+−，作A 关于直线l （OB所在直线）的对称圆，1C 的对称点记为3C ，知1(0,2)A ，则1232B C B C B C B C +=+′′′′，如图，由图可知，当132,,,,A C B C A ′′共线时，32||||C B C B ′′+存在最小值，因为111,2A A A A r r ′===′，所以32||||C B C B ′′+最小值为3.故答案为：3−【点睛】关键点点睛：利用向量的的几何表示，原问题转化为求32||||C B C B ′′+最小值，数形结合，利用共线线段最短得解.四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17. 在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且______，请从下列两个条件中任选一个填入上方的横线中作为已知条件，并解答本题（如果选择多个条件分别解答，则按第一个解答计分）：①sinsin 2B Cc a C +=；②)222ABC S b c a =+− ，（1）求A ；（2）若D 为边BC 上一点，且2CD AD BD ==，试判断ABC 是锐角三角形、直角三角形还是钝角三角形，并说明理由. 【答案】（1）π3A =（2）直角三角形，理由见解析【解析】【分析】（1）选①：利用诱导公式化简，再由正弦定理边化角，然后由二倍角公式化简可得；选②：根据面积公式和余弦定理列方程可解；（2）根据已知先得1233AD AB AC =+，然后平方，联立余弦定理求解可得2c b =，a ，然后可判断三角形形状. 【小问1详解】若选①：πsin sin cos 222B C A A c c c +−== ，cos sin 2A c a C ∴=，sin cos sin sin 2AC A C ∴=， ()0,π,sin 0C C ∈> ，cossin 2sin cos 222A A AA ∴==， π0,,cos 0222A A ∈>，1sin 22A ∴=，所以π26A =，解得π3A =.若选②：)2222cos cos ABC S b c a bc A A =+−== ，1cos sin 2A bc A =， sin A A =，tan A ∴，因为()0,πA ∈，故π3A =. 【小问2详解】 2CD BD AD == ，212,,333AD a CD a BD a ∴===且2BD DC = 22AD AB AC AD ∴−=−，即1233AD AB AC =+ ， 222144999AD AB AC AB AC ∴=++⋅，22241429999a cb bc ∴=++，即222442a c b bc =++①，又由余弦定理得222a b c bc =+−②，联立①②可得2c b =，a ，从而222+=a b c ，故ABC 是直角三角形.18. 已知函数()sin cos (0)f x x x ωωω=+>的图象关于直线π8x =对称，且()f x 在π0,6上没有最小值.（1）求()f x 的单调增区间；（2）已知函数()()log 242x a g x a a =−+（0a >且1a ≠），对任意1ππ,42x∈，总存在[]21,2x ∈，使得()()12f x g x ≤，求实数a 的取值范围. 【答案】（1）)3πππ,πZ 88k k k−++∈（2）2a ≥或112a ≤<. 【解析】【分析】（1）由两角和的正弦公式化简，再由对称轴及在π0,6上没有最小值求出解析式，由正弦型函数的单调性求单调区间即可；（2）根据存在性及任意性问题转化为()()12max max f x g x ≤，分别利用三角函数及对数型函数的性质求最值，解不等式即可. 【小问1详解】()πsin cos 4f x x x x ωωω=++.()f x 的图象关于直线π8x =对称. ππππ,Z 842k k ω∴+=+∈，解得82,Z k k ω=+∈. 当π0,6x∈时，ππππ,4464x ωω+∈+ . ()f x 在π0,6上没有最小值.ππ3π642ω∴+≤，解得152ω≤.又0ω>，所以2ω=，所以()π24f x x=+.令()πππ2π22πZ 242k x k k −+≤+≤+∈，解得()3ππππZ 88k x k k −+≤≤+∈. 所以()f x 的单调增区间为()3πππ,πZ 88k k k−++∈.【小问2详解】任意1ππ,42x∈，均存在[]20,2x ∈，使得()()12f x g x ≤. ()()12max max f x g x ∴≤.1ππ,42x ∈ .1π3π5π2,444x ∴+∈ .()m x 11a sin 1π24f x x∴ +≤≤=.又log ,242x a y t t a a ==−+ （0a >且1a ≠）单调性相同， ()()log 242x a g x a a ∴=−+在定义域上是增函数.()()()2max 2log 2421a g x g a a ∴==−+≥.21242a a a a > ∴ −+≥或2010242a a a a << <−+≤ 2a ∴≥或112a ≤<. 19. 航班正点率是指航空旅客运输部门在执行运输计划时，航班实际出发时间与计划出发时间较为一致的航班数量与全部航班数量的比率.人们常用航班正点率来衡量一个航空公司的运行效率和服务质量.现随机抽取10家航空公司，对其近一年的航班正点率和顾客投诉次数进行调查，得到数据如下：航空公司编号 1 2 3 4 5 6 7 8 9 10航班正点率ix/% 82 7777 76 74 73 71 70 9169顾客投诉次数iy/次21 58 79 68 74 93 72 122 18 125 整理数据得：10153620i iix y=≈∑，102158150iix=≈∑，102164810iiy=≈∑，101760iix==∑，101730iiy==∑，70≈.（1）（i）证明：样本相关系数nnx yr=；（ii）根据以上数据计算样本相关系数（结果保留2位小数），并由此推断顾客投诉次数与航班正点率之间的线性相关程度（若0.81r≤≤，则认为线性相关程度很强；若0.30.8r≤<，则认为线性相关程度一般；若0.3r<，则认为线性相关程度很弱）.（2）用一元线性回归模型对上表中的样本数据进行拟合，得到顾客投诉次数关于航班正点率的经验回归方程为5y x a=−+.数，并希望一年内收到的顾客投诉不超过73次，试估计该公司的航班正点率应达到多少？参考公式：样本相关系数nx yr=【答案】（1）（i）证明见解析；（ii）0.89−；顾客投诉次数与航班正点率之间的线性相关程度很强（2）76%.【解析】【分析】（1）（i）将()()1ni iix x y y=−−∑展开，结合平均数意义化简可得()()11n ni i i ii ix x y y x y nx y=−−=−∑∑，然后分别用,i x x,i x x替代,i y y，用,i y y分别替代,i x x可证；（ii）根据所给数据代入公式计算,然后可作出判断；（2）利用样本中心点求 a，然后根据回归方程解不等式可得. 【小问1详解】（i ）证明：()()()11ni iiini i i i x x x y x y x y y y x y ===+−−−−∑∑1111n n nni i i ii i i i x y x y x y x y =====−−+∑∑∑∑ 1111nnnniii ii i i i x y y x x y x y =====−−+∑∑∑∑1()()ni ii x y y nx x ny nx y ==−−+∑1ni ii x y nx y ==−∑，在上式中分别用,i x x 替代,i y y ，得()22211nni i i i x x x nx ==−=−∑∑，同理，也有()22211nni i i i y y y n y ==−=−∑∑，故样本相关系数nnx yr =.（ii ）可知10117610i i x x ===∑，10117310i i y y ===∑.10110536201076731860i i i x y x y =∴−≈−××=−∑，10222110581501076390ii xx =−≈−×=∑， 1022211064810107311520ii yy =−≈−×=∑，1010x y x yr−∴≈620.8970≈−≈−，故顾客投诉次数与航班正点率之间的线性相关程度很强.【小问2详解】557673453a x y =+=×+=令545373ˆyx =−+≤，得76x ≥. 即该公司的航班正点率应达到76%.20. 2023年4月23日是第28个“世界读书日”.为了倡导学生享受阅读带来的乐趣、尊重和保护知识产权，立德中学举办了一次阅读知识竞赛.初赛中每支队伍均要参加两轮比赛，只有两轮比赛均通过的队伍才能晋级.现有甲、乙两队参赛，初赛中甲队通过第一轮和第二轮的概率均为34，乙队通过第一轮和第二轮的概率分别为35，23，且各队各轮比赛互不影响. （1）记甲、乙两队中晋级的队伍数量为X ，求X 的分布列和数学期望；（2）经过激烈的比拼，甲、乙两队成功进入决赛争夺冠军.决赛共有两道抢答题.第一题中，某支队伍若抢到并答对则加10分，若抢到但答错则对方加10分.第二题中，某支队伍若抢到并答对则加20分，若抢到但答错则对方加20分.最终得分高的队伍获胜.假设两支队伍在每一题中抢到答题权的概率均为12，且每一题答对的概率分别与初赛中通过对应轮次的概率相等.各队各题作答互不影响.已知甲队获得了冠军，计算第二题是由甲队抢到答题权的概率. 【答案】（1）分布列见解析，7780（2）57【解析】【分析】（1）设“甲队晋级”为事件M ，“乙队晋级”为事件N ，求得9()16P M =，2()5P N =，得到X 的可能取值为0,1,2，求得相应的概率，出分布列，结合期望的公式，即可求解；（2）记事件A = “甲队获得冠军”，B = “该题由甲队抢到答题权”，结合条件概率的公式，即可求解. 【小问1详解】解：设“甲队晋级”为事件M ，“乙队晋级”为事件N ，可得339()4416P M =×=，322()535P N =×=，则随机变量X 的可能取值为0,1,2，可得()922101116580P X==−×−=；()92924111116516580P X==−×+×−=. ()929216540P X ==×=.所以随机变量X 的分布列为则期望()214197701280804080E X =×+×+×=. 【小问2详解】解：根据题意，设甲乙两队通过初赛的事件分布为12,A A ，可得12339322(),()4416535P A P A =×==×=，即甲乙进入决赛的概率分别为916和25，记事件A = “甲队获得冠军”，B = “该题由甲队抢到答题权”，可得()()()()()191393||21625160P A P B P A B P B P A B =+=×+×=，又由()()()199()(|)()21632P AB P AB P B P B P A B P B =⋅==×=，故()()()9532|937160P AB P B A P A ===. 21. 如图，四面体ABCD 中，平面ABC⊥平面BCD ，AB AC ⊥，AB AC ==1CD =，（1）若AD AB ⊥，证明：CD ⊥平面ABC ；（2）设过直线AD 且与直线BC 平行的平面为α，当BD 与平面ABC 所成的角最大时，求平面α与平面BCD 的夹角的余弦值.【答案】（1）证明见解析（2【解析】【分析】（1）利用面面垂直的性质定理证得⊥AE 平面BCD ，进而得到AE CD ⊥，从而利用线面垂直的判定定理依次证得AB ⊥平面ACD ，CD ⊥平面ABC ；（2）先由题意推得BD 与平面ABC 所成的角最大时DF 的值，再推得平面α与平面BCD 的夹角的平面角为AGE ∠，从而在Rt AEG △中求得所求. 【小问1详解】过点A 作AE BC ⊥，垂足为E ，平面ABC⊥平面BCD ，平面ABC ∩平面BCD BC =，AE BC ⊥，AE ⊂平面ABC ，AE ∴⊥平面BCD ，又CD ⊂平面BCD ，AE CD ∴⊥，AD AB ⊥ ，AB AC ⊥，AC AD A = ，AC AD ⊂ 平面ACD ，AB ∴⊥平面ACD ，又CD ⊂平面ACD ，AB CD ∴⊥，又,,AE AB A AE AB =⊂ 平面ABC ，故CD ⊥平面ABC .【小问2详解】过点D 作DF BC ⊥，垂足为F平面ABC⊥平面BCD ，平面ABC ∩平面BCD BC =，DF BC ⊥，DF ⊂平面BCD ，DF ⊥∴平面ABC ，DBC ∴∠是BD 与平面ABC 所成的角，在ABC 中，ABAC ⊥，AB AC ==2BC =，故sin sin CD BC DBC BDC=∠∠，即12sin sin DBC BDC =∠∠，则1sin sin 2DBC BDC ∠=∠，∴当sin 1BDC ∠=，即CD BD ⊥时，sin DBC ∠最大，且最大值为12，此时π6DBC ∠=，BD =，DF =，记l α= 平面BCD ，过点E 作EG l ⊥，垂足为G ，连接AG ，//BC α ，BC ⊂平面BCD ，l α= 平面BCD ，//l BC ∴，故平面ADG 就是平面α，AE 平面BCD ，AE l ∴⊥，EG l ⊥ ，EG AE E ∩=，,EG AE ⊂平面AGE ，l ∴⊥平面AGE ，又AG ⊂平面AGE ，l AG ∴⊥，AGE ∴∠是平面α与平面BCD 的夹角，则π02AGE <∠<，又因为DF BC ⊥，//l BC ，所以//GE DF ，所以四边形DFEG 是平行四边形，故GE DF ==，则在Rt AEG △中，AG ，所以平面α与平面BCD的夹角余弦值为cos GE AGE AG ∠=. .22. 已知()1f x x =+，()22g x x =+.定义{},min ,,a a b a b b b a ≤ =≤ ，设()()(){}min ,2m x f x t g x t =−−，R t ∈．（1）若3t =，（i ）画出函数()m x 的图象；（ii ）直接写出函数()m x 的单调区间；（2）定义区间(),A p q =的长度()L A q p =−.若()*12Nn B A A A n =∪∪∪∈ ，(1)i j A A i j n =∅≤<≤ ，则()1()ni i L B L A ==∑.设关于x 的不等式()m x t <的解集为D .是否存在t ，使得()6L D =？若存在，求出t 的值；若不存在，请说明理由.【答案】（1）（i ）作图见解析；（ii ）单调减区间为(),3−∞，()5,6，单调增区间为()3,5，()6,+∞ （2）存在，3t = 【解析】【分析】（1）（i ）3t =时，(){}2min 31,1238m x x x x =−+−+，求出方程221238x x x −=−+的根，即可画出()m x 的图象；（ii ）由()m x 的图象即可写出其单调区间；（2）由()min 1m x =得不等式()m x t <有解必要条件是1t >，再对t 的值分情况讨论即可. 【小问1详解】（i ）若3t =，则()31f x t x −=−+，()()222621238g x t x x x −=−+=−+.(){}2min 31,1238m x x x x ∴=−+−+. 令221238x x x −=−+，得15=x ，28x =.故函数()m x 的图象如图所示.（ii ）由函数()m x 的图象可知()m x 的单调减区间为(),3−∞，()5,6，单调增区间为()3,5，()6,+∞.- 【小问2详解】()min 1f x = ，()min 2g x =.()min 1m x ∴=. ∴不等式()m x t <有解的必要条件是1t >.①当12t <≤时，如图①所示，令()m x t <，即()f x t <，得()1,21D t =−.的()222L D t ∴=−≤，不符合题意.当2t >时，令()1x t g x −+=，得()2241410x t x t t −++++=解得1x =，2x =令11x t t −+=，得3t =.②当23t <≤时，如图②所示，()f x t <的解集为()1,21t −，()g x t <的解集为(2t t −+，此时()22L D t =−+. 令()6L D =，解得3t =.③当3t >时，如图③所示，2220t x t +−=+=< ，22t x ∴+< ，令()m x t <，得(1,2D t =.()21L D t ∴=+−.令()6L D =，解得3t =或174t =，均舍去. 综上所述，3t =..【点睛】思路点睛：本题考查了函数的新定义问题，对于第（2）小题，突破口是由()min 1m x =得不等式()m x t <有解的必要条件是1t >，再对t 与()f x 和()g x 的最小值进行分类讨论求解.。

高二数学下学期期末联考试题

高二数学下学期期末联考试题本试卷分第I卷（选择题）和第n卷（非选择题）两部分，共150分•考试用时120 分钟•祝各位同学考试顺利！第I卷一、选择题：每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的•1 •若a , b • （0 , •：：），则“ a2 b2：：： 1 ”是“ ab 1 a b”的（）.（A）必要非充分条件；（B）充分非必要条件；（C）充要条件；（D）既不充分也不必要条件.2.经过点（0, 0）,且与以（2,—1）为方向向量的直线垂直的直线方程为（）.（A）x 2y=0; （B）x_2y=0;（C）2x y = 0 ; （D）2x - y = 0 .3.已知动点P （x , y ）满足J（x-1） +y = x + y，则点P的轨迹是（）.（A）椭圆；（B ）双曲线；（C）抛物线；（D）两相交直线.4.（文科）给出以下四个命题：①如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行；②如果一条直线和一个平面内的两条直线都垂直，那么这条直线垂直于这个平面；③如果两条直线都平行于一个平面，那么这两条直线互相平行；④如果两条直线同垂直一个平面，那么这两条直线平行.其中真命题的个数是（)•(A) 4 ；( B 3；(C) 2；(D) 1（理科）对于任意的直线l与平面「，在平面:- 内必有直线m，使m与1 （)（A）平行；（B 相交；（C）垂直；（D ）互为异面直线.5.若关于x的不等式x-1+x+1c a的解集为0,则实数a的取值范围为（）.(A)(-二,2) ；(B)(-二,2] ；( C) (2, ：：) ；(D) [2,二).6.已知直线l : y =ax +2与以A (1,4)、B (3, 1)为端点的线段相交，则实数a的取值范围是( ).1 1 1(A) a ；(B) a_2 ；(C) a_2 ；( D) a 或a_2 .3 3 37.已知圆C: (x - a)2(^2)-4 (a 0)及直线I : x - y • 3 = 0 •当直线l被圆C 截得的弦长为2、. 3时，贝y a =().(A ) ...2 ；8.已知点A(3,2),F 为抛物线y 2 =2x 的焦点，点P 在抛物线上移动，当PA+|PF11.如图 1, PA 丄平面 ABC ，/ ACB = 90 ,2•与 =1(a b - 0)的左，右焦点分别为b取得最小值时，点 P 的坐标是( ). (A ) ( 0, 0); ( B ) (2, 2);1 9.(文科)已知a 0 , b 0,- a (C ) (-2,— 2)(D) (2, 0).(A ) 4、. 2 ; =1，则a b 的最小值是().(B ) 32.2 ; (C )2 2 ;(D ) 5.(理科)已知X _ 4，则y5(A )最大值一；4 (B)2 x _4x 5 士 / 、有( ).2x - 4 5 最小值一； 4 (C )最大值1; (D )最小值1 . 10.点P 是双曲线x 22 y =1上的一点，F 1和F 2分别是双曲线的左、右焦点, 12PF 1 PF 2 =0，则F 1PF 2的面积是( ). (A) 24;(B ) 16; (C ) 8;(D) 12.PB 与AC 所成的角是().(B) arcta n 、、2 ；(D) arctan 、、3 . 在椭圆上，且 PF/=3PF 2 , 则此椭圆的离心率的最小值为( ).(B) (理科)已知E 、2x F 是椭圆一2=1的左、右焦点, l 是椭圆的一条准线，点 P且 PA = AC = BC = a ，则异面直线12.(文科)已知椭圆F 1、F 2，点 P在I上，则/ EPF的最大值是( )•(A) 15 ; (B) 30 ; (C) 45 ;(D) 60第口卷二、填空题：本大题共4小题，每小题4分，共16分•把答案填在题中横线上.13. m , n是空间两条不同直线，? /■是两个不同平面，下面有四个命题：①若m 丨.、，n // :,②若m _ n ,〉// :，③若m _ n , 〉// :,④若m _〉，m // n, ：• // :,则n _ :.其中真命题的编号是____________ .(写出所有真命题的编号)2 214.对于圆x (y -1) =1上任一点P(x , y)，不等式x • y • m _ 0恒成立，则实数m的取值范围 ____________ .x y — 1,15.___________________________________________________________________设x,y满足约束条件：2x-y_0,则目标函数2x y的最大值是 _____________________________ .x -2y _ 0 ,2 216.________________________ 已知抛物线x -2xy y -8x -8y = 0的对称轴为x - y = 0 ,焦点为(1, 1), 则此抛物线的准线方程是 .三、解答题：本大题共6小题，共74分.解答应写出文字说明，证明过程或演算步骤.17.(12分)设a 0 ,解关于x的不等式：空2) :: 1.x—1218. (12分)过抛物线y =2px的焦点的一条直线和此抛物线相交于两个点A、B, 经过点A和抛物线顶点的直线交准线于点M .求证：([)y A y B = _p2;(n)直线MB平行于抛物线的对称轴.19.(12分)如图2，已知四边形ABCD为矩在I上，则/ EPF的最大值是( )•形，PA丄平面ABCD , M、N分别为AB、PC的中点.(I)求证：MN丄CD .(n)在棱PD上是否存在一点E,使得 B 图2 CAE //平面PMC ?若存在，请确定点E的位置；若不存在，请说明理由.2 2 220.( 12分)如图3，过圆x y ^R上的动点P向圆x2y2 = r2( R r 0 )引两条切线PA、PB，切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点，求△ MON面积的最小值.21.(12 分)已知a , b • R , x 1,2 2 . x . 2 2已知点B ( 2, 0), O A=(0,2J2) , O为坐标原点，动点P满足求证：x a ( ) b 一(a b).x -122.(14分)文科做(I)、(n)；理科做(I)O P +OA + OP -OA =4J3 .(I)求点P的轨迹C的方程；(n)当m为何值时，直线l : y^;<3x m与轨迹C相交于不同的两点M、N,且满足BM = BN ?(川)是否存在直线I : y =kx・m(k=0)与轨迹C相交于不同的两点M、N，且满足BM = BN ?若存在，求出m的取值范围；若不存在，请说明理由.答案与提示：一、选择题1 —5 BDBCB ; 6 —12 BCBBD BB .提示：2 21 .由a b ：：1 = 0 ：：a ：：1, 0 ：：b ：：1 = （1 - a）（1 — b） 0 二ab 1 a b ；反之由（1 - a）（1 -b）• 0 不能推得0 :：: a ：：：1,0 ：：：b ：：：1 .故"a2 b2：：：1 ”是"ab 1 a b”的充分非必要条件.选（B）.12.由题设知已知直线的斜率为，•••所求直线的斜率为2;2又所求直线过原点，故2x「y =0为所求.选（D）.3.由题设知动点P到定点（1, 0）的距离和它到定直线x - y=0的距离的比是常数2，根据双曲线的第二定义可得点P的轨迹为双曲线.选（B）.4.（文科）①、④正确，选（C）.（理科）对于任意的直线I与平面：•，若I在平面内，则存在直线m丄I ;若I不在平面〉内，且I丄〉，则平面:-内任意一条直线都垂直于I ;若I不在平面〉内，且I与：•不垂直，则它的射影在平面:'内为一条直线，在平面:' 内必有直线m垂直于它的射影，则m丄I .故选（C）.5.由x_1|+|x+1| 日（1_x）+（x+1）|=2知a 兰2.选（B）.6.由A （1, 4）、B （3, 1）在直线I上或其异侧得（a—2）（3a+1）兰0.1解得a乞2 .选（B）.37.设截得的弦为AB，圆心为C（a , 2），作CH丄AB于H，则由平几知识得CH =1 .a—2+3 厂由此得CH =——=1，解得a = 12 —1 .选（C）.V28 .点A在抛物线含焦点区域，过A作AP垂直于抛物线的准线交抛物线于点P,则由抛物线的定义知点P （2, 2）为所求点.选（B）.5 3AQA Kr -9.（文科）a ' b =（a - b ）（- -^3 一 - -3^2，选（B ）.a bb a2（理科）令t =x -2（t —2），则f （t ）=x 也主二丄住〕）.2x —42 t一5f （t ）在［2, •：：）上是单调递增函数，故y 的最小值是f （2） .选（B ）.4* 210.由 PR PF 2 =0得 PF ! + PF 2 = 4c 2 =64 , PF — PF 2 2a = ： 4 .1即e .选（B ）.2（理科）不妨设右准线I 交x 轴于点A ,由平几知识知过 E 、F 的圆且与|相切于点P易得/ FPA = 30，/ EPA = 60，从而/ EPF = 30为所求最大值，故选（B ）. 二、填空题：本大题共 4小题，每小题4分，共16分.把答案填在题中横线上. 13.①、④；14. ［ 72 — 1 , + °° ）； 15. 5 ；16. x + y + 2 =0 .3提示：13.②、③为假命题；①、④为真命题.14.设点 P(cos 二，1 sin 旳，由题设得 COST V si • m _ 0 .-m 乞1 --€2 .故m 的取值范围为［i 2 -1，•:：）.和直线I : 2x y =0，将I 向右上方平行移动，使其经过可1 一 —--S 禹PF 2 =2 PF 1 ' PF 2 = 12.选（11.如图，过B 作BD // CA ，且满足则/ PBD 为PB 与AC 所成的角. 易得四边形ADBC 为正方形，由PA 丄平面 ABC 得BD _ PD . D )•BD = CA ,在 Rt △ PDB 中，PD 二 2a ,DB 二 a , tan . PBD =竺=.2 .DB12.（文科）由题设和焦半径公式得2a 二 PR +|PF 2 =4PF 2 =4(a —ex p ).0 :: x P 乞 a .••• a = 2ex P 乞 2ea . 时，/ EPF 最AP 2=AE AF即 - m 込 u = COST 1 sin v 恒成立.而 u = 2 sin( x •15.如图，作出不等式表示的可行域（阴影部分）x5 3一 2 1行域内的点A （―,）时，z=2x ，y 取得最大值. 3 3 2 1」 x , y 时，Z max33故当16.对称轴x - y =0与抛物线的交点（0, 0）为抛物线的顶点，且抛物线的准线垂直于对称轴，焦点（1, 1）关于顶点（0, 0）的对称点（—1,—1 ）在准线上，故所求准线方程为x y 2 =0.三、解答题& 击（a —1）x —（2a —1）17.不等式整理得0 .X—12a —1（a -1）（x - ）当a=1时，不等式为0. ......... （3分）x-12a —1①当0 ：：：a :: 1时，1，原不等式解集为a —1—2 a -1 —（v , ............................）_• （1, ■二）；（6分）a -1②当a =1时，不等式解集为（1,，：：）; ... （9分）2a —1 2a —1③当a 1时，兰一1■ 1，原不等式解集为（1,竺一）. ........................... （12分）a—1 a—1P 218.（1）AB方程为x=my ，代入抛物线y =2px方程得22 2y -2 pmy - p =0 . ............. （ 3 分）由韦达定理得y A y^ - - p2. ........... （ 5 分）（n）OA方程为y =心乂，与准线方程联立解得M （-卫，坐）.X A 2 2X AY B故直线MB平行于抛物线的对称轴. ............ （12分）19. （I）取AC的中点0,连结NO，MO，由N为PC的中点得NO // PA. .......... （2分）又PA丄平面ABCD，• NO丄平面ABCD . ............. （4分）又••• OM丄AB，由三垂线定理得AB丄MN . （8 分）•-Y M2-PY A _- P Y A2X A Y A （11 分）Y A又••• CD // AB，• MN 丄CD . ........ （6 分）（n）存在点E，使得AE //平面PMC .此时点E为PD的中点. ............ （8分）证明如下：取PD的中点E，连结NE，53x -1 即_J2x—L (x -1)21 由N是PC的中点得NE // CD , NE CD21 又MA // CD, MA CD2 ，••• MA // NE , MA = NE .由此可知四边形MNEA是平行四边形，•AE // MN .由MN 平面PMC, AE二平面PMC ,•AE //平面PMC . .......... ( 12 分)2 2 220.设P(x。

高二数学下学期期末考试试题含解析试题 10

智才艺州攀枝花市创界学校二零二零—二零二壹高二数学下学期期末考试试题〔含解析〕一、单项选择题：在每一小题给出的四个选项里面，只有一项为哪一项哪一项符合题目要求的. 1.假设全集U =R ，集合{}11A x x =-<<，{}(2)0B x x x =-≤，那么()U A C B ⋂为〔〕A.{}02x x <<B.{}01x x <<C.{}01x x ≤<D.{}10x x -<<【答案】B 【解析】 ∵集合(){}20B x x x =-≤∴{0Bx x =≤或者}2x ≥ ∴{}02U C B x x =<<∵集合{}11A x x =-<<∴{}()01U A C B x x ⋂=<<应选B.2.“θ为第一或者第四象限角〞是“cos 0θ>〞的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据x 轴正半轴上的角的余弦值也大于0以及充分条件、必要条件的定义可得答案. 【详解】当θ为第一或者第四象限角时，cos 0θ>，所以“θ为第一或者第四象限角〞是“cos 0θ>〞的充分条件，当cos 0θ>时，θ为第一或者第四象限角或者x 轴正半轴上的角，所以“θ为第一或者第四象限角〞不是“cos 0θ>〞的必要条件，所以“θ为第一或者第四象限角〞是“cos 0θ>〞的充分不必要条件.应选：A【点睛】此题考察了三角函数的符号规那么，考察了充分必要条件的概念，属于根底题. 3.函数()ln 1f x x =+的图象大致是〔〕A. B.C. D.【答案】A 【解析】【分析】先确定定义域，舍去B;再根据(1,)-+∞单调性舍去CD ，即可得结果. 【详解】()ln 1,101f x x x x =+∴+≠≠-，,所以舍B;当(1,)x ∈-+∞时,()ln(1)f x x =+单调递增，所以舍去CD ，应选：A【点睛】此题考察根据函数解析式选择图象、函数定义域、函数单调性，考察根本分析识别才能，属根底题. 4.盒中装有3只螺口灯池与9只卡口灯泡，这些灯泡的外形都一样且灯口向下放假设，现需要一只卡口灯泡，电工师傅每次从中任取一只且不放回，那么在他第1次抽到的是螺口灯泡的条件下，第2次抽到的是卡口灯泡的概率为〔〕 A.14B.944C.911D.79【答案】C 【解析】【分析】根据题意转化为从装有2只螺口灯池与9只卡口灯泡中抽取一只，恰为卡口灯泡的概率，再根据古典概型概率公式求解，也可利用条件概率公式求解.【详解】方法一：因为电工师傅每次从中任取一只且不放回，且第1次抽到的是螺口灯泡，所以第1次抽到的是螺口灯泡，第2次抽到的是卡口灯泡的概率等价于：从装有2只螺口灯池与9只卡口灯泡中抽取一只，恰为卡口灯泡的概率，即为992+911=，方法二：设事件A 为：第1次抽到的是螺口灯泡，事件B 为：第2次抽到的是卡口灯泡,那么第1次抽到的是螺口灯泡，第2次抽到的是卡口灯泡的概率为39()91211(|)3()1112P AB P B A P A ⨯⨯=== 应选：C【点睛】此题考察条件概率，考察根本分析求解才能，属根底题.5.角α的顶点为坐标原点，始边为x 轴的非负半轴，角α的终边绕原点逆时针旋转2π后经过点34,55⎛⎫- ⎪⎝⎭，那么sin α=〔〕A.35 B.35C.45-D.45【答案】B【解析】【分析】先根据三角函数定义得cos()2πα+，再根据诱导公式求sin α.【详解】根据题意得33cos()25πα-+==-所以3sin cos()25παα=-+=，应选：B【点睛】此题考察三角函数定义以及诱导公式，考察根本分析求解才能，属根底题. 6.甲射击命中目的的概率为12，乙射击命中日标的概率为13，甲、乙是否命中目的互相之间无影响，如今甲、乙两人同时射击目的一次，那么目的被击中的概率是〔〕 A.16B.13C.23D.56【答案】C 【解析】【分析】先转化对立事件，根据HY 事件概率乘法公式以及对立事件概率公式求解，即得结果.【详解】因为目的被击中,指甲、乙两人至少有一人命中目的，其对立事件为甲、乙两人都未命中目的，所以目的被击中的概率是1121(1)(1)233---=，应选：C【点睛】此题考察HY 事件概率乘法公式以及对立事件概率公式，考察根本分析求解才能，属根底题. 7.为考察某种药物预防疾病的效果，进展动物试验，得到如以下联表：据此推断药物有效，那么这种推断犯错误的概率不超过〔〕附表及公式：参考公式：()()()()()22n ad bc K a b c d a c b d -=++++A0.025 B.0.010【答案】A 【解析】【分析】先根据卡方公式求卡方，再根据数据作判断.【详解】()2210510302045 6.109(5.024,6.635)55503075K ⨯-⨯=≈∈⨯⨯⨯ 所以这种推断犯错误的概率不超过，应选：A【点睛】此题考察卡方公式及其应用，考察根本分析求解才能，属根底题.8.2sin cos 2αα+=，α∈R ，那么tan α=〔〕 A.13-B.3C.13-或者3 D.3-或者13【答案】D【解析】【分析】先对条件平方，再利用弦化切解得结果.【详解】2252sin cos 4sin 4sin cos cos 22αααααα+=++= tan 3α∴=-或者1tan 3α=当1tan 3α=时，sin cos 1010αα==当tan 3α=-时，sin cos αα== 应选：D【点睛】此题考察弦化切，考察根本分析求解才能，属根底题.二、多项选择题：在每一小题给出的四个选项里面，有多项符合题目要求. 9.i 〕 A.假设复数3i z =+，那么131010iz =-．B.复数z 满足21z i -=，z 在复平面内对应的点为(),x y ，那么()2221x y +-=．C.假设复数1z ，2z 满足21z z =，那么120z z ≥．D.复数13zi =-的虚部是3．【答案】ABC 【解析】【分析】直接运算可判断A ；由复数的几何意义和复数模的概念可判断B ；由一共轭复数的概念，运算后可判断C ；由复数虚部的概念可判断D ；即可得解.【详解】由()()11333i 3i 3i 1010i i z -===-++-，故A 正确；由z 在复平面内对应的点为(),x y ，那么()221z i x y i -=+-=1=，那么()2221xy +-=，故B 正确；设复数1z a bi =+，那么2z a bi =-，所以()()21220a bi a b z bi z a +-=+=≥，故C 正确；复数13zi =-的虚部是-3，故D 不正确.应选：A 、B 、C【点睛】此题综合考察了复数的相关问题，属于根底题.10.将函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移4π个单位长度后，所得图象对应的函数为()y g x =，那么以下结论正确的选项是〔〕 A.函数()gx 的图象关于直线3x π=对称B.函数()gx 的图象关于点,03π⎛-⎫⎪⎝⎭对称C.函数()gx 在5,2424ππ⎡⎤-⎢⎥⎣⎦上单调递减D.函数()gx 在[]0,2π上恰有4个极值点【答案】AD 【解析】【分析】先根据图象变换得()y g x =，再根据余弦函数性质研究对称性、单调性以及极值点，即可作出选择.【详解】将函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向右平移4π个单位长度后得()2sin 2()cos(2)433g x x x πππ⎛⎫=-+=-+ ⎪⎝⎭因为()13g π=，所以函数()g x 的图象关于直线3x π=对称，即A 正确；因为1()32g π-=-，所以函数()g x 的图象不关于点,03π⎛-⎫⎪⎝⎭对称，即B 错误；因为53,,2,2424344x x πππππ⎡⎤⎡⎤∈-+∈⎢⎥⎢⎥⎣⎦⎣⎦，所以函数()g x 单调递增，即C 错误；因为[]0,2,2[,4]333x x πππππ∈+∈+，所以当2,2,3,43x πππππ+=时函数()gx 获得极值，即函数()gx 在[]0,2π上恰有4个极值点，D 正确；应选：AD【点睛】此题考察三角函数图象变换、余弦函数性质，考察根本分析求解才能，属中档题.1021年3月，为促进疫情后复工复产期间平安消费，某派出甲、乙、丙、丁4名医生到A ，B ，C 三家企业开展“新冠肺炎〞防护排查工作，每名医生只能到一家企业工作，那么以下结论正确的选项是〔〕 A.假设C 企业最多派1名医生，那么所有不同分派方案一共48种 B.假设每家企业至少分派1名医生，那么所有不同分派方案一共36种 C.假设每家企业至少分派1名医生，且医生甲必须到A 企业，那么所有不同分派方案一共12种D.所有不同分派方案一共34种【答案】ABC 【解析】【分析】利用排列组合知识对每一个选项的情况进展计算，可得正确选项.【详解】对于选项A ：假设C 企业没有派医生去，每名医生有2种选择，那么一共用4216=种，假设C 企业派1名医生那么有134232C ⋅=种，所以一共有163248+=种.对于选项B ：假设每家企业至少分派1名医生，那么有211342132236C C C A A ⋅=种，对于选项C ：假设每家企业至少分派1名医生，且医生甲必须到A 企业，假设甲企业分2人，那么有336A =种；假设甲企业分1人，那么有2123126C C A =种，所以一共有6612+=种.对于选项D ：所有不同分派方案一共有43种. 应选：ABC【点睛】此题主要考察了排列组合分组分配问题，属于中档题. 12.定义域为R 的函数()f x 是奇函数，且满足()()11f x f x -=+，当01x <≤时，()2f x x =，那么以下结论正确的选项是〔〕 A.()f x 的最小正周期为2B.11x -<≤时，()2f x x =C.()f x 在[]11,13上单调递增D.()28,4141()284,4143,x k k x k f x k Z x k k x k --<≤+⎧=∈⎨-+++<≤+⎩【答案】BCD 【解析】【分析】根据对称性以及奇偶性求周期，判断A;根据奇偶性求11x -<≤上解析式，判断B;根据周期转化到[]1,1-，结合11x -<≤上解析式，判断C;根据周期以及对称性求解析式，判断D.【详解】()()()()112f x f x f x f x -=+∴=-因为()f x 是奇函数，所以()()f x f x =--,()()(2)(4)(2)4f x f x f x f x f x T ∴--=-∴-=--=-∴=，即A 错误；10x -<<时，因为()f x 是奇函数，所以()()(2)2f x f x x x =--=--=因为定义域为R 的函数()f x 是奇函数，所以()()()0000f f f =-∴=因此11x -<≤时，()2f x x =，即B 正确；因为周期为4，所以()f x 在[]11,13上单调性与()f x 在[]1,1-上单调性一样，因为11x -<≤时，()2f x x =单调递增，所以()f x 在[]11,13上单调递增，即C 正确；因为周期为4，所以()(4),f x f x k k Z =-∈当4141k x k -<≤+时，141x k -<-≤()(4)2(4)f x f x k x k ∴=-=-因为11x -<≤时，()2f x x =，所以13x <<时，121x -<-<()(2)2(2)f x f x x ∴=-=-，3x =时，()3(34)(1)22(23)f f f =-=-=-=-即13x <≤时，()2(2)f x x =-当4143k x k +<≤+时，143x k <-≤()(4)2[2(4)]f x f x k x k ∴=-=--综上，()28,4141()284,4143,x k k x k f x k Z x k k x k --<≤+⎧=∈⎨-+++<≤+⎩，即D 正确；应选：BCD【点睛】此题考察函数对称性、奇偶性、周期性、单调性、解析式，考察综合分析求解才能，属中档题. 三、填空题： 13.随机变量()2~1,X N σ，假设()20.2P X >=，那么()P X >0=______.【答案】【解析】【分析】先根据正态分布对称性求()P X <0，再求().P X >0【详解】因为随机变量()2~1,X N σ，()20.2P X >=，所以()()20.2P X P X >==<0因此()()110.20.8PX P X >0=-≤0=-=故答案为：【点睛】此题考察利用正态分布对称性求概率，考察根本分析求解才能，属根底题.14.()()2log 1,11,12x x x f x x ⎧->⎪=⎨⎛⎫≤⎪ ⎪⎝⎭⎩，那么20212020f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭______. 【答案】2021 【解析】【分析】根据自变量范围代入对应解析式，计算再根据20212020f ⎛⎫ ⎪⎝⎭范围代入对应解析式得结果. 【详解】22211log log log 202020202020222021202111(log (1))(log )()2220202020202020202f f f f -⎛⎫⎛⎫=-===== ⎪ ⎪⎝⎭⎝⎭故答案为：2021【点睛】此题考察分段函数求值、指对数运算，考察根本分析求解才能，属根底题.15.521x x ⎛⎫+- ⎪⎝⎭的展开式中各项系数之和为______；展开式中含3x 项的系数为______〔用数字答题〕.【答案】(1).32(2).20 【解析】【分析】令1x =即得展开式中各项系数之和，先按52()1x x ⎛⎫+- ⎪⎝⎭展开，再研究展开式中各项含3x 项的系数，最后求和的结果.【详解】令1x =，那么5521232x x ⎛⎫⎪⎭= ⎝=+- 所以含3x 项的系数为0412055532101020C C C C =+=+故答案为：32，20【点睛】此题考察利用赋值法求展开式中各项系数之和、利用二项式定理求展开式中特定项系数，考察根本分析求解才能，属根底题.16.己知a ，b 为正实数，直线y =x －a 与曲线y =ln(x +b )相切于点(x 0，y 0)，那么11a b+的最小值是_______________. 【答案】4 【解析】【分析】由题意结合导数的几何意义、导数的运算可得01x b =-、00y =，进而可得1b a +=，再利用()1111a b a b a b ⎛⎫+=++ ⎪⎝⎭，结合根本不等式即可得解. 【详解】对()ln y x b =+求导得1y x b'=+，因为直线y =x －a 与曲线y =ln(x +b )相切于点(x 0，y 0)，所以011x b=+即01x b =-，所以()()00ln ln 10y x b b b =+=-+=，所以切点为()1,0b -，由切点()1,0b -在切线y =x －a 上可得10b a --=即1b a +=，所以()1111224b a a b a b a b a b ⎛⎫+=++=++≥+⎝= ⎪⎭，当且仅当12b a==时，等号成立. 所以11a b+的最小值是4. 故答案为：4.【点睛】此题考察了导数的运算、导数几何意义的应用，考察了根本不等式求最值的应用及运算求解才能，属于中档题.四、解答题：解容许写出文字说明、证明过程或者演算步骤. 17.如图，在OAB 中，P 为边AB 上的一点2BP PA =，6OA =，2OB =且OA 与OB 的夹角为60︒. 〔1〕设OP xOA yOB =+，求x ，y 的值；〔2〕求OP AB ⋅的值.【答案】〔1〕23x =，13y =；〔2〕623-.【解析】【分析】〔1〕由向量的加减运算，可得()2233=+=+=+-OPOB BP OB BA OB OA OB，进而可得答案.〔2〕用OAOB ，表示OP AB ⋅，利用向量数量积公式，即可求得结果. 【详解】〔1〕因为2BPPA =，所以23BPBA =. ()22213333OP OB BP OB BA OB OA OB OA OB =+=+=+-=+.又OP xOA xOB =-，又因为OA 、OB 不一共线，所以，23x=，13y =〔2〕结合〔1〕可得：()2133OP AB OA OB OB OA ⎛⎫⋅=+⋅- ⎪⎝⎭.22121333=⋅-+OA OB OA OB ，因为6OA =，2OB =，且OA 与OB 的夹角为60︒.所以22112162626232333OP AB⋅=⨯⨯⨯-⨯+⨯=-. 【点睛】此题考察了向量的加减运算、平面向量根本定理、向量的数量积运算等根本数学知识，考察了运算求解才能和转化的数学思想，属于根底题目.18.函数()()2101x x f x m m -=>+，且()325f =. 〔1〕求m 的值，并指出函数()y f x =在R 上的单调性〔只需写出结论即可〕；〔2〕证明：函数()f x 是奇函数；〔3〕假设()()2230f m f m +-<，务实数m 的取值范围.【答案】〔1〕2，()f x 在R 上为增函数；〔2〕证明见解析；〔3〕〔3-，1〕.【解析】【分析】〔1〕由()325f =，代入解析式，解方程求出m 的值，利用指数函数的单调性即可求解. 〔2〕利用函数的奇偶性定义即可判断. 〔3〕利用函数为奇函数，将不等式转化为()()232f m f m <-，再利用函数为增函数可得232m m <-，解不等式即可求解.【详解】〔1〕因为()325f =，所以2221315m -=+，即24m =，因为0m >，所以2m =.函数()21212121x x xf x -==-++在R 上为增函数. 〔2〕由〔1〕知()2121x xf x -=+定义域为(),-∞+∞. 对任意(),x ∈-∞+∞，都有()()211221211221x x x x xx f x f x --------====-+++. 所以函数()f x 是奇函数，〔3〕不等式()()2230f m f m +-<等价于()()223f m f m <--，因为函数()f x 是奇函数，所以()()232f m f m <-，又因为函数()f x 在R 上为增函数，所以232m m <-，即2230m m +-<.解得231m -<<.所以实数m 的取值范围为〔3-，1〕.【点睛】此题考察了利用定义判断函数的奇偶性、利用函数的单调性解不等式，考察了根本运算求解才能，属于根底题.19.HYHY 在HY 报告中指出，必须树立和践行“绿水青山就是金山银山〞的生态文明开展理念，这将进一步推动新能源汽车产业的迅速开展.以下是近几年我国某新能源乘用车的年销售量数据及其散点图：〔1〕某位同学根据以上数据和散点图，得出y 与x 的销售〔万辆〕两种回归模型①y bx a =+，②2y cx d =+，请判断哪一种模型更适宜？〔给出判断即可，不必说明理由〕〔2〕根据〔1〕的判断结果及表中数据，建立y 关于x 的回归方程，并预测2021年我国某新能源采用车的销售量(准确到).〔3〕我们可以用()()22121ˆ1ni i i ni i y yRy y ==-=--∑∑来刻画模型的拟合效果，2R 越接近于1，表示回归的效果越好，现由散点图的样本点分布，也可以认为样本点集中在曲线nx y me =的附近，用非线性回归模型求得y 关于x 的回归方程为0.90ˆ0.84x ye =，且20.9588R =.试与〔2〕中所求的回归模型比较，请用2R 说明哪种模型的拟合效果更好.附：最小二乘估计公式：()()()121ˆnii i ni i tty y bt t ==--=-∑∑，ˆˆa y bt=- 参考数据〔下面的2i ix ω=，5115i i ωω==∑〕22.72y =，()()51135.2iii x x y y =--=∑，()521374ii ωω=-=∑，()()51851.2i i i y y ωω=--=∑，()521ˆ 5.86iii y y=-=∑，()5211943i i y y =-=∑【答案】〔1〕2y cx d =+；〔2〕2ˆ 2.28 2.36y x =-，万辆；〔3〕第〔2〕问中的回归模型拟合效果更好. 【解析】【分析】〔1〕根据散点图点的分布直接判断；〔2〕先求均值，再代公式得ˆˆc d，，即得回归方程，最后把6x =代入得估计值；〔3〕根据公式先求〔2〕中所求的回归方程对应2R 值，再比较大小即可作判断. 【详解】〔1〕根据散点图，2y cx d =+更适宣作为年销量y 关于年份代码x 的回归方程；〔2〕依题意11ω=，()()()51521851.2ˆ 2.28374iii i i y y cωωωω==--==≈-∑∑， ˆˆ22.72 2.2811 2.36dy c ω=-=-⨯=-， 2ˆ 2.28 2.36 2.28 2.36yx ω=-=-，所以2ˆ 2.28 2.36yx =-. 把6x=代入，得ˆ79.72y=. 故预测2021年我国某新能源乘用车的销量为万辆.〔3〕对于〔2〕中所求得的线性回归模型，()521ˆ 5.86iii y y=-=∑，()5211943i i i y y =-=∑，()()5221521ˆ 5.86110.99701943i i i i i i y yR y y ==-=-=-≈-∑∑. 因为0.95880.9970<，所以〔2〕中的回归模型拟合效果更好.【点睛】此题考察散点图、求线性回归方程、利用线性回归方程估计、计算相关系数，考察根本分析求解才能，属中档题. 20.函数()()sin f x A x =+ωϕ，〔0A >，0>ω，2πϕ<〕的最小正周期为4π.〔1〕从①03f π⎛⎫-= ⎪⎝⎭；②2 13f π⎛⎫-=- ⎪⎝⎭；③x R ∀∈，都有()23f x f π⎛⎫≤ ⎪⎝⎭这三个条件中，选择适宜的两个条件，求函数()f x 的解析式；〔2〕求〔1〕中所求得的函数()f x 在区间2,33ππ⎡⎤-⎢⎥⎣⎦上的最大值和最小值.【答案】〔1〕()12sin 26x f x π⎛⎫=+ ⎪⎝⎭；〔2〕最小值为-1【解析】【分析】〔1〕先根据周期得ω，①或者③都能确定ϕ，所以选①②或者②③，再根据②确定A ；〔2〕先根据自变量范围得126x π+范围，再根据正弦函数性质求最值.【详解】〔1〕因为()f x 的最小正周期为4π，所以24ππω=，解得12ω=. 选①②：因为03f π⎛⎫-= ⎪⎝⎭，所以sin 06πϕ⎛⎫-+= ⎪⎝⎭，解得6k πϕπ=+，k ∈Z .因为2πϕ<，所以6π=ϕ. 又因为213f π⎛⎫-=- ⎪⎝⎭，所以sin 136A ππ⎛⎫-+=- ⎪⎝⎭，即sin 16A π⎛⎫-=- ⎪⎝⎭，所以2A =.所以()12sin 26x f x π⎛⎫=+ ⎪⎝⎭.选②③：因为x ∀∈R ，都有()23f x f π⎛⎫≤ ⎪⎝⎭，所以23x π=时，()f x 获得最大值，即sin 13πϕ⎛⎫+= ⎪⎝⎭，所以232k ππϕπ+=+，k Z ∈，所以2πϕ<，所以6π=ϕ. 又因为213f π⎛⎫-=- ⎪⎝⎭，所以sin 136A ππ⎛⎫-+=- ⎪⎝⎭，即sin 16A π⎛⎫-=- ⎪⎝⎭，所以2A =.所以()12sin 26x f x π⎛⎫=+ ⎪⎝⎭.〔2〕因为2,33x ππ⎡⎤∈-⎢⎥⎣⎦，所以1,2663x πππ⎡⎤+∈-⎢⎥⎣⎦，所以1sin 2622x π⎡⎛⎫+∈⎢ ⎪⎝⎭⎣⎦，当23xπ=-时，()f x 获得最小值为-1；当3x π=时，()f x所以()f x 获得最小值为-1【点睛】此题考察根据三角函数性质求函数解析式、根据正弦函数性质求最值，考察综合分析求解才能，属中档题.21.根据某水文观测点的历史统计数据，得到某河流每年最高水位X〔单位：米〕的频率分布表如下：将河流最高水位落入各组的频率视为概率，并假设每年河流最高水位互相HY. 〔1〕求在将来3年里，至多有1年河流最高水位[)25,29X ∈的概率；〔2〕该河流对沿河一蔬菜科植户影响如下：当[)23,25X ∈时，因河流水位较低，影响蔬菜正常灌溉，导致蔬菜干旱，造成损失；当[]29,33X ∈时，因河流水位过高，导致蔬菜内涝，造成损失.现有三种应对方案：方案一：不采取措施，蔬菜销售收人情况如下表：方案二：只建立引水灌溉设施，每年需要建立费5000元，蔬菜销售收入情况如下表；方案三：建立灌溉和排涝配套设施，每年需要建立费7000元，蔬莱销售收入情况如下表：每年的蔬菜种植本钱为60000元，请你根据三种方案下该蔬菜种植户所获利润的均值为根据，比较哪种方案较好，并说明理由.〔注：蔬菜种植户所获利润＝蔬菜销售收入－蔬菜种植本钱－建立费〕【答案】〔1〕；〔2〕方案三较好，理由见解析. 【解析】【分析】〔1〕先根据频率分布表得[)25,29X ∈的概率，再根据二项分布概率公式求结果；〔2〕先依次求出三种方案下概率分布以及数学均值，再根据大小确定选择. 【详解】〔1〕由频率分布表，得设在将来3年里，河流最高水位[)25,29X ∈发生的年数Y ，那么()3,0.8YB ~.记事件“在将来3年，至多有1年河流最高水位[)25,29X ∈〞为事件A ，那么()()()()()3201330110.80.810.80.104PA P Y P Y C C ==+==-+⨯-=.所以，在将来三年，至多有1年河流最高水位[)25,29X ∈的概率为0.104.〔2〕由题设得()29330.05P X ≤≤=.用1X ，2X ，3X 分别表示方案一、方案二、方案三的蔬菜销售收入，由题意得：1X 的分布列如下：所以()1400000.151200000.800.05102000E X =⨯+⨯+⨯=；2X 的分布列如下：所以()2700000.151200000.800.05106500E X =⨯+⨯+⨯=；3X 的分布列如下：所以()3700000.151200000.8700000.05110000E X =⨯+⨯+⨯=.设三种方案下蔬菜种植户所获利润分别为1Y ，2Y ，3Y ，那么1160000Y X =-，2265000Y X =-，3367000Y X =-，所以()()116000042000E Y E X =-=，()()226500041500E Y E X =-=，()()336700043000E Y E X =-=.因为()()()213E Y E Y E Y <<，所以采取方案三利润的均值最大，故方案三较好.【点睛】此题考察概率分布与数学期望、二项分布概率公式，考察根本分析求解才能，属中档题.22.函数()cos x f x e x -=-.〔1〕求函数()f x 在[],2ππ上的最大值；〔2〕讨沦函数()f x 在区间()0,2π上的零点的个数.【答案】〔1〕1e π-+；〔2〕2. 【解析】【分析】〔1〕求出导函数，判断出函数的单调性，利用单调性即可求出最值.〔2〕求出导函数，利用导数判断函数的单调性，再利用零点存在性定理判断函数的零点即可.【详解】〔1〕()sin x f x e x -'=-+，当[],2x ππ∈时，sin 0x ≤，0x e --<，所以()0f x '<，即函数()f x 在[],2ππ上是减函数.所以，当xπ=时，()f x 取最大值()1f e ππ-=+. 〔2〕因为()sin x f x e x -'=-+， ①当[),2x ππ∈时，由〔1〕知()f x 在[),2ππ上单调递减. 因为()10f e ππ-=-+>，()2210f e ππ-=-<，所以()f x 在[),2ππ有唯一零点.②当()0,x π∈时，令()()sin x x f x e x ϕ-'==-+，那么()cos x x e x ϕ-'=+在()0,π为减函数. 因为202e ππϕ-⎛⎫'=> ⎪⎝⎭，()10e πϕπ-'=-<，所以0,2x ππ⎛⎫∃∈ ⎪⎝⎭，使得()00x ϕ'=，所以当()00,x x ∈时，()0x ϕ'>，()f x '单调递增；当()0,x x π∈时，()0x ϕ'<，()f x '单调递减；所以()20102f x f e ππ-⎛⎫''>=-> ⎪⎝⎭，因为()010f '=-<.()f e ππ-'=-<0. 所以10,2x π⎛⎫∃∈ ⎪⎝⎭，()10f x '=；2,2x ππ⎛⎫∃∈ ⎪⎝⎭，()20f x '=. 当()10,x x ∈时，()0f x '<，函数()f x 单调递减；当()12,x x x ∈时，()0f x '>，函数()f x 单调递增；当()2,x x π∈时，()0f x '<，函数()f x 单调递减；又()00f =，所以()10f x '<.而()2202f x f e ππ-⎛⎫>=> ⎪⎝⎭，()10f e ππ-=+>. 所以()f x 在()10,x 上无零点；在()12,x x 上有唯一零点；在()2,x π上无零点。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

孝感高中2009—2010学年度下学期高二期末考试数学（文）一、选择题（本大题共10个小题，每小题5分，共50分，每小题的四个选项中，只有一个符合题目要求。

）1.先后抛掷2枚均匀硬币，出现2枚反面的概率是（） A.1B.14C.13D.122.在正方体ABCD —1111A B C D 中，1A B 与CD 所成的角为（）A.90°B. 60°C.45°D.30°3.若771111=+yx C C C ,则x ,y 的值分别是（） A.126==x ,y B.117==x ,y C.116==x ,y D.127==x ,y4.以正方体的顶点为顶点的三棱锥的个数是（）A.1387C CB.48CC.48C —6D.48C —125.某校高一、高二、高三三个年级的学生数分别为1500人、1200人和1000人，现采用按年级分层抽样法了解学生的视力状况，已知在高一年级抽查了75人，则这次调查三个年级共抽查了（） A.185人 B.180人 C.182人 D.190人 6.函数322()=--+f x x ax bx a 在1=x 时有极值10,则a ,b 的值为（） A.33=⎧⎨=-⎩a b 或411a b =-⎧⎨=⎩B.41=-⎧⎨=⎩a b 或411=-⎧⎨=⎩a bC.15=-⎧⎨=⎩a bD.以上都不对7.从0，1，2，3，4，5，6，7，8，9十个数字中，选出一个偶数和三个奇数，组成一个没有重复数字的四位数，这样的四位数共有（） A.1480个 B.1440个 C.1200个 D.1140个8.某班有48名学生，某次数学考试，算术平均分为70分，方差为s ,后来发现成绩记录有误，某甲得80分却误记为50分，某乙得70分却误记为100分，更正后计算得方差为1s ，则1s 与s 的大小关系为（） A.1<s s B.1s s >C.1=s sD.1s 与s 的大小关系不确定9.如图，在半径为3的球面上有A,B,C 三点，90∠=︒=ABC ,BA BC ，球心O到平面ABC ,则B,C 两点的球面距离是（） A 3πB.πC.43πD.2π10.考察正方体6个面的中心，甲从这6个点中任意选两个点连成直线，乙也从这6个点任意选两个点连成直线，则所得的两条直线相平行但不重合的概率等于（） A.175B.275C.375D.475二、填空题（本大题共5小题，每小题5分，共25分。

请把答案填在题中的横线上。

）11.在(12)n x -的展开式中，各项系数的和是 .12.正方形的面积与其水平放置的直观图的面积的比为 . 13. 已知曲线33=+y |x |x ，则曲线在点(2,2)--A 处的切线方程为 .14.某铁路货运站对6列电煤货运列车进行编组调度，决定将这6列列车编成两组，每组3列，且甲、乙两列列车不在同一小组。

如果甲所在小组的3列列车先开出，那么这6列列车先后不同的发车顺序共有__________________种。

（用数字作答）15.已知菱形ABCD 的角A 是60°，将菱形ABCD 沿对角线BD 折成直二面角A —BD —C ，有如下四个结论：①⊥AC BD ；②AB 与平面BCD 成60°的角；③AB 与CD 所成角为60°；④二面角B —AC —D 的大小为90°，其中所有正确的结论的序号是 .三、解答题（本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤.） 16. （本小题满分12分）如图所示，在一段线路中并联着3个自动控制的常开开关，只要其中有1个开关能够闭合，线路就能正常工作.假定在某段时间内每个开关能够闭合的概率都是0.7,计算在这段时间内线路正常工作的概率.17. （本大题满分12分）已知8()-ax x的展开式中常数项为1120.（Ⅰ）求实数a 的值;（Ⅱ）求二项展开式中含2x 的项.18.（本小题满分12分）用边长为60cm 的正方形铁皮做一个无盖水箱，先在四角截去一个小正方形，然后把四边翻转90°角，再焊接而成（如图所示）.水箱底边的长取多少时，水箱容积最大？最大容积是多少？在某农场棉花试验基地，抽样测得某品种棉花纤维的纤度（表示纤维粗细的一种量）共有100个数据，将这些数据分组如右表：（Ⅰ）请补全答卷上的频率分布表和频率分布直方图；（Ⅱ）估计纤度落在[1.34,1.46)中的概率及纤度不小于1.42的概率是多少？（Ⅲ）统计方法中，同一组数据常用该组区间的中点值（例如，[1.30,1.34)）的中点值是1.32)作为代表，据此，估计这块棉花试验基地的棉花纤维纤度的平均值（结果精确到0.01）.20.（本小题满分13分）△ABC 和△DBC 所在平面互相垂直，且(0)===>AB BC BD a a ,120∠=∠=CBA D BC °,求：（Ⅰ）AD 的连线和平面BCD 所成的角；（Ⅱ）AD 的连线与直线BC 所成的角；（Ⅲ）是否存在实数a ,使二面角A —BD —C 为arctan2π-,若存在，求出所有a 的值;若不存在，请说明理由.21.（本小题满分14分）已知函数32()4()=-+-∈R f x x ax a .若函数()=y f x 的图象在点P （1，f (1)）处的切线的倾斜角为4π. （Ⅰ）求a ;（Ⅱ）设()f x 的导数函数是()'f x .若m ,n [1,1]∈-,求()()'+f m f n 的最小值; （Ⅲ）就实数m 的值，讨论关于x 的方程()=f x m 的解的个数.孝感高中2009~2010学年度下学期高二期末考试数学（文）参考答案二、填空题：11.(1)-n12.13. 9160-+=x y 14. 21615. ①②三、解答题:16.分别记这段时间内开关,,A B C J J J 能够闭合为事件A ，B.由题意，这段时间内3个开关是否能够闭合相互之间没有影响.………………………………………………………………（2分） ∴这段时间内3个开关都不能闭合的概率是()()()()= P A B C P A P B P C ………………………………………………………………（6分）=[1()][1()][1()]---P A P B P C (10.7)(10.7)(10.7)0.027=---=…………………………（9分）于是这段时间内至少有1个开关能够闭合，从而使线路能正常工作的概率是 1()10.0270.973-=-= P A B C …………………………………………………………（11分）答：在这段时间内线路正常工作的概率是0.973.……………………………………（12分） 17.解：（Ⅰ）设通项为882188()()--+=-=- r r r r r r r a T C x a C xx,………………………（2分）令820-=r ,则4=r ,所得的项为常数项，即448()1120,-=a C 解得2=±a ;…………………………………………………………（6分）（Ⅱ）在通项中令822,3-=∴=r r ……………………………………………………（8分）若2=-a ,则所求的项为332318()+=- T a C x ,即2448x …………………………………（10分）若2=a ,则所求的项为332318()+=- T a C x ,即2448-x .…………………………………（12分）18.解：设水箱底边长为x cm ，则水箱高（单位：cm ）602xh -=………………（2分）水箱容积（单位：cm 3）23260()(060)2x x V V x x h x -===<<……………………（5分）得23()602V x x x '=-.令()0V x '=,即236002x x -=,解得10x =（不合题意，舍去），240.x =……………（7分）当x 在（0，60）内变化时，导数()V x '的正负如下表.因此在40x =处，函数()V x 取得极大值，并且这个极大值就是函数()V x 的最大值.……（9分）将40x =代入()V x ，得最大容积2604040160002V -=⨯=.………………………………（11分）答：水箱底边长取40 cm 时，容积最大.最大容积为16000 cm 3.………………………（12分） 19.解：注：填正确频率分布表与频率分布直方图分别得2分，3分.（纵坐标填对得2分）（Ⅱ）纤度落在[1.34,1.46)中的概率估计为 0.16+.132+0.24=0.72; 纤度不少于1.42的概率为0.24+0.16+0.08=0.48.…………（9分）（Ⅲ）由1.32×0.04+1.36×0.16+1.40×0.32+1.44×0.24+1.48×0.16+1.52×0.08≈1.42即估计这块棉花试验基地的棉花纤维纤度的平均值为 1.45……………………………（12分）20. （Ⅰ）解：过A 作BC 的反向延长线的垂线，交于点E ，连ED ，∵面ACB BCD ⊥面，∴AE ⊥面BCD∴ADE ∠为AD 与平面BDC 所成角.……………………（2分）又,120AB BC BD ABC CBD ==∠=∠=︒ ∴2ACAE ED ==.∴45AD E ∠=︒.…………………………（4分）（Ⅱ）解法1：∵()AD BC BD BA BC =- 0BD BC BA BC =-=.解法2：过D 作EC 的平行线与过C 平行于ED 的直线交于F. 由（1）知，EDFC 为矩形,∵DF DE ⊥,∴DF AD ⊥，即BC AD ⊥.…………………………………………（7分）（Ⅲ）当0a >时，使二面角A —BD —C 为arctan2π-，证明如下.……………………（8分）过E 作EG BD ⊥于G ，连结AG.由三垂线定理知，AG BD ⊥.∴AGE ∠是二面角A —BD —E 的平面角……………（10分）由EG BD BE ED = ,可知EG,AE == 在Rt △AEG 中，tan 2,arctan 2AGE AGE ∠=∠=.∴当0a >时，二面角A —BD —C 的度数为arctan2π-.…………………………（13分）1 24 6 821.解：（Ⅰ）2()32f x x ax '=-+.………………………………………………………………（1分）据题意，(1)tan 14f π'==,∴321a -+=,即2a =.…………………………………（3分）（Ⅱ）由（Ⅰ）知322()24,()34f x x x f x x x '=-+-=-+，由()0,'=f x 有0=x 或43=x .∴对于[1,1],()m f m ∈-的最小值为(0)4f =-.…………………………………………（6分） ∵2()34f x x x '=-+的对称轴为23x =，且抛物线开口向下.∴[1,1]x ∈-时，()f x '最小值为(1)f '-与(1)f '中较小的. ∵(1)1,(1)7f f ''=-=-，∴当[1,1]x ∈-时,()f x '的最小值为7-,∴当[1,1]n ∈-时，()f n '的最小值为7-……（7分） ∴()()f m f n '+的最小值，值为11-…………(8分) （Ⅲ）由（Ⅰ）求得476(0)4,()327f f =-=-.……（10分）依题意可画出函数()y f x =草图，得：当7627m >-或4m <-时，方程有一解; ……（12分）当76427m -<<-时，方程有三解; 当7627m =-或4m =-时，方程有两解. ………(14分)。

高二数学下册期末联考检测试题10

合集下载

浙江省宁波市九校高二下学期期末联考数学试卷-含答案

2024河南省新未来高二下学期7月期末联考数学试题及答案

浙江省温州市十校联合体2022-2023学年高二下学期期末联考数学试题高二数学试题

广东省四校(华附、省实、广雅、深中)2023-2024学年高二下学期期末联考数学试题(解析版)

青海省部分名校2023-2024学年高二下学期期末联考数学试题(含答案)

高二数学下学期期末考试试题理含解析试题 10

福建省福州市八县(市)协作校2023-2024学年高二下学期期末联考试题数学含答案

浙江省宁波市九校2022-2023学年高二下学期期末联考数学试题(解析版)

高二数学下学期期末联考试题

高二数学下学期期末考试试题含解析试题 10

文档推荐

最新文档

高二数学下册期末联考检测试题10

合集下载

浙江省宁波市九校高二下学期期末联考数学试卷-含答案

2024河南省新未来高二下学期7月期末联考数学试题及答案

浙江省温州市十校联合体2022-2023学年高二下学期期末联考数学试题高二数学试题

广东省四校(华附、省实、广雅、深中)2023-2024学年高二下学期期末联考数学试题(解析版)

青海省部分名校2023-2024学年高二下学期期末联考数学试题(含答案)

高二数学下学期期末考试试题理含解析试题 10

福建省福州市八县(市)协作校2023-2024学年高二下学期期末联考试题 数学含答案

浙江省宁波市九校2022-2023学年高二下学期期末联考数学试题(解析版)

高二数学下学期期末联考试题

高二数学下学期期末考试试题含解析 试题 10

文档推荐

最新文档

福建省福州市八县(市)协作校2023-2024学年高二下学期期末联考试题数学含答案

高二数学下学期期末考试试题含解析试题 10