理论力学 第四章 平面任意力系

理论力学第2版(唐国兴王永廉主编)课后答案理论力学第2版内容简介第2版前言第1版前言第一章静力学基础知识要点解题方法难题解析习题解答第二章平面汇交力系知识要点解题方法难题解析习题解答第三章力矩、力偶与平面力偶系知识要点解题方法习题解答第四章平面任意力系知识要点解题方法难题解析习题解答第五章空间力系知识要点解题方法习题解答第六章静力学专题知识要点解题方法习题解答第七章点的运动学知识要点解题方法难题解析习题解答第八章刚体的基本运动知识要点解题方法习题解答第九章点的合成运动知识要点解题方法难题解析习题解答第十章刚体的平面运动知识要点解题方法难题解析习题解答第十一章质点动力学基本方程知识要点解题方法难题解析第十二章动量定理知识要点解题方法难题解析习题解答第十三章动量矩定理知识要点解题方法难题解析习题解答第十四章动能定理知识要点解题方法难题解析习题解答第十五章动静法知识要点解题方法习题解答参考文献理论力学第2版目录机械工业出版社本书是与唐国兴、王永廉主编的《理论力学》(第2版)配套的教学与学习指导书。

本书按主教材的章节顺序编写，每章分为知识要点、解题方法、难题解析与习题解答四个部分。

其中，“知识要点”部分提纲挈领地对该章的基本概念、基本理论和基本公式进行归纳总结，以方便读者复习、记忆和查询;“解题方法”部分深入细致地介绍解题思路、解题方法和解题技巧，以提高读者分析问题和解决问题的能力;“难题解析”部分精选若干在主教材的例题与习题中没有涉及的典型难题进行深入分析，以拓展读者视野，满足读者深入学习的需要;“习题解答”部分对主教材中该章的全部习题均给出求解思路和答案，但不提供详细解题过程，以期在帮助读者自主学习和练习的同时为他们留出适量的思考空间。

本书继承了主教材的风格特点，结构严谨、层次分明、语言精练、通俗易懂。

本书虽与主教材配套，但其结构体系完整，亦可单独使用。

本书可作为应用型本科院校与民办二级学院工科各专业学生的.学习和应试指导书，同样适合高职高专、自学自考和成人教育的学生使用，对考研者、教师和工程技术人员也是一本很好的参考书。

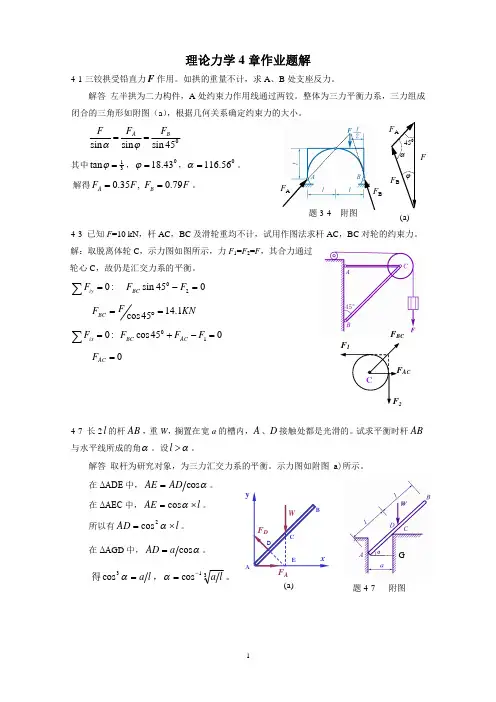
理论力学4章作业题解4-1三铰拱受铅直力F 作用。

如拱的重量不计，求A 、B 处支座反力。

解答 左半拱为二力构件，A 处约束力作用线通过两铰。

整体为三力平衡力系，三力组成闭合的三角形如附图（a ），根据几何关系确定约束力的大小。

45sin sin sin B A F F F ==j a其中31tan =j ，043.18=j ，056.116=a 。

解得F F F F B A 79.0 ,35.0==。

4-3 已知F =10 kN ，杆AC ，BC 及滑轮重均不计，试用作图法求杆AC ，BC 对轮的约束力。

解：取脱离体轮C ，示力图如图所示，力F 1=F 2=F ，其合力通过轮心C ，故仍是汇交力系的平衡。

:0=åiyF 045sin 20=-F F BCKN FF BC 1.1445cos =°=045cos :010=-+=åF F F FAC BC ix0=AC F4-7 长2l 的杆AB ，重W ，搁置在宽a 的槽内，A 、D 接触处都是光滑的。

试求平衡时杆AB 与水平线所成的角a 。

设a >l 。

解答 取杆为研究对象，为三力汇交力系的平衡。

示力图如附图(a)所示。

在ΔADE 中，a cos AD AE =。

在ΔAEC 中，l AE ´=a cos 。

所以有l AD ´=a 2cos 。

在ΔA GD 中，a cos a AD =。

得a =a 3cos ，31cosl a -=a 。

F BCAC题3-4 附图F BF AF BF AFa45j(a)A (a)题4-7 附图G4-9 AB ，AC ，AD 三连杆支撑一重物，如图所示。

已知W=10kN ，AB =4m ，AC =3 m ，且ABEC 在同一水平面内，试求三连杆所受的力。

解：取铰A 研究，示力图如图示，为汇交力系的平衡。

0=åix F ： 05430sin =´°+AD AB F F 0=åiy F ： 05330sin =´°+AD AC F F 0=åiZF： 030cos =-°W F AD联立求解KNF KNF KN F AD AC AB 5.115.36.4=-=-=4-8 图示结构上作用一水平力F 。

理论力学(40)-答案第一篇静力学第一章静力学的基本量与计算1-1判断题（1）由力的解析表达式F=F某i+Fyj+Fzk能确定力的大小、方向和作用线。

（√）（2）力在空间直角坐标轴上的投影和此力沿该轴的分力相同。

（某）（3）合力一定比分力大。

（某）（4）合力对于某一轴之矩，等于力系中所有力对同一轴之矩的代数和。

（√）（5）力矩和力偶矩相同。

（某）（6）力偶矩矢是自由矢量，力对点的矩矢也是自由矢量。

（某）（7）位于两相交平面内的两力偶能等效组成平衡力系。

（某）（8）空间力偶对坐标轴之矩等于力偶矩矢在坐标轴上的投影。

（√）（9）力偶不能合成为合力，也不能与力等效。

（√）（10）力偶中两个力在任一轴上投影的代数和可以不等于零。

（某）1-2已知力F沿六面体一个面的对角线AD作用，且F1000N。

则该力在某轴上的投影为0N，力在y轴上的投影为5003N，力在z轴上的投影为500N。

zzDF10cmyAFO某yA某O103cm10cmD1-3在边长为a的正方体内，沿对角线DA方向作用一个力F。

该力对某轴的力矩为3Fa3对z轴的力矩0对O点力矩大小为6Fa31-4水平圆盘的半径为r，外缘C处作用有已知力F。

力F位于圆盘C 处的切平面内，且与C处圆盘切线夹角为60，尺寸如图所示。

求力F对某，y，z轴之矩。

or3r,h)解：力F的作用点C的坐标为(,22力F沿三个坐标轴的投影为：3F某Fco600in600F41FyFco600co600F43FzFin600F2则有：zBFO60r30Chy某331Fr(F)h(F)(h3r)22443r33FMyzF某某FzhF(F)(rh) 4224r133FrMz某FyyF某(F)rF24242M某yFzzFyoAo1-5已知：F100N，30，60，求力F在某，y，z轴上的投影以及力F对某，y，z轴之矩。

解：力F在某，y，z轴上的投影为zF某Finco25NFyFco503NFzFinin253N力F对某，y，z轴之矩为某F2myM某2532503NmMy0Mz25250Nm21-6已知：F102kN，M5kNm，求图示力系对某，y，z轴之矩。

四、平面任意力系试用力系向已知点简化的方法说明图所示的力F 和力偶(F 1，F 2)对于轮的作用有何不同？在轮轴支撑A 和B 处的约束反力有何不同？设F 1=F 2=F /2，轮的半径为r 。

[答]：考虑约束，则力和力偶对轮的作用相同；而A 处的约束反力大小等于F ，B 处的约束反力大小等于0。

怎样判定静定和静不定问题？图中所示的六种情况那些是静定问题，那些是静不定问题？为什么？静定问题： (c)、(e)静不定问题：(a)、(b)、(d)、(f)FFF(d)(e) (f)PP 1=150N ，P 2=200N ，P 3=300N ，。

力偶的臂等于8cm ，力偶的力F =200N 。

试将平面力系向O [解]X X X X R X 6.4373005220010115022321-=⨯-⨯-⨯-=++==∑Y Y Y Y R Y .1613005120010315022321-=⨯+⨯-⨯-=++==∑合力R 大小为：N R R R Y X 5.466)6.161()6.437(2222=-+-=+=方向： ︒===3.2037.0arctg R R arctgXYα 合力偶矩大小为：Nm F M M O O 44.2108.02002.0513001.022150)(=⨯-⨯⨯+⨯⨯==∑ 与原点距离为： cm RM dO96.45==A 点之矩。

[解](a) 对A 点之矩为: (b) 对A 点之矩为:(c) 对A 点之矩为：22121qaaqa M A -=⨯-=2313221qLLqL M A -=⨯-=2211221)2(61)(3121L q qLq q L q M A +-=---=(a)求下列各梁和刚架的支座反力，长度单位为m 。

[解](a)AB 梁受力如图(a)所示：045cos 2:0=︒⨯+=∑A X X ∑=︒⨯-+=045sin 2:0B A N Y Y∑=⨯︒⨯-⨯+-=0645sin 245.1:0B AN M联立方程组可解得：;KN 50.2;KN 09.1;KN 41.1=-=-=B A A N Y X(b)AB 梁受力如图(b)所示:∑==0:0A X X∑=⨯⨯--+=031212:0BA N Y Y ∑=⨯⨯⨯-⨯+⨯=013121212:0BA N M 解得：;KN 25.0;KN 75.3;KN 0-===B A A N Y X(C)AC 梁受力如图(c)所示:∑==0:0A X X∑=-⨯-=0534:0A Y Y∑=⨯⨯-⨯-=05.13435:0A AM M由上述方程可解得：;KNm 33;KN 17;KN 0===A A A M Y XG =1.8KN ，其它重量不计，求铰链A 的约束反力和杆BC 所受的力。

理论力学平面任意力系的平衡条件及方程一、平面任意力系的平衡条件平面任意力系平衡的必要和充分条件为：力系的主矢和对任一点的主矩M O 都等于零，F R'=M O =∑M O (F i )二、平面任意力系的平衡方程∑F ix =0∑F iy =0∑M (F )=0O i ⎧⎪⎨⎪⎩⎧∑F x =0⎨∑M A (F )=0⎩∑M B (F )=0条件：x AB⎪⎪⎧∑M A (F )=0⎨∑M B (F )=0⎩∑M C(F )=0条件：A ，B ，C 点⎪⎪上式只有 个独立方程，只能求出 个未知数。

[例]求图示刚架的约束力。

解：以刚架为研究对象，受力如图。

q∑F x =0:F Ax -qb =0∑F y =0:F Ay -F =0∑M A (F )=0:M -Fa -1qb 2=02=qb A解 ：F Ax F Ay =F 212A M =Fa +qbq[例]求图示梁的支座约束力。

解：以梁为研究对象，受力如图。

∑F x =0:F Ax +F cos θ=0∑F y =0:F Ay +F B -F sin θ=0∑M A (F )=0:F B a -F sin θ⋅(a +b )-M =0解 ：=-F cos θF Ax =M +F sin θ(a +b )aB F =-M +Fb sin θAyFa[例] 外伸梁的尺寸及载荷如图所示，F 1=2 kN ，F 2=1.5 kN ，M =1.2 kN·m ， l 1=1.5 m ，l 2=2.5 m ，试求铰支座A 及支座B 的约束力。

60解：1、 梁为研究对象，受力分 如图2、 平衡方程3、解方程∑MA(F )=0F B l 2-M -F 1l 1-F 2(l 1+l 2)sin60=Fx=0F Ax -F 2cos ∑60=0=0∑FyF Ay +F B -F 1-F 2sin 60=0=0.75kN F =3.56kN=-0.261kNF Ax B F Ay[例]悬臂吊车如图所示。