二进制与十进制相互转化

二进制八进制十进制十六进制之间的进制转换详情可参考百度百科：进制转换这个词条【主要搞懂1和2两条，其他的进制之间的转化就迎刃而解，很好懂了】1. 十进制-> 二进制：将这个十进制数连续除以2的过程，第一步除以2，得到商和余数，将商再继续除以2，得到又一个商和余数，直到商为0。

最后将所有余数倒序排列，得到的数就是转换成二进制的结果。

2. 二进制-> 十进制：二进制数第1位的权值是2的0次方，第2位的权值是2的1次方，第3位的权值是2的2次方。

（例如1258这个十进制数，实际上代表的是：1x1000+2x100+5x10+8x1=1258）那么1011这个二进制数，实际上代表的是：1x8+0x4+1x2+1x1=11（十进制数11）。

（这里的8就是2的3次方，4就是2的2次方，2就是2的1次方，1就是2的0次方）3. 十进制-> 八进制：十进制数转换成八进制的方法，和转换为二进制的方法类似，唯一变化：除数由2变成8。

4. 八进制-> 十进制和转换为二进制的方法类似，唯一变化是，底数变成8，第1位表示8的0次方，第二位表示8的一次方，第三位表示8的2次方，第四位表示8的3次方。

例如1314这个八进制数，十进制数就是1x512+3x64+1x8+4x1=716（十进制）5. 十进制-> 十六进制10进制数转换成16进制的方法，和转换为2进制的方法类似，唯一变化：除数由2变成16。

十六进制是0123456789ABCDEF这十六个字符表示。

那么单独一个A就是10，单独一个B就是11，CDEF，就分表表示12，13，14，15。

而10这个十六进制数，实际就是十进制中的16。

6. 十六进制-> 十进制和转换为二进制的方法类似，唯一变化是，底数变成16，第1位表示16的0次方，第二位表示16的一次方，第三位表示16的2次方，第四位表示16的3次方。

7. 二进制<--->八进制，之间的相互转换，更简单一些，因为8本身是2的三次方。

二进制数与十进制数转换概述及解释说明1. 引言1.1 概述本文将会讨论二进制数与十进制数之间的转换方法及相关概念。

在计算机科学中，二进制和十进制是最常用的数字表示方式。

二进制由两个数字0和1组成，而十进制则由0到9的十个数字组成。

了解这两种表示方法以及它们之间的转换过程对于理解计算机编程和数据处理非常重要。

1.2 文章结构这篇文章分为五个主要部分。

首先，我们将介绍二进制数和十进制数的基本概念，包括定义和表示方法。

然后，我们会详细介绍将二进制数转换为十进制数的方法，并提供简单示例和步骤说明以帮助读者更好地理解。

接着，我们会介绍一种称为进位计算法的具体转换方法，并通过演示加深对其原理的理解，并举例说明其在实际应用场景中的意义。

1.3 目的本文旨在帮助读者全面了解二进制数与十进制数之间的转换过程，并能够掌握相关方法和技巧。

通过学习这些知识，读者将能够更好地理解计算机中数字的表示和运算方式，提升对计算机科学的理解和应用能力。

此外，本文还会探讨二进制与十进制转换在计算机科学中的重要性，并提供一些优化或改进建议，以扩展读者的思考。

2. 二进制数与十进制数的基本概念2.1 二进制数的定义和表示方法:二进制数是一种以2为基数的计数系统，只使用两个数字0和1来表示所有的数值。

在二进制中，每一位上的数字称为比特（bit）。

比特代表了数字的位置权值，从右往左依次增加。

例如，一个八位二进制数可以表示0到255之间的整数。

2.2 十进制数的定义和表示方法:十进制是我们常用的计数系统，它使用10个数字0-9来表示所有的数值。

在十进制中，每一位上的数字代表了10的不同次幂，并且从右往左依次增加。

例如，一个三位十进制数可以表示从0到999之间的整数。

总结：二进制和十进制是两种常见而重要的计数系统。

理解它们之间的差异以及如何进行转换对于学习计算机科学和编程非常关键。

接下来我们将详细介绍如何将二进制转换为十进制以及如何将十进制转换为二进制。

二进制,八进制,十进制，十六进制之间的相互转换和相关概念二进制:计算机只认识0或1,也就是高电平和低电平.所以所有的数据格式最终会转化为2进制形式,计算机硬件才能识别。

二进制逢二进一,八进制逢八进一,十进制逢十进一，十六进制逢十六进一。

下边是各进制之间的转换公式.二进制转十进制0110 0100(2) 换算成十进制第0位 0 * 2^0 = 0第1位 0 * 2^1 = 0第2位 1 * 2^2 = 4第3位 0 * 2^3 = 0第4位 0 * 2^4 = 0第5位 1 * 2^5 = 32第6位 1 * 2^6 = 64第7位 0 * 2^7 = 0 ＋---------------------------100二进制转八进制可采用8421法1010011(2)首先每三位分割即: 001,010,011不足三位采用0补位.然后采用8421法: 001=1010=2011=3所以转换成8进制是123二进制转十六进制1101011010100(2)首先每四位分割即: 0001,1010,1101,0100不足四位采用0补位.然后采用8421法: 0001:11010:A1101:D0100:4所以转换成十六进制是1AD4十六进制当数字超过9后将采用A代替10,B代替11,C代替12,D代替13,E 代替14,F代替15;下边是十进制的各种转换:十进制转二进制6(10)10进制数转换成二进制数，这是一个连续除2的过程：把要转换的数，除以2，得到商和余数，将商继续除以2，直到商为0。

最后将所有余数倒序排列，得到数就是转换结果。

商余数6/2 3 03/2 1 11/2 0 1最后把余数从下向上排列写出110即是转换后的二进制.十进制转换八进制10进制数转换成八进制数，这是一个连续除8的过程：把要转换的数，除以8，得到商和余数，将商继续除以8，直到商为0。

最后将所有余数倒序排列，得到数就是转换结果。

120(10)商余数120/8 15 015/8 1 71/8 0 1最后把余数从下向上排列写出170即是转换后的八进制.十进制转换十六进制10进制数转换成十六进制数，这是一个连续除16的过程：把要转换的数，除以16，得到商和余数，将商继续除以16，直到商为0。

二进制和十进制之间的转换方法
二进制和十进制之间的转换方法如下：
1. 二进制转十进制：
- 二进制数的每一位按权展开，从右到左分别为2的0次方、2的1次方、2的2次方...
- 将每一位乘以对应的权重，并将结果相加即可得到十进制数。

例如，将二进制数1101转换为十进制数：
1 * 2^3 + 1 * 2^
2 + 0 * 2^1 + 1 * 2^0 = 13
2. 十进制转二进制：
- 将十进制数不断除以2，每次取余数，直到商为0为止。

- 将得到的余数从下往上排列即可得到二进制数。

例如，将十进制数26转换为二进制数：
26 / 2 = 13 0
13 / 2 = 6 (1)
6 / 2 = 3 0
3 / 2 = 1 (1)
1 / 2 = 0 (1)
所以，26的二进制表示为11010。

以上就是二进制和十进制之间的转换方法。

二进制转化规则在计算机科学中，二进制是一种非常常用的数制，它由0和1组成，具有简洁、运算规则简单、适合逻辑运算等特点。

在计算机内部，所有的信息都被表示为二进制形式。

然而，在实际应用中，我们经常需要将十进制数转换为二进制数，或者将二进制数转换为十进制数。

本文将介绍二进制转化的规则。

一、十进制转二进制将十进制数转换为二进制数的方法是采用“除2取余法”。

具体步骤如下：1. 将十进制数的整数部分除以2，得到商和余数（1或0）；2. 将商再次除以2，得到新的商和余数；3. 重复上述步骤，直到商为0为止；4. 将每一步的余数从低位到高位依次排列，即为该十进制数的二进制表示。

例如，将十进制数23转换为二进制数的过程如下：23 ÷ 2 = 11 余 111 ÷ 2 = 5 余 15 ÷ 2 = 2 余 12 ÷ 2 = 1 余 01 ÷2 = 0 余 1将每一步的余数从低位到高位依次排列，得到23的二进制表示为10111。

二、二进制转十进制将二进制数转换为十进制数的方法是采用“乘权求和法”。

具体步骤如下：1. 从二进制数的最低位开始，每个位上的数字乘以该位的权值（2的幂次方），得到每个位的值；2. 将每个位的值相加，得到该二进制数的十进制表示。

例如，将二进制数10111转换为十进制数的计算过程如下：1×2^4 + 0×2^3 + 1×2^2 + 1×2^1 + 1×2^0 = 23因此，二进制数10111等于十进制数23。

三、注意事项在进行二进制转化时，需要注意以下几点：1. 在不同的场合下，二进制数的表示可能采用不同的基数和字母表示。

例如，在计算机科学中，常用的基数为2，字母表示为0和1；而在物理学中，常用的基数为8，字母表示为0、1、2、3、4、5、6和7。

因此，在进行转换时，需要明确所采用的基数和字母表示；2. 在进行转换时，需要注意进位或借位的处理。

二进制,八进制,十进制，十六进制之间的相互转换和相关概念二进制:计算机只认识0或1,也就是高电平和低电平.所以所有的数据格式最终会转化为2进制形式,计算机硬件才能识别。

二进制逢二进一,八进制逢八进一,十进制逢十进一，十六进制逢十六进一。

下边是各进制之间的转换公式.二进制转十进制0110 0100(2) 换算成十进制第0位0 * 2^0 = 0第1位0 * 2^1 = 0第2位 1 * 2^2 = 4第3位0 * 2^3 = 0第4位0 * 2^4 = 0第5位 1 * 2^5 = 32第6位 1 * 2^6 = 64第7位0 * 2^7 = 0 ＋---------------------------100二进制转八进制可采用8421法1010011(2)首先每三位分割即: 001,010,011不足三位采用0补位.然后采用8421法: 001=1010=2011=3所以转换成8进制是123二进制转十六进制1101011010100(2)首先每四位分割即: 0001,1010,1101,0100不足四位采用0补位.然后采用8421法: 0001:11010:A1101:D0100:4所以转换成十六进制是1AD4十六进制当数字超过9后将采用A代替10,B代替11,C代替12,D代替13,E代替14,F代替15;下边是十进制的各种转换:十进制转二进制6(10)10进制数转换成二进制数，这是一个连续除2的过程：把要转换的数，除以2，得到商和余数，将商继续除以2，直到商为0。

最后将所有余数倒序排列，得到数就是转换结果。

商余数6/2 3 03/2 1 11/2 0 1最后把余数从下向上排列写出110即是转换后的二进制.十进制转换八进制10进制数转换成八进制数，这是一个连续除8的过程：把要转换的数，除以8，得到商和余数，将商继续除以8，直到商为0。

最后将所有余数倒序排列，得到数就是转换结果。

120(10)商余数120/8 15 015/8 1 71/8 0 1最后把余数从下向上排列写出170即是转换后的八进制.十进制转换十六进制10进制数转换成十六进制数，这是一个连续除16的过程：把要转换的数，除以16，得到商和余数，将商继续除以16，直到商为0。

二进制数与十进制数的相互转换文章标题：深度探讨二进制数与十进制数的相互转换一、引言在日常生活和工作中，我们经常会接触到二进制数和十进制数。

二进制数是计算机中使用的一种数制，而十进制数则是我们常见的数学表示方法。

本文将深入探讨二进制数与十进制数的相互转换，帮助读者更深入地了解这两种数制的关系。

二、二进制数与十进制数的基本概念1. 二进制数的表示方法二进制数是由0和1组成的数字系统，每一位上的数称为一个二进制位。

1011表示十进制的11。

2. 十进制数的表示方法十进制数是由0到9组成的数字系统，每一位上的数表示对应的数量级。

123表示1*100 + 2*10 + 3*1。

三、二进制数转换为十进制数1. 从右向左的求和方法以二进制数1011为例，按照2的幂次方从右向左求和，即1*2^3 + 0*2^2 + 1*2^1 + 1*2^0，得到十进制数11。

2. 通用公式转换对于任意长度的二进制数，可以使用通用公式进行转换，即将每一位上的二进制数乘以2的对应次方再求和。

四、十进制数转换为二进制数1. 除2取余法以十进制数11为例，通过反复除2取余的方法可以得到二进制数1011。

即11÷2=5余1，5÷2=2余1，2÷2=1余0，1÷2=0余1。

2. 通用公式转换对于任意十进制数，同样可以使用通用公式进行转换，即反复除2取余直至商为0，再将余数倒序排列得到二进制数。

五、总结与回顾通过本文的深度探讨，我们了解了二进制数与十进制数之间的转换方法。

无论是从二进制数转换为十进制数，还是相反，都可以通过简单的算法和公式来实现。

这种转换方法在计算机领域具有重要意义，同时也有助于我们对数制间的转换有更深刻的理解。

六、个人观点与理解在我看来，二进制数与十进制数的转换虽然在表面上涉及了不同的数制与算法，但本质上都是在不同的进位制下表示和计算数值。

通过学习和掌握转换方法，我们可以更好地理解计算机运行原理，以及更灵活地处理数字计算和逻辑运算。

整数时十进制与二进制相互转换：二进制的1101转化成十进制1101（2）=1*2^0+0*2^1+1*2^2+1*2^3=1+0+4+8=13转化成十进制要从右到左用二进制的每个数去乘以2的相应次方，不过次方要从0开始。

相反，用十进制的13除以2，每除一下将余数就记在旁边，最后按余数从下向上排列就可得到1101。

由二进制数转换成十进制数的基本做法是，把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。

这种做法称为“按权相加”法。

2的0次方是12的1次方是22的2次方是42的3次方是82的4次方是162的5次方是322的6次方是642的7次方是1282的8次方是2562的9次方是5122的10次方是10242的11次方是20482的12次方是40962的13次方是81922的14次方是163842的15次方是32768有小数点的十进制与二进制之间的转换：十进制数转换为二进制数时，由于整数和小数的转换方法不同，所以先将十进制数的整数部分和小数部分分别转换后，再加以合并。

例如19.95 转2进制分为两个步骤：(1) 小数点前：19/2=9余19/2=4 余14/2=2 余02/2=1 余01/2=0 余1由下往上取余数10011(2) 小数点后0.95*2 = 1.9 取整1（1.9-1）*2 = 1.8 取整1（1.8-1）*2 = 1.6 取整1（1.6-1）*2 = 1.2 取整1（1.2-1）*2 = 0.4 取整0（0.4-0）*2 = 0.8 取整0（0.8-0）*2 = 1.6 取整1（1.6-1）*2 = 1.2 取整1假设小数精度为8位，从上往下去则小数点后为0.11110011故19.95 转化为二进制为10011.11110011整数时八进制数转换为十进制数：八进制就是逢8进1。

八进制数采用0～7这八数来表达一个数。

八进制数第0位的权值为8的0次方，第1位权值为8的1次方，第2位权值为8的2次方，以此类推。

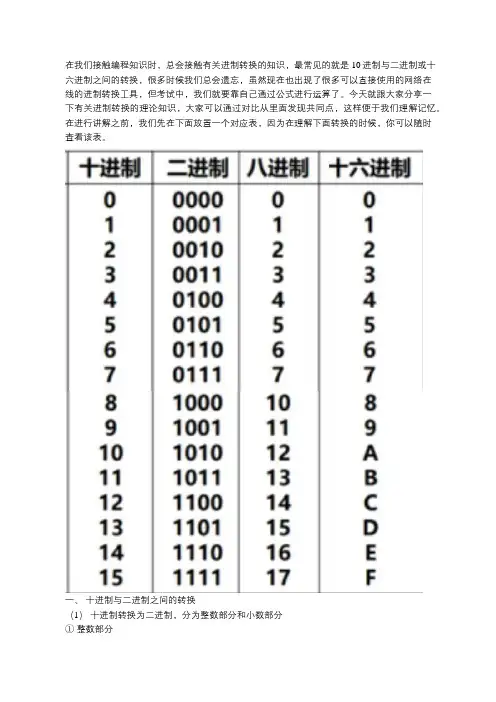
在我们接触编程知识时，总会接触有关进制转换的知识，最常见的就是10进制与二进制或十六进制之间的转换，很多时候我们总会遗忘，虽然现在也出现了很多可以直接使用的网络在线的进制转换工具，但考试中，我们就要靠自己通过公式进行运算了。

今天就跟大家分享一下有关进制转换的理论知识，大家可以通过对比从里面发现共同点，这样便于我们理解记忆。

在进行讲解之前，我们先在下面放置一个对应表，因为在理解下面转换的时候，你可以随时查看该表。

一、十进制与二进制之间的转换（1）十进制转换为二进制，分为整数部分和小数部分①整数部分方法：除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。

下面举例：例：将十进制的168转换为二进制得出结果将十进制的168转换为二进制，（10101000）2分析:第一步，将168除以2商84余数为0。

第二步，将商84除以2，商42余数为0。

第三步，将商42除以2，商21余数为0。

第四步，将商21除以2，商10余数为1。

第五步，将商10除以2，商5余数为0。

第六步，将商5除以2，商2余数为1。

第七步，将商2除以2，商1余数为0。

第八步，将商1除以2，商0余数为1。

第九步，读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，即10101000②小数部分方法：乘2取整法，即将小数部分乘以2，然后取整数部分，剩下的小数部分继续乘以2，然后取整数部分，剩下的小数部分又乘以2，一直取到小数部分为零为止。

如果永远不能为零，就同十进制数的四舍五入一样，按照要求保留多少位小数时，就根据后面一位是0还是1，取舍，如果是零，舍掉，如果是1，向入一位。

换句话说就是0舍1入。

读数要从前面的整数读到后面的整数，下面举例：例1：将0.125换算为二进制得出结果：将0.125换算为二进制（0.001）2分析：第一步，将0.125乘以2，得0.25则整数部分为0小数部分为0.25;第二步将小数部分0.25乘以2得0.5则整数部分为0小数部分为0.5;第三步将小数部分0.5乘以2得1.0则整数部分为1小数部分为0.0;第四步读数从第一位读起读到最后一位即为0.001。

二进制数转换成十进制数二进制的1101转化成十进制1101（2）=1*2^0+0*2^1+1*2^2+1*2^3=1+0+4+8=13 转化成十进制要从右到左用二进制的每个数去乘以2的相应次方不过次方要从0开始相反用十进制的数除以 2 每除一下将余数就记在旁边最后按余数从下向上排列就可得到1101或者用下面这种方法：13=8+4+0+1=8+4+1（算出等于13就行了）由二进制数转换成十进制数的基本做法是，把二进制数首先写成加权系数展开式，然后按十进制加法规则求和。

这种做法称为"按权相加"法。

例如二进制数1000110转成十进制数可以看作这样：数字中共有三个1 即第二位一个，第三位一个，第七位一个，然后十进制数即2的2-1次方+2的3-1次方+2的7-1次方即2+4+64=70 次方数即1的位数减一。

2的0次方是1 2的1次方是2 2的2次方是4 2的3次方是8 2的4次方是16 2的5次方是32 2的6次方是64 2的7次方是128 2的8次方是256 2的9次方是512 2的10次方是1024 2的11次方是2048 2的12次方是4096 2的13次方是8192 2的14次方是16384 2的15次方是32768 2的16次方是65536 2的17次方是131072 2的18次方是262144 2的19次方是524288 2的20次方是1048576编辑本段十进制数转换为二进制数十进制数转换为二进制数时，由于整数和小数的转换方法不同，所以先将十进制数的整数部分和小数部分分别转换后，再加以合并。

1. 十进制整数转换为二进制整数十进制整数转换为二进制整数采用"除2取余，逆序排列"法。

具体做法是：用2去除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为0时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。

一、十进制与二进制之间的转换1、十进制转换为二进制（1）整数部分方法1（除2取余法）：每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。

举例：将十进制的10转换为二进制第一步，将商10除以2,商5余数为0;第二步，将商5除以2,商2余数为1;第三步，将商2除以2,商1余数为0;第四步，将商1除以2,商0余数为1;第五步，读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，得结果（1010）2;（2）小数部分（方法：乘2取整法）将小数部分乘以2，然后取整数部分，剩下的小数部分继续乘以2，然后取整数部分，剩下的小数部分又乘以2，一直取到小数部分为零为止。

如果永远不能为零，就同十进制数的四舍五入一样，按照要求保留多少位小数时，就根据后面一位是0还是1，取舍，如果是0，舍掉，如果是1，向入一位。

换句话说就是0舍1入。

读数要从前面的整数读到后面的整数，下面举例：将0.45转换为二进制（保留到小数点第四位）0.45＊2=0.9取0;0.9＊2=1.8取1;0.8＊2=1.6取1;0.6＊2=1.2取1;0.2＊2=0.4取0;0.4＊2=0.8取0;0.8＊2=1.6取1;大家从上面步骤可以看出，当第五次做乘法时候，得到的结果是0.4，那么小数部分继续乘以2，得0.8，0.8又乘以2的，到1.6这样一直乘下去，最后不可能得到小数部分为零，因此，这个时候只好学习十进制的方法进行四舍五入了，但是二进制只有0和1两个，于是就出现0舍1入。

这个也是计算机在转换中会产生误差，但是由于保留位数很多，精度很高，所以可以忽略不计。

那么，我们可以得出结果将0.45转换为二进制约等于 (0.0111)2。

注：整数的转换是精确的，小数的转换可能出现无穷小数或循环小数的情况。

二进制与十进制间的转换方法(图文教程)二进制与十进制是计算机中最常用的两种数字表示和计算方法，它们之间的转换是非常简单的。

下面通过图文教程来介绍如何进行二进制和十进制之间的转换。

一、二进制转十进制1.求权重首先需要明确的是，二进制每一位的权重是2的n次方，其中n从0开始逐位递增。

例如二进制数1010的权重依次为2的0次方，2的1次方，2的2次方，2的3次方，即1，2，4，8。

2.计算只要按照权重和二进制数的规则来计算即可，例如二进制数1010的十进制数为：1 * 2的3次方 + 0 * 2的2次方 + 1 * 2的1次方 + 0 * 2的0次方 = 8 + 0 + 2 + 0 = 10注意：计算过程中需要按照从右往左的顺序计算，也就是从低位到高位。

二、十进制转二进制1.除2取余法十进制转二进制通常采用除2取余法，即将十进制数不断除以2，每次将余数作为当前位的二进制数，直到商为0为止，然后将所有的余数倒序排列即可。

例如十进制数12的二进制数为：第一步：12 / 2 = 6 余0第二步：6 / 2 = 3 余0第三步：3 / 2 = 1 余1第四步：1 / 2 = 0 余1则12的二进制数为1100。

2.补位法另外一种十进制转二进制的方法是补位法，即根据数值大小和位数确定，先将转换后的二进制数补成相应位数，然后根据位权求和来确定十进制数。

例如将十进制数12转换为8位二进制数为00001100，然后再分别求出每位的权重和对应的二进制位是否为1，最终确定二进制数的值为12。

总结：以上就是二进制与十进制之间的转换方法，其中二进制转换时需要注意权重和从低位到高位的顺序，十进制转换时则需要注意数值大小和位数的补全。

细心认真的操作可以帮助我们更好地运用计算机中的数字表示和计算方法，提高计算效率和准确度。

二进制与十进制是计算机中最常用的两种数字表示和计算方法。

在计算机科学中，二进制由0和1表示，常被用来表示位于电子电路中的开关状态，而十进制是人们最常使用和理解的数字表示方法。

十进制、二进制、八进制，十六进制之间相互转换方
法详解
1.十进制想要转换为n进制：
整数部分不停地除以n，直到商为0即可，记录下每次的余数，从最后一个余数开始排列即可。

小数部分不停地乘以n,每次乘完后把个位数的数字记录后再变为0，再进行下一次乘法运算，直到小数部分为0即可，记录下每次乘法结束后个位数的数字为多少，从第一个数字开始排列即可。

2.n进制转换为十进制：
n进制上的每一个数字乘以位权再把它们全部加起来。

（如果不懂位权是啥的，请看：所谓位权，是指一个数值的每一位上的数字的权值的大小。

例如十进制数4567从低位到高位的位权分别为10^0、10^1、10^2、10^3。

因为：4567＝4x10^3＋5x10^2＋6x10^1＋7x10^0），
3.二进制转换为八进制:
从右至左，每3个为一组，不足的补0，通过转换为十进制的方法把它们转换为数字，再依次写下了即可。

4.八进制转换为二进制：
每一个数转化为3位的二进制数即可，不足的补0，再按顺序排列即可。

5.二进制转换为16进制：
从右至左，每4个为一组，不足的补0，通过转换为十进制的
方法把它们转换为数字，需注意的是十六进制中10-15为A-F，再依次写下了即可。

6.十六进制转换为二进制：
每一个数转化为4位的二进制数即可，不足的补0，再按顺序排列即可。

7.八进制转换为十六进制：
先转换为二进制，再转换为十六进制即可。

8。

十六进制转换为八进制：
先转换为二进制，再转换为八进制即可。

二进制，八进制,十进制，十六进制之间的转换算法一、十进制与二进制之间的转换（1）十进制转换为二进制，分为整数部分和小数部分①整数部分方法：除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。

下面举例：例：将十进制的168转换为二进制得出结果将十进制的168转换为二进制，（10101000）2分析:第一步，将168除以2,商84,余数为0。

第二步，将商84除以2，商42余数为0。

第三步，将商42除以2，商21余数为0。

第四步，将商21除以2，商10余数为1。

第五步，将商10除以2，商5余数为0。

第六步，将商5除以2，商2余数为1。

第七步，将商2除以2，商1余数为0。

第八步，将商1除以2，商0余数为1。

第九步，读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，即10101000（2）小数部分方法：乘2取整法，即将小数部分乘以2，然后取整数部分，剩下的小数部分继续乘以2，然后取整数部分，剩下的小数部分又乘以2，一直取到小数部分为零为止。

如果永远不能为零，就同十进制数的四舍五入一样，按照要求保留多少位小数时，就根据后面一位是0还是1，取舍，如果是零，舍掉，如果是1，向入一位。

换句话说就是0舍1入。

读数要从前面的整数读到后面的整数，下面举例：例1：将0.125换算为二进制得出结果：将0.125换算为二进制（0.001）2分析：第一步，将0.125乘以2，得0.25,则整数部分为0,小数部分为0.25;第二步, 将小数部分0.25乘以2,得0.5,则整数部分为0,小数部分为0.5;第三步, 将小数部分0.5乘以2,得1.0,则整数部分为1,小数部分为0.0;第四步,读数,从第一位读起,读到最后一位,即为0.001。

例2,将0.45转换为二进制（保留到小数点第四位）大家从上面步骤可以看出，当第五次做乘法时候，得到的结果是0.4，那么小数部分继续乘以2，得0.8，0.8又乘以2的，到1.6这样一直乘下去，最后不可能得到小数部分为零，因此，这个时候只好学习十进制的方法进行四舍五入了，但是二进制只有0和1两个，于是就出现0舍1入。