当前位置：文档之家 › 数学物理方法第二章复变函数的积分

数学物理方法第二章复变函数的积分

  • 格式：ppt
  • 大小：524.00 KB
  • 文档页数：7

下载文档原格式

  / 7

合集下载

数学物理方法第二章2012

数学物理方法第二章2012


0, dz I l z 2i.
1 f ( z ) f ( ) z dz =0 2 i c
( S l ) ( S l )
f ( )
1 f ( ) z dz 2 i l

C
max f ( z ) f ( ) f ( z ) f ( ) dz 2 0 z
Sl . Sl
Sl
CR
R
l

并且
( z ) n dz 0,
l
整数
n 1
16
2.4 柯西公式 柯西积分公式: 若f (z)在闭单通区域B上解析，l 为B境界线，为B内的任一点，那么
1 f ( z) f ( ) z dz 2 i l
证明：由于 只需证明
沿此区域边界的积分为零。
（二）复通区域情形
有时，所研究的函数在区域上并非处处解析 奇点：复变函数不解析的点 若f(z)在z=b 不解析（或没有定义），而在z=b的去心 邻域 0<z−b <R内解析，则z=b为f(z)的孤立奇点。 含孤立奇点的区域，可将其每个奇点的有限小邻域 挖掉，使原区域变为复通区域
L L L
(4) f ( z )dz f ( z )dz f ( z )dz, 其中L是
L L1 L2
由L1和L2组成的
(5) f ( z)dz f ( z) ds
L L
dz (dx) 2 (dy ) 2 ds
(6) L f ( z)dz ML
若，f ( z ) M
第二章 复变函数的积分
在复变函数中，微分法、积分法是研究复变函数 性质的重要方法和解决实际问题的有力工具 2.1复变函数的积分 ——复平面上的线积分 (与实函数积分相似，定义为和的极限)
数学物理方法1-2复变函数的积分

数学物理方法1-2复变函数的积分


莫雷拉定理
总结词
莫雷拉定理是复变函数中一个关于全 纯函数的积分性质的定理。
详细描述
莫雷拉定理说明，如果全纯函数f(z)在圆盘 |z| < R内有界，那么对于任意实数t，积分 ∫f(z)e^(it)dz在|z| = R的边界上非零。这个 定理在研究全纯函数的性质以及解决一些数 学物理问题时非常有用。
柯西定理
总结词
柯西定理是复变函数中的一个基本定理，它表明如果一个函数在某个区域内的点上满足某种条件，则 该函数在该区域内可积。
详细描述
柯西定理说明，如果函数f(z)在某个区域D内是解析的，并且存在常数C使得对于D内的任意点z，都有 |f(z)|≤C，那么函数f(z)在D内是可积的。这意味着满足一定条件的解析函数在一定区域内具有可积性。
幂级数展开的收敛性
幂级数展开的收敛性取决于函数的性质和级数的收敛条件。
幂级数展开的应用
幂级数展开在数学物理中广泛应用于求解微分方程和积分方程。
泰级数展开
泰勒级数展开定义
01
将一个复变函数表示为多项式的无穷级数。
泰勒级数展开的收敛性
02
泰勒级数展开的收敛性取决于函数的性质和级数的收敛条件。
泰勒级数展开的应用
个定理在解决一些数学物理问题时非常有用。
柯西不等式
总结词
柯西不等式是复变函数中一个基本的积分不等式，它反映了函数与其共轭函数之间的积分关系。
详细描述
柯西不等式表明，对于任意实数a和b，以及在全平面上的非负函数f和g，有∫f(z)g(z*)dz ≥ |∫f(z)dz * ∫g(z*)dz|， 其中z*是z的共轭复数。这个不等式在处理一些积分问题时非常有用。
积分路径
积分性质
复数函数的积分具有线性性质、可加 性、可交换性等基本性质。
数学物理方法第2章复变函数积分-2016方案

数学物理方法第2章复变函数积分-2016方案


(2.1.3)
(2) 化为参数积分计算．设积分曲线L的参数方程为z(t)，
将z(t)及dz(t)＝z'(t)dt代入式(2.1.4)，可得
3
【例2.1.1】计算积分I=
其中曲线L是
(1)沿1+ i 到2+4 i 的直线，见图2.2(a)；
(2)沿1+ i 到2+i，再到2+4 i 的折线，见图2.2(b)；
§2.2.1 单通区域的柯西定理
定理 若函数f(z)在单通区域D 内解析，则f(z)在D内沿任意 闭曲线的积分为零
∮l f(z)dz = 0 (2.2.1)
证明 这个定理的严格证明比较复 杂, 为简单起见, 我们在“f(z)在D 内连续” 附加条件下证明这个定 理．
先将复变积分化为两个实变积 分的线性叠加
29
这就是解析函数的定积分公式，它与实变 函数中的牛顿-莱布尼茨公式具有相同的形 式。
通常把f(z)的原函数的集合
称f(z)的不定积分，式中C为复常数。
30
(2.2.8)
31
§2.2.3 复通区域的柯西定理
定理 若f(z)在闭复通区域 解析，则f(z)沿所
有内、外边界线(L=L0+ 之和为零
37
【2.2.2】试计算 其中积分回路分别(图2.11) (1) |z-i|＝2；(2) |z+i|＝2；(3) |z|＝3.
38
解 首先，将被积函数分解为部分分式(利用通 分可以凑出来)
≠0
=0
39
40
【例2.2.3】若f(z)=1/(z-a) 在z=a的无心邻域内 连续，积分回路是以a点为圆心的圆弧
由于a点在D内随意变动时，柯西公式依然成立， 有时分别用z和x代替式 (2.3.1)的a和z。将柯西公 式改写为
数学物理方法 第二章 复变函数的积分

数学物理方法 第二章 复变函数的积分

wuxia@
证明： 1 dz 1 f (α )dz (1)已知f (α ) = f (α ) ⋅ ∫l z − α = 2πi ∫l z − α 2πi 1 f ( z )dz 1 f ( z ) − f (α ) 与f (α ) = 比较，只需证明 ∫l z − α ∫l z − α dz = 0即可. 2πi 2πi f ( z ) − f (α ) (2)因为z = α为 的奇点，因此，以α为圆心，取任意小 z −α f ( z ) − f (α ) ε为半径做小圆Cε , 这样在l及Cε 所围复通区域上 单值解析。 z −α f ( z ) − f (α ) 1 f ( z ) − f (α ) 1 根据柯西定理， ∫ dz = ∫Cε z − α dz l 2πi z −α 2πi 对于Cε 上的z有：z − α = εe iϕ , dz = iεeiϕ dϕ 于是, 有： 1 f ( z ) − f (α ) 1 2π f ( z ) − f (α ) iϕ 1 iεe dϕ = iϕ ∫l z − α dz = 2πi ∫0 εe 2πi 2π
wuxia@
∫
2π
0
[ f ( z ) − f (α )]dϕ
(3)现在需要对上式右端做估计 因为f ( z )连续，一定可以找到∆ > 0,当 | z − α |≤ ∆时， | f ( z ) − f (α ) |≤ ε ′ 因而有： 1 2π 1 2π 1 ∫0 [ f ( z ) − f (α )]dϕ ≤ 2π ∫0 | f ( z ) − f (α ) |⋅ | dϕ |< 2π 2π =ε 1 f ( z ) − f (α ) 1 f ( z) ∴ dz = 0, f (α ) = ∫l z − α ∫l z − α dz 2πi 2πi
数学物理方法课件-2 复变积分

数学物理方法课件-2 复变积分


其中，M (R) max f (z) , n 1,2, z R
证：
f (n) ( )

n!
2i

(
f ( ) )n1
d

n!
2

M (R) R n 1
2R

n!M (R) Rn
即
f
(n) ( )

n!M R
(
n
R)
，得证.
整函数: 在整个复平面上解析的函数称为整函数.
49

1
0 1
z100 k 1 z 2k
98!!
§2.5 解析函数的高阶导数
1.高阶导数
2. 柯西不等式与刘维尔定理
柯西不等式：设f (z)在区域B上解析，为B内一点，以
为圆心作圆周： R，只要及其所包含区域均含于
B, 则有
f
(n) ( )

n!M (R) Rn
0 2i 2i 0 0
即
C
1 z2
z
dz

0
§2.3 不定积分
证:
B
§2.4 柯西公式
1.有界区域柯西公式
( )

证: 如图，根据复连通区域柯西定理有
1 f (z)
1 f (z)
dz
dz
2i C z
2i Cr z
欲证原式，即证
第二章 复变积分
§2.1 复变积分
性质:
例:
补:简单曲线 光滑曲线
1. 简单曲线
设曲线C的参数方程为 x x(t), y y(t), z z(t) (a t b)
其中，x(t), y(t), z(t)在[a, b]连续，当t1 t2 (a t1, t2 b)时, (x(t1), y(t1), z(t1)) (x(t2 ), y(t2 ), z(t2 ))
数学物理方法第2章复变函数积分-2016

数学物理方法第2章复变函数积分-2016


49
50
【例2.3.2】试计算积分，
积分回路L为x2 + y2=2x 解 (1) 积分回路的形状： (x-1)2+y2=1
(2)被积函数的奇点．

方程z4+1=0有四个根：z=exp[i (p+2kp)/4]， k=0,1,2,3，因此，被积函数有四个奇点，但仅有 z1与z4位于积分回路之内
51
2. 复通区域的柯西公式

设f (z)在闭复通区域D中解析，a为D的内点， 则 式中积分沿D的内外边界线的正方向．
32

证明 为了应用单通区域的柯西定理，作割线把外边界线 L0与内边界线连接起来，将闭复通区域变成闭单通区域。
33
推论3 在f(z)的解析区域中，积分回路连 续变形时，其积分值不变．

证明 取变形前后的积分回路 作为复通区域 的内外边界 线，如图2.9所示．由式 (2.2.21a) 可得
移项后，改变l2的积分方向，即有

复变积分性质(5)及式(2.2.34)，可证
43
由于e可任意地小，(q2-q1)为常量，式
(2.2.35)表明
可任意地小根据极限的定义，可得
44
2. 大圆弧引理

若j(z)在无穷远点的无心邻域内连续，在大 圆弧CR(z=Reiq, R→∞,q1<q<q2 )上

这两个引理为计算沿圆弧的积分带来方便． 2.3节将分别用来证明单通区域及无界区域的 柯西公式．
(3)按复通区域的柯西定理及柯西公式计算以小圆周c1 和c2分别包围奇点z1和z4 ，则被积函数在外边界线l 与内边界线c1 ， c2 所围的复通区域解析。按复通区 域的柯西定理，沿l的积分等于沿C1与C2积分之和， 后两个积分可按柯西公式算出，即
第02章 复变函数的积分

第02章 复变函数的积分

第二章复变函数的积分基本要求：1．正确理解复变数函数路积分的概念；2．深刻理解柯西定理及孤立奇点的定义；3．理解并会熟练运用柯西公式。

教学内容：§2.1 复数函数的积分，路积分及其与实变函数曲线积分的联系。

§2.2 柯西定理。

柯西定理的内容和应用，孤立奇点，单连通区域，复连通区域，回路积分。

§2.3 不定积分*。

原函数。

§2.4 柯西公式。

柯西公式的导出，高阶导数的积分表达式。

（模数原理及刘维定理不作要求）本章重点：柯西定理，柯西公式和孤立奇点。

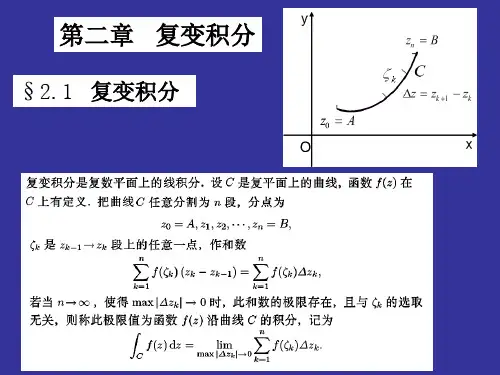
§2.1 复变函数的积分（一）复变函数的积分（简称复积分）1.复积分的定义曲线l 是分段光滑曲线（起点0()A z ，终点()n B z ）；()f z 在l 上连续；（光滑曲线：曲线上每一点都有切线）。

把曲线l 分成n 小段，1k k z z -→是第k 小段，在1[]k k z z --上任取一点k ζ，求和111()()=()nnkk k k k k k f z z f z ζζ-==-∆∑∑，当n →∞而且每个k z ∆都趋于零时，如果这个和的极限存在，而且其值与各个k ζ的选取无关，则这个和的极限称为函数()f z 沿曲线l 从A ，终点B 的路积分，记作()lf z dz ⎰，即max 01()lim()k nkk lz k f z dz f z ζ∆→==∆∑⎰(2.1.1)2. 复积分的计算方法复变函数积分可以分解为两个实积分来计算。

即：()(,)(,)f z u x y iv x y =+，dz dx idy =+(,)(,)(()[(,),(,)]())(,)llllu x y dx v x y d f z dz u x y iv x y dx idy i y v x y dx u x y dy-+=++=+⎰⎰⎰⎰3. 复积分的性质复变函数的路积分可以归结为两个实变函数的线积分，因而实变函数线积分的许多性质也对路积分成立，如(1)常数因子可以移到积分号之外；()d ()d llcf z z c f z z =⎰⎰(2)函数和的积分等于各个函数的积分和；[]1212()()......()()().......()nnll l l f z f z f z dz f z dz f z dz f z dz +++=+++⎰⎰⎰⎰(3)反转积分路径，积分变号；()()l lf z dz f z dz +-=-⎰⎰(4)全路径上的积分等于各段上的积分和。

第一节(复变函数的积分)

第一节(复变函数的积分)

C C2
1
C1
C3
C3
= ∫ tdt+ ∫ (1−it)idt = 1 + i + 1 =1+ i 0 0 2 2
1
C 2 z1
∫ f (z )dz = ∫α
C
β
f [z (t )]z ′ (t )dt .
8
三.积分的性质
i )∫ f (z )dz = − ∫
C C C
−1
f (z )dz
i i )∫ kf (z )dz = k ∫ f (z )dz
∫ f (z )dz = ∫ udx − vdy + i ∫ vdx + udy
C C C
6
C 3 . 例2 计算∫Czdz，其中 为从原点到 + 4i的直线段
解 C : z = t (3 + 4i )， t从 0到1.
∴ ∫ zdz = ∫ t (3 + 4i )(3 + 4i )dt = ∫
1 C 0 1 0
y l 2 l2 O l1
1+i l1
解 先计算 1， 先计算I ，
1 I1 = ∫ xdx + i ∫ dy = + i 0 0 2
1 1
x
而对于I2， 而对于 ，
1
1 I 2 = ∫ o ⋅ idy + ∫ xdx = 0 0 2
1
被积函数相同，起点终点都相同，但积分路径不同， 被积函数相同，起点终点都相同，但积分路径不同，结果 也不相同，一般地，对于复变函数的积分， 也不相同，一般地，对于复变函数的积分，值不仅依赖于 起点和终点，还跟积分路径有关。 起点和终点，还跟积分路径有关。
l
理工类专业课复习资料-数学物理方法总结(改)

理工类专业课复习资料-数学物理方法总结(改)

数学物理方法总结第一章 复变函数复数的代数式:z=x+iy复数的三角式和指数式:(cos sin )z ρϕϕ=+和i z e ϕρ=欧拉公式:{1sin ()21cos ()2iz iz iz izz e e iz e e --=-=+柯西-黎曼方程(或称为柯西-黎曼条件):{u u x yv v x y∂∂=∂∂∂∂=-∂∂ (其中f(z)=u+iv)函数f(z)=u+iv 在点0z 及其领域上处处可导,则称f(z)在0z 点解析.在区域B 上每一点都解析,则称f(z)是在区域B 上的解析函数.解析函数的性质:1.若函数f(z)=u+iv 在区域B 上解析,则12(,),(,)u x y C v x y C ==(12,C C 为常数)是B 上的两组正交曲线族.2.若函数在区域B 上解析,则u,v 均为B 上的调和函数,即22220u vx y ∂∂+=∂∂ 例题: 已知某解析函数f(z)的实部22(,)u x y x y =-,求虚部和这个解析函数.解答: 由于22ux∂∂=2;22v y ∂∂=-2;则22220u v x y ∂∂+=∂∂曲线积分法u x ∂∂=2x;u y ∂∂=-2y.根据C-R 条件有:v x∂∂=2y;v y ∂∂=2x.于是 22dv ydx xdy =+;(,0)(,)(0,0)(,0)(,)(,)(,0)(22)(22)(22)22x x y x x y x y x v ydx xdy C ydx xdy ydx xdy Cxdy C xy C=++=++++=+=+⎰⎰⎰⎰凑全微分显式法由上式可知dv=2ydx+2xdy贝易得dv=d(2xy)则显然v=2xy+C不定积分法上面已有—=2y;丝=2xdx dy则第一式对y积分,x视为参数，有v=J2xy+(p(x)=2xy+(p(x)......................dv...上式对x求导有一=2y+^\x),而由C-R条件可知(p\x)=0,dx从而(p(x)=C.故v=2xy+C.f(z)=x2-y2+i(2x y+C)=z2+iC第二章复变函数的积分单连通区域柯西定理如果函数f(z)在闭单连通区域B上解析，则沿B上任意一分段光滑闭合闭合曲线1(也可以是B的边界)，有血/⑵也=0.复连通区域柯西定理如果f(z)是闭复连通区域上的单值解析函数，则山任)也+£由/(z)也=0.式中1为区域外边界线，诸l为区域内边界线，积分均沿边界线的正方向进行.即血力＞)也=力血/(z)d z.柯西公式f(a)=t^-也""dz2m z-an次求导后的柯西公式f(〃)(z)=£山声舄化2mi中(。

第二章_复变函数的积分

第二章_复变函数的积分

l
数学物理方法
★由格林公式
（曲线积分与曲面积分的关系） 曲线积分与曲面积分的关系）
∂Q ∂P ∫ Pdx + Qdy = ∫∫ ( ∂x − ∂y )dxdy l S
P = [u( x, y) + iv( x, y)], Q = [−v( x, y) + iu( x, y)
∂v ∂u ∂u ∂v ∫ f (z)dz = −∫∫ (∂x + ∂y )dxdy + i∫∫ ( ∂x − ∂y )dxdy l S S
n inϕ 2π iϕ 0
2π
= iR
n+1
∫
0
e
i (n+1)ϕ
dϕ
数学物理方法
I = iR
n+1
∫
2π
0
ei(n+1)ϕ dϕ
2π 0
= iR
n+1
1 i (n+1)ϕ e i(n +1)
C R
α
l
1 i ( n+1) 2π = iR (e −1) i(n +1) 1 n+1 i ( n+1)ϕ I = iR e n ≠ −1 i(n +1)
∫ Re zdz = ∫ xdx+ ixdy
l l
(1)路径 路径
l l1
ቤተ መጻሕፍቲ ባይዱ
O l1 ⇒ O →C → A
OC CA
B 1
∫ Re zdz = ∫ xdx + ixdy = ∫ xdx + ixdy + ∫ = ∫ 0 + i0dy + ∫ xdx + ix0 1 = ∫ i0dy + ∫ xdx = 2
第二章+复变函数的积分

第二章+复变函数的积分

第二章 复变函数的积分基本要求：1．正确理解复变数函数路积分的概念； 2．深透理解柯西定理及孤立奇点的定义； 3．理解并会熟练运用柯西公式。

本章重点：柯西定理，柯西公式和孤立奇点。

§2.1．复变函数的积分 1、复变函数积分复数积分是复平面上的线积分。

设l 是复平面上的一条由A 到B 点的光滑曲线，在曲线上复变函数f (z )有定义，在曲线上任意分为n 段，曲线上各分点为01211,,,,,,,k k k n z A z z z z z z B -+=⋯⋯,=ξk 是[z k -1, z k ]段上的任意一点。

作和数()()()111n nk k k k k k k f z z f z ξξ-==-=∆∑∑当n 无限增大，使每一Δz k 都趋于零时，如果这个和数的极限存在，且其值与各个点ξk 的选取无关，则这极限值称为函数沿曲线由A 到B 的路积分：()()max 01d limk nkklz k f z z f zξ∆→==∆∑⎰因()()();,,z x iy f z u x y i x y υ=+=+因此()()()()()()d ,,d d d d d ll llf z z u x y i x y x iy u x y i x u y υυυ=++⎡⎤⎣⎦=-++⎰⎰⎰⎰即，复变函数的路积分归为两个实变函数的线积分。

2、复变函数积分的性质由上一积分式知，复变积分具有实变函数线积分所具有的一般性质。

（1）常数因子可以移到积分号之外：()()d d llAf z z A f z z =⎰⎰ A 为常数（2）函数的和的积分等于各个函数的积分之和：()()()()()()1212+++d d d d nnll llf z f z f z z f z z f z z f z z ⋯=++⋯+⎡⎤⎣⎦⎰⎰⎰⎰ （3）反转积分路径，积分变号：()()d d llf z z f z z -=-⎰⎰l －表示l 的逆向（4）全路径上的积分等于各段积分之和：()()()()12d d d d nll l l f z z f z z f z z f z z =++⋯+⎰⎰⎰⎰ l = l 1 + l 2 + ⋯+ l n此外，还有经常用到的： （5）()()d d llf z z f z z≤⎰⎰（6）()d lf z zMC ≤⎰，其中M 为()f z 在l 上的上界，C 为l 的长度。

《数学物理方法》电子教案：第二章 复变函数的积分


dz d (t it 2 ) (1 i 2 t ) dt
24i
2
2
2
z2dz (t it2 )2 (1 i2t)dt [(t2 t4 ) 4t4 ]dt i [2t3 2t(t2 t4 )]dt
1i
1
1
1
２．
1和y 3t 2
二、 复通区域的柯西定理 定理4. 若f(z)在闭复通区域D 中解析，则f(z)沿所有边界线正
方向积分之和为零。 正方向：沿边界线的正方向环绕时，D 保持在左边。
证明：作割线将闭复通区域变成闭单通区域。闭单通区域
的边界线L由 L1, L', L2 和 L'' 组成，则
L f (z)dz 0
又
D
内的偏导数
P y
和
Q x
连续，并且
P y
Q x
由于复变函数的积分可转化为两个实变线积分：
z2
z2
z2
f (z)dz (udx vdy) i vdx udy)
z1
z1
z1
因此可得到复变函数的积分与路径无关的充要条件。
一、单通区域的柯西定理
定理 1. 若 f(z)在单通区域 D 内解析，则 f(z)在 D 内 的积分与路径无关。
w=f(z)在 L 上有定义；
(2)将 L 任意分成n 段，k 为第k 段[zk 1, zk ]上的任意一点;
(3)当 n ，且 max zk 0时，若和式的极限
n
lim f (k)zk
max zk 0 k 1
存在，并且极限值与 zk 和 k 的选取方式无关，则称它 为 f(z)沿 L 从 A 到 B 的积分，记作：
F’(z)=f(z)

数学物理方法第二章

积分 Cf(z)dz一定.存在
证 设光滑曲 C由线参数方程给出
zz(t)x(t)i y(t), t
正方向为参数增加的方向,
参数 及 对应A 于 及起 终 B , 点 点
数学物理方法第二章
6
并 z ( t) 且 0 , t,
如f(果 z) u (x ,y) iv(x ,y)在 D 内处 , 处 那u 么 (x,y)和 v(x,y)在 D内均为连 , 续函
n
n
f(k)zk [u(k,k)xkv(k,k)yk]
k1
k1
n
i[v(k,k)xku(k,k)yk]
k1
C f(z)dz CudxvdyiCvdxudy
数学物理方法第二章
9
公式 C f(z)dz CudxvdyiCvdxudy
在形式上可以看成是
f(z)uiv与 dzdxidy相乘后求 : 积
f(z)dzf ( z ) d z f ( z ) d z f ( z ) d z .
C
C 1
C 2
C n
在今后讨论的积分中, 总假定被积函数是连续的, 曲线 C 是按段光滑的.
数学物理方法第二章
12
性质：
设L是简单逐段光滑曲线，f,g在L上连续，则
(1)f(z)dz f(z)d;z反转积分路径，积分反号
z2
z2
f(z)dzudxvdyivdxudy
z1
z1
z1
因此可得到复变函数的积分与路径无关的充要条件
数学物理方法第二章
24
单连通区域柯西定理：
如果函数f (z)在闭单连通域B 上解析，则沿B上任一分段光滑 闭曲线l（也可以是B的边界）， 有
f (z)dz 0

02_复变函数的积分

l AB l1 B ' A' CD l2 D 'C '
B B
l1
D
l2 D
C C

f ( z)dz f ( z)dz f ( z)dz 0
l l1 l2
l
总结：单连通和复连通区域的柯西定理说的是： (1) 闭单连通区域中的解析函数沿境界线或区域内任一闭合 曲线的积分为零；
1 xdx i 1dy i 0 0 2
1 1
l2 0 l1
x
I 2 xdz xdx i xdy
l2 l2 l2
1 xdx i 0 dy 0 0 2
1 1
y 1+i l2 0 l1 x
课堂练习：计算积分
I1 zdz ,
l
I 2 zdz
是任取的， f ( z ) 1 常把记作z 2πi
f ( ) l z d
例:

z i 1

z 2
e dz 2πieiz z i 2πei z i z z 5 z z dz z i dz 2πi 5 z (5 z )( z i )
f ( z )dz 0
l
u v v u ; x y x y
(2) 复通区域情形
一般来说，在区域内，只要有一个简单的闭合曲线其内有 不属于该区域的点，这样的区域便是复通区域。 或者形象地说，把奇点(即函数不可导、不连续或者根本 无定义的点)挖掉而形成的某种带“孔”的区域，即所谓的复 通区域。
f ( z )dz 0
l
证明：
f ( z )dz udx v dy i v dx udy l l l Q P l Pdx Qdy S x y dxdy

数学物理方法第二章复变函数的积分


d z b ln b ln a ln i Arg b Arg a az a
b
ln z ln(| z |e )
Arg z
此积分与路径有关系！因z = 0 是1/z的一个奇点。 如被积函数有奇点，则由不定积分给出的函数可能是 多值的。被积函数的奇点，可能是该函数的支点。
x d y y d x d d f ( z ) d z u v d t i u v d t l t d t t d t d t d t A A
t B t B
几个重要性质 1.常数因子可以移到积分号之外
c f ( z ) d z c f ( z ) d z
推广：若 f (z)在单连通域B上解析，在闭单连通 域 B 上连续，则沿 B 上任一分段光滑闭合曲 线 l (也可以是 B 的边界)，有

l
f (z)d z 0
（二）复连通域情形 如果区域内存在： (1)奇点 ；(2)不连续线段；(3)无定义区 为了把这些奇异部分排除在外，需要作适当的 围道 l1、l2、 l3 把它们分隔开来，形成带孔的区 域—复连通区域。
C 2
只要起点和终点固定不变，当积分路径连续变形时 （不跳过“孔”）时，函数的路积分值不变。
§2.3 不定积分（原函数）
根据 Cauchy 定理，若函数 f (z) 在单连通
区域B上解析， 则沿B上任一分段光滑曲线 l
的积分

l
f ( z) dz 只与起点和终点有关，而与
路径无关。因此如果固定起点 z0 而变化终点 z, 这个不定积分便定义了一个单值函数 F(z):

l
f (z)d z 0
George Green

数学物理方法1课件——第二章 复变函数的积分


y=x2
1) 沿着c1 的积分
I=−1 − i 32
O
x
2) 沿着c2 的积分
I = −1+1i 33
f (z) = x − y + ix2，即u = x − y, v = x2
∂u = 1, ∂u = −1, ∂v = 2x, ∂v = 0
∂x
∂y
∂x
∂y
一般来讲，复变函数的积分与以下三个要素有关：
v∫ ∫ ∫ ∫ z dz z−1=1 z −1
=
2π 1 + eiθ 0 eiθ
ieiθdθ
=
2π idθ +
0
2π ieiθ dθ
0
∫ = 2π i + 2π eiθ diθ = 2π i 0
v∫ 练习
z−2 =1 ( z
z2 − 2)3
dz
=
2π i ?
or
0?
§ 2.2 柯西定理
单连通区域：是指在该区域D中作任何简单的闭合围道，围道 内的点都属于该区域的点。 复连通区域：是指在该区域D内，只要有一个简单的闭合曲线， 其内有不属于D内的点，则区域D为复连通区域。
∫ ∫ ∫ ∫ 若c = c1 + c2 + ... + cn，则有 c f (z)dz =
f (z)dz +
c1
c2
f (z)dz + ... +
cn
f (z)dz
3）反转积分路径，积分改变符号：
∫ ∫ f (z)dz = − f (z)dz，其中，c−表示与c方向相反
c
c−
4）常系数可提到积分号外面：
k =1
k =1

第二章复变函数的积分

柯西公式的应用前面我们讨论了柯西公式背后蕴含的数学意义，发现了解析函数和奇点之间的密切关系。

关于奇点性质的进一步分析需要用到级数展开作为工具，将在下一章中展开讨论。

柯西公式本身应用非常广泛，不仅可用于回路积分的计算，还可以用于定理的证明。

下面具体讨论柯西公式的一些应用。

3/17/2012 61 应用1: 计算回路积分计算回路积分 : 被积函数f ( z = 积分路分为l1和l2的回路积分。

1 1 i ，其中a = + ，2 2 z ( z − a 对于l1的积分, 路径位于z = 0附近。

积分形式: I = ∫ l1 1 dz, 可改写成：z ( z − a I =∫ 似乎可以归纳出这样一个积分公式：当l中只有一个奇点z = z0时，1 /( z − a 1 /(ζ − a dz = ∫ dζ , 而柯西公式形式是：ζ −0 z −0 l1 l1 f (ζ 1 f (ζ δζ , 化成2πif ( z = ∫ δζ . ζ −z 2πi ∫ ζ − z l1 l1 f ( z = ∫ f ( zdz = ∫ l l ( z − z0 f ( z dz = 2πi lim ( z − z0 f ( z z → z0 z − z0 这个公式普遍成立吗？3/17/2012 两者对比，有z = 0，f (ζ = 1 /(ζ − a。

2πi 所以I = 2πif (0 = = −2π − 2πi − 0.5 − 0.5i 62应用1: 计算回路积分对于l2的积分, 尝试使用刚才的积分公式: I = 2πi lim ( z − z0 f ( z z → z0 将z 0 = a = 1 i 1 代入，直接有： + 和f ( z = 2 2 z ( z − a 1 I = 2πi lim( z − a z →a z ( z − a 1 = 2πi lim z →a z 2πi = = 2π + 2πi 0.5 + 0.5i 数值结果：∫ f ( z dz = −6.285 − 6.285i l1 3/17/2012 l2 ∫ f ( z dz = 6.285 + 6.285i 和数值计算结果吻合63 刚才的积分公式普遍成立吗？如果f ( z 形式变为f ( z = 的回路积分。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 1
一般而言,复变函数的积分不仅与起点和终点有 关, 同时还与路径有关。
§2.2 柯西（Cauchy）定理
——研究积分与路径之间的关系 （一）单连通域情形 单连通域： 在其中作任何简单闭合围线，围 线内的点都是属于该区域内的点。 单连通区域的Cauchy 定理 ：如果函数 f (z) 在闭 单连通区域 B 中单值且解析， 则沿 B 中任 何一个分段光滑的闭合曲线 l (也可以是 B 的 边界 l0 ), 函数的积分为零。
lim f( z z ) k)( k k 1
n
存在且与 k 的选取无关, 则这个和的极限称为 函数 f (z) 沿曲线 l 从 A 到 B 的路积分，记为
即

l
f (z) dz
n k k k 1
z ) d z lim f ( )( z z f(
l n k 1 max | z | 0 k
l 1 l 2
f (z)=Re (z)不是解析函数!
y i l2 o l1 1 l2
I1 Rez d z xd( x iy) 1 xd x i d y i 0 0 2 ( y = 0) (x=1)
1 1
1+i
l1 x
1 I 0 id y x d x 2 0 0 (x=0) ( y=i ) 2
l l l
v u u v d x d y i d x d y s s x y y x
又u、v 满足C-R条件 u v u v , x y y x
y
f ( z ) d z 0
l
B
l
o

沿 l 环线正向走 环域在左侧
f ( z ) d z
l
ud x vd y i( x ud y ) vd
l l
u u v v 因 f (z)在 B 上解析，因而 , , , x y x y 在 B 上连续。
f ( z ) d z f ( z ) d z
l

l
4. 全路径上的积分等于各分段上的积分之和 即： 如果 l=l1+l2+……+ln
l l 1 l 2 l n
f ( z ) d z f ( z ) d z f ( z ) d z ...... f ( z ) d z
l l
2.函数和的积分等于各函数积分的和
d f( z ) f( z ) ...... f( z ) z f ( z ) d z f ( z ) d z ....... f ( z ) d z
l 1 2 n l 1 l 2 l n
3.反转积分路径，积分值变号
After graduation Green stayed on at Cambridge, writing on Optics, Acoustics and Hydrodynamics. However, in 1840 he became ill and returned to Nottingham where he died the 10 following year.
第二章 复变函数的积分 §2.1 复变函数的积分
复平面上的路积分 定义: 复平面分段光滑曲线l 上的连续函数 f (z)，作和
y
zn
zk-1 •
k • l
zk • •
• B
f ( )(z z
k 1 k k
n
k 1
)
A•
o
z0
• z1
x
若
n k 1 m ax | z | 0 k
)
分量形式：f (z) = u(x,y)+ i v(x,y), z = x + i y
f (z) dz=( u+ i v) d (x + i y)
l l l
f ( z ) d z u d x v d y i ( u d y v d x )
参数形式：曲线l 的参数方程 {x = x (t), y = y (t)}, 起始点 A tA, 结束点 B tB
5. 积分不等式1：
z ) d z z )d z f( f(
l l
6.积分不等式2：
f (z) dz ML
l
其中 M 是 | f (z) | 在 l 上的最大值，L 是 l 的全长。
例：计算积分 解：
l1 l1
I Re z d z , I Re z d z , 1 2
x d y y d x d d f ( z ) d z u v d t i u v d t l t d t t d t d t d t A A
t B t B
几个重要性质 1.常数因子可以移到积分号之外
c f ( z ) d z c f ( z ) d z
对实部虚部分别应用格林公式
平面内曲线积 Q P P d x Q d y d x d y分和二重积分 l s y x 之间关系
将回路积分化成面积分
z ) d z u d x v d y i( d x u d y ) f( v

l
f (z)d z 0
George Green
(14 July 1793–31 May 1841) was a British mathematician and physicist , who wrote "An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism". Green's life story is remarkable in that he was almost entirely self-taught, having only had about one year of formal schooling as a child between the ages of 8 and 9. He entered Cambridge University as an Undergraduate in 1833 aged 40 and graduated in 1837.