定积分的应用之微元法

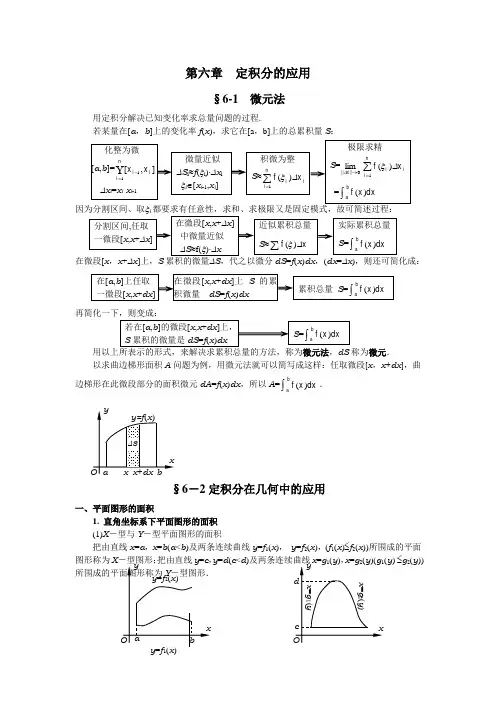
第六章 定积分的应用§6-1 微元法用定积分解决已知变化率求总量问题的过程.若某量在[a ，b ]上的变化率f (x )，求它在[a ，b]上的总累积量S ： 因为分割区间、取i 都要求有任意性，求和、求极限又是固定模式，故可简述过程：再简化一下，则变成：称为微元．以求曲边梯形面积A 问题为例，用微元法就可以简写成这样：任取微段[x ，x +dx ]，曲边梯形在此微段部分的面积微元dA =f (x )dx ，所以A =⎰ba dx x f )(．§6－2定积分在几何中的应用一、平面图形的面积1. 直角坐标系下平面图形的面积 (1)X －型与Y －型平面图形的面积把由直线x =a，x =b (a <b )及两条连续曲线y =f 1(x )， y =f 2(x )，(f 1(x )≤f 2(x ))所围成的平面图形称为X y =d (c <d )y ) ≤g 2(y ))注意 构成图形的两条直线，有时也可能蜕化为点．把X －型图形称为X －型双曲边梯形，把Y －型图形称为Y －型双曲边梯形．１）用微元法分析X －型平面图形的面积取横坐标x 为积分变量，x ∈[a ，b ]．在区间[a ，b ]上任取一微段[x ，x +dx ]，该微段上的图形的面积dA 可以用高为f 2(x )－f 1(x )、底为dx 的矩形的面积近似代替．因此dA =[ f 2(x )－f 1(x )]dx ， 从而 A =.)]()([ 12⎰-ba dx x f x f (1)２）微元法分析Y －型图形的面积A =.)]()([ 12⎰-dc dy y g y g (2)对于非X －型、非Y －型平面图形，我们可以进行适当的分割，划分成若干个X －型图形和Y －型图形，然后利用前面介绍的方法去求面积．例1 求由两条抛物线y 2=x ， y =x 2所围成图形的面积A ．解 解方程组,,22x y x y ==得交点(0，0)，(1，1)．将该平面图形视为X －型图形，确定积分变量为x ，积分 区间为[0，1]．由公式(1)，所求图形的面积为A =1 0 31 0 23132)(23x x dx x x -=-⎰=31． 例2 求由曲线y 2=2x 与直线y =－2x +2所围成图形的面积A ． 解解方程组,22 ,22+-==x y x y 得交点(21，1)，(2，－2)． 积分变量选择y ，积分区间为[－2，1]．所求图形的面积为 A =12- 31 2- 22]6141[]21)211[(y y y dy y y ⎰--=--=49．例3 求由曲线y =sin x ，y =cos x 和直线x =2π及y 轴所围成图形的面积A ．解 在x =0与x =2π之间，两条曲线有两个交点： B (4π，22)，C (45π，－22)． 由图易知，整个图形可以划分为[0，4π]，[4π，45π]，[45π，2π]三段，在每一段上都是X －型图形．应用公式(1)，所求平面图形的面积为A =⎰⎰⎰-+-+-4455 02)sin (cos )cos (sin )sin (cos πππππdx x x dx x x dx x x =42．2. 极坐标系中曲边扇形的面积在极坐标系中，称由连续曲线r =r (θ)及两条射线θ=α， θ=β，(α<β)所围成的平面图形为曲边扇形．在[α，β]上任取一微段[θ，θ+d θ]，面积微元dA 表示1这个角内的小曲边扇形面积，dA =21[r (θ)]2d θ 所以 A =⎰βαθθ 2)]([21d r ． (3) 例5 求心形线r =a (1+cos θ)，(a >0)所围成图形的积A ．解 因为心形线对称于极轴，所以所求图形的面积 A 是极轴上方图形A 1的两倍．极轴上方部分所对应的极角变化范围为θ∈[0，π]，由 公式(3)，所求图形的面积为A =2⨯⎰βαθθ 2)]([21d r=⎰⎰++=+ππθθθθθ 022 02)cos cos 21()]cos 1([d a d a=)23|2sin 41sin 22302=++ ⎝⎛πθθθa πa 2．二、空间立体的体积 1. 一般情形设有一立体，它夹在垂直于x 轴的两个平面x =a ， x =b 之间(包括只与平面交于一点的情况)，其中a <b ，如图所示．如果用任意垂直于x 轴的平面去截它，所得的截交面面积A 可得为A =A (x )，则用微元法可以得到立体的体积V 的计算公式．过微段[x ，x +dx ]两端作垂直于x 轴的平面，截得立体一微片，对应体积微元dV =A (x )dx ． 因此立体体积V =.)( ⎰ba dx x A (4)例5 经过一如图所示的椭圆柱体的底面的短轴、与底面交成角α的一平面，可截得圆柱体一块楔形块， 求此楔形块的体积V ．解 据图，椭圆方程为64422y x +=1． 过任意x ∈[－2，2]处作垂直于x 轴的平面，与楔形块 截交面为图示直角三角形，其面积为A (x )=21y ⋅y tan α=21y 2tan α=32(1－42x )tan α=8(4－x 2)tan α， 应用公式(4)V =⎰--22 2)4(tan 8dx x α=16tan α⎰-22)4(dx x =3256tan α．2. 旋转体的体积旋转体就是由一个平面图形绕这平面内的一条直线l 旋转一周而成的空间立体，其中直线l 称为该旋转体的旋转轴．把X －型图形的单曲边梯形绕x 旋转得到旋转体，则公式(4)中的截面面积A (x )是很容易得到的．如图，设曲边方程为y =f (x )， x ∈[a ，b ](a <b )，旋转体体积记作V x ．过任意x ∈[a ，b ]处作垂直于x 轴的截面，所得截面是半径为|f (x )|的圆，因此截面面积 A (x )= π|f (x )|2．应用公式(4)，即得V x =π⎰ba dx x f 2)]([ (5)类似可得Y －型图形的单曲边梯形绕y 轴旋转得到的旋转体的体积V y 计算公式 V y =π⎰d c dy y g 2)]([ (6)其中的x =g (y )是曲边方程，c ，d (c <d )为曲边梯形的上下界．例6 求曲线y =sin x (0≤x ≤π)绕x 轴旋转一周所得的旋转体体积V x ．解 V x =π⎰b a dx x f 2)]([=π⎰π0 2)(sin dx x=⎰-=-ππππ0 0 ]22sin [2)2cos 1(2x x dx x =22π． 例7 计算椭圆2222bya x +=1(a >b >0)绕x 轴及y 轴旋转而成的椭球体的体积V x ，V y ． 解 (1)绕x 轴旋转，旋转椭球体如图所示，可看作上半椭圆y =22x a ab-及x 轴围成的单曲边梯形绕x 轴旋转而成的，由公式(5)得V x =π⎰-a a dx x a a b - 222)(=⎰-a dx x a a b 02222)(2π =a 0 3222]3[2x x a a b -π=34πab 2．(2)绕y 轴旋转，旋转椭球体如图所示，可看作右半 椭圆x =22y b ba-及y 轴围成的单曲边梯形绕y 轴旋转而成的，由公式(6)得V y =π⎰-bb dy y b b a - 222)(=⎰-b dy y b ba 0 2222)(2π =b 0 3222]3[2y y b ba -π=34πa 2b ．f (x当a =b =R 时，即得球体的体积公式V =34πR 3． 例8 求由抛物线y =x 与直线y =0，y =1和y 轴围成的平面图形，绕y 轴旋转而成的旋转体的体积V y ．解 抛物线方程改写为x =y 2，y ∈[0，1]． 由公式(６)可得所求旋转体的体积为 V y =π55])[(1 0514122ππ===⎰⎰y dy y dy y ．三、平面曲线的弧长1. 表示为直角坐标方程的曲线的长度计算公式称切线连续变化的曲线为光滑曲线．若光滑曲线C 由直角坐标方程y =f (x )，(a ≤x ≤b )，则导数f '(x )在[a ，b ]上连续．如图所示，在[a ，b ]上任意取一微段[x ，x +dx ]，对应的曲线微段为AB ，C 在点A 处的切线也有对应微段AP ．以AP 替代AB ，注意切线改变量是微分，即得曲线长度微元d s 的计算公式d s=22)()(dy dx +， (7) 得到的公式称为弧微分公式．以C 的方程y =f (x )代入，得 ds =2)]([1x f '+dx.据微元法，即得直角坐标方程表示的曲线长度的一般计算公式s =⎰ba ds =⎰'+ba dx x f 2)]([1 (8)若光滑曲线C 由方程x =g (y )(c ≤y ≤d )给出，则g '(y )在[c ，d ]上连续，根据弧微分公式(7)及微元法，同样可得曲线C 的弧长计算公式为 s =⎰'+d cdy y g 2)]([1 (9)例9 求曲线y =41x 2－21ln x (1≤x ≤e )的弧长s ． 解 y '=21x －x 21=21(x －x1)，ds =2)]([1x f '+dx =)1(21)1(4112x dx x x +=-+dx ， 所求弧长为s =⎰ba ds =41]ln 21[21)1(21e1 2 1=+=+⎰x x dx x x e (e 2+1)． 例10 求心形线r =a (1+cos θ) (a >0)的全长．解 θ∈[0，2π]；又因为心形线关于极轴对称，全长是其半长的两倍，所以θ∈[0，π]．ds =22)]([)]([θθr r +'d θ=2)cos 1(2θ+d θ=2a cos 2θd θ，所以 s =2⎰πθθ2cos2d a =8a ．§6—3 定积分在物理中的部分应用一、变力做功物体在一个常力F 的作用下，沿力的方向作直线运动，则当物体移动距离s 时，F 所作的功W =F ⋅s ．物体在变力作用下做功的问题，用微元法来求解．设力F 的方向不变，但其大小随着位移而连续变化；物体在F 的作用下，沿平行于力的作用方向作直线运动．取物体运动路径为x 轴，位移量为x ，则F =F (x )．现物体从点x =a 移动到点x =b ，求力F 作功W ．在区间[a ，b ]上任取一微段[x ，x +dx ]，力F 在此微段上做功微元为dW ．由于F (x )的连续性，物体移动在这一微段时，力F (x )的变化很小，它可以近似的看成不变，那么在微段dx 上就可以使用常力做功的公式．于是，功的微元为dW =F (x )dx ． 作功W 是功微元dW 在[a ，b ]上的累积，据微元法W =⎰ba dW =⎰ba dx x F )(． (12)例1 在弹簧弹性限度之内，外力拉长或压缩弹簧，需要克服弹力作功．已知弹簧每拉长0.02m 要用9.8N 的力，求把弹簧拉长0.1m 时，外力所做的功W ．解 据虎克定律，在弹性限度内，拉伸弹簧所需要的外力F 和弹簧的伸长量x 成正比，即 F (x )=kx ，其中k 为弹性系数． 据题设，x =0.02m 时，F =9.8N ，所以 9.8=0.02k ，得k =4.9⨯102(N/m).所以外力需要克服的弹力为 F (x )=4.9⨯102x ．由(12)可知，当弹簧被拉长0.1m 时，外力克服弹力作功W =⎰⨯1.0 0 2109.4xdx =21⨯4.9⨯1021.0 0 2x =2.45(J)．例2 一个点电荷O 会形成一个电场，其表现就是对周围的其他电荷A 产生沿径向OA作用的引力或斥力；电场内单位正电荷所受的力称为电场强度．据库仑定律，距点电荷r =OA 处的电场强度为F (r )=k 2r q(k 为比例常数，q 为点电荷O 的电量)． 现若电场中单位正电荷A 沿OA 从r =OA =a 移到r =OB =b (a <b )，求电场对它所作的功W ．解 这是在变力F (r )对移动物体作用下作功问题．因 为作用力和移动路径在同一直线上，故以r 为积分变量，可应用公式(12)，得W =⎰b adr rq k 2=kq b a r ]1[-=kq (b a 11-)．二、液体的压力单位面积上所受的垂直于面的压力称为压强，即p=ρ⋅h，(其中ρ是液体密度，单位是kg/3m，h是深度，单位是m)．如果沉于一定深度的承压面平行于液体表面，则此时承压面上所有点处的h是常数，承压面所受的压力P=ρ⋅h⋅A，其中A是单位为m2的承压面的面积．若承压面不平行于液体表面，此时承压面不同点处的深度未必相同，压强也就因点而异．考虑一种特殊情况：设承压面如图那样为一垂直于液体表面的薄板，薄板在深度为x 处的宽度为f(x)，求液体对薄板的压力．薄板沿深度为x的水平线上压强相同，为ρ⋅x，现在在薄板深x处取一高为dx的微条(见图中斜线阴影区域)，设其面积为dA．微条上受液体压力为压力微元dP．近似认为在该微条上压强相同，为ρ⋅x，则dP=ρ⋅xdA；又深度为x处薄板宽为f(x)，故dA=f(x)dx，因此dP=ρ⋅x⋅f(x)dx．若承压面的入水深度从a到b(a<b)，则薄板承压面上液体总压力是x从a到b所有压力微元dP的累积．据微元法P=⎰badxxxf)(ρ=ρ⎰badxxxf)(．(13)。

定积分微元法及其应用摘要：积分学中的定积分在几何、物理、经济管理等方面有着极其广泛的应用。

由于定积分的微元法通常往往能使一些实际问题简单化，因此，定积分的微元法在定积分的应用方面至关重要。

本文首先简介定积分的微元法适用的所求量以及定积分微元法在应用中的步骤，重点介绍积分微元法在几何、物理、经济管理及日常生活等方面的应用。

关键词：定积分：微元法：应用一、定积分的微元法适用的所求量定积分的微元法是将实际问题设法转化为定积分问题的一种方法，通常，如果所求量满足三条：1.关于某一个区间有关；2.在区间上具有可加性，即当把区间分成任意n个小区间时，相应的所求量也分成n个小部分，且所求量等于n个小部分之和，即；3.在上任取一个小区间，所求量的部分量能够近似表示成（即所求量的微分元素），那么所求量就可以用定积分的微元法来求，即。

二.定积分微元法在应用中的步骤定积分微元法就是将所研究的所求量进行无限细分，从中抽取某一微小部分进行探探讨，通过分析，研究找出所求量的整体变化规律的方法。

通常利用定积分微元法解决一些具体问题时，采用将所研究的所求量细分成很多微小的“元素”，而这些微小的“元素”具有相同的几何形态或物理规律，因此，我们仅需要分析和研究其中的一个微小部分，利用所学的数学或物理的理论知识进行处理，以期达到用一个定积分表达式来求所求量的效果。

用定积分微元法将实际问题中的所求量抽象为定积分的步骤也基本相同，分为3步，1.根据题意，建立适当坐标系，画出草图（使得后面的选积分变量、确定积分区间、寻找所求量的微分元素比较直观）；由于函数关系的建立是由所建立的坐标系来决定的，坐标系的建立是否恰当，往往直接影响到寻找微分元素的难易以及定积分计算的繁简程度。

因此，建立坐标系时，既要考虑到较易寻找所求量的微分元素，还要考虑到后面的定积分的计算要相对较简单。

2.选取积分变量，并确定其变化区间。

积分变量选择的是否恰当，往往直接决定着定积分的计算是简单还是繁琐。

第五讲 定积分的微元法 定积分在几何中的应用(一)一、定积分的微元法由引入定积分概念的两个实例不难看出， 可用定积分所求的量 A 具有以下 三个特点：1、量A 是分布在区间［a,b ］上的整体量，即A 与区间［a,b ］有关，在［a,b ］上连续分布。

3、量A 在区间［a,b ］上的分布是非均匀的。

现在来讨论如何用定积分解决一些实际问题。

复习求曲边梯形面积的方法，给出微元法的概念。

设f(x)在区间［a,b ］上连续，且f(x) 0，求以曲线取近 似 计算每 个小 区 间 上 面 积 A i 的 近 似 值 A if( i ) x i2、量A 具有可加性，即整体量等与部分量的和:nA i ；i1f (X )为曲边的［a,b ］上的曲边梯形的面积A .把这个面积A 表示为定积分A a bf (x)dx，求面积A 的思路是“分割、 取近似、求和、取极限”即: 1、分割 将［a,b ］分成n 个小区间，相应地把曲边梯形分成n 个小曲边梯形,其面积记作 A(i 1,2,,n),则 A A ；i12、(x i 1ix n ) ；3、求和求和得A 的近似值A nf( i )i1x i ；4、 n取极限 取极限得 A limi1f( i ) x ibf(x)dx ．为了以后使用方便，可把上述四步概括为下面两步， 设所求量为A ，区间yA 「为[a,b],1、无限细分，化整为零A f x dx ;2、连续求和，积零为整xbbbdA dA x d f x dx f x dx ， A dA dA x faaaa由此不难看出，f x dx 实际上就是量A 在点x 出的微分，将dA f x dx 称为量A 的微元，上述方法称为微元分析法，简称为微元法。

二、定积分在几何中的应用(一)平面图形的面积1、直角坐标系下面积的计算在dx 0时，将A 从a 到b 连续求和，则有：A f(x)dx. y n由于A 与区间［a,b ］有关，且在［a,b ］上连续分布,上限函数的定义则有：A x f x dx ，从而， x有积分axb X1、当平面图形是由曲线f(x)及直线xb 、y 0所围成时;bb细分区间［a,b ］，从中任取一小区间［x,x dx ］(dx x )，并求出相应于这个小区间的部分量a oA 的近似值///Jx X dx b Xx dx ；xxxf x dxd f x dx f x dxacbf x dx .d2、当平面图形是由曲线 伞yy iX 、y 2 f 2 x 及直线x a 、x b 所围成时;yy i f i xy 2 To xb x若y i y 2时，则有：A f 2 xf i xdxb bf 2 x dxf i aax dx般地,f 2 xf l x dxacf i x af 2 xd dxcf 2 bxf i x dxdf i x f 2 x dx3、当平面图形是由曲线 X i f i y 、 X 2 f 2 y 及直线yd 所围成时;d则：A 2 y 1 y dy .cx 例1、计算由两条抛物线y 2x例2、计算抛物线y22x与圆x2寸8所围平面图形的面积。

定积分中微元法及其应用研究1. 引言1.1 什么是定积分中微元法及其应用研究定积分中微元法是微积分学中的重要概念，它通过将被积函数分割成无穷小的微元，然后对这些微元进行求和，从而得到整个函数的定积分值。

微元法在定积分中的应用非常广泛，可以解决各种形式的积分计算问题，同时也可以帮助我们更好地理解积分的几何意义。

微元法在实际问题中的应用也非常广泛，例如在物理学、工程学、经济学等领域都有重要的应用价值。

通过微元法，我们可以更准确地描述和分析各种现实问题，为科学研究和工程实践提供有力的支持。

虽然微元法在定积分中有着重要的作用，但它也存在一定的局限性，例如在处理复杂函数或高维度的积分问题时会比较困难。

我们在使用微元法时需要结合具体情况，选择合适的方法和技巧来求解问题。

定积分中微元法是微积分学中的重要工具，它不仅可以简化积分计算的过程，还可以帮助我们更深入地理解函数的性质和应用。

在未来的研究中，我们可以进一步探讨微元法在更复杂问题中的应用，以及不同类型积分的求解方法，从而拓展微元法在定积分中的应用范围。

2. 正文2.1 定积分的基本概念定积分是微积分中的一个重要概念，是对曲线下面积的一种计算方法。

在定积分中，我们将给定的区间分成许多小区间，并在每个小区间内取一个点，然后求出这些小区间上的面积之和，最后取极限得到整个区间的面积。

在进行定积分运算时，我们通常利用微元法来计算。

微元法是一种运用微小部分求和的方法，将函数进行分割，然后在每个微小的部分上进行计算，最后将所有微小部分相加得到整体的结果。

在定积分中，微元法能够帮助我们将曲线下的面积分解成无穷个微小的长方形或梯形，进而求得整个区间的面积。

需要注意的是，定积分的基本概念中还包括对积分上下限的理解和确定，以及对被积函数的理解和计算。

通过对定积分的基本概念的理解和掌握，我们可以更好地应用微元法进行定积分的计算，并进一步应用到实际问题的求解中。

2.2 微元法在定积分中的应用微元法在定积分中的应用是定积分中非常重要和常见的方法之一。

定积分中微元法及其应用研究1. 引言1.1 研究背景定积分中微元法及其应用研究引言定积分是微积分的重要组成部分，是对曲线下方面积的概念。

在实际问题中，我们经常需要求解曲线下的面积，例如计算图形的面积、求解物体的质量和体积等。

定积分中的微元法是一种重要的计算方法，通过将曲线分成无穷小的微元，然后对每个微元进行求和从而得到整个曲线下的面积。

微元法的应用可以帮助我们更准确、快速地计算定积分，提高计算效率。

在过去的研究中，人们对微元法在定积分中的应用逐渐深入探讨，积累了大量的经验和知识。

随着科学技术的不断发展和社会需求的不断增加，对定积分中微元法的研究也面临着新的挑战和机遇。

有必要对定积分中微元法及其应用进行深入研究，以满足不断增长的科学研究和工程实践的需要。

【内容到此结束】1.2 研究目的研究目的是深入探究定积分中微元法及其应用，通过对定积分的基本概念和微元法的具体应用进行分析和研究，探讨微元法在定积分中的实际应用价值和解决问题的能力。

通过研究微元法在定积分中的求解过程和步骤，揭示微元法在不定积分、定积分和定积分应用中的差异和联系，从而为定积分中微元法的理论基础提供更加全面的理解和认识。

结合定积分中微元法在实际问题中的应用，探讨微元法在解决实际问题和应用方面的优势和局限性，为定积分中微元法的未来研究和应用提供启示和指导。

通过对定积分中微元法的研究目的和意义的探讨，旨在加深对定积分中微元法的理论认识和应用实践，提高定积分问题求解的准确性和效率，为相关学科领域的学术研究和技术应用提供理论支持和指导。

1.3 研究意义定积分中微元法及其应用研究的研究意义在于深化对定积分概念的理解，拓展数学方法在实际问题中的应用。

微元法作为定积分中的重要方法，通过将函数分割成无限小的小块，将复杂问题简化为简单的求和问题，极大地提高了计算效率和准确性。

定积分中微元法的研究意义在于通过微元法的应用，可以更好地解决现实生活中复杂的变化问题，如曲线的长度、曲线围成的面积等。

第六章定积分的应用
定积分是求某种总量的数学模型，它在几何学、物理学、经济学、社会学等方面都有着广泛的应用，显示了它的巨大魅力. 也正是这些广泛的应用，推动着积分学的不断发展和完善. 因此，在学习的过程中，我们不仅要掌握计算某些实际问题的公式，更重要的还在于深刻领会用定积分解决实际问题的基本思想和方法——微元法，不断积累和提高数学的应用能力.
第一节定积分的微元法
分布图示
★面积表为定积分的步骤
★定积分的微元法
★内容小结
★返回
内容要点
在应用学科中广泛采用的将所求量（总量）表示为定积分的方法——微元法，这个方法的主要步骤如下：
一、由分割写出微元根据具体问题，选取一个积分变量，例如为积分变量，并确定它的变化区间，任取的一个区间微元，求出相应于这个区间微元上部分量的近似值，即求出所求总量的微元
；
二、由微元写出积分根据写出表示总量的定积分
应用微元法解决实际问题时，应注意如下两点：
（1）所求总量关于区间应具有可加性，即如果把区间分成许多部分区间, 则相应地分成许多部分量, 而等于所有部分量之和. 这一要求是由定积分概念本身所决定的;
（2）使用微元法的关键是正确给出部分量的近似表达式，即使得. 在通常情况下，要检验是否为的高阶无穷小并非易事，因此，在实际应用要注意的合理性.。

微元法在利用定积分解决实际问题中所起的作用张志军一、能利用定积分来解决的实际问题有什么特点？能利用定积分来解决的实际问题，总可归结为求一个确定在某一区间上且一般来说在上非均匀分布的量。

这个量有以下两个特点：1、对区间具有可加性设是与变量的变化区间有关的待求量，在内任意插入分点，把分成个小区间，相应地量也被分成个部分量，那么等于这些部分量的和，即2、能找出部分量的近似表达式如果对每个部分量可以找到如下形式的近似值，其中为上的连续函数，那么待求量的近似值为我们要求的是的精确值，而用的近似值累加，其误差也将累加，所以就要求累加的误差能随所有而趋于零。

因此，希望相应于任一长为的小区间的部分量都满足表达式：且当时，（并与无关）。

这样我们可以证明量即可用定积分来计算二、如何理解和运用微元法来解决可化为定积分的实际问题？微元法也成为元素法，它是用来化实际问题为定积分问题的一种简便方法，也是物理学、力学和工程技术上普遍采用的方法。

如问题一所述，可化为定积分来计算的待求量有两个特点，对区间的可加性这一特点，是容易看出来的，因此，关键在于另一特点，即找任仪部分量的表达式：（1）然而，人们往往根据问题的几何或物理的特征，自然地将注意力集中于去找这一项上。

但不能忘记，这一项与之差，当时，应是比高阶的无穷小量，借用微分的记号，将这项记为（2）这个量称为待求量的微元或元素。

用定积分来解决实际问题的关键就在于求出微元。

若连续，我们由（1）式即知，（2）式表示的微元实际上是的微分，因为在区间上的待求量为，故。

因此，要求出在区间上的待求量，先要求出的微分。

然后把在上积分，即可求出，这就是所谓微元法或元素法。

按数学的定义，量的微分是它的线性主部，但从工程实际应用的角度看，量的微分就是在一定的条件下，将一些变动的量视为常量而得到的与成正比的的近似值。

按此理解，把数学与工程实际应用结合起来考虑，那么量的微分一般说来就比较易求，同时，化实际问题为定积分问题的步骤也得到了简化。