D-S证据推理的应用

火灾的发生是一个伴有光、烟、温升、辐射和气体浓度变化的综合现象，需要利用各种火灾传感器检测和捕捉这些信息，我们可以根据具体的情况，选择两种或两种以上火灾传感器组来检测火灾状况。

本火灾预警报警系统采用了两级传感器信息融合，一级是局部(即象素级)融合，采用经典的自适应加权融合估计算法，克服了单个传感器的不确定性和局限性，获得被测对象的一致性解释与描述。

二级是在全局(即决策层)进行融合，采用证据理论。

Dempster-shafer(D-S)证据理论是概率论的推广，它允许人们对不确定性问题进行建模，并进行推理，能够更加客观的反映事物的不确定性。

在具体设计时，本文分三个模块进行处理，D-S 合成模块、BPA 模块、局部决策模块。

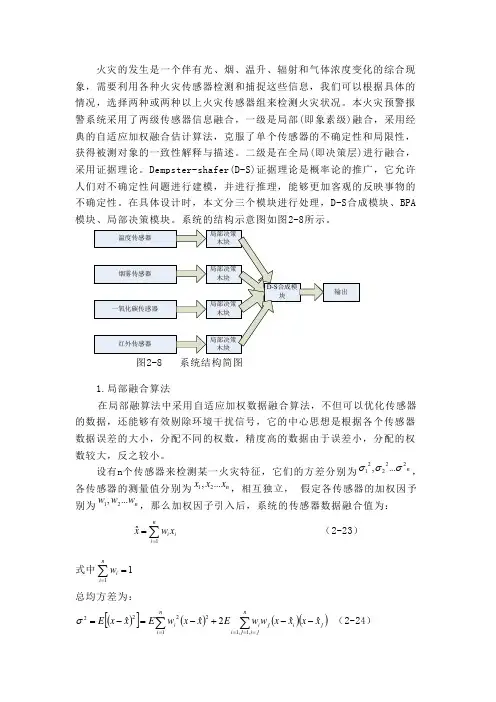
系统的结构示意图如图2-8所示。

图2-8 系统结构简图1.局部融合算法在局部融算法中采用自适应加权数据融合算法，不但可以优化传感器的数据，还能够有效剔除环境干扰信号，它的中心思想是根据各个传感器数据误差的大小，分配不同的权数，精度高的数据由于误差小，分配的权数较大，反之较小。

设有n 个传感器来检测某一火灾特征，它们的方差分别为n 22221...,σσσ，各传感器的测量值分别为n x x x ...,21，相互独立， 假定各传感器的加权因予别为n w w w ...,21，那么加权因子引入后，系统的传感器数据融合值为： ∑==ni i i x w x1ˆ （2-23） 式中11=∑=ni i w总均方差为：()[]()()()∑∑====--+-=-=ni nji j i jijii x x xx w w E x x w E xx E 1,1,12222ˆˆ2ˆˆσ （2-24）因为n x x x ...,21彼此相互独立，且是x 的无偏估计，所以：()()0ˆˆ=--j i x x xx E ()n j i j i ...2,1,,=≠ （2-25）则有：()∑∑==--=ni ni i i i w xx w 112222ˆσσ （2-26）上式中的σ是各加权因子i w 的多元二次函数，它的最小值的求取就是在加权因子n w w w ...,21满足归一化约束条件下多元函数极值的求取。

《改进D-S证据理论的决策融合算法研究及应用》篇一一、引言随着现代科技的不断发展，决策融合算法在各个领域得到了广泛应用。

其中，Dempster-Shafer（D-S）证据理论作为决策融合的重要方法之一，已经得到了广泛关注。

然而，D-S证据理论在处理决策信息时仍存在一些局限性，如对冲突信息的处理不够完善、对证据的独立性和一致性要求过于严格等。

因此，本文旨在研究改进D-S证据理论的决策融合算法，以提高决策的准确性和可靠性。

二、D-S证据理论概述D-S证据理论是一种基于信任度的决策融合方法，通过对证据进行分配函数描述和合并过程来达到信息融合的目的。

然而，在应用过程中，D-S证据理论仍存在一些问题。

首先，当存在冲突信息时，传统的D-S证据理论往往无法有效地处理这些信息，导致决策的准确性下降。

其次，D-S证据理论对证据的独立性和一致性要求较高，这在实际情况中往往难以满足。

三、改进D-S证据理论的决策融合算法针对上述问题，本文提出了一种改进的D-S证据理论决策融合算法。

该算法通过引入权重因子来调整每个证据的信任度分配，从而降低冲突信息对决策结果的影响。

同时，该算法还采用了基于相似度的证据关联性分析，以提高证据之间的相互关系信息在合并过程中的作用。

此外，针对不同情况下的实际应用场景，我们提出了更加灵活的调整策略来应对各种不确定性因素。

四、算法实现及性能分析为了验证改进算法的有效性，本文在多个实际应用场景中进行了实验。

实验结果表明，改进后的D-S证据理论决策融合算法能够更好地处理冲突信息，提高了决策的准确性。

同时，该算法能够更灵活地应对不同场景下的不确定性因素，具有较强的实用性和通用性。

五、应用案例分析本文以某智能交通系统为例，详细介绍了改进D-S证据理论决策融合算法在交通流量预测中的应用。

通过将多种交通信息作为证据进行融合处理，该算法能够更准确地预测交通流量变化趋势。

同时，我们还探讨了该算法在医疗诊断、机器人智能决策等其他领域的应用潜力。

证据理论的应用举例1 D-S 证据理论1.1关于D-S 证据理论的概念D-S 理论假定有一个用大写希腊字母 Θ 表示的环境（environment ），该环境是一个具有互斥和可穷举元素的集合：Θ = { θ1 , θ2 , ⋯ , θn }术语环境在集合论中又被称之为论域（the universe of discourse ）。

在D-S 理论中，习惯上把证据的信任度类似于物理对象的质量去考虑，即证据的质量（Mass ）支持了一个信任。

关于质量这一术语也被称为基本概率赋值（BPA , the Basic Probability Assignment ）或简称为基本赋值（Basic Assignment ）。

为了避免与概率论相混淆，我们将不使用这些术语，而是简单的使用质量（Mass ） 一词。

1.2 D-S 证据理论与概率论的区别D-S 理论和概率论的基本区别是关于无知的处理。

即使在无知的情况下，概率论也必须分布一个等量的概率值。

假如你没有先验知识，那么你必须假定每一种可能性的概率值都是P, NP 1=其中，N 是可能性的总数。

事实上，这赋值为P 是在无可奈何的情况下作出的。

但是，概率论也有一种冠冕堂皇的说法，即所谓的中立原理（the principle of indifference ）。

当仅仅有两种可能性存在的时候，比方说“有石油”和“没有石油”，分别用H 和⌝H 表示，那么出现应用中立原理的极端情况。

在与此相类似的情况中，即使在没有一点知识的条件下，那么也必须是P = 50 % ，因为概率论要求P(H)+P(⌝H) = 1，就是说，要么赞成H ，要么反对H ，对H 无知是不被允许的。

表1-1为证据理论与概率论的区别。

表1-1 证据理论与概率论的区别D-S理论不要求必须对无知假设H和反驳假设H赋以信任值，而是仅仅将Mass分配给你希望对其分配信任的环境的子集。

任一未被分配给具体子集的‘信任’被看成‘未表达意见’，并将其分配给环境 ，反驳一个假设的‘信任’，实际上，是对该假设的‘不信任’，但不是对该假设‘未表达意见’。