测量技术基础 第二章
- 格式:ppt
- 大小:4.88 MB
- 文档页数:7


第二章技术测量的基本知识及常用计算器具一、填空题1、测量实质上是将被测几何量与作为计量单位的标准量进行,从而确定被测几何量是的倍数或分数的过程。
2、一个完整的测量过程应包括、、和等四个方面。
3、检验是确定被测几何量是否在规定的之内,从而判断被测对象是否合格,而无须得出。
4、测量对象主要是指几何量,包括、、、和等。
5、我国的法定计量单位是以确定的。
6、测量方法是指测量时采用的和的综合。
7、测量结果有效值的准确性是由确定的。
8、计量器具按结构特点可以分为、、和等四类。
9、量仪与量具在结构上最主要的区别是:前者一般具有,系统,而后者没有此系统。
10、按原始信号转换原理的不同,量仪可分为:、、和等几种。
其中量仪使用最为广泛。
11、间接测量是指通过测量与被测尺寸有一定的其它尺寸,然后通过获得被测尺寸量值的方法。
12、间接测量法存在误差,故仅用在不能或不宜采用的场合。
13、相对测量是指将被测量与同它只有微小差别的已知同种量(一般为标准量),通过测量这两个量值间的以确定被测量值的方法。
14、综合测量能得到工件上几个有关几何量的,以判断工件是否,因而实质上综合测量一般属于。
15、接触测量时,计量器具的测量元件与工件表面,并有机械作用的,会使被测表面和计量器具的有关部分产生而影响测量精度。
16、根据在加工过程中,测量可分为主动测量与被动测量。
主动测量的目的是;被动测量的目的是;17、对于静态测量,被测量的量值是的;对于动态测量,被测量的量值是的。
18、动态测量可测出工件某些参数情况,经常用于测量工件的参数。
19、刻度间距是指标尺或刻度盘上两相邻刻线的;刻度值是指标尺或刻度盘上每一刻度间距所代表的。
刻度间距太小,影响测量的;刻度值越小,计量器具的。
20、示值范围是指计量器具标尺或刻度盘所指示的值到值的范围。
21、测量范围是指计量器具能够测出的被测尺寸的值到值的范围。
22、示值误差是指计量器具的与被测尺寸之差。
示值误差由仪器设计、和等因素产生。



第二章测量技术基础一、重点名词测量误差随机误差二、重点掌握/熟练掌握1.掌握量块的特性及量块的组合方法;2.掌握各种测量分类法的特点;3.掌握计量器具的分类及其技术性能指标。
4.掌握测量误差的含义及其表示法;5.掌握测量误差的基本类型及其处理原则;6.掌握随机误差的概念及测量结果的表示法;7.掌握测量误差的合成。
三、一般掌握1.掌握有关测量的概念;2.一般了解尺寸的传递系统。
88题一、判断题(正确的打√,错误的打╳)1.我国法定计量单位中,长度单位是米(m),与国际单位不一致。
(╳)2.量规只能用来判断零件是否合格,不能得出具体的尺寸。
(√)3.计量器具的示值范围即测量范围。
(╳)4.间接测量就是相对测量。
(╳)5.使用的量块越多,组合的尺寸越精确。
(╳)6.测量所得的值即为零件的真值。
(╳)7.通常所说的测量误差,一般是指相对误差。
(╳)8.多数随机误差是服从正态分布规律的。
(√)9.精密度高,正确度就一定高。
(╳)10.选择计量器具时,应保证其不确定度不大于其允许值u1。
(√)11.直接测量必为绝对测量。
(×)12.为减少测量误差,一般不采用间接测量。
(√)13.为提高测量的准确性,应尽量选用高等级量块作为基准进行测量。
(×)14.使用的量块数越多,组合出的尺寸越准确。
( ×)15.0~25mm千分尺的示值范围和测量范围是一样的。
(√)16.用多次测量的算术平均值表示测量结果,可以减少示值误差数值。
(×)17.某仪器单项测量的标准偏差为ζ=0.006mm,若以9次重复测量的平均值作为测量结果,其测量误差不应超过0.002mm。
(×)18.测量过程中产生随机误差的原因可以一一找出,而系统误差是测量过程中所不能避免的。
( ×)19.选择较大的测量力,有利于提高测量的精确度和灵敏度。
( × )20.对一被测值进行大量重复测量时其产生的随机误差完全服从正态分布规律。




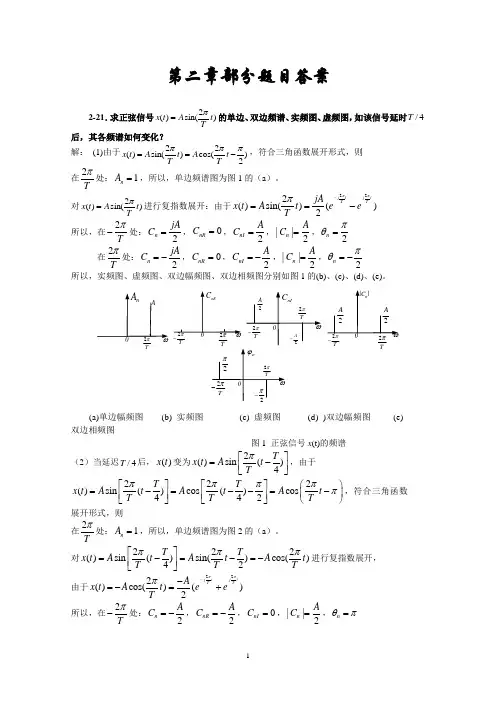
第二章部分题目答案2-21.求正弦信号)2sin()(t TA t x π=的单边、双边频谱、实频图、虚频图,如该信号延时4/T 后,其各频谱如何变化?解: (1)由于22()sin()cos()2x t A t A t T T πππ==-,符合三角函数展开形式,则 在2Tπ处:1n A =,所以,单边频谱图为图1的(a )。
对)2sin()(t T A t x π=进行复指数展开:由于222()sin()()2j t j tT T jA x t A t e e T πππ-==- 所以,在2Tπ-处:2n jA C =,0nR C =,2nI A C =,||2n A C =,2n πθ=在2T π处:2n jA C =-,0nR C =,2nI A C =-,||2n A C =,2n πθ=- 所以,实频图、虚频图、双边幅频图、双边相频图分别如图1的(b)、(c)、(d)、(e)。
2Tπ2Tπ-(a)单边幅频图 (b) 实频图 (c) 虚频图 (d) )双边幅频图 (e) 双边相频图图1 正弦信号x (t)的频谱 (2)当延迟4/T 后,()x t 变为2()sin ()4T x t A t Tπ⎡⎤=-⎢⎥⎣⎦,由于222()sin ()cos ()cos 442T T x t A t A t A t T T T πππππ⎡⎤⎡⎤⎛⎫=-=--=- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭,符合三角函数展开形式,则在2Tπ处:1n A =,所以,单边频谱图为图2的(a )。
对222()sin ()sin()cos()42T T x t A t A t A t TT T πππ⎡⎤=-=-=-⎢⎥⎣⎦进行复指数展开, 由于222()cos()()2j t j tT TA x t A t e e T πππ--=-=+ 所以,在2Tπ-处:2n A C =-,2nR A C =-,0nI C =,||2n A C =,n θπ=在2T π处:2n A C =-,2nR A C =-,0nI C =,||2n AC =,n θπ= 所以,实频图、虚频图、双边幅频图、双边相频图分别如图2的(b)、(c)、(d)、(e)。
