第9讲 圆轴扭转时的变形和刚度条件
- 格式:doc
- 大小:299.50 KB
- 文档页数:9




圆轴扭转的受力特点和变形特点
圆轴在受到扭矩作用时,其受力特点和变形特点与直轴不同。
下面我们来详细探讨一下圆轴扭转的受力特点和变形特点。
一、受力特点
在圆轴扭转过程中,受到的力主要是扭矩。
扭矩是使物体产生转动的力,其大小可以用公式T=FT*d来计算,其中T是扭矩,F是力,T是距离,d是轴的直径。
在圆轴扭转时,扭矩会使圆轴上的横截面产生剪切应力,剪切应力的大小与扭矩成正比。
二、变形特点
圆轴在受到扭矩作用时,会产生扭转变形。
这种变形主要表现为圆轴的各个横截面发生相对转动。
在圆轴扭转时,横截面之间的距离保持不变,因此不会出现拉伸或压缩变形。
同时,由于圆轴的刚度较大,所以扭转变形量相对较小。
三、影响圆轴扭转的因素
圆轴的扭转性能受到多种因素的影响,包括材料性质、截面形状、尺寸和边界条件等。
例如,圆轴的材料强度越高,其抵抗扭矩的能力就越强;截面形状和尺寸也会影响圆轴的扭转性能;边界条件如支撑条件和固定方式也会对圆轴的扭转性能产生影响。
四、圆轴扭转的应用
圆轴的扭转性能在机械工程中有着广泛的应用。
例如,在汽车和自行车中,车轴就是一种圆轴,它们需要承受来自轮子和车轮的扭矩。
在设计这些车轴时,需要考虑其受力特点和变形特点,以确保其具有足够的强度和刚度。
此外,在建筑工程和桥梁工程中,钢结构和钢筋混凝土结构的连接节点也需要利用圆轴的扭转性能来传递力和转矩。


第五节圆轴的扭转变形与刚度条件一、圆周的扭转变形圆轴受扭转时,除了考虑强度条件外,有时还要满足刚度条件。
例如机床的主轴,若扭转变形太大,就会引起剧烈的振动,影响加工工件的质量。
因此还需对轴的扭转变形有所限制。
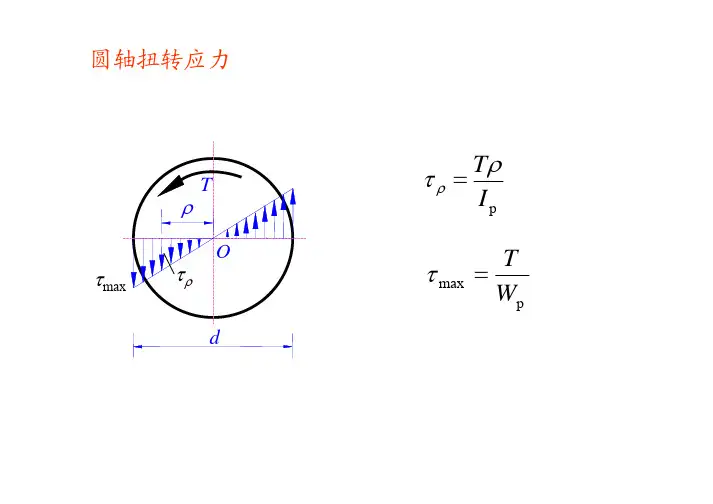
轴受扭转作用时所产生的变形,是用两横截面之间的相对扭转角ϕ表示的,如下图所示。
由于γ角与ϕ角对应同一段弧长,故有ϕ·R = γ·l (a)式中的R是轴的半径,由剪切虎克定律,τ=G·γ,所以可得ϕ=τ·l/ (G·γ)(b)式中τ=M·R/ Jρ,代入(b)得:ϕ=M·l/ (G·Jρ)(1-46)公式(1-46)是截面A、B之间的相对扭转角计算公式,ϕ的单位是rad。
两截面间的相对扭转角与两截面间的距离l成正比,为了便于比较,工程上一般都用单位轴长上的扭转角θ表示扭转变形的大小:θ=ϕ/ l=M/ (G·Jρ)(1-47)θ的单位是rad/m。
如果扭矩的单位是N·m,G的单位MP a,Jρ的单位m4。
但是工程实际中规定的许用单位扭转角[θ]是以°/m 为单位的,则公式(1-47)可改写为:(1-48)式中G·Jρ称为轴的抗扭刚度,取决于轴的材料与截面的形状与尺寸。
轴的G·Jρ值越大,则扭转角θ越小,表明抗扭转变形的能力越强。
二、扭转的刚度条件圆轴受扭转时如果变形过大,就会影响轴的正常工作。
轴的扭转变形用许用扭转角[θ]来加以限制,其单位为°/m,其数值的大小根据载荷性质、工作条件等确定。
在一般传动和搅拌轴的计算中,可选取[θ]=0.5°/m~10°/m。
由此得出轴的扭转刚度条件:θ=M/ (G·Jρ)·(180/ π)≤[θ](1-49)圆轴设计时,一般要求既满足强度条件(1-45),又要满足刚度条件(1-49)。



圆轴扭转时的变形与刚度计算圆轴扭转时的变形与刚度计算是机械工程中的一项重要内容。
圆轴扭转是指轴材受到扭矩作用产生的变形现象。
在圆轴扭转中,轴材会经历弹性变形和塑性变形。
弹性变形是指轴材在扭矩作用下恢复原状的变形,而塑性变形则是指超过轴材弹性限度后产生的永久变形。
圆轴扭转可通过弹性力学原理进行分析。
根据胡克定律,弹性体的应力与应变之间有线性关系。
对圆轴来说,变形主要体现为轴材的剪切变形。
剪切形变角度φ与应力τ之间的关系为:τ=G*φ其中,G是剪切模量,表示材料抵抗剪切变形的能力。
φ是单位长度的圆周上小弧δs扭转对应的形变角。
通过积分可得到实际的扭转角θ与应力之间的关系:τ=G*θ/L其中,L是轴材的长度。
对于圆轴来说,扭转力矩T与应力分布之间的关系为:T=τ*A其中,A是轴材的横截面积。
将τ带入等式可得到扭转角与扭转力矩之间的关系:T=G*θ*A/L从上述公式可知,轴材扭转角度与扭转力矩之间存在一线性关系,即扭转刚度k。
k=G*A/L通过上述公式,可以得到轴材的扭转刚度。
扭转刚度越大,则轴材对于扭转力矩的抵抗能力越强。
此外,圆轴扭转时的变形也与材料的断裂强度有关。
当扭转力矩超过材料的断裂强度时,轴材会发生塑性变形,产生永久变形。
在实际应用中,通常会根据所需要的刚度和工作条件来选择合适的轴材及其横截面积。
在计算中需要考虑到轴材的材料特性、几何形状和所受的载荷等因素。
此外,还可以通过模拟实验或数值计算的方法对扭转变形和刚度进行验证和评估。
总之,圆轴扭转时的变形与刚度计算是机械工程中的一项重要内容。
通过弹性力学原理,可以分析轴材在扭转力矩作用下的变形情况,并计算出轴材的扭转刚度。
这对于轴类零件的设计和工程应用具有重要意义。
第9讲教学方案——圆轴扭转时的变形和刚度条件非圆截面杆的扭转§3-5 圆轴扭转时的变形和刚度条件扭转角是指受扭构件上两个横截面绕轴线的相对转角。
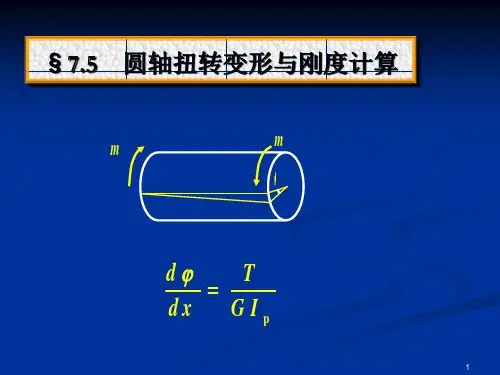
对于圆轴,由式(4-10) pGI Tdxd =φ 所以p l0plGI Tldx GI T d ===⎰⎰φφ(rad ) (4-17) 式中p GI 称为圆轴的抗扭刚度,它为剪切模量与极惯性矩乘积。
p GI 越大,则扭转角φ越小。
让dxd φϕ=,为单位长度相对扭角,则有pGI T=ϕ(rad/m ) 扭转的刚度条件:[]ϕϕ≤=Pmax GI T(rad/m ) (4-18) 或[]ϕπϕ≤⨯=180GI T P max (°/m ) (4-19) 例3-3 如图4-13的传动轴,500=n r/min ,5001=N 马力,2002=N 马力,3003=N 马力,已知[]70=τMPa ,[]1=ϕ°/m ,80=G GPa 。
求:确定AB 和BC 段直径。
解: 1)计算外力偶矩702470241==nN m A (N ·m ) 6.280970242==nN m B (N ·m ) 4.421470243==nN m C (N ·m ) 作扭矩T 图,如图4-13b 所示。
2)计算直径d AB 段:由强度条件,[]τπτ≤==31max 16d T W T t[]801070702416163631≈⨯⨯⨯=≥πτπTd (mm ) 由刚度条件[]ϕππϕ≤⨯=18032dG T 416.8411080180702432][G 180T 32d 429421=⨯⨯⨯⨯⨯=⨯≥πϕπ(mm ) 取 6.841=d mmBC 段:同理,由扭转强度条件得 672≥d mm 由扭转刚度条件得 5.742≥d mm 取5.742=d mm例3-4 如图4-14所示等直圆杆,已知10m 0=KN ·m ,试绘扭矩图。
解:设两端约束扭转力偶为A m ,B m(1)由静力平衡方程0=∑x m 得000=-+-B A m m m mB A m m = (a ) 此题属于一次超静定。
(2)由变形协调方程(可解除B 端约束),用变形叠加法有0321B B B B =+-=φφφφ (b )(3)物理方程p 0B GI a m 1⋅-=φ,p 0B GI a 2m 2⋅+=φ,pB B GI a3m 3⋅-=φ (c ) 由式(c ),(b )得0GI a 3m GI a 2m GI a m pB p 0p 0=⋅-⋅+⋅-即0m 3m 2m B 00=-+-并考虑到(a ),结果3m m m 0B A == 假设的力偶转向正确,绘制扭矩图如图4-14c 所示。
§3-6 圆柱形密圈螺旋弹簧的应力和变形计算螺旋弹簧如图4-15a 所示。
当螺旋角5<α时,可近似认为簧丝的横截面与弹簧轴线在同一平面内1.弹簧丝横截面上的应力如图4-15b 以簧丝的任意横截面取出密圈弹簧的上部分为研究对象,根据平衡方程,横截面上剪力由Q 引起的剪应力214d P A Q πτ==,而且认为1τ均匀分布于横截面上(图4-15c );若将簧丝的受力视为直杆的纯扭转,由T 引起的最大剪应力(图4-15d )332816d PDd T W T t ππτ=== P Q =,扭矩PD T 21=。
,一般将这种弹簧称为密圈螺旋弹簧。
所以在簧丝横截面内侧A 点有3321max 8218dPDk D d d PD ππτττ=⎪⎭⎫ ⎝⎛+=+= (4-20) 其中 D2d1k += (4-21) 当101Dd<,略去剪应力1τ所引起的误差005<τ,可用近似式3max dPD8πτ=(4-22) 对某些工程实际问题,如机车车辆中的重弹簧,Dd的值并不太小,此时不仅要考虑剪力,还要考虑弹簧丝曲率的影响,进一步理论分析和修正系数k 的选取可见有关参考书。
密圈弹簧丝的强度条件是[]ττ≤max (4-23)式中:[]τ—弹簧丝材料的许用剪应力2. 弹簧的变形设弹簧在轴向压力(或拉力)作用下,轴线方向的总缩短(或伸长)量为λ,这是弹簧的整体的压缩(或拉伸)变形。
如图4-16a 、b ,外力对弹簧做功λP 21W =。
簧丝横截面上,距圆心为ρ的任意点的扭转剪应力为44163221dPD d PD I T P πρπρρτρ=== (a ) 如认为簧丝是纯扭转,则其相应的单位体积变形能是8222221282d G D P G u πρτρ== (b ) 弹簧的变形能应为⎰=VudV U (c )此处ds dA dV ⋅=,其中ρπρd 2dA ⋅=,弹簧丝总长为n D S ⋅=π,n 为弹簧有效圈数。
于是积分式(c )得4322d82222Gd nD P 4d 2d G D P 128Dn U =⋅=⎰ρπρπρπ (d )由λP W U 21==,则得到 4343648Gd n PR Gd n PD ==λ (4-24)式中2D R =是弹簧圈的平均半径。
若引入记号nD Gd c 348= 则式(4-24)可写成cP=λ (4-25) c 代表弹簧抵抗变形的能力,称为弹簧刚度。
可见λ与c 成反比,c 越大则λ越小。
例3-5 某柴油机的气阀弹簧,簧圈平均半径mm 5.59=R ,簧丝直径mm 14=d ,有效圈数5=n 。
GPa 80=G 。
弹簧工作时受3P max =KN ,求此弹簧的最大压缩量与最大剪应力(略去弹簧曲率的影响)解:由变形公式求最大压缩量43933343)1014(10805)105.59(105.264Gd n PR 64--⨯⨯⨯⨯⨯⨯==λ mm m 8.5410543=⨯=-考虑剪切力时33333max )1014(105.592105.28)5.594141(d PD 8)D 2d 1(--⨯⨯⨯⨯⨯⨯⨯+=+=ππτ MPa 292276059.1=⨯=不考虑剪力影响时MPa 276'm ax =τ,相差5.9% 。
由于1018.11Dd >= ,还应考虑曲率影响,此处从略。
§3-7 非圆截面杆的扭转问题工程上受扭转的杆件除常见的圆轴外,还有其他形状的截面,下面简要介绍矩形截面,如图4-17a 。
杆件受扭转力偶作用发生变形,变形后其横截面将不再保持平面,而发生“翘曲”(图4-17b )。
扭转时,若各横截面翘曲是自由的,不受约束,此时相邻横截面的翘曲处处相同,杆件轴向纤维的长度无变化,因而横截面上,只有剪应力没有正应力,这种扭转称为自由扭转。
此时横截面上剪应力规律如下(图14-7c ):1)边缘各点的剪应力τ与周边相切,沿周边方向形成剪流。
2)max τ发生在矩形长边中点处,大小为:kmax W T=τ , 2k hb W α= (4-26)次大剪应力发生在短边中点,大小为max 1v ττ=四个角点处剪应力0=τ。
3)杆件两端相对扭转角φ kGI Tl=φ , 2k hb I β= (4-27) 其中系数v ,,βα与bh有关,可查表(见有关参考书)。
注意到:对非圆截面扭转,平面假设不再成立。
上面计算公式是将弹性力学的分析结果写成圆轴公式形式。
当10>bh 时,截面成为狭长矩形,此时31≈=βα,若以δ表示狭长矩形的短边长度,则式(4-26)化为⎪⎪⎭⎪⎪⎬⎫==k k max GI Tl W T φτ (4-28)其中2k h 31W δ=,3k h 31I δ=,此时长边上应力趋于均匀,如图4-17d 所示。
在工程实际结构中受扭构件某些横截面的翘曲要受到约束(如支承处,加载面处等)。
此扭转为约束扭转,其特点是轴向纤维的长度发生改变,导致横截面上除扭转剪应力外还出现正应力。
对非圆截面杆件约束扭转提示:(1)对薄壁截面(如型钢)将引起较大的正应力。
有关内容可参“开口薄壁杆件约束扭转”专题;(2)对实心截面杆件(如矩形,椭圆形)正应力一般很小可以略去,仍按自由扭转处理。
例3-6 某柴油机曲轴的曲柄截面Ⅰ—Ⅰ可以认为是矩形的,如图4-18。
在实用计算中,其扭转剪应力近似地按矩形截面杆受扭计算。
若mm 22=b ,mm 102=h ,已知曲柄所受扭矩为m N 281⋅=T ,试求这一矩形截面上的最大剪应力。
解:由截面Ⅰ—Ⅰ的尺寸求得64.422102==b h 查表,并利用插入法,求出 287.0=a于是得()MPa 8.19102210102287.02812332max =⨯⨯⨯==--ahb T τ。