下载文档原格式
哲学是一门思考人生、世界和知识的学科，而哲学家 f.b.希尔德布兰德(Frederick B. Hilbrandt) 倡导并应用数学方法来探索哲学问题，这在哲学界引起了广泛的关注和讨论。
本文将以从简到繁、由浅入深的方式来探讨 f.b.希尔德布兰德应用数学方法的哲学意义，希望能够更深入地理解这个主题。
1. f.b.希尔德布兰德的数学方法f.b.希尔德布兰德提出的数学方法主要包括概率、统计和逻辑推理。
他认为，通过运用数学的严谨性和逻辑性，可以更准确地分析和解决哲学上的一些复杂问题。
他运用概率和统计学的方法来分析道德问题，通过数据和逻辑推理来探讨道德决策的合理性和影响因素。
这种方法的提出引发了广泛的讨论，也为哲学研究开辟了新的思路。
2. 应用数学方法的哲学意义f.b.希尔德布兰德提出的数学方法使得哲学问题可以更加客观地被分析和讨论。
传统的哲学思考往往缺乏严密的逻辑和数据支持，而数学方法的运用可以弥补这一不足，使得哲学问题不再只是主观的臆测，而能够通过数据和逻辑得到更具说服力的解释。
数学方法的应用也拓展了哲学研究的范围和深度。
通过运用概率统计方法，可以更好地解释人类行为和决策背后的规律，使得道德哲学不再停留在理论层面，而能够更深入地理解人类行为的本质和动机。
3. 个人观点在我看来，f.b.希尔德布兰德应用数学方法的做法值得肯定，因为他为哲学研究提供了新的视角和方法。
数学是一门严谨的科学，它的运用可以使得哲学不再停留在纷繁的言辞和主观的臆测中，而能够更加客观地进行分析和讨论。
数学方法的应用也拓展了哲学的研究领域，使得哲学更具有现代科学的特点和魅力。
总结起来，f.b.希尔德布兰德提出的应用数学方法在哲学研究中具有重要的意义。
通过数学的严谨性和逻辑性，可以更客观、深入地分析和解决哲学问题，同时也拓展了哲学研究的范围和深度。
希望未来能有更多的哲学家借鉴和运用数学方法，为哲学研究带来更多的新思路和发现。
f.b.希尔德布兰德在哲学界倡导并应用数学方法来探索哲学问题确实引起了广泛的关注和讨论。
JOURNAL OF FORMALIZED MATHEMATICSV olume10,Released1998,Published2003Inst.of Computer Science,Univ.of BiałystokA Theory of Boolean Valued Functions and PartitionsShunichi Kobayashi Shinshu UniversityNaganoKui Jia Shinshu UniversityNaganoSummary.In this paper,we define Boolean valued functions.Some of their algebraic properties are proved.We also introduce and examine the infimum and supremum of Booleanvalued functions and their properties.In the last section,relations between Boolean valuedfunctions and partitions are discussed.MML Identifier:BVFUNC_1.WWW:/JFM/Vol10/bvfunc_1.htmlThe articles[11],[4],[13],[1],[16],[15],[14],[2],[3],[9],[12],[8],[10],[7],[5],and[6]provide the notation and terminology for this paper.1.B OOLEAN O PERATIONSIn this paper Y denotes a set.Let k,l be boolean sets.The functor k⇒l is defined as follows:(Def.1)k⇒l=¬k∨l.The functor k⇔l is defined as follows:(Def.2)k⇔l=¬(k⊕l).Let us note that the functor k⇔l is commutative.Let k,l be boolean sets.Note that k⇒l is boolean and k⇔l is boolean.Let us note that every set which is boolean is also natural.Let k,l be boolean sets.Let us observe that k≤l if and only if:(Def.3)k⇒l=true.We introduce k l as a synonym of k≤l.2.B OOLEAN V ALUED F UNCTIONSLet us consider Y.The functor BVF(Y)is defined as follows:(Def.4)BVF(Y)=Boolean Y.Let Y be a set.Note that BVF(Y)is functional and non empty.Let Y be a set.Note that every element of BVF(Y)is boolean-valued.In the sequel Y is a non empty set.Let a be a boolean-valued function and let x be a set.We introduce Pj(a,x)as a synonym of a(x).1c Association of Mizar UsersLet us consider Y and let a be an element of BVF(Y).Then¬a is an element of BVF(Y).Let b be an element of BVF(Y).Then a∧b is an element of BVF(Y).Let p,q be boolean-valued functions.The functor p∨q yielding a function is defined as follows: (Def.5)dom(p∨q)=dom p∩dom q and for every set x such that x∈dom(p∨q)holds(p∨q)(x)= p(x)∨q(x).Let us note that the functor p∨q is commutative.The functor p⊕q yields a function and is defined by:(Def.6)dom(p⊕q)=dom p∩dom q and for every set x such that x∈dom(p⊕q)holds(p⊕q)(x)= p(x)⊕q(x).Let us note that the functor p⊕q is commutative.Let p,q be boolean-valued functions.One can check that p∨q is boolean-valued and p⊕q is boolean-valued.Let A be a non empty set and let p,q be elements of Boolean A.Then p∨q is an element of Boolean A and it can be characterized by the condition:(Def.7)For every element x of A holds(p∨q)(x)=p(x)∨q(x).Then p⊕q is an element of Boolean A and it can be characterized by the condition:(Def.8)For every element x of A holds(p⊕q)(x)=p(x)⊕q(x).Let us consider Y and let a,b be elements of BVF(Y).Then a∨b is an element of BVF(Y).Then a⊕b is an element of BVF(Y).Let p,q be boolean-valued functions.The functor p⇒q yields a function and is defined as follows:(Def.9)dom(p⇒q)=dom p∩dom q and for every set x such that x∈dom(p⇒q)holds(p⇒q)(x)=p(x)⇒q(x).The functor p⇔q yielding a function is defined as follows:(Def.10)dom(p⇔q)=dom p∩dom q and for every set x such that x∈dom(p⇔q)holds(p⇔q)(x)=p(x)⇔q(x).Let us note that the functor p⇔q is commutative.Let p,q be boolean-valued functions.One can check that p⇒q is boolean-valued and p⇔q is boolean-valued.Let A be a non empty set and let p,q be elements of Boolean A.Then p⇒q is an element of Boolean A and it can be characterized by the condition:(Def.11)For every element x of A holds(p⇒q)(x)=¬Pj(p,x)∨Pj(q,x).Then p⇔q is an element of Boolean A and it can be characterized by the condition:(Def.12)For every element x of A holds(p⇔q)(x)=¬(Pj(p,x)⊕Pj(q,x)).Let us consider Y and let a,b be elements of BVF(Y).Then a⇒b is an element of BVF(Y).Then a⇔b is an element of BVF(Y).Let us consider Y.The functor false(Y)yields an element of Boolean Y and is defined by: (Def.13)For every element x of Y holds Pj(false(Y),x)=false.Let us consider Y.The functor true(Y)yielding an element of Boolean Y is defined as follows: (Def.14)For every element x of Y holds Pj(true(Y),x)=true.One can prove the following propositions:(4)1For every boolean-valued function a holds¬¬a=a.1The propositions(1)–(3)have been removed.(5)For every element a of Boolean Y holds ¬true (Y )=false (Y )and ¬false (Y )=true (Y ).(6)For all elements a ,b of Boolean Y holds a ∧a =a .(7)For all elements a ,b ,c of Boolean Y holds (a ∧b )∧c =a ∧(b ∧c ).(8)For every element a of Boolean Y holds a ∧false (Y )=false (Y ).(9)For every element a of Boolean Y holds a ∧true (Y )=a .(10)For every element a of Boolean Y holds a ∨a =a .(11)For all elements a ,b ,c of Boolean Y holds (a ∨b )∨c =a ∨(b ∨c ).(12)For every element a of Boolean Y holds a ∨false (Y )=a .(13)For every element a of Boolean Y holds a ∨true (Y )=true (Y ).(14)For all elements a ,b ,c of Boolean Y holds a ∧b ∨c =(a ∨c )∧(b ∨c ).(15)For all elements a ,b ,c of Boolean Y holds (a ∨b )∧c =a ∧c ∨b ∧c .(16)For all elements a ,b of Boolean Y holds ¬(a ∨b )=¬a ∧¬b .(17)For all elements a ,b of Boolean Y holds ¬(a ∧b )=¬a ∨¬b .Let us consider Y and let a ,b be elements of Boolean Y .The predicate a b is defined as follows:(Def.15)For every element x of Y such that Pj (a ,x )=true holds Pj (b ,x )=true .Let us note that the predicate a b is reflexive.The following propositions are true:(18)For all elements a ,b ,c of Boolean Y holds if a b and b a ,then a =b and if a b andb c ,then a c .(19)For all elements a ,b of Boolean Y holds a ⇒b =true (Y )iff a b .(20)For all elements a ,b of Boolean Y holds a ⇔b =true (Y )iff a =b .(21)For every element a of Boolean Y holds false (Y ) a and a true (Y ).3.I NFIMUM AND S UPREMUMLet us consider Y and let a be an element of Boolean Y .The functor INF a yields an element of Boolean Y and is defined as follows:(Def.16)INF a = true (Y ),if foreveryelement x of Y holds Pj (a ,x )=true ,false (Y ),otherwise.The functor SUP a yields an element of Boolean Y and is defined by:(Def.17)SUP a = false (Y ),if foreveryelement x of Y holds Pj (a ,x )=false ,true (Y ),otherwise.We now state two propositions:(22)For every element a of Boolean Y holds ¬INF a =SUP ¬a and ¬SUP a =INF ¬a .(23)INF false (Y )=false (Y )and INF true (Y )=true (Y )and SUP false (Y )=false (Y )andSUP true (Y )=true (Y ).Let us consider Y.Observe that false(Y)is constant.Let us consider Y.One can check that true(Y)is constant.Let Y be a non empty set.Note that there exists an element of Boolean Y which is constant.We now state several propositions:(24)For every constant element a of Boolean Y holds a=false(Y)or a=true(Y).(25)For every constant element d of Boolean Y holds INF d=d and SUP d=d.(26)For all elements a,b of Boolean Y holds INF(a∧b)=INF a∧INF b and SUP(a∨b)=SUP a∨SUP b.(27)For every element a of Boolean Y and for every constant element d of Boolean Y holdsINF(d⇒a)=d⇒INF a and INF(a⇒d)=SUP a⇒d.(28)For every element a of Boolean Y and for every constant element d of Boolean Y holdsINF(d∨a)=d∨INF a and SUP(d∧a)=d∧SUP a and SUP(a∧d)=SUP a∧d.(29)For every element a of Boolean Y and for every element x of Y holds Pj(INF a,x) Pj(a,x).(30)For every element a of Boolean Y and for every element x of Y holds Pj(a,x) Pj(SUP a,x).4.B OOLEAN V ALUED F UNCTIONS AND P ARTITIONSLet us consider Y,let a be an element of Boolean Y,and let P1be a partition of Y.We say that a is dependent of P1if and only if:(Def.18)For every set F such that F∈P1and for all sets x1,x2such that x1∈F and x2∈F holds a(x1)=a(x2).Next we state two propositions:(31)For every element a of Boolean Y holds a is dependent of I(Y).(32)For every constant element a of Boolean Y holds a is dependent of O(Y).Let us consider Y and let P1be a partition of Y.We see that the element of P1is a subset of Y.Let us consider Y,let x be an element of Y,and let P1be a partition of Y.Then EqClass(x,P1) is an element of P1.We introduce Lift(x,P1)as a synonym of EqClass(x,P1).Let us consider Y,let a be an element of Boolean Y,and let P1be a partition of Y.The functor INF(a,P1)yields an element of Boolean Y and is defined by the condition(Def.19).(Def.19)Let y be an element of Y.Then(i)if for every element x of Y such that x∈EqClass(y,P1)holds Pj(a,x)=true,thenPj(INF(a,P1),y)=true,and(ii)if it is not true that for every element x of Y such that x∈EqClass(y,P1)holds Pj(a,x)= true,then Pj(INF(a,P1),y)=false.Let us consider Y,let a be an element of Boolean Y,and let P1be a partition of Y.The functor SUP(a,P1)yields an element of Boolean Y and is defined by the condition(Def.20).(Def.20)Let y be an element of Y.Then(i)if there exists an element x of Y such that x∈EqClass(y,P1)and Pj(a,x)=true,thenPj(SUP(a,P1),y)=true,and(ii)if it is not true that there exists an element x of Y such that x∈EqClass(y,P1)and Pj(a,x)= true,then Pj(SUP(a,P1),y)=false.Next we state a number of propositions:(33)For every element a of Boolean Y and for every partition P1of Y holds INF(a,P1)is depen-dent of P1.(34)For every element a of Boolean Y and for every partition P1of Y holds SUP(a,P1)is depen-dent of P1.(35)For every element a of Boolean Y and for every partition P1of Y holds INF(a,P1) a.(36)For every element a of Boolean Y and for every partition P1of Y holds a SUP(a,P1).(37)For every element a of Boolean Y and for every partition P1of Y holds¬INF(a,P1)=SUP(¬a,P1).(38)For every element a of Boolean Y holds INF(a,O(Y))=INF a.(39)For every element a of Boolean Y holds SUP(a,O(Y))=SUP a.(40)For every element a of Boolean Y holds INF(a,I(Y))=a.(41)For every element a of Boolean Y holds SUP(a,I(Y))=a.(42)For all elements a,b of Boolean Y and for every partition P1of Y holds INF(a∧b,P1)=INF(a,P1)∧INF(b,P1).(43)For all elements a,b of Boolean Y and for every partition P1of Y holds SUP(a∨b,P1)=SUP(a,P1)∨SUP(b,P1).Let us consider Y and let f be an element of Boolean Y.The functor GPart f yielding a partition of Y is defined by:(Def.21)GPart f={{x;x ranges over elements of Y:f(x)=true},{x ;x ranges over elements of Y: f(x )=false}}\{/0}.The following two propositions are true:(44)For every element a of Boolean Y holds a is dependent of GPart a.(45)For every element a of Boolean Y and for every partition P1of Y such that a is dependent ofP1holds P1isfiner than GPart a.R EFERENCES[1]Grzegorz Bancerek.Sequences of ordinal numbers.Journal of Formalized Mathematics,1,1989./JFM/Vol1/ordinal2.html.[2]Czesław Byli´n ski.Functions and their basic properties.Journal of Formalized Mathematics,1,1989./JFM/Vol1/funct_1.html.[3]Czesław Byli´n ski.Functions from a set to a set.Journal of Formalized Mathematics,1,1989./JFM/Vol1/funct_2.html.[4]Czesław Byli´n ski.Some basic properties of sets.Journal of Formalized Mathematics,1,1989./JFM/Vol1/zfmisc_1.html.[5]Shunichi Kobayashi and Kui Jia.A theory of partitions.Part I.Journal of Formalized Mathematics,10,1998./JFM/Vol10/partit1.html.[6]Jarosław Kotowicz.Monotone real sequences.Subsequences.Journal of Formalized Mathematics,1,1989./JFM/Vol1/seqm_3.html.[7]Adam Naumowicz and MariuszŁapi´n ski.On T1reflex of topological space.Journal of Formalized Mathematics,10,1998.http:///JFM/Vol10/t_1topsp.html.[8]Takaya Nishiyama and Yasuho Mizuhara.Binary arithmetics.Journal of Formalized Mathematics,5,1993./JFM/Vol5/binarith.html.[9]Beata Padlewska.Families of sets.Journal of Formalized Mathematics,1,1989./JFM/Vol1/setfam_1.html.[10]Konrad Raczkowski and PawełSadowski.Equivalence relations and classes of abstraction.Journal of Formalized Mathematics,1,1989./JFM/Vol1/eqrel_1.html.[11]Andrzej Trybulec.Tarski Grothendieck set theory.Journal of Formalized Mathematics,Axiomatics,1989./JFM/Axiomatics/tarski.html.[12]Andrzej Trybulec.Function domains and Frænkel operator.Journal of Formalized Mathematics,2,1990./JFM/Vol2/fraenkel.html.[13]Zinaida Trybulec.Properties of subsets.Journal of Formalized Mathematics,1,1989./JFM/Vol1/subset_1.html.[14]Edmund Woronowicz.Relations and their basic properties.Journal of Formalized Mathematics,1,1989./JFM/Vol1/relat_1.html.[15]Edmund Woronowicz.Interpretation and satisfiability in thefirst order logic.Journal of Formalized Mathematics,2,1990.http:///JFM/Vol2/valuat_1.html.[16]Edmund Woronowicz.Many-argument relations.Journal of Formalized Mathematics,2,1990./JFM/Vol2/margrel1.html.Received October22,1998Published January2,2004。
线性代数英语词汇大集合========================================================================= Aadjont(adjugate) of matrix A A 的伴随矩阵augmented matrix A 的增广矩阵Bblock diagonal matrix 块对角矩阵block matrix 块矩阵basic solution set 基础解系CCauchy-Schwarz inequality 柯西- 许瓦兹不等式characteristic equation 特征方程characteristic polynomial 特征多项式coffcient matrix 系数矩阵cofactor 代数余子式cofactor expansion 代数余子式展开column vector 列向量commuting matrices 交换矩阵consistent linear system 相容线性方程组Cramer's rule 克莱姆法则Cross- product term 交叉项DDeterminant 行列式Diagonal entries 对角元素Diagonal matrix 对角矩阵Dimension of a vector space V 向量空间V 的维数Eechelon matrix 梯形矩阵eigenspace 特征空间eigenvalue 特征值eigenvector 特征向量eigenvector basis 特征向量的基elementary matrix 初等矩阵elementary row operations 行初等变换Ffull rank 满秩fundermental set of solution 基础解系Ggrneral solution 通解Gram-Schmidt process 施密特正交化过程Hhomogeneous linear equations 齐次线性方程组Iidentity matrix 单位矩阵inconsistent linear system 不相容线性方程组indefinite matrix 不定矩阵indefinit quatratic form 不定二次型infinite-dimensional space 无限维空间inner product 内积inverse of matrix A 逆矩阵JKLlinear combination 线性组合linearly dependent 线性相关linearly independent 线性无关linear transformation 线性变换lower triangular matrix 下三角形矩阵Mmain diagonal of matrix A 矩阵的主对角matrix 矩阵Nnegative definite quaratic form 负定二次型negative semidefinite quadratic form 半负定二次型nonhomogeneous equations 非齐次线性方程组nonsigular matrix 非奇异矩阵nontrivial solution 非平凡解norm of vector V 向量V 的范数normalizing vector V 规范化向量Oorthogonal basis 正交基orthogonal complemen t 正交补orthogonal decomposition 正交分解orthogonally diagonalizable matrix 矩阵的正交对角化orthogonal matrix 正交矩阵orthogonal set 正交向量组orthonormal basis 规范正交基orthonomal set 规范正交向量组Ppartitioned matrix 分块矩阵positive definite matrix 正定矩阵positive definite quatratic form 正定二次型positive semidefinite matrix 半正定矩阵positive semidefinite quadratic form 半正定二次型Qquatratic form 二次型Rrank of matrix A 矩阵A 的秩r(A )reduced echelon matrix 最简梯形阵row vector 行向量Sset spanned by { } 由向量{ } 所生成similar matrices 相似矩阵similarity transformation 相似变换singular matrix 奇异矩阵solution set 解集合standard basis 标准基standard matrix 标准矩阵Isubmatrix 子矩阵subspace 子空间symmetric matrix 对称矩阵Ttrace of matrix A 矩阵A 的迹tr ( A )transpose of A 矩阵A 的转秩triangle inequlity 三角不等式trivial solution 平凡解Uunit vector 单位向量upper triangular matrix 上三角形矩阵Vvandermonde matrix 范得蒙矩阵vector 向量vector space 向量空间WZzero subspace 零子空间zero vector 零空间==============================================================================向量：vector 向量的长度（模）：零向量: zero vector负向量: 向量的加法：addition 三角形法则：平行四边形法则：多边形法则减法向量的标量乘积：scalar multiplication 向量的线性运算线性组合：linear combination 线性表示，线性相关（linearly dependent），线性无关（linearly independent），原点（origin）位置向量（position vector）线性流形（linear manifold）线性子空间（linear subspace）基（basis）仿射坐标（affine coordinates），仿射标架（affine frame），仿射坐标系（affine coordinate system）坐标轴（coordinate axis）坐标平面卦限（octant）右手系左手系定比分点线性方程组（system of linear equations齐次线性方程组（system of homogeneous linear equations）行列式（determinant）维向量向量的分量（component）向量的相等和向量零向量负向量标量乘积维向量空间（vector space）自然基行向量（row vector）列向量（column vector）单位向量（unit vector）直角坐标系（rectangular coordinate system），直角坐标（rectangular coordinates），射影（projection）向量在某方向上的分量，正交分解，向量的夹角，内积（inner product）标量积（scalar product），数量积，方向的方向角，方向的方向余弦；二重外积外积（exterior product），向量积（cross product），混合积（mixed product，scalar triple product）==================================================================================（映射（mapping）），（象（image）），（一个原象（preimage）），（定义域（domain）），（值域（range）），（变换（transformation）），（单射（injection）），（象集），（满射（surjection）），（一一映射，双射（bijection）），（原象），（映射的复合，映射的乘积），（恒同映射，恒同变换（identity mapping）），（逆映射（inverse mapping））；（置换（permutation）），（阶对称群（symmetric group）），（对换（transposition）），（逆序对），（逆序数），（置换的符号（sign）），（偶置换（even permutation）），（奇置换（odd permutation））；行列式（determinant），矩阵（matrix），矩阵的元（entry），（方阵（square matrix）），（零矩阵（zero matrix）），（对角元），（上三角形矩阵（upper triangular matrix）），（下三角形矩阵（lower triangular matrix）），（对角矩阵（diagonal matrix）），（单位矩阵（identity matrix）），转置矩阵（transpose matrix），初等行变换（elementary row transformation），初等列变换（elementary column transformation）；（反称矩阵（skew-symmetric matrix））；子矩阵（submatrix），子式（minor），余子式（cofactor），代数余子式（algebraic cofactor），（范德蒙德行列式（Vandermonde determinant））；（未知量），（系数矩阵），（方程的系数（coefficient）），（常数项（constant）），（线性方程组的解（solution）），（增广矩阵（augmented matrix）），（零解）；子式的余子式，子式的代数余子式===================================================================================线性方程组与线性子空间（阶梯形方程组），（方程组的初等变换），行阶梯矩阵（row echelon matrix），主元，简化行阶梯矩阵（reduced row echelon matrix），（高斯消元法（Gauss elimination）），（解向量），（同解），（自反性（reflexivity）），（对称性（symmetry）），（传递性（transitivity）），（等价关系（equivalence））；（齐次线性方程组的秩（rank））；（主变量），（自由位置量），（一般解），向量组线性相关，向量组线性无关，线性组合，线性表示，线性组合的系数，（向量组的延伸组）；线性子空间，由向量组张成的线性子空间；基，坐标，（自然基），向量组的秩；（解空间），线性子空间的维数（dimension），齐次线性方程组的基础解系（fundamental system of solutions）；（平面束（pencil of planes））（导出组），线性流形，（方向子空间），（线性流形的维数），（方程组的特解）；（方程组的零点），（方程组的图象），（平面的一般方程），（平面的三点式方程），（平面的截距式方程），（平面的参数方程），（参数），（方向向量）；（直线的方向向量），（直线的参数方程），（直线的标准方程），（直线的方向系数），（直线的两点式方程），（直线的一般方程）；=====================================================================================矩阵的秩与矩阵的运算线性表示，线性等价，极大线性无关组；（行空间，列空间），行秩（row rank），列秩（column rank），秩，满秩矩阵，行满秩矩阵，列满秩矩阵；线性映射（linear mapping），线性变换（linear transformation），线性函数（linear function）；（零映射），（负映射），（矩阵的和），（负矩阵），（线性映射的标量乘积），（矩阵的标量乘积），（矩阵的乘积），（零因子），（标量矩阵（scalar matrix）），（矩阵的多项式）；（退化的（degenerate）方阵），（非退化的（non-degenerate）方阵），（退化的线性变换），（非退化的线性变换），（逆矩阵（inverse matrix）），(可逆的（invertible），（伴随矩阵（adjoint matrix））；（分块矩阵（block matrix）），（分块对角矩阵（block diagonal matrix））；初等矩阵（elementary matrix），等价（equivalent）；（象空间），（核空间（kernel）），（线性映射的秩），（零化度（nullity））==================================================================================== transpose of matrix 倒置矩阵; 转置矩阵【数学词汇】transposed matrix 转置矩阵【机械专业词汇】matrix transpose 矩阵转置【主科技词汇】transposed inverse matrix 转置逆矩阵【数学词汇】transpose of a matrix 矩阵的转置【主科技词汇】permutation matrix 置换矩阵; 排列矩阵【主科技词汇】singular matrix 奇异矩阵; 退化矩阵; 降秩矩阵【主科技词汇】unitary matrix 单式矩阵; 酉矩阵; 幺正矩阵【主科技词汇】Hermitian matrix 厄密矩阵; 埃尔米特矩阵; 艾米矩阵【主科技词汇】inverse matrix 逆矩阵; 反矩阵; 反行列式; 矩阵反演; 矩阵求逆【主科技词汇】matrix notation 矩阵符号; 矩阵符号表示; 矩阵记号; 矩阵运算【主科技词汇】state transition matrix 状态转变矩阵; 状态转移矩阵【航海航天词汇】torque master 转矩传感器; 转矩检测装置【主科技词汇】spin matrix 自旋矩阵; 旋转矩阵【主科技词汇】moment matrix 动差矩阵; 矩量矩阵【航海航天词汇】Jacobian matrix 雅可比矩阵; 导数矩阵【主科技词汇】relay matrix 继电器矩阵; 插接矩阵【主科技词汇】matrix notation 矩阵表示法; 矩阵符号【航海航天词汇】permutation matrix 置换矩阵【航海航天词汇】transition matrix 转移矩阵【数学词汇】transition matrix 转移矩阵【机械专业词汇】transitionmatrix 转移矩阵【航海航天词汇】transition matrix 转移矩阵【计算机网络词汇】transfer matrix 转移矩阵【物理词汇】rotation matrix 旋转矩阵【石油词汇】transition matrix 转换矩阵【主科技词汇】circulant matrix 循环矩阵; 轮换矩阵【主科技词汇】payoff matrix 报偿矩阵; 支付矩阵【主科技词汇】switching matrix 开关矩阵; 切换矩阵【主科技词汇】method of transition matrices 转换矩阵法【航海航天词汇】stalling torque 堵转力矩, 颠覆力矩, 停转转矩, 逆转转矩【航海航天词汇】thin-film switching matrix 薄膜转换矩阵【航海航天词汇】rotated factor matrix 旋转因子矩阵【航海航天词汇】transfer function matrix 转移函数矩阵【航海航天词汇】transition probability matrix 转移概率矩阵【主科技词汇】energy transfer matrix 能量转移矩阵【主科技词汇】fuzzy transition matrix 模糊转移矩阵【主科技词汇】canonical transition matrix 规范转移矩阵【主科技词汇】matrix form 矩阵式; 矩阵组织【主科技词汇】stochastic state transition matrix 随机状态转移矩阵【主科技词汇】fuzzy state transition matrix 模糊状态转移矩阵【主科技词汇】matrix compiler 矩阵编码器; 矩阵编译程序【主科技词汇】test matrix 试验矩阵; 测试矩阵; 检验矩阵【主科技词汇】matrix circuit 矩阵变换电路; 矩阵线路【主科技词汇】reducible matrix 可简化的矩阵; 可约矩阵【主科技词汇】matrix norm 矩阵的模; 矩阵模; 矩阵模量【主科技词汇】rectangular matrix 矩形矩阵; 长方形矩阵【主科技词汇】running torque 额定转速时的转矩; 旋转力矩【航海航天词汇】transposed matrix 转置阵【数学词汇】covariance matrix 协变矩阵; 协方差矩阵【主科技词汇】unreduced matrix 未约矩阵; 不可约矩阵【主科技词汇】receiver matrix 接收机矩阵; 接收矩阵变换电路【主科技词汇】torque 传动转矩; 转矩; 阻力矩【航海航天词汇】pull-in torque 启动转矩; 输入转矩, 同步转矩, 整步转矩【航海航天词汇】parity matrix 奇偶校验矩阵; 一致校验矩阵【主科技词汇】bus admittance matrix 母线导纳矩阵; 节点导纳矩阵【主科技词汇】matrix printer 矩阵式打印机; 矩阵形印刷机; 点阵打印机【主科技词汇】dynamic matrix 动力矩阵; 动态矩阵【航海航天词汇】connection matrix 连接矩阵; 连通矩阵【主科技词汇】characteristic matrix 特征矩阵; 本征矩阵【主科技词汇】regular matrix 正则矩阵; 规则矩阵【主科技词汇】flexibility matrix 挠度矩阵; 柔度矩阵【主科技词汇】citation matrix 引文矩阵; 引用矩阵【主科技词汇】relational matrix 关系矩阵; 联系矩阵【主科技词汇】eigenmatrix 本征矩阵; 特征矩阵【主科技词汇】system matrix 系统矩阵; 体系矩阵【主科技词汇】system matrix 系数矩阵; 系统矩阵【航海航天词汇】recovery diode matrix 恢复二极管矩阵; 再生式二极管矩阵【主科技词汇】inverse of a square matrix 方阵的逆矩阵【主科技词汇】torquematic transmission 转矩传动装置【石油词汇】torque balancing device 转矩平衡装置【航海航天词汇】torque measuring device 转矩测量装置【主科技词汇】torque measuring apparatus 转矩测量装置【航海航天词汇】torque-tube type suspension 转矩管式悬置【主科技词汇】steering torque indicator 转向力矩测定仪; 转向转矩指示器【主科技词汇】magnetic dipole moment matrix 磁偶极矩矩阵【主科技词汇】matrix addressing 矩阵寻址; 矩阵寻址时频矩阵编址; 时频矩阵编址【航海航天词汇】stiffness matrix 劲度矩阵; 刚度矩阵; 劲度矩阵【航海航天词汇】first-moment matrix 一阶矩矩阵【主科技词汇】matrix circuit 矩阵变换电路; 矩阵电路【计算机网络词汇】reluctance torque 反应转矩; 磁阻转矩【主科技词汇】pull-in torque 启动转矩; 牵入转矩【主科技词汇】induction torque 感应转矩; 异步转矩【主科技词汇】nominal torque 额定转矩; 公称转矩【航海航天词汇】phototronics 矩阵光电电子学; 矩阵光电管【主科技词汇】column matrix 列矩阵; 直列矩阵【主科技词汇】inverse of a matrix 矩阵的逆; 逆矩阵【主科技词汇】lattice matrix 点阵矩阵【数学词汇】lattice matrix 点阵矩阵【物理词汇】canonical matrix 典型矩阵; 正则矩阵; 典型阵; 正则阵【航海航天词汇】moment matrix 矩量矩阵【主科技词汇】moment matrix 矩量矩阵【数学词汇】dynamic torque 动转矩; 加速转矩【主科技词汇】indecomposable matrix 不可分解矩阵; 不能分解矩阵【主科技词汇】printed matrix wiring 印刷矩阵布线; 印制矩阵布线【主科技词汇】decoder matrix circuit 解码矩阵电路; 译码矩阵电路【航海航天词汇】scalar matrix 标量矩阵; 标量阵; 纯量矩阵【主科技词汇】array 矩阵式组织; 数组; 阵列【计算机网络词汇】commutative matrix 可换矩阵; 可交换矩阵【主科技词汇】标准文档实用文案。
Three Theories of TruthCORRESPONDENCE THEORY Bertrand Russell The correspondence theory of truth corresponds to objective reality. A claim is made about the universe.We check out the claim with observations and physical measuring devices.While this theory properly emphasizes the notion that propositions are true when they correspond toreality, its proponents often have difficulty explaining what facts are and how propositions are related to them.Problems:•Verification involves subjective experiences as to both observations and requires interpretations.•Claims are made about things that are very large such as galaxies and the entire universe, as to its shape and size and duration that are beyond the ability of any human to have a directexperience of it.•Claims are made about things that are very small such as sub-atomic particle and small quanta of energy, bosons, gluons, neutrinos, charm particles and the like of which no human can have adirect experience.COHERENCE THEORY Bland Blanshard This explains how scientists can make claims about the very large and small objects using asystem of claims already accepted to be true.The theory is the belief that a proposition is true to the extent that it agrees with othertrue propositions. In contrast with the correspondence theory's emphasis on an independentreality, this view supposes that reliable beliefs constitute an inter-related system, each element of which entails every other.Truth is a property of a related group of consistent statements e.g., Mathematics, ScienceTruth is a systemic coherence of propositions interconnectedness of beliefsProblems:1.what if other judgments (statements) are false? Consistent error is possible.2.coherence theory in the last analysis seems to involve a correspondence since the firstjudgments must be verified directly.PRAGMATIC THEORY C.S. Peirce, William James, James DeweyThe theory is the belief that a proposition is true when acting upon it yields satisfactorypractical results. As formulated by William James, the pragmatic theory promises (in the long term) a convergence of human opinions upon a stable body of scientific propositions that have been shown in experience to be successful principles for human action.Examines how beliefs work in practice, the practical difference.This makes TRUTH something that is PSYCHOLOGICAL.TRUTH is whatever has met a society's criteria for justification.Problems:1. What is justified for one community to believe may not be true.2. How to explain errors? Falsehoods?3. It makes truth RELATIVE. NO ABSOLUTE TRUTH. NO OBJECTIVE TRUTH.MANY TRUTHS AT ONCE.There is a difference between truth and justified belief which pragmatism overlooks.Truth = what an ideal community would believe in the long run of timeREVIEWCorrespondence: Check it out using observation and physical measurements.Coherence: Does it fit in with other accepted beliefs?Pragmatic:Does it work?Justified True BeliefIn Plato's dialogue the Theaetetus, Socrates considers a number of definitions of knowledge. One of the prominent candidates is justified true belief. We know that, for something to count as knowledge, it must be true, and be believed to be true. Socrates argues that this is insufficient; in addition one must have a reason or justification for that belief.One implication of this definition is that one cannot be said to "know" something just because one believes it and that belief subsequently turns out to be true. An ill person with no medical training but a generally optimistic attitude might believe that she will recover from her illness quickly, but even if this belief turned out to be true, on the Theaetetus account the patient did not know that she would get well, because her belief lacked justification.Knowledge, therefore, is distinguished from true belief by its justification, and much of epistemology is concerned with how true beliefs might be properly justified. This is sometimes referred to as the theory of justification.The Theaetetus definition agrees with the common sense notion that we can believe things without knowing them. Whilst knowing p entails that p is true, believing in p does not, since we can have false beliefs. It also implies that we believe everything that we know. That is, the things we know form a subset of the things we believe.。
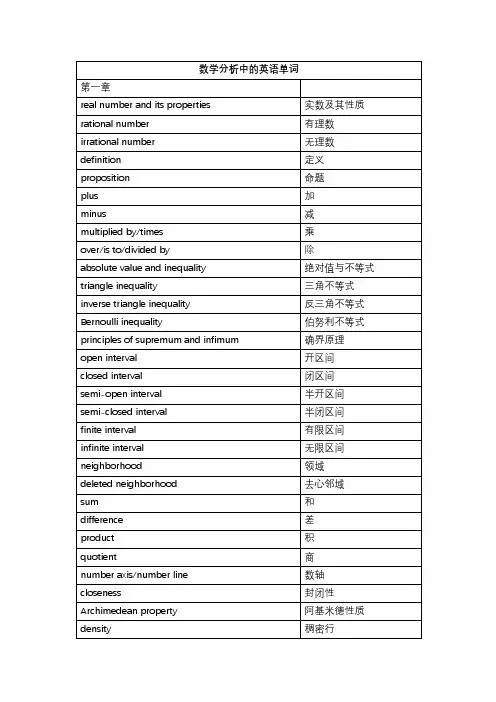
数学分析中的英语单词第一章real number and its properties 实数及其性质 rational number 有理数 irrational number 无理数 definition 定义 proposition 命题plus 加minus 减multiplied by/times 乘over/is to/divided by 除absolute value and inequality 绝对值与不等式 triangle inequality 三角不等式 inverse triangle inequality 反三角不等式 Bernoulli inequality 伯努利不等式 principles of supremum and infimum 确界原理open interval 开区间closed interval 闭区间semi-open interval 半开区间semi-closed interval 半闭区间finite interval 有限区间 infinite interval 无限区间 neighborhood 领域deleted neighborhood 去心邻域sum 和difference 差product 积quotient 商number axis/number line 数轴 closeness 封闭性 Archimedean property 阿基米德性质 density 稠密行upper and lower bounds 上界和下界 bounded set 有界集 unbounded set 无界集 existence domian 存在域 supremum 上确界 infimum 下确界order-complete set 有序完备集 completeness of real numbers 实数的完备性 complete ordered field 全序域 axiom of completeness 完备性公理 Dedekind cut 戴德金分割 Dedekind property 戴德金性质 constant and variable quantities 常量与变量 definition of function 函数的定义域 domain 定义域 range 值域 independent variable 自变量 dependent variable 因变量 intermediate variable 中间量 elementary function 初等函数 constant function 常量函数 power function 幂函数 exponential function 指数函数 logarithmic function 对数函数 trigonometric function 三角函数 inverse trigonometric function 反三角函数 compound function 复合函数 mapping 映射inverse mapping 逆映射 image 像primary image 原像 piecewise function 分段函数sign function 符号函数 Dirichlet function 狄利克雷函数 Riemann function 黎曼函数 bounded function 有界函数 monotone function 单调函数 monotone increasing function 单调增函数 strictly monotone function 严格单调函数 odd(even) function 奇函数（偶函数） minimal positive period 最小正周期 absolute value function 绝对值函数 identity function 恒等函数 polynomial function 多项式函数linear function 线性函数 quadratic function 二次函数rational function 有理函数 hyperbolic sine 双曲正弦 hyperbolic cosine 双曲余弦 trigonometric identity 三角恒等式odd-even identity 奇偶恒等式 cofunction identity 余函数恒等式 Pythagorean identity 毕达哥拉斯恒等式 half-angle identity 半角恒等式 product identity 积恒等式sum identity 和恒等式 addition identity 加法恒等式 double-angle identity 倍角恒等式第二章 数列极限limit of sequence 数列极限 divergent sequence 发散数列 infinitesimal sequence 无穷小数列 convergent sequence 收敛数列 uniqueness theorem 唯一性定理boundedness theorem 有界性定理 inheriting order properties 保序性inheriting inequality 保不等式 subsequence 子列strictly increasing 严格递增 monotone increasing sequence 单调递增序列 monotone decreasing sequence 单调递减序列 necessary condition 必要条件sufficient condition 充分条件squeeze principle 夹逼定理Cauchy convergence criterion 柯西收敛准则第三章 函数极限limit of function 函数极限infinite limit 无穷极限one-sided limit 单侧极限right(left)limit/right(left) hand limit 右（左）极限 property of limit of function 函数极限的性质 local boundedness 局部有界性Heine theorem 海涅定理infinity 无穷大量order of infinitesimal 无穷小量的阶 infinitesimal of higher(lower) order 高（低）阶无穷小量 infinitesimal of same order 同阶无穷小量 equivalent infinitesimal 等价无穷小量k-order infinitesimal k-阶无穷小量 vertical asymptote 垂直渐近线oblique asymptote 斜渐进线 horizontal asymptote 水平渐近线第四章函数的连续性increment of independent variable 自变量的增量 increment of function 函数的增量right(left) continuous 右(左)连续discontinuity point and its classification 间断点及其分类 removable discontinuity 可去间断点jump discontinuity 跳跃间断点 discontinuity of the first kind 第一类间断点 discontinuity of the second kind 第二类间断点local properties of continuous function 连续函数的局部性质 composition properties of continuous function 连续函数的复合性质闭区间上连续函数的性质 properties of continuous function over closedintervalextreme value theorem 极值定理maximum and minimum value theorem 最大值和最小值定理 intermediate value theorem 介值性定理zero-point theorem 零点定理uniform continuity theorem 一致连续定理continuity of inverse function 反函数的连续性local inheriting order property 局部保号性continuity of elementary function 初等函数的连续性第五章 导数和微分finite increment formula 有限增量公式rate of change 变化率difference quotient 差商left(right) derivative 左（右）导数 derivative function 导函数derivable function 可导函数geometric meaning of derivative 导数的集合意义Fermat theorem 费马定理Darboux theorem 达布定理intermediate value theorem of derivative function 导函数的介值定理 algebra of derivatives 导数的四则运算 derivative of sum 和的导数derivatives of difference 差的导数derivative of product 积的导数derivative of quotient 商的导数 derivative of inverse function 反函数的导数 maximum value 最大值minimum value 最小值 derivative of composite function 复合函数的导数 logarithmic derivative 对数求导法 parametric equation of circle 圆的参数方程 parametric equation of ellipse 椭圆的参数方程 parametric equation of cycloid 摆线的参数方程 parametric equation of asteroid 星形线的参数方程 second derivative 二阶导数third derivative 三阶导数n-th derivative n阶导数Leibniz formula 莱布尼茨公式 acceleration 加速度physical interpretation 物理解释 concept of differential 微分的概念 differentiable function 可微函数linear principal part 线性主部 differential of independent variable 自变量的微分 operational rules of differential 微分的运算法则 invariance of differential form 微分形式的不变性 geometric meaning of differential 微分的几何意义 higher-order differential 高阶微分第六章 微分中值定理Rolle mean value theorem 罗尔中值定理 Lagrange mean value theorem 拉格朗日中值定理 Cauchy mean value theorem 柯西中值定理 Taylor theorem 泰勒定理L’Hospital rule 洛必达法则limit of indeterminate form of type 0/0 0/0型不定式极限 indeterminate form of type ∞/∞ ∞/∞型不定式other indeterminate forms 其他类型不定式Taylor formula with Peano remainder 带有皮亚诺型余项的泰勒公式Taylor coefficient 泰勒系数Taylor polynomial 泰勒多项式remainder of Taylor formula 带有拉格朗日型余项的泰勒公式Taylor formula with Lagrange remainder 带有拉格朗日型余项的麦克劳林公式extreme value of function 函数的极值test of extreme value 极值判断the first sufficient condition of extreme value 极值的第一充分条件 convexity and inflection point of function 函数的凸性和拐点 convex function 凸函数concave function 凹函数strictly convex function 严格凸函数strictly concave function 严格凹函数Jenson inequality 琴生不等式第七章实数的完备性实数击完备性的基本定理 fundamental theorems of completeness in the setof real numbersnested interval theorem 闭区间套定理Cauchy convergence criterion 柯西收敛准着 accumulation theorem 聚点定理finite covering theorem 有限覆盖定理upper and lower limits 上极限和下极限第八章 不定积分indefinite integral 不定积分primitive function 原函数integrand function 被积函数integral sign 积分符号expression of integrand 积分表达式integral constant 积分常数table of basic integrals 基本积分表 geometric meaning of indefinite 不定积分的几何意义 integral curve 积分曲线initial condition 初始条件 integration by parts 分部积分法 integration by substitutions 换元积分法formula of substitution of the first kind 第一换元公式 indefinite integral of rational function 有理函数的不定积分 proper fraction 真分式improper fraction 假分式 decomposition into partial fractions 部分分式分解 method of undermined coefficients 待定系数法第九章 定积分definite integral 定积分curvilinear trapezoid 曲边梯形dividing/partition 分割norm/modulus 模Riemann sum 黎曼和Riemann integral 黎曼积分 integrability in the sense of Riemann 黎曼可积interval of integration 积分区间upper and lower limits 上限和下限 geometric meaning of definite integral 定积分的几何意义 upper sum 上和lower sum 下和Darboux upper sum 达布上和Darboux lower sum 达布下和Newton-Leibniz formula 牛顿-莱布尼茨公式 necessary condition for integrability 可积的必要条件 necessary and sufficient conditions for integrability 可积的充要条件 integrable function class 可积函数类linear property of definite integral 定积分的线性性质 additive with respect to integral interval/additivityover integral interval积分区间的可加性 mean value theorem of integral 积分中值定理 average value 平均值integral with variant upper limit 变上限积分 existence of primitive function 原函数的存在性 integration by substitution 换元积分法 integration by parts 分部积分法integral form of reminder of Taylor formula 泰勒公式的积分类型 第十章 定积分的应用area of plane figure 平面图形的面积method of finding volume of a solid from the knows area of parallel sections 由平行截面面积求体积的方法arc length and curvature of plane curve 平面的曲线的弧长与曲率 smooth curve 光滑曲线differential of arc 弧微分circle of curvature 曲率圆radius of curvature 曲率半径area of revolution surface 旋转曲面的面积some applications of definite integral in physics 定积分在物理中的某些应用gravitation 引力work 功approximate computation of definite integral 定积分的近似计算 trapezoidal method 梯形法parabola method 抛物线法第十一章反常积分notion of improper integral 反常积分的概念 improper integral on infinite interval 无穷区间上的反常积分 improper integral of unbounded function 无界函数的反常积分 property of infinite integral and test of 无穷积分的性质和收敛判convergence 别absolutely convergent 绝对收敛comparison test 比较收敛法Cauchy test 柯西判别法Dirichlet test 狄利克雷判别法Abel test 阿贝尓判别法第十二章数项级数series with number terms 数项级数infinite series 无穷级数convergence of series 级数的收敛性 sequence of partial sum 部分和序列geometric series 几何级数harmonic series 调和级数Cauchy convergence criterion for series 级数收敛的柯西准则 series with positive terms 正项级数necessary condition for convergence 收敛的必要条件root test 根式判别法D’alembert(ratio) test 达朗贝尔判别法（比式判别法）limit form of ratio test 比式判别法的极限形式 Gauss test 高斯判别法integral test 积分判别法Raabe test 拉贝尓判别法p-series p级数series with arbitraty terms 一般项级数alternating series 交错级数Leibnitz test 莱布尼茨判别法 rearrangement of series 级数的重排Abel test 阿贝尓判别法Dirichlet test 狄利克雷判别法第十章 函数列与函数项级数convergent at x"在点x"收敛convergence domain/region of convergence 收敛域sum function 和函数limit function 极限函数series of functions 函数项级数uniform convergence 一致收敛test of uniform convergence 一致收敛判别法魏尔斯特拉判别法 Weierstrass’s test/Weierstrass uniformconvergence criterion/Weierstrass m-test foruniform convergenceuniform boundedness 一致有界Dirichlet test 狄利克列判别法第十四章幂级数power series 幂级数interval of convergence 收敛区间radius of convergence 收敛半径Abel theorem 阿贝尓定理operations of power series 幂级数的运算taylor series 泰勒级数expansion of power series of elementary function 初等函数的幂级数展开式 exponential function of complex variable 复变量的指数函数Euler formula 欧拉公式第十五章傅里叶级数Fourier series 傅里叶级数 trigonometric series 三角级数system of orthogonal functions 正交函数系simple harmonic vibration 简谐振动Fourier series for function of period 2π以2π为周期的函数的傅立叶级数angular frequency 角频率piecewise smooth 分段光滑Fourier coefficient 傅立叶系数 convergence theorem 收敛定理Fourier series of even and odd functions 奇函数与偶函数的傅立叶级数amplitude 振幅sine series 正弦级数cosine series 余弦级数periodic extension 周期延拓第十六章多元函数的极限与连续functions of several variables 多元函数plane point set 平面点集coordinate plane 坐标平面interior point 内点outer point 外点boundary point 界点boundary 边点isolated point 孤立点open set 开集closed set 闭集connectedness 连通性connected open set 连通开集open domain(region) 开域closed domain(region) 闭域bounded point set 有界点集unbounded point set 无界点集nested closed domain theorem 闭域套定理function of two variables 二元函数n-dimensional vector space n-维向量空间improper limit 非正常极限double limit 二重极限properties of continuous functions on bounded closed region 有界闭区域上连续函数的性质repeated limits 累次极限 total increment 全增量partial increment 偏增量第十七章多元函数微分学total differential 全微分partial derivative 偏导数continuously differentiate 连续可微tangent plane of surface 曲面的切平面normal plane of curve 曲线的法平面 differentiation of composite function 复合函数微分法chain rule for functions of several variables 多元函数的链式法则 invariance of differential form of first order 一阶微分形式的不变性 directional derivative and gradient 方向导数与梯度 differentiability 可微性Taylor formula 泰勒公式problem of extreme value 极值问题partial derivative of higher order 高阶偏导数mixed partial derivative 混合偏导数第十八章隐函数定理及其应用existence and uniqueness theorem of implicit隐函数存在唯一性定理 functionssystem of implicit functions 隐函数组functional determinant (Jacobian determinant) 函数行列式（雅可比行列式）system of inverse functions 反函数组coordinate transformation 坐标变换geometrical application 几何应用tangent line and normal line of plane curve 平面曲线的切线与法线 tangent line and normal plane of space curve 空间曲线的切线与法平面 conditional extremum 条件极值Lagrange multiplier method 拉格朗日乘数法第十九章 含参变量积分proper integral with parameter 含参量的正常积分 improper integral with parameter 含参量的反常积分Euler integral 欧拉积分 Weierstrass test 魏尔斯特拉判别法 Dicichlet test 狄利克雷判别法 improper integral with infinite bound 无穷限的反常积分 improper integral with unbounded 无界函数的反常积分 Gamma functionBeta function第二十章inner area 内面积outer area 外面积cylindrical body with tip surface 曲顶柱体fineness 细度integral region 积分区域double integral 二重积分x-type region x型区域y-type region y型区域triple integral 三重积分change of variable in triple integral 三重积分换元法 transformation of cylindrical 柱面坐标变换 transformation of spherical coordinates 球面坐标变换area of surface 曲面面积第十一章曲线积分第一型曲线积分 curvilinear integrals of the first kind/line integrationof 1-form第二型曲线积分 curvilinear integrals of the first kind/line integrationof 2-formrelation between two classes of curvilinear两次曲线积分的联系 integralsGreen formula 格林公式 independence of curvilinear integrals with曲线积分与路径无关性 pathsimple connected region 单连通区域complex connected region 复连通区域第二十二章曲面积分surface integral of the first kind 第一型曲面积分 surface integral of the second kind 第二型曲面积分 unilateral surface 单侧曲面bilateral surface/two sided face 双侧曲面right-hand rule 右手法则relation between two classes of surface integrals 两类曲面积分的关系 Gauss formula 高斯公式Stokes formula 斯托克斯公式 introduction to field 场论初步field of vectors 向量场gradient field 梯度场gravitation field 引力场divergence field 散度场rotation field 旋度场circulation 环流量。
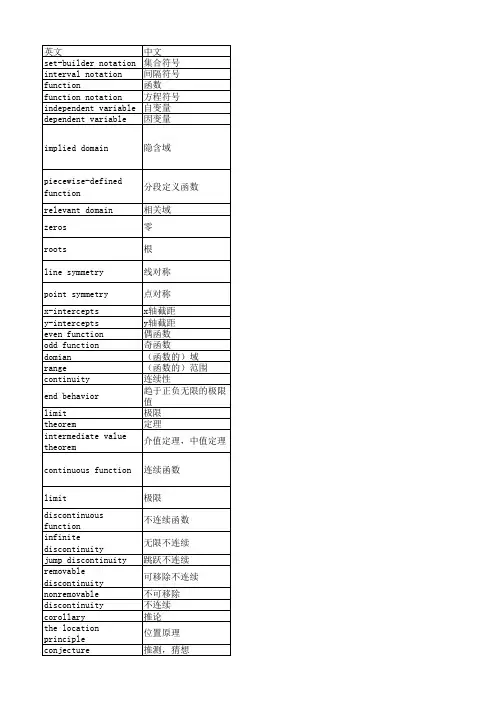
常用离散数学名词中英文对照集合：set元素：element严格定义:well defined成员:member外延原理:principle of extension泛集(全集):universal set空集:empty set(null set)子集:subset文氏图:venn diagram并:union交:intersection相对补集:relative complement绝对补集:absolute complement补集:complement对偶性:duality幂等律:idempotent laws组合律:associative laws交换律:commutative laws分配律:distributive laws同一律:identity laws对合律:involution laws求补律:complement laws对偶原理:principle of duality有限集:finite set计算原理:counting principle类:class幂集:power set子类:subclass子集合:subcollection命题:proposition命题计算:proposition calculus语句:statement复合:compound子语句:substatement合取:conjunction析取:disjuction否定:negation真值表:truth table重言式:tautology矛盾:contradiction逻辑等价:logical equivalence命题代数:algebra of propositions 逻辑蕴涵:logicalimplication关系:relation有序对:ordered pair划分:parti-on偏序:partial order整除性:divisibility常规序:usual order上确界:supremum下确界:infimum上(下)界:upper(lower) bound乘积集:product set笛卡儿积:cartesian product笛卡儿平面:cartesian plane二元关系:binary relation定义域:domain值域:range相等:equality恒等关系:identity relation全关系:universal ralation空关系:empty ralation图解:graph坐标图:coordinate diagram关系矩阵:matrix of the relation 连矢图:arrow diagram有向图:directed graph逆关系:inverse relation转置:transpose复合:composition自反:reflexive对称的:symmetric反对称的:anti-symmetric可递的:transitive等价关系:equivalence relation半序关系:partial ordering relation 函数:function映射:mapping变换:transformation像点:image象:image自变量:independent variable因变量:dependent variable函数图象:graph of a function合成函数:composition function可逆函数:invertible function一一对应:one to one correspondence 内射:injective满射:surjective双射:bijective基数度:cardinality基数:cardinal number图论:graph theory多重图:multigraphy顶点:vertix(point,node)无序对:unordered pair边:edge相邻的adjacent端点:endpoint多重边:multiple edge环:loop子图:subgraph生成子图:generated subgraph平凡图:trivial graph入射:incident孤立点:isolated vertex连通性:connectivity通路:walk长度:length简单通路:chain(trail)圈:path回路:cycle连通的:connected连通分支:connected component距离:distance欧拉图:eulerian graph欧拉链路:eulerian trail哈密顿图:hamilton graph哈密顿回路:hamilton cycle货郎行程问题:traveling salesman完全图:complete graph正则图:regular graph偶图:bipartive graph树图:tree graph加权图:labeled graph同构图:isomorphic graph同构:isomorphism同胚的:homeomorphic平面图:planar graph着色问题:colortion区域:region地图:map非平面图:nonplanargraph着色图:colored graphs顶点着色:vertex coloring色散:chromatic number四色原理:four color theorem对偶地图:dual map退化树:degenerate tree生成树:spanning tree有根树:rooted tree根:root水平(深度):level(depth)叶子:leaf分支:branch有序有根树:ordered rooted tree二元运算符:binary operational symbol半群:semigroup单位元素:identity element右(左)单位元素:right(left) identity左(右)消去律:left(right) cancellation law) 逆:inverse并列:juxtaposition有限群:finite group正规子群:normal subgroup非平凡子群:nontrivial subgroup循环群:cyclic group环:ring整环:integral domain域:field交换环:commutative ring加性环:additive group汇合:meet格:lattice有界格:bounded lattice分配格:distributeve lattice补格:complemented lattice表示定理:representation theorem。
高等数学中定义定理的英文表达Value of function ：函数值Variable ：变数Vector ：向量Velocity ：速度Vertical asymptote ：垂直渐近线Volume ：体积X-axis ：x轴x-coordinate ：x坐标x-intercept ：x截距Zero vector ：函数的零点Zeros of a polynomial ：多项式的零点TTangent function ：正切函数Tangent line ：切线Tangent plane ：切平面Tangent vector ：切向量Total differential ：全微分Trigonometric function ：三角函数Trigonometric integrals ：三角积分Trigonometric substitutions ：三角代换法Tripe integrals ：三重积分SSaddle point ：鞍点Scalar ：纯量Secant line ：割线Second derivative ：二阶导数Second Derivative Test ：二阶导数试验法Second partial derivative ：二阶偏导数Sector ：扇形Sequence ：数列Series ：级数Set ：集合Shell method ：剥壳法Sine function ：正弦函数Singularity ：奇点Slant asymptote ：斜渐近线Slope ：斜率Slope-intercept equation of a line ：直线的斜截式Smooth curve ：平滑曲线Smooth surface ：平滑曲面Solid of revolution ：旋转体Space ：空间Speed ：速率Spherical coordinates ：球面坐标Squeeze Theorem ：夹挤定理Step function ：阶梯函数Strictly decreasing ：严格递减Strictly increasing ：严格递增Sum ：和Surface ：曲面Surface integral ：面积分Surface of revolution ：旋转曲面Symmetry ：对称RRadius of convergence ：收敛半径Range of a function ：函数的值域Rate of change ：变化率Rational function ：有理函数Rationalizing substitution ：有理代换法Rational number ：有理数Real number ：实数Rectangular coordinates ：直角坐标Rectangular coordinate system ：直角坐标系Relative maximum and minimum ：相对极大值与极小值Revenue function ：收入函数Revolution , solid of ：旋转体Revolution , surface of ：旋转曲面Riemann Sum ：黎曼和Riemannian geometry ：黎曼几何Right-hand derivative ：右导数Right-hand limit ：右极限Root ：根P、QParabola ：拋物线Parabolic cylinder ：抛物柱面Paraboloid ：抛物面Parallelepiped ：平行六面体Parallel lines ：并行线Parameter ：参数Partial derivative ：偏导数Partial differential equation ：偏微分方程Partial fractions ：部分分式Partial integration ：部分积分Partiton ：分割Period ：周期Periodic function ：周期函数Perpendicular lines ：垂直线Piecewise defined function ：分段定义函数Plane ：平面Point of inflection ：反曲点Polar axis ：极轴Polar coordinate ：极坐标Polar equation ：极方程式Pole ：极点Polynomial ：多项式Positive angle ：正角Point-slope form ：点斜式Power function ：幂函数Product ：积Quadrant ：象限Quotient Law of limit ：极限的商定律Quotient Rule ：商定律M、N、OMaximum and minimum values ：极大与极小值Mean Value Theorem ：均值定理Multiple integrals ：重积分Multiplier ：乘子Natural exponential function ：自然指数函数Natural logarithm function ：自然对数函数Natural number ：自然数Normal line ：法线Normal vector ：法向量Number ：数Octant ：卦限Odd function ：奇函数One-sided limit ：单边极限Open interval ：开区间Optimization problems ：最佳化问题Order ：阶Ordinary differential equation ：常微分方程Origin ：原点Orthogonal ：正交的LLaplace transform ：Leplace 变换Law of Cosines ：余弦定理Least upper bound ：最小上界Left-hand derivative ：左导数Left-hand limit ：左极限Lemniscate ：双钮线Length ：长度Level curve ：等高线L'Hospital's rule ：洛必达法则Limacon ：蚶线Limit ：极限Linear approximation：线性近似Linear equation ：线性方程式Linear function ：线性函数Linearity ：线性Linearization ：线性化Line in the plane ：平面上之直线Line in space ：空间之直线Lobachevski geometry ：罗巴切夫斯基几何Local extremum ：局部极值Local maximum and minimum ：局部极大值与极小值Logarithm ：对数Logarithmic function ：对数函数IImplicit differentiation ：隐求导法Implicit function ：隐函数Improper integral ：瑕积分Increasing/Decreasing Test ：递增或递减试验法Increment ：增量Increasing Function ：增函数Indefinite integral ：不定积分Independent variable ：自变数Indeterminate from ：不定型Inequality ：不等式Infinite point ：无穷极限Infinite series ：无穷级数Inflection point ：反曲点Instantaneous velocity ：瞬时速度Integer ：整数Integral ：积分Integrand ：被积分式Integration ：积分Integration by part ：分部积分法Intercepts ：截距Intermediate value of Theorem ：中间值定理Interval ：区间Inverse function ：反函数Inverse trigonometric function ：反三角函数Iterated integral ：逐次积分HHigher mathematics 高等数学/高数E、F、G、HEllipse ：椭圆Ellipsoid ：椭圆体Epicycloid ：外摆线Equation ：方程式Even function ：偶函数Expected Valued ：期望值Exponential Function ：指数函数Exponents , laws of ：指数率Extreme value ：极值Extreme Value Theorem ：极值定理Factorial ：阶乘First Derivative Test ：一阶导数试验法First octant ：第一卦限Focus ：焦点Fractions ：分式Function ：函数Fundamental Theorem of Calculus ：微积分基本定理Geometric series ：几何级数Gradient ：梯度Graph ：图形Green Formula ：格林公式Half-angle formulas ：半角公式Harmonic series ：调和级数Helix ：螺旋线Higher Derivative ：高阶导数Horizontal asymptote ：水平渐近线Horizontal line ：水平线Hyperbola ：双曲线Hyper boloid ：双曲面DDecreasing function ：递减函数Decreasing sequence ：递减数列Definite integral ：定积分Degree of a polynomial ：多项式之次数Density ：密度Derivative ：导数of a composite function ：复合函数之导数of a constant function ：常数函数之导数directional ：方向导数domain of ：导数之定义域of exponential function ：指数函数之导数higher ：高阶导数partial ：偏导数of a power function ：幂函数之导数of a power series ：羃级数之导数of a product ：积之导数of a quotient ：商之导数as a rate of change ：导数当作变率right-hand ：右导数second ：二阶导数as the slope of a tangent ：导数看成切线之斜率Determinant ：行列式Differentiable function ：可导函数Differential ：微分Differential equation ：微分方程partial ：偏微分方程Differentiation ：求导法implicit ：隐求导法partial ：偏微分法term by term ：逐项求导法Directional derivatives ：方向导数Discontinuity ：不连续性Disk method ：圆盘法Distance ：距离Divergence ：发散Domain ：定义域Dot product ：点积Double integral ：二重积分change of variable in ：二重积分之变数变换in polar coordinates ：极坐标二重积分CCalculus ：微积分differential ：微分学integral ：积分学Cartesian coordinates ：笛卡儿坐标图片一般指直角坐标Cartesian coordinates system ：笛卡儿坐标系Cauch’s Mean Value Theorem ：柯西均值定理Chain Rule ：连锁律Change of variables ：变数变换Circle ：圆Circular cylinder ：圆柱Closed interval ：封闭区间Coefficient ：系数Composition of function ：函数之合成Compound interest ：复利Concavity ：凹性Conchoid ：蚌线Cone ：圆锥Constant function ：常数函数Constant of integration ：积分常数Continuity ：连续性at a point ：在一点处之连续性of a function ：函数之连续性on an interval ：在区间之连续性from the left ：左连续from the right ：右连续Continuous function ：连续函数Convergence ：收敛interval of ：收敛区间radius of ：收敛半径Convergent sequence ：收敛数列series ：收敛级数Coordinate：s：坐标Cartesian ：笛卡儿坐标cylindrical ：柱面坐标polar ：极坐标rectangular ：直角坐标spherical ：球面坐标Coordinate axes ：坐标轴Coordinate planes ：坐标平面Cosine function ：余弦函数Critical point ：临界点Cubic function ：三次函数Curve ：曲线Cylinder：圆柱Cylindrical Coordinates ：圆柱坐标A、BAbsolute convergence ：绝对收敛Absolute extreme values ：绝对极值Absolute maximum and minimum ：绝对极大与极小Absolute value ：绝对值Absolute value function ：绝对值函数Acceleration ：加速度Antiderivative ：反导数Approximate integration ：近似积分Approximation ：逼近法by differentials ：用微分逼近linear ：线性逼近法by Simpson’s Rule ：Simpson法则逼近法by the Trapezoidal Rule ：梯形法则逼近法Arbitrary constant ：任意常数Arc length ：弧长Area ：面积under a curve ：曲线下方之面积between curves ：曲线间之面积in polar coordinates ：极坐标表示之面积of a sector of a circle ：扇形之面积of a surface of a revolution ：旋转曲面之面积Asymptote ：渐近线horizontal ：水平渐近线slant ：斜渐近线vertical ：垂直渐近线Average speed ：平均速率Average velocity ：平均速度Axes, coordinate ：坐标轴Axes of ellipse ：椭圆之轴Binomial series ：二项级数。
Derandomization,witnesses for Boolean matrix multiplication and construction of perfect hash functions∗Noga Alon†Moni Naor‡To appear in Algorithmica,final versionAbstractSmall sample spaces with almost independent random variables are applied to de-sign efficient sequential deterministic algorithms for two problems.Thefirst algorithm,motivated by the attempt to design efficient algorithms for the All Pairs Shortest Pathproblem using fast matrix multiplication,solves the problem of computing witnesses forthe Boolean product of two matrices.That is,if A and B are two n by n matrices,andC=AB is their Boolean product,the algorithmfinds for every entry C ij=1a witness:an index k so that A ik=B kj=1.Its running time exceeds that of computing theproduct of two n by n matrices with small integer entries by a polylogarithmic factor.The second algorithm is a nearly linear time deterministic procedure for constructinga perfect hash function for a given n-subset of{1,...,m}.∗Part of this paper was presented at the IEEE33rd Symp.on Foundations of Computer Science†Incumbent of the Florence and Ted Baumritter Combinatorics and Computer Science Chair,Depart-ment of Mathematics,Raymond and Beverly Sackler Faculty of Exact Sciences,Tel Aviv University,Tel Aviv,Israel.Research supported in part by a USA Israeli BSF grant and by the Fund for Basic Research administered by the Israel Academy of Sciences.e-mail:noga@math.tau.ac.il.‡Incumbent of the Morris and Rose Goldman Career Development Chair,Department of Applied Math and Computer Science,Weizmann Institute,Rehovot76100,Israel.Supported by an Alon Fellowship and by a grant from the Israel Science Foundation administered by the Israeli Academy of Sciences.e-mail: naor@wisdom.weizmann.ac.il.Some of this work was done while the author was with the IBM Almaden Research Center.1IntroductionIn this paper we show how to make two very efficient probabilistic algorithms deterministic at a relatively small degradation in their performance.The random choices made by a probabilistic algorithm define naturally a probability space where each choice corresponds to a random variable.In order to remove randomness from an algorithm one should come up with a way offinding deterministically a successful assignment to these choices.One approach for achieving it,known as the method of conditional probabilities,is to search the probability space for a good choice by bisecting the probability space at every iteration byfixing an additional choice.The value of the next bit is chosen according to some estimator function that should approximate the probability of success given the choicesfixed so far.The number of steps is therefore proportional to the number of choices made by the probabilistic algorithm and each step involves evaluating an estimator which usually takes time proportional to the input size.Thus,the cost of derandomization though polynomial, can considerably increase the complexity of the algorithm.This approach is taken in[29],[25],(cf.,also[6].)A different approach forfinding a good point is to show that the random choices made need not be fully independent,i.e.even if some limited form of independence is obeyed, then the algorithm is successful.A smaller probability space where the random choices obey this limited independence is constructed.If this space is exhaustively searched,then a good point is found.The complexity is increased by a factor proportional to the size of the space. The size of the space is usually some polynomial in the input size.Thus again this approach suffers from considerable increase in time.This approach is taken in[17],[1],[15]using probability spaces that are k-wise independent,and in[5],[23]using small bias probability spaces and almost k-wise independence(see definition below in subsection1.3).Our goal in this work is to use these methods without incurring a significant penalty in the run time.We exploit the fact that very small(polylogarithmic)probability spaces exist if one is willing to live with very limited independence.This form of independence is usually too limited to be applicable directly for replacing the random choices in a probabilistic algorithm.Our tactic will be to divide the random choices into a small(logarithmic or polylogarithmic)number of sets of random variables with complete independence between the sets.However within each set we will require only very limited independence.The search algorithmfinds a good assignment byfixing the sets one by one.At every iteration all the points of a small probability space corresponding to the current set of random variables is examined and the one that maximizes some estimator function of the probability of success is chosen.Since we have only a few sets of random variables and since each probability space is small the total work is increased by only a polylogarithmic factor.We note that the two approaches described above had been combined in a different way previously in[18,7,22].The random variables used there were k-wise independent resulting in a probability space of size O(n k).This probability space was then searched using an estimator function in O(k log n)steps.This method does not seem applicable for the problems considered here,since we could not come up with appropriate estimator functions that were efficiently computable.In the following two subsections we describe the two algorithmic problems for which2applying the above mentioned method yields efficient deterministic algorithms:the compu-tation of Boolean matrix multiplication with witnesses and the(deterministic)construction of perfect hash functions.Although the two problems are not related,the algorithms we suggest for both are similar,and are based on the same approach outlined above.In sub-section1.3we review the probability spaces that have the independence properties used for both applications.1.1Witnesses for matrix multiplicationConsider a Boolean matrix multiplication:C=AB,C ij= n k=1(A ik∧B kj).The n3time method that evaluates these expressions gives for every i,j for which C ij=1all the k’s for which A ik=B kj=1.The subcubic methods on the other hand(see,e.g.,[8])consider A and B as matrices of integers and do not provide any of these k’s.We call a k such that A ik=B kj=1a witness(for the fact that C ij=1).We want to compute in addition to the matrix C a matrix of witnesses.When there is more than one witness for a given i and j we are satisfied with one such witness.We use O(nω)to denote the running time of some subcubic algorithm for Boolean matrix multiplication.Our algorithm for this problem can be derived from any such algorithm yielding a corresponding time bound as a function of w.The best asymptotic bound known at present is the one with the exponentω<2.376and is due to Coppersmith and Winograd[8].For two functions f(n)and g(n)we let g(n)=˜O(f(n))denote the statement that g(n) is O(f(n)(log n)O(1)).Several researchers(see,e.g.,[28],[4])observed that there is a simple randomized algo-rithm that computes witnesses in˜O(nω)time.In Section2we describe a deterministic algorithm for computing the witnesses in˜O(nω)time.It is essentially a derandomization of a modified version of the simple randomized algorithm using the approach outlined in the Introduction,i.e.the combination of small sample spaces and the method of conditional probabilities.A different,more complicated algorithm for this problem,whose running time is slightly inferior,i.e.not˜O(nω)(but is also O(nω+o(1))),has been found by Galil and Margalit[20],[14].The main motivation for studying the computation of witnesses for Boolean matrix mul-tiplication is the observation of Galil and Margalit that this problem is crucial for the design of efficient algorithms for the All-Pairs-Shortest-Path problem for graphs with small integer weights which are based on fast matrix multiplication.Efficient algorithms for computing the distances in this way were initiated in[3]and improved(for some special cases)in[13], [28].The attempt to extend this method for computing the shortest paths as well leads naturally to the above problem,which already found other(related)applications as well. See[4,14,20,28]for more details.1.2Perfect hash functionsFor a set S⊂{1,...,m}a perfect hash function is a mapping h:{1,...,m}→{1,...,n} which is1-1on S.H is an(m,n,k)-family of perfect hash functions if∀S⊂{1,...,m}of size k there is an h∈H that is perfect for S.We will be interested mainly in the case k=n.3The requirements from a perfect hash function are•Succinct representation-the mapping h can be described by a relatively small number of bits.•Efficient evaluation-given a value x∈{1,...,m}and the description of h,there should be an efficient method of computing h(x).•An efficient construction-given S there should be an efficient way offinding h∈H that is perfect for SPerfect hash functions have been investigated extensively(see e.g.[9,10,11,12,16,19, 21,26,27,30]).It is known(and not too difficult to show,see[11],[16],[24])that the minimum possible number of bits required to represent such a mapping isΘ(n+log log m) for all m≥2n.Fredman,Koml´o s and Szemer´e di[12]developed a method for constructing perfect hash functions.Given a set S,their method can supply a mapping with the required properties in almost linear expected randomized running time.Deterministically,however,they only describe a variant of their algorithm that works in worst-case running time O(n3log m).In Section3we describe a construction of perfect hash functions and a deterministic algorithm that for a given S in time O(n log m log4n)finds a mapping with the above properties. Note that the size of the input isΘ(n log m)and hence this algorithm is optimal,up to a polylogarithmic factor.In case m is polynomial in n,the representation of the mapping h constructed requires O(n)bits.Given x computing h(x)takes O(1)operations.In the general case,the size of the mapping h requires O(n+log n log log m)bits.The time to evaluate h(x)depends on the computational model(i.e.what operations can be performedin one step):it is either O(log mlog n )in a weak model or O(1)in a strong one(see more aboutthe model in Section3).1.3Small bias probability spacesLetΩbe a probability space with n random variables x1,x2,...x n.We say thatΩis a c-wise -bias probability space if for any nonempty subset S of x1,x2,...x n of size at most c we have|P rob[ i∈S x i=0]−P rob[ i∈S x i=1]|< .The property of a c-wise -bias probability space that we use is that for any subset S of x1,x2,...x n of size i≤c the probability that the random variables of S attain a certain configuration deviates from1/2i by at most .Therefore c-wise -bias probability spaces are described as almost c-wise independent.The known constructions of these probability spaces are of size polynomial in c,1/ and log n(often described by saying that the number of random bits required to sample from them is O(log1/ +log c+log log n)).Therefore if1/ is logarithmic in n and c is at most logarithmic in n the size of the probability space is still polylogarithmic in n.To be more precise,the construction of[23],as optimized in[2],yields a probability space of size O(c log n3)and the ones in[5]yield probability spaces of size O(c2log2n2).42Boolean matrix multiplication with witnessesAll the matrices in this section are n by n matrices,unless otherwise specified.If M is such a matrix,we let M ij denote the entry in its i th row and j th column.Let A and B be two matrices with{0,1}entries,and let C be their product over the integers.Our objective is tofind witnesses for all the positive entries of C,i.e.,for each entry C ij>0of C we wish tofind a k such that A ik=B kj=1.This is clearly equivalent to the problem of finding witnesses in the Boolean case.As observed by several researchers there is a simple randomized algorithm that solves this problem in expected running time˜O(nω).Here we consider deterministic algorithms for the problem.Our algorithm,described in the next two subsections,is a derandomized version of a modification of the simple randomized solution. Its running time is˜O(nω).The analysis of the algorithm is presented in subsection2.3, where it is also shown how to replace the probabilistic steps with deterministic ones.2.1Outline and intuition of the algorithmThe starting observation is thatfinding witnesses for entries which are1is easy:if E and F are two matrices with{0,1}entries and G=EF is the result of their multiplication over the integers,then one multiplication of matrices with entries of size at most n suffices forfinding witnesses for all the entries of G which are precisely1.Indeed,simply replace every1-entry in the k th row of F by k(for all1≤k≤n)to get a matrix F and compute G =EF .Now observe that if G ij=1and Gij =k then k is a witness for G ij.The idea(of both the randomized and deterministic algorithms)is to dilute F gradually, thus making the entries of G go down to0,however not before passing through1.Therefore if G ij= and every entry in F is made zero with probability roughly1/ ,then G ij becomes1 with probability bounded away from zero.A way of achieving it simultaneously for all entries is to work in phases,where in each phase every’1’entry of F is zeroed with probability1/2. At each phase alsofind witnesses for all entries of G that became1.If G ij= then for the (i,j)entry of EF after log such phases there is a constant probability of turning G ij into a 1and thus enabling the discovery of a witness.By repeating this process log n times,there is a high probability of discovering all the witnesses.The choices we must make in the execution of the algorithm is which entries of F to zero at what phase.In the randomized algorithm all choices are independent,and thus the size of the probability is exponential in O(n log2n).In order to remove the randomness from the witnessfinding algorithm we follow the paradigm outlined in the Introduction.Random choices corresponding to different phases remain independent,however,the choices made in a phase will be highly dependent.We must alsofind a good estimate of progress.The key point is that for our estimate of progress it is sufficient that the choices within a phase be made according to a c-wise -bias sample space for c and1/ that are logarithmic in n.Our notion of progress is defined by two“contradicting”conditions:first the total sum of entries in G must go down significantly at every round(by at least a constant fraction).This implies that in O(log n)rounds we get that G vanishes.The second condition is that we do not lose too many entries of G,where by lose we mean that they go from a large value to0without passing through1.5The second condition turns out to be too strong.We relax it by specifying some bound c (not coincidently,the same c as above)such that we would like every entry to pass through the range{1,...,c}before vanishing.We show how tofind a witness in this case as well. The fraction of entries that disobey the second condition should be small enough to assure that at least a constant fraction of the entries do not skip the desired range.The set of good assignments to the choices of a phase is obtained by an exhaustive search among all the sample space for an assignment that progresses nicely.This is repeated for all phases and the whole process is repeated O(log n)times until all entries have a witness.2.2Detailed description of the algorithmDefine c= log log n+9 andα=82c .For two matrices E and F with{0,1}entries defineG=E∧F by G ij=E ij∧F ij.Besides A,B and C=AB our algorithm employs two sequences of{0,1}matrices: R1,R2...,R t+1and D1,D2,...D t+1where t= 1+3log4/3n .For matrices R and R we say that R is a dilution of R if for every1≤j,k≤n we have R j,k≥R j,k.The sequence R1,R2...R t+1is monotonically decreasing,i.e.for every1≤i≤t R i+1is a dilution of R i. We now describe the algorithm;the way to perform steps4b and4c will be described later. The definition of a good dilution is given below.•While not all witnesses are known1.Let L be the set of all positive entries of C for which there are no known witnesses.2.Let R1be the all1matrix.3.Let D1←A·(B∧R1)4.For i=1to t= 1+3log4/3n ,Perform the following:(a)Let L be the set of all non-zero entries of D i in L which are at most c.(b)Find witnesses for all entries in L .(c)R i+1←good dilution of R i(see definition of“good”below)(d)D i+1←A·(B∧R i+1)(The matrix multiplication is over the integers)A matrix R i+1is good with respect to R i(in step4c above)if the following two conditions hold:a)The total sum of the entries of D i+1=A·(B∧R i+1)is at most3/4of the total of theentries of D i=A·(B∧R i).(Observe that this guarantees that after1+3log4/3n iterations of good R i’s all the entries of D will vanish.)b)The fraction of entries in L that are0in D i+1,among those larger than c in D i is atmostα.62.3Analysis of the algorithmWefirst analyse one iteration of a randomized version of the algorithm(Lemma1),then analyse it when the sample space has a small bias(Lemma2)andfinally we show that this suffices for achieving a deterministic algorithm.Lemma1For any1≤i≤t,suppose that R i+1←R i∧S in step4c where S is a random 0,1matrix,then the R i+1is good with probability at least1/6.The lemma follows from the following three claims:Claim1The probability that the sum of entries of D i+1is at most3/4the sum of entries of D i is at least1/3.To see this,observe that the expected sum of entries of D i+1is1/2the sum of entries of D i,since for every1≤j,k,l≤n such that A jk=(B∧R i)kl=1the probability that (B∧R i+1)kl=1is exactly1/2.The claim then follows from Markov’s Inequality.2 Claim2The probability that afixed entry of D i which is at least c drops down to0in D i+1 is at most1/2c.This is obvious.Observe that the claim holds even if we only assume that every c entries of S are independent.2Claim3The probability that more than a fractionαof the entries in L that had a value atleast c in D i drop to0in D i+1is at most12c 1α=18.This follows from Claim2by Markov’s Inequality.2Since Claims1and3describe the event we are interested in and1/3−1/8>1/6the lemma follows.2Define =12c+1.The crucial point is to observe that the proof of the above lemma stillholds,with almost no change,if the matrix S is not totally random but its entries are chosen from a c-wise -dependent distribution in the sense of[23],[5].Recall that if m random variables whose range is{0,1}are c-wise -dependent then every subset of j≤c of them attains each of the possible2j configurations of0and1with probability that deviates from 1/2j by at most .Lemma2If R i+1←R i∧S in step4c where the entries of S are chosen as n2random variables that are c-wise -dependent,then R i+1is good with probability at least1/12−2 .We note that in fact it is sufficient to choose only one column from a c-wise -dependent sample space and copy it n times.However,this changes the size of the sample space by a constant factor only.The proof of Lemma2is by the following modified three claims,whose proofs are analogous to those of the corresponding previous ones.Claim4The probability that the sum of entries of D i+1is at most3/4the sum of entries of D i is at least1/3−2 .27Claim5The probability that afixed entry of D i which is at least c drops down to0in D i+1 is at most1/2c+ .2Claim6The probability that more than a fractionαof the entries in L that had a valueleast c in D i drop to0in D i+1is at most(1c + )1<2c1=1/4.2Since Claims4and6describe the event we are interested in and1/3−2 −1/4>1/12−2 the lemma follows.2As shown in[23]and in[5]there are explicit probability spaces with n2random variables which are c-wise -dependent,whose size is(log(n)·c·1)2+o(1),which is less than,e.g.,O((log n)5).Moreover,these spaces can be easily constructed in time negligible with respect to the total running time of our algorithm.Suppose that in step4c all the matrices S defined by such a probability space are searched, until a good one is found.Checking whether a matrix is good requires only matrix multipli-cation plus O(n2)operations.Therefore the inner loop(starting at step4)takes polynomial in log n times matrix multiplication time.Executing Step4b:It is important to note that during the performance of step4c,while considering all possible matrices S provided by our distribution,we can accomplish step4b (of the next iteration)as well.To see this we needClaim7If R i+1←R i∧S in step4c where the entries of S are chosen as n2random variables that are c-wise -dependent,then for each entry in L there is a positive probability to be precisely1in D i+1.This follows since if S is chosen uniformly at random,then the probability that an entry in L is precisely1in D i+1is at least c/2c and this event depends on at most c variables.2 To apply the claim,recall the observation at the beginning of Section2.1,that we can find witnesses for entries that are at most1.If we replace each matrix multiplication in the search for a good S by two matrix multiplications as described in that observation,we complete steps4b and4c together.Analysis of the outer loop:In every iteration of the inner loop4at most anαfraction of the entries of L are“thrown”(i.e.their witness will not be found in this iteration of the outer loop).Therefore at least1−(1+3log4/3n)αfraction of the entries of D in L will not be thrown during the completion of these iterations.For those entries,which are at least 1/2of the entries in L,a witness is found.Therefore,only O(log n)iterations of the outer loop are required,implying the desired˜O(nω)total running time.We have thus proved the following:Theorem1The witnesses for the Boolean multiplication of two n by n matrices can be found in deterministic˜O(nω)time.83Efficient deterministic construction of perfect hash functionsIn this Section we describe an efficient method of constructing perfect hash functions.Recall that for a set S⊂{1,...,m}a perfect hash function is a mapping of{1,...,m}onto {1,...,n}which is1-1on S.We are given a set of n elements out of{1,...,m}and the goal is to build a perfect hash function from{1,...,m}to a range which is O(n)with the properties listed in Section1.2 (Given a function that maps to a range of size O(n),another function which maps to a range of size n can be constructed using the technique in[12]or in[10].)Outline of the FKS scheme:Our scheme has the same structure as the one of Fredman, Koml´o s and Szemer´e di[12]which we now review:The FKS scheme consists of two levels. Thefirst level function,denoted by h,maps the elements of{1,...,m}into a range of size O(n);all the elements that were sent to the same location i are further hashed using a second level hash function h i.The second level hash function h i should be1-1on the subset that was hashed to location i by h.For every i in the range of h we allocate as much space as the range of h i which we denote by r i.The perfect hash function is now defined as follows: if x∈{1,...,m}is mapped to i by h,then the scheme maps x to h i(x)+ 1≤j<i r j.The size of the range is therefore i r i.Let s i(h)=|{x|x∈S and h(x)=i}|,i.e s i=s i(h)denotes the number of elements mapped to i.The property we require h to satisfy is that n i=1 s i(h)2 should be O(n).The size of the range of h i will be O( s i2 ).The functions suggested by[12]for both levels were of the form(k·x mod p)mod r where p is an appropriate prime,r is n for thefirst level ands2 i for the second level.Overview of the new scheme:The scheme consists of more than one level of hashing.Thefirst level is a hash functionwhich is used to partition the elements according to their hash value,where S i is the setof all elements with hash value i.Then,each S i is going to be mapped to a separatefinalregion,say R i,where the size of R i depends on|S i|.Thisfirst hash function is of the same form h(x)=Ax where A is a log(n)×log(m)matrix over GF[2]and x is treated as a vectorof length log m over GF[2].The mapping of S i into R i consists of either one more level ofhashing or two more levels,depending on how large S i is.If S i is sufficiently small,thenthere is only one more hash function that maps S i into R i,and it is of the same form as[12].If S i is large enough,then there are two more levels of hashing to map S i into R i,where the bottom level is the same form as[12]but the upper level(which we will refer toas the intermediate)is of the form h(x)=Ax where A is a matrix over GF[2]of appropriatedimensions.Our main difficulty is coming up with thefirst level hash function h.Given the proper hwe can allocate relatively long time forfinding the second and third level functions:even ifconstructing a good(i.e.1-1)h i takes time proportional to O(s2i ),then the total amount ofwork in the second step would still be linear.In fact,finding a perfect hash function of theform(k·x mod p)mod r requires time proportional to s3i log m.For the sake of completenesswe outline in Section3.2how to achieve this.9Finding the top level hash function h and the intermediate level h i’s is done using the approach outline in the Introduction to the paper.Instead of choosing h from a collection at random we select it by considering it a concatenation of one-bit functions andfixing each one in turn.We must show that the one-bit functions can be chosen from a very small collection (defined by a small bias sample space)and that there is a good estimator of progress(which will be the number of pairs that must be separated).Model:Since we are interested in fast on-line evaluation of the constructed perfect hash function we must specify the computational power of the evaluator.The weakest model we consider only assumes that the evaluator can access in one operation the memory that stores the description of the perfect hash function and retrieve a word of width at most log n.It needs only very simple arithmetic,basically addition.Note that in this weak model we can perform a lot of computation in O(1)time using pre-stored tables of of size O(n)as we can see in the following example.Consider the function f r(x)=r·x where r and x are in{0,1}log m and f r computes their inner product over GF[2].Partition r into k=log m parts r1,r2,...r k.For each r j arrange a table of size n/log m such that for0≤y<n/log m entry y in the table contains the inner product of y and r j where y and r j are considered as vectors of length log n−log log m over GF[2].Given these tables,evaluating f rj(x)requires k operations: access the tables at entries x1,x2,x k and Xor the results.If m is polynomial in n than this is O(1)operations and in general takes O(log m/log n)time.This example is important to us,since the top level hash function is of the form h(x)=Ax where the multiplication is over GF[2]A stronger model is to assume that any operation on words of size O(log m)takes constant time.Thus we count only accesses to the memory(which may be interesting sometimes).3.1First level hash functionTofind thefirst level hash function we solve the following problem for all t in the range {1,...log n}:given a set S⊂{1,...,m}of size n,construct a function h:{1,...,m}→{1,...2t}such that if s i(h)=|{x|x∈S and h(x)=i}|then 2t i=1 s i(h)2 ≤q=e2 n2 /2t. Note that q is only a constant factor larger than the expected value of i s i2 in case h is chosen at random from all functions{1,...,m}→{1,...2t}.Wefind h in a step by step manner,forming it as a concatenation of one bit functions f1,f2,...,f t where f j:{1,...,m}→{0,1}.After we have decided on f1,f2,...f j we determine f j+1using an estimator function which we try to reduce.The estimator which weuse isP j(f1,f2,...f j)= i∈{0,1}j s i(f1,f2,...f j)2where s i(f1,f2,...f j)=|S i(f1,...,f j)|and S i(f1,...,f j)={x|x∈S and f1f2...f j(x)=i} is the set of all elements that were mapped by thefirst j functions to i.The motivation for choosing this estimator is the observation that P j(f1,...,f j)/2t−j is the conditional expec-tation of the number of pairs mapped to the same point by h given the chosen f1...f j and assuming the rest of the bit functions will be chosen randomly.10。
