当前位置：文档之家 › 西南交大经管院《运筹学》运输与整数规划

西南交大经管院《运筹学》运输与整数规划

  • 格式：pdf
  • 大小：359.30 KB
  • 文档页数：71

下载文档原格式

  / 71

合集下载

西南交大853运筹学重要考点(不明年限)

西南交大853运筹学重要考点(不明年限)

运筹学重要考点第一部分：线性规划1、线性规划与单纯形法（1）线性规划问题的数学模型（2）线性规划问题解的概念（3）线性规划问题的图解法（4）单纯形法①将所给问题标准化②计算、迭代步骤③最优性的判定（解的判定定理）④人工变量法：大M法和两阶段法2、对偶问题⑴原问题转化为对应的对偶问题⑵对偶问题的基本性质⑶对偶单纯形法的计算⑷影子价格3、灵敏度分析⑴价值系数灵敏度分析⑵约束条件灵敏度分析⑶技术系数灵敏度分析4、运输问题⑴表上作业法①初始基的确定：最小元素法、伏格尔法②最优解的判别：闭回路法、位势法③改进方法：闭环回路调整法⑵产销不平衡运输问题的求解第二部分：整数规划⑴分支定界法⑵割平面法⑶0-1规划建模及解法（隐枚举法）⑷指派问题①解法：匈牙利法②非标准指派问题第三部分：动态规划1、动态规划的基本思想2、动态规划的解题步骤⑴建立动态规划模型⑵采用逆序法求解3、动态规划的应用⑴最短路问题（一维资源分配问题）⑵生产经营问题①生产——库存问题②库存——销售问题③限期采购问题⑶可靠性问题⑷背包问题⑸设备更新问题第四部分：图与网路计划1、图的基本概念和性质2、最小树（Kruskal算法）3、最短路问题及算法⑴Dijcskra算法⑵Ford算法4、网路最大流问题5、最小费用最大流问题6、中国邮递员问题（奇偶图上作业法）7、网络计划⑴绘制网络图⑵计算时间参数和确定关键路径⑶网络计划的调整和优化单纯型对偶单纯型（改进单纯计算及参数灵敏度不考）运输整数规划（分支定界和割平面计算不考）动态规划（会计算即可）动态规划应用（只考一维资源费配背包可靠度排序）图论网络计划（知道关键路线特征及虚工作意义即可不考计算）。

西南交大经管院《运筹学》运输与整数规划

西南交大经管院《运筹学》运输与整数规划

凑整法
例：max: z = 3x1 + x2
s.t.
2x1 + x2
≤5
2x1 + 3x2 = 5 x1, x2 为非负整数 松弛问题解: x = (2.5, 0 ) T, 四舍五入得不到可行解;
整数最优解: x = (1, 1) T
凑整法
例：max: x1 + 5x2
x2
s.t. x1 + 10x2 ≤ 20
-
Month Installed
2
3
1.10
1.11
1.12
1.13
1.11
1.13
1.12
1.14
-
1.10
-
1.11
-
-
-
-
4 1.13 1.15 1.14 1.15 1.12 1.13 1.13 1.15
Units Produced
1
1 (RT) 10
1 (OT) 0
2 (RT) 0
Month 2 (OT) 0
如指派问题、背包问题、旅行推销商问题都是整数规划问 题； 整数规划又是最难求解的问题之一，至今还没有找到有效算 法。
邮局排班问题
例1：邮局一年365天都要有人值班，每天需要的职工数因 业务忙闲而异，据统计邮局每天需要的人数按周期变化， 一周内每天需要的人数如下表：
排班要符合每周连续工作五天，休息两天的规定。如 何排班可使用人最少。
operationsresearch运输与整数规划西南交通大学经济管理学院transportationproblem运输问题sourcesdestinations运输问题的特征每一个出发地都有一定的供应量supply配送到目的地每一个目的地都有需要从一定的需求量demand接收从出发地发出的产品需求假设therequirementsassumption可行解特性thefeasiblesolutionsproperty成本假设thecostassumption数解性质integersolutionsproperty选择顾客耐芙迪公司在3个工厂中专门生产一种产品这种产品有着优良的品质所以现在公司接到了许多订单产品供不应求

《运筹学》第6章 整数规划

《运筹学》第6章 整数规划
整数规划（Integer Programming，简称IP），是 要求全部或部分决策变量为整数的规划。整数规 划分为线性整数规划和非线性整数规划。本章只 介绍线性整数规划，简称为整数规划。
整数规划分为两大类：一般整数规划与0-1整数规 划（Binary Integer Programming，简称BIP）。
6.3 0-1整数规划
例6.2 分公司选址问题。某销售公司打算通过在武汉 或长春设立分公司（也可以在两个城市都设分公司） 以增加市场份额，管理层同时也在考虑建立一个配送 中心（也可以不建配送中心），但配送中心地点限制 在新设分公司的城市。
经过计算，每种选择使公司收益的净现值和所需费 用如表6-2所示。总的预算费用不得超过1000万元。目 标是在满足以上约束的条件下使总的净现值最大。
100万元 500万元
2
大型飞机
500万元 5000万元 没有限制
可获得的总资金 1亿元
6.1 整数规划基本概念、分类与解的特点
解：
(1)决策变量
设小型飞机与大型飞机的购买 数量分别为x1、x2(架)。 (2)目标函数
目标是年总净利润最大。
M ax z x1 5 x2
(3) 约束条件 ① 资金限制 ② 小型飞机数量限制（最多
在长春设立分公司 在武汉设立分公司 在长春建配送中心 在武汉建配送中心
净现值（万元） 800 500 600 400
所需资金（万元） 600 300 500 200
6.3 0-1整数规划
解：
（1）决策变量
本题的决策变量是是非决策的0-1决策变量，每一个决策只有 两种选择，是或者否，1表示对于这个决策选择“是”，0表 示对于这个决策选择“否” 。
是非决策问题

管理运筹学讲义整数规划

管理运筹学讲义整数规划

管理运筹学讲义整数规划整数规划是管理运筹学中一种重要的优化技术，它在实际问题中具有广泛的应用。

本文将介绍整数规划的基本概念、建模方法以及解决算法，并通过实例展示其在实际问题中的应用。

一、整数规划的基本概念整数规划是线性规划的一种扩展形式，其决策变量被限制为整数。

在实际问题中，往往存在某些变量只能取整数值的约束条件，这时就需要使用整数规划方法进行求解。

与线性规划相比，整数规划的求解难度更大，但可以提供更精确的结果。

二、整数规划的建模方法在进行整数规划建模时，需要确定决策变量、目标函数和约束条件。

1. 决策变量决策变量是问题中需要优化的变量，其取值决定了问题的解。

在整数规划中，决策变量通常表示为整数。

2. 目标函数目标函数是整数规划问题中需要最小化或最大化的目标。

它可以是线性函数或非线性函数，但在整数规划中，通常只考虑线性目标函数。

3. 约束条件约束条件是问题的限制条件，限制了决策变量的取值范围。

在整数规划中，约束条件可以是线性等式或线性不等式。

三、整数规划的解决算法解决整数规划问题的常见算法包括割平面法、分支定界法和动态规划法等。

这些算法通过不断对问题进行优化，逐步逼近最优解。

1. 割平面法割平面法是一种通过添加额外的约束条件来逼近最优解的方法。

它首先求解一个松弛问题，然后根据松弛问题的解加入新的约束条件，直到找到最优解。

2. 分支定界法分支定界法是一种将整数规划问题划分为多个子问题，并对每个子问题进行求解的方法。

它通过不断分支和剪枝来找到最优解。

3. 动态规划法动态规划法是一种通过将问题分解为多个子问题，并通过求解子问题的最优解来求解原始问题的方法。

它采用自底向上的求解方式，将所有可能的决策情况进行组合，得到最优解。

四、整数规划在实际问题中的应用整数规划在实际问题中有着广泛的应用。

以下是一个应用整数规划解决的实际问题示例：某公司生产两种产品A和B，每天的生产时间为8小时。

产品A每单位利润为100元，产品B每单位利润为150元。

《管理运筹学》02-7运输问题

《管理运筹学》02-7运输问题
在运输问题中，混合整数规划可以处理更为复 杂的约束条件和多阶段决策过程。
通过将问题分解为多个子问题，并应用分支定 界法等算法，可以找到满足所有约束条件的整 数解，实现运输资源的合理配置。
04运Leabharlann 问题的实际案例物资调拨案例
总结词
物资调拨案例是运输问题中常见的一种，主要涉及如何优化物资从供应地到需 求地的调配。
02
动态运输问题需要考虑运输过 程中的不确定性，如交通拥堵 、天气变化等，需要建立动态 优化模型来应对这些变化。
03
解决动态运输问题需要采用实 时优化算法，根据实际情况不 断调整运输计划，以实现最优 的运输效果。
多式联运问题
1
多式联运是指将不同运输方式组合起来完成一个 完整的运输任务，需要考虑不同运输方式之间的 衔接和配合。
生产计划案例
总结词
生产计划案例主要关注如何根据市场需求和生产能力制定合理的生产计划。
详细描述
生产计划案例需要考虑市场需求、产品特性、生产成本、生产周期等因素。通过 优化生产计划，可以提高生产效率、降低生产成本，并确保产品按时交付给客户 。
05
运输问题的扩展研究
动态运输问题
01
动态运输问题是指运输需求随 时间变化而变化的运输问题， 需要考虑时间因素对运输计划 的影响。
2
多式联运问题需要考虑不同运输方式的成本、时 间、能力等因素，需要建立多目标优化模型来平 衡这些因素。
3
解决多式联运问题需要采用混合整数规划或遗传 算法等算法，以实现多目标优化的效果。
逆向物流问题
1
逆向物流是指对废旧物品进行回收、处 理和再利用的物流活动，需要考虑废旧 物品的回收、分类、处理和再利用等环 节。
的情况。如果存在这些问题，就需要进行调整，直到找到最优解为止。

交通运筹学第3章 整数规划

交通运筹学第3章 整数规划

X1 4
(2)
4 2.1
X2 2 (4) 4 2 340
349.0 X2 3 (5) 340 (6) 5.444 1
5 341.39 1.571
X2 1 340 X2 2 (7) 无解
20
1.428 327.12 3
307.76
第3节 割平面法

割平面法的基本思想： 在整数规划问题的松弛问题中依次引进线性 约束条件(称Gomory约束，高莫雷约束或割 平面)，使问题的可行域逐步缩小。但每次 切割时，只割去问题的部分非整数解，而不 切割任何整数的可行解，直到使问题的目标 函数值达到最优的整数点成为缩小后可行域 的一个顶点，这样就可以用求解线性规划问 题的方法找出这个最优解。
31
第四节 0-1整数规划





将0-1规划的变量改为并且为整数，就可以用分支定界 法或割平面法求解。由于0-1规划的特殊性，用隐枚举 法更为简便。其求解步骤如下： 寻找一个初始可行解，得到目标函数值的下界，（最 小值为题则为上界）。 列出2个变量取值的组合，当组合解对应的目标值小于 （max）时，认为不可行，当大于等于（max）时，再 检验是否满足约束条件，得到0-1规划的可行解。 依据的值确定最优解。 这里的下界可以动态移动，当某个大于时，则将作为 新的下届。
X为整数 (B)为(A)的松弛问题。
14
（2）替代问题的求解 max Z=CX
(B)
AX=b X 0
采用相应的方法（如图解法）求解出替代问题的 最优解，观察其是否满足整数解的要求。如其最 优解就为整数，则结束；如含有分数，则需要进 行分支定界操作。
15
（3）分支与定界—增加约束
•如替代问题的解不符合整数条件，则需要对原问题进行分支。

运筹学2运输问题及目标规划

运筹学2运输问题及目标规划
M N
另外要注意（记忆）： 1、对于运输问题模型，在m＋n个约束条 件中，因为隐含着一个总产量等于总销量的等式，所以相 互独立的约束条件个数为m＋n－1个，因此秩≤m＋n－1 2、区别于一般的线性规划问题，产销平衡 的运输问题一定具有可行解，同时也一定存在最优解。
这种模型用单纯形法完全可以求解。 但是如果用单纯形法求 解，先得在每个约束条件上加入一个人工变量(以便求出初始基可 行解)。因此，即使是 m = 3， n = 4 这样的简单问题, 变量数就有 （3×4）＋（3＋4）＝19个之多，计算起来非常复杂。
A B C 销量bj
3 1 7 3
11 9 4 6
3 2 10 5
10 8 5 6
7 4 9
对于运输问题，关键要素有三：产量、销量和运费。 解：设xij代表从第I个产地到第j个销地的运输量（I＝1，2，3； J＝1，2，3，4），用cij代表从第I个产地到第j个销地的运价，于是 可构造数学模型
Min Z cij xij
（2）求各非基变量（空格或非数字格）的检验数。即在表上求空 格的检验数，判别是否达到最优解。如果达到最优解，则停止计算， 否则转入下一步； （3）迭代。确定换入变量和换出变量，找出新的基可行解，在表 上用闭回路法进行调整。 （4）重复（2）、（3）步，直到求得最优解为止。
表上作业法的难点是 1、找出初始基可行解
A2 的产品供应 B1 。由于A2 每天生产4吨，B1 每天只需要
3吨，即 A2 除每日能满足B1 的需要外还余1吨。因此在产
销平衡表 (A2 , B1) 交叉处填上3，表示 A2 调运3吨给B1 ，
再在单位运价表中将B1 这一列运价划去，表示 B1 的需求
已满足，不需要继续调运 (即x21 =3=min(a2,b1)=min(4 , 3).

第二讲 运输问题与整数规划介绍

第二讲 运输问题与整数规划介绍
用表上作业法求出空船的最优调度方案见表7.
港 口 C D F 每天缺少船只 A 1 B 1 1 1 E 1 1 1 3 每天多余船只 2 2 1 5
由表7知最少需周转的空船数为 2×1+13×1+5×1+17×1+3×1=40条。这样在不考虑维 修、储备等情况下,该公司至少应配备40+91=131条船。
应用举例
表上作业法比单纯形法简单，可将其他 问题转化为运输问题的形式来求解。
例1 某厂按合同规定须于当年每个季度末分别提供10， 15，25，20台同一规格的柴油机。已知该厂各季度 15 25 20 的生产能力及生产每台柴油机的成本如表1所示。又 如果生产出来的柴油机当季不交货的，每台每积压 一个季度需储存、维护等费用0.15万元。要求在完 成合同的情况下，作出使该厂全年生产(包括储存、 维护)费用最小的决策.
产大于销问题
应用举例(1)
当i＞j时，xij=0，令对应的cij=M，再加上一个假想的 需求D，就可以把这个问题变成产销平衡的运输模型: 表3 产销平衡表与单位运价表(合表)
销地 产地
Ⅰ 10.8 M M M 10
Ⅱ 10.95 11.10 M M 15
Ⅲ 11.10 11.25 11.00 M 25
无转运问题 新增“产地”： am+j= 0 新增“销地”： bi= 0
有转运问题
j =1,2,..., n i =1,2,..., m
转运问题
第一步，将产地、转运点、销地重新编排， 第一步，将产地、转运点、销地重新编排， 转运点既作为产地又作为销地； 转运点既作为产地又作为销地； 第二步，各地之间的运距（或运价） 第二步，各地之间的运距（或运价）在原 问题运距（运价）表基础上进行扩展： 问题运距（运价）表基础上进行扩展：从 一地运往自身的单位运距（运价）记为零， 一地运往自身的单位运距（运价）记为零， 不存在运输线路的则记为M 不存在运输线路的则记为M（一个足够大 的正数） 的正数）；

运筹学-第三章-整数规划

运筹学-第三章-整数规划

于是，对原问题增加两个新约束条件，将原问题分为两个 子问题，即有
max z 40x1 90x2
max z 40x1 90x2
9x1 7x2 56
s.t
7 x1
20 x2
70
x1 4
x1, x2 0
（LP1）
9x1 7x2 56
和
s.t
7
x1
20
x2
70
（LP2）
x1 5
表 3.1
货物 体积（米 3/箱） 重量（百公斤/箱） 利润（百元/箱）
甲
5
2
20
乙
4
5
10
托运限制 24 米 3
13 百公斤
解： 设x1，x2 分别为甲、乙两种货物的托运箱数，则数 学模型可以表示为：
max z 20x1 10x2
5x1 4x2 24 2x1 5x2 13 x1, x2 0, x1, x2整数
其中，目标函数表示追求最大的卫星实验价值；第1,2个约
束条件表示体积和重量的限制；第3-5个约束条件表示特定的卫
星装载要求,该问题的决策变量是0-1整数变量。
3.2.3隐枚举法 从上面两个例子可以看出，此类型问题是整数规划中的特
殊情形，其中决策变量 xi 的取值只能为0或1，此时变量 xi 称 为0-1变量，这类问题被称为0-1整数规划。对于 xi 的取值的 0-1约束，可以转化成下述整数约束条件：xi 1, xi 0, xi Z
目前对于整数规划问题的求解主要有两种方法：分支 定解法和割平面法。本章仅介绍分枝定界法，该方法在上 世纪60年代由Land Doig和Dakin等人提出，其具有灵活 且便于计算机求解的优点，所以现在已成为解决整数规划 问题的重要方法。下面通过例子说明分支定界方法的算法 思想和步骤。

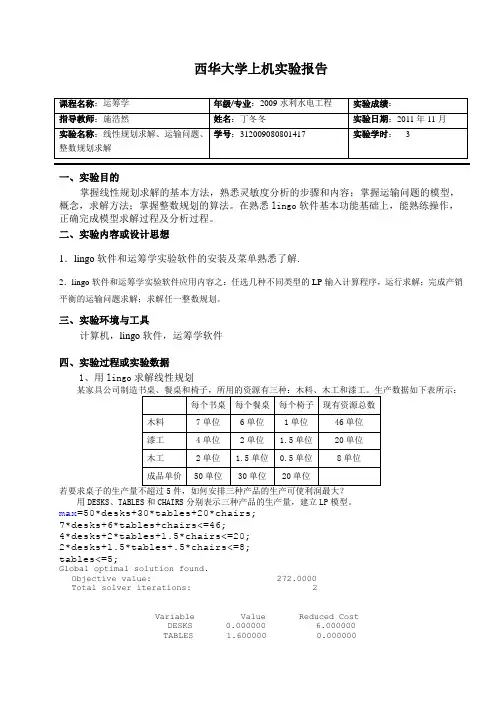
运筹学实验一线性规划求解、运输问题、整数规划求解

运筹学实验一线性规划求解、运输问题、整数规划求解

西华大学上机实验报告一、实验目的掌握线性规划求解的基本方法，熟悉灵敏度分析的步骤和内容；掌握运输问题的模型，概念，求解方法；掌握整数规划的算法。

在熟悉lingo软件基本功能基础上，能熟练操作，正确完成模型求解过程及分析过程。

二、实验内容或设计思想1．lingo软件和运筹学实验软件的安装及菜单熟悉了解.2．lingo软件和运筹学实验软件应用内容之：任选几种不同类型的LP输入计算程序，运行求解；完成产销平衡的运输问题求解；求解任一整数规划。

三、实验环境与工具计算机，lingo软件，运筹学软件四、实验过程或实验数据1、用lingo求解线性规划用DESKS、TABLES和CHAIRS分别表示三种产品的生产量，建立LP模型。

max=50*desks+30*tables+20*chairs;7*desks+6*tables+chairs<=46;4*desks+2*tables+1.5*chairs<=20;2*desks+1.5*tables+.5*chairs<=8;tables<=5;Global optimal solution found.Objective value: 272.0000Total solver iterations: 2Variable Value Reduced CostDESKS 0.000000 6.000000TABLES 1.600000 0.000000Row Slack or Surplus Dual Price1 272.0000 1.0000002 25.20000 0.0000003 0.000000 12.000004 0.000000 4.0000005 3.400000 0.0000002、用LINGO软件计算运输问题model:sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsetsmin=@sum(links: cost*volume);@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataendGlobal optimal solution found.Objective value: 638.0000Total solver iterations: 16Variable Value Reduced CostCAPACITY( WH3) 57.00000 0.000000 CAPACITY( WH4) 43.00000 0.000000 CAPACITY( WH5) 41.00000 0.000000 CAPACITY( WH6) 52.00000 0.000000 DEMAND( V1) 35.00000 0.000000 DEMAND( V2) 37.00000 0.000000 DEMAND( V3) 25.00000 0.000000 DEMAND( V4) 32.00000 0.000000 DEMAND( V5) 41.00000 0.000000 DEMAND( V6) 36.00000 0.000000 DEMAND( V7) 43.00000 0.000000 DEMAND( V8) 38.00000 0.000000 COST( WH1, V1) 8.000000 0.000000 COST( WH1, V2) 2.000000 0.000000 COST( WH1, V3) 6.000000 0.000000 COST( WH1, V4) 7.000000 0.000000 COST( WH1, V5) 4.000000 0.000000 COST( WH1, V6) 2.000000 0.000000 COST( WH1, V7) 9.000000 0.000000 COST( WH1, V8) 5.000000 0.000000 COST( WH2, V1) 4.000000 0.000000 COST( WH2, V2) 9.000000 0.000000 COST( WH2, V3) 5.000000 0.000000 COST( WH2, V4) 3.000000 0.000000 COST( WH2, V5) 8.000000 0.000000 COST( WH2, V6) 5.000000 0.000000 COST( WH2, V7) 8.000000 0.000000 COST( WH2, V8) 2.000000 0.000000 COST( WH3, V1) 5.000000 0.000000 COST( WH3, V2) 2.000000 0.000000 COST( WH3, V3) 1.000000 0.000000 COST( WH3, V4) 9.000000 0.000000 COST( WH3, V5) 7.000000 0.000000 COST( WH3, V6) 4.000000 0.000000 COST( WH3, V7) 3.000000 0.000000 COST( WH3, V8) 3.000000 0.000000 COST( WH4, V1) 7.000000 0.000000 COST( WH4, V2) 6.000000 0.000000 COST( WH4, V3) 7.000000 0.000000 COST( WH4, V4) 3.000000 0.000000 COST( WH4, V5) 11.00000 0.000000 COST( WH4, V6) 2.000000 0.000000 COST( WH4, V7) 7.000000 0.000000 COST( WH4, V8) 1.000000 0.000000 COST( WH5, V1) 2.000000 0.000000 COST( WH5, V2) 3.000000 0.000000 COST( WH5, V3) 9.000000 0.000000 COST( WH5, V4) 5.000000 0.000000 COST( WH5, V5) 7.000000 0.000000 COST( WH5, V6) 2.000000 0.000000 COST( WH5, V7) 6.000000 0.000000 COST( WH5, V8) 5.000000 0.000000 COST( WH6, V1) 5.000000 0.000000 COST( WH6, V2) 5.000000 0.000000 COST( WH6, V3) 2.000000 0.000000 COST( WH6, V4) 2.000000 0.000000 COST( WH6, V5) 8.000000 0.000000 COST( WH6, V6) 1.000000 0.000000 COST( WH6, V7) 4.000000 0.000000VOLUME( WH1, V2) 37.00000 0.000000 VOLUME( WH1, V3) 0.000000 3.000000 VOLUME( WH1, V4) 0.000000 4.000000 VOLUME( WH1, V5) 41.00000 0.000000 VOLUME( WH1, V6) 2.000000 0.000000 VOLUME( WH1, V7) 0.000000 4.000000 VOLUME( WH1, V8) 0.000000 4.000000 VOLUME( WH2, V1) 0.000000 2.000000 VOLUME( WH2, V2) 0.000000 7.000000 VOLUME( WH2, V3) 0.000000 2.000000 VOLUME( WH2, V4) 14.00000 0.000000 VOLUME( WH2, V5) 0.000000 4.000000 VOLUME( WH2, V6) 0.000000 3.000000 VOLUME( WH2, V7) 0.000000 3.000000 VOLUME( WH2, V8) 0.000000 1.000000 VOLUME( WH3, V1) 0.000000 5.000000 VOLUME( WH3, V2) 0.000000 2.000000 VOLUME( WH3, V3) 14.00000 0.000000 VOLUME( WH3, V4) 0.000000 8.000000 VOLUME( WH3, V5) 0.000000 5.000000 VOLUME( WH3, V6) 0.000000 4.000000 VOLUME( WH3, V7) 43.00000 0.000000 VOLUME( WH3, V8) 0.000000 4.000000 VOLUME( WH4, V1) 0.000000 5.000000 VOLUME( WH4, V2) 0.000000 4.000000 VOLUME( WH4, V3) 0.000000 4.000000 VOLUME( WH4, V4) 5.000000 0.000000 VOLUME( WH4, V5) 0.000000 7.000000 VOLUME( WH4, V6) 0.000000 0.000000 VOLUME( WH4, V7) 0.000000 2.000000 VOLUME( WH4, V8) 38.00000 0.000000 VOLUME( WH5, V1) 35.00000 0.000000 VOLUME( WH5, V2) 0.000000 1.000000 VOLUME( WH5, V3) 0.000000 6.000000 VOLUME( WH5, V4) 0.000000 2.000000 VOLUME( WH5, V5) 0.000000 3.000000 VOLUME( WH5, V6) 6.000000 0.000000 VOLUME( WH5, V7) 0.000000 1.000000 VOLUME( WH5, V8) 0.000000 4.000000 VOLUME( WH6, V1) 0.000000 4.000000 VOLUME( WH6, V2) 0.000000 4.000000 VOLUME( WH6, V3) 11.00000 0.000000 VOLUME( WH6, V4) 13.00000 0.000000 VOLUME( WH6, V5) 0.000000 5.000000 VOLUME( WH6, V6) 28.00000 0.000000 VOLUME( WH6, V7) 0.000000 0.000000 VOLUME( WH6, V8) 0.000000 3.000000 Row Slack or Surplus Dual Price1 638.0000 -1.0000002 0.000000 -2.0000003 0.000000 -2.0000004 0.000000 -3.0000005 0.000000 -3.0000006 0.000000 -4.0000007 0.000000 -2.0000008 0.000000 -5.0000009 0.000000 -1.00000010 0.000000 0.00000012 0.000000 2.00000013 0.000000 0.00000014 0.000000 0.00000015 0.000000 1.0000003、用lingo解整数规划问题min=5*x1+x2+3*x3+7*x4+x5+x6+3*x7;6*x1+3*x2+2*x3+x4+x5>=50;x2+2*x4+x5+5*x6>=35;x3+x5+3*x7>=10;在lingo窗口输入以下代码，min=5*x1+x2+3*x3+7*x4+x5+x6+3*x7;6*x1+3*x2+2*x3+x4+x5>=50;x2+2*x4+x5+5*x6>=35;x3+x5+3*x7>=10;@gin(x1);@gin(x2);@gin(x3);@gin(x4);@gin(x3);@gin(x6);@gin(x7);END运行结果为：Global optimal solution found.Objective value: 27.00000Extended solver steps: 0Total solver iterations: 4Variable Value Reduced CostX1 0.000000 5.000000X2 14.00000 1.000000X3 0.000000 2.000000X4 0.000000 7.000000X5 10.00000 0.000000X6 3.000000 1.000000X7 0.000000 0.000000Row Slack or Surplus Dual Price1 27.00000 -1.0000002 2.000000 0.0000003 4.000000 0.0000004 0.000000 -1.000000五、总结正确安装了运筹学的lingo实验软件，对lingo软件的菜单有了一定的了解和熟悉，掌握了线性规划求解的基本方法，了解灵敏度分析的步骤和内容；掌握了运输问题的模型，概念，求解方法；掌握了整数规划的算法。

运输问题、整数规划简介

运输问题、整数规划简介

纯整数规划： 纯整数规划：如果所有决策变量都要求取 整数，则称为“纯整数规划” 整数，则称为“纯整数规划” 混合整数规划： 混合整数规划：如果仅有一部分的决策变 量要求取整数，则称为“混合型整数规划” 量要求取整数，则称为“混合型整数规划”。 还有一种特殊情况， 还有一种特殊情况， 0－1整数规划：所有决策变量仅限于取 0 或 － 整数规划 整数规划： 1 两个整数，这种规划问题称为“0-1规划” 两个整数，这种规划问题称为“ 规划”
运输问题的一般提法： 运输问题的一般提法： 某种物资有若干产地和销地， 某种物资有若干产地和销地 ， 现 在需要把这种物资从各个产地运到 各个销地，产量总数等于销量总数。 各个销地， 产量总数等于销量总数。 已知各产地的产量和各销地的销量 产量和各销地的 已知各产地的 产量 和各销地的 销量 以及各产地到各销地的单位运价 或运距） 问应如何组织调运， （ 或运距 ） ， 问应如何组织调运 ， 才能使总运费 或总运输量） 总运费（ 才能使 总运费 （ 或总运输量 ） 最省 或最多） （或最多）？
M inZ = ∑∑cij xij
i= 1 j= 1 m n
n i =1 m , , ∑xij = ai j =1 m s.t.∑xij = bj j =1 n , , i=1 , m , , xij ≥ 0, i =1 ; j =1 n
n m ∑ai = ∑bj j =1 i=1
指派问题（分配问题） 指派问题（分配问题） (Assignment Problem) 假定有n项任务分配给n 假定有n项任务分配给n个人去完 并指定每人完成其中一项， 成，并指定每人完成其中一项， 每项只交给其中一个人去完成， 每项只交给其中一个人去完成， 应如何分配使总效率为最高。 应如何分配使总效率为最高。

运筹学目标规划与整数规划

运筹学目标规划与整数规划
目标规划
单击此处添加副标题
运筹学
01
02
可能的弹性约束：
方案优劣并不以单一准则为目标，而是以多重准则为目标 约束条件并不完全符合严格的刚性条件，具有一定的弹性
最好等于 最好不大于 最好不小于
实际问题决策经常面临的问题：
多目标决策问题
弹性约束的处理方法
实际量＋
d
－
－
d
+
=
目标值
负偏差变量
正偏差变量
S1
B: x1=2,x2=23/9 Z=41/9
S11
无可行解
S12
D: x1=33/14,x2=2 Z=61/14
对S12分枝：
1
2
3
1
1
3
2
X
2
5
4
X
S2
构造约束：
和
形成分枝问题S121和S122，得解E和F
S121
ቤተ መጻሕፍቲ ባይዱ
S122
S
A: x1=3/2,x2=10/3 Z=29/6
S2
C: x1=1,x2=7/3 Z=10/3
经典指派问题
n个员工分配作n项工作，一致的i个员工作的j项工作的成本为cij，i=1,…,n; j=1,…,n。求最佳分配方案。
指派问题的数学模型
t.
指派问题的解应对应于成本矩阵的不同行与不同列，且总成本最小
例
cij
指派问题的性质
定理：对于指派问题，成本矩阵的任一行(或列)减去(或加上)一个相同的数得到的新指派问题与原问题同解
100
200
300
400
500
1
(1)
(2)

整数规划及运输问题

整数规划及运输问题

（2）选择了S3或S4就不能选择S5，反 过来也一样;
（3）在S5，S6 ，S7，S8中最多只能选 两个。 问如何选择井位使总费用最小？
课堂练习1: 某钻井队要从S1~S10共10个井位中确定五个钻井探油，
如果选Si，估计钻探费用为ci元，并且井位选择上要满足下列条件： （1）或选择S1和S7，或选择S8 （2）选择了S3或S4就不能选择S5，反过来也一样 （3）在S5，S6 ，S7，S8中最多只能选两个 问如何选择井位使总费用最小？
min Z x1 5 x2 x1 x2 2 5 x1 6 x2 30 x 4 1 ( IP6) x1 2 x2 3 x 3 1 x1 , x2 0且为整数
只要求出（LP5）和（LP6）的最优解即可。
先求（ LP5 ） , 如图所示。此时 E
3
3
x1
按整数规划约束条件，其可行解肯定在线性规划问题的可
行域内且为整数点。故整数规划问题的可行解集是一个有限集，
如图所示。
整数规划与线性规划的关系
因此，可将集合内的整数点一一找出，其最
大目标函数的值为最优解，此法为完全枚举法。
如上例：其中（ 2 ， 2 ）（ 3 ， 1 ）点为最大值， Z=4。
记为（LP）
用图解法求（LP）的最 优解，如图所示。
分枝定界法 ⑵
x2
3
⑴
(18/11,40/11)
⑶
x1＝18/11, x2 =40/11
Z(0) =－218/11≈(－19.8)
即Z(0) 是（IP）最小值的下限。 对于x1＝18/11≈1.64，
取值x1 ≤1， x1 ≥2
对于x2 =40/11 ≈3.64，取值x2 ≤3 ，x2 ≥4

运筹学运输问题、整数规划、目标规划和动态规划

运筹学运输问题、整数规划、目标规划和动态规划

整数规划案例一案例二案例三动态规划案例四:某开发区养老保险定量分析模型养老保险属于社会保障系统的重要内容，社会保障系统作为一个国家社会制度的重要组成部分，其内容、形式和其中所使用的各种计算方法不仅关系到国民的自身利益，而且对一个国家的政治和社会经济的发展具有重要的作用。

社会保障系统中所包含的定量分析和计算是多种多样的，主要包括三个方面：第一，对社会保障基金提取量的测算；第二，对职工享受社会保障待遇的标准测算；第三，对社会保障基金各阶段收付额的预测。

基本养老保险金的提取比例一般是一年或若干年调整一次，从数学模型的角度看两者并无实质性区别，这里定义一年为一个阶段。

考虑到养老保险制度是一个长期制度，具体年限并不确定，因而阶段数可以根据实际问题的研究目标制定。

如：要确定10年内各年的提取比例，则阶段数就定为10；也可以将老龄化程度最高、养老保险金支付额最大的年份作为决策过程的终止年。

不失一般性，将整个决策过程定义为n个阶段。

状态变量x k定义为阶段k开始时的储备基金，M是最大储备金额。

为阶段k基本养老保险金按工资总额提取的比例，这一比例也决策变量uk应在一定范围之内。

按照国际标准，提取比例达到20%时即为社会预警线，29%即达到社会承受的极限，因此我们设定R为提取的最大比例，若s为阶段k的k工资总额，则有：d k -xk≤sk•uk≤min{sk•R,dk+dk+1+…+dn+A-xk}其中sk•R就是基本养老保险金所能提取的最大金额。

已知阶段k开始时的储备基金是x k，阶段k的基本养老保险金收入额为s k•u k ，支付额是dk。

假定储备基金的年增值率为ik，考虑资金的时间价值，则阶段末即阶段k+1的初始储备基金为：x k+1=（1+ik）xk+sk•uk-dk，即状态转移方程。

可以看出，k+1阶段的储备基金xk+1完全由k阶段的储备基金xk和基本养老保险金的提取比例uk所决定，与前面的状态和决策无关，即满足无后效性。

西南交大交通运输规划与管理专业

西南交大交通运输规划与管理专业

选修课程
智能交通系统
交通运输政策与法规
介绍智能交通系统的基本原理和应用 ，包括交通信号控制、智能车辆导航 、交通信息采集与处理等。
介绍交通运输政策的基本理论和法规 ，包括交通运输政策制定、实施和评 估的方法和工具。
城市交通规划
介绍城市交通规划的基本理论和方法 ，包括城市道路网规划、公共交通规 划、停车设施规划等。
01
引言
专业背景与意义
01
交通运输行业的重要性
交通运输是国民经济的基础性、先导性产业，对于促进经济社会发展、
改善人民生活具有重要意义。
02
交通运输规划与管理在行业中的地位
交通运输规划与管理是交通运输行业的重要组成部分，对于提高运输效
率、保障交通安全、促进可持续发展具有重要作用。
03
专业设置的必要性
习。
教学软件应用
利用专业教学软件，如交通规划 软件、仿真软件等，辅助理论和
实践教学。
04
交通运输规划与管理专业人才 培养目标与要求
人才培养目标
培养具备交通运输规划与管理领域的 基本理论、基本知识和基本技能，具 有创新精神和实践能力的高级专门人 才。
培养具备交通运输规划、交通设计、 交通运营管理等方面能力的人才，能 够从事城市交通规划、交通设计、交 通管理、交通工程等工作。
03
交通运输规划与管理专业教学 方法与手段
理论教学方法
讲授法
通过教师讲授，学生听讲 的方式，系统传授专业知 识。
讨论法
组织小组讨论或课堂讨论 ，引导学生主动思考和交 流。
案例分析法
通过分析实际案例，帮助 学生理解理论知识在ຫໍສະໝຸດ 践 中的应用。实践教学方法
实验法

西南交大经管院《运筹学》线性规划

西南交大经管院《运筹学》线性规划

Linear Programming With Spreadsheet每个小组都有一组拼装玩具(8个小块和6 大块) ，这些是你们的原材料（raw materials ），你们要用这些原材料去生产桌和椅（tables and chairs ）这两种产品（products ），具体拼装图如下一个幻灯片。

你怎么去分析呢？The Lego Production Problem拼装玩具生产自己动手想想看！自己动手原材料6 大块8 小块产品桌椅Profit = $20/Table Profit = $15/Chair自己动手为了最小化成本或最大化利润的目的需要对一些稀缺资源进行配置Maximize ($15)Chairs+($20)Tablessubject toLarge Bricks:Chairs+2Tables≤6Small Bricks:2Chairs+2Tables≤8andChairs≥0, Tables≥0.你的答案是什么？Components of the Model模型的组成部分Decision variables 决策变量Objective function 目标函数Constraints 约束使用EXCEL求解线性规划Excel自1991年问世，目前已有几千万用户；其免费的规划求解软件由Frontline System提供()，专为大多数没有受过OR/MS专门训练的用户设计；Excel将GUI，各种函数功能，模型语言，优化软件和编程功能(VBA) 结合在统一的环境下；Excel 提供了强大的数据组织、运算和呈现功能，在Excel 表格中可用更工程化的方式提供模型使用的数据，并可将输出结果用各种图表的方式表示出来；EXCEL模型的基本构成Excel通过表格(cell)所含数据或公式来表示运筹模型的变量、目标函数、约束方程和模型参数:y数据：Excel强大的数据组织与呈现功能可使模型数据组织的更简洁明了；y变量：Excel中的可变单元格定义决策变量，决策变量是模型求解的未知量，也称为可变量；y目标函数：由目标单元格中的数学表达式表示；y约束：约束由表示约束左边项与右边项的数学表达式或数值的单元格定义，通常约束的左边项是数学表达式，右边项既可是表达式，也可是参数如何进入Excel中的优化模块选择主菜单“工具”→“规划求解”可进入“规划求解参数”定义窗口；如找不到“规划求解”项，可通过“工具”→“加载宏”加入该项功能。

运筹学中的线性规划和整数规划

运筹学中的线性规划和整数规划

运筹学中的线性规划和整数规划运筹学是一门涉及决策分析、优化、模型构建和仿真等知识领域的学科，应用广泛，如供应链管理、交通规划、制造业生产、金融投资等方面。

其中，线性规划和整数规划是运筹学中最为基础和重要的优化技术，被广泛应用于各个领域。

一、线性规划线性规划是一种在一组线性约束条件下，求解线性目标函数极值问题的数学方法。

在生产、运输、选址等问题中，线性规划都有着重要的应用。

其数学模型可以表示为：$\max c^Tx$$s.t. Ax \leq b,x\geq 0$其中$c$为目标函数的向量，$x$为决策变量向量，$A$为约束矩阵，$b$为约束向量，$c^Tx$表示目标函数的值，$\leq$表示小于等于。

如果目标函数和约束都是线性的，则可以通过线性规划的求解方法来确定决策变量的最优值。

线性规划的求解方法一般分为单纯形法和内点法两种方法。

单纯性法是线性规划中最为常用的方法，通过对角线交替调整，逐步从可行解中寻找最优解，收敛速度较快，但是存在不稳定的情况。

内点法是近年来发展起来的用于求解大规模线性规划问题的数值方法，其核心思想是迭代求解一系列线性方程组，每次保持解在可行域内部，直到找到最优解为止。

这种方法对大规模问题求解能力强，使用较多。

二、整数规划整数规划是线性规划的升级版，它要求决策变量必须取整数值。

整数规划在很多实际问题中都有着重要的应用，比如很多生产过程中需要将生产数量取整数，物流路径问题需要选取整数条路径等。

与线性规划不同的是，整数规划是NP难问题，没有一种有效的算法能够完全解决所有的整数规划问题。

因此，通常需要采用分支定界、割平面等方法来求解。

分支定界是一种常用的整数规划求解方法。

它通过将整数规划问题分为多个子问题，依次求解这些子问题并优化当前最优解，以逐步逼近最优解。

割平面法则是在分支定界方法的基础上加入约束条件，使得求解过程更加严格化，最终得到更好的结果。

总的来说，运筹学中线性规划和整数规划是不可或缺的优化工具，我们可以通过理论和实践加深对它们的理解。

管理运筹学(西南交通大学)

管理运筹学(西南交通大学)

西南交通大学2014年全日制硕士研究生入学试题解析试题名称：管理运筹学二一、问题题（60分，共10小题，每小题6分）（答在试卷上的内容无效）1、简述单纯形法的基本思路。

解析：这是一道考查单纯形法基本知识的题目，是很容易出简答题的知识点。

解：详见寇伟华《运筹学》P40。

2、简述线性规划问题求解出现退化解的特征。

解析：P58线性规划问题各种解的情况都容易出问答题，应理解并会用自己的语言组织。

解：如果出现基变量等于零，就会造成基本可行解中非零变量的个数小于约束条件方程的个数，这就是退化现象。

在用单纯形法求解时，退化现象表现为，若确定的换出变量同时有两个或两个以上，就会造成下一次迭代时有一个或几个基变量的取值为0。

3、什么是对偶问题的弱对偶性？解析：考查的是对偶问题的性质，对偶问题的性质是常考题目，应熟练掌握。

解：详见寇伟华《运筹学》P76定理3.24、简述影子价值与边际值的区别。

解析：这是考查概念的问题，影子价格和边际值是两个简单的概念，理解了自然能说出他们的区别。

解：详见寇伟华《运筹学》P95影子价格和边际值概念5、简述闭回路法求取运输问题检验数的步骤。

解析：闭回路法求运输问题检验数是基本知识和方法，运输问题这里可以问的问题很多，可以问你表上作业法，可以问你差值法求初试基本可行解的步骤，可以问你位势法求运输问题检验数的步骤等等，需要对运输问题的表上作业法的过程非常熟悉，才能有助于解决这类问答题以及计算题。

解：详见寇伟华《运筹学》P128。

6、简述指派问题等效矩阵的方法及性质。

解析：考查指派问题的简答问答题，理解并用自己的语言组织即可。

解：详见寇伟华《运筹学》P154定理6.1。

7、简述无向图中连通图与完备图的区别。

解析：考查的是图与网络这章的基本知识的概念和区别，应理解并掌握基础知识。

解：详见寇伟华《运筹学》P216和P217完备图和连通图的概念。

8、判别可行流是最小费用流的依据是什么？解析：考查图与网络中的基本判别条件，熟练掌握了最小费用流的解题过程也就能自己组织出答案。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

5
20 <=
20
0
0
<=
10
0
10 <=
30
0
0
<=
15
0
25 <=
25
10
10 <=
10
5
5
<=
5
0
0
<=
10
20
=
Total Cost
20
($millions)
77.4
北方飞机制造公司的最优生产进度安排
月份 1 (RT) 2 (RT) 3 (RT) 3 (OT) 4 (RT)
产量 20 10 25 10 5
序 服装 市场 租金 生产 销售 人工 设备 可用工 种类 需求 元/台 成本 价格 工时 工时 时/台
1 西服 150 5000 280 400 5 3 300 2 衬衫 800 2000 30 40 1 0.5 500 3 羽绒服 350 3000 200 300 4 2 300
服装厂生产模型
20
5
10
1.13
1.15
Northern Airplane Co. Production-Scheduling Problem
Production Cost Regular
Storage Cost
($millions)
Time Overtime ($millions per month)
Month 1 1.08
Nifty Co. Product-Distribution Problem
Unit Profit
Customer 1
Plant 1
$55
Plant 2
$37
Plant 3
$29
Customer 2 $42 $18 $59
Customer 3 $46 $32 $51
Customer 4 $53 $48 $35
x1 = 1.000 x2 = 4.333
x2 ≤ 4
zU = 5.33 zL = 5.00
SUB 3
z3 = 5.0 x1 = 1.0 x2 = 4.0
LP松弛
z0 = 5.545 x1 = 1.477 x2 = 4.068
SUB 2
max x1 + x2
s.t. 6x1 + 2x2 ≤ 17
5x1 + 9x2 ≤ 44
问题：每月生产多少发动机的计划，使制造和存储的总成本达到最小
月份
1 2 3 4
计划安装量
最大产量 正常时间 加班时间
单位生产成本（百万 美元）
正常时间 加班时间
单位存储 成本（美
元）
10
20
10
1.08
1.10
15000
15
30
15
1.11
1.12
15000
25
25
10
1.10
1.11
15000
x1 + x2 + x3
+x6 + x7 ≥ 15
x1 + x2 + x3 + x4
+x7 ≥ 19
x1 + x2 + x3 + x4 + x5
≥ 14
x2 + x3 + x4 + x5 + x6
≥ 16
x3 + x4 + x5 + x6 + x7 ≥ 11
xi ≥ 0 i = 1, 2, . . . , 7
规模问题。
穷举法
方法简单，只可解小问题，计算量很大；对0-1整数规 划，计算量为2n，按指数增长：
n
计算量
计算时间
10
1.02×103
1.02毫秒
20
1.05×106
1.05秒
30
1.07×109
18 分钟
40
1.10×1012
13 天
50
1.73×1015
36 年
100
1.27×1030
4 亿亿年
选择顾客
耐芙迪公司在３个工厂中专门生产一种产品 这种产品有着优良的品质，所以现在公司接到了许多订单，产
品供不应求． 主要是由于运输成本的差异，销售一个产品得到的净利润也不
同，很大程度上取决于哪个工厂供应哪个顾客． 问题：公司需要向每一位顾客供应的产品数量是多少？每一个
工厂向每一个顾客供应多少单位的货物？
6x1+ 2x2 ≤ 17
0
1.0
2.0
3.0
4.0 x1
x2
5.0
整数最优解
线性规划最优解
4.0
5x1+ 9x2 ≤ 44
目标函数线 3.0
2.0
x1 ≤ 1
1.0
x1 ≥ 2
6x1+ 2x2 ≤ 17
0
1.0
2.0
3.0
4.0
x1
SUB 1
max: x1 + x2
s.t. 6x1 + 2x2 ≤ 17
Total
Shipment
Customer 1 Customer 2 Customer 3 Customer 4 Production
Plant 1 7,000
0
1,000
0
8,000
=
Plant 2
0
0
0
5,000
5,000
=
Plant 3
0
6,000
1,000
0
7,000
=
Min Purchase Total Shipped Max Purchase
x2
整数规划问题：
5.0
max: z = x1 + x2
4.0
s.t. 6x1 + 2x2 ≤ 17
5x1 + 9x2 ≤ 44 3.0
x1, x2 为整数
按线性规划求解： 2.0
x1= 1.477, x2= 4.068 1.0 z = 5.545
整数规划最优解 线性规划最优解 5x1+ 9x2 ≤ 44 目标函数线
LP解： x = (1.3, 3.3, 2, 7.3, 0, 3.3, 5) z = 22.3
整数解：x = ( 4, 4, 2, 6, 0, 4, 3)
z = 23
固定费用问题
例2: 服装厂可生产西服、衬衫和羽绒服。生产不同服装要使 用不同设备，该厂可从租赁公司租用这些设备（每种设备 可租用多台）。服装厂每月可用人工工时为 3000小时，该 厂如何安排生产可使每月利润最大。市场需求、设备租金 和其它经济参数见下表：
4 . 0 x1
求解整数规划方法
穷举法：方法简单，只可解小问题，计算量很 大；对0-1整数规划，计算量为2n，按指数增长；
凑整法：解的质量差，有时无法得到可行解 分枝定界: 计算效率高, 应用广泛; 割平面法: 有理论意义, 但计算效率较低； 启发算法: 效率高, 但不能保证找到最优解, 可解大
一二三四五六日 17 13 15 19 14 16 11
邮局排班模型
解：设 xi 为第 i 天开始上班的人数：
min: z = x1 + x2 + x3 + x4 + x5 + x6 + x7
s.t.
x1
+x4 + x5 + x6 + x7 ≥ 17
x1 + x2
+x5 + x6 + x7 ≥ 13
-
Month Installed
2
3
1.10
1.11
1.12
1.13
1.11
1.13
1.12
1.14
-
1.10
-
1.11
-
-
-
-
4 1.13 1.15 1.14 1.15 1.12 1.13 1.13 1.15
Units Produced
1
1 (RT) 10
1 (OT) 0
2 (RT) 0
Month 2 (OT) 0
运筹学 Operations Research
运输与整数规划
西南交通大学经济管理学院
The Transportation Problem 运输问题
Sources
Destinations
运输问题的特征
每一个出发地都有一定的供应量（supply）配送到目 的地，每一个目的地都有需要从一定的需求量（ demand），接收从出发地发出的产品 需求假设（The Requirements Assumption） 可行解特性（The Feasible Solutions Property） 成本假设（The Cost Assumption） 整数解性质（Integer Solutions Property）
2.0
x1 ≤ 2
x1, x2 为非负整数
1.0
松弛问题解：x = (2, 1.8 ) T z = 11 四舍五入解：x = (2, 2.0 ) T 不是可行 0
解；
x = (2, 1.0 ) T z = 7 整数最优解：x = (0, 2.0 ) T z = 10
1.0 2.0 x1
分枝定界算法举例
7,000 <=
7,000 <=
7,000
3,000 <=
6,000 <=
9,000
2,000 <=
2,000 <=