八年级数学下册 22.1 多边形练习(无答案) 沪教版五四

22.1 多边形的内角和教学目标：1.理解多边形及其有关概念，掌握多边形内角和定理，并会运用定理解决简单的计算问题；2. 经历多边形及其有关概念的形成过程，体验类比思想；经历多边形内角和的探索过程，体验化归思想。

3.体会多边形内角和计算公式中所蕴含的函数思想。

教学重难点：重点：多边形内角和定理的探索、归纳及运用定理进行简单计算．难点：多边形内角和定理的探索过程。

教学过程：【环节一】复习引入回忆三角形的概念：由平面内不在同一直线上的三条线段首尾顺次联结所组成的封闭图形叫做三角形．意图：通过类比三角形的概念，引出多边形的概念。

【环节二】新课学习（一）多边形的有关概念1．多边形的概念问：那四边形、五边形、……、多边形的概念呢？由平面内不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形。

组成多边形的线段最少有3条，所以三角形是最简单的多边形。

由n条线段组成的多边形就称为n边形，如三角形、四边形、五边形……等等。

2.师生例举生活中的多边形。

设计意图：通过例举生活中的多边形，提高学习多边形的积极性。

3.多边形的相关概念多边形的边、顶点、内角、对角线组成多边形的每一条线段叫做多边形的边；相邻的两条线段的公共端点叫做多边形的顶点；多边形的各顶点通常用大写的英文字母表示；多边形相邻两边所在的射线组成的角叫做多边形的内角；联结多边形的两个不相邻顶点的线段叫做多边形的对角线。

凸多边形和凹多边形的定义。

对于一个多边形，画出它的任意一边所在的直线，如果其余各边都在这条直线的一侧，那么这个多边形叫做凸多边形；否则叫做凹多边形。

DCBA备注：本章所讨论的多边形都是凸多边形。

(二)合作交流，探索多边形内角和定理思考：我们已经知道三角形的内角和为180°，那么四边形的内角和等于多少度？五边形呢？六边形呢？n边形的内角和等于多少度吗？设计意图：通过复习三角形内角和为180°，引出课题并板书课题。

（引导学生把求多边形内角和的问题转化成三角形内角和的问题。

-------------多边形（★★）1．了解多边形的有关概念，认识多边形的边、内角、外角、顶点、对角线；2．通过归纳，得出n边形对角线条数公式；3．经历探索多边形的内角和公式的过程，了解多边形的内角和公式，进一步发展学生的合情推理意识，主动探究的习惯，体会数学与现实世界的紧密联系；4．会用多边形的对角线条数与内角和公式进行简单的计算与说理．知识结构边形的内角和等于180°（n-2）。

360°。

边形的对角线条数等于1/2·n（n-3）3、4、6/。

拼成360度的角．：3、4。

“知识结构”这一部分的教学，可采用下面的策略：1.本部分建议时长5分钟.2.请学生先自己说本节内容的知识点，通过学生的叙述，教师以知识框架的形式出现，因为学生用知识框架的形式总结出来，还是有一定的难度的。

1.本部分建议时长20分钟.2.进行例题讲解时，教师宜先请学生试着自行解答.若学生能正确解答，则不必做过多的讲解；若学生不能正确解答，教师应对相关概念、公式进行进一步辨析后再讲解例题.3.在每一道例题之后设置了变式训练题，应在例题讲解后鼓励学生独立完成，以判断学生是否真正掌握了相关考点和题型.4.教师应正确处理好例题与变式训练题之间的关系，宜采用讲练结合的方式，切不可将所有例题都讲完后再让学生做变式训练题.题型一：多边形内角和及外角和定理应用：例题1一个多边形的内角和等于它的外角和的5倍，它是几边形？(★) 思路点拨:本题实际告诉了这个多边形的内角和是.解析：设这个多边形是边形， 则它的内角和是， 所以，解得.所以这个多边形是十二边形．本题是多边形的内角和定理和外角和定理的综合运用. 只要设出边数，根据条件列出关于的方程，求出的值即可，这是一种常用的解题思路．例题2“典例精讲”这一部分的教学，可采用下面的策略：一个多边形除了一个内角外，其余各内角和为2750°，求这个多边形的内角和是多少？(★★★) 【答案】设这个多边形的边数为，这个内角为，则，即.因为等式左边是180°的整数倍，所以等式右边也是180°的整数倍.又因为，所以，此时.所以这个多边形的内角和是：.１．注意内角和的计算公式，以及内角和与变数之间的关系；２．要熟悉借助于未知数通过建立方程，通过讨论的思想进行求解．我来试一试！１．若一个多边形的内角和与外角和的总度数为1800°，求这个多边形的边数．(★★)【答案】设这个多边形的边数为，根据题意得：，解得.所以多边形的边数为10．２．一个多边形的内角和与某一个外角的度数总和为1350°，求这个多边形的边数．（★★）【答案】可设多边形的边数为n，某一个外角为α．则(n－2)×180＋α＝135．从而(n－2)=．因为边数n为正整数，所以α＝90，n＝9．题型二：多边形对角线公式的运用例题1某校七年级六班举行篮球比赛，比赛采用单循环积分制（即每两个班都进行一次比赛）.你能算出一共需要进行多少场比赛吗？（★★）思路点拨：本题体现与体育学科的综合，解题方法参照多边形对角线条数的求法，即多边形的对角线条数加上边数.如图：解析：共需要比赛（场）.所以一共需要进行15场比赛．对于其他学科问题要善于把它与数学知识联系在一起，便于解决．我来试一试！一个多边形共有20条对角线，则多边形的边数是（）（★★）A．6；B．7；C．8；D．9．【答案】C. 提示：一个多边形的对角线条数为条，将6、7、8、9分别代入，结果为20的即为正确答案.例题2一个十二边形有几条对角线．（★★）解析：过十二边形的任意一个顶点可以画9条对角线，那么十二个顶点可以画12×9条对角线，但每条对角线在每个顶点都数了一次，所以实际对角线的条数应该为12×9÷2＝54（条）∴十二边形的对角线共有54条．对于一个n 边形的对角线的条数，我们可以总结出规律条，牢记这个公式，以后只要用相应的n的值代入即可求出对角线的条数，要记住这个公式只有在理解的基础之上才能记得牢．例题3已知一个多边形共有27条对角线.求：（1）这个多边形是几边形？ （2）此多边形的内角和的度数．（★★）分析：要求多边形的边数是多少，实际上是要求掌握对角线与边数之间的关系式，即对角线数2)3(-=n n ，若求出了边数，内角和就容易求到. 解答：（1）设边数为n ，根据题意得：272)3(=-n n ， 解得9=n 或6-=n （舍）∴ 这个多边形是9边形. （2）∵︒=︒⨯-1260180)29(，∴此多边形的内角和为︒1260.我来试一试！过m 边形的一个顶点有7条对角线，n 边形没有对角线，k 边形共有k 条对角线，则()______nm k -=．（★★★）答案：125．（提示：可求5,3,10===k n m ）说明：本部分为专题测试，学生做完后教师进行评分（建议10分钟做完）。

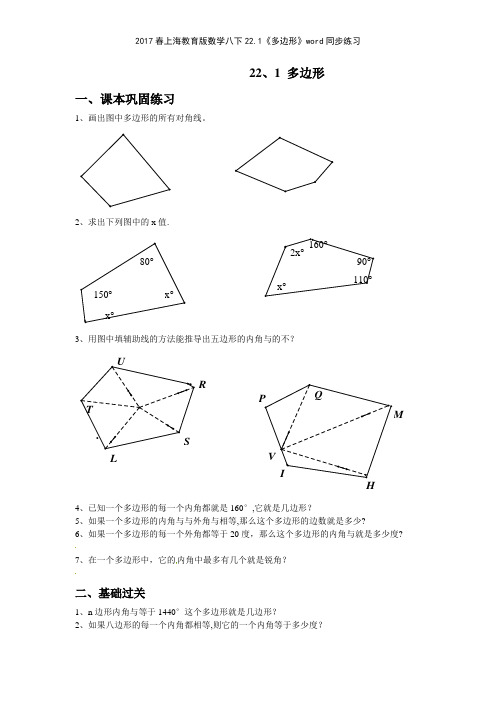
22、1 多边形一、课本巩固练习1、画出图中多边形的所有对角线。

2、求出下列图中的x 值. 90°110°160°2x°x°x°80°x°150°3、用图中填辅助线的方法能推导出五边形的内角与的不？IL MP Q RSTUV4、已知一个多边形的每一个内角都就是160°,它就是几边形？5、如果一个多边形的内角与与外角与相等,那么这个多边形的边数就是多少?6、如果一个多边形的每一个外角都等于20度，那么这个多边形的内角与就是多少度?7、在一个多边形中，它的内角中最多有几个就是锐角？二、基础过关1、n 边形内角与等于1440°这个多边形就是几边形？2、如果八边形的每一个内角都相等,则它的一个内角等于多少度？3、n 边形由一个顶点可引__________________________条对角线，共有____________条对角线。

4、一个多边形的每一个内角比每一个外角的3倍20°，求这个多边形的内角与5、五边形共有______________条对角线.6、正方形的对角线长为10,它的面积就是多少？7、填空题：1、四边形任意相邻内角互补，那么四边形就是 .2、一个四边形的四边长分别就是a,b,c,d ，且有)(22222bd ac d c b a +=+++,则此四边形就是。

3、 一个多边形的内角与为1440°,则它的边数为4、若平行四边形中有一个内角为90°，则其余三个角的度数之比为: 。

5、 如果ABCD 的周长为28cm,且AB ：BC=2∶5，那么AB= cm ，BC= cm,CD= cm,CD= c m8、已知一个多边形的内角与与一个外角的差为1560°,求这个多边形的边数与这个外角的度数。

9、已知一个多边形的每个内角都相等，且一个内角比一个外角大36°，求这个多边形的边数.。

最新精选数学八年级下册第二十二章四边形第一节多边形沪教版练习题第三篇第1题【单选题】用同一种正多边形地砖不能镶嵌成平整的地面的是( )A、正三角形地砖B、正方形地砖C、正五边形地砖D、正六边形地砖【答案】：【解析】：第2题【单选题】如图，把△ABC纸片沿DE折叠，当点A在四边形BCDE的外部时，记∠AEB为∠1，∠ADC为∠2，则∠A、∠1与∠2的数量关系，结论正确的是( )A、∠1＝∠2＋∠AB、∠1＝2∠A＋∠2C、∠1＝2∠2＋2∠AD、2∠1＝∠2＋∠A【答案】：【解析】：第3题【单选题】一个正多边形，它的每一个外角都等于45°，则该正多边形是( )A、正六边形B、正七边形C、正八边形D、正九边形【答案】：【解析】：第4题【单选题】六边形的对角线的条数为( )A、15B、9C、8D、6【答案】：【解析】：第5题【单选题】若一个多边形的内角和900°，则这个多边形的边数为( )A、5B、7C、9D、12【答案】：【解析】：第6题【单选题】一个多边形的内角和是外角和的2倍，这个多边形是( )A、三角形B、四边形C、五边形D、六边形【答案】：【解析】：第7题【单选题】若一个多边形的内角和为720°，则该多边形为( )边形．A、四B、五C、六D、七【答案】：【解析】：第8题【单选题】如果一个多边形的内角和等于720°，则这个多边形是( )A、四边形B、五边形C、六边形D、七边形【答案】：【解析】：第9题【单选题】一个多边形的每一个外角都等于36有误，则该多边形的内角和等于( )A、1080°B、900°C、1440°D、720°【答案】：【解析】：第10题【填空题】过五边形的一个顶点可作______条对角线，可将五边形分成_______个三角形．【答案】：【解析】：第11题【填空题】若一个正多边形的一个外角是40°，则这个正多边形的边数是______．A、9【答案】：【解析】：第12题【解答题】一底角为60°的等腰梯形的腰长和一个正三角形的边长相等，同时使用这两种图形能否铺满平面？若能，请设计一个图案；若不能，请说明理由．【答案】：【解析】：第13题【解答题】如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.【答案】：【解析】：第14题【解答题】我们经常看到的人行道上由各种地砖铺砌成美丽的图案，构成图案的每一块地砖都是全等图形吗？请你自己设计一种地砖，让每一块地砖都是全等的，并且能够密铺（拼在一起没有缝隙、没有重叠）成美丽的图案．【答案】：【解析】：第15题【综合题】探究与发现：图1 图2 图3探究一：三角形的一个内角与另两个内角的平分线所夹的角之间的关系已知：如图1，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系，并说明理由．探究二：四边形的两个个内角与另两个内角的平分线所夹的角之间的关系已知：如图2，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试探究∠P与∠A＋∠B的数量关系，并说明理由．探究三：六边形的四个内角与另两个内角的平分线所夹的角之间的关系已知：如图3，在六边形ABCDEF中，DP、CP分别平分∠EDC和∠BCD，请直接写出∠P与∠A＋∠B＋∠E＋∠F的数量关系：【答案】：【解析】：。

数学八年级下 第二十二章 四边形22.1 多边形（1）一、选择题1．四边形ABCD 中，如果∠A+∠C+∠D=280°，则∠B 的度数是 （ ）A ．80°B ．90°C ．170°D ．20°2．一个多边形的内角和等于1080°，这个多边形的边数是 （ ）A ．9B ．8C ．7D ．63．内角和等于外角和2倍的多边形是 （ ）A ．五边形B ．六边形C ．七边形D ．八边形4．凸n 边形的内角中，锐角的个数最多有 （ ）A ．1个B ．2个C ．3个D ．4个5．一个多边形的每一个顶点处取一个外角，这些外角中最多有钝角 （• ）A ．1个B ．2个C ．3个D ．4个6、各内角相等的n 边形的一个外角等于 （ ）A 、n n )2(1800-B 、n 0180C 、nn )2(3600- D 、n 0360 7、n 边形所有的对角线条数是 （ ）A 、2)1(-n nB 、2)2(-n nC 、22nD 、2)3(-n n 8、如果正n 边形的一个内角等于一个外角的2倍，那么n 的值是 （ ）A 、4B 、5C 、6D 、7二、填空题9. 五边形的内角和等于_______度．10．六边形的内角和等于_______度．11．正十边形的每一个内角的度数等于______，每一个外角的度数等于_______．12．如图，你能数出 个不同的四边形。

第12题13、如图所示，∠1=∠C+________，∠2=∠B+___________。

∠A+∠B +∠C +∠D+∠E= ________+∠1+∠2=________度。

14、一个多边形的每一个外角等于300，则这个多边形为___________ 边形。

15、当多边形边数增加一条边时，其内角和增加___________度 。

16、若正多边形的一个外角等于其一个内角的52，则这个多边形的内角和是___________ 。

章节测试题1.【答题】若凸n边形的每个外角都是36°，则从一个顶点出发引的对角线条数是（）A. 6B. 7C. 8D. 9【答案】B【分析】根据多边形的对角线的规律，n边形的一个顶点处有n-3条对角线，总共有条对角线.【解答】360°÷36°=10，10−3=7.故从一个顶点出发引的对角线条数是7.选B.2.【答题】一个n边形共有20条对角线，则n的值为（）A. 5B. 6C. 8D. 10【答案】C【分析】根据多边形的对角线的规律，n边形的一个顶点处有n-3条对角线，总共有条对角线.【解答】设这个多边形是n边形，则=20，∴n2−3n−40=0，(n−8)(n+5)=0，解得n=8,n=−5(舍去).故选C.3.【答题】从五边形的一个顶点，可以引几条对角线（）A. 2B. 3C. 4D. 5【答案】A【分析】根据多边形的对角线的规律，n边形的一个顶点处有n-3条对角线，总共有条对角线.【解答】根据n边形从一个顶点出发可引出（n-3）条对角线可直接得到从五边形的一个顶点可以引：5−3=2条对角线。

选A.4.【答题】多边形的一个顶点处的所有对角线把多边形分成了11个三角形，则经过这一点的对角线的条数是（）A. 8B. 9C. 10D. 11【答案】C【分析】根据多边形的对角线的规律，n边形的一个顶点处有n-3条对角线，总共有条对角线.【解答】设多边形有n条边，则n−2=11，解得n=13.故这个多边形是十三边形。

故经过这一点的对角线的条数是13−3=10.选C.5.【答题】十五边形从一个顶点出发有（）条对角线．A. 11B. 12C. 13D. 14【答案】B【分析】本题主要涉及多边形对角线的问题，熟练掌握多边形对角线的计算公式是解题的关键；连接多边形不相邻的两个顶点的线段，叫做多边形的对角线，n边形过一个顶点有(n-3)条对角线.【解答】n边形(n>3)从一个顶点出发可以引(n−3)条对角线，所以十五边形从一个顶点出发有：15−3=12条对角线。

第二十二章四边形专题22.1 多边形（重点练）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1.一个n边形的内角和比它的外角和大180°，则n等于（）A．3 B．4 C．5 D．6【答案】C【分析】根据n边形的内角和为（n﹣2）•180°，外角和等于360°列出方程求解即可．【解答】解：根据题意得：（n﹣2）•180°﹣360°＝180°，解得n＝5．故选：C．【知识点】多边形内角与外角2.一个多边形的内角和比它的外角和的2倍少180°，这个多边形的边数是（）A．5 B．6 C．7 D．8【答案】A【分析】根据多边形的内角和、外角和的求法列方程求解即可．【解答】解：设这个多边形为n边形，由题意得，（n﹣2）×180°＝360°×2﹣180°，解得n＝5，即这个多边形为五边形，故选：A．【知识点】多边形内角与外角3.如图，△ABC的高CD、BE相交于O，如果∠A＝55°，那么∠BOC的大小为（）A．125°B．135°C．105°D．145°【答案】A【分析】因为CD、BE均为△ABC的高，则有∠BEC＝∠ADC＝90°；又知∠A＝55°，可根据三角形的内角和定理得到∠OCE＝90°﹣∠A＝90°﹣55°＝35°，最后依据三角形的外角性质定理即三角形的一个外角等于与它不相邻的两个内角之和，得到∠BOC＝∠BEC+∠OCE＝90°+35°＝125°．【解答】解：∵CD、BE均为△ABC的高，∴∠BEC＝∠ADC＝90°＝90°，∵∠A＝55°，∴∠OCE＝90°﹣∠A＝90°﹣55°＝35°，则∠BOC＝∠BEC+∠OCE＝90°+35°＝125°．故选：A．【知识点】多边形内角与外角4.如图，在五边形ABCDE中，若去掉一个30°的角后得到一个六边形BCDEMN，则∠1+∠2的度数为（）A．210°B．110°C．150°D．100°【答案】A【分析】解法一：根据多变的内角和定理可求解∠B+∠C+∠D+∠E＝510°，∠1+∠2+∠B+∠C+∠D+∠E ＝（6﹣2）×180°＝720°，进而可求解．解法二：利用三角形的内角和定理和平角的定义也可求解．【解答】解：解法一：∵∠A+∠B+∠C+∠D+∠E＝（5﹣2）×180°＝540°，∠A＝30°，∴∠B+∠C+∠D+∠E＝510°，∵∠1+∠2+∠B+∠C+∠D+∠E＝（6﹣2）×180°＝720°，∴∠1+∠2＝720°﹣510°＝210°，解法二：在△ANM中，∠ANM+∠AMN＝180°﹣∠A＝180°﹣30°＝150°，∴∠1+∠2＝360°﹣（∠AMN+∠ANM）＝360°﹣150°＝210°故选：A．【知识点】多边形内角与外角5.如图，四边形ABCD中，∠A＝90°，∠C＝110°，点E，F分别在AB，BC上，将△BEF沿EF翻折，得△GEF，若GF∥CD，GE∥AD，则∠D的度数为（）A．60°B．70°C．80°D．90°【答案】C【分析】依据平行线的性质，即可得到∠BEG＝∠A＝90°，∠BFG＝∠C＝110°，再根据四边形内角和为360°，即可得到∠D的度数．【解答】解：∵GF∥CD，GE∥AD，∴∠BEG＝∠A＝90°，∠BFG＝∠C＝110°，由折叠可得：∠B＝∠G，∴四边形BEGF中，∠B＝＝80°，∴四边形ABCD中，∠D＝360°﹣∠A﹣∠B﹣∠C＝80°，故选：C．【知识点】翻折变换（折叠问题）、三角形内角和定理、多边形内角与外角、平行线的性质二、填空题（共5小题）6.一个凸多边形的内角和是其外角和的2倍，则这个多边形是边形．【答案】6【分析】多边形的外角和是360度，多边形的内角和是它的外角和的2倍，则多边形的内角和是720度，根据多边形的内角和可以表示成（n﹣2）•180°，依此列方程可求解．【解答】解：设多边形边数为n．则360°×2＝（n﹣2）•180°，解得n＝6．故答案为：6．【知识点】多边形内角与外角7.四边形不具有稳定性．如图，面积为25的正方形ABCD变成面积为20的菱形BCEF后，则AF的长为．【分析】延长EF，与AB交于G，作FH⊥BC于H，利用正方形的性质以及菱形的面积公式分别求出BC、FH，进而求出AG的长度，利用勾股定理可得FG的长度，从而得出AF的长度．【解答】解：延长EF，与AB交于G，作FH⊥BC于H．由已知，AB＝BC＝5，，∴FH＝4，∴AG＝1，∴GF＝＝3，∴AF＝．故答案为：．【知识点】三角形的稳定性、多边形8.小明同学在计算某n边形的内角和时，不小心少输入一个内角，得到和为2005°，则n等于．【答案】14【分析】根据多边形的内角和定理及多边形的每一个内角都小于180°解答即可．【解答】解：n边形内角和为：（n﹣2）•180°，并且每个内角度数都小于180°，∵少算一个角时度数为2005°，根据公式，13边形内角和为1980°，14边形内角和为2160°，∴n＝14．故答案为：14．【知识点】多边形内角与外角9.如图，是中国象棋残局图的一部分，请用线段将图中棋子所在的格点按指定方向顺次连接，组成一个多边形．连接顺序为：将→象→炮→兵→马→車→将，则组成的多边形的内角和为度．【答案】720【分析】根据题意可知，组成的多边形是六边形，根据多边形内角和定理即可求解．【解答】解：根据题意可知，组成的多边形是六边形，（6﹣2）×180°＝720°．故组成的多边形的内角和为720度．故答案为：720．【知识点】多边形内角与外角10.如图所示：下列正多边形都满足BA1＝CB1，在正三角形中，我们可推得：∠AOB1＝60°；在正方形中，可推得：∠AOB1＝90°；在正五边形中，可推得：∠AOB1＝108°，依此类推在正八边形中，∠AOB1＝°，在正n（n≥3）边形中，∠AOB1＝°．【分析】如图4，根据正八边形的性质可以得出AB＝BC，∠ABC＝∠BCD＝135°，就可以得出△ABA1≌△BCB1，就可以得出∠CBB1＝∠BAA1，就可以得出∠AOB1＝135°，由正三角形中∠AOB1＝60°＝，正方形中，∠AOB1＝90°＝；正五边形中，∠AOB1＝108°＝，…正n（n≥3）边形中，∠AOB1＝，就可以得出结论．【解答】解：∵多边形ABCDEFGH是正八边形，∴AB＝BC，∠ABC＝∠BCD＝135°．在△ABA1和△BCB1中，，∴△ABA1≌△BCB1（SAS）∴∠CBB1＝∠BAA1．∵∠AOB1＝∠ABO+∠BAA1．∴∠AOB1＝∠ABO+∠CBB1∴∠AOB1＝∠ABO+∠CBB1＝135°；∵在正三角形中∠AOB1＝60°＝，在正方形中∠AOB1＝90°＝；在正五边形中，∠AOB1＝108°＝；…∴在正n（n≥3）边形中，∠AOB1＝，故答案为：135，．【知识点】全等三角形的判定与性质、多边形内角与外角三、解答题（共5小题）11.如图，在四边形ABCD中，∠A＝80°，∠ABC＝70°，∠C＝90°，DF平分∠ADC交BC于点F，点E在AD上，连接BE，且∠ABE：∠EBC＝4：3，求证：BE∥DF．【分析】根据四边形内角和定理求得∠ADC＝120°，继而由角平分线的性质和直角三角形两锐角互余知∠DFC＝∠EBC＝30°，据此可得．【解答】证明：∵∠A+∠ABC+∠C+∠ADC＝360°，∠A＝80°，∠ABC＝70°，∠C＝90°，∴∠ADC＝120°，∵DF平分∠ADC，∴∠FDC＝∠ADC＝60°，∵∠C＝90°，∴∠DFC＝30°，又∵∠ABE：∠EBC＝4：3，∴∠EBC＝∠ABC＝30°，∴∠DFC＝∠EBC，∴BE∥DF．【知识点】平行线的判定、多边形内角与外角12.如图，小亮从点O处出发，前进5米后向右转15°，再前进5米后又向右转15°，这样走n次后恰好回到出发点O处．（1）小亮走出的这个n边形的每个内角是多少度？这个n边形的内角和是多少度？（2）小亮走出的这个n边形的周长是多少米？【分析】（1）这个n边形每个内角度数为180°﹣15°＝165°；根据多边形外角和360°，用360除以15求出边数，再利用内角和公式即可求解；（2）周长为边数乘以边长．【解答】解：（1）这个n边形每个内角度数为180°﹣15°＝165°；∵多边形外角和为360°，∴15n＝360，解得n＝24．∴这个n边形的内角和是（24﹣2）×180°＝3960度；（2）5×24＝120（米），所以小亮走出的这个n边形的周长是120米．【知识点】多边形内角与外角13.如图所示，直线EF分别交四边形ABDC的边CA与BD的延长线于点M和N，且∠1＝∠3，∠B＝∠C，∠N＝30°．求∠M的度数．【分析】利用平行线的判定定理及平行线的性质定理，可求得答案．【解答】解：∵∠1＝∠2，∠1＝∠3，∴∠2＝∠3（等量代换），∴AB∥CD（同位角相等，两直线平行），∴∠MAB＝∠C（两直线平行，同位角相等），又∵∠B＝∠C，∴∠NAB＝∠B（等量代换），∴CM∥BN（内错角相等，两直线平行），∴∠M＝∠N（两直线平行，内错角相等），∵∠N＝30°，∴∠M＝30°．【知识点】多边形内角与外角14.如图，AC，BD为四边形ABCD的对角线，∠ABC＝90°，∠ABD+∠ADB＝∠ACB，∠ADC＝∠BCD．（1）求证：AD⊥AC；（2）探求∠BAC与∠ACD之间的数量关系，并说明理由．【分析】（1）根据直角三角形的两个锐角互余可得∠ACB+∠BAC＝90°，根据三角形内角和定理可得∠ABD+∠ADB+∠BAD＝180°，再根据∠ABD+∠ADB＝∠ACB，可得∠ACB+∠BAD＝180°，即∠ACB+∠BAC+∠CAD＝180°，进而得出∠CAD＝90°，从而得证；（2）由题意可得∠BAC＝90°﹣∠ACB＝90°﹣（∠BCD﹣∠ACD），由（1）的结论可得∠DAC＝90°，可得∠ADC＝90°﹣∠ACD，再由∠ADC＝∠BCD，可得∠BCD＝90°﹣∠ACD，据此即可得出∠BAC＝2∠ACD．【解答】解：（1）∵在△ABC中，∠ABC＝90°，∴∠ACB+∠BAC＝90°，在△ABD中，∠ABD+∠ADB+∠BAD＝180°，∵∠ABD+∠ADB＝∠ACB，∴∠ACB+∠BAD＝180°，即∠ACB+∠BAC+∠CAD＝180°，∴∠CAD＝90°，∴AD⊥AC．（2）∠BAC＝2∠ACD；∵∠ABC＝90°，∴∠BAC＝90°﹣∠ACB＝90°﹣（∠BCD﹣∠ACD），∵∠DAC＝90°，∴∠ADC＝90°﹣∠ACD，∵∠ADC＝∠BCD，∴∠BCD＝90°﹣∠ACD，∴∠BAC＝90°﹣（90°﹣∠ACD﹣∠ACD）＝2∠ACD．【知识点】多边形内角与外角15.已知在四边形ABCD中，∠A＝∠C＝90°．（1）∠ABC+∠ADC＝°；（2）如图①，若DE平分∠ADC，BF平分∠ABC的外角，请写出DE与BF的位置关系，并证明；（3）如图②，若BE，DE分别四等分∠ABC、∠ADC的外角（即∠CDE＝∠CDN，∠CBE＝∠CBM），试求∠E的度数【答案】180【分析】（1）根据四边形内角和等于360°列式计算即可得解；（2）延长DE交BF于G，根据角平分线的定义可得∠CDE＝∠ADC，∠CBF＝∠CBM，然后求出∠CDE＝∠CBF，再利用三角形的内角和定理求出∠BGE＝∠C＝90°，最后根据垂直的定义证明即可；（3）先求出∠CDE+∠CBE，然后延长DC交BE于H，再根据三角形的一个外角等于与它不相邻的两个内角的和求解即可．【解答】（1）解：∵∠A＝∠C＝90°，∴∠ABC+∠ADC＝360°﹣90°×2＝180°；故答案为：180°；（2）解：延长DE交BF于G，∵DE平分∠ADC，BF平分∠CBM，∴∠CDE＝∠ADC，∠CBF＝∠CBM，又∵∠CBM＝180°﹣∠ABC＝180°﹣（180°﹣∠ADC）＝∠ADC，∴∠CDE＝∠CBF，又∵∠BED＝∠CDE+∠C＝∠CBF+∠BGE，∴∠BGE＝∠C＝90°，∴DG⊥BF，即DE⊥BF；（3）解：由（1）得：∠CDN+∠CBM＝180°，∵BE、DE分别四等分∠ABC、∠ADC的外角，∴∠CDE+∠CBE＝×180°45°，延长DC交BE于H，由三角形的外角性质得，∠BHD＝∠CDE+∠E，∠BCD＝∠BHD+∠CBE，∴∠BCD＝∠CBE+∠CDE+∠E，∴∠E＝90°﹣45°＝45°【知识点】三角形的外角性质、三角形内角和定理、多边形内角与外角。

22.1多边形一、填空题1.一个多边形的内角和与外角和相等，则这个多边形的边数为．2.一个多边形的内角和是1440∘，那么这个多边形边数是．3.五边形从一个顶点出发，能引出条对角线，一共有条对角线．4.五边形共有条对角线．5.四边形任意相邻内角互补，那么四边形是．6.一个四边形的边长依次为a，b，c，d，且满足a2+b2+c2+d2=2ac+2bd，则这个四边形为．7.一个多边形的内角和为1440∘，则它的边数为．8.若平行四边形中有一个内角为90∘，则其余三个角的度数之比为：．9.如果平行四边形ABCD的周长为28cm，且AB:BC=2:5，那么AB=cm，BC=cm，CD=cm．二、解答题10.画出图中多边形的所有对角线．11.求出下列图中的x值．12.已知一个多边形的每一个内角都是160∘，它是几边形？13.如果一个多边形的每一个外角都等于20度，那么这个多边形的内角和是多少度？14.在一个多边形中，它的内角中最多有几个是锐角？15.如果八边形的每一个内角都相等，则它的一个内角等于多少度？16.已知一个多边形的每个内角都比相邻外角的3倍还多20∘，求这个多边形的内角和．17.正方形的对角线长为10，它的面积是多少？18.已知一个多边形的内角和与一个外角的差为1560∘，求这个多边形的边数和这个外角的度数．19.已知一个多边形的每个内角都相等，且一个内角比一个外角大36∘，求这个多边形的边数．答案一、填空题1. 【答案】四2. 【答案】10【解析】设它的边数为n，根据题意，得(n−2)⋅180∘=1440∘，所以n=10．3. 【答案】2；5【解析】对于n边形从一个顶点出发可以引出(n−3)条对角线，共有n(n−3)2条对角线，然后根据公式代入进行计算即可得出答案．4. 【答案】5【解析】∵n边形共有n(n−3)2条对角线，∴五边形共有5(5−3)2=5，∴答案为5．5. 【答案】平行四边形【解析】∵四边形的任意两个相邻内角都互补，∴四边形的对角相等，∴四边形是平行四边形．6. 【答案】平行四边形【解析】∵a2+b2+c2+d2=2ac+2bd，∴(a2−2ac+c2)+(b2−2bd+d2)=0，∴(a−c)2+(b−d)2=0，∴a−c=0，b−d=0，∴a=c，b=d．∴四边形是平行四边形．7. 【答案】10【解析】设多边形的边数为n，则有：180∘(n−2)=1440∘，解得：n=10．8. 【答案】1:1:1【解析】若平行四边形有一个内角为90∘，则这个四边形是矩形，其余三个角都是90∘，故其余三角之比为1:1:1．9. 【答案】4；10；4【解析】∵平行四边形ABCD的周长为28cm，∴AB+BC=14cm，∵AB:BC=2:5，∴CD=AB=22+5×14=4(cm)，BC=52+5×14=10(cm)．二、解答题10. 【答案】分别将两个图形中的与每个顶点不相邻的顶点连接起来，如图：11. 【答案】由四边形的内角和为360∘，则有150∘+80∘+2x∘=360∘，解得x=65；由五边形内角和为180∘×(5−2)=540∘，则有3x∘+160∘+90∘+110∘=540∘，解得x=60．12. 【答案】∵多边形的每一个内角都等于160∘，∴多边形的每一个外角都等于180∘−160∘=20∘，∴边数n=360∘÷20∘=18．∴该图形为十八边形．13. 【答案】∵多边形每一个外角都等于20∘，∴它的边数为：360∘÷20∘=18，∴它的内角和：180∘(18−2)=2880∘．故这个多边形的内角和是：2880∘．14. 【答案】∵任意多边形的外角和是360∘，∴在任意多边形的外角中，最多有3个钝角．∴内角中，最多有3个锐角．15. 【答案】∵正八边形的外角和为360∘，∴正八边形的每个外角的度数=360∘÷8=45∘，∴正八边形的每个内角=180∘−45∘=135∘．16. 【答案】设多边形内角的相邻角为α，则内角等于3α+20∘．∴(3α+20∘)+α=180∘，α=40∘．∵每个内角都比相邻的外角的3倍还多20∘，即多边形的每个外角为40∘，又∵多边形的外角和为360∘，=9，∴多边形的外角个数=36040∴多边形的边数=9，多边形的内角和=(9−2)⋅180∘=1260∘．17. 【答案】设正方形的边长是x，则有x2+x2=102，x=5√2．面积为：5√2×5√2=50．故正方形面积为50．18. 【答案】设这个内角度数为x．根据题意，得(n−2)×180∘−(180−x)=1560∘．解得：x=1560∘−180∘n+540∘=2100∘−180∘n，由于0<x<180，即0<2100∘−180∘n<180∘，解得：1023<n <1123，∴n =11．将 n =11 代入 x =2100∘−180∘n 中得：x =120∘，∴ 这个外角为 180∘−120∘=60∘．故多该多边形的边数是 11，这个外角的度数为 60∘．19. 【答案】设内角是 x ∘，外角是 y ∘，得到一个方程组{x −y =36,x +y =180.解得：{x =108,y =72.由任何多边形的外角是 360∘，则多边形中外角的个数是360÷72=5.所以这个多边形的边数是 5．。