数值传热学第一次大作业
- 格式:pdf
- 大小:1.05 MB
- 文档页数:16

数值传热学是热力学的重要分支之一,研究物质中热量的传递和分布规律。
与传统的实验方法相比,数值传热学采用计算机模拟技术,通过数学模型和计算实验方法,能够更加深入、系统地研究热传递现象的规律和特性,为工程设计和实际生产提供重要的技术支持。
数值传热学的本质是热传递方程的数值求解。
热传递方程是描述物质中热量传递和分布的方程,它包含了热传导、热对流和热辐射三种传热方式。
热传导是指热量沿着物质内部的温度梯度传递,主要发生在固体和液体中;热对流是指热量随物质的流动而传递,主要发生在液体和气体中;热辐射是指热量通过辐射传递,主要发生在光学和辐射热转换材料中。
通过数值方法求解热传递方程,可以得到物体的温度分布、热传递速率和热流密度等参数,为材料和工程设计提供准确的数据支持。
数值传热学的核心是数值方法,主要包括有限差分、有限元和边界元等方法。
有限差分法是一种利用离散化方法求解微分方程的数值方法,它将微分方程中的连续变量离散化,将求解微分方程转化为求解线性方程组。
有限元法是一种利用有限元逼近方法解决偏微分方程的数值方法,采用对物体进行简单的几何划分,将问题离散化,通过数学建模来表示物体的温度分布和热流密度分布。
边界元法是一种较新的有限元法补充,它能够快速解决边界值问题,并且可以减少问题的维数。
数值传热学的应用范围广泛,包括热工和物理问题的研究、能源系统分析和设计、建筑工程中的热传递和能源效率研究等。
例如,在太阳能发电系统设计中,数值传热学可以帮助设计人员确定集热器表面温度和吸收率等参数,提高太阳能效率并减少系统成本。
在建筑工程中,数值传热学可以帮助设计师分析建筑物的保温性能,合理评估保温材料的性能和使用效果,确保建筑节能和环保。
在机械加工领域中,数值传热学可以帮助工程师分析材料切削过程中的热量和温度分布,挑选适合材料和刀具的加工工艺,提高机械切削效率。
数值传热学是现代科学技术的重要分支之一,是研究物质中热传递和分布规律的重要工具。


一维非稳态导热的数值解法一、导热问题数值解法的认识(一)背景所谓求解导热问题,就是对导热微分方程在规定的定解条件下的积分求解。
这样获得的解称为分析解。
近100年来,对大量几何形状及边界条件比较简单的问题获得了分析解。
但是,对于工程技术中遇到的许多几何形状或边界条件复杂的导热问题,由于数学上的困难目前还无法得出其分析解。
另一方面,在近几十年中,随着计算机技术的迅速发展,对物理问题进行离散求解的数值方法发展十分迅速,并得到日益广泛的应用。
这些数值方法包括有限差分法、有限元法及边界元法等。
其中,有限差分法物理概念明确,实施方法简便,本次大作业即采用有限差分法。
(二)基本思想把原来在时间、空间坐标系中连续的物理量的场,如导热物体的温度场,用有限个离散点上的值的集合来代替,将连续物理量场的求解问题转化为各离散点物理量的求解问题,将微分方程的求解问题转化为离散点被求物理量的代数方程的求解问题。
(三)基本步骤(1)建立控制方程及定解条件。
根据具体的物理模型,建立符合条件的导热微分方程和边界条件。
(2)区域离散化。
用一系列与坐标轴平行的网格线把求解区域划分成许多子区域,以网格线的交点作为需要确定温度值的空间位置,称为节点。
每一个节点都可以看成是以它为中心的一个小区域的代表,将小区域称之为元体。
(3)建立节点物理量的代数方程。
建立方法主要包括泰勒级数展开法和热平衡法。
(4)设立迭代初场。
(5)求解代数方程组。
(6)解的分析。
对于数值计算所获得的温度场及所需的一些其他物理量应作仔细分析,以获得定性或定量上的一些结论。
对于不符合实际情况的应作修正。
二、问题及求解(一)题目一厚度为0.1m 的无限大平壁,两侧均为对流换热边界条件,初始时两侧流体温度与壁内温度一致,1205f f t t t ===℃;已知两侧对流换热系数分别为h 1=11 W/m 2K 、h 2=23W/m 2K ,壁的导热系数λ=0.43W/mK ,导温系数a=0.3437×10-6 m 2/s 。

数值传热学习题答案数值传热学习题答案数值传热学是热力学的一个重要分支,主要研究热量在物质中传递的机理和规律。
在实际工程中,我们经常会遇到各种与传热有关的问题,通过数值计算可以得到准确的答案。
下面我将为大家提供一些数值传热学习题的答案,希望能够帮助大家更好地理解和应用这门学科。
1. 一个铝制热交换器的表面积为10平方米,其表面温度为100摄氏度,环境温度为20摄氏度。
已知铝的导热系数为200 W/(m·K),求热交换器的传热速率。
答:根据传热定律,传热速率与传热面积、传热系数和温度差之间成正比。
传热速率 = 传热系数× 传热面积× 温度差。
将已知数据代入公式中,可得传热速率= 200 × 10 × (100 - 20) = 160,000 W。
2. 一个房间的尺寸为5米× 5米× 3米,墙壁和天花板的厚度为0.2米,墙壁和天花板的导热系数为0.5 W/(m·K),室内温度为25摄氏度,室外温度为10摄氏度。
求房间的传热损失。
答:房间的传热损失可以通过计算墙壁和天花板的传热速率来得到。
墙壁和天花板的传热速率 = 传热系数× 传热面积× 温度差。
墙壁和天花板的传热面积 = 2 × (5 × 5) + 2 × (5 × 3) = 70平方米。
将已知数据代入公式中,可得墙壁和天花板的传热速率= 0.5 × 70 × (25 - 10) = 525 W。
因此,房间的传热损失为525瓦特。
3. 一个水箱的体积为1立方米,初始温度为20摄氏度,水的密度为1000千克/立方米,比热容为4186 J/(千克·摄氏度),水箱的表面积为2平方米,表面温度为100摄氏度。
已知水的传热系数为0.6 W/(m^2·K),求水箱内水的温度随时间的变化。

第一次作业情况总结(能动1503)复习题:3. 导热系数、表面传热系数及传热系数的单位各是什么?哪些是物性参数,哪些与过程有关?分析:基本无问题,个别同学将表面传热系数单位写错。
例如W/(K*m2)和W/(m2*K4)。
6. 用一只手握住盛有热水的杯子,另一只手用筷子快速搅拌热水,握杯子的手会显著地感到热。
试分析其原因。
分析:一些同学未抓住“由自然对流变为强制对流”这一本质原因。
大部分同学均回答正确。
7. 什么是串联热阻叠加原则,它在什么前提下成立?以固体中的导热为例,试讨论有哪些情况可能使热量传递方向上不同截面的热流量不相等。
分析:错误率最高的一道题。
第一问“串联热阻叠加原则”全部回答正确。
第二问“前提”有些同学未作答,其余所有同学的答案为“各个环节热流量相同”。
第三问全部同学都认为横截面的不同会导致热流量不相等,其中部分同学认为通过圆筒壁各个环节热流量不相等,均未提到“无内热源或非稳态情况”。
习题:1-4 对于附图所示的两种水平夹层,试分析冷、热表面间热量交换的方式有何不同?如果要通过实验来测定夹层中流体的导热系数,应采用哪一种布置?分析:个别同学未能看出(a)装置热上冷下无法产生自然对流。
大部分同学均回答正确。
1-5一个内部发热的圆球悬挂于室内,对于附图所示的三种情况,试分析:(1)圆球表面散热的方式;(2)圆球表面与空气之间的换热方式。
分析:错误率同样很高。
几乎所有同学都未能辨析出(1)(2)问的区别。
一些同学将(1)或(2)问简单的回答为“散热”或者“表面换热”,且相当一部分同学未考虑到(1)中存在热辐射。
1-6一宇宙飞船的外形如附图所示,其中外遮光罩是凸出于飞船体之外的一个光学窗口,其表面的温度状态直接影响到飞船的光学遥感器。
船体表面各部分的表面温度与遮光罩的表面温度不同。
试分析,飞船在太空中飞行时与遮光罩表面发生热交换的对象可能有哪些?换热的方式是什么?分析:基本无问题,一些同学未考虑到外遮光罩与飞船船体之间的热传导。

传热学数值计算大作业传热学数值计算大作业一选题《传热学》第四版P179页例题 4-3二相关数据及计算方法1.厚2δ=0.06m的无限大平板受对称冷却,故按一半厚度作为模型进行计算2. δ=0.03m,初始温度t0=100℃,流体温度t∞=0℃;λ=40W/(m.K),h=1000W/(m2.K),Bi=h*△x/λ=0.25;3.设定Fo=0.25和Fo=1两种情况通过C语言编程(源程序文件见附件)进行数值分析计算;当Fo=0.25时,Fo<1/(2*(1+Bi)),理论上出现正确的计算结果;当Fo=1时,Fo>1/(2*(1+Bi)),Fo>0.5,理论上温度分布出现振荡,与实际情况不符。
三网格划分将无限大平面的一半划分为6个控制体,共7个节点。
△x=0.03/N=0.03/6=0.005,即空间步长为0.005m四节点离散方程绝热边界节点即i=1时,tij+1=2Fo△ti+1j+(1-2Fo△)tij 内部节点即0tij+1=tij(1-2Fo△Bo△-2Fo△)+2Fo△ti-1j+2Fo△Bo△tf五温度分布线图(origin)六结果分析1 空间步长,时间步长对温度分布的影响空间步长和时间步长决定了Bo和Fo,两者越小计算结果越精确,但同时计算所需的时间就越长。
2 Fo数的大小对计算结果的影响编程时对Fo=1及0.25的情况分别进行了计算,发现当Fo=1时,各点温度随时间发生振荡,某点的温度高反而会使下一时刻的温度变低,违反了热力学第二定律,因此在计算中对Fo的选取有限制。
为了保证各项前的系数均为正值,对于内节点,Fo>0.5;对于对流边界节点,Fo<1/(2*(1+Bi))。
3 备注在Fo=0.25时,为了反映较长时间后温度的分布,取T=600,并选取了其中部分时刻的温度输出进行画图。
图像显示,随着时间的增长,各点温度趋向一致。
而当Fo=1时由于结果会出现振荡,只取T=6观察即可。

传热学数值计算大作业航14 艾迪2011011537 如图所示,有一个正方形截面的无限长的水泥柱,热导率为,密度为,比热容为。
水泥柱的边长为。
水泥柱的左侧靠墙,可以认为保持温度为。
水泥柱被包围在温度为°的热空气中。
三个面上均只考虑对流换热,并且对流换热系数分别为,,。
请编写程序数值求解该稳态导热问题(可使用Fortran 或C 或Matlab 语言)。
作业要求提交源代码和报告,报告内容包括:(1) 给出该导热问题的数学描述; (2) 描述所采用的差分格式和求解过程;(3) 验证求解结果的准确性,给出网格无关性验证; (4) 给出求解结果(温度云图、边界热流、平均温度等); (5) (选做)讨论对流换热系数、热导率等参数对求解结果的影响。
解:(1)、因为无内热源,温度分布:222201230(0,0)(x,0)t(0,y)t ,((x,0))(,y)(x,)((,y)),((x,H))f f f t tx H y H x ydt h t t dx dt H dt H h t H t h t t dx dxλλλ∂∂+=<<<<∂∂⎧=-=-⎪⎪⎨⎪-=--=-⎪⎩(2)、采用热平衡法建立内节点和边界节点的离散方程,x 、y 方向各取n 个节点,即()()11n n -⨯- 个网格,且x y ∆=∆ 。
对于任意内节点(i ,j ),有:,1,1,,1,1t (t t t t )/4i j i j i j i j i j -+-+=+++D边界三边界一边界节点:边界1、 1,0(1j )j t t n =≤≤边界2、11,1,21,11,1h 2h 2(2)t 2t t t (1k n)k k k k f xxt λλ-+∆∆+=+++<<边界3、22,k n 1,k n,k 1,k 1h 2h 2(2)t 2t t t (1k n)n n f xxt λλ--+∆∆+=+++<<边界4、33k,n k,n 11,n k 1,n h 2h 2(2)t 2t t t (1k n)k fxxt λλ--+∆∆+=+++<<C 点、2121n,1n 1,1n,2(h h )(h )(2)t t t f xh xt λλ-+∆+∆+=++D 点、2323n,n ,n 11,n (h h )(h )(2)t t t n n f xh xt λλ--+∆+∆+=++(3)、由于各个节点都写成了差分显示表达,可用高斯—赛德尔迭代法求解。

简答题集锦1.流动与传热数值模拟的基本任务是什么?(把原来在时间域及空间域上连续的物理量的场,如速度场和压力场,用一系列有限个离散点上的变量值的集合来代替,通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数方程组,然后求解代数方程组获得场变量的近似值CFD可以看做是在流动基本方程(质量守恒方程飞动量守恒方程、能量守恒方程)控制下对流动的数值模拟。
通过这种数值模拟,我们可以得到极其复杂问题的流场内各个位置上的基本物理量(如速度、压力、温度、浓度等)的分布,以及这些物理量随时间的变化情况,确定旋涡分布特性、空化特性及脱流区等。
)2.数值模拟过程如何实现,主要步骤是那些?(建模、网格划分、坐标系、数学方程、求解、后处理)a.建立反映工程问题或物理过程本质的数学模型;b.选择与计算区域的边界相适应的坐标系;c.建立网格;d.建立离散方程;e.求解代数方程组;f.后处理,显示计算结果3.建立离散方程有哪些主要方法?比较说明各种方法的优缺点?(有限差分、有限体积、有限元、有限分析等)4什么叫控制方程?常见的控制方程有哪几个?各用在什么场合?5试写出控制方程的通用形式,并说明通用形式中各项的意义?(写明通式,以及各个方程中通式的表达形式)6推导x 方向的动量控制方程中的源项u S 的表达式。
由此证明当密度和黏度为常数时,u S 变为0。
X 方向N-S 方程:Mx S xw z u z x v y u y divu x u x x p Dt Du +∂∂+∂∂∂∂+∂∂+∂∂∂∂++∂∂∂∂+∂∂-=)][()]([)2(μμλμρ)()())()())())()()()()()][()]([)2(gradu div divu xz w y v x u x gradu div S divu xz w y v x u x S S divu xz w y v x u x gradu div S xw z x v y x u x z u z y u y x u x S xw z u z x v y u y divu x u x Mx u Mx Mx Mx μλμμλμλμμμμμμμμμμλμ+∂∂+∂∂+∂∂+∂∂∂∂=++∂∂+∂∂+∂∂+∂∂∂∂=+∂∂+∂∂+∂∂+∂∂∂∂+=+∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂∂∂+∂∂∂∂=+∂∂+∂∂∂∂+∂∂+∂∂∂∂++∂∂∂∂((()()( 因为密度为常数,所以连续性方程:0=∂∂+∂∂+∂∂z w y v x u ρρρ 推 得:0=∂∂+∂∂+∂∂z w y v x u 所以:Su= 0)()=∂∂+∂∂+∂∂+∂∂∂∂divu x z w y v x u x λμ(7区域离散为分几种,说明各自的特点。

1、二维非稳态导热微分方程:S YT X T t T p +∂∂+∂∂=)2222c (λδδρ。
对于时间步进(x 方向,y 方向)及空间而言,该方程为何种类型的方程?解: 将二维非稳态导热微分方程化为:0c 2222=+-∂∂+∂∂S tT Y T X T p δδρλλ (1)x 方向:0,0,a ===c b λ。
则:04b 2=-=∆ac ,所以该二维非稳态导热方程为抛物型方程。
(2)y 方向:0,0,a ===c b λ。
则:04b 2=-=∆ac ,所以该二维非稳态导热方程也为抛物型方程。
(3)对于空间而言,二维非稳态导热方程可知:,0,a b c λλ===则:2240b ac λ∆=-=-<,所以该二维非稳态导热方程为椭圆型方程。
2、(补充不可压、常物性的条件。
写出守恒型和非守恒型控制方程,并推导二者关系。
) 解:由题可知,该流体为不可压缩、常物性流体,而且是有内热源的二维问题。
守恒型控制方程: 质量守恒方程:0=∂∂+∂∂yv x u ; 由于流体自身条件,使得0==v u S S ,得动量守恒方程:()()⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂22221y u x u v x p y vu x uu ρ ()()⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂22221y v x v v y p y vv x uv ρ ; 能量守恒方程:()()T S y T x T a y vT x uT +⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂+∂∂2222 . 非守恒型控制方程:质量守恒方程:无非守恒型 动量守恒方程:⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂22221y u x u v x p y u v x u u ρ ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂-=∂∂+∂∂22221y v x v v y p y v v x v u ρ ;能量守恒方程:T S y T xT a y T v x T u +⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂+∂∂2222流速及温度的边界条件:进口截面:c T in =,()y u u =,0=v ;在两平板界面上:0=∂∂yT ,0=v ,()y u u =; 出口截面:0=∂∂x T ,0=∂∂x u ,0=∂∂y v .。
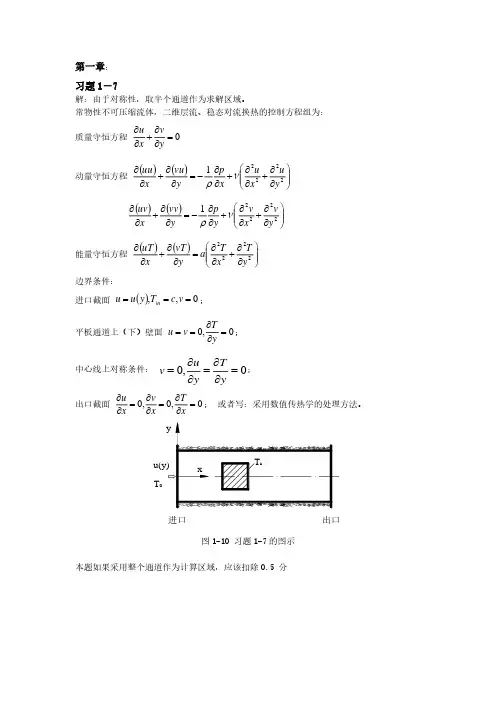
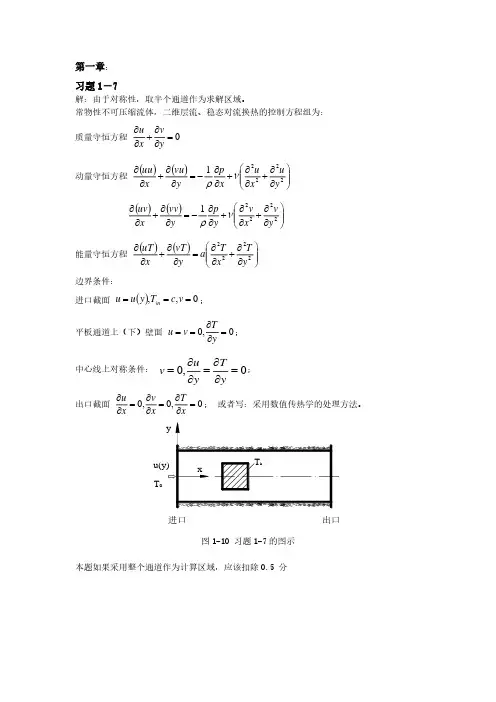
习题1-7解:由于对称性,取半个通道作为求解区域。
常物性不可压缩流体,二维层流、稳态对流换热的控制方程组为: 质量守恒方程0=∂∂+∂∂yv x u 动量守恒方程 ()()⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂−=∂∂+∂∂22221y u x u x py vu x uu νρ ()()⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂−=∂∂+∂∂22221y v x v y p y vv x uv νρ 能量守恒方程 ()()⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=∂∂+∂∂2222y T xT a y vT x uT 边界条件:进口截面 ()0,,===v c T y u u in ; 平板通道上(下)壁面 0,0=∂∂==yTv u ; 中心线上对称条件: 0,0u T v y y∂∂===∂∂; 出口截面0,0,0=∂∂=∂∂=∂∂xT x v x u ; 或者写:采用数值传热学的处理方法。
图1-10 习题1-7的图示本题如果采用整个通道作为计算区域,应该扣除0.5 分2-3.解:由u x u ∂∂=()xuu ∂∂21=η22y u ∂∂得: 其守恒形式为:()xuu ∂∂=2η22y u ∂∂ 对方程两端在t ∆时间间隔内对其控制容积积分得:()dxdydt x uu t t t nsew ⎰⎰⎰∆+∂∂=⎰⎰⎰∆+∂∂t t t e w n s dydxdt y u 222η()()[]dxdt y u y u dydt uu uu s n t t t ewtt t w e n s ][2⎪⎪⎭⎫ ⎝⎛∂∂−⎪⎪⎭⎫ ⎝⎛∂∂=−⎰⎰⎰⎰∆+∆+η 将()()2)(PE e uu uu uu +=, ()()()2P W w uu uu uu +=,()n PN n y u u y u δ−=⎪⎪⎭⎫ ⎝⎛∂∂,()sSP s y u u y u δ−=⎪⎪⎭⎫ ⎝⎛∂∂。
y y y s n ∆==)()(δδ 带入,得:xdt y u u u ydt uu uu t t t S P N tt tW E ∆∆+−=∆⎥⎦⎤⎢⎣⎡−⎰⎰∆+∆+]2[22)()(η t x yu u u t y uu uu tSt P t N t W t E ∆∆∆+−=∆∆−222)()(η整理得离散方程为:()()0242=∆−+−∆−yu u u xuu uu t P t S t N tWt E η2—3:解:由2221()u 2u u ux x y η∂∂∂===∂∂∂得:原方程的守恒形式为: 222()2u ux yη∂∂=∂∂ 对方程两端在t ∆时间间隔内对其控制容积积分,把可积的部分积出后得:22()t tsne wtu u dtdy +∆−⎰⎰= 2t te wtn s u u dtdx y y η+∆⎡⎤⎛⎫⎛⎫∂∂−⎢⎥ ⎪ ⎪∂∂⎝⎭⎝⎭⎣⎦⎰⎰选定2u 随y 而变化的型线,这里取为阶梯式,即在控制容积内沿y 方向不变,则2222()=y ()t tt ts ne we w ttu u dtdy u u dt +∆+∆−∆−⎰⎰⎰选定2u 随t 而变化的规律,这里采用阶梯式显式,则22()t tewty u u dt +∆∆−⎰= ()()22t t e w u u t y ⎡⎤−∆∆⎢⎥⎣⎦选定uy∂∂随x 而变化的型线,这里取为阶梯式,即在控制容积内沿x 方向不变,则22t tt t e wtt n s n s u u u u dtdx x dt y y y y ηη+∆+∆⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂∂−=∆−⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎰⎰⎰ 选定uy∂∂随t 而变化的规律,这里采用阶梯显式,则 2t ttn s u u x dt y y η+∆⎡⎤⎛⎫⎛⎫∂∂∆−⎢⎥ ⎪ ⎪∂∂⎝⎭⎝⎭⎣⎦⎰= 2t t n s u u t x y y η⎡⎤⎛⎫⎛⎫∂∂−∆∆⎢⎥ ⎪ ⎪∂∂⎢⎥⎝⎭⎝⎭⎣⎦进一步选取u 随x,y 分段线性变化,则2222E Pe u u u += , 222w 2W P u u u +=()nt PtN ty uu y u δ−=⎪⎪⎭⎫ ⎝⎛∂∂n , ()stSt p ts y u u y u δ−=⎪⎪⎭⎫ ⎝⎛∂∂。
数值传热学大作业燃烧室出口换热与流动的数值模拟学院专业班级学号姓名燃烧室出口换热与流动的数值模拟摘要:本文针对稳态、层流、常物性的燃烧室出口的换热与流动问题,采用商业软件FLUENT 进行了数值模拟。
通过数值模拟,本文得到了温度分布和速度分布,计算得到三种流体各自的换热量以及漏斗状壁面两侧烟气和空气的局部的表面对流换热系数。
1物理问题描述某圆柱形燃烧室出口截面结构如图1-1所示,燃烧产生的高温烟气从燃烧室流出后在图1标号为①的位置进入图中漏斗结构,最终从②流出。
冷却水从标号为⑤的位置进入“水套”结构,由⑥流出;常温空气从标号为③的位置流入空气流道,分别与高温烟气和冷却水发生热交换,最终从④流出。
图1-1 燃烧室出口结构:①烟气入口;②烟气出口;③空气流道入口;④空气流道出口⑤冷却水入口;⑥冷却水出口表1给出了该结构的几何参数,漏斗状的结构(图1中标号为A的结构)、水套(图1中标号为B的结构)的壁厚均为5mm,材料为钢,过程是稳态。
给定工况和给定的流体参数如表2所示:表2 工质工矿与流体参数为了方便计算,在数值模拟中,本文做了一些假设:(1)流体的物性都是固定的;(2)流体中的粘性耗散度忽略不计;(3)流动及换热处于稳态、层流、充分发展状态;(4)假设流体流动过程中不存在热辐射的情况。
2控制方程及求解方法考虑几何对称性,将问题简化为一个2D模型,则该问题中的控制方程如下。
连续性方程:动量方程:能量方程:本文采用了SIMPLE算法进行求解。
SIMPLE算法自1972年问世以来在世界各国计算流体力学及计算传热学界得到了广泛的应用,这种算法提出不久很快就成为计算不可压流场的主要方法,随后这一算法以及其后的各种改进方案成功的推广到可压缩流场计算中,已成为一种可以计算任何流速的流动的数值方法。
SIMPLE 算法的基本假设:速度场的假定与压力场的假定各自独立进行,二者无任何联系。
对假定压力场的修正通过已求解的速度场的质量守恒条件得到。
数值传热学习题答案权威版习题4-2⼀维稳态导热问题的控制⽅程:022=+??S xTλ依据本题给定条件,对节点2节点3采⽤第三类边界条件具有⼆阶精度的差分格式,最后得到各节点的离散⽅程:节点1: 1001=T 节点2: 1505105321-=+-T T T 节点3:75432=+-T T 求解结果:852=T ,403=T对整个控制容积作能量平衡,有:02150)4020(15)(3=?+-?=?+-=?+x S T T h x S q f f B即:计算区域总体守恒要求满⾜习题4-5在4-2习题中,如果25.03)(10f T T h -?=,则各节点离散⽅程如下:节点1: 1001=T节点2: 1505105321-=+-T T T节点3:25.03325.032)20(4015])20(21[-?+=-?++-T T T T对于节点3中的相关项作局部线性化处理,然后迭代计算;求解结果:818.822=T ,635.353=T (迭代精度为10-4)迭代计算的Matlab 程序如下: x=30; x1=20;while abs(x1-x)>0.0001a=[1 0 0;5 -10 5;0 -1 1+2*(x-20)^(0.25)]; b=[100;-150; 15+40*(x-20)^(0.25)]; t=a^(-1)*b; x1=x; x=t(3,1); endtcal=t习题4-12的Matlab程序%代数⽅程形式A i T i=C i T i+1+B i T i-1+D imdim=10;%计算的节点数A=cos(x);%TDMA的主对⾓元素B=sin(x);%TDMA的下对⾓线元素C=cos(x)+exp(x); %TDMA的上对⾓线元素T=exp(x).*cos(x); %温度数据%由A、B、C构成TDMAcoematrix=eye(mdim,mdim);for n=1:mdimcoematrix(n,n)=A(1,n);if n>=2coematrix(n,n-1)=-1*B(1,n);endif ncoematrix(n,n+1)=-1*C(1,n);endend%计算D⽮量D=(coematrix*T')';%由已知的A、B、C、D⽤TDMA⽅法求解T%消元P(1,1)=C(1,1)/A(1,1);Q(1,1)=D(1,1)/A(1,1);for n=2:mdimP(1,n)=C(1,n)/(A(1,n)-B(1,n)*P(1,n-1));Q(1,n)=(D(1,n)+B(1,n)*Q(1,n-1))/(A(1,n)-B(1,n)*P(1,n-1)); end%回迭Tcal(1,mdim)=Q(1,mdim);for n=(mdim-1):-1:1Tcal(1,n)=P(1,n)*Tcal(1,n+1)+Q(1,n);endTcom=[T;Tcal];%绘图⽐较给定T值和计算T值plot(Tcal,'r*')hold on结果⽐较如下,由⽐较可知两者值⾮常切合(在⼩数点后8位之后才有区别):习题4-14充分发展区的温度控制⽅程如下:)(1rTr r r x T uc p =??λρ对于三种⽆量纲定义w b w T T T T --=Θ、∞∞--=ΘT T T T w 、ww T T T T --=Θ∞进⾏分析如下1)由wb wT T T T --=Θ得:w w b T T T T +Θ-=)(由T 可得:x T x T x T T T x T w b w w b ??Θ-+??Θ=?+Θ-?=??)1(])[(rT r T T r T T T r T w w b w w b ??Θ-+?Θ?-=?+Θ-?=??)1()(])[( 由b T 与r ⽆关、Θ与x ⽆关以及x T ??、rT的表达式可知,除了w T 均匀的情况外,该⽆量纲温度定义在⼀般情况下是不能⽤分离变量法的; 2)由∞∞--=ΘT T T T w 得: ∞∞+Θ-=T T T T w )(由T 可得:xT x T T T x T w w ??Θ=?+Θ-?=??∞∞])[(rx T ??、rT的表达式可知,在常见的四种边界条件中除了轴向及周向均匀热流const q w =的情况外,有0=??rT w,则该⽆量纲温度定义是可以⽤分离变量法的; 3)由wwT T T T --=Θ∞得: w w T T T T +Θ-=∞)(由T 可得:xT x T T T x T w w w ??Θ-=?+Θ-?=??∞)1(])[(rT r T T r T T T r T w w w w ??Θ-+?Θ-=+Θ-?=??∞∞)1()(])[( 同2)分析可知,除了轴向及周向均匀热流const q w =温度定义是可以⽤分离变量法的;习题4-181)采⽤柱坐标分析,写出统⼀的稳态柱坐标形式动量⽅程:S r r r r r r x x w r v r r r u x +++=??+??+??)(1)(1)()(1)(1)(θφλθφλφλφρθφρφρ x 、r 和θ分别是圆柱坐标的3个坐标轴,u 、v 和w 分别是其对应的速度分量,其中x 是管内的流动⽅向;对于管内的层流充分发展有:0=v 、0=w ,0=??xu;并且x ⽅向的源项:x pS ??-=r ⽅向的源项:r pS ??-=r S 1由以上分析可得到圆柱坐标下的动量⽅程: x ⽅向:0)(1)(1=??-+x pu r r r u r r r θλθλ r ⽅向:0=??r pθ⽅向:0=??θp边界条件: R r =,0=u0=r ,0=??r u ;对称线上,0=??θu不考虑液体的轴向导热,并简化分析可以得到充分发展的能量⽅程为:)(1)(1θλθλρ+=??Tr r r T r r r x T uc p 边界条件: R r =,w q r T =??λ;0=r ,0=??rTπθ/0=,0=??-θλT2)定义⽆量纲流速:dxdp R uU 2-=λ并定义⽆量纲半径:R r /=η;将⽆量纲流速和⽆量纲半径代⼊x ⽅向的动量⽅程得:0))1((1))1((122=??-?-+?-xp U dx dp R R R R U dx dp R RR R θληλθηηλληηη上式化简得:ηθηηηηηU U 边界条件:1=η,0=U0=η,0=??ηU;对称线上,0=??θU 定义⽆量纲温度:λ/0R q T T b -=Θ其中,0q 是折算到管壁表⾯上的平均热流密度,即:Rq q wπ=0;由⽆量纲温度定义可得:b T Rq T +Θ=λ将T 表达式和⽆量纲半径η代⼊能量⽅程得:)(1)(100θληλθηηλληηηρ?Θ+?Θ=??R q R R R R q R R R x T uc b p 化简得:)1(1)(10θηθηηηηηρ?Θ+?Θ=??x T u c q R b p (1)由热平衡条件关系可以得:mm m b m p b p p RU U q R u u R q A u u dx dT A u c x T u c x T u c 020221221)(===??=??ππρρρ将上式代⼊式(1)可得:)1(1)(12θηθηηηηη?Θ+?Θ=m U U 边界条件:0=η,0=?Θ?η;1=η,R q q w πη10==?Θ?0=?Θ?θ;πθ=,0=?Θθ单值条件:由定义可知:0/0=-=ΘλR q T T b b b 且: ??Θ=ΘAAb U d AU d A 即得单值性条件:0=Θ??AA UdAUdA3)由阻⼒系数f 及Re 定义有:228)(2/Re ??? ??=-=D D U D u u dx dp D f e m e m me νρ且:m W b m W b m W R q T T D T T q Nu ,0,,0~2)/(2Θ=-=-=λλ5-21.⼀维稳态⽆源项的对流-扩散⽅程如下所⽰:xx u 22??Γ=??φφρ(取常物性)边界条件如下:L L x x φφφφ====,;,00上述⽅程的精确解如下:11)/(00--=--?PeL x Pe L e e φφφφΓ=/uL Pe ρ 2.将L 分成20等份,所以有:=P Pe 201 2 3 4 5 6 ………… …………… 17 18 19 20 21 对于中⼼差分、⼀阶迎风、混合格式和QUICK 格式分别分析如下: 1)中⼼)5.01()5.01(11-?+?++-=i i i P P φφφ 20,2 =i2)⼀阶迎风中间节点: ?-?++++=P P i i i 2)1(11φφφ 20,2 =i3)混合格式当1=?P 时,中间节点:2)5.01()5.01(11-?+?++-=i i i P P φφφ20,2 =i当10,5=?P 时,中间节点: 1-=i i φφ 20,2 =i 4) QUICK 格式*12111)35(8122121---++++++=+--??-??+?i i i i i i i P P P P P φφφφφφφ 2≠i *1111)336(8122121--++++++=+-?-??+?i i i i i i P P P P P φφφφφφ 2=i数值计算结果与精确解的计算程序如下:%except for HS, any other scheme doesnt take Pe<0 into consideration %expression of exact solution y=dsolve('a*b*Dy=c*D2y','y(0)=y0,y(L)=yL','x')y=subs(y,'L*a*b/c','t')y=simple(subs(y,'a*b/c*x','t*X'));ysim=simple(sym(strcat('(',char(y),'-y0)','/(yL-y0)')))y=sym(strcat('(',char(ysim),')*(yL-y0)','+y0'))% in the case of Pe=0y1=dsolve('D2y=0','y(0)=y0,y(L)=yL','x')%grid Pe numbertt=[1 5 10];%dimensionless lengthm=20;%mdim is the number of inner nodemdim=m-1;X=linspace(0,1,m+1);%initial value of variable during calculationy0=1;yL=2;%cal exact solutionfor n=1:size(tt,2)t=m*tt(1,n);if t==0yval1(n,:)=eval(y1);elseyval1(n,:)=eval(y);endend%extra treatment because max number in MATLAB is 10^308 if max(isnan(yval1(:)))yval1=yval1';yval1=yval1(:);indexf=find(isnan(yval1));for n=1:size(indexf,1)if rem(indexf(n,1),size(X,2))==0yval1(indexf(n),1)=yL;elseyval1(indexf(n),1)=y0;endendyval1=reshape(yval1,size(X,2),size(yval1,1)/size(X,2));yval1=yval1';endd=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*tt(1,n))*y0;d(n,mdim)=0.5*(1-0.5*tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval2=TDMA(a,b,c,d,mdim);yval2=[repmat([1],size(tt,2),1),yval2,repmat([2],size(tt,2),1)]; Fig(1,X,yval1,yval2,tt); title('CD Vs. Exact Solution')% FUS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval3=TDMA(a,b,c,d,mdim);yval3=[repmat([1],size(tt,2),1),yval3,repmat([2],size(tt,2),1)]; Fig(2,X,yval1,yval3,tt); title('FUS Vs. Exact Solution')% HS solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);t=tt(1,n);if t>2b(n,:)=repmat([0],1,mdim);c(n,:)=repmat([1],1,mdim);d(n,1)=y0;elseif t<-2b(n,:)=repmat([1],1,mdim);c(n,:)=repmat([0],1,mdim);d(n,mdim)=yL;elseb(n,:)=repmat([0.5*(1-0.5*t)],1,mdim);c(n,:)=repmat([0.5*(1+0.5*t)],1,mdim);d(n,1)=0.5*(1+0.5*t)*y0;d(n,mdim)=0.5*(1-0.5*t)*yL;endendc(:,1)=0;b(:,mdim)=0;% numerical cal by using TDMA subfuctionyval4=TDMA(a,b,c,d,mdim);yval4=[repmat([1],size(tt,2),1),yval4,repmat([2],size(tt,2),1)]; Fig(3,X,yval1,yval4,tt); title('HS Vs. Exact Solution')%QUICK Solutiond=zeros(size(tt,2),mdim);a=repmat([1],size(tt,2),mdim);for n=1:size(tt,2)t=tt(1,n);b(n,:)=repmat([1/(2+t)],1,mdim);c(n,:)=repmat([(1+t)/(2+t)],1,mdim);d(n,1)=(1+tt(1,n))/(2+tt(1,n))*y0;d(n,mdim)=1/(2+tt(1,n))*yL;endc(:,1)=0;b(:,mdim)=0;%numerical cal by using TDMA subfuctionyval5=zeros(size(tt,2),mdim);yval5com=yval5+1;counter=1;%iterativewhile max(max(abs(yval5-yval5com)))>10^-10if counter==1yval5com=TDMA(a,b,c,d,mdim);endfor nn=1:size(tt,2)for nnn=1:mdimif nnn==1d(nn,nnn)=((6*yval5com(nn,nnn)-3*y0-3*yval5com(nn,nnn+1))*tt(1,nn))/(8*(2+tt(1, nn)))+((1+tt(1,nn))/(2+tt(1,nn))*y0);elseif nnn==2d(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-y0)*tt (1,nn))/(8*(2+tt(1,nn)));elseif nnn==mdimd(nn,nnn)=((5*yval5com(nn,nnn)-3*yL-yval5com(nn,nnn-1)-yval5com(nn,nnn-2))*tt (1,nn))/(8*(2+tt(1,nn)))+(1/(2+tt(1,nn))*yL); elsed(nn,nnn)=((5*yval5com(nn,nnn)-3*yval5com(nn,nnn+1)-yval5com(nn,nnn-1)-yval5 com(nn,nnn-2))*tt(1,nn))/(8*(2+tt(1,nn))); endendendyval5=TDMA(a,b,c,d,mdim);temp=yval5;yval5=yval5com;yval5com=temp;counter=counter+1;endyval5=yval5com;yval5=[repmat([1],size(tt,2),1),yval5,repmat([2],size(tt,2),1)];Fig(4,X,yval1,yval5,tt);title('QUICK Vs. Exact Solution')%-------------TDMA SubFunction------------------function y=TDMA(a,b,c,d,mdim)%form a b c d resolve yval2 by using TDMA%eliminationp(:,1)=b(:,1)./a(:,1);q(:,1)=d(:,1)./a(:,1);for n=2:mdimp(:,n)=b(:,n)./(a(:,n)-c(:,n).*p(:,n-1));q(:,n)=(d(:,n)+c(:,n).*q(:,n-1))./(a(:,n)-c(:,n).*p(:,n-1));end%iterativey(:,mdim)=q(:,mdim);for n=(mdim-1):-1:1y(:,n)=p(:,n).*y(:,n+1)+q(:,n);end%-------------ResultCom SubFunction------------------ function y=ResultCom (a,b,c)for n=1:max(size(c,2))y(2*n-1,:)=a(n,:);y(2*n,:)=b(n,:);end%-------------Fig SubFunction------------------ function y=Fig(n,a,b,c,d)figure(n);plot(a,b);hold onplot(a,c,'*');str='''legend(';for n=1:size(d,2)if n==size(d,2)str=strcat(str,'''''Pe=',num2str(d(1,n)),''''')''');elsestr=strcat(str,'''''Pe=',num2str(d(1,n)),''''',');endendeval(eval(str));精确解与数值解的对⽐图,其中边界条件给定10=φ,2=L φ。
数值计算大作业一、用数值方法求解尺度为100mm ×100mm 的二维矩形物体的稳态导热问题。
物体的导热系数λ为1.0w/m ·K 。
边界条件分别为: 1、上壁恒热流q=1000w/m2; 2、下壁温度t1=100℃; 3、右侧壁温度t2=0℃; 4、左侧壁与流体对流换热,流体温度tf=0℃,表面传热系数 h 分别为1w/m2·K 、10 w/m2·K 、100w/m2·K 和1000 w/m2·K;要求:1、写出问题的数学描述;2、写出内部节点和边界节点的差分方程;3、给出求解方法;4、编写计算程序(自选程序语言);5、画出4个工况下的温度分布图及左、右、下三个边界的热流密度分布图;6、就一个工况下(自选)对不同网格数下的计算结果进行讨论;7、就一个工况下(自选)分别采用高斯迭代、高斯——赛德尔迭代及松弛法(亚松弛和超松弛)求解的收敛性(cpu 时间,迭代次数)进行讨论;8、对4个不同表面传热系数的计算结果进行分析和讨论。
9、自选一种商业软件(fluent 、ansys 等)对问题进行分析,并与自己编程计算结果进行比较验证(一个工况)。
(自选项)1、写出问题的数学描述 设H=0.1m微分方程 22220t tx y∂∂+=∂∂x=0,0<y<H :()f th t t xλ∂-=-∂ 定解条件 x=H ,0<y<H :t=t 2 y=0,0<x<H :t=t1t 1t 2h ;t fq=1000 w/m 2y=H ,0<x<H :tq yλ∂-=∂ 2、写出内部节点和边界节点的差分方程 内部节点:()()1,,1,,1,,122220m n m n m nm n m n m n t t t t t t x y -+-+-+-++=∆∆左边界: (),1,,1,1,,,022m n m n m n m nm n m n f m n t t t t t t x x h y t t y y y xλλλ-++---∆∆∆-+++∆=∆∆∆右边界: t m,n =t 2上边界: 1,,1,,,1,022m n m n m n m nm n m n t t t t t t y y q x x x x yλλλ-+----∆∆∆+++∆=∆∆∆ 下边界: t m,n =t 13、求解过程利用matlab 编写程序进行求解,先在matlab 中列出各物理量,然后列出内部节点和边界节点的差分方程,用高斯-赛德尔迭代法计算之后用matlab 画图。
目录一、物理问题的描述及分析 (2)二、离散过程及算法分析 (2)2.1 离散过程………………………………………………………………………………...错误!未定义书签。
2.2 算法分析……………………………………………………………………...................错误!未定义书签。
装三、结果演示 (2)四、结论 (11)五、心得体会 (11)六、附件 (12)订线一、物理问题的描述及分析对如图所示的二维方腔顶盖驱动流问题,顶盖拖动速度为u top ,方腔的长度和高度均为H ,流体密度为ρ、动力粘度为μ。
流动与传热的控制方程如下:0u v x y∂∂+=∂∂ 22221u u u p u u u v t x y x x y μρρ⎛∂∂∂∂∂∂++=-++ ∂∂∂∂∂∂⎝其中,u 、v 分别为x 、y 方向速度分量,p 为压力。
用高度H 、流体密度ρ和拖动速度u top 作为无量纲标尺,将控制方程无量纲化,流场初始状态为静止,Re =1000 (top u HRe ρμ=),求流动达到稳定状态时,x 方向中垂线(/2x H =)上的无量纲速度U x ,y 方向中垂线(/2y H =)上的无量纲速度V ,绘制出速度分布曲线 ;绘出压力场、速度场。
二、离散过程及算法分析2.1 离散过程无量纲化后的控制方程:0U VX Y∂∂+=∂∂ (1) 22221Re U U U P U U U V X Y X X Y τ⎛⎫∂∂∂∂∂∂++=-++ ⎪∂∂∂∂∂∂⎝⎭ (2) 22221Re V V V P V V U V X Y Y X Y τ⎛⎫∂∂∂∂∂∂++=-++ ⎪∂∂∂∂∂∂⎝⎭(3) 利用有限差分,同位网格方法对其进行离散,空间项采用中心差分,速度用显式,压力用隐式:u22221v v v p v v u v t x y y x y μρρ⎛∂∂∂∂∂∂++=-++ ∂∂∂∂∂∂⎝1,,n ni j i jU U U ττ+-∂=∂∆ (4a ) 1,1,,2n n i j i j n i j U U U U U X X +--∂=∂∆;,1,1,2n ni j i j n i j U U U V V Y Y+--∂=∂∆ (4b ) 111,,n n i j i jP P P X X+++-∂-=-∂∆ (4c ) 21,,1,222n n n i j i j i j U U U U X X +--+∂=∂∆;2,1,,1222n n ni j i j i j U U U U Y Y +--+∂=∂∆ (4d ) 以下对边界邻点进行特殊处理:U 的左边界邻点:()1,,1,2,343i j i j i ji jU U U UO X X X+-+-∂=+∆∂∆ ()21,,1,2,2281243i j i j i ji jU U U U O X X X -+-+∂=+∆∂∆U 的右边界邻点:()1,,1,2,433i j i j i ji jU U U U O X X X+---∂=+∆∂∆ ()21,,1,2,221283i j i j i ji jU U U U O X X X-+-+∂=+∆∂∆U 的下边界邻点:(),1,,12,343i j i j i j i jU U U U O Y Y Y+-+-∂=+∆∂∆ ()2,1,,12,2281243i j i j i j i jU U U U O Y Y Y -+-+∂=+∆∂∆U 的上边界邻点:(),1,,12,433i j i j i j i jU U U U O Y Y Y+---∂=+∆∂∆ ()2,1,,12,221283i j i j i j i jU U U U O Y Y Y-+-+∂=+∆∂∆同理,可以写出V 的边界邻点的表达式,这里不再赘述。
大作业一、假设0,1x y≤≤的方腔内充满不可压缩流体,左、右、下壁面固定,上壁面以()22161u x x=--运动。
试求腔内的定常解。
(流体的物性取20℃的水。
同时,可以使用20℃的甘油作为对比)二、求解二维圆柱坐标中的Poisson-Nernst-Plack(PNP)方程,PNP方程来描述纳米孔内带电离子在浓度梯度及电场作用下的迁移行为和离子浓度分布。
具体方程如下所示:其中i=+/-,分别代表阴阳离子。
以及连续性方程:其中Φ是局域的电动势,c i表示i种离子的浓度,左侧边界上c+=10,c-=10,右侧边界上c+=1,c-=1。
j i表示离子流,D i为离子的扩散系数2×10-9,z i为离子的带电量,z i=1,T为溶液的温度,T=300。
e是电子电量1.602×10-19,ε0×εr=80,k B为波尔兹曼常数,k B=1.38×10-23。
边界上的电势Φ由高斯定律决定:对于带电的纳米孔壁(图中红色实线所示),有σs=σ(σ为纳米孔的表面电荷密度,数值为0.05);对于其余区域有σs=0。
离子流j i在边界上的法向分量为零,即,求解φ、浓度c i以及ij的场。
(备注:求解区域为一圆柱形区域,长度为1200,直径为d=10。
建议步骤:可首先猜想浓度场c+和c-,并求解电动势场φ,通过连续性方程修正离子流场ij)大作业要求:1-3人为一组,完成以上任选一题目。
最终截止时间为12月26日。
在最终截止时间之前可以提交1次,若不满意得分可以继续修改。
大作业以报告形式提交,内容至少包括计算域的网格划分、方程的离散化、边界条件的处理、计算收敛的判据、计算的结果、结果的图形化显式、结果分析等。
源代码作为附录附在报告的最后。