下载文档原格式
《电⼯电⼦》问答题答案电⼯电⼦问答题答案1、电位的定义答：电位是指电路中各点相对于参考点之间的电压。
电路中各点的点位与参考点有关，参考点不同，电路中各点点位随之⽽异。
2、负载从电源获得最⼤功率的条件是什么？答：当负载电路RL 等于信号源内阻时，max P P =有最⼤值，电路中的电流LS R U I 2=，负载上得到的最⼤功率LS L L S R U R R U P 4)2(22max == 3、R 、L 、C 元件的特性⽅程是什么？4、应⽤叠加原理时，要注意的事项有哪些？答：①叠加原理不适⽤于⾮线性电路；②多个电源共同作⽤时，可将多个电源单独作⽤，对于不作⽤的电压源⽤短路线代替，不作⽤的电流源做开路处理；③叠加原理只能求⽀路电路和电压，不能⽤来求解功率；④在使⽤叠加原理前，必须标明各⽀路电流、电压的⽅向。
5、⽤戴维宁定理解题的步骤是什么？答：①断开原电路中要求电流或电压的负载⽀路；②求开路电压U0；③求⽆源⼆端⽹络的⼊端电阻；④画出等效电压源⽀路，接上断开的负载，⽤等效电路求解。
6、何为换路定则？7、暂态过程初始值的求解步骤有哪些？答：①求出)0()0(--L C i u 或②依据换路定则，得出)0()0(++L C i u 或③画出0+的等效电路，求出)0()0()0()0(++++R R L C u i u i 、、、等其他电压、电流的初始值。
8、什么是⼀阶电路暂态分析的三要素法？答：在直流电源作⽤下，⼀阶线性电路任⼀之路的电压或电流均有如下的解：⼀般式τte f f f t f -+∞-+∞=)]()0([)()( 其中：f(∞)是电路新的稳态值，f(0+)为初始值，τ为换路后电路的时间常数。
f(∞)、f(0+)、τ称之为⼀阶电路的三要素。
9、正弦交流电常采⽤哪四种表⽰法？举例说明答：①三⾓函数 )sin(ψω+=t U u m ②波形图例如（略）③相量图例如（略）④复数式ψψ∠==+=?U Ue jU U U j b a10、确定⼀个正弦量需要哪些要素？答：最⼤振幅A 、⾓频率ω、初相ψ为确定⼀个正弦量的三要素。
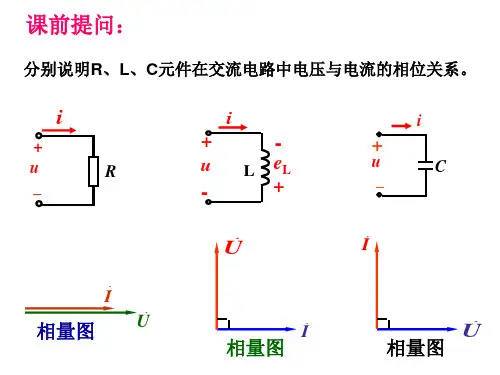
§6-5 R 、L 、C 的相量模型在正弦稳态电路中，三种基本电路元件R 、L 、C 的电压、电流之间的关系都是同频率正弦电压、电流之间的关系，所涉及的有关运算都可以用相量进行，因此这些关系的时域形式都可以转换为相量形式。
一． 正弦交流电路中的电阻元件1. 电阻元件伏安关系在电压和电流的参考方向关联时，电阻R 的伏安关系的时域形式R R ()()u t R i t =⋅当正弦电流i R ＝2I R cos(ωt +ψi )通过电阻R 时， 则 R Rm i u ()cos()cos()Rm u t RI t U t ωψωψ=+=+Rm Rm R R U RI U RI =⎫⎬=⎭电压、电流的最大值(有效值)之间符合欧姆定律；u i u i 0ψψϕψψ=⎫⎬=-=⎭R u 与R i 同相令：R R R iRR R R u R i ()()i t I I u t U U RI R I ψψψ⇒=∠⇒=∠=∠=则在电压和电流关联参考方向下电阻的伏安关系的相量形式为R R U R I = Rm Rm U R I =线性电阻的相量电路、相量图如下。
u R (t )R UR IR I 与R U 共线2. 功率：①瞬时功率：由于瞬时功率p 是由同一时刻的电压与电流的乘积来确定的，因此当流过电阻R 的电流为i R (t )＝I R m cos(ωt +Ψi )时，电阻所吸收的瞬时功率为R R R Rm u Rm i 2R R i R R R R i ()()()cos()cos() 2cos ()cos(2)0p t u t i t U t I t U I t U I U I t ωψωψωψωψ==++=+=++≥常量 两倍于原频率的正弦量可以看出，电阻吸收的功率是随时间变化的，但p R 始终大于或等于零，表明了电阻的耗能特性。
上式还表明了电阻元件的瞬时功率包含一个常数项和一个两倍于原电流频率的正弦项，即电流或电压变化一个循环时，功率变化了两个循环。
1 .电阻元件的功率设正弦稳态电路中，在关联参考方向下，瞬时功率为p R(t)=u(t)I(t)设流过电阻元件的电流为I R (t)=I m sinωt A其电阻两端电压为 u R(t)=I m R sinωt =U m sinωt V则瞬时功率为p R(t)= u(t) i(t)=2U R I R sin2ωt =U R I R（1-cos2ωt）W由于cos2ωt≤1,故此p R（t）=U R I R（1-cos2ωt）≥0其瞬时功率的波形图如图所示由图可见，电阻元件的瞬时功率是以两倍于电压的频率变化的，而且p R（t）≥0，说明电阻元件是耗能元件。
电阻的平均功率可见对于电阻元件，平均功率的计算公式与直流电路相似。
2. 电感元件的功率在关联参考方向下，设流过电感元件的电流为i L(t)=√2I L sinωt A则电感电压为：上式表明，电感元件的瞬时功率也是以两倍于电压的频率变化的；且p L(t)的值可正可负。
其波形图如图所示。
从图上看出，当u L(t)、i L(t)都为正值时或都为负值时，p L(t)为正，说明此时电感吸收电能并转化为磁场能量储存起来；反之，当p L(t)为负时，电感元件向外释放能量。
p L(t)的值正负交替，说明电感元件与外电路不断地进行着能量的交换。
电感消耗的平均功率为：电感消耗的平均功率为零，说明电感元件不消耗功率，只是与外界交换能量。
3．电容元件的功率在电压、电流为关联参考方向下，设流过电容元件的电流为: i c (t)=√2I c sinωt A则电容电压为：其瞬时功率为：u c (t)、I c(t)、p c(t)的波形如图所示。
从图上看出，p c(t)、与p L(t)波形图相似，电容元件只与外界交换能量而不消耗能量。
电容的平均功率也为零，即：电感元件以磁场能量与外界进行能量交换，电容元件是以电场能量与外界进行能量交换。
二端电路的功率1.有功功率（也叫平均功率）和功率因素式中称为二端电路的功率因素，功率因素的值取决于电压与电流之间的相位差，也叫功率因素角。
1 .电阻元件的功率
设正弦稳态电路中，在关联参考方向下，瞬时功率为p R(t)=
u(t)I(t)
设流过电阻元件的电流为I R (t)=I m sinωt A
其电阻两端电压为 u R(t)=I m R sinωt =U m sinωt V
则瞬时功率为p R(t)= u(t) i(t)=2U R I R sin2ωt =U R I R（1-cos2ωt）W
由于cos2ωt≤1,故此p R（t）=U R I R（1-cos2ωt）≥0
其瞬时功率的波形图如图所示
由图可见，电阻元件的瞬时功率是以两倍
于电压的频率变化的，而且p R（t）≥0，
说明电阻元件是耗能元件。
电阻的平均功率
可见对于电阻元件，平均功率的计算公式与
直流电路相似。
2. 电感元件的功率
在关联参考方向下，设流过电感元件的电流为i L(t)=√2I L sinωt A
则电感电压为：
上式表明，电感元件的瞬时功率也是以两倍于电压的频率变化的；且p L(t)的值可正可负。
其波形图如图所示。
从图上看出，当u L(t)、i L(t)
都为正值时或都为负值时，
p L(t)为正，说明此时电感吸收
电能并转化为磁场能量储存起
来；反之，当p L(t)为负时，
电感元件向外释放能量。
p L(t)的值正负交替，说明电
感元件与外电路不断地进行着
能量的交换。
电感消耗的平均功率为：
电感消耗的平均功率为零，说
明电感元件不消耗功率，只是
与外界交换能量。
3．电容元件的功率
在电压、电流为关联参考方向下，设流过电容元件的电流为: i c (t)=
√2I c sinωt A
则电容电压为：
其瞬时功率为：
u c (t)、I c(t)、p c(t)的波形如图所示。
从图上看出，p c(t)、与p L(t)波形图相似，电容元件只与外界交换能量而不消耗能量。
电容的平均功率也为零，即：
电感元件以磁场能量与外界进行能量交换，电容元件是以电场能量与外界进行能量交换。
二端电路的功率
1.有功功率（也叫平均功率）和功率因素
式中
称为二端电路的功率因素，功率因素的值取决于电压与电
流之间的相位差
，
也叫功率因素角。
2.无功功率、视在功率和复功率 无功功率用Q 表示，定义
通常将二端电路电压和电流有效值的乘积称为视在功率，用S 表示，即S=UI
P 、Q 、S 之间存在如下关系：
工程上为了计算方便，把有功功率作为实部，无功功率作为虚部，组成复数，称为复功率，用
表示复功率，即=P+jQ
3.正弦稳态电路的最大功率传输
如图所示，交流电源的电压为 ，其内阻抗
为Z s =R s +jx s ，负载阻抗Z L =R L +jX L ,电路中电流
为：
电流有效值为：
负载吸收的功率为：
要求出P L的最大值为此需求出P L对R L的导数，并使之为零，即：
由上式得到：（R S+R L)2-2R L(R S+R L）=0 解得：R L=R S
负载获取最大功率的条件为：
上式表明，当负载阻抗等于电源内阻抗的共轭复数时，负载能获得最大功率，称为最大功率匹配或共轭匹配。
此时最大功率为：
三相电路
1 三相电路的基本概念
三相交流电源是三个单相交流电源按一定方式进行的组合，且单相交流电源的频率相等，幅值（最大值）相等，相位彼此相差120°。
设第一相初相为0°，第二相为-120°，第三相为120°，所以瞬时电动势为：e1=E m sinωt e2=E m sin（ωt-120°） e3=E m sin（ωt+120°）这样的电动势叫对称三相电动势。
其相量图和波形图见下图。
对称三相电动势相量和为零，即： =0 由波形图可知，三相电动势对称时任一瞬间的代数和为零，即：e1+e2+e3=0
2.三相电源的连接
将三相电源按一定方式连接之后，再向负载供电，通常采用星形连接方式，如图所示。
低压配电系统中，采用三根
相线和一根中线输电，称为
三相四线制；高压输电工程
中，由三根相线组成输电，
称为三相三线制。
每相绕组
始端与末端之间的电压，也
就是相线和中线之间的电
压，叫相电压，其瞬时值用
u1、u2、u3表示，通用u p表
示。
任意两相线与相线之间
的电压，叫线电压，瞬时值
用u12、u23、u31表示，通用
u l表示。
由于u12=u1-u2，
u23=u2-u3，u31=u3-u1作出线电
压和相电压的相量图，
如图所示。
由于构成
等腰三角形，
所以
同理一般写为
作星形连接时，三
个相电压和三个线电压均为三相
对称电压，各线电压的有效值为相
电压有效值的倍，且线电压相
位比对应的相电压超前30°。
3 三相负载的星形连接
三相电路负载有星形连接和三角形连接两种方式。
负载的星形连接
如图所示是三相负载作星形莲接时的电路图。
显然，在负载星形连接时，线电流等于相电流，即
相负载对称，即 Z1=Z2=Z3=Z p，因各相电压对称，所以各相电流相等，即：I1=I2=I3=I YP=同时，三个相电流的相位差互为120°，
满足由基尔霍夫电流定律知
iN=i1+i2+i3略去电线上的电压降，则各相负载的相电压就等于电源的相电压，这样，电源的线电压为负载相电压的倍，即：
U YP为星形联接负载相电压。
三相电路中，流过每根相线的电流叫线电流，即I1、I2、I3，用表示，方向规定为由电源流向负载；而流过负载的电流叫相电流，用
I YP表示，其方向与相电压方向一致；流过中线的电流叫中线电流，用I N表示，其方向规定由负载中点N/流向电源中点N。
这样，对称的三相负载作星形联接时，中线电流为零。
这时，可以省略中线而成为三相三线制，并不影响电路工作。
如果三相负载不对称，各相电流大小就不相等，相位差也不一定是120°，中线电流不为零，此时就
不能省去中线。
否则会影响电路正常工作，甚至造成事故。
所以三相四线制中除尽量使负载平衡运行之外，中线上不准安装熔丝和开关。
负载的三角形连接
如图所示，将三相负载分别接在三相电源的两根相线之间，称为三相负载的三角形连接。
不论负载对称与否，各相负载承受的电压均为对称的电源线电压。
对于对称三相负载，相电压等于线电压，即相电
流同时，各相电压与各相电流的相位差也相同。
即三相电流的相位差也互为120°。
各相电流的方向与该相的电压方向一致。
由KCL知i1=i12-i31i2=i23-i12i3=i31-i23 作出线电流和相电流的相量，如图所示。
从图中看出：各线电流在相
位上比各相电流滞后30°。
由于相电流对称，所以线电
流也对称，各线电流之间相
差120°。
可以看出
I l=2I12cos30=
所以
这些说明：对称三相负载
呈三角形连接时，线电流的
有效值为相电流有效值的
倍，线电流在相位上滞后
于相电流30°。
三相电路的功率
三相电路的功率等于各相负载吸收功率的总
P=P1+P2+P3
和：
Q=Q1+Q2+Q3
S=S1+S2+S3
当三相负载对称时，各相功率相等，总功率为一相即
功率的三倍。
通常，相电压和相电流不易测量，计算三相电路的功率时，是通过线电压和线电流来计算。
不论负载作星形连接还是三角形连接，总的有功功率、无功功率和视在功率，计算三相负载总功率的公式是相同的，即：。
