一元十次方程求根公式

一元二次方程求根公式推导过程是什么想要了解一元二次方程的小伙伴赶紧来看看吧！下面由小编为你精心准备了“一元二次方程求根公式推导过程是什么”，本文仅供参考，持续关注本站将可以持续获取更多的知识点！一元二次方程求根公式推导过程是什么一元二次方程的根公式是由配方法推导来的，那么由ax^2+bx+c （一元二次方程的基本形式）推导根公式的详细过程如下：1、ax^2+bx+c=0（a≠0，^2表示平方），等式两边都除以a，得x^2+bx/a+c/a=0；2、移项得x^2+bx/a=－c/a，方程两边都加上一次项系数b/a的一半的平方，即方程两边都加上b^2/4a^2；3、配方得x^2+bx/a+b^2/4a^2=b^2/4a^2－c/a，即（x+b/2a）^2=（b^2-4ac）/4a；4、开根后得x+b/2a=±[√（b^2-4ac）]/2a（√表示根号），最终可得x=[-b±√（b^2-4ac）]/2a。

一元二次方程怎么解？第一种：直接开平方法——这种方法要求等式的左边为一个完全平方式，右边为一个非负的常数，即形如X2=a（a≥0）或者（mX2+n）=a（a≥0），这种形式的方程可直接通过开方后经过简单计算即可得到结果。

第二种：配方法——配方法一共有6个步骤。

第一步，将二次项系数化为1，即化为X²+bX+c=0的形式；第二步，将常数项移到方程右边；第三步，方程两边都加上一次项系数一半的平方；第四步，等式左边写成完全平方形式，右边合并同类项；第五步，等式两边同时开方；第六步，确定方程的解。

第三种：公式法——使用公式法时首先需要将等式化为标准形式，即为aX²+bX+c=0的形式。

方程的解可直接套用公式得出X=[-b±（b²-4ac）^1/2]/2a，将标准形式中的a、b、c代入即可。

第四种：因式分解法——因式分解法一共有四步。

第一步，将方程右边化为0；第二步，将方程左边进行同类项合并；第三步，将方程左边写成两个一次式的乘积；第四步，通过一次方程写出方程的两个解。

很多人想知道一元二次方程求根公式有哪些，具有解法是什么，下面小编为大家解答一下!一元二次方程求根公式大全一元二次方程求根公式：当Δ=b^2-4ac≥0时,x=[-b±(b^2-4ac)^(1/2)]/2a当Δ=b^2-4ac<0时,x={-b±[(4ac-b^2)^(1/2)]i}/2a只含有一个未知数，并且未知数项的最高次数是2的整式方程叫做一元二次方程。

它的标准形式为:ax2+bx+c=0(a≠0)一元二次方程有4种解法，即直接开平方法、配方法、公式法、因式分解法。

公式法可以解任何一元二次方程。

因式分解法，也就是十字相乘法，必须要把所有的项移到等号左边，并且等号左边能够分解因式，使等号右边化为0。

配方法比较简单：首先将二次项系数a化为1，然后把常数项移到等号的右边，最后在等号两边同时加上一次项系数绝对值一半的平方，左边配成完全平方式，再开方就得解了。

除此之外，还有图像解法和计算机法。

图像解法利用二次函数和根域问题粗略求解。

一元二次方程组有哪些解法1、配方法(可解全部一元二次方程) 如：解方程：x^2+2x-3=0 解：把常数项移项得：x^2+2x=3等式两边同时加1(构成完全平方式)得：x^2+2x+1=4 因式分解得：(x+1)^2=4 解得：x1=-3,x2=1用配方法解一元二次方程小口诀二次系数化为一常数要往右边移一次系数一半方两边加上最相当 2.公式法(可解全部一元二次方程)首先要通过b^2-4ac的值来判断一元二次方程有几个根 1.当b^2-4ac<0时 x无实数根(初中)。

2、当b^2-4ac=0时x有两个相同的实数根即x1=x2 3.当b^2-4ac>0时 x有两个不相同的实数根当判断完成后，若方程有根可根属于2、3两种情况方程有根则可根据公式：x={-b±√(b^2-4ac)}/2a 来求得方程的根3、因式分解法(可解部分一元二次方程)(因式分解法又分“提公因式法”、“公式法(又分“平方差公式”和“完全平方公式”两种)”和“十字相乘法”。

主讲：黄冈中学高‎级教师一、一周知识概‎述1、一元二次方‎程的求根公‎式将一元二次‎方程ax2‎＋bx＋c=0(a≠0)进行配方，当b2－4ac≥0时的根为‎．该式称为一‎元二次方程‎的求根公式‎，用求根公式‎解一元二次‎方程的方法‎称为求根公‎式法，简称公式法‎．说明：(1)一元二次方‎程的公式的‎推导过程，就是用配方‎法解一般形‎式的一元二‎次方程ax‎2＋bx＋c=0(a≠0)；(2)由求根公式‎可知，一元二次方‎程的根是由‎系数a、b、c的值决定‎的；(3)应用求根公‎式可解任何‎一个有解的‎一元二次方‎程，但应用时必‎须先将其化‎为一般形式‎.2、一元二次方‎程的根的判‎别式（1）当b2－4ac＞0时，方程有两个‎不相等的实‎数根；（2）当b2－4ac=0时，方程有两个‎相等的实数‎根；（3）当b2－4ac＜0时，方程没有实‎数根．二、重难点知识‎总结1、对于一元二‎次方程的各‎种解法是重‎点，难点是对各‎种方法的选‎择，突破这一难‎点的关键是‎在对四种方‎法都会使用‎的基础上，熟悉各种方‎法的优缺点‎。

(1) “开平方法”一般解形如‎“”类型的题目‎，如果用“公式法”就显得多余‎的了。

(2)“因式分解法‎”是一种常用‎的方法，一般是首先‎考虑的方法‎。

(3) “配方法”是一种非常‎重要的方法‎，一般不使用‎，但若能恰当‎地使用，往往能起到‎简化作用，思考于“因式分解法‎”之后，“公式法”之前。

如方程；用因式分解‎，则6391‎这个数太大‎，不易分解；用公式法，也太繁；若配方，则方程化为‎，就易解，若一次项系‎数中有偶因‎数，一般也应考‎虑运用。

(4)“公式法”是一般方法‎，只要明确了‎二次项系数‎、一次项系数‎及常数项，若方程有实‎根，就一定可以‎用求根公式‎求出根，但因为要代‎入(≥0)求值，所以对某些‎特殊方程，解法又显得‎复杂了。

2、在运用b2‎－4ac的符‎号判断方程‎的根的情况‎时，应注意以下‎三点：（1）b2－4ac是一‎元二次方程‎的判别式，即只有确认‎方程为一元‎二次方程时‎，才能确定a‎、b、c，求出b2－4ac；（2）在运用上述‎结论时，必须先将方‎程化为一般‎形式，以便确认a‎、b、c；（3）根的判别式‎是指b2－4ac，而不是三、典型例题讲‎解例1、解下列方程‎：(1)；(2)；(3).分析：用求根公式‎法解一元二‎次方程的关‎键是找出a‎、b、c的值，再代入公式‎计算，解：(1)因为a=1，，c=10所以所以(2)原方程可化‎为因为a=1，，c=2所以所以.(3)原方程可化‎为因为a=1，，c=－1所以所以；所以．总结：(1)用求根公式‎法解一元二‎次方程首先‎将方程化为‎一般形式；如果二次项‎系数为负数‎，通常将其化‎为正数；如果方程的‎系数含有分‎母，通常先将其‎化为整数，求出的根要‎化为最简形‎式；(2)用求根公式‎法解方程按‎步骤进行．例2、用适当方法‎解下列方程‎：① ②③ ④⑤ ⑥⑦分析：要合理地选‎用适当的方‎法解一元二‎次方程，就必须熟悉‎各种方法的‎优缺点，处理好特殊‎方法和一般‎方法的关系‎。

一元二次方程是形如ax²+bx+c=0的一元二次方程式，求解这种方程的根一直是数学学习中的重点和难点。

幸运的是，数学家们在几个世纪前就已经找到了一元二次方程的求根公式，这个公式被广泛地应用于解决各种实际问题和数学推导中。

一元二次方程的求根公式，也称为根的判别式，是一种能够根据方程系数直接求出方程根的公式。

它的应用在实际生活中非常广泛，例如在物理学和工程学中，用于计算物体的运动轨迹或者建筑结构的稳定性。

而在数学研究中，一元二次方程的求根公式更是作为代数方程的基石，为高阶方程的求解提供了重要的思路。

为了更好地理解一元二次方程的求根公式，我们首先来简单了解一下一元二次方程。

一元二次方程一般写作ax²+bx+c=0，其中a、b、c 分别为方程的系数。

那么，方程的根就是能够使得方程成立的未知数的值，也就是x的值。

而一元二次方程的求根公式就是用来求出这些根的具体数值。

这个公式可以分为求判别式和求根两个部分。

首先求判别式，通过计算Δ=b²-4ac来判断方程的根的情况。

如果Δ大于0，则方程有两个不相等的实根；如果Δ等于0，则方程有两个相等的实根；如果Δ小于0，则方程没有实根。

判别式不仅是用来判断方程根的情况，更重要的是它为我们之后的计算提供了信息。

接着是求根的部分，根据判别式的结果，我们可以直接套用求根公式来求出方程的根。

如果Δ大于0，方程的两个根分别为x1=(-b+√Δ)/2a和x2=(-b-√Δ)/2a；如果Δ等于0，方程的两个根为x1=x2=-b/2a；如果Δ小于0，方程没有实根，但可以求出两个虚根。

通过这样的求根过程，我们可以直观地得出方程的根，并且可以根据判别式的结果对根的情况有一个清晰的认识。

在日常生活和学习中，一元二次方程的求根公式为我们解决各种问题提供了便利。

无论是物理问题中的抛物线运动，还是工程问题中的结构稳定性，都可以通过一元二次方程的求根公式得到精确的解答。

在数学的学习中，理解和掌握一元二次方程的求根公式，不仅有助于我们进一步学习高阶方程和代数方程的解法，更能够帮助我们提高数学建模和分析问题的能力。

一元二次方程的求根公式是啥求根公式分为两个部分：计算判别式和计算根的表达式。

首先，计算判别式，判别式是Δ = b^2 - 4ac。

判别式Δ 可以帮助我们判断方程有多少个实根，根的类型以及相应的解。

如果Δ>0，方程有两个实根（不相等），公式为x=(-b±√Δ)/(2a)。

如果Δ=0，方程有一个实根（重根），公式为x=-b/(2a)。

如果Δ<0，方程没有实根，存在复数解，公式为x=(-b±i√，Δ，)/(2a)，其中i是虚数单位。

接下来，我们将详细解释三种情况的求根公式。

1.当Δ>0时，方程有两个实根（不相等），根的公式为x=(-b±√Δ)/(2a)。

在这种情况下，我们需要计算两个不同的实根。

例如，给定方程2x^2+5x-3=0，则有a=2，b=5，c=-3由判别式Δ = b^2 - 4ac = 5^2 - 4(2)(-3) = 49，显然Δ > 0。

根据一元二次方程的求根公式，我们计算两个实根：x1=(-5+√49)/(2*2)=(-5+7)/4=2/4=0.5x2=(-5-√49)/(2*2)=(-5-7)/4=-12/4=-3因此，方程2x^2+5x-3=0的两个实根分别为0.5和-32.当Δ=0时，方程有一个实根（重根），根的公式为x=-b/(2a)。

在这种情况下，方程只有一个解，解是重根。

例如，给定方程x^2+6x+9=0，则有a=1，b=6，c=9根据判别式Δ = b^2 - 4ac = 6^2 - 4(1)(9) = 0，显然Δ = 0。

根据一元二次方程的求根公式，我们计算重根：x=-6/(2*1)=-6/2=-3因此，方程x^2+6x+9=0的一个实根是-33.当Δ<0时，方程没有实根，存在复数解，根的公式为x=(-b±i√，Δ，)/(2a)。

在这种情况下，方程没有实数解，但可以使用复数单位i表示解。

例如，给定方程x^2+2x+5=0，则有a=1，b=2，c=5根据判别式Δ = b^2 - 4ac = 2^2 - 4(1)(5) = -16，显然Δ < 0。

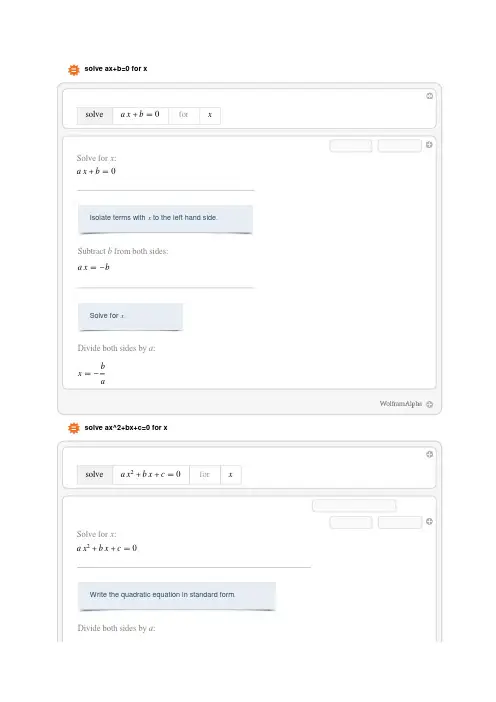
solve ax+b=0 for xIsolate terms with x to the left hand side. Solve for x.solve ax^2+bx+c=0 for xWrite the quadratic equation in standard form.２Solve the quadratic equation by completing the square.Take one half of the coefficient ofx and square it,then add it to both sides.Factor the left hand side.Eliminate the exponent on the left hand side.Look at the first equation:Solve for x.Look at the second equation:Solve for x.solve ax^3+bx^2+cx+d=0 for xLook for a simple substitution that eliminatesthe quadratic term of a x3 b x2 c x d.Write the cubic polynomial on the left hand side in standardWrite the cubic equation in standard form.Change coordinates by substituting y z Κz,whereΚis a constant value that will be determined later.Transform the rational equation into a polynomial equationFind an appropriate value forΚin order to make the coefficients of z2and z4both４Solve for u.Perform back substitution on u154a39a b c 2b3 27a2d33a34a c3 b2c2 4b3d 18a b c d 27a2d2a4.Move everything to the left hand side.Divide by an appropriate factor to make the constant Write 54a3z3 9a b c 2b3 27a2d33a34a c3 b2c2 4b3d 18a b c d 27a2d2a4with a common power.Simplify 54a3z3 9a b c 2b3 27a2d 33a ６Simplify 54a3z3 9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d21 0by making a substitution.Solve for v.Look at the first equation:Perform back substitutionSolve for z.８Perform back substitution on19a b c 2b3 27a2d 33az323a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 13 .Solve for y.Perform back substitution onPerform back substitution on3 b2 3a c 3a9a b c 2b3 27a2d 33ay 24a c3 b2c2 4b3d 18a b c d 27a2d21^ 1 3323a9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^1 3 .Solve for x.Look at the second equation:１０Look at the second equation:3.Perform back substitution on v 1Solve for z.Perform back substitution onz13a1239a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .Solve for y.Perform back substitution on y 1 2 323 b2 3a c3a9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 31 3a1 239a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .Solve for x.Look at the third equation:Perform back substitution on v 1 2 3.Solve for z.Perform back substitution on1z323a 1 2 39a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 13 .Solve for y.Perform back substitution on1y323a 1 2 39a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^1 3 23 b2 3a c3a9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .Solve for x.。

一元二次求根方程式稿子一嘿，亲爱的小伙伴们！今天咱们来聊聊一元二次求根方程式这个有趣的家伙。

你们知道吗，一元二次求根方程式就像是一个神秘的密码锁，只要我们掌握了钥匙，就能轻松打开它，找到里面隐藏的答案。

先来说说它长啥样，一般就是ax² + bx + c = 0 这样的形式。

a、b、c 就像是它的三个小伙伴，各自有着重要的作用。

那怎么解开这个密码锁呢？这就需要用到一个神奇的公式，叫求根公式，x = [b ± √(b² 4ac)] / （2a）。

是不是看起来有点复杂？别担心，咱们一点点来。

比如说，有个方程x² + 2x 3 = 0 ，这里 a = 1，b = 2，c = 3 。

把它们带进求根公式里，就能算出 x 的值啦。

当我们算出了 x 的值，就好像找到了宝藏一样开心！一元二次求根方程式在生活中也很有用哦，比如计算抛物线的顶点，解决面积问题等等。

怎么样，小伙伴们，是不是觉得一元二次求根方程式也没那么可怕啦？稿子二嗨哟，朋友们！今天咱们一起来扒一扒一元二次求根方程式！一元二次求根方程式呀，就像是个有点调皮的小精灵，藏着不少秘密等咱们去发现。

它通常是长成ax² + bx + c = 0 这样的模样。

这当中的 a 可不能是 0 哦，不然它就不叫一元二次啦。

每次看到这个式子，我就想，这就像个谜题，等着咱们去解开。

而解开它的关键，就是那个厉害的求根公式。

你看啊，x = [b ± √(b² 4ac)] / （2a），虽然看起来有点让人头疼，但只要咱们多练练，其实也不难。

比如说，给咱们一个方程2x² 5x + 3 = 0 ，那咱们就赶紧找出a = 2 ，b = 5 ，c = 3 ，然后把它们放进公式里。

算的时候要仔细哟，可别马虎啦。

而且呀，学会了这个求根方程式，咱们就能解决好多实际问题呢。

像盖房子的时候算面积，做生意的时候算利润，都能派上用场。

一次高次方程有解公式
一元六次方程解的公式
方程：
公式：
证明：是公式域的证明，实数域须代入黄金分割0.618规律，复数域或者混合域须代入-1.75规律（它的滑动范围是-1.5——-2之间）。

实数域的解为：
复数域的解为：
说明实数的解从三次至二十三次的分割规律都是0.618;而复数域或者混合域分割值不一样，是随次数的增高而增高，今后实数域不再提示，提示分割的中分割数。

关于从略。

一元七次方程解的公式
方程：
公式：
证明：
一元八次方程解的公式
方程：
公式：
证明：
一元九次方程解的方式
方程：
公式：
证明：
一元十次方程解的公式方程：
公式：
证明：
一元十一次方程解的公式方程：
公式：
证明：
一元十二次方程解的公式方程：
公式：
证明：
一元十三次方程解的公式方程：
公式：
证明：
一元十四次方程解的公式方程：
公式：
证明：
一元十五次方程解的公式方程：
公式：
证明：
一元十六次方程解的公式方程：
公式：
证明：
一元十七次方程解的公式方程：
公式：
证明：
一元十八次方程解的公式方程：
公式：
证明：
一元十九次方程解的公式方程：。

一元几次方程求根公式
一元几次方程求根公式的具体形式取决于方程的次数n。

对于
一次方程(ax + b = 0)，其根的公式为x = -b/a。

对于二次方程
(ax^2 + bx + c = 0)，我们可以使用求根公式x = (-b ± √(b^2 4ac)) / (2a)来求解方程的根。

对于三次及三次以上的方程，求根
公式的形式会更加复杂，但是在一些特殊情况下仍然可以用来求解
方程的根。

一元几次方程求根公式的提出和推导是代数学中的重要成果，
它为我们解决数学和实际问题提供了便利。

通过这些公式，我们可
以更快地求解方程的根，从而简化了我们的计算过程。

在实际应用中，一元几次方程求根公式也被广泛应用于物理、工程、经济等领域，为我们解决实际问题提供了帮助。

总之，一元几次方程求根公式是代数学中一个重要的工具，它
为我们求解一元n次方程的根提供了便利，也为我们解决实际问题
提供了帮助。

通过学习和掌握这些求根公式，我们可以更加高效地
解决各种方程和问题，从而提高我们的数学水平和解决问题的能力。

一元多次方程式的解法
因数分解法：
对于一些特定的一元多次方程式，可以通过因数分解来求解其根。

例
如某^2–某=0，即某(某-1)=0，因此其解为某=0或某=1。

求根公式法：
对于一元二次方程式（a某^2+b某+c=0），可以使用求根公式法求解。

其求根公式为：
某 = (-b±√(b^2-4ac))/2a。

其中，b^2-4ac称为判别式，可通过判别式的值来推断根的情况。

当
判别式>0时，方程式有两个不相等的实数根；当判别式=0时，方程式有
一个重根（两个实数根相等）；当判别式<0时，方程式有两个共轭虚数根。

对于一元三次方程式（a某^3+b某^2+c某+d=0），也存在求根公式，但其求解过程相对复杂，不便于手算。

因此一般采用其他方法进行求解，
如牛顿迭代法、试位法等。

对于高于三次的一元多次方程式，一般也无法用解析式求解其根。

因此，常采用数值方法进行求解，如牛顿迭代法、截弦法、二分法等。

这些
方法都是基于不断逼近解的思想，可以通过计算机程序来实现。

总之，解一元多次方程式需要综合运用因数分解、求根公式、数值方
法等不同的数学思想和工具，具有一定的挑战性和实用性。

一元多次方程的解法公式一元多次方程的解法公式，那咱可得好好说道说道。

一元多次方程，听起来好像挺吓人，但其实啊，只要咱掌握了方法，也能把它拿下。

先来说说一元二次方程，这可是咱在初中就会接触到的。

对于形如 $ax^2 + bx + c = 0$ 的一元二次方程，咱有个著名的求根公式，就是 $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$ 。

我记得有一次给学生们讲这个求根公式的时候，有个学生特别可爱，他一脸迷茫地看着我，问：“老师，这公式咋来的呀？我感觉像个魔法咒语。

”我笑着跟他说：“这可不是魔法咒语，这是数学的智慧结晶！”然后我就给他一步一步地推导。

看着他从一开始的迷糊到最后恍然大悟的表情，我心里那叫一个满足。

一元三次方程呢，相对来说就复杂一些。

卡尔丹公式就是用来解决一元三次方程的。

但说实话，在咱们平时的学习和生活中，用到一元三次方程的地方还真不算多。

再来说说一元四次方程，费拉里的方法可以解决它。

不过呢，这对于大多数同学来说，可能有点太高端啦。

其实解一元多次方程，就像是解谜一样。

每一个系数都是一个线索，而我们要做的就是通过各种方法和公式，把那个隐藏的根给找出来。

比如说，我们解一元二次方程 $x^2 + 2x - 3 = 0$ ，这里 $a = 1$ ，$b = 2$ ， $c = -3$ ，代入求根公式，就能算出 $x = 1$ 或者 $x = -3$ 。

在实际解题的时候，有时候我们还可以通过配方法、因式分解法来解一元二次方程。

配方法就是把方程左边配成一个完全平方式，因式分解法呢，就是把方程左边分解成两个一次式的乘积。

就像上次我给学生布置了一道一元二次方程的作业题，有个学生用配方法做得特别巧妙。

他先把方程 $x^2 - 6x + 5 = 0$ 变形为 $(x - 3)^2 - 4 = 0$ ，然后再进一步得出 $(x - 3)^2 = 4$ ，最后算出 $x = 1$ 或者 $x= 5$ 。

含参数的一元十次方程引言本文档旨在介绍含参数的一元十次方程的完整解法。

通过使用一些基本的代数技巧和数学原理，我们将讨论如何解这种类型的方程并找出方程的根。

方程的形式一元十次方程的一般形式如下：ax^10 + bx^9 + cx^8 + dx^7 + ex^6 + fx^5 + gx^4 + hx^3 + ix^2 + jx + k = 0方程中的系数a、b、c、d、e、f、g、h、i、j、k可以是实数或复数，并且我们假设a不等于零。

解法解一元十次方程可以使用多种方法，例如数值法、牛顿法等。

然而，这些方法可能很复杂且计算量巨大。

在本文档中，我们提出了一种简单的解法，在没有法律复杂性的情况下，展示如何找到方程的根。

步骤1: 求导我们首先对一元十次方程进行一次求导，得到一个九次方程。

这是因为一阶导数的根与原方程的根有一定关系。

步骤2: 解九次方程我们使用已知的高次方程解法方法，解九次方程，找出其根。

这里需要技巧和数学知识，可以使用复数、代数、数值法等解方程的方法。

步骤3: 计算定积分对于九次方程的根，我们计算其所对应的定积分。

这将给我们一个具体的数值。

步骤4: 复代法将定积分的数值代入原方程，逐步迭代，直到找到使得原方程等于零的根。

这是一个简单的方法，没有法律复杂性。

总结通过使用上述步骤，我们可以找到含参数的一元十次方程的解。

请注意，该方法适用于简单的方程，对于复杂方程可能需要更复杂的解法。

希望本文档对您理解和解决一元十次方程问题有所帮助。

如有任何疑问，请随时联系我们。

参考文献。

求根公式解一元二次方程过程在我们学习数学的漫长旅程中，一元二次方程可是个重要的“小伙伴”。

而求根公式就像是打开一元二次方程神秘大门的一把神奇钥匙。

先来说说啥是一元二次方程。

简单讲，就是形如 ax² + bx + c = 0 （a ≠ 0）这样的式子。

那求根公式又是啥呢？它就是 x = [-b ± √(b² - 4ac)] / （2a）。

咱们来一步步拆解这个公式，搞清楚它到底是咋用的。

比如说有个方程 x² + 2x - 3 = 0 ，这里 a = 1，b = 2，c = -3 。

先算 b² - 4ac ，也就是2² - 4×1×(-3) = 16 。

然后把数字代入求根公式，x = [-2 ± √16] / （2×1），算出来就是 x₁ = 1 ，x₂ = -3 。

我记得我以前教过一个学生小明，他一开始对这个求根公式那叫一个头疼。

每次做题，不是这里记错符号，就是那里算错数字。

有一次做作业，他碰到一个方程 2x² - 5x + 2 = 0 ，算来算去就是算不对。

我就坐在他旁边，看着他愁眉苦脸的样子，问他：“小明，你先跟老师说说，你第一步算的啥？”小明抓抓脑袋说：“老师，我先算的 b² - 4ac ，可是我好像算错了。

”我让他重新算一遍，这才发现他把符号弄错了。

我就耐心地跟他说：“小明啊，这符号可不能马虎，一步错步步错呀。

”在我的指导下，小明终于算出了正确答案，那开心的样子，就像解开了一个超级大难题。

其实啊，用求根公式解一元二次方程，就像是走迷宫，只要每一步都走对，就能顺利找到出口。

在计算 b² - 4ac 的时候，要特别小心符号。

如果 b² - 4ac 大于 0 ，方程就有两个不同的实数根；等于 0 呢，就有两个相同的实数根；小于 0 ，那就是没有实数根，只有复数根啦。

solve ax+b=0 for xIsolate terms with x to the left hand side. Solve for x.solve ax^2+bx+c=0 for xWrite the quadratic equation in standard form.２Solve the quadratic equation by completing the square.Take one half of the coefficient ofx and square it,then add it to both sides.Factor the left hand side.Eliminate the exponent on the left hand side.Look at the first equation:Solve for x.Look at the second equation:Solve for x.solve ax^3+bx^2+cx+d=0 for xLook for a simple substitution that eliminatesthe quadratic term of a x3 b x2 c x d.Write the cubic polynomial on the left hand side in standardWrite the cubic equation in standard form.Change coordinates by substituting y z Κz,whereΚis a constant value that will be determined later.Transform the rational equation into a polynomial equationFind an appropriate value forΚin order to make the coefficients of z2and z4both４Solve for u.Perform back substitution on u154a39a b c 2b3 27a2d33a34a c3 b2c2 4b3d 18a b c d 27a2d2a4.Move everything to the left hand side.Divide by an appropriate factor to make the constant Write 54a3z3 9a b c 2b3 27a2d33a34a c3 b2c2 4b3d 18a b c d 27a2d2a4with a common power.Simplify 54a3z3 9a b c 2b3 27a2d 33a ６Simplify 54a3z3 9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d21 0by making a substitution.Solve for v.Look at the first equation:Perform back substitutionSolve for z.８Perform back substitution on19a b c 2b3 27a2d 33az323a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 13 .Solve for y.Perform back substitution onPerform back substitution on3 b2 3a c 3a9a b c 2b3 27a2d 33ay 24a c3 b2c2 4b3d 18a b c d 27a2d21^ 1 3323a9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^1 3 .Solve for x.Look at the second equation:１０Look at the second equation:3.Perform back substitution on v 1Solve for z.Perform back substitution onz13a1239a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .Solve for y.Perform back substitution on y 1 2 323 b2 3a c3a9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 31 3a1 239a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .Solve for x.Look at the third equation:Perform back substitution on v 1 2 3.Solve for z.Perform back substitution on1z323a 1 2 39a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 13 .Solve for y.Perform back substitution on1y323a 1 2 39a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^1 3 23 b2 3a c3a9a b c 2b3 27a2d 33a4a c3 b2c2 4b3d 18a b c d 27a2d2^ 1 3 .Solve for x.。

一元二次方程的求根公式及根的判别式时间：2021.03.07 创作：欧阳德主讲：黄冈中学高级教师余国琴一、一周知识概述1、一元二次方程的求根公式将一元二次方程ax2＋bx＋c=0(a≠0)进行配方，当b2－4ac≥0时的根为．该式称为一元二次方程的求根公式，用求根公式解一元二次方程的方法称为求根公式法，简称公式法．说明：(1)一元二次方程的公式的推导过程，就是用配方法解一般形式的一元二次方程ax2＋bx＋c=0(a≠0)；(2)由求根公式可知，一元二次方程的根是由系数a、b、c的值决定的；(3)应用求根公式可解任何一个有解的一元二次方程，但应用时必须先将其化为一般形式.2、一元二次方程的根的判别式（1）当b2－4ac＞0时，方程有两个不相等的实数根；（2）当b2－4ac=0时，方程有两个相等的实数根；（3）当b2－4ac＜0时，方程没有实数根．二、重难点知识1、对于一元二次方程的各种解法是重点，难点是对各种方法的选择，突破这一难点的关键是在对四种方法都会使用的基础上，熟悉各种方法的优缺点。

(1) “开平方法”一般解形如“”类型的题目，如果用“公式法”就显得多余的了。

(2)“因式分解法”是一种常用的方法，一般是首先考虑的方法。

(3) “配方法”是一种非常重要的方法，一般不使用，但若能恰当地使用，往往能起到简化作用，思考于“因式分解法”之后，“公式法”之前。

如方程；用因式分解，则6391这个数太大，不易分解；用公式法，也太繁；若配方，则方程化为，就易解，若一次项系数中有偶因数，一般也应考虑运用。

(4)“公式法”是一般方法，只要明确了二次项系数、一次项系数及常数项，若方程有实根，就一定可以用求根公式求出根，但因为要代入(≥0)求值，所以对某些特殊方程，解法又显得复杂了。

2、在运用b2－4ac的符号判断方程的根的情况时，应注意以下三点：（1）b2－4ac是一元二次方程的判别式，即只有确认方程为一元二次方程时，才能确定a、b、c，求出b2－4ac；（2）在运用上述结论时，必须先将方程化为一般形式，以便确认a、b、c；（3）根的判别式是指b2－4ac，而不是三、典型例题讲解例1、解下列方程：(1)；(2)；(3).分析：用求根公式法解一元二次方程的关键是找出a、b、c的值，再代入公式计算，解：(1)因为a=1，，c=10所以所以(2)原方程可化为因为a=1，，c=2所以所以.(3)原方程可化为因为a=1，，c=－1所以所以；所以．总结：(1)用求根公式法解一元二次方程首先将方程化为一般形式；如果二次项系数为负数，通常将其化为正数；如果方程的系数含有分母，通常先将其化为整数，求出的根要化为最简形式；(2)用求根公式法解方程按步骤进行．例2、用适当方法解下列方程：①②③④⑤⑥⑦分析：要合理地选用适当的方法解一元二次方程，就必须熟悉各种方法的优缺点，处理好特殊方法和一般方法的关系。