立体几何求体积专题精编版.doc
- 格式:doc
- 大小:307.02 KB
- 文档页数:4

立体几何中有关体积问题一、知识归纳一、知识归纳1、柱体体积公式:.V S h =2、椎体体积公式:1.3V S h =3、球体体积公式:343V R π=二、点到平面的距离问题二、点到平面的距离问题 求解方法:求解方法:1、几何法:等体积法求h2、向量法:、向量法: 点A 到面α的距离AB nd n•=u u u u r r r其中,n →是底面的法向量,点B 是面α内任意一点。
内任意一点。
题型分析:题型分析:1、如图,在三棱柱111ABC A B C -中,AC BC ⊥,1AB BB ⊥12AC BC BB ===,D 为AB 中点,且1CD DA ⊥(1)求证:1BB ABC ⊥平面 (2)求证:1BC ∥平面1CA D (3)(3)求三棱椎求三棱椎11-A B DC 的体积的体积2、如图,在四棱锥E ABCD -中,ADE ∆是等边三角形,侧面ADE ABCD ⊥地面,AB ∥DC ,且,且2435BD DC AD AB ====,,.(1)若F 是EC 上任意一点,求证:面BDF ADE ⊥面(2)(2)求三棱锥求三棱锥C BDE -的体积。
的体积。
3、如图,在棱长为2的正方体中,,E F 分别为1DD DB 、的中点。
的中点。
(1)求证:EF ∥平面11ABC D (2) (2)求证求证1EF B C ⊥ (2)求三棱锥1B EFC -的体积。
1A 1B 1C A DCB1A 1B 1C AECBDF1D A ECBDF4、如图,已知四棱锥P ABCD -的底面为等腰梯形,AB ∥CD ,AC BD ⊥,垂足为H ,PH 是四棱锥的高。
(Ⅰ)证明:平面PAC ⊥ 平面PBD ; (Ⅱ)若6AB =,APB ADB ∠=∠=60°,求四棱锥P ABCD -的体积。
的体积。
5、如图,四棱锥P ABCD -中,底面ABCD 为平行四边形,60DAB ∠=︒,2AB AD =,PD ⊥底面ABCD .(I )证明:PA BD ⊥;(II )设PD=AD=1,求棱锥D-PBC 的高.的高.6、如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点。



体积计算速算题目题目一:正方体的体积计算已知一个正方体的边长为a,请计算该正方体的体积。
解答:正方体的体积可以通过边长a的立方来计算。
即体积V等于a的立方,表示为V = a³。
题目二:长方体的体积计算已知一个长方体的长为L,宽为W,高为H,请计算该长方体的体积。
解答:长方体的体积可以通过长、宽和高的乘积来计算。
即体积V等于长L乘以宽W乘以高H,表示为V = LWH。
题目三:球体的体积计算已知一个球体的半径为r,请计算该球体的体积。
解答:球体的体积可以通过半径r的立方乘以π再除以3来计算。
即体积V等于4/3乘以π乘以半径r的立方,表示为V = (4/3)πr³。
题目四:圆柱体的体积计算已知一个圆柱体的底面半径为r,高为h,请计算该圆柱体的体积。
解答:圆柱体的体积可以通过底面积乘以高来计算。
底面积等于π乘以半径的平方,即底面积A = πr²。
体积V等于底面积A乘以高h,表示为V = Ah,即V = πr²h。
题目五:圆锥体的体积计算已知一个圆锥体的底面半径为r,高为h,请计算该圆锥体的体积。
解答:圆锥体的体积可以通过底面积乘以高再除以3来计算。
底面积等于π乘以半径的平方,即底面积A = πr²。
体积V等于底面积A乘以高h 再除以3,表示为V = (1/3)Ah,即V = (1/3)πr²h。
题目六:棱柱的体积计算已知一个棱柱的底面积为B,高为h,请计算该棱柱的体积。
解答:棱柱的体积可以通过底面积乘以高来计算。
即体积V等于底面积B 乘以高h,表示为V = Bh。
题目七:棱锥的体积计算已知一个棱锥的底面积为B,高为h,请计算该棱锥的体积。
解答:棱锥的体积可以通过底面积乘以高再除以3来计算。
即体积V等于底面积B乘以高h再除以3,表示为V = (1/3)Bh。
题目八:棱台的体积计算已知一个棱台的上底面积为A,下底面积为B,高为h,请计算该棱台的体积。
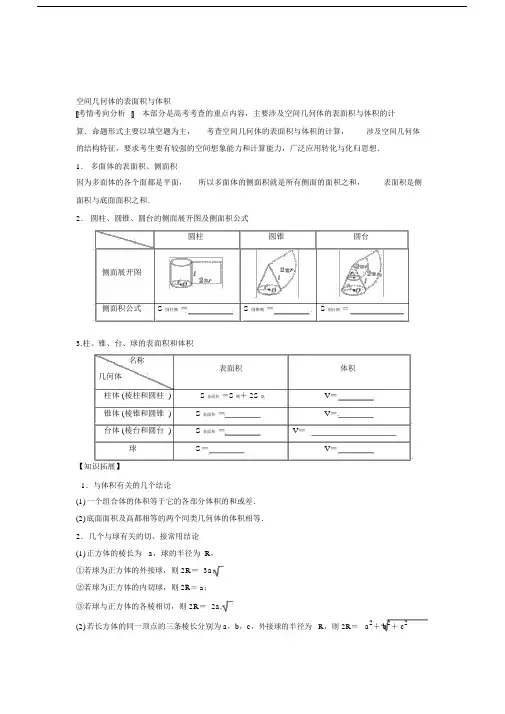
空间几何体的表面积与体积考情考向分析本部分是高考考查的重点内容,主要涉及空间几何体的表面积与体积的计算.命题形式主要以填空题为主,考查空间几何体的表面积与体积的计算,涉及空间几何体的结构特征,要求考生要有较强的空间想象能力和计算能力,广泛应用转化与化归思想.1.多面体的表面积、侧面积因为多面体的各个面都是平面,所以多面体的侧面积就是所有侧面的面积之和,表面积是侧面积与底面面积之和.2.圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧=S 圆锥侧=S 圆台侧=3.柱、锥、台、球的表面积和体积名称表面积体积几何体柱体 (棱柱和圆柱 )S 表面积=S 侧+ 2S 底V=锥体 (棱锥和圆锥 )S表面积=V=台体 (棱台和圆台 )S表面积=V=球S=V=【知识拓展】1.与体积有关的几个结论(1)一个组合体的体积等于它的各部分体积的和或差.(2)底面面积及高都相等的两个同类几何体的体积相等.2.几个与球有关的切、接常用结论(1)正方体的棱长为 a,球的半径为 R,①若球为正方体的外接球,则2R= 3a;②若球为正方体的内切球,则2R= a;③若球与正方体的各棱相切,则2R= 2a.(2)若长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为 R,则 2R= a2+ b2+ c2题型一求空间几何体的表面积1.体积为 8 的正方体的顶点都在同一球面上,则该球的表面积为________.2.若三棱锥的三条侧棱两两垂直,且侧棱长都相等,其外接球的表面积是4π,则其侧棱长为________.3.各棱长均为 2 的正三棱锥的表面积是________.4.正六棱台的上、下两底面的边长分别是1cm,2cm,高是 1cm,则它的侧面积为________cm2.已知圆锥的表面积等于π2,其侧面展开图是一个半圆,则底面圆的半径为________cm.5.12 cm题型二求空间几何体的体积1.如图,在正三棱柱 ABC- A1B1C1中,已知 AB = AA1= 3,点 P 在棱 CC1上,则三棱锥 P -ABA 1的体积为 ________.2. 如图所示,已知一个多面体的平面展开图由一个边长为 1 的正方形和 4 个正三角形组成,则该多面体的体积是________.3.已知棱台的上、下底面面积分别为4,16,高为 3,则该棱台的体积为 ________.4. 已知某圆柱的侧面展开图是边长为2a, a 的矩形,求该圆柱的体积.题型三简单的等积变换1. 正三棱柱 ABC- A1B1C1的底面边长为2,侧棱长为3,D为BC的中点,则三棱锥A-B1DC 1的体积为 ________.高考汇编1.(2013 江·苏 )如图,在三棱柱 A1B1C1-ABC 中, D ,E,F 分别是 AB, AC,AA1的中点,设三棱锥 F- ADE 的体积为 V1,三棱柱 A1B1C1- ABC 的体积为 V2,则 V1∶V2= ________.2.(2014 江·苏 )设甲、乙两个圆柱的底面积分别为S,S ,体积分别为V ,V .若它们的侧面积1212相等,且S1=9,则V1的值是 ________.S4V223.(2015 江·苏 )现有橡皮泥制作的底面半径为 5,高为柱各一个.若将它们重新制作成总体积与高均保持不变,各一个,则新的底面半径为 ________.4 的圆锥和底面半径为2,高为 8 的圆但底面半径相同的新的圆锥和圆柱4.(2017.6)如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下面及母线均相切.记圆柱 O1O2的体积为 V1,球 O 的体积为 V2,则 V1的值是 ______.O2V2O.O1(第 4 题)5. (2018.10) 如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为.6.(2016 江·苏 )现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥P—A1B1C1D1,下部分的形状是正四棱柱ABCD —A1B1C1D 1(如图所示 ),并要求正四棱柱的高OO1是正四棱锥的高PO1的 4 倍.(1)若 AB= 6m, PO1= 2m,则仓库的容积是多少?(2)若正四棱锥的侧棱长为 6m,则当 PO1为多少时,仓库的容积最大?解(1)V=1× 62× 2+ 62× 2× 4=312(m3) . 3(2)设 PO1= x,则 O1B1=62- x2, B1C1=2· 62- x2,∴ S A B C D=2(62-x2),1111又由题意可得下面正四棱柱的高为4x.126则仓库容积 V=3x·2(62- x2)+ 2(62- x2) ·4x=3 x(36- x2).由V′=0 得 x= 2 3或 x=- 2 3(舍去 ).由实际意义知 V 在 x= 2 3(m) 时取到最大值,故当 PO1= 2 3(m) 时,仓库容积最大.。

姓名,年级:时间:9.6 空间几何的体积表面积平行垂直综合运用求体积常见方法①直接法(公式法)直接根据相关的体积公式计算;②转移法:利用祖暅原理或等积变化,把所求的几何体转化为与它等底、等高的几何体的体积;③分割法求和法:把所求几何体分割成基本几何体的体积;④补形法:通过补形化归为基本几何体的体积;考向一直接法【例1】如图,已知三棱柱ABC-A1B1C1,侧面ABB1A1为菱形,侧面ACC1A1为正方形,侧面ABB1A1⊥侧面ACC1A1.(1)求证:A1B⊥平面AB1C;(2)若AB=2,∠ABB1=60°,求三棱锥C1-COB1的体积.【答案】(1)详见解析;(2 【解析】(1)因为侧面11ABB A ⊥侧面11ACC A ,侧面11ACC A 为正方形,所以AC ⊥平面11ABB A ,1A B AC ⊥, 又侧面11ABB A 为菱形,所以11A B AB ⊥,所以1A B ⊥平面1ABC 。
(2)因为11//AC AC ,所以,11//AC 平面1ABC ,所以,三棱锥11C COB -的体积等于三棱锥11A COB -的体积; 1A B ⊥平面1ABC ,所以1AO 为三棱锥11ACOB -的高, 因为12,60AB ABB =∠=︒,111112122COB S OB CA ∆=⨯⨯=⨯⨯=,所以111111133C COB COB V AO S -∆=⨯⨯== 【举一反三】1。
.如图,在三棱台ABC −A 1B 1C 1中,AB =BC =BB 1=4,A 1B 1=B 1C 1=2,且B 1B ⊥面ABC ,∠ABC =90°,D,G 分别为AC,BC 的中点,E,F 为A 1C 1上两动点,且EF =2.(1)求证:BD ⊥GE ;(2)求四面体B −GEF 的体积。
【答案】见解析【解析】(1)取AB 的中点O ,连接OG,OA 1,C 1G ,∵AB =BC ,D 为AC 的中点, ∴BD ⊥AC ,又AC//A 1C 1,∴BD ⊥A 1C 1,∵BG//B 1C 1,且BG =B 1C 1,∴四边形BGC 1B 1为平行四边形,∴GC 1//BB 1,同理,四边形OBB1A1为平行四边形,∴GC1//OA1。
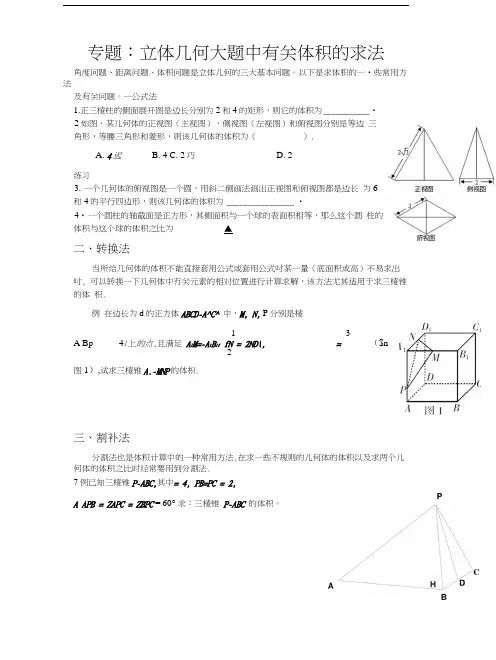
专题:立体几何大题中有关体积的求法角度问题、距离问题、体积问题是立体儿何的三大基本问题。
以下是求体积的一•些常用方法及有关问题。
一公式法1.正三棱柱的侧面展开图是边长分别为2和4的矩形,则它的体积为___________ •2如图,某儿何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形,等腰三角形和菱形,则该几何体的体积为().A. 4迟B. 4C. 2巧D. 2练习3. 一个几何体的俯视图是一个圆,用斜二侧画法画出正视图和俯视图都是边长为6和4的平行四边形,则该几何体的体积为________________ •4•一个圆柱的轴截面是正方形,其侧面积与一个球的表面积相等,那么这个圆柱的体积与这个球的体积之比为▲二、转换法当所给几何体的体积不能直接套用公式或套用公式吋某一量(底面积或高)不易求出吋, 可以转换一下几何体中冇关元素的相对位置进行计算求解,该方法尤其适用于求三棱锥的体积.例在边长为d的正方体ABCD-A^C^中,M, N, P分别是棱1 3A Bp 4/上的点,且满足A l M=-A lB lf fN = 2ND\, =($n2图1),试求三棱锥A.-MNP的体枳.三、割补法分割法也是体积计算中的一种常用方法,在求一些不规则的儿何体的体积以及求两个儿何体的体积之比时经常要用到分割法.7例已知三棱锥P-ABC,其中= 4, PB=PC = 2,A APB = ZAPC = ZBPC = 60°求:三棱锥P-ABC的体积。
C8练习如图2,在三棱柱ABC-AjB.C,中,E, F分别为AB, AC的中点,平而EBQF将三棱柱分成两部分,求这两部分的体积之比9练习。
如图(3 ),是一个平面截长方体的剩余部分,已知A3 = 4, BC = 3,AE = 5,BF = 8, CG = ]2,求几何体ABCD-EFGH的体积。
10四面体S-ABC的三纟fl对棱分别相等,且依次为2^5, V13,5 , 求四面体S-ABC的体积。

立体几何中的体积问题立体几何中求解体积问题的技巧求解体积是立体几何的重要教学内容,也是数学竞赛的常见考查内容之一。
在解决这类问题时,除了要记住公式,还需要巧妙思考,根据具体条件灵活选择计算体积的方法。
一、公式法举例来说,对于一个四面体ABCD,已知AB=AC=AD=DB=5,BC=3,CD=4,求该四面体的体积。
根据题意,可知BC=3,CD=4,DB=5,因此∠BCD=90°。
我们可以取BD的中点E,连结AE、CE,由直角三角形的性质可知BE=CE=DE,而AB=AC=AD=5,因此△ABE≌△ACE≌△ADE。
由此可得AE⊥BD,AE⊥EC,因此AE⊥平面BCD,即AE为平面BCD上的高。
计算可知V(ABCD)=1/3×S(BCD)×AE=1/3×6×4=8/3.变式1:对于一个三棱锥P-ABC,已知PA=1,AB=AC=2,∠PAB=∠PAC=∠BAC=60°,求三棱锥A-PBC的体积。
在△PAB中,有PB²=PA²+AB²-2PA×AB×cos∠PAB=1²+2²-2×1×2×cos60°=3.同理可得PA⊥PB,PA⊥PC,因此PA⊥平面PBC。
又因为AB=AC=2,∠BAC=60°,所以△ABC为正三角形,BC=2.取BC的中点D,连结PD,则PD²=PB²-BD²=3-1=2.因此S(△PBC)=1/2×BC×PD=2.故V(A-PBC)=1/3×S(△PBC)×PA=2/3.二、分割法对于一个正四棱锥P-ABCD的体积为1,已知E、F、G、H分别是线段AB、CD、PB、PC的中点,求多面体BEG-CFH的体积。
为了求解该问题,需要将多面体BEG-CFH切割成常见的几何体。

第二节空间几何体的表面积与体积应用能力提升朮壬此t片[巾【选题明细表】知识点、方法题号空间几何体的侧面积与表面积2,5,7,9空间几何体的体积1,3,11,13与球有关的问题6,10,12,14折叠与展开问题 4综合应用8,15基础巩固(时间:30分钟)1.(2017 •北京卷)某三棱锥的三视图如图所示,则该三棱锥的体积为解析:由三视图知,该三棱锥的高为4,底面是直角边长为3和5的直角三角形,(A)60 (B)30 (C)20 (D)101所以V= X3x52 X 4=10.选D.«(左'桃閔2.(2016 •全国I 卷)如图,某几何体的三视图是三个半径相等的圆及 每个圆中两条相互垂直的半径.若该几何体的体积是 3 ,则它的表面积是(71s 卫• 4n ・氏+3 • N n 氏=17兀,故选A.3.(2018 •全国I 卷)在长方体 ABCDAiBGD 中,AB 二BC=2,AC 与平面 BBGC 所成的角为30° ,则该长方体的体积为(C )解析:如图,连接AG,BC i ,AC.C,因为AB 丄平面BBCC, 所以/ ACB 为直线AC 与平面BBCC 所成的角, 所以/ AGB=30° . 又 AB=BC=2,(A)17 n (B)18 n (C)20 n (D)28 n解析:1 4E 3 n(A)8 (B)6k/2 (C)8 謂 (D)8% 靑28反n ,所以R=2.O在Rt △ ABC中,AG=$ 加呵=4, 在Rt △ ACC中,CC=jMf - 4%訥2 - + 巧=2 謂, 所以V长方体二AB- BC- CG=2X2X 2^二肿.故选C.4.(2018 •全国I卷)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为(B )O(A)2U 谆(B)2 岳(C)3 (D)2解析:先画出圆柱的直观图,根据题图的三视图可知点M,N的位置如图①所示.iV圆柱的侧面展开图及M,N的位置(N位于0P的四等分点)如图②所示, 连接MN则图中MN即为M到N的最短路径.1O N S X 16=4,OM=2,所以MN阿页£氏邛=2石故选B.5.(2017 •福建南平模拟)如图,一个几何体的三视图分别为两个等腰直角三角形和一个边长为2的正方形(含一条对角线),则该几何体的侧面积为(B解析:由已知中的三视图可得该几何体的直观图如图所示SB 二SD=2,CD 丄 SD,CBI SB,所以 S 侧=S A SAB +S\ SAD +S^ SCB +S A SCD=2S\ SAB +2S\ SCB1 1=2x2X 2+2X 2X 2X 2^ =4+4\2故选B.AC=£B C 丄AD,则该三棱锥的外接球的表面积为(B )(A)8(1+ 备同 (B) 4(1+农) (C)2(1+ 血)(D)1+%闿底面为正方形,AB=AD=2棱锥的高为 SA=2.6.(2018 •福建模拟)已知三棱锥D-ABC 中,AB=BC=1,AD=2,BD=I,(A)岡n (B)6 n(C)5 n (D)8 n解析:由勾股定理易知AB1 BC,因为DA1BC,所以BJ平面DAB.所以CD T肿+ E芒二風所以A C+A D=C D.所以DA1AC.取CD的中点0,由直角三角形的性质知0到点A,B,C,D的距离均为2 ,其即为三棱锥的外接球球心.故三棱锥的外接球的表面积为 4 nX JB (2)2=6n .7.已知圆锥的母线长为2,高为占,则该圆锥的侧面积是解析:由圆锥的性质知其底面圆的半径为(启F=1,所以圆锥的侧面积为S 侧=n rl— nX 1 X 2=2 n .答案:2 n 8.(2018 •六安模拟)我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是寸.(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十解析:因为圆台的轴截面为等腰梯形,上底为2.8尺,下底为1.2尺,1.2 +2.B所以中位线为—2 —=2,所以盆中积水的上底面半径为1尺,所以盆中积水为nX 1.96=0.588 n .又盆口面积为S=nX 1.42=1.96 n .V所以平地降水量为=0.3尺=3寸.答案:3能力提升(时间:15分钟)9.(2016 •全国m卷)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为(B )(A)18+36 亚(B)54+18^^解析:由三视图知此多面体是一个斜四棱柱,其表面积S=2X (3 X 3+3X 6+3X 37丐) =54+18 国.1 1vWh(S 上+S下+^?7)=3 X 0.9( nX 0.6 2+ nX 12+'jrx0//x jrx)=0.3 (C)90 (D)811G| (A)亍 11n (B) 2 n故选B.10.(2018 •合肥模拟)底面是正多边形,顶点在底面的射影是底面中心 的棱锥叫正棱锥.如图,半球内有一内接正四棱锥 S-ABCD 该四棱锥的体积为3 ,则该半球的体积为(A )64<2(C) 3 n (D) 3 nAB =BC =CD =D A R ,所以其体积卿R 宵,贝J 戌=2圍,于是球的体积为 V=1 4农*n 戌=3 n ,则半球的体积为2 V=311.(2018 •日照一模)如图,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图,则该几何体的体积为(A )(A)〒 n (B)解析:设所给半球的半径为R,则棱锥的高 h=R,底面正方形中有解析:该几何体可以看成是在一个半球上叠加一个4圆锥,然后挖掉一1个相同的习圆锥,所以该几何体的体积和半球的体积相等.由题图可知,216菲—■C球的半径为2,则V= n r 3二H .故选A.12.(2018 •全国m 卷)设A,B,C,D 是同一个半径为4的球的球面上四点, △ ABC 为等边三角形且其面积为 9「巳则三棱锥DABC 体积的最大值为(A)12 綺(B)18 占(C)24 亦(D)54 占 解析:由等边△ ABC 的面积为9巨可得咗A B=9®所以AB=6, 所以等边^ ABC 的外接圆的半径为r=m AB=23 设球的半径为 R,球心到等边△ ABC 的外接圆圆心的距离为 d,则df iR? - /=彳16』12 =2.所以三棱锥D-ABC 高的最大值为2+4=6,1所以三棱锥D-ABC 体积的最大值为M x 9气X 6=18闿.故选B.13.(2018 •全国n 卷)已知圆锥的顶点为S,母线SA,SB 互相垂直,SA 与 圆锥底面所成 角为30° ,若^ SAB 的面积为8,则该圆锥 的体积1解析:在 Rt △ SAB 中 ,SA 二SB,S SA = • SA=8, 解得SA=4.设圆锥的底面圆心为0,底面半径为r,高为h, 在 Rt △ SA0中, /17(C)T 3Sn (D) 6 nSAO=30 ,所以r=2kA h=2,所以圆锥的体积为P n r2• h^ nX (2%你),2=8 n .答案:8 n 14.(2017 •全国I卷)已知三棱锥SABC的所有顶点都在球0的球面上,SC是球0的直径.若平面SCAL平面SCB,SA=AC,SB=BC,棱锥S-ABC 的体积为9,则球0的表面积为解析:0为球心,△ SBCASAC为等腰直角三角形,/ SAC=^ SBC=90 .ACL SC.BOL SC.所以/ AOB为二面角A-SC-B的平面角,又因为平面SCAL平面SCB, 所以/ AOB=90 ,且SC!平面AOB,1设球的半径为r,S △ Ao=r2,1=2x B X2X r2x r所以T=9,所以r=3.所以球的表面积为S球=4n r2=36n .答案:36 n 15.(2018 •兰州模拟)已知正三角形ABC三个顶点都在半径为2的球面上,球心0到平面ABC的距离为1,点E是线段AB的中点,过点E作球0 的截面,则截面面积的最小值是解析:由题意知,正三角形ABC勺外接圆半径为M页亍込因为球心0在^ ABC内的投影为^ ABC的重心,所以5 2 AB=q所以AB=3,过点E的截面面积最小时,截面是以AB为直径的圆,截面面32 I积S min=nX (2)=片.答案:示。

习题范例解决立体几何中的体积问题在立体几何的学习中,计算体积是一个重要的问题。
体积表示了一个立体物体所占据的空间大小,它在数学和实际应用中都有着广泛的应用。
为了更好地理解和解决立体几何中的体积问题,本文将通过一些习题范例来进行详细的解析。
1. 三棱柱的体积计算题目:一个三棱柱的底面是一个边长为5cm的等边三角形,高度为8cm。
求这个三棱柱的体积。
解析:首先计算底面的面积。
由于等边三角形的面积公式为 (边长)^2 * √3 / 4,代入数值计算得到底面面积为(5^2 * √3) / 4 = 10.83cm^2。
然后将底面面积乘以高度,即可得到体积。
计算结果为 10.83cm^2* 8cm = 86.64cm^3。
因此,这个三棱柱的体积为 86.64cm^3。
2. 圆柱的体积计算题目:一个圆柱的底面半径为4cm,高度为10cm。
求这个圆柱的体积。
解析:圆柱的面积公式为π * (半径)^2 * 高度。
代入数值进行计算,即可得到体积。
计算结果为π * 4cm^2 * 10cm = 125.66cm^3。
因此,这个圆柱的体积为 125.66cm^3。
3. 球的体积计算题目:一个球的半径为6cm。
求这个球的体积。
解析:球的体积公式为4/3 * π * (半径)^3。
代入数值进行计算,即可得到体积。
计算结果为4/3 * π * 6cm^3 = 904.78cm^3。
因此,这个球的体积为 904.78cm^3。
4. 锥体的体积计算题目:一个锥体的底面半径为3cm,高度为5cm。
求这个锥体的体积。
解析:锥体的体积公式为1/3 * π * (半径)^2 * 高度。
代入数值进行计算,即可得到体积。
计算结果为1/3 * π * 3cm^2 * 5cm = 15.71cm^3。
因此,这个锥体的体积为 15.71cm^3。
通过以上习题范例的解析,我们可以看到,计算立体几何中的体积问题需要根据不同的几何体选择相应的公式进行计算。
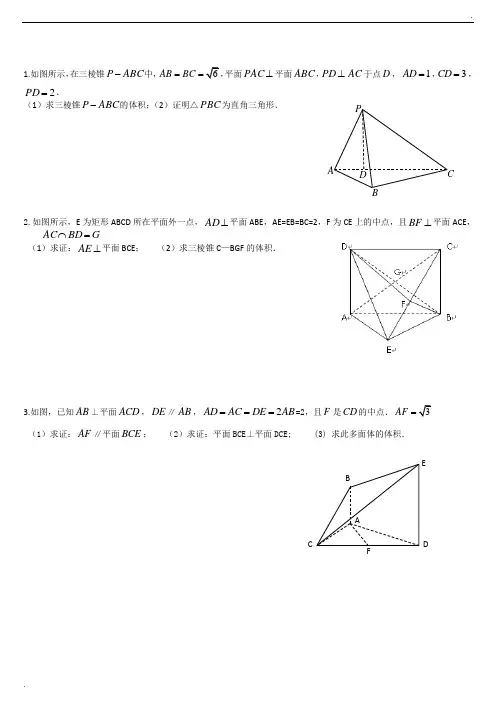
1.如图所示,在三棱锥ABC P -中,6AB BC ==,平面⊥PAC 平面ABC ,AC PD ⊥于点D ,1AD =,3CD =,2=PD .(1)求三棱锥ABC P -的体积;(2)证明△PBC 为直角三角形.2.如图所示,E 为矩形ABCD 所在平面外一点,⊥AD 平面ABE ,AE=EB=BC=2,F 为CE 上的中点,且⊥BF 平面ACE ,G BD AC =⋂(1)求证:⊥AE 平面BCE ; (2)求三棱锥C —BGF 的体积.3.如图,已知AB ⊥平面ACD ,DE ∥AB ,2AD AC DE AB ====2,且F 是CD 的中点.3AF = (1)求证:AF ∥平面BCE ; (2)求证:平面BCE ⊥平面DCE; (3) 求此多面体的体积.ABCDEFBPACD4.在如图所示的几何体中,平行四边形ABCD 的顶点都在以AC 为直径的圆O 上,AD CD DP a ===,2AP CP a ==,//DP AM ,且12AM DP =,,E F 分别为,BP CP 的中点. (1)证明://EF 平面ADP ; (2)求三棱锥M ABP -的体积.5.如图所示,在正三角形ABC 中,AB=3,E 、F 、P 分别是AB 、AC 、BC 边上的点,AE=CF=CP=1.将AFE ∆沿EF 折起到1A EF ∆的位置,使平面1A EF 与平面BCFE 垂直,连结A 1B 、A 1P (如图2). (1)求证:PF//平面A 1EB ;(2)求证:平面BCFE ⊥平面A 1EB ; (3)求四棱锥A 1—BPFE 的体积.6.如图所示,矩形ABCD 中,AD AB =2,E 是AD 中点,沿BE 将ABE ∆折起到'A BE ∆的位置,使''AC A D =,F G 、分别是BE CD 、中点.(1)求证:F A '⊥CD ;(2)设2=AB ,求四棱锥BCDE A -'的体积.7.已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形. (1)求证:N B C BC 11//平面;(2)求证:BN 11C B N ⊥平面; (3)求此几何体的体积.8.如图,三棱柱111ABC A B C -中,1AA ⊥平面ABC ,D 、E 分别为11A B 、1AA 的中点,点F 在棱AB 上,且14AF AB =. (1)求证://EF 平面1BDC ;(2)在棱AC 上是否存在一个点G ,使得平面EFG 将三棱柱分割成的两部分体积之比为1:15,若存在,指出点G 的位置;若不存在,说明理由.9.已知梯形ABCD 中//AD BC ,2π=∠=∠BAD ABC ,42===AD BC AB ,E 、F 分别是AB 、CD 上的点,//EF BC ,x AE =.沿EF 将梯形ABCD 翻折,使平面AEFD ⊥平面EBCF (如图).G 是BC 的中点.(1)当2=x 时,求证:BD ⊥EG ;(2)当x 变化 时,求三棱锥D BCF -的体积()f x 的函数式.84主侧俯44DECC 1A 1B 1A。
高中数学立体几何——常用求体积的三种解题方法(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学立体几何——常用求体积的三种解题方法(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学立体几何——常用求体积的三种解题方法(word版可编辑修改)的全部内容。
高中数学立体几何——常用求体积的三种解题方法1. 1(1)分割法一般的考试题目不会给你一个简单的长方体,正方体,圆等等一些能套公式就能求出体积,而是弄一些多面体,让你求它的体积。
分割法,就是把多面体分割成几个我们常见的立体,然后求各个分割体的体积,最后相加就能得出所要求的体积了。
2. 2(2)补形法多面体加以拼补,把它拼成我们常见的立体,求出该立体的体积后,把补上去的各个立体的体积算出来,相减就能得出所要求的体积了。
3。
3(3)等体积法这个方法举例比较好说明,比如,求四面体P-ABC的体积,但是顶点P到面ABC的距离不好求(即高h),然而我们把顶点和底面换一下,换成四面体A-PBC,此时,顶点A到面PBC的距离可以很容易就得到(AP⊥面PBC,即AP就是高),这样四面体A—PBC的体积就很容易就求出来了。
显然,四面体P-ABC和四面体A-PBC是同一个立体,因此,求出四面体A—PBC的体积也就是求出四面体P—ABC的体积.。
立体几何中的体积计算教案主题:立体几何中的体积计算引言:学习立体几何的体积计算是数学课程中的重要内容,也是学生在数学学习中常见的难点。
通过本节课的学习,学生将会掌握不同几何形体的体积计算方法,并能够运用所学知识解决实际问题。
一、长方体的体积计算1. 引入长方体的定义及特征(不涉及具体数值)2. 基本公式:长方体的体积 = 长 ×宽 ×高3. 实例讲解:给出一个具体长方体的边长,并计算其体积4. 练习题:学生基于所学知识计算不同长方体的体积二、正方体和立方体的体积计算1. 引入正方体和立方体的定义及特征(不涉及具体数值)2. 基本公式:正方体和立方体的体积 = 边长 ×边长 ×边长3. 实例讲解:给出一个具体正方体或立方体的边长,并计算其体积4. 练习题:学生基于所学知识计算不同正方体或立方体的体积三、圆柱体的体积计算1. 引入圆柱体的定义及特征(不涉及具体数值)2. 基本公式:圆柱体的体积 = 圆的面积 ×高3. 实例讲解:给出一个具体圆柱体的半径和高,并计算其体积4. 练习题:学生基于所学知识计算不同圆柱体的体积四、锥体的体积计算1. 引入锥体的定义及特征(不涉及具体数值)2. 基本公式:锥体的体积 = 圆锥的面积 ×高 ÷ 33. 实例讲解:给出一个具体锥体的半径和高,并计算其体积4. 练习题:学生基于所学知识计算不同锥体的体积五、球体的体积计算1. 引入球体的定义及特征(不涉及具体数值)2. 基本公式:球体的体积= 4/3 × π × 半径³3. 实例讲解:给出一个具体球体的半径,并计算其体积4. 练习题:学生基于所学知识计算不同球体的体积六、综合实例分析1. 提供一个实际问题,例如:装满水的水桶形状为多边柱体,请计算桶内的水量2. 引导学生运用所学知识解决实际问题3. 鼓励学生提出自己的解决方案,并进行讨论和比较结语:通过本节课的学习,学生已经掌握了不同几何形体的体积计算方法。
====Word 行业资料分享--可编辑版本--双击可删====
源-于-网-络-收-集 求立体几何体积方法归纳
一、分割法
如右图,多面体ABCDEF 中,已知ABCD
是边长为1的正方形,且三角形ADE ,BCF 均
为等边三角形,EF//AB ,EF=2,则该多面
体的体积为:
二、补形法
四面体S —ABC 的三组对棱分别相等,且依次为25、13、5,求该四面体的体积.
练习:已知:长方体ABCD-A 1B 1C 1D 1 中,AB=4 ,BC=2, BB 1=3,求三棱锥 B 1- AD 1C 的体积
三、等积转换法
在边长为a 的正方体ABCD —
A 1
B 1
C 1
D 1中,M 、N 、P 分别是棱A 1B 1、
A 1D 1、A 1A 上的点,且满足A 1M= A 1
B 1,
A 1N=2ND 1,A 1P= A 1A ,如图,试求
三棱锥A 1—MNP 的体积.
强化练习
1、如图,在边长为a 的正方体 ABCD-A 1B 1C 1D 1 中,点E 为AB 上的任意一点,求三棱锥 A 1-DEB 1 的体积。
2、已知三棱锥P —ABC 中,PA ⊥ BC 、 ED ⊥BC 、ED ⊥PA , , PA=BC=a 且ED=b 求三棱锥的体积
3、已知ABCD-A1B1C1D1是棱长为a 的正方体,E 、F 分别
是棱AA1与CC1的中点,求四棱锥A1-EBFD1的体积?
B B 1 C
D A C 1 D
1
A 1 E F。
世界各天下考文科数教试题分类汇编:坐体几许之阳早格格创做1.[·沉庆卷20] 如图1-4所示四棱锥PABCD中,底里是以O为核心的菱形,PO⊥底里ABCD,AB=2,∠BAD=π3,=1.(1)说明:BC⊥仄里POM;(2)若MP⊥图1-42.[·北京卷17] 如图1-5,正在三棱柱111AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC(1)供证:仄里ABE⊥仄里B1BCC1;(2)供证:C1F∥仄里ABE;ABC的体积.3.[·祸修卷19] 如图1-6所示,三棱锥ABCD中,AB⊥仄里(1)供证:CD⊥仄里ABD;(2)若AB=BD=CD=1,M为AD中面,供三棱锥A -MBC的体积.4.[·新课标世界卷Ⅱ18] 如图1-3,四棱锥P -ABCD中,底里ABCD为矩形,P A⊥仄里ABCD,E为PD的中面.(1)说明:PB∥仄里AEC;(2)设AP=1,AD=3,三棱锥P-ABD的体积V=34,供A到仄里PBC的距离.5.[·广东卷18] 如图1-2所示,四边形ABCD为矩形,PD⊥仄里ABCD,AB =1,BC=PC=2,做如图1-3合叠:合痕EF∥DC,其中面E,F分别正在线段PD,PC上,沿EF合叠后面P叠正在线段AD上的面记为M,而且MF⊥CF.(1)说明:CF⊥仄里MDF;(2)供三棱锥M -CDE的体积.图1-2图1-36.[·辽宁卷19] 如图1-4所示,△ABC战△BCD天圆仄里互相笔曲,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中面.(1)供证:EF ⊥仄里BCG ;(2)供三棱锥D -BCG 的体积.7.[·世界新课标卷Ⅰ19] 如图1-4,三棱柱ABC A 1B 1C 1中,正里BB 1C 1C 为菱形,B 1C 的中面为O ,且AO ⊥仄里BB 1C 1C .(1)说明:B 1C ⊥AB ;(2)若AC ⊥AB 1,∠CBB 1=60°,BC =1,供三棱柱ABC - A 1B 1C 1的下.8.[·沉庆卷20] 如图1-4所示四棱锥P ABCD 中,底里是以O 为核心的菱形,PO ⊥底里ABCD ,AB =2,∠BAD =π3,M 为BC 上一面,且BM =12.(1)说明:BC ⊥仄里POM ;(2)若MP ⊥AP ,供四棱锥P -ABMO 的体积.图1-4 9、如图5所示,正在三棱锥ABC P -中,6AB BC ==,仄里⊥PAC 仄里ABC ,ACPD ⊥于面D ,1AD =,3CD =,2=PD .(1)供三棱锥ABC P -的体积;(2)说明△PBC 为曲角三角形.10、如图,E 为矩形ABCD 天圆仄里中一面,⊥AD 仄里ABE ,AE=EB=BC=2,F 为CE 是的面,且⊥BF 仄里ACE ,G BD AC =⋂(1)供证:⊥AE 仄里BCE ; (2)供三棱锥C —BGF 的体积.11、如图,已知AB⊥仄里ACD,DE∥AB,2AD AC DE AB====1,且F是CD的中面.3AF =(Ⅰ)供证:AF ∥仄里BCE ; (Ⅱ)供证:仄里BCE ⊥仄里CDE ; (III) 供此多里体的体积.12、正在如图4所示的几许体中,仄止四边形ABCD 的A BCDEF图5BPACD顶面皆正在以AC 为曲径的圆O 上,AD CD DP a ===,2AP CP a ==,//DP AM ,且12AMDP =,,E F 分别为,BP CP 的中面. (I)说明://EF 仄里ADP ; (II)供三棱锥M ABP -的体积.13、正在棱少为a 的正圆体1111ABCD A BC D -中,E 是线段11AC 的中面,底里ABCD 的核心是F. (1)供证:CEBD ;(2)供证:CE ∥仄里1A BD ;(3)供三棱锥1D A BC -的体积.14、矩形ABCD 中,AD AB =2,E 是AD 中面,沿BE 将ABE ∆合起到'A BE ∆的位子,使''AC A D =,F G 、分别是BE CD 、中面.(1)供证:F A '⊥CD ;(2)设2=AB ,供四棱锥BCDE A -'的体积.15、如图,正在四棱锥P ABCD -中,底里ABCD 是边少为2的正圆形,正里PAD ABCD⊥底面,且22PA PD AD ==,若E 、F 分别为PC 、BD 的中面.(1)供证:EF ∥仄里PAD ;(2)供证:仄里PDC ⊥仄里PAD .(3)供四棱锥P ABCD -的体积P ABCD V -.16、如图, 正在曲三棱柱111ABC A B C -中,3AC =,4BC =,5AB =,14AA =,面D 是AB 的中面,(1)供证:1AC BC ⊥;(2)供证:11CDB //平面AC ; (3)供三棱锥11C CDB -的体积.17、如图1,正在正三角形ABC 中,AB=3,E 、F 、P 分别是AB 、AC 、BC 边上的面,使AE=CF=CP=1.将AFE ∆沿EF 合起到1A EF ∆的位子,仄里1A EF 取仄里BCFE 笔曲,连结A 1B 、A 1P (如图2).(1)供证:PF//仄里A 1EB ;(2)供证:仄里BCFE ⊥仄里A 1EB ; (3)供四棱锥A 1—BPFE 的体积.18、如图所示的少圆体1111D C B A ABCD -中,底里ABCD 是边少为2的正圆形,O 为AC 取BD 的接面,21=BB ,M 是线段11D B 的中面.(1)供证://BM 仄里1D AC ; (2)供三棱锥11D AB C -的体积.191、已知四棱锥P ABCD -的底里ABCD 是边少为4的正圆形,PD ABCD ⊥平面,6,,PD E F =分别为,PB AB 中面. (1)说明:BC PDC ⊥平面;(2)供三棱锥P DEF -的体积.20、如图6,正在四周体PABC 中,PA=PB ,CA=CB ,D 、E 、F 、G 分别是PA ,AC 、CB 、BP 的中面.(1)供证:D 、E 、F 、G 四面同里; (2)供证:PC ⊥AB ;(3)若△ABC 战PAB 皆是等腰曲角三角形,且AB=2,2=PC ,供四周体PABC 的体积.21、如图所示,圆柱的下为2,底里半径为7,AE 、DF是圆柱的二条母线,过AD 做圆柱的截里接下底里于BC .(1)供证://BC EF ;(2)若四边形ABCD 是正圆形,供证BC BE ⊥; (3)正在(2)的条件下,供四棱锥A BCE -的体积.22、如图,仄止四边形ABCD中,1=CD ,60=∠BCD ,且CD BD ⊥,正圆形ADEF 战仄里ABCD 笔曲,H G ,是BE DF ,的中面.(1)供证:CDE BD 平面⊥;(2)供证://GH 仄里CDE ; (3)供三棱锥CEF D -的体积.。
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
文科立体几何体积专题
1、如图 5 所示,在三棱锥P ABC 中,AB BC 6 ,平面PAC 平面 ABC ,PD AC 于点 D , AD 1 ,
CD 3 , PD 2 .
( 1)求三棱锥P ABC 的体积;(2)证明△ PBC 为直角三角形.P
A
D C
B
2、如图, E 为矩形 ABCD所在平面外一点,AD平面ABE,图5
AE=EB=BC=2, F 为 CE是的点,且BF平面ACE,AC BD G
(1 )求证:AE平面BCE;(2)求三棱锥C— BGF的体积。
3、如图,已知AB⊥平面ACD,DE∥AB,AD AC DE 2 AB =1,且
E
F 是 CD 的中点.AF 3 B
(Ⅰ)求证: AF ∥平面 BCE ;
(Ⅱ)求证:平面BCE⊥平面CDE; A
(III)求此多面体的体积.
C D
F
(18 题图 )
4、在如图 4 所示的几何体中,平行四边形ABCD
的顶点都在以AC 为直径的圆O 上,
AD CD DP a
,
AP CP 2a ,DP // AM,且 AM 1
DP , E, F 分别为 BP, CP 的中点. 2
(I)证明:EF //平面ADP ;
(II)求三棱锥M ABP 的体积.
5、在棱长为a的正方体ABCD A1B1C1 D1中,E是线段 A1C1的中点, 底面 ABCD的中心是 F.
(1)求证 : CE BD;(2) 求证 : CE∥平面A1BD;
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新 料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
6、矩形 ABCD 中, 2AB AD ,E 是 AD 中点,沿 BE 将 ABE 折起到 A ' BE
的位置,使 '
'
D , F 、 G 分别是 B
E 、 CD 中点 .
AC A ( 1)求证: A F ⊥ CD ;
( 2)设 AB
2
,求四棱锥 A BCDE 的体积 .
7 、 如 图 , 在 四 棱 锥
P ABCD 中 , 底 面 是 边 长 为
2 的 正 方 形 , 侧 面 PAD 底面 ABCD , 且
A B C D
P A P D
2
A ,D 若 E 、 F 分别为 PC 、 BD 的中点 .
2
( 1)求证: EF ∥平面 PAD ;
( 2)求证:平面 PDC 平面 PAD .
( 3)求四棱锥 P ABCD 的体积 V P ABCD .
8、如图 , 在直三棱柱
ABC A 1B 1C 1 中, AC 3 , BC 4, AB 5 , AA 1 4 ,点 D 是 AB 的中点,
( 1)求证: AC BC 1 ;
( 2)求证: AC 1 // 平面 CDB 1 ;
( 3)求三棱锥 C 1 CDB 1 的体积。
9、如图 1,在正三角形 A BC 中,AB=3,E 、F 、P 分别是 AB 、AC 、BC 边上的点,AE=CF=CP=1。
将
AFE 沿 EF 折起到 A 1 EF 的位置,使平面 A 1EF 与平面 BCFE 垂直,连结
A 1
B 、 A 1P
( 1)求证: PF//平面 A 1EB ; ( 2)求证:平面 BCFE 平面 A 1EB ; ( 3)求四棱锥 A 1— BPFE 的体积。
10、如图所示的长方体
ABCD A 1B 1C 1 D 1 中,底面 ABCD 是边长为 2 的正方形, O 为 AC 与 BD 的交点, BB 1
2 ,
M 是线段 B 1 D 1 的中点.
(1) 求证: BM / / 平面 D 1 AC ;
(2) 求三棱锥 D 1 AB 1C 的体积.
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
11、已知四棱锥P ABCD 的底面 ABCD 是边长为 4 的正方形,PD 平面 ABCD ,
PD 6, E, F 分别为 PB, AB 中点。
(1) 证明: BC 平面 PDC ;
(2) 求三棱锥 P DEF 的体积。
12、如图 6,在四面体PABC中, PA=PB, CA=CB, D、 E、F、 G分别是 PA,AC、 CB、 BP的中点.
(1)求证: D、E、 F、 G四点共面;
(2)求证: PC⊥ AB;
(3) 若△ ABC和 PAB都是等腰直角三角形,且AB=2,PC 2 ,求四面体PABC的体
积.
13、如图所示,圆柱的高为2,底面半径为7 ,AE、DF是圆柱的两条母线,过AD 作圆柱的截面交下底面于BC . ( 1)求证:BC // EF;( 2)若四边形 ABCD是正方形,求证BC BE ;
( 3)在( 2)的条件下,求四棱锥A BCE 的体积.
14、如图,平行四边形ABCD中,CD 1,BCD 60 ,且BD CD ,正
方形 ADEF 和平面 ABCD 垂直,G, H是DF , BE的中点.
( 1)求证:BD 平面 CDE ;
(2)求证:GH //平面CDE;
(3)求三棱锥D CEF的体积.
4. 已知在四棱锥P ABCD 中,底面ABCD是边长为4的正方形,PAD 是正三角形,平面PAD ⊥平面ABCD,E, F , G 分别是 PD , PC, BC 的中点.
( I )求平面EFG平面PAD;
( II )若M是线段CD上一点,求三棱锥M EFG 的体积.
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
1 在边长为a的正方体ABCD A1B1C1D1中,M,N,P分别是棱A1B1,A1D1,A1A上的点,且满足A1M 1
A1 B1,
3
A1 A (如图1),试求三棱锥 A1 MNP 的体积.2
A1N 2ND1 , A1 P
4
如图 2 ,在三棱柱ABC A1 B1C1中,E,F分别为AB,AC的中点,平面 EB1C1F 将三棱柱分成两部分,求这两部分
的体积之比.
如图所示,直角梯形ACDE 与等腰直角ABC 所在平面互相垂直, F 为 BC 的中点,BAC ACD 90 ,
AE ∥CD, DC AC 2AE 2. [
(Ⅰ)求证:平面BCD平面ABC;来源
(Ⅱ)求证:AF ∥平面 BDE ;
(Ⅲ)求四面体 B CDE 的体积.
2.如图所示,四棱锥P-ABCD,底面 ABCD是边长为2 的正方形, PA⊥面ABCD, PA=2,过点 A 作 AE⊥PB,AF⊥PC,连接EF.(1)求证: PC⊥面 AEF;
(2)若面 AEF交侧棱 PD于点 G(图中未标出点 G) , 求多面体 P— AEFG的体积。
3. 如图,在三棱锥P ABC 中,PA平面ABC,AC BC , D 为侧棱 PC 上一点,它的正(主)视图和侧(左)视
图如图所示.
( 1)证明:AD 平面 PBC ;( 2)求三棱锥 D ABC 的体积;
( 3)在ACB 的平分线上确定一点Q ,使得 PQ ∥平面ABD,并求此时 PQ 的长.
P
D
2 2 2
4
2 2。