下载文档原格式
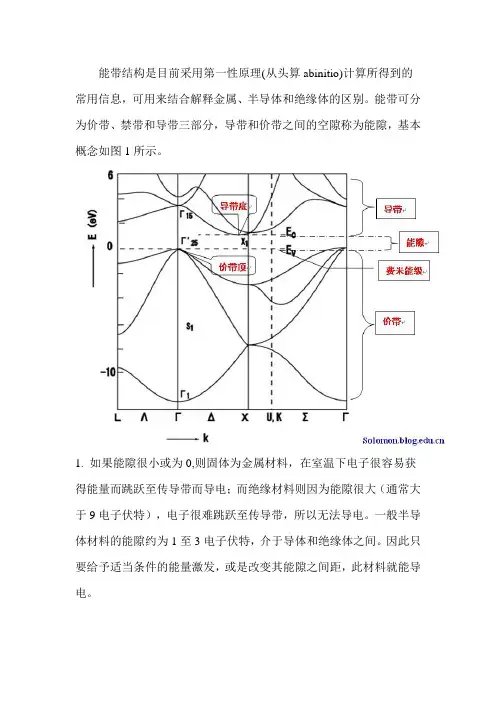
能带结构是目前采用第一性原理(从头算abinitio)计算所得到的常用信息，可用来结合解释金属、半导体和绝缘体的区别。
能带可分为价带、禁带和导带三部分，导带和价带之间的空隙称为能隙，基本概念如图1所示。
1. 如果能隙很小或为0,则固体为金属材料，在室温下电子很容易获得能量而跳跃至传导带而导电；而绝缘材料则因为能隙很大（通常大于9电子伏特），电子很难跳跃至传导带，所以无法导电。
一般半导体材料的能隙约为1至3电子伏特，介于导体和绝缘体之间。
因此只要给予适当条件的能量激发，或是改变其能隙之间距，此材料就能导电。
2. 能带用来定性地阐明了晶体中电子运动的普遍特点。
价带（valence band），或称价电带，通常指绝对零度时，固体材料里电子的最高能量。
在导带（conduction band）中，电子的能量的范围高于价带（v alence band），而所有在传导带中的电子均可经由外在的电场加速而形成电流。
对于半导体以及绝缘体而言，价带的上方有一个能隙（b andgap），能隙上方的能带则是传导带，电子进入传导带后才能再固体材料内自由移动，形成电流。
对金属而言，则没有能隙介于价带与传导带之间，因此价带是特指半导体与绝缘体的状况。
3. 费米能级(Fermi level)是绝对零度下电子的最高能级。
根据泡利不相容原理，一个量子态不能容纳两个或两个以上的费米子(电子)，所以在绝对零度下，电子将从低到高依次填充各能级，除最高能级外均被填满，形成电子能态的“费米海”。
“费米海”中每个电子的平均能量为（绝对零度下）为费米能级的3/5。
海平面即是费米能级。
一般来说，费米能级对应态密度为0的地方，但对于绝缘体而言，费米能级就位于价带顶。
成为优良电子导体的先决条件是费米能级与一个或更多的能带相交。
4. 能量色散（dispersion of energy）。
同一个能带内之所以会有不同能量的量子态，原因是能带的电子具有不同波向量（wave vector），或是k-向量。
费米面上的能态密度物理学家费米（EnricoFermi）的名字被用在关于粒子物理的许多领域中。
最著名的是他在原子核理论上的发现，他发现原子核中存在被称为“费米”的粒子，这些粒子在粒子物理学中起到了重要的作用。
费米还发现了另一个重要的概念，即费米面上的能态密度（Fermi surface density of states）。
这个概念对于帮助我们理解半导体、超导体和金属表面的性质非常有用。
费米面上的能态密度是指在金属表面上，费米粒子被收缩到空间量子中，形成的能态的密度，它代表了金属表面的电子的能态的密度。
费米面上的能态密度包括了金属表面电子的表示、电子结构、电子-核结构间的相互作用、电子激发状态和结构变化等，这些都能左右金属表面电子的性质。
费米面上的能态密度与金属表面电子的性质有关，它可以用来测量金属表面电子的能态密度，以及金属表面电子在外力作用下的性质变化。
当电子能态的密度大于一定的数值时，说明金属表面电子的能态发生了变化，造成了金属表面的性质发生变化。
这就为我们研究半导体、超导体和金属表面的性质提供了一个重要的参考。
费米面上的能态密度的量化通常是通过量子力学理论来实现的。
它通过量子力学方法，可以计算金属表面电子在某一能量水平上的能态密度，可以把所有金属表面电子的能态都统一放到能态密度图上，从而可以准确计算出金属表面电子的能态密度。
费米面上的能态密度可以用来估算金属表面电子性质的变化，从而更有效地研究半导体、超导体和金属表面的性质。
费米面上的能态密度的研究也可以为我们研究半导体、超导体等新型材料的构造提供重要的参考意见。
费米面上的能态密度也可以用来探索金属表面电子在外力作用下的性质变化，例如金属表面电子在温度变化、磁场作用、压力等情况下的能态变化，这些都可以从费米面上的能态密度中研究出来，从而更好地了解金属表面电子的性质变化。
综上所述，费米面上的能态密度越来越受到研究者的关注，不仅可以用来研究半导体、超导体和金属表面的性质，而且也可以用来探索金属表面电子在外力作用下的性质变化，为我们研究粒子物理提供了重要的参考依据。
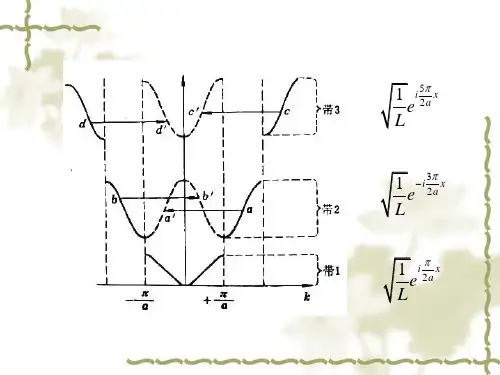
能带理论能带理论是目前研究固体中电子运动的一个主要理论基础，它预言固体中电子能量会落在某些限定范围或“带"中，因此，这方面的理论称为能带理论。
对于晶体中的电子，由于电子和周围势场的相互作用，晶体电子并不是自由的,因而其能量与波失间的关系E （k ）较为复杂，而这个关系的描述这是能带理论的主要内容.本章采用一些近似讨论能带的形成,并通过典型的模型介绍能带理论的一些基本结论和概念。
一、三个近似绝热近似：电子质量远小于离子质量，电子运动速度远高于离子运动速度，故相对于电子的运动，可以认为离子不动，考察电子运动时,可以不考虑离子运动的影响，取系统中的离子实部分的哈密顿量为零。
平均场近似:让其余电子对一个电子的相互作用等价为一个不随时间变化的平均场。
周期场近似: 无论电子之间相互作用的形式如何，都可以假定电子所感受到的势场具有平移对称性。
原本哈密顿量是一个非常复杂的多体问题，若不简化求解是相当困难的，但 经过三个近似处理后使复杂的多体问题成为周期场下的单电子问题，从而本章的中心任务就是求解晶体周期势场中单电子的薛定谔方程，即其中二、两个模型(1）近自由电子模型1、模型概述 在周期场中，若电子的势能随位置的变化（起伏）比较小，而电子的平均动能要比其势能的绝对值大得多时，电子的运动就几乎是自由的.因此,我们可以把自由电子看成是它的零级近似，(222U m ∇+)()(r U R r U n=+而将周期场的影响看成小的微扰来求解。
（也称为弱周期场近似）2、怎样得到近自由电子模型近自由电子近似是晶体电子仅受晶体势场很弱的作用，E （K ）是连续的能级。
由于周期性势场的微扰 E （K ）在布里渊区边界产生分裂、突变形成禁带,连续的能级形成能带，这时晶体电子行为与自由电子相差不大，因而可以用自由电子波函数来描写今天电子行为。
3、近自由电子近似的主要结果1) 存在能带和禁带：在零级近似下，电子被看成自由粒子，能量本征值 E K0 作为 k 的函数具有抛物线形式.由于周期势场的微扰，E （k ）函数将在 处断开，本征能量发生突变,出现能量间隔2︱V n ︱,间隔内不存在允许的电子能级，称禁带；其余区域仍基本保持自由电子时的数值。
费米面上的能态密度费米面上的能态密度是一个重要的物理概念，它是1926年由美国物理学家爱因斯坦提出的。
它代表了系统里具有恒定能量的粒子的最大密度。
这一概念可以用于研究物理、化学和其他复杂的科学系统，也可以用于理解空间、时间和质量的联系。
费米面上的能态密度的最初定义是，它是指一个平面上一点的能量，该能量能在其上容纳的粒子的最大数量。
水平的，它可以被认为是一个物理限制，它限制了物质体系里的粒子的数量及其能量分布模式。
例如，费米面上的能态密度可以用来解释为什么动能会在费米面上截断，以及加热等运动会使粒子的能量间隔发生变化等现象。
费米面上的能态密度的重要性不容小觑，它为众多科学系统的研究提供了令人满意的解释。
举例来说，它已经被用于研究量子力学模型、热力学体系、摩擦系统等。
此外，它也被广泛应用于物理学领域，如空气动力学、流体力学、激光物理学、电磁学等，从而为现代技术打下坚实基础。
费米面上的能态密度还可以用于探测温度及能量之间的关系。
研究表明，费米面上的能态密度与温度之间存在一种恒定的关系，即费米能态密度的大小越高，温度越高。
由此可以间接测量温度，在某些情况下可以代替温度计。
同时，费米面上的能态密度还可以用于探测质量和时间之间的关系，这是研究物质空间结构和动态行为的基础。
此外，费米面上的能态密度在研究粒子物理学中也发挥着重要的作用。
它可以帮助人们更好地理解粒子的行为及其物理性质，为物质的宏观结构和小观性质的研究提供依据。
费米面上的能态密度还可以为研究粒子的相互作用提供参考，从而有助于弄清他们的行为特征。
总之，费米面上的能态密度是一个重要的物理概念，它在众多科学领域均发挥着重要作用，无论是探测温度、能量、质量、时间或研究粒子物理学，它都提供了有价值的参考。
此外，费米面上的能态密度也为现代技术打下了坚实的基础，它使科学研究成为可能，并且有助于人类更好地理解自然界的物质世界。
电荷密度图、能带结构、态密度的分析能带图的横坐标是在模型对称性基础上取的K点。
为什么要取K点呢？因为晶体的周期性使得薛定谔方程的解也具有了周期性。
按照对称性取K点，可以保证以最小的计算量获得最全的能量特征解。
能带图横坐标是K点，其实就是倒格空间中的几何点。
纵坐标是能量。
那么能带图应该就是表示了研究体系中，各个具有对称性位置的点的能量。
我们所得到的体系总能量，应该就是整个体系各个点能量的加和。
主要是从以下三个方面进行定性/定量的讨论：1、电荷密度图（charge density）；2、能带结构（Energy Band Structure）；3、态密度（Density of States，简称DOS）。
电荷密度图是以图的形式出现在文章中，非常直观，因此对于一般的入门级研究人员来讲不会有任何的疑问。
唯一需要注意的就是这种分析的种种衍生形式，比如差分电荷密图（def-ormation charge density）和二次差分图（difference charge density）等等，加自旋极化的工作还可能有自旋极化电荷密度图（spin-polarized charge density）。
所谓“差分”是指原子组成体系（团簇）之后电荷的重新分布，“二次”是指同一个体系化学成分或者几何构型改变之后电荷的重新分布，因此通过这种差分图可以很直观地看出体系中个原子的成键情况。
通过电荷聚集（accumulation）/损失（depletion）的具体空间分布，看成键的极性强弱；通过某格点附近的电荷分布形状判断成键的轨道（这个主要是对d轨道的分析，对于s或者p轨道的形状分析我还没有见过）。
分析总电荷密度图的方法类似，不过相对而言，这种图所携带的信息量较小。
成键前后电荷转移的电荷密度差。
此时电荷密度差定义为：delta_RHO = RHO_sc - RHO_atom其中RHO_sc 为自洽的面电荷密度，而RHO_atom 为相应的非自洽的面电荷密度，是由理想的原子周围电荷分布堆彻得到的，即为原子电荷密度的叠加(a superposition of atomic charge densities)。
