固体物理学_能带理论之能态密度和费密面
- 格式:ppt
- 大小:4.67 MB
- 文档页数:36


电子结构中的能带与费米面研究在固体物理学的研究领域中,电子结构是一个非常关键的概念。
电子结构描述了固体中电子的分布和能量状态,对于理解物质的性质和行为有着重要的影响。
在电子结构的研究中,能带与费米面是两个重要的概念。
首先我们来看能带。
在固体中,电子受到晶格势场的约束,形成了离散的能量状态,这些能量状态被称为能级。
当晶体中的原子数目很大时,能级间的间隔变得很小,几乎可以看作连续分布。
这时,我们可以用能带来描述这种连续能级的分布情况。
能带理论最早是由布洛赫(Bloch)于1928年提出的。
该理论认为,电子在晶格势场下的波函数可以表示为平面波与周期性函数的乘积形式。
由于周期性函数具有晶格周期性,因此电子的波函数具有相应的晶格周期性,其能量和动量都可以用一个波矢k来描述。
根据能带理论,电子的能量和动量之间有个非常重要的关系,即能量-动量关系。
根据这个关系,我们可以得到能量与波矢之间的关系,即能带结构。
在能带结构中,能量-波矢关系是用能量-波矢图来表示的,其中横轴表示波矢k,纵轴表示能量E。
在能带结构图中,能带的宽度代表了相应能级的分布范围,而能带间的间隙则代表了能级间的能量间隔。
在导体中,能带之间的间隙非常小,电子可以自由地跃迁到其他能级,因此电子能够自由导电。
而在绝缘体中,能带之间存在较大的间隙,电子无法跃迁到其他能级,因此无法导电。
在半导体和绝缘体中,我们还可以看到分离的价带和导带。
价带是占据态电子能级较低的能带,而导带则是未占据态电子能级较高的能带。
能隙就是这两个能带之间的间隔。
费米面是固体中一个非常特殊的曲面。
它描述了在绝对零度下,具有最高能量的电子所占据的波矢和能量状态。
费米面的形状与固体的导电性质密切相关。
在金属中,费米面穿过一些能带,使得电子在这些态之间能够自由跃迁,从而导致金属的良好导电性。
而在绝缘体和半导体中,费米面处于能隙中,使得电子无法在价带和导带之间跃迁,因此无法导电。
除了金属、半导体和绝缘体之外,还有一种特殊的物质叫拓扑绝缘体。

固体物理学中的费米面与能带结构在固体物理学中,费米面与能带结构是两个重要的概念。
它们描述了在晶体中的电子行为,对于理解电导、磁性以及其他物质的性质至关重要。
一、费米面费米面是描述电子运动的一个概念。
在凝聚态物理学中,电子遵循泡利不相容原理,即每个量子态只能容纳一个电子。
由于这个原理,电子填满能级时会填充到一定的能量范围内。
费米面是描述这个能量范围边界的一个表面。
费米面实际上是指在零温下,电子填满能级时所占据的最高能级。
费米面上方的电子就是导电带。
费米面的形状可以通过电子的能带结构以及能级的填充情况来决定。
二、能带结构能带结构描述了电子在晶体中能量分布的情况。
在固体中,电子的能量是由晶格结构以及电子相互作用决定的。
晶格会对电子的能量造成影响,从而形成能带。
根据波尔兹曼方程,电子在晶体中的运动可以通过能带结构来描述。
能带结构分为导带和禁带两部分。
导带是指电子可以容纳的能级范围,而禁带则是指电子无法取得的能级范围。
禁带中的能量被称为带隙。
带隙决定了固体的电导性质。
对于导电材料来说,带隙较小,电子可以轻易地跃迁到导带中,而对于绝缘体来说,带隙较大,电子无法跃迁到导带中,因此不能导电。
能带结构可以通过实验技术如X射线衍射和光电子能谱来研究。
通过这些实验,科学家可以测量电子的能量分布,从而揭示晶体的能带结构。
三、费米面与能带结构的关系费米面和能带结构之间有着紧密的联系。
费米面的形状取决于能带结构以及电子的填充情况。
对于导体来说,费米能级与导带重叠,费米面呈现为一个封闭曲面,形状非常复杂。
而对于绝缘体来说,费米能级位于禁带中,费米面是一个简单的球面。
这个球面上的每个点对应着一个电子的量子态。
费米面上的电子数量取决于晶体中电子的填充情况。
费米面附近的电子具有决定导电性质的重要作用。
在固体中的费米面形状和所处位置是非常重要的。
这些特性不仅决定了电子的运动行为,也决定了很多物质的性质,如电导、磁性等。
总结固体物理学中的费米面与能带结构是了解电子行为的重要工具。






HUBEI UNIVERSITYCh4.7 能态密度和费米面3ds2V⎰Ch4.7 能态密度和费米面5Ch4.7 能态密度和费米面7作业:求解一维、二维情况下自由电子能态密度N(E))E k∇Ch4.7 能态密度和费米面9k yk xA·C ··BE E B 时:N (E )由0迅速增大。
()V dE dZ E N ==2Ch4.7 能态密度和费米面13紧束缚近似等能面简立方晶格的s带对应的能态密度函数图⇀Ch4.7 能态密度和费米面15Ch4.7 能态密度和费米面17kFCh4.7 能态密度和费米面19Ch4.7 能态密度和费米面21公有化态—能带)晶体中电子波函数是布洛赫函数,它反映晶体电子共有化运动和围绕Ch4.7 能态密度和费米面23取值所对应的许之关系方程的能量区域称作能带或允带:两个相邻能带间的间隔禁带中不存在电子的定态;★禁带的宽度对晶体的导电性:晶体中最低能带的各个能级都被Ch4.7 能态密度和费米面25在外电场的作用下,导带中的电子可以进入同一能带中未被填充的稍高的能级,这个转移过程没有反向的电子转移与之抵消。
所以导带中的电Ch4.7 能态密度和费米面27Ch4.7 能态密度和费米面29二价碱土金属——最外层2个s态电子,似乎刚好填充满和s相应的能带。
由于与s对应的能带和上面的能带发生重叠,2N个尚未填充满s态能带,就开始填充上面的能带,形成两个能带都是部分填充——碱土金属为金属导体——第一布里渊区中的状态尚未填满,第二布里渊区已填充电子,此时的费米面由两部分构成Ch4.7 能态密度和费米面31Ch4.7 能态密度和费米面33——在低能量区域Na、Mg、Al和金刚石、硅的X光子发射能量逐渐上升的——反映了电子的能量从带底逐渐增大,其能态密度逐渐增大的规律Ch4.7 能态密度和费米面35——在高能量的一端金刚石、硅的X光子发射谱逐渐下降——反映了电子填充了导带中所有的状态,即满带。
能带和态密度引言能带和态密度是固体物理学中的重要概念,它们对于理解物质的电子结构和导电性质具有重要意义。
能带理论是固体物理学中最基本的理论之一,它描述了电子在晶体中的运动方式和能量分布。
态密度则是描述在一定能量范围内,单位体积内存在的电子态数目。
本文将深入探讨能带和态密度的概念、性质以及在固体物理学研究中的应用。
一、能带1.1 能带结构在晶体中,原子之间存在相互作用力,导致了电子在晶格中运动时受到周期性势场的束缚。
根据量子力学原理,电子具有波粒二象性,在晶格势场下形成了波动性质。
根据布洛赫定理,在周期势场下,波函数可以表示为平面波与周期函数之积。
通过对波函数解析形式进行数学推导,可以得到离散化的能量分布。
根据离散化得到的能量分布图谱,在一维情况下可以将其表示为离散化点之间相连的线段,称为能带。
能带的形状和特征取决于晶体的结构和原子之间的相互作用。
晶体中存在多个能带,其中价带和导带是最为重要的两个能带。
价带是电子在晶体中受束缚状态下的能量分布,而导带则是电子在晶体中具有较高能量状态下的分布。
两者之间存在禁闭区域,称为禁闭区。
1.2 能带理论为了更好地理解电子在固体中运动和分布规律,科学家提出了多种模型和理论。
其中最著名且广泛应用于固体物理学研究中的是紧束缚模型和自由电子模型。
紧束缚模型假设原子之间存在较强相互作用力,电子主要局域在原子附近运动。
该模型通过考虑原子轨道之间的重叠以及相互作用力来描述电子在晶格中运动。
该模型更适用于描述局域化电子行为以及强关联效应。
自由电子模型则假设固体中的电子可以自由地运动,并且不受到其他粒子或者势场限制。
该模型通过简化数学形式,将电子视为自由粒子,从而得到了一维、二维和三维情况下的能带结构。
自由电子模型适用于描述弱关联电子行为以及导体、半导体等材料的电子结构。
二、态密度2.1 态密度的概念态密度是描述在一定能量范围内,单位体积内存在的电子态数目。
在固体物理学中,态密度是研究材料中电子行为和导电性质的重要物理量。
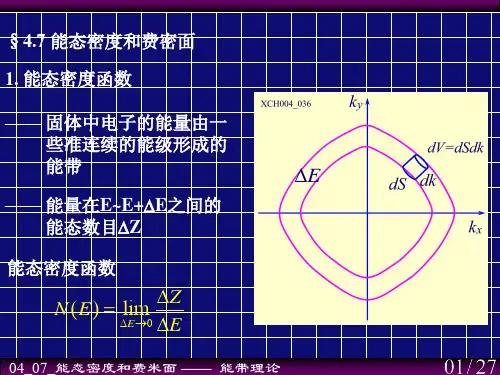
5.8 能态密度和费米面:一. 能态密度二. 费米面见黄昆书4.7节与孤立原子中的本征能态形成一系列的分立能级不同,固体中电子的能级是非常密集的,形成准连续的分布,和孤立原子那样去标注每个能级是没有意义的,为了概括晶体中电子能级的状况,我们引入“能态密度”的概念,这个函数在讨论晶体电子的各种过程时特别在输运现象的分析中是非常重要的。
费米面是固体物理中最重要的概念之一。
在自由电子论中费米面的重要性在于:只有费米面附近的电子才能参与热跃迁或输运过程,决定着晶体的各种物理性质。
这里费米面的含义不变,只是晶体势场的影响使费米面的形状变得复杂,从而对性质的影响变得复杂罢了,自由电子气模型受周期场的微弱影响,近自由电子的等能面偏离自由电子的球形。
并受到布里渊区界面影响和自由电子态密度相比近自由电子的能态密度发生了明显变化。
E A原因是明显的:在4.2节已经指出,周期场的微扰使布里渊区附近界面内的能量下降,而等能面的凸出正意味着达到同样的能量E ,需要更大的k 值,当能量E 超过边界上A 点的能量E A ,一直到E 接近于在顶角C 点的能量E C (即达到第一能带的顶点)时,等能面将不再是完整的闭合面,而成为分割在各个顶角附近的曲面。
由此我们给出对近自由电子能态密度的估计:在能量没有接近E A 时,N (E)和自由电子的结果相差不多,随着能量的增加,等能面一个比一个更加强烈地向外突出,态密度也超过自由电子,在E A 处达到极大值,之后,等能面开始残破,面积开始下降,态密度下降,直到E C 时为零。
所以近自由电子近似下的N (E)如图所示。
BCC LiFermi surface[100][010]Fermi surface is distortedfrom a spherenear the zone boundary.A cusp is caused by interactionN (E )N (E )E B E BE CE C EE 。