4.5 紧束缚近似、能态密度和费米面
- 格式:ppt
- 大小:1.06 MB
- 文档页数:38

§5-4 紧束缚近似理论原子结合为原子时,电子的状态发生了根本性的变化,电子从孤立原子的束缚态变为晶体中的共有化状态。
电子状态变化的大小取决于电子在某原子附近所受该原子势场的作用与其它诸原子势场作用的相对大小。
若原子所处原子势场的作用较之其它原子势场的作用要大得多,例如对于原子中内层电子,或晶体间距较大时,上面讨论的近自由电子近似就不适用,这时共有化运动状态与束缚态之间有直接联系,即紧束缚近似理论。
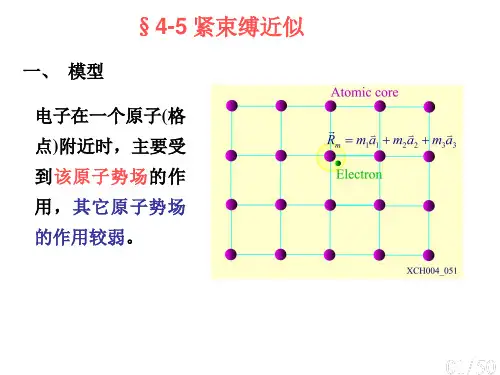
紧束缚理论的实质是把原子间相互作用影响看成微扰的简并微扰方法,微扰后的状态是N 个简并态的线性组合,即用原子轨道()i m ϕ-r R 的线性组合来构成晶体中的电子共有化运动的轨道(,)ψk r ,也称原子轨道线性组合法,简写为LCAO 。
5.4.1 原子轨道线性组合设晶体中第m 个原子的位矢为:112233m m m m =++R a a a ……………………………………………………………………………(5-4-1)若将该原子看作一个孤立原子,则在其附近运动的电子将处于原子的某束缚态()i m ϕ-r R ,该波函数满足方程:22()()()2m i m i i m V m ϕεϕ⎡⎤-∇+--=-⎢⎥⎣⎦r R r R r R ………………………………………………(5-4-2) 其中()m V -r R 为上述第m 个原子的原子势场,i ε是与束缚态i ϕ相对应的原子能级。
如果晶体为N 个相同的原子构成的布喇菲格子,则在各原子附近将有N 个相同能量i ε的束缚态波函数i ϕ。
因此不考虑原子之间相互作用的条件下,晶体中的这些电子构成一个N 个简并的系统:能量为i ε的N 度简并态()i m ϕ-r R ,m=1,2,…,N 。
实际晶体中的原子并不是真正孤立、完全不受其它原子影响的。
由于晶体中其它诸原子势场的微扰,系统的简并状态将消除,而形成由N 个能级构成的能带。
根据以上的分析和量子力学的微扰理论,我们可以取上述N 个简并态的线性组合(,)()()mi m maψϕ=-∑k r k r R ………………………………………………………………………(5-4-3)作为晶体电子共有化运动的波函数,同时把原子间的相互影响当作周期势场的微扰项,于是晶体中电子的薛定谔方程为:22()()()2U E m ψψ⎡⎤-∇+=⎢⎥⎣⎦r r r …………………………………………………………………(5-4-4) 其中晶体势场U (r )是由原子势场构成的,即 ()()()nl nU V U =-=+∑r r Rr R …………………………………………………………………(5-4-5)5.4.2 微扰计算(5-4-4)式可以转化为如下形式:()()22()()()2m m V U V E m ψψ⎡⎤-∇+-+--=⎢⎥⎣⎦r R r r R r r 代入(5-4-2)和(5-4-3)后,可得:[()()()]()0mi m i m maE U V εϕ-+---=∑r r R r R ………………………………………………(5-4-5)在紧束缚近似作用下,可认为原子间距较i ϕ态的轨道大得多,不同原子的i ϕ重叠很小,从而有:()()*in i m nm d ϕϕδ--=⎰r R r R r …………………………………………………………………(5-4-6)现以()*in ϕ-r R 左乘方程(5-4-5),并对整个晶体积分,可以得: *()()[()()]()n i m i m m i m ma E a U V d 0εϕϕ-+---⋅-∑⎰r R r r R r R r =…………………………(5-4-7)首先讨论(5-4-7)式中的积分。


(1)Hall 系数—— Hall 系数 对于自由电子:q =-e ,所以, 其中,n 为单位体积中的载流子数,即载流子浓度。
由Hall 系数的测量不仅可以判断载流子的种类(带正电还是带负电),而且还是测量载流子浓度的重要手段。
载流子浓度越低,Hall 系数就越大,Hall 效应就越明显。
(2)F-D 分布函数——Fermi -Dirac 分布函数其中 μ是电子的化学势,其物理意义是在体积不变的情况下,系统增加一个电子所需的自由能。
从分布几率看,当E =μ时,f(μ)=1/2 ,代表填充几率为1/2的能态。
当E -μ >几个kBT 时,exp[(E -μ)/ kBT] >>1 ,有: 这时,Fermi -Dirac 分布过渡到经典的Boltzmann 分布。
且f(E)随E 的增大而迅速趋于零。
这表明: E -μ >几个kBT 的能态是没有电子占据的空态。
(3)Bloch 函数及其物理意义Bloch 函数 行进波因子 表明在晶体中运动的电子已不再局域于某个原子周围,而是可以在整个晶体中运动的,这种电子称为共有化电子。
它的运动具有类似行进平面波的形式。
那么,周期函数 的作用则是对这个波的振幅进行调制,使它从一个原胞到下一个原胞作周期性振荡,但这并不影响态函数具有行进波的特性。
(4)波失k 的物理意义,态空间点阵,分布密度,简约区,k 取值总数波失k 的物理意义:表示不同原胞间电子波函数的位相变化。
不同的波矢量k 表示原胞间位相差不同,即描述晶体中电子不同的运动状态。
态空间点阵:k 取值不连续,在k 空间中,k 的取值构成一个空间点阵,称为态空间点阵。
分布密度:的分布密度为 简约区:(—— 简约区) k 取值总数:在简约区中波失k (5)金属,半导体电导率随温度变化的差异金属而言:Fermi 能级位于导带内,所以温度变化激发的载流子的贡献可以基本不用考虑;那么:随温度升高,晶格的振动加剧,从而导致载流子受到晶格振动所引起的散射,也就是声子的散射加强;从而电阻率增加,电导率下降;半导体而言:Fermi 能级位于导带和价带之间,温度变化激发的载流子的贡献必须考虑;随温度升高,从价带激发到导带的载流子数目增加,即有更多的载流子参与了导电,从而电阻率降低,电导率上升。


能带理论课程总结能带理论是一种近似的理论,在固体中存在大量的电子,它们的运动是相互联系着的,每个电子的运动都要受到其它电子运动的牵连。
这种多电子系统严格的解显然是不可能的。
能带理论是单电子近似的理论,就是把每个电子的运动看成是独立的在一个等效势场中的运动。
能带理论的出发点是固体中的电子不再束缚于个别的原子,而是在整个固体内运动,称为共有化电子。
在讨论共有化电子的运动状态时假定原子实处在平衡位置,而把原子实偏离平衡位置的影响看成微扰,对于理想晶体,原子规则排列成晶格,晶格具有周期性,因而等效势场也具有周期性,晶体中的的电子就是在一个具有晶格周期性的等效势场中运动,其波动方程为:也有:为任意晶格矢量。
在研究能带理论时,我们往往通过近似模型的转化,将相关问题简单化。
通过假定体积为V=,有N个带正电荷Ze的例子是,结合系统哈密顿量和体系中的薛定谔方程,首先应用绝热近似的观点将系统哈密顿量简化,实现多粒子问题到多电子问题的转化,再通过单电子近似即用分离变量法对单个电子独立求解得单电子所受势场为:从而实现了多电子问题到单电子问题的转化,最后假定电子所受到的势场具有平移对称性即存在周期场近似,则把能带理论顺利转化为周期性场中的单电子近似问题了。
1、布洛赫定理布洛赫定理指出,当势场具有晶格周期性时,波动方程的解具有以下性质:上式就是布洛赫定理。
根据该定理得到波函数:即布洛赫函数。
Bloch 发现,不管周期势场的具体函数形式如何,在周期势场中运动的单电子的波函数不再是平面波,而是调幅平面波,其振幅也不再是常数,而是按晶体的周期而周期变化。
具体波动图像如下所示:2、近自由电子模型在周期场中,若电子的势能随位置的变化(起伏)比较小,而电子的平均动能要比其势能的绝对值大得多时,电子的运动就几乎是自由的。
因此,我们可以把自由电子看成是它的零级近似,而将周期场的影响看成小的微扰来求解。
近自由电子(NFE)模型的定性描述:在NFE 模型中,是以势场严格为零的Schrödinger方程的解(即电子完全是自由的)为出发点的,但必须同时满足晶体平移对称性的要求,我们称之为空格子模型。





紧束缚近似公式(一)紧束缚近似公式紧束缚近似(Tight Binding Approximation)是一种描述电子在固体晶格中行为的数学方法。
在紧束缚近似中,电子波函数被表示为原子轨道的线性组合,通过求解薛定谔方程来得到能级结构和电子态密度等信息。
Bloch定理Bloch定理表明在理想晶体中,电子波函数可以表示为平面波和某个周期函数的乘积形式。
根据Bloch定理,电子波函数可以用下式表示:Ψk(r)=e ik⋅r u k(r)其中,e ik⋅r是平面波,u k(r)是周期函数。
紧束缚近似基本公式紧束缚近似基本公式是在Bloch定理的基础上,进一步假设电子波函数由最近邻原子的原子轨道线性组合构成。
根据紧束缚近似,电子在晶体中的波函数可以用下式表示:e ik⋅R n u n(r−R n)Ψk(r)=∑c nn其中,R n是最近邻原子的位置矢量,u n(r−R n)是最近邻原子的原子轨道。
紧束缚近似能带关系根据紧束缚近似基本公式,可以得到能带关系,即能量与波矢之间的关系。
能带关系可以用下式表示:E k=∑c n∗c n e ik⋅(R n−R m)ϵnmn其中,E k是能量,c n∗和c n是电子的系数,e ik⋅(R n−R m)是相位因子,ϵnm是最近邻原子间的相互作用能。
紧束缚近似的应用举例紧束缚近似在描述材料的能带结构和电子态密度等方面有广泛的应用。
以下是一些应用举例:1.能带计算:通过紧束缚近似,可以计算材料的能带结构,进而分析材料的导电性、绝缘性等特性。
2.电子态密度计算:紧束缚近似可以用于计算材料的电子态密度,这对于研究材料的化学反应等方面非常重要。
3.值得注意的是,紧束缚近似也有其局限性,适用于描述弱相互作用体系,如共价键、金属键等。
对于强相互作用系统,如强关联电子体系,紧束缚近似可能不适用。
总之,紧束缚近似是一种重要的描述电子在晶体中行为的方法,在材料科学和凝聚态物理等领域有着广泛的应用。