昆明理工大学理论力学第一章答案

第一章静力学公理和物体的受力分析、是非判断题1.1.1 在任何情况下，体内任意两点距离保持不变的物体称为刚体。

1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、直线1.1.3 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

（x ）1.1.4力的可传性只适用于刚体，不适用于变形体。

（V ）1.1.5 两点受力的构件都是二力杆。

1.1.6只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

（1.1.7 力的平行四边形法则只& ）1.1.8 凡矢量都可以应用平行四（V ）1.1.9只要物体平衡，都能应用加减平衡力系公理。

1.1.10凡是平衡力系，它的作用效果都等于零。

1.1.11 合力总是比（x ）1.1.12只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

（x）1.1.13若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

（V）1.1.14当软绳受两个等值反向的压力时，可以平衡。

（x）1.1.15静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

（V）1.1.16静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

1.1.17 凡是两端用较链连接的直杆都是二力杆。

（x ）1.1.18如图所示三较拱，受力F，只作用，其中F作用于较C的销子上，则AC、BC构件都不是二力构件。

二、填空题（V ）方向相反，沿同一适用于刚边形法则合（（分力大x )体。

成。

x )X )图图1.2.1力对物体的作用效应一般分为外效应和内效应。

1.2.2 对非自由体的运动所预加的限制条件称为束约束；约束力的方向总是与约所能阻止的物体的运动趋势的方向相反；约束力由主动力引起，且随主动力的改变而改变。

123 如图所示三钱拱架中，若将作用于构件AC上的力偶M搬移到构件BC上，则A、B、C各处的约束力A.都不变；C.都改变；三、受力图1.3.1画出各物体的受力图。

第一章 静力学公理和物体的受力分析
答 案
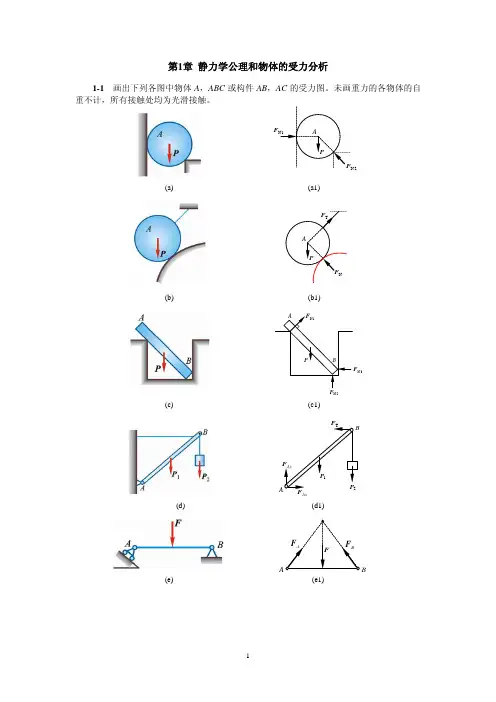
1-1
（1）若F1=F2表示力，则一般只说明两个力大小相等，方向相同。

（2）若F1=F2表示力，则一般只说明两个力大小相等，方向是否相同，难以判定。

（3）说明两个力大小、方向、作用效果均相同。

1-2
前者为两个矢量相加，后者为两个代数量相加。

1-3
（1）B处应为拉力，A处力的方向不对。

（2）C、B处力方向不对，A处力的指向反了。

（3）A处力的方向不对，本题不属于三力汇交问题。

（4）A、B处力的方向不对。

受力图略。

1-4
不能。

因为在B点加和力F等值反向的力会形成力偶。

1-5
不能平衡。

沿着AB的方向。

1-6略。

1-7
提示：单独画销钉受力图，力F作用在销钉上；若销钉属于AC，则力F作用在AC上。

受力图略。

理论力学习题册答案班级姓名学号第一章静力学公理与受力分析(1)一．是非题1、加减平衡力系公理不但适用于刚体，还适用于变形体。

（）2、作用于刚体上三个力的作用线汇交于一点，该刚体必处于平衡状态。

（）3、刚体是真实物体的一种抽象化的力学模型，在自然界中并不存在。

（）4、凡是受两个力作用的刚体都是二力构件。

（）5、力是滑移矢量，力沿其作用线滑移不会改变对物体的作用效果。

（）二．选择题1、在下述公理、法则、原理中，只适于刚体的有（）①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三．画出下列图中指定物体受力图。

未画重力的物体不计自重，所有接触处均为光滑接触。

多杆件的整体受力图可在原图上画。

(a)球A(b)杆AB- 1 -(c)杆AB、CD、整体(d)杆AB、CD、整体(e)杆AC、CB、整体(f)杆AC、CD、整体四．画出下列图中指定物体受力图。

未画重力的物体不计自重，所有接触处均为光滑接触。

多杆件的整体受力图可在原图上画。

(a)球A、球B、整体(b)杆BC、杆AC、整体- 2 -班级姓名学号第一章静力学公理与受力分析（2）一．画出下列图中指定物体受力图。

未画重力的物体不计自重，所有接触处均为光滑接触。

多杆件的整体受力图可在原图上画。

(a)杆AB、BC、整体(c)杆AB、CD、整体CAFAxDBFAyFBWEW(b)杆ABOriginal Figure、BC、轮E、整体FBD of the entire frame(d)杆BC带铰、杆AC、整体- 3 -(e)杆CE、AH、整体(g)杆AB带轮及较A、整体(f)杆AD、杆DB、整体(h)杆AB、AC、AD、整体- 4 -班级姓名学号第二章平面汇交和力偶系一．是非题1、因为构成力偶的两个力满足F= - F’，所以力偶的合力等于零。

（）2、用解析法求平面汇交力系的合力时，若选用不同的直角坐标系，则所求得的合力不同。

（）3、力偶矩就是力偶。

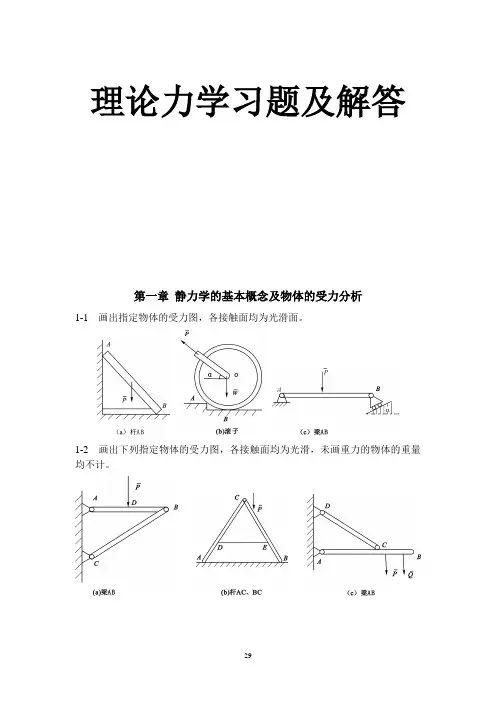
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图，各接触面均为光滑面。

1-2 画出下列指定物体的受力图，各接触面均为光滑，未画重力的物体的重量均不计。

1-3 画出下列各物体以及整体受力图，除注明者外，各物体自重不计，所有接触处均为光滑。

(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN，用绳子挂在支架的滑轮B上，绳子的另一端接在铰车D 上，如图所示。

转动铰车，物体便能升起，设滑轮的大小及滑轮转轴处的摩擦忽略不计，A、B、C三处均为铰链连接。

当物体处于平衡状态时，试求拉杆AB和支杆CB所受的力。

2-2 用一组绳悬挂重P=1kN的物体，求各绳的拉力。

2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN，P2=800kN及制动力T=193kN，桥墩自重W=5280kN，风力Q=140kN。

各力作用线位置如图所示，求将这些力向基底截面中心O简化的结果，如能简化为一合力，试求出合力作用线的位置。

2-4 水平梁的支承和载荷如图所示，试求出图中A、B处的约束反力。

2-5 在图示结构计算简图中，已知q=15kN/m，求A、B、C处的约束力。

2-6 图示平面结构，自重不计，由AB、BD、DFE三杆铰接组成，已知：P=50kN，M=40kN·m，q=20kN/m，L=2m，试求固定端A的反力。

图2-6 图2-72-7 求图示多跨静定梁的支座反力。

2-8 图示结构中各杆自重不计，D、E处为铰链，B、C为链杆约束，A为固定端，已知：q G=1kN/m，q=1kN/m，M=2kN·m，L1=3m，L2=2m，试求A、B、C 处约束反力。

图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成，O、B处为铰链，A、E是固定铰支座，尺寸如图，已知：r=20cm，在滑轮上吊有重Q=1000N的物体，杆及轮重均不计，试求支座A和E以及AO杆上的O处约束反力。

第一章静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。

（）2．在理论力学中只研究力的外效应。

（）3．两端用光滑铰链连接的构件是二力构件。

（）4．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。

（）5．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。

（）6．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。

（）7．平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。

（）8．约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。

（）二、选择题1．若作用在A点的两个大小不等的力F1和F2，沿同一直线但方向相反。

则其合力可以表示为。

①F1－F2；②F2－F1；③F1＋F2；2．作用在一个刚体上的两个力F A、F B，满足F A=－F B的条件，则该二力可能是。

①作用力和反作用力或一对平衡的力；②一对平衡的力或一个力偶。

③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。

3．三力平衡定理是。

①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡，必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。

4．已知F1、F2、F3、F4为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形，由此。

①力系可合成为一个力偶；②力系可合成为一个力；③力系简化为一个力和一个力偶；④力系的合力为零，力系平衡。

5．在下述原理、法则、定理中，只适用于刚体的有。

①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。

三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。

2．已知力F沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。

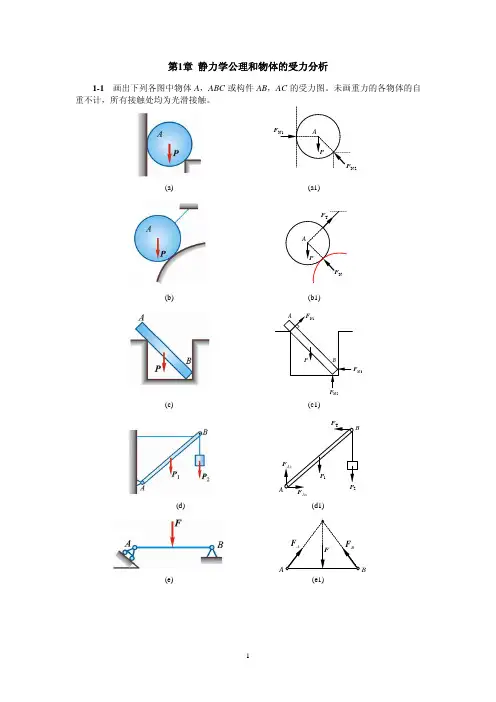
习题7-1图Oυ(a)υυ(b)习题7-3图第7章 点的复合运动7-1 图示车A 沿半径R 的圆弧轨道运动，其速度为v A 。

车B 沿直线轨道行驶，其速度为v B 。

试问坐在车A 中的观察者所看到车B 的相对速度v B /A ，与坐在车B 中的观察者看到车A 的相对速度v A /B ，是否有B A A B //v v -=？（试用矢量三角形加以分析。

）答：B A A B //v v -≠1．以A 为动系，B 为动点，此时绝对运动：直线；相对运动：平面曲线；牵连运动：定轴转动。

为了定量举例，设R OB 3=，v v v B A ==，则v v 3e =∴ ⎩⎨⎧︒==6021/θv v A B2．以B 为动系，A 为动点。

牵连运动为：平移；绝对运动：圆周运动；相对运动：平面曲线。

此时⎪⎩⎪⎨⎧︒==4522/θv v B A ∴ B A A B //v v -≠7-3 图示记录装置中的鼓轮以等角速度0ω转动，鼓轮的半径为r 。

自动记录笔连接在沿铅垂方向并按)sin(1t a y ω=规律运动的构件上。

试求记录笔在纸带上所画曲线的方程。

解：t r x 0ω= （1） )sin(1t a y ω=（2）由（1）0ωr xt =代入（2），得)sin(01r xa y ωω=7-5 图示铰接四边形机构中，O 1A = O 2B = 100mm ，O 1O 2 = AB ，杆O 1A 以等角速度ω= 2rad/s 绕轴O 1转动。

AB 杆上有一套筒C ，此套筒与杆CD 相铰接，机构的各部件都在同一铅垂面内。

试求当ϕ= ︒60，CD 杆的速度和加速度。

解：1．动点：C （CD 上），动系：AB ，绝对：直线，相对：直线，牵连：平移。

2．r e a v v v +=（图a ） v e = v A01.02121.0cos e a =⨯⨯==ϕv v m/s （↑）3． r e a a a a +=（图b ）4.021.022e =⨯==ωr a m/s 2 346.030cos e a =︒=a a m/s 2（↑）习题7-5图习题7-7图习题7-9图υ(a) (b)(a)7-7 图示瓦特离心调速器以角速度ω绕铅垂轴转动。

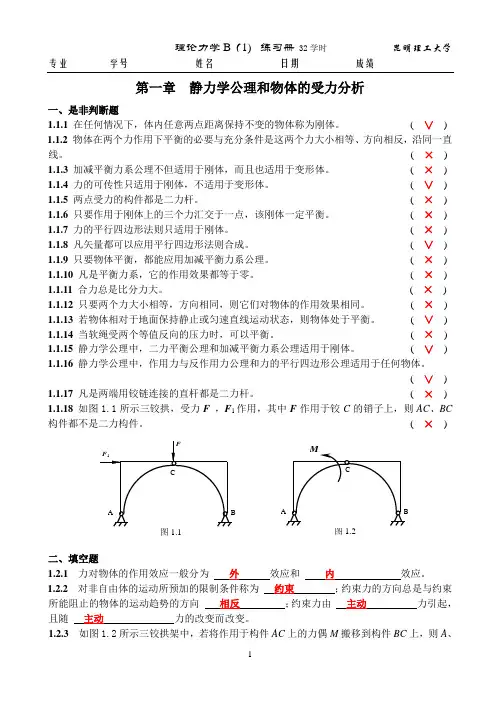
第一章 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下，体内任意两点距离保持不变的物体称为刚体。

( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。

( × ) 1.1.3 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

( × ) 1.1.4 力的可传性只适用于刚体，不适用于变形体。

( ∨ ) 1.1.5 两点受力的构件都是二力杆。

( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

( × ) 1.1.7 力的平行四边形法则只适用于刚体。

( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。

( ∨ ) 1.1.9 只要物体平衡，都能应用加减平衡力系公理。

( × ) 1.1.10 凡是平衡力系，它的作用效果都等于零。

( × ) 1.1.11 合力总是比分力大。

( × ) 1.1.12 只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

( ∨ ) 1.1.14 当软绳受两个等值反向的压力时，可以平衡。

( × ) 1.1.15 静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

( ∨ ) 1.1.16 静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。

( × ) 1.1.18 如图1.1所示三铰拱，受力F ，F 1作用，其中F 作用于铰C 的销子上，则AC 、BC 构件都不是二力构件。

( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。

1.2.2 对非自由体的运动所预加的限制条件称为 约束 ；约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ；约束力由 主动 力引起，且随 主动 力的改变而改变。

1.01 解：A 点运动已知，欲求D 点运动，可以从D 点和A 点的几何关系出发求解。

取图示的坐标系，以,,(,,,,)i i x y i A B C D E =分别表示各点的,x y 坐标。

由OA AB =，CD DE AC AE ===可知：运动过程中ACDE 始终为一个平行四边形，故 D A x x =，2A D C y y y += OA 绕O 轴转动，转角为5t πϕ=∴cos 200cos5A t x OA π=ϕ=，sin 200sin 5A ty OA π=ϕ= sin ()sin 150sin 5C ty OC OA AC π=ϕ=-ϕ=∴ 200cos 5D A t x x π==(mm)， D C 2100sin 5A ty y y π=-=(mm)得到D 点的运动方程为22221200100D Dx y +=， 运动轨迹为椭圆的一部分。

1.02 图示AB 杆长为l ，绕B 点按t ϕω=的规律转动。

与杆连接的滑块按sin s a b t ω=+的规律沿水平方向作简谐振动，其中a 、b 、ω为常数，求A 点的轨迹。

解：在t 时刻，点A 的在oxy 坐标中的坐标为x x l y l A B A =+=sin ,cos ϕϕ将x s a b B ==+sin ϕ代入上式，可得A 的运动方程为x a b l y l A A -+⎛⎝ ⎫⎭⎪+⎛⎝ ⎫⎭⎪=221， 运动轨迹为椭圆。

1.03 半径为r 的半圆形凸轮以等速0v 在水平面上滑动，如图所示，求当︒=30θ瞬时顶杆上升的速度大小与加速度大小（杆与凸轮的接触点为M ）。

解：取如图所示的坐标系，y 轴沿着顶杆向上，x 轴在水平面上沿着凸轮运动方向。

由已知条件可得M 点的坐标为0=x ，22002022)(t v t rv t v r r y -=--=，则y 方向上的速度和加速度分别为：y =0022rv 0t -v 02t2 （1）22002200220022002022/)(2tv t rv tv t rv t v r v t v t rv v y------= （2）当30=θ时，r t v r 230=-，即r t v )231(0-= 代入（1）式和（2）式，可以得到0303|v y== θ， rr y 20308|-== θ1.04 半径为R 的圆弧与AB 墙相切，在圆心O 处有一光源，点M 从切点C 处开始以等速度0υ沿圆弧运动，如图所示，求M 点在墙上影子'M 的速度大小与加速度大小。

理论力学（第二版）参考答案上部（一~三章）第一章1.2写出约束在铅直平面内的光滑摆线上运动的质点的微分方程，并证明该质点在平衡位置附近作振动时，振动周期与振幅无关. 解：设s为质点沿摆线运动时的路程，取=0时，s=0S== 4 a (1)设为质点所在摆线位置处切线方向与x轴的夹角，取逆时针为正，即切线斜率=受力分析得：则，此即为质点的运动微分方程。

该质点在平衡位置附近作振动时，振动周期与振幅无关，为.1.3证明：设一质量为m的小球做任一角度θ的单摆运动运动微分方程为θθθFrrm=+)2(θθsinmgmr= ①给①式两边同时乘以dθθθθθdgdr s i n=对上式两边关于θ 积分得cgr+=θθc o s212②利用初始条件θθ=时0=θ 故cosθgc-=③由②③可解得c o sc o s2-θθθ-∙=lg上式可化为dtdlg=⨯-∙θθθcoscos2-两边同时积分可得θθθθθθθθd g l d g l t ⎰⎰---=--=020222002sin 12sin 10012cos cos 12进一步化简可得θθθθd g l t ⎰-=0002222sin sin 121由于上面算的过程只占整个周期的1/4故⎰-==02022sin2sin124T θθθθd g l t由ϕθθsin 2sin /2sin 0=两边分别对θϕ微分可得ϕϕθθθd d cos 2sin2cos=ϕθθ202sin 2sin 12cos-=故ϕϕθϕθθd d 202sin 2sin 1cos 2sin2-= 由于00θθ≤≤故对应的20πϕ≤≤故ϕϕθϕθϕθθθθπθd g l d g l T ⎰⎰-=-=202022cos 2sinsin 2sin 1/cos 2sin42sin2sin 2故⎰-=2022sin 14πϕϕK d g l T 其中2sin 022θ=K通过进一步计算可得g lπ2T =])2642)12(531()4231()21(1[224222 +⨯⨯⨯⨯-⨯⨯⨯⨯++⨯⨯++n K nn K K1.5解：如图，在半径是R的时候，由万有引力公式，对表面的一点的万有引力为, ①M为地球的质量；可知，地球表面的重力加速度g , x为取地心到无限远的广义坐标，，②联立①，②可得：,M为地球的质量；③当半径增加,R2=R+,此时总质量不变，仍为M,此时表面的重力加速度可求：④由④得：⑤则，半径变化后的g 的变化为⑥对⑥式进行通分、整理后得：⑦对⑦式整理，略去二阶量，同时远小于R ，得⑧则当半径改变 时，表面的重力加速度的变化为：。

只限自己使用，请不要传播 —— 李鹏程第一章 静力学基础一、是非判断题 1.1 ( ∨ ) 1.2 ( × ) 1.3 ( × ) 1.4 ( ∨ ) 1.5 ( × ) 1.6 ( × ) 1.7 ( × ) 1.8 ( ∨ ) 1.9 ( × ) 1.10 ( × ) 1.11 ( × ) 1.12 ( × ) 1.13 ( ∨ ) 1.14 ( × ) 1.15 ( ∨ )1.162.1 2.2 2.3 外 内 。

2.4 约束 ； 相反 ； 主动 主动 。

2.5 3 ，2.6 力偶矩代数值相等（力偶矩的大小相等，转向相同） 。

三、选择题3.1 (c) 。

3.2 A 。

3.3 D 。

3.4 D 。

3.5 A 。

3.6 B 。

3.7 C 。

3.8四、计算题4.14.2(e)(d) (a)mm KN F M ⋅-=18030)(mm KN F M ⋅=-=3.2815325)(20mm KN F M ⋅-=25210.)(01=)(F M x m N F M y ⋅-=501)(01=)(F M z m N F M x ⋅-=2252)(m N F M y ⋅-=2252)(mN F M z ⋅=2252)(mN F M x ⋅=2253)(mN F M y ⋅-=2253)(mN F M z ⋅=2253)(只限自己使用，请不要传播 —— 李鹏程五 、受力图 5.15.2(a)(b) B B(b) (c) P 2(d)只限自己使用，请不要传播 —— 李鹏程5.3(1) 小球 (2) 大球 (3) 两个球合在一起 P 2P 1A CB (a)(1) AC 杆 (2) CB 杆 (3)整体(1) AC 段梁 (2) CD 段梁 (3)整体 (1) AB 杆 (2) CD 杆(3)整体只限自己使用，请不要传播——李鹏程第二章力系的简化一、是非判断题1.1( ×) 1.2( ∨) 1.2( ×)二、填空题2.1 平衡。

1 / 27第一章 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下，体内任意两点距离保持不变的物体称为刚体。

( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。

( × ) 1.1.3 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

( × ) 1.1.4 力的可传性只适用于刚体，不适用于变形体。

( ∨ ) 1.1.5 两点受力的构件都是二力杆。

( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

( × ) 1.1.7 力的平行四边形法则只适用于刚体。

( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。

( ∨ ) 1.1.9 只要物体平衡，都能应用加减平衡力系公理。

( × ) 1.1.10 凡是平衡力系，它的作用效果都等于零。

( × ) 1.1.11 合力总是比分力大。

( × ) 1.1.12 只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

( ∨ ) 1.1.14 当软绳受两个等值反向的压力时，可以平衡。

( × ) 1.1.15 静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

( ∨ ) 1.1.16 静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。

( × ) 1.1.18 如图1.1所示三铰拱，受力F ，F 1作用，其中F 作用于铰C 的销子上，则AC 、BC 构件都不是二力构件。

( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。

第一章 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下，体内任意两点距离保持不变的物体称为刚体。

( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反，沿同一直线。

( × ) 1.1.3 加减平衡力系公理不但适用于刚体，而且也适用于变形体。

( × ) 1.1.4 力的可传性只适用于刚体，不适用于变形体。

( ∨ ) 1.1.5 两点受力的构件都是二力杆。

( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点，该刚体一定平衡。

( × ) 1.1.7 力的平行四边形法则只适用于刚体。

( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。

( ∨ ) 1.1.9 只要物体平衡，都能应用加减平衡力系公理。

( × ) 1.1.10 凡是平衡力系，它的作用效果都等于零。

( × ) 1.1.11 合力总是比分力大。

( × ) 1.1.12 只要两个力大小相等，方向相同，则它们对物体的作用效果相同。

( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态，则物体处于平衡。

( ∨ ) 1.1.14 当软绳受两个等值反向的压力时，可以平衡。

( × ) 1.1.15 静力学公理中，二力平衡公理和加减平衡力系公理适用于刚体。

( ∨ ) 1.1.16 静力学公理中，作用力与反作用力公理和力的平行四边形公理适用于任何物体。

( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。

( × ) 1.1.18 如图1.1所示三铰拱，受力F ，F 1作用，其中F 作用于铰C 的销子上，则AC 、BC 构件都不是二力构件。

( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。

1.2.2 对非自由体的运动所预加的限制条件称为 约束 ；约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ；约束力由 主动 力引起，且随 主动 力的改变而改变。