第七讲散射一、散射截面

微分散射截面的卢瑟福公式引言：微分散射截面是研究微观粒子与物质相互作用的重要参数之一。

卢瑟福公式是描述微分散射截面的经典理论，它为我们理解原子核结构和粒子之间相互作用提供了关键线索。

本文将介绍卢瑟福公式的基本原理和应用，并探讨其在科学研究和工程应用中的重要性。

一、卢瑟福散射实验卢瑟福散射实验是物理学历史上的里程碑之一。

实验中，卢瑟福用α粒子轰击金箔，观察其在金属箔上的散射情况。

实验结果显示，大多数α粒子直线通过金箔，但少数粒子发生明显的散射。

这一观察揭示了原子核的存在，并推翻了汤姆逊的“杏仁布丁模型”。

二、微分散射截面的定义微分散射截面是描述入射粒子在散射过程中与靶粒子相互作用的参数。

它表示在单位立体角范围内，入射粒子被散射到该方向的概率。

微分散射截面通常用符号σ表示，单位为平方米或玻尔恩。

三、卢瑟福公式的推导卢瑟福公式是描述微分散射截面的经典理论。

根据卢瑟福实验的结果，可以推导出以下公式：σ(θ) = (1/4πε₀) * (Z₁Z₂e²/mv²) * (1/sin²(θ/2))其中，σ(θ)表示微分散射截面，Z₁和Z₂分别是入射和靶粒子的电荷数，e是元电荷，m是入射粒子的质量，v是入射粒子的速度，θ是散射角度。

四、卢瑟福公式的应用卢瑟福公式在原子核物理和粒子物理研究中有广泛的应用。

通过测量散射角度和微分散射截面，可以推断出粒子和原子核的结构信息。

此外，卢瑟福公式还可以用于设计粒子加速器和核反应堆等工程应用。

五、卢瑟福公式的局限性尽管卢瑟福公式在经典物理下是有效的，但它忽略了量子力学效应。

在高能散射和微观粒子研究中，需要使用量子力学的散射理论来描述粒子的行为。

因此，卢瑟福公式只适用于低能和经典散射情况。

六、结论卢瑟福公式是描述微分散射截面的重要理论，它为我们研究原子核结构和粒子相互作用提供了关键线索。

虽然卢瑟福公式在经典物理下是有效的，但在高能和微观领域需要使用量子力学的散射理论。

飞机雷达散射截面(rcs)公式
飞机雷达散射截面（Radar Cross Section，RCS）是描述目标对雷达波的散射能力的重要参数。

在雷达系统中，RCS公式是用来计算目标散射的电磁波能量的数学表达式。

RCS公式通常是基于目标的几何形状、材料特性和入射波的频率等因素进行建模的。

RCS公式可以用来预测目标在雷达系统中的探测性能，以及设计隐身技术和电磁干扰技术。

它对于军事和民用航空领域都具有重要意义。

RCS公式的一般形式如下：
RCS = σ A.
其中，σ表示目标的散射截面，A表示目标的有效面积。

散射截面σ是描述目标对入射电磁波的反射能力的参数，通常是一个与频率有关的函数。

目标的有效面积A则是描述目标在雷达波束中所占的实际面积。

RCS公式的具体形式会根据目标的几何形状和材料特性而有所
不同。

对于复杂的目标，RCS公式可能需要进行数值模拟或实验测
量来获得准确的数值。

在现代雷达技术中，研究人员不断努力寻求降低目标的RCS，
以实现隐身和减少雷达探测距离。

因此，RCS公式的研究和应用对
于提高雷达系统的性能具有重要意义。

总之，飞机雷达散射截面（RCS）公式是描述目标对雷达波的散
射能力的重要数学表达式，对于雷达技术和隐身技术具有重要意义。

吸收截面和散射截面
吸收截面和散射截面是物理学中的重要概念，它们是用来描述物体对物理现象的反应的。

吸收截面是指物体对物理现象的吸收能力，它是一个物体对物理现象的反应的度量。

它可以用来衡量物体对物理现象的吸收能力，以及物体对物理现象的敏感程度。

它可以用来衡量物体对物理现象的吸收能力，以及物体对物理现象的敏感程度。

散射截面是指物体对物理现象的散射能力，它是一个物体对物理现象的反应的度量。

它可以用来衡量物体对物理现象的散射能力，以及物体对物理现象的敏感程度。

它可以用来衡量物体对物理现象的散射能力，以及物体对物理现象的敏感程度。

吸收截面和散射截面是物理学中重要的概念，它们可以用来衡量物体对物理现象的反应能力，以及物体对物理现象的敏感程度。

它们可以用来研究物体对物理现象的反应，以及物体对物理现象的敏感程度。

它们也可以用来研究物体对物理现象的反应，以及物体对物理现象的敏感程度。

总之，吸收截面和散射截面是物理学中重要的概念，它们可以用来衡量物体对物理现象的反应能力，以及物体对物理现象的敏感程度。

它们可以用来研究物体对物理现象的反应，以及物体对物理现象的敏感程度。

它们也可以用来研究物体对物理现象的反应，以及物体对物理现象的敏感程度。

因此，吸收截面和散射截面在物理学中具有重要的意义。

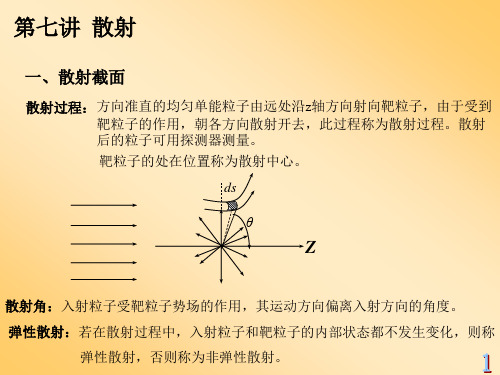
第七讲散射理论一、散射现象的一般描述1、什么是散射？简单地说，散射就是指粒子与粒子之间或粒子与力场之间的碰撞（相互作用）过程，是一种具有重要实际意义的现象，所以散射现象也称碰撞现象，其可以示意为：粒子流散射中心如：原子物理中的α粒子散射实验。

2、散射的分类：弹性散射：一粒子与另一粒子碰撞的过程中，只有动能的交换，粒子内部状态并无改变。

非弹性散射：两粒子碰撞中粒子的内部状态有所改变（例如原子被激发或电离）。

在这里我们只讨论弹性散射，即假设碰撞过程中粒子的内部状态未变，并假设散射中心质量很大、碰撞对其运动没有影响。

3、散射的经典力学描述从经典力学来看，在散射过程中，每个入射粒子都以一个确定的碰撞参数（瞄准距离）b 和方位角0ϕ射向靶子，由于靶子的作用，入射粒子的轨道将发生偏转，沿某方向(,)θϕ出射。

例如在α粒子的散射实验中，有22cot 422M b Ze θυπε= （偏转角θ与瞄准距离之间的关系） 那些瞄准距离在b b db -和之间的α粒子，散射后，必定向着d θθθ+和之间的角度射出，如下图所示：凡通过图中所示环形面积d σ的α粒子，必定散射到角度在d θθθ+和之间的一个空心圆锥体之中。

环形面积d σ称为有效散射截面，又称微分截面。

且2222401()()4sin 2Ze d d M σθπευΩ= 然而，在散射实验中，人们并不对每个粒子的轨道感兴趣，而是研究入射粒子束经过散射后沿不同方向出射的分布。

设一束粒子流以稳定的入射流强度沿Z 轴方向射向靶粒子A ，由于靶粒子的作用，设在单位时间内有dn 个粒子沿(,)θϕ方向的立体角d Ω中射出，显然，,(,)dn Nd dn q Nd θϕ∝Ω=Ω令，即1(,)()dn q N d θϕ=Ω显然，(,)q θϕ具有面积的量纲，称为微分散射截面。

微分散射截面),(ϕθq 表示单位时间内散射到单位立体角Ωd （面积/距离平方）的粒子数占总粒子数比率，即Ω=Nd q dn ),(ϕθ。

散射截面和透过率
散射截面和透过率是物理学中常用的两个概念。

散射截面指的是一个粒子与另一个粒子或场的相互作用中，被散射到某个固定方向的概率与入射粒子数的比值。

而透过率则是指入射粒子通过一个物体时，能够穿过该物体的概率。

在实际应用中，散射截面和透过率常常被用于描述光、电子、中子等粒子在材料中传播的行为。

例如，透过率可以用来描述光在不同材料中的传播特性，可以用来设计光学元件；散射截面则可以用来描述中子在核物质中的相互作用，有助于了解核反应过程。

在计算散射截面和透过率时，一般会考虑入射粒子的能量、入射角度、目标物质的物理性质等因素。

通过精确的计算和实验数据的比较，可以进一步了解材料的微观结构和相互作用特性，为材料的研究和应用提供重要参考。

- 1 -。

第七讲散射理论一、散射现象的一般描述1、什么是散射？简单地说，散射就是指粒子与粒子之间或粒子与力场之间的碰撞（相互作用）过程，是一种具有重要实际意义的现象，所以散射现象也称碰撞现象，其可以示意为：粒子流散射中心如：原子物理中的α粒子散射实验。

2、散射的分类：弹性散射：一粒子与另一粒子碰撞的过程中，只有动能的交换，粒子内部状态并无改变。

非弹性散射：两粒子碰撞中粒子的内部状态有所改变（例如原子被激发或电离）。

在这里我们只讨论弹性散射，即假设碰撞过程中粒子的内部状态未变，并假设散射中心质量很大、碰撞对其运动没有影响。

3、散射的经典力学描述从经典力学来看，在散射过程中，每个入射粒子都以一个确定的碰撞参数（瞄准距离）b 和方位角0ϕ射向靶子，由于靶子的作用，入射粒子的轨道将发生偏转，沿某方向(,)θϕ出射。

例如在α粒子的散射实验中，有22cot 422M b Ze θυπε= （偏转角θ与瞄准距离之间的关系） 那些瞄准距离在b b db -和之间的α粒子，散射后，必定向着d θθθ+和之间的角度射出，如下图所示：凡通过图中所示环形面积d σ的α粒子，必定散射到角度在d θθθ+和之间的一个空心圆锥体之中。

环形面积d σ称为有效散射截面，又称微分截面。

且2222401()()4sin 2Ze d d M σθπευΩ= 然而，在散射实验中，人们并不对每个粒子的轨道感兴趣，而是研究入射粒子束经过散射后沿不同方向出射的分布。

设一束粒子流以稳定的入射流强度沿Z 轴方向射向靶粒子A ，由于靶粒子的作用，设在单位时间内有dn 个粒子沿(,)θϕ方向的立体角d Ω中射出，显然，,(,)dn Nd dn q Nd θϕ∝Ω=Ω令，即1(,)()dn q N d θϕ=Ω显然，(,)q θϕ具有面积的量纲，称为微分散射截面。

微分散射截面),(ϕθq 表示单位时间内散射到单位立体角Ωd （面积/距离平方）的粒子数占总粒子数比率，即Ω=Nd q dn ),(ϕθ。

量子力学中的散射问题量子力学是一门研究微观世界中粒子运动和相互作用的科学，它提供了一种描述和预测微观粒子在不同能量条件下碰撞和散射行为的理论框架。

其中，散射问题是量子力学中的一个重要研究方向，涉及到粒子与势场相互作用后的运动轨迹、角度以及能量转移等关键性问题。

一、经典散射与量子散射经典散射理论是散射问题的最早研究方法，它基于经典力学的基本原理，描述了粒子在经典力场中的运动行为。

经典散射理论认为粒子以一定的入射角度和速度进入势场，通过与势场中的粒子相互作用后，会发生散射运动，出射角度和速度也会发生变化。

然而，在微观世界中，经典散射理论已不能准确描述粒子的行为，因为量子力学规定了微观粒子以波粒二象性存在。

因此，量子散射理论的出现填补了这一空白，成为研究微观粒子散射行为的有效工具。

二、量子散射的数学描述在量子力学中，散射问题的数学描述基于薛定谔方程，该方程描述了粒子的波函数随时间和空间的变化规律。

利用波函数的数学性质，可以导出相应的散射理论。

对于一个粒子从无穷远处入射到势场中的散射问题，可以通过薛定谔方程的求解，得到入射波、反射波和散射波的解析表达式。

通过计算这些波函数的幅度和相位，可以得到入射角度和出射角度之间的关系，进而揭示粒子在散射过程中的运动规律。

三、散射振幅和散射截面在量子散射理论中，散射振幅和散射截面是两个重要的物理量，可以用来描述粒子与势场相互作用的强度和模式。

散射振幅描述了入射波和散射波之间的干涉程度，它与势场的形状和强度密切相关。

通过计算散射振幅的模值和相位，可以得到散射过程中动力学信息，例如动量转移和能量转移等。

散射截面则是描述粒子被散射的概率密度，它与散射振幅直接相关。

通常采用微分散射截面和总散射截面来描述粒子在不同方向上被散射的概率。

通过计算和测量散射截面，可以研究和验证不同势场对粒子散射行为的影响。

四、应用和研究进展量子散射问题在物理学和化学领域中具有广泛的应用价值。

例如，在凝聚态物理中，散射理论可以用来解释电子在晶格中的散射行为，进而揭示材料的导电性和导热性等性质。