整式加减易错题-整体代入法
- 格式:doc
- 大小:73.50 KB
- 文档页数:1

七年级数学整式整体代入法好呀,今天我们来聊聊七年级的数学,特别是整式整体代入法。
这个听起来好像有点高深,其实就像我们生活中的小窍门,掌握了就能轻松搞定。
整式是什么呢?想象一下,你在做一道数学题,看到一堆字母像是打成了一团,别担心,这就是整式。
它们就像是你家的调料,可能有点杂乱,但只要用得当,味道就会变得美味可口。
整体代入法,简单来说,就是我们在做题的时候,把某个变量想象成一个“整体”,这样一来,问题看起来就没那么复杂了,仿佛一瞬间让一锅杂烩变成了美味的火锅,嗯,开始流口水了。
好比说,假设我们有一个整式,比如说 (x^2 + 3x + 2),我们想要解这个方程。
如果把这个 (x) 看作一块大蛋糕,我们可以想象成把蛋糕切成几块,先把它分开,再一个个解决。
整式整体代入法的意思就是,先把这块蛋糕的整体放在脑子里,想象一下,如果我把 (x) 设为某个具体的数,比如 1,哇,立刻算出来的结果就像咬了一口蛋糕,甜得让人心花怒放。
数学就像个迷宫,让人觉得无从下手。
你一头扎进去,转来转去就是找不到出口。
不过整体代入法就像是一把金钥匙,帮你打开那扇通往正确答案的大门。
比如说,你有一个方程 (f(x) = x^2 4),你想找它的零点,哦,这个时候我们可以把 (x) 代入一些数,看看结果如何。
比如当 (x = 2) 时,哎呀,结果就是 0,这就说明在这儿有个零点,就像找到了一颗闪闪发光的宝石。
整体代入法不仅仅是在解题,它还教会我们一种思考方式。
生活中,我们也常常需要把复杂的事情简单化。
比如,你在筹备一个派对,想想看,先决定主题,然后再考虑菜单、邀请谁,这样一步一步来,不就简单多了吗?整式代入法和这种思考方式有点像,把一个复杂的方程,先简化,再逐步破解,这样就能轻松应对各种数学难题。
咱们还可以说说这个方法的妙用。
很多同学看到复杂的方程就像见到了鬼,心里一惊,其实只要用上整体代入法,就能把“鬼”变成“小猫”。
例如,一个问题里有多个整式相加相减,我们可以找一个变量,先把它当成整体,然后逐步代入,这样解题就像是在解谜,挺有趣的。

第三讲整式的加减(一)一、常考题型题型总结【题型1】抄错题问题【例1】小郑在一次测验中计算一个多项式A 减去xz yz xy 235+-时,不小心看成加上xz yz xy 235+-,计算出错误结果为xz yz xy 462-+,试求出正确答案。
【例2】数学课上七年级一班的张老师给同学们写了这样一道题“当2,2-==b a 时,求多项式⎪⎭⎫ ⎝⎛---+-2233233414213b b a b a b b a b a ⎪⎭⎫ ⎝⎛++b a b a 23341322+-b 的值”,马小虎做题时把2=a 错抄成2-=a ,王小真没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由.【培优练习】1、李明在计算一个多项式减去2245x x -+时,误认为加上此式,计算出错误结果为221x x -+-,试求出正确答案。
2、2、某同学做一道数学题,误将求“A-B ”看成求“A+B ”,结果求出的答案是3x 2-2x+5.已知A=4x 2-3x-6,请正确求出A-B.3、一位同学做一道题:“已知两个多项式A ,B ,计算2A+B ”。
他误将“2A+B ”看成“A+2B ”,求得的结果为。
已知B=,求原题的正确答案。
4、计算下式的值:甲同学把错抄成,但他计算的结果也是正确的,你能说明其中的原因吗? 7292+-x x 232-+xx【题型2】分类讨论型问题【例1】如果关于x 的多项式21424-+x ax 与x x b 53+是次数相同的多项式,求4322123-+-b b b 的值 【培优练习】1、多项式12423232+++-+x x x ax x a 是关于x 的二次多项式,求a a a ++221 【题型3】绝对值双值性【例1】已知3x 2y |m|-(m-1)y+5是关于x ,y 的三次三项式,求2m 2-3m+1的值. 【培优练习】1、若多项式()22532m xy n y +--是关于x y ,的五次二项式,求222m mn n -+的值 2、如果()1233m x y m xy x ---+为四次三项式,则m =________。

1.如图,是小刚在电脑中设计的一个电子跳蚤,每跳一次包括上升和下降,即由点A—B—C为一个完整的动作.按照图中的规律,如果这个电子跳蚤落到9的位置,它需要跳的次数为 ( )A.5次B.6次C.7次D.8次C解析:C【分析】首先观察图形,得出一个完整的动作过后电子跳骚升高2个格,根据起始点为-5,终点为9,即可得出它需要跳的次数.【详解】解:由图形可得,一个完整的动作过后电子跳骚升高2个格,如果电子跳骚落到9的位置,则需要跳9(5)72--=次.故选C.此题考查数字的规律变化,关键是仔细观察图形,得出一个完整的动作过后电子跳骚升高2个格,难度一般.2.与(-b)-(-a)相等的式子是( )A.(+b)-(-a) B.(-b)+aC.(-b)+(-a) D.(-b)-(+a)B解析:B【分析】将各选项去括号,然后与所给代数式比较即可﹒【详解】解: (-b)-(-a)=-b+aA. (+b)-(-a)=b+a;B. (-b)+a=-b+a;C. (-b)+(-a)=-b-a;D. (-b)-(+a)=-b-a;故与(-b)-(-a)相等的式子是:(-b)+a﹒故选:B﹒【点睛】本题考查了去括号的知识,熟练去括号的法则是解题关键﹒3.某公司今年2月份的利润为x万元,3月份比2月份减少8%,4月份比3月份增加了10%,则该公司4月份的利润为(单位:万元)()A.(x﹣8%)(x+10%)B.(x﹣8%+10%)C.(1﹣8%+10%)x D.(1﹣8%)(1+10%)x D解析:D【分析】首先利用减小率的意义表示出3月份的利润,然后利用增长率的意义表示出4月份的利润.【详解】解:由题意得3月份的产值为(1﹣8%)x,4月份的产值为(1﹣8%)(1+10%)x.故选:D.【点睛】本题考查了列代数式,正确理解增长率以及下降率的定义是关键.4.如图,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是()A.y=2n+1 B.y=2n+n C.y=2n+1+n D.y=2n+n+1B解析:B【详解】∵观察可知:左边三角形的数字规律为:1,2,…,n,右边三角形的数字规律为:2,22,…,2n,n+,下边三角形的数字规律为:1+2,222+, (2)∴最后一个三角形中y与n之间的关系式是y=2n+n.故选B.【点睛】考点:规律型:数字的变化类.5.已知一个多项式与3x2+9x的和等于5x2+4x﹣1,则这个多项式是()A.2x2﹣5x﹣1 B.﹣2x2+5x+1 C.8x2﹣5x+1 D.8x2+13x﹣1A解析:A【分析】根据由题意可得被减式为5x2+4x-1,减式为3x2+9x,求出差值即是答案.【详解】由题意得:5x2+4x−1−(3x2+9x),=5x2+4x−1−3x2−9x,=2x 2−5x−1. 故答案选A. 【点睛】本题考查了整式的加减,解题的关键是熟练的掌握整式的加减运算.6.已知5a b +=,4ab =,则代数式()()35834ab a b a ab +++-的值为( ) A .36 B .40C .44D .46A解析:A 【分析】原式去括号整理后,将已知等式代入计算即可求出值. 【详解】 ∵a+b=5,ab=4,∴原式=3ab+5a+8b+3a−4ab=8(a+b)−ab=40−4=36, 故选A. 【点睛】本题考查的是代数式的求值,熟练掌握先化简再求值是解题的关键.7.把有理数a 代数410a +-得到1a ,称为第一次操作,再将1a 作为a 的值代入410a +-得到2a ,称为第二次操作,...,若a =23,经过第2020次操作后得到的是( ) A .-7 B .-1C .5D .11A解析:A 【分析】先确定第1次操作,a 1=|23+4|-10=17;第2次操作,a 2=|17+4|-10=11;第3次操作,a 3=|11+4|-10=5;第4次操作,a 4=|5+4|-10=-1;第5次操作,a 5=|-1+4|-10=-7;第6次操作,a 6=|-7+4|-10=-7;…,后面的计算结果没有变化,据此解答即可. 【详解】解:第1次操作,a 1=|23+4|-10=17; 第2次操作,a 2=|17+4|-10=11; 第3次操作,a 3=|11+4|-10=5; 第4次操作,a 4=|5+4|-10=-1; 第5次操作,a 5=|-1+4|-10=-7; 第6次操作,a 6=|-7+4|-10=-7; 第7次操作,a 7=|-7+4|-10=-7; …第2020次操作,a 2020=|-7+4|-10=-7. 故选:A . 【点睛】本题考查了绝对值和探索规律.解题的关键是先计算,再观察结果是按照什么规律变化的.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.8.已知单项式2x 3y 1+2m 与3x n +1y 3的和是单项式,则m ﹣n 的值是( ) A .3 B .﹣3 C .1 D .﹣1D解析:D 【分析】根据同类项的概念,首先求出m 与n 的值,然后求出m n -的值. 【详解】 解:单项式3122mx y+与133n xy +的和是单项式,3122m x y +∴与133n x y +是同类项,则13123n m +=⎧⎨+=⎩∴12m n =⎧⎨=⎩, 121m n ∴-=-=-故选:D . 【点睛】本题主要考查同类项,掌握同类项定义中的两个“相同”:(1)所含字母相同;(2)相同字母的指数相同,从而得出m ,n 的值是解题的关键. 9.下面去括号正确的是( ) A .2()2y x y y x y +--=+- B .2(35)610a a a a --=-+ C .()y x y y x y ---=+- D .222()2x x y x x y +-+=-+ B解析:B 【分析】根据去括号法则对四个选项逐一进行分析,要注意括号前面的符号,以选用合适的法则. 【详解】A. 2()2y x y y x y +--=--,故错误;B. 2(35)610a a a a --=-+,故正确;C. ()y x y y x y ---=++,故错误;D. 222()22x x y x x y +-+=-+,故错误; 故选:B 【点睛】本题考查去括号的方法:去括号时,运用乘法的分配律,先把括号前的数字与括号里各项相乘;括号前是“+”,去括号后,括号里的各项都不改变符号;括号前是“一”,去括号后,括号里的各项都改变符号.10.下列式子中,是整式的是( ) A .1x + B .11x + C .1÷x D .1x x+ A 解析:A【分析】根据整式的定义即单项式和多项式统称为整式,找出其中的单项式和多项式即可. 【详解】解:A. 1x +是整式,故正确; B.11x +是分式,故错误; C. 1÷x 是分式,故错误;D.1x x +是分式,故错误. 故选A. 【点睛】本题主要考查了整式,关键是掌握整式的概念.11.把一个大正方形和四个相同的小正方形按图①、②两种方式摆放,则大正方形的周长与小正方形的周长的差是( )A .2+a bB .+a bC .3a b +D .3a b + D解析:D 【分析】利用大正方形的周长减去4个小正方形的周长即可求解. 【详解】解:根据图示可得:大正方形的边长为2a b +,小正方形边长为4a b-,∴大正方形的周长与小正方形的周长的差是: 2a b +×4-4a b-×4=a+3b. 故选;D. 【点睛】本题考查了列代数式,正确求出大小正方形的边长列代数式,以及整式的化简,正确对整式进行化简是关键.12.有20个数排成一行,对于任意相邻的三个数,都有中间的数等于前后两数的和.如果第一个数是0,第二个数是2,这20个数的和是( ) A .2 B .﹣2C .0D .4A解析:A 【分析】根据题意可以写出这组数据的前几个数,从而发现数字的变化规律,再利用规律求解. 【详解】解:由题意可得,这列数为:0,2,2,0,﹣2,﹣2,0,2,2,…,∴这20个数每6个为一循环,且前6个数的和是:0+2+2+0+(﹣2)+(﹣2)=0, ∵20÷6=3…2,∴这20个数的和是:0×3+(0+2)=2. 故选:A . 【点睛】本题考查了数字的变化规律,正确理解题意,发现题目中数字的变化规律:每6个数重复出现是解题的关键.13.下列说法:①在数轴上表示a -的点一定在原点的左边;②有理数a 的倒数是1a;③一个数的相反数一定小于或等于这个数;④如果a b >,那么22a b >;⑤235x y的次数是2;⑥有理数可以分为整数、正分数、负分数和0;⑦27m ba -与2abm 是同类项.其中正确的个数为( ) A .1个 B .2个C .3个D .4个A解析:A 【分析】根据字母可以表示任意数可判断①,根据特殊例子0没有倒数可判断②,根据负数的相反数可判断③,根据特殊例子a=1,b=-2,可判断④,根据单项式次数的定义可判断⑤,根据有理数的分类判断⑥,根据同类项的概念判断⑦. 【详解】字母可以表示任意数,当a <0时,-a >0,故①错误; 0没有倒数,故②错误;负数的相反数是正数,正数大于负数,故③错误; 若a=1,b=-2,a b >,但是22a b <,故④错误;235x y的次数是3,故⑤错误; 0属于整数,故⑥这种分类不正确;27m ba -与2abm 是同类项,⑦正确,故选A.【点睛】本题考查有理数和代数式的相关概念,熟记这类知识点是解题的关键.14.小明乘公共汽车到白鹿原玩,小明上车时,发现车上已有(6a ﹣2b )人,车到中途时,有一半人下车,但又上来若干人,这时车上共有(10a ﹣6b )人,则中途上车的人数为( ) A .16a ﹣8b B .7a ﹣5bC .4a ﹣4bD .7a ﹣7b B解析:B 【分析】根据题意表示出途中下车的人数,再根据车上总人数即可求得中途上车的人数. 【详解】由题意可得:(10a ﹣6b )﹣[(6a ﹣2b )﹣(3a ﹣b )]=10a ﹣6b ﹣6a +2b +3a ﹣b =7a ﹣5b . 故选B . 【点睛】本题考查了整式加减的应用,根据题意正确列出算式是解决问题的关键. 15.下列说法错误的是( ) A .23-2x y 的系数是32-B .数字0也是单项式C .-x π是二次单项式D .23xy π的系数是23πC 解析:C 【分析】根据单项式的有关定义逐个进行判断即可. 【详解】A. 23-2x y 的系数是32-,故不符合题意;B. 数字0也是单项式 故不符合题意;C. -x π是一次单项式 ,故原选项错误D.23xy π的系数是23π,故不符合题意. 故选C . 【点睛】本题考查对单项式有关定义的应用,能熟记单项式的有关定义是解此题关键. 1.观察下列顺序排列的等式:9×0+1 = 1,9×1+2 = 11,9×2+3=21, 9×3+4=31,9×4+5=41,……,猜想:第n 个等式(n 为正整数)用n 表示,可表示成_________.【分析】根据数据所显示的规律可知:第一数列都是9第2数列开始有顺序且都是所对序号的数减去1加号后的数据有顺序且与所在的序号项吻合等号右端是的规律所以第n 个等式(n 为正整数)应为【详解】根据分析:即第 解析:109n -【分析】根据数据所显示的规律可知:第一数列都是9,第2数列开始有顺序且都是所对序号的数减去1,加号后的数据有顺序且与所在的序号项吻合,等号右端是()10?11n -+的规律,所以第n 个等式(n 为正整数)应为()()9110?11n n n -+=-+. 【详解】根据分析:即第n 个式子是()()9110?11109n n n n -+=-+=-. 故答案为:109n -. 【点睛】本题主要考查了数字类规律探索题.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后直接利用规律求解.2.a-b,b-c,c-a三个多项式的和是____________0【解析】(a-b)+(b-c)+(c-a)=a-b+b-c+c-a=a-a+b-b+c-c=0故答案为0解析:0【解析】(a-b)+(b-c)+(c-a)=a-b+b-c+c-a=a-a+b-b+c-c=0,故答案为0.3.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示,按照这样的规律,摆第n个图,需用火柴棒的根数为_______________.6n+2【解析】寻找规律:不难发现后一个图形比前一个图形多6根火柴棒即:第1个图形有8根火柴棒第2个图形有14=6×1+8根火柴棒第3个图形有20=6×2+8根火柴棒……第n个图形有6n+2根火柴棒解析:6n+2.【解析】寻找规律:不难发现,后一个图形比前一个图形多6根火柴棒,即:第1个图形有8根火柴棒,第2个图形有14=6×1+8根火柴棒,第3个图形有20=6×2+8根火柴棒,……,第n个图形有6n+2根火柴棒.4.将连续正整数按以下规律排列,则位于第7行第7列的数x是________________.?136********259142027?48131926??7121825??111724??1623??22?????x?【分析】先根据第一行的第一列的数以及第二行的第二列的数第三行的第三列数第四行的第四列数进而得出变化规律由此得出结果【详解】第一行的第一列的数是1;第二行的第二列的数是5=1+4;第三行的第三列的数是解析:85【分析】先根据第一行的第一列的数,以及第二行的第二列的数,第三行的第三列数,第四行的第四列数,进而得出变化规律,由此得出结果.【详解】第一行的第一列的数是 1;第二行的第二列的数是 5=1+4;第三行的第三列的数是 13=1+4+8;第四行的第四列的数是 25=1+4+8+12;......第n行的第n列的数是1+4+8+12+...+4(n-1)=1+4[1+2+3+...+(n+1)]=1+2n(n-1);∴第七行的第七列的数是1+2×7×(7-1)=85;故答案为:85.【点睛】本题考查数字的变化规律,学生通过观察、分析、归纳发现其中的规律,从而利用规律解决问题.5.观察下列式子:1×3+1=22;7×9+1=82;25×27+1=262;79×81+1=802;…可猜想第2 019个式子为__________.(32019-2)×32019+1=(32019-1)2【分析】观察等式两边的数的特点用n表示其规律代入n=2016即可求解【详解】解:观察发现第n个等式可以表示为:(3n-2)×3n+1=(3n-解析:(32 019-2)×32019+1=(32 019-1)2【分析】观察等式两边的数的特点,用n表示其规律,代入n=2016即可求解.【详解】解:观察发现,第n 个等式可以表示为:(3n -2)×3n +1=(3n -1)2, 当n =2019时,(32019-2)×32019+1=(32019-1)2,故答案为:(32019-2)×32019+1=(32019-1)2. 【点睛】此题主要考查数的规律探索,观察发现等式中的每一个数与序数n 之间的关系是解题的关键.6.当x =1时,ax +b +1=﹣3,则(a +b ﹣1)(1﹣a ﹣b )的值为_____.-25【分析】由x=1时代数式ax+b+1的值是﹣3求出a+b 的值将所得的值整体代入所求的代数式中进行计算即可得解【详解】解:∵当x =1时ax+b+1的值为﹣3∴a+b+1=﹣3∴a+b =﹣4∴(a解析:-25. 【分析】由x =1时,代数式ax +b +1的值是﹣3,求出a +b 的值,将所得的值整体代入所求的代数式中进行计算即可得解. 【详解】解:∵当x =1时,ax +b +1的值为﹣3, ∴a +b +1=﹣3, ∴a +b =﹣4,∴(a +b ﹣1)(1﹣a ﹣b )=(a +b ﹣1)[1﹣(a +b )]=(﹣4﹣1)×(1+4)=﹣25. 故答案为:﹣25. 【点睛】此题考查整式的化简求值,运用整体代入法是解决问题的关键.7.计算7a 2b ﹣5ba 2=_____.2a2b 【分析】根据合并同类项法则化简即可【详解】故答案为:【点睛】本题考查了合并同类项解题的关键是熟练运用合并同类项的法则本题属于基础题型解析:2a 2b 【分析】根据合并同类项法则化简即可. 【详解】()22227a b 5ba =75a b=2a b ﹣﹣.故答案为:22a b 【点睛】本题考查了合并同类项,解题的关键是熟练运用合并同类项的法则,本题属于基础题型. 8.如果关于x 的多项式42142mx x +-与多项式35n x x +的次数相同,则2234n n -+-=_________.【分析】根据多项式的次数的定义先求出n 的值然后代入计算即可得到答案【详解】解:∵多项式与多项式的次数相同∴∴;故答案为:【点睛】本题考查了求代数式的值以及多项式次数的定义解题的关键是正确求出n 的值解析:24-【分析】根据多项式的次数的定义,先求出n 的值,然后代入计算,即可得到答案.【详解】解:∵多项式42142mx x +-与多项式35n x x +的次数相同, ∴4n =,∴22234243443212424n n -+-=-⨯+⨯-=-+-=-;故答案为:24-.【点睛】本题考查了求代数式的值,以及多项式次数的定义,解题的关键是正确求出n 的值. 9.两堆棋子,将第一堆的2个棋子移到第二堆去之后,第二堆棋子数就成了第一堆棋子数的2倍.设第一堆原有a 个棋子,第二堆原有______个棋子.【分析】根据题意可得第二堆现在的棋子数是2(a-2)因此原来的棋子数为2(a-2)-2【详解】解:由题意可得:现在第二堆有2(a-2)个棋子因此原来第二堆有2(a-2)-2=2a-6个棋子故答案为:解析:()26a -【分析】根据题意可得第二堆现在的棋子数是2(a -2),因此原来的棋子数为2(a -2)-2.【详解】解:由题意可得:现在第二堆有2(a -2)个棋子,因此原来第二堆有2(a -2)-2=2a -6个棋子.故答案为:(2a -6).【点睛】本题考查了整式加减的应用,根据题意列出代数式是解决此题的关键.10.求值:(1)()()22232223a a a a a -++-=______,其中2a =-;(2)()()222291257127a ab ba ab b -+-++=______,其中12a =,12b =-; (3)()()222222122a b ab a b ab +----=______,其中2a =-,2b =.60【分析】先根据去括号合并同类项法则进行化简然后再代入求值即可【详解】(1)原式=当时原式=;(2)原式=当时原式=;(3)原式=【点睛】本题考查整式的化简求值掌握去括号合并同类项法则是解题的关键解析:6 0【分析】先根据去括号、合并同类项法则进行化简,然后再代入求值即可.【详解】(1)原式= 2222342268a a a a a a a --+-=-,当2a =-时,原式=()()228241620--⨯-=+=;(2)原式=222222912571272242a ab b a ab b a ab b -+---=--, 当12a =,12b =-时,原式=22111111224266222222⎛⎫⎛⎫⎛⎫⨯-⨯⨯--⨯-=+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭; (3)原式=22222222220a b ab a b ab +-+--=.【点睛】本题考查整式的化简求值,掌握去括号、合并同类项法则是解题的关键.11.图中阴影部分的面积为______. 【分析】图中阴影部分面积为半径为R 的半圆面积减去直径为R 的圆的面积进行计算即可【详解】解:【点睛】本题考查圆的面积计算公式熟记公式并根据题意找出阴影部分面积为半径为R 的半圆面积减去直径为R 的圆的面积解析:21π4R【分析】图中阴影部分面积为半径为R 的半圆面积减去直径为R 的圆的面积,进行计算即可.【详解】解:2221=()224R R S R πππ-=阴影 【点睛】本题考查圆的面积计算公式,熟记公式并根据题意找出阴影部分面积为半径为R 的半圆面积减去直径为R 的圆的面积是解题关键.1.如图所示,一个点从数轴上的原点开始,先向右移动3单位长度,再向左移动5个单位长度,可以看到终点表示的数是﹣2,已知点A ,B 是数轴上的点,请参照下图并思考,完成下列各题.(1)如果点A 表示数-3,将A 点向右移动7个单位长度,那么终点B 表示的数是 ,A ,B 两点间的距离为 .(2)如果点A 表示数3,将A 点向左移动7个单位长度,再向右移动5个单位长度,那么终点B 表示的数是 ,A ,B 两点间的距离为 .(3)如果点A 表示数4-,将A 点向右移动168个单位长度,再向左移动256个单位长度,那么终点B 表示的数是 ,A ,B 两点间的距离是 .(4)一般地,如果A 点表示数为m ,将A 点向右移动n 个单位长度,再向左移动P 个单位长度,那么,请你猜想终点B 表示什么数?A ,B 两点间的距离为多少?解析:(1)4,7;(2) 1,2;(3) -92,88;(4)m+n-p ,|n-p|【分析】(1)根据数轴上的点向右平移加,向左平移减,可得B 点表示的数为-3+7=4,根据数轴上两点间的距离是大数减小数,可得答案;(2)根据数轴上的点向右平移加,向左平移减,可得B 点表示的数3-7+5=1,根据数轴上两点间的距离是大数减小数,可得答案;(3)根据数轴上的点向右平移加,向左平移减,可得B 点表示的数-4+168-256=-92,根据数轴上两点间的距离是大数减小数,可得答案;(4)按照(1)(2)(3)中的方法讨论更加一般的情况即可求解.【详解】解:(1)∵点A 表示数-3,∴将A 点向右移动7个单位长度,那么终点B 表示的数是-3+7=4,A ,B 两点间的距离为4-(-3)=7,故答案为:4,7;(2)∵点A 表示数3,∴将A 点向左移动7个单位长度,再向右移动5个单位长度,那么终点B 表示的数是3-7+5=1,A ,B 两点间的距离为3-1=2,故答案为:1,2;(3)∵点A 表示数-4,将A 点向右移动168个单位长度,再向左移动256个单位长度,那么终点B 表示的数是-4+168-256=-92,A ,B 两点间的距离是-4-(-92)=88,故答案为:-92,88;(4)∵A 点表示的数为m ,∴将A 点向右移动n 个单位长度,再向左移动p 个单位长度, 那么点B 表示的数为m+n-p ,A ,B 两点间的距离为|m-(m+n-p)|=|n-p|.故答案为:m+n-p ,|n-p|.【点睛】本题考查的是数轴上点的平移规律及数轴上两点之间的距离公式,点在数轴上平移遵循“左减右加”原则;注意数轴上两点之间的距离为大数减小数,当不确定谁大谁小时记得加绝对值符号;正确利用数形结合分析是解题关键.2.化简:(1)()()22224232a b ab ab a b ---;(2)2237(43)2x x x x ⎡⎤----⎣⎦.解析:(1)22105a b ab -;(2)2533x x --【分析】(1)先去括号,再合并同类项即可得到答案;(2)先去括号,再合并同类项即可得到答案.【详解】(1)()()22224232a b ab ab a b ---22224236a b ab ab a b =--+22105a b ab =-.(2)2237(43)2x x x x ⎡⎤----⎣⎦2237(43)2x x x x =-+-+2237432x x x x =-+-+2533x x =--.【点睛】本题主要考查了整式的加减,整式加减的实质就是去括号,合并同类项,一般步骤是:先去括号,然后再合并同类项.3.日历上的规律:下图是2020年元月的日历,图中的阴影区域是在日历中选取的一块九宫格.(1)九宫格中,四个角上的四个数之和与九宫格中央这个数有什么关系?(2)请你自选一块九宫格进行计算,观察四个角上的四个数之和与九宫格中央那个数是否还有这种关系.(3)试说明原理.解析:(1)四个角上的四个数之和等于九宫格中央这个数的4倍;(2)四个角上的四个数之和等于九宫格中央这个数的4倍,选取九宫格见解析;(3)见解析.【分析】(1)求出四个角上的四个数之和与九宫格中央这个数,从而验证它们的关系. (2)选择如下图的九宫格,验证他们的关系即可.(3)设九宫格中央这个数为a ,列等式进行验证即可.【详解】(1)四个角上的四个数之和等于九宫格中央这个数的4倍.理由如下:6228202828414+++=+=⨯.(2)如图,9112325174+++=⨯,所以四个角上的四个数之和等于九宫格中央这个数的4倍.(选取的九宫格不唯一).(3)设九宫格中央这个数为a ,那么左上角的数为71a --,右上角的数为71a -+,左下角的数为71a +-,右下角的数为71a ++,四个数的和为(71)(71)(71)(71)4a a a a a --+-+++-+++=.即四个角上的四个数之和等于九宫格中央这个数的4倍.【点睛】本题考查了整式的加减应用,掌握整式的加减运算法则是解题的关键.4.古人云:凡事宜先预后立.我们做任何事情都要先想清楚,然后再动手去做,才能避免盲目从事.一天,需要小亮计算一个L 形的花坛的面积,在动手测量前,小亮依花坛形状画出示意图,并用字母表示出了将要测量的边长(如图所示),小亮在列式进行面积计算时,发现还需要再测量一条边的长度,你认为他还需要测量哪条边的长度?请你在图中用字母n 表示出来,然后求出它的面积.解析:图详见解析,am bn mn +-【分析】由图可知花坛是由两块矩形组成,若想求解矩形面积就必需知道矩形的长和宽,而图中少了左边矩形的宽.【详解】解:需要测量的边如图所示(或测量剩下的那条边的长度).图形的面积为am bn mn +-.【点睛】不规则的几何图形的面积的计算要转化为规则的几何图形面积的和差.。


专题03 整体代入法【规律总结】整体代入法,在求代数式值中应用求代数式的值最常用的方法,即把字母所表示的数值直接代入,计算求值。
有时给出的条件不是字母的具体值,就需要先进行化简,求出字母的值,但有时很难求出字母的值或者根本就求不出字母的值,根据题目特点,将一个代数式的值整体代入,求值时方便又快捷,这种整体代入的技法经常用到。
【典例分析】例1、在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD−AB=2时,S2−S1的值为()A. 2aB. 2bC. 2a−2bD. −2b【答案】B【解析】解:S1=(AB−a)⋅a+(CD−b)(AD−a)=(AB−a)⋅a+(AB−b)(AD−a),S2=AB(AD−a)+(a−b)(AB−a),∴S2−S1=AB(AD−a)+(a−b)(AB−a)−(AB−a)⋅a−(AB−b)(AD−a)=(AD−a)(AB−AB+b)+(AB−a)(a−b−a)=b⋅AD−ab−b⋅AB+ab=b(AD−AB)=2b.故选:B.利用面积的和差分别表示出S1和S2,然后利用整式的混合运算计算它们的差.本题考查了整式的混合运算:“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.也考查了正方形的性质.例2、若m是方程2x2−3x−1=0的一个根,则6m2−9m+2015的值为______.【答案】2018【解析】解:由题意可知:2m2−3m−1=0,∴2m2−3m=1∴原式=3(2m2−3m)+2015=2018故答案为:2018根据一元二次方程的解的定义即可求出答案.本题考查一元二次方程的解,解题的关键是正确理解一元二次方程的解的定义,本题属于基础题型.例3、解下列各题:(1)若n满足(n−2023)(2021−n)=−6,求(n−2023)2+(2021−n)2的值.(2)已知:m2=n+2,n2=m+2(m≠n),求:m3−2mn+n3的值.【答案】解:(1)∵(n−2023)(2021−n)=−6,∴原式=(n−2023+2021−n)2−2(n−2023)(2021−n)=(−2)2−2×(−6)=4+12=16;(2)∵m2=n+2①,n2=m+2(m≠n)②,∴m2−n=2,n2−m=2,∵m≠n,∴m−n≠0,∴①−②得m2−n2=n−m∴(m−n)(m+n)=−(m−n),∵m−n≠0,∴m+n=−1∴原式=m3−mn−mn+n3=m(m2−n)+n(n2−m)=2m +2n =2(m +n) =2×(−1) =−2.【解析】本题主要考查的是代数式求值,完全平方公式,运用了整体代入法的有关知识. (1)将给出的代数式进行变形为(n −2023+2021−n)2−2(n −2023)(2021−n),然后整体代入求值即可;(2)先根据m 2=n +2,n 2=m +2(m ≠n),求出m +n =−1,然后将给出的代数式进行变形,最后整体代入求解即可.【好题演练】一、选择题1. 已知a +b =12,则代数式2a +2b −3的值是( )A. 2B. −2C. −4D. −312【答案】B【解析】解:∵2a +2b −3=2(a +b)−3, ∴将a +b =12代入得:2×12−3=−2 故选:B .注意到2a +2b −3只需变形得2(a +b)−3,再将a +b =12,整体代入即可 此题考查代数式求值的整体代入,只需通过因式解进行变形,再整体代入即可.2. 若α、β为方程2x 2−5x −1=0的两个实数根,则2α2+3αβ+5β的值为( )A. −13B. 12C. 14D. 15【答案】B 【解析】 【分析】本题考查了根与系数的关系:若x 1,x 2是一元二次方程ax 2+bx +c =0(a ≠0)的两根时,x 1+x 2=−b a,x 1x 2=ca .也考查了一元二次方程解的定义.根据一元二次方程解的定义得到2α2−5α−1=0,即2α2=5α+1,则2α2+3αβ+5β可表示为5(α+β)+3αβ+1,再根据根与系数的关系得到α+β=52,αβ=−12,然后利用整体代入的方法计算. 【解答】解:∵α为2x 2−5x −1=0的实数根, ∴2α2−5α−1=0,即2α2=5α+1,∴2α2+3αβ+5β=5α+1+3αβ+5β=5(α+β)+3αβ+1, ∵α、β为方程2x 2−5x −1=0的两个实数根, ∴α+β=52,αβ=−12,∴2α2+3αβ+5β=5×52+3×(−12)+1=12.故选B .3. 如果a 2+2a −1=0,那么代数式(a −4a ).a 2a−2的值是( )A. −3B. −1C. 1D. 3【答案】C 【解析】 【分析】本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.根据分式的减法和乘法可以化简题目中的式子,然后根据a 2+2a −1=0,可以得到a 2+2a =1,从而可以求得所求式子的值. 【解答】解:(a −4a )⋅a 2a−2=a 2−4a⋅a 2a−2=(a+2)(a−2)a⋅a 2a−2=a 2+2a ,由a 2+2a −1=0得a 2+2a =1,故原式=1. 故选C .4.已知1x −1y=3,则代数式2x+3xy−2yx−xy−y的值是()A. −72B. −112C. 92D. 34【答案】D【解析】解:∵1x−1y=3,∴y−xxy=3,∴x−y=−3xy,则原式=2(x−y)+3xy(x−y)−xy=−6xy+3xy−3xy−xy=−3xy−4xy=34,故选:D.由1x −1y=3得出y−xxy=3,即x−y=−3xy,整体代入原式=2(x−y)+3xy(x−y)−xy,计算可得.本题主要考查分式的加减法,解题的关键是掌握分式加减运算法则和整体代入思想的运用.5.已知x1,x2是方程x2−3x−2=0的两根,则x12+x22的值为()A. 5B. 10C. 11D. 13【答案】D【解析】【分析】本题考查了完全平方公式以及根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=−ba ,x1x2=ca,利用根与系数的关系得到x1+x2=3,x1x2=−2,再利用完全平方公式得到x12+x22=(x1+x2)2−2x1x2,然后利用整体代入的方法计算.【解答】解:根据题意得x1+x2=3,x1x2=−2,所以x12+x22=(x1+x2)2−2x1x2=32−2×(−2)=13.故选:D.6.小慧去花店购买鲜花,若买5支玫瑰和3支百合,则她所带的钱还剩下10元;若买3支玫瑰和5支百合,则她所带的钱还缺4元.若只买8支玫瑰,则她所带的钱还剩下()A. 31元B. 30元C. 25元D. 19元【答案】A【解析】【分析】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.设每支玫瑰x元,每支百合y元,根据总价=单价×数量结合小慧带的钱数不变,可得出关于x,y的二元一次方程,整理后可得出y=x+7,再将其代入5x+3y+10−8x中即可求出结论.【解答】解:设每支玫瑰x元,每支百合y元,依题意,得:5x+3y+10=3x+5y−4,∴y=x+7,∴5x+3y+10−8x=5x+3(x+7)+10−8x=31.故选A.二、填空题7.已知ab=a+b+1,则(a−1)(b−1)=______.【答案】2【解析】【分析】本题考查多项式乘多项式,解题的关键是掌握多项式乘多项式的运算法则及整体代入思想的运用,属于基础题.将ab=a+b+1代入原式=ab−a−b+1,合并即可得.【解答】解:当ab=a+b+1时,原式=ab−a−b+1=a+b+1−a−b+1=2,故答案为:2.8.将抛物线y=ax2+bx−1向上平移3个单位长度后,经过点(−2,5),则8a−4b−11的值是______.【答案】−5【解析】解:将抛物线y=ax2+bx−1向上平移3个单位长度后,表达式为:y=ax2+bx+2,∵经过点(−2,5),代入得:4a−2b=3,则8a−4b−11=2(4a−2b)−11=2×3−11=−5,故答案为:−5.根据二次函数的平移得出平移后的表达式,再将点(−2,5)代入,得到4a−2b=3,最后将8a−4b−11变形求值即可.本题考查了二次函数的平移,二次函数图象上点的坐标特征,解题的关键是得出平移后的表达式.9.若a+b=1,则a2−b2+2b−2=______.【答案】−1【解析】解:∵a+b=1,∴a2−b2+2b−2=(a+b)(a−b)+2b−2=a−b+2b−2=a+b−2=1−2=−1.故答案为:−1.由于a+b=1,将a2−b2+2b−2变形为a+b的形式,整体代入计算即可求解.本题考查了平方差公式,注意整体思想的应用.10.若实数x满足x2−2x−1=0,则2x3−7x2+4x−2017=______.【答案】−2020【解析】【分析】把−7x2分解成−4x2与−3x2相加,然后把所求代数式整理成用x2−2x表示的形式,然后代入数据计算求解即可.本题考查了提公因式法分解因式,利用因式分解整理出已知条件的形式是解题的关键,整体代入思想的利用比较重要.【解答】解:∵x2−2x−1=0,∴x2−2x=1,2x3−7x2+4x−2017=2x3−4x2−3x2+4x−2017,=2x(x2−2x)−3x2+4x−2017,=6x−3x2−2017,=−3(x2−2x)−2017=−3−2017=−2020,故答案为−2020.11.已知|x−y+2|+√x+y−2=0,则x2−y2的值为________.【答案】−4【解析】【分析】本题考查了非负数的性质,解题关键是掌握几个非负数的和等于0,那么这几个非负数都等于0.由非负数的性质得出x、y的值,再代入所求代数式求解即可.【解答】解:∵|x−y+2|+√x+y−2=0,∴x−y+2=0,x+y−2=0,即x−y=−2,x+y=2,∴x 2−y 2=(x +y)(x −y)=2×(−2)=−4, 故答案为−4.12. 已知m +n =3mn ,则1m +1n 的值为______.【答案】3 【解析】 【试题解析】 【分析】本题考查了分式的化简求值,利用通分将原式变形为m+nmn 是解题的关键. 原式通分后可得出m+nmn ,代入m +n =3mn 即可求出结论. 【解答】 解:原式=1m +1n =m+n mn ,又∵m +n =3mn , ∴原式=m+n mn=3.故答案为:3.三、解答题13. 已知x =√2+1,y =√2−1,分别求下列代数式的值;(1)x 2+y 2; (2)yx +xy .【答案】解:(1)∵x =2+1=√2−1,y =2−1=√2+1, ∴x −y =−2,xy =2−1=1,∴x 2+y 2=(x −y)2+2xy =(−2)2+2×1=6;(2)∵x 2+y 2=6,xy =1, ∴原式=x 2+y 2xy=61=6.【解析】本题考查二次根式的化简求值,分母有理化,解题的关键是运用完全平方公式以及整体思想,本题属于基础题型.(1)先将x 、y 进行分母有理化,得到x =√2−1,y =√2+1,再求出x −y 与xy 的值,然后根据完全平方公式得出x 2+y 2=(x −y)2+2xy ,再整体代入即可; (2)将所求式子变形为x 2+y 2xy,再整体代入即可.14. 阅读材料,然后解方程组.材料:解方程组{x −y −1=0, ①4(x −y)−y =5. ②由①得x −y③,把③代入②,得4×1−y =5. 解得y =−1.把y =−1代入③,得x =0. ∴{x =0y =−1这种方法称为“整体代入法”.你若留心观察,有很多方程组可采用此方法解答,请用这种方法解方程组{2x −3y −2=0,①2x−3y+57+2y =9.②.【答案】解:由①得:2x −3y =2③, 将③代入②得:1+2y =9,即y =4, 将y =4代入③得:x =7, 则方程组的解为{x =7y =4.【解析】由第一个方程求出2x −3y 的值,代入第二个方程求出y 的值,进而求出x 的值,即可确定出方程组的解.此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.15. 阅读材料,善于思考的小军在解方程组{2x +5y =3①4x +11y =5②时,采用了一种“整体代换”的解法:解:将方程②变形:4x +10y +y =5即2(2x +5y)+y =5③ 把方程①代入③得2×3+y =5 ∴y =−1把y =−1代入①得x =4 ∴方程组的解为{x =4y =−1 请你解决以下问题:(1)模仿小军的“整体代换”法解方程组{3x −2y =5 ①9x −4y =19②(2)已知x 、y 满足方程组{5x 2−2xy +20y 2=822x 2−xy +8y 2=32,求x 2+4y 2的值; 【答案】解:(1)由②得:3x +6x −4y =19,即3x +2(3x −2y)=19③, 把①代入③得:3x +10=19,即x =3, 把x =3代入①得:y =2, 则方程组的解为{x =3y =2;(2)由5x 2−2xy +20y 2=82得:5(x 2+4y 2)−2xy =82,即x 2+4y 2=82+2xy5,由2x 2−xy +8y 2=32得:2(x 2+4y 2)−xy =32,即2×82+2xy5−xy =32,整理得:xy =4, ∴x 2+4y 2=82+2xy5=82+85=18.【解析】此题考查了解二元一次方程组,弄清阅读材料中的“整体代入”方法是解本题的关键.(1)模仿小军的“整体代换”法,求出方程组的解即可;(2)方程组第一个方程变形表示出x 2+4y 2,第二个方程变形后代入求出xy 的值,进而求出x 2+4y 2的值.16. (1)已知x 3⋅x a ⋅x 2a+1=x 31求a 的值;(2)若n 为正整数,且x 2n =4,求(3x 3n )2−4⋅(x 2)2n 的值。

专题03 整体代入法【规律总结】整体代入法,在求代数式值中应用求代数式的值最常用的方法,即把字母所表示的数值直接代入,计算求值。
有时给出的条件不是字母的具体值,就需要先进行化简,求出字母的值,但有时很难求出字母的值或者根本就求不出字母的值,根据题目特点,将一个代数式的值整体代入,求值时方便又快捷,这种整体代入的技法经常用到。
【典例分析】例1、在矩形ABCD内,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),矩形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.当AD−AB=2时,S2−S1的值为()A. 2aB. 2bC. 2a−2bD. −2b【答案】B【解析】解:S1=(AB−a)⋅a+(CD−b)(AD−a)=(AB−a)⋅a+(AB−b)(AD−a),S2=AB(AD−a)+(a−b)(AB−a),∴S2−S1=AB(AD−a)+(a−b)(AB−a)−(AB−a)⋅a−(AB−b)(AD−a)=(AD−a)(AB−AB+b)+(AB−a)(a−b−a)=b⋅AD−ab−b⋅AB+ab=b(AD−AB)=2b.故选:B.利用面积的和差分别表示出S1和S2,然后利用整式的混合运算计算它们的差.本题考查了整式的混合运算:“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.也考查了正方形的性质.例2、若m是方程2x2−3x−1=0的一个根,则6m2−9m+2015的值为______.【答案】2018【解析】解:由题意可知:2m2−3m−1=0,∴2m2−3m=1∴原式=3(2m2−3m)+2015=2018故答案为:2018根据一元二次方程的解的定义即可求出答案.本题考查一元二次方程的解,解题的关键是正确理解一元二次方程的解的定义,本题属于基础题型.例3、解下列各题:(1)若n满足(n−2023)(2021−n)=−6,求(n−2023)2+(2021−n)2的值.(2)已知:m2=n+2,n2=m+2(m≠n),求:m3−2mn+n3的值.【答案】解:(1)∵(n−2023)(2021−n)=−6,∴原式=(n−2023+2021−n)2−2(n−2023)(2021−n)=(−2)2−2×(−6)=4+12=16;(2)∵m2=n+2①,n2=m+2(m≠n)②,∴m2−n=2,n2−m=2,∵m≠n,∴m−n≠0,∴①−②得m2−n2=n−m∴(m−n)(m+n)=−(m−n),∵m−n≠0,∴m+n=−1∴原式=m3−mn−mn+n3=m(m2−n)+n(n2−m)=2m +2n=2(m +n)=2×(−1)=−2.【解析】本题主要考查的是代数式求值,完全平方公式,运用了整体代入法的有关知识.(1)将给出的代数式进行变形为(n −2023+2021−n)2−2(n −2023)(2021−n),然后整体代入求值即可;(2)先根据m 2=n +2,n 2=m +2(m ≠n),求出m +n =−1,然后将给出的代数式进行变形,最后整体代入求解即可.【好题演练】一、选择题1. 已知a +b =12,则代数式2a +2b −3的值是( ) A. 2B. −2C. −4D. −312 【答案】B 【解析】解:∵2a +2b −3=2(a +b)−3,∴将a +b =12代入得:2×12−3=−2故选:B .注意到2a +2b −3只需变形得2(a +b)−3,再将a +b =12,整体代入即可此题考查代数式求值的整体代入,只需通过因式解进行变形,再整体代入即可.2. 若α、β为方程2x 2−5x −1=0的两个实数根,则2α2+3αβ+5β的值为( ) A. −13B. 12C. 14D. 15【答案】B【解析】【分析】 本题考查了根与系数的关系:若x 1,x 2是一元二次方程ax 2+bx +c =0(a ≠0)的两根时,x 1+x 2=−b a,x 1x 2=c a .也考查了一元二次方程解的定义. 根据一元二次方程解的定义得到2α2−5α−1=0,即2α2=5α+1,则2α2+3αβ+5β可表示为5(α+β)+3αβ+1,再根据根与系数的关系得到α+β=52,αβ=−12,然后利用整体代入的方法计算.【解答】解:∵α为2x 2−5x −1=0的实数根,∴2α2−5α−1=0,即2α2=5α+1,∴2α2+3αβ+5β=5α+1+3αβ+5β=5(α+β)+3αβ+1,∵α、β为方程2x 2−5x −1=0的两个实数根,∴α+β=52,αβ=−12,∴2α2+3αβ+5β=5×52+3×(−12)+1=12. 故选B .3. 如果a 2+2a −1=0,那么代数式(a −4a ).a 2a−2的值是( )A. −3B. −1C. 1D. 3【答案】C【解析】【分析】 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.根据分式的减法和乘法可以化简题目中的式子,然后根据a 2+2a −1=0,可以得到a 2+2a =1,从而可以求得所求式子的值.【解答】解:(a −4a )⋅a 2a−2=a 2−4a ⋅a 2a−2=(a+2)(a−2)a ⋅a 2a−2=a 2+2a ,由a 2+2a −1=0得a 2+2a =1,故原式=1.故选C .4.已知1x −1y=3,则代数式2x+3xy−2yx−xy−y的值是()A. −72B. −112C. 92D. 34【答案】D【解析】解:∵1x−1y=3,∴y−xxy=3,∴x−y=−3xy,则原式=2(x−y)+3xy(x−y)−xy=−6xy+3xy−3xy−xy=−3xy−4xy=34,故选:D.由1x −1y=3得出y−xxy=3,即x−y=−3xy,整体代入原式=2(x−y)+3xy(x−y)−xy,计算可得.本题主要考查分式的加减法,解题的关键是掌握分式加减运算法则和整体代入思想的运用.5.已知x1,x2是方程x2−3x−2=0的两根,则x12+x22的值为()A. 5B. 10C. 11D. 13【答案】D【解析】【分析】本题考查了完全平方公式以及根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=−ba ,x1x2=ca,利用根与系数的关系得到x1+x2=3,x1x2=−2,再利用完全平方公式得到x12+x22=(x1+x2)2−2x1x2,然后利用整体代入的方法计算.【解答】解:根据题意得x1+x2=3,x1x2=−2,所以x12+x22=(x1+x2)2−2x1x2=32−2×(−2)=13.故选:D.6.小慧去花店购买鲜花,若买5支玫瑰和3支百合,则她所带的钱还剩下10元;若买3支玫瑰和5支百合,则她所带的钱还缺4元.若只买8支玫瑰,则她所带的钱还剩下()A. 31元B. 30元C. 25元D. 19元【答案】A【解析】【分析】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.设每支玫瑰x元,每支百合y元,根据总价=单价×数量结合小慧带的钱数不变,可得出关于x,y的二元一次方程,整理后可得出y=x+7,再将其代入5x+3y+10−8x中即可求出结论.【解答】解:设每支玫瑰x元,每支百合y元,依题意,得:5x+3y+10=3x+5y−4,∴y=x+7,∴5x+3y+10−8x=5x+3(x+7)+10−8x=31.故选A.二、填空题7.已知ab=a+b+1,则(a−1)(b−1)=______.【答案】2【解析】【分析】本题考查多项式乘多项式,解题的关键是掌握多项式乘多项式的运算法则及整体代入思想的运用,属于基础题.将ab=a+b+1代入原式=ab−a−b+1,合并即可得.【解答】解:当ab=a+b+1时,原式=ab−a−b+1=a+b+1−a−b+1=2,故答案为:2.8.将抛物线y=ax2+bx−1向上平移3个单位长度后,经过点(−2,5),则8a−4b−11的值是______.【答案】−5【解析】解:将抛物线y=ax2+bx−1向上平移3个单位长度后,表达式为:y=ax2+bx+2,∵经过点(−2,5),代入得:4a−2b=3,则8a−4b−11=2(4a−2b)−11=2×3−11=−5,故答案为:−5.根据二次函数的平移得出平移后的表达式,再将点(−2,5)代入,得到4a−2b=3,最后将8a−4b−11变形求值即可.本题考查了二次函数的平移,二次函数图象上点的坐标特征,解题的关键是得出平移后的表达式.9.若a+b=1,则a2−b2+2b−2=______.【答案】−1【解析】解:∵a+b=1,∴a2−b2+2b−2=(a+b)(a−b)+2b−2=a−b+2b−2=a+b−2=1−2=−1.故答案为:−1.由于a+b=1,将a2−b2+2b−2变形为a+b的形式,整体代入计算即可求解.本题考查了平方差公式,注意整体思想的应用.10.若实数x满足x2−2x−1=0,则2x3−7x2+4x−2017=______.【答案】−2020【解析】【分析】把−7x2分解成−4x2与−3x2相加,然后把所求代数式整理成用x2−2x表示的形式,然后代入数据计算求解即可.本题考查了提公因式法分解因式,利用因式分解整理出已知条件的形式是解题的关键,整体代入思想的利用比较重要.【解答】解:∵x2−2x−1=0,∴x2−2x=1,2x3−7x2+4x−2017=2x3−4x2−3x2+4x−2017,=2x(x2−2x)−3x2+4x−2017,=6x−3x2−2017,=−3(x2−2x)−2017=−3−2017=−2020,故答案为−2020.11.已知|x−y+2|+√x+y−2=0,则x2−y2的值为________.【答案】−4【解析】【分析】本题考查了非负数的性质,解题关键是掌握几个非负数的和等于0,那么这几个非负数都等于0.由非负数的性质得出x、y的值,再代入所求代数式求解即可.【解答】解:∵|x−y+2|+√x+y−2=0,∴x−y+2=0,x+y−2=0,即x−y=−2,x+y=2,∴x 2−y 2=(x +y)(x −y)=2×(−2)=−4,故答案为−4.12. 已知m +n =3mn ,则1m +1n 的值为______.【答案】3【解析】【试题解析】【分析】本题考查了分式的化简求值,利用通分将原式变形为m+n mn 是解题的关键.原式通分后可得出m+n mn ,代入m +n =3mn 即可求出结论.【解答】解:原式=1m +1n =m+n mn ,又∵m +n =3mn ,∴原式=m+n mn =3.故答案为:3.三、解答题13. 已知x =√2+1,y =√2−1,分别求下列代数式的值;(1)x 2+y 2;(2)y x +x y .【答案】解:(1)∵x =2+1=√2−1,y =2−1=√2+1,∴x −y =−2,xy =2−1=1,∴x 2+y 2=(x −y)2+2xy =(−2)2+2×1=6;(2)∵x 2+y 2=6,xy =1,∴原式=x 2+y 2xy =61=6.【解析】本题考查二次根式的化简求值,分母有理化,解题的关键是运用完全平方公式以及整体思想,本题属于基础题型.(1)先将x 、y 进行分母有理化,得到x =√2−1,y =√2+1,再求出x −y 与xy 的值,然后根据完全平方公式得出x 2+y 2=(x −y)2+2xy ,再整体代入即可;(2)将所求式子变形为x 2+y 2xy ,再整体代入即可.14. 阅读材料,然后解方程组.材料:解方程组{x −y −1=0, ①4(x −y)−y =5. ②由①得x −y③,把③代入②,得4×1−y =5.解得y =−1.把y =−1代入③,得x =0.∴{x =0y =−1这种方法称为“整体代入法”.你若留心观察,有很多方程组可采用此方法解答,请用这种方法解方程组{2x −3y −2=0,①2x−3y+57+2y =9.②. 【答案】解:由①得:2x −3y =2③,将③代入②得:1+2y =9,即y =4,将y =4代入③得:x =7,则方程组的解为{x =7y =4.【解析】由第一个方程求出2x −3y 的值,代入第二个方程求出y 的值,进而求出x 的值,即可确定出方程组的解.此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.15. 阅读材料,善于思考的小军在解方程组{2x +5y =3①4x +11y =5②时,采用了一种“整体代换”的解法:解:将方程②变形:4x +10y +y =5即2(2x +5y)+y =5③把方程①代入③得2×3+y =5∴y =−1把y =−1代入①得x =4∴方程组的解为{x =4y =−1请你解决以下问题:(1)模仿小军的“整体代换”法解方程组{3x −2y =5 ①9x −4y =19② (2)已知x 、y 满足方程组{5x 2−2xy +20y 2=822x 2−xy +8y 2=32,求x 2+4y 2的值; 【答案】解:(1)由②得:3x +6x −4y =19,即3x +2(3x −2y)=19③,把①代入③得:3x +10=19,即x =3,把x =3代入①得:y =2,则方程组的解为{x =3y =2; (2)由5x 2−2xy +20y 2=82得:5(x 2+4y 2)−2xy =82,即x 2+4y 2=82+2xy 5, 由2x 2−xy +8y 2=32得:2(x 2+4y 2)−xy =32,即2×82+2xy 5−xy =32, 整理得:xy =4,∴x 2+4y 2=82+2xy 5=82+85=18.【解析】此题考查了解二元一次方程组,弄清阅读材料中的“整体代入”方法是解本题的关键.(1)模仿小军的“整体代换”法,求出方程组的解即可;(2)方程组第一个方程变形表示出x 2+4y 2,第二个方程变形后代入求出xy 的值,进而求出x 2+4y 2的值.16. (1)已知x 3⋅x a ⋅x 2a+1=x 31求a 的值;(2)若n 为正整数,且x 2n =4,求(3x 3n )2−4⋅(x 2)2n 的值。

整式的加减重难点和易错点一、选择题1、整式-(a-(b-c))去括号为()A。
-a-b+cB。
-a+b-cC。
-a+b+cD。
-a-b-c2、在(a-b+c)(a+b-c)=[a+(b-c)][a-(b-c)]的括号内填入的代数式分别()A。
c-b,c-bB。
b+c,b+cC。
b+c,b-cD。
c-b,c+b3、当k取1/3时,多项式x^2-3kxy-3y^2+xy-8中不含xy 项。
A。
0B。
1C。
1/9D。
-1/34、如果多项式(a+1)x^4-bx-3x-5是关于x的四次三项式,则ab的值是()A、4B、-4C、5D、-55、若|a|=2,|b|=3,且a>b,则|a-b|的值是()A、-5或-1B、1或-1C、5或3D、5或16、若|m|=3,|n|=7.且m-n>0,则m+n的值()A、10B、4C、-10或-4D、4或-47、若M=3x^2-5x-2,N=3x^2-4x-2,则M,N的大小关系()A、M>NB、M=NC、M<ND、以上都有可能8、设a是最小的自然数,b是最大的负整数,c,d分别是单项式-xy^2的系数和次数,则a,b,c,d四个数的和是()A、-1B、0C、1D、39、若多项式y^2+(m-3)xy+2x|m|是三次三项式,则m的值为()A、-3B、3C、3或-3D、210、如果a是最小的正整数,b是绝对值最小的数,c与a^2互为相反数,那么(a+b)^2009-c^2009=11、当a<3时,|a-3|+a=12、有理数a,b满足a|b|,则代数式|a+b|+|2a-b|化简后结果为___________13、去括号a-b)-(-c-d)a-b)+(c-d)________________14、化简(x+2)-(x-3x)4x-(-6x)+(-9x)=15、化简3-5x-4(x-x+3x)/22=16、当a^2+b^2=1时,(a+b)^2的最小值为__________17、计算m+n-(m-n)的结果为2n。

七年级数学上册整式加减章节期末复习专题“看错题”问题20
个附详细答案
“看错题”问题常见问法是,对于某个多项式运算,某同学计算过程中看错了某个运算符号,或者看错了某个字母导致运算结果出错,让求出这个正确的多项式,并求出正确的值。
这类问题也是整式加减章节常见问题,解决这类问题的关键是对于多项式计算过程中对多项式某一项看成一个整体,注意变号,看错就将错就错计算,把题干中“错误”的算式算出来,这样可以求出来这个多项式中其中一项多项式的值,求出多项式的值这类题目就做对了一半,接下来就需要结合题目信息,将算出来正确的多项式的值带入到整个多项式运算当中算出正确结果。
这类题常见错误点是,去括号容易变号,不能够将整个运算过程中的某个多项式看成一个整体,解不出来某项多项式正确的值导致计算出错。
今天老师给大家整理了“看错题”问题常见解答题20个附详细答案,同学们可以练习一下。
如果资料帮助到你,麻烦分享给需要的同学
点赞/转发是老师更新最大的动力
分享知识点复习资料、真题试卷、电子课本、中考/会考复习资料。
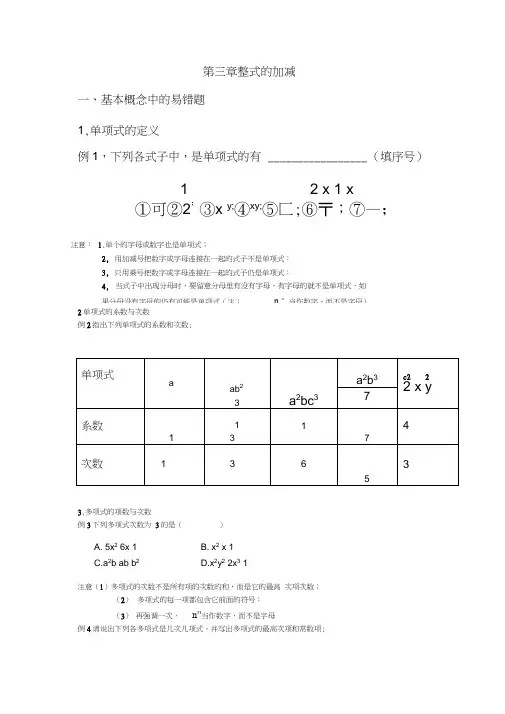
第三章整式的加减一、基本概念中的易错题1,单项式的定义例1,下列各式子中,是单项式的有_________________ (填序号)1 2 x 1 x①可②2;③x y;④xy;⑤匚;⑥〒;⑦—;注意:1,单个的字母或数字也是单项式;2,用加减号把数字或字母连接在一起的式子不是单项式;3,只用乘号把数字或字母连接在一起的式子仍是单项式;4,当式子中出现分母时,要留意分母里有没有字母,有字母的就不是单项式,如果分母没有字母的仍有可能是单项式(注:n ”当作数字,而不是字母)2单项式的系数与次数例2指出下列单项式的系数和次数;3,多项式的项数与次数例3下列多项式次数为3的是()A. 5x2 6x 1B. x2 x 1C.a2b ab b2D.x2y2 2x3 1注意(1)多项式的次数不是所有项的次数的和,而是它的最高次项次数;(2)多项式的每一项都包含它前面的符号;(3)再强调一次,n”当作数字,而不是字母例4请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;(1)25______________ x2y xy3是____________________________ 次项式,最高次项是 ____ ,常数项是_________________________ ;3 2 2 1(2)—U—1是次项式,最高次项是,常数项是34,书写格式中的易错点例5下列各个式子中,书写格式正确的是( )1A.a bB. 1 abC.a 32a2bD.a3 E . 1ab F .31、代数式中用到乘法时,若是数字与数字乘,要用’乂”若是数字与字母乘,乘号通常写成” •或省略不写,如3X y应写成3 y或3y,且数字与字母相乘时,字母与字母相乘,乘号通常写成“ •或省略不写;2、带分数与字母相乘,要写成假分数;3、代数式中出现除法运算时,一般用分数写,即用分数线代替除号;4、系数一般写在字母的前面,且系数“1往往会省略;例6王强班上有男生m人,女生比男生的一半多5人,王强班上的总人数(用m表示)为______ 人。

初一数学易错点:整式化简之整体代入和“无关”与“不含”问题一.考点分析:知识点:整体代入需识别整体,再进行代入计算;“无关”与“不含”问题需先化简整式,再将“无关”与“不含”的那一项系数化为0.考查内容:基础运算能力之一——整式化简易错点:整体代入找不到应该代入的整体部分;整式化简出现计算错误。
解题方法:识别关键点进行整式组合,发现整体部分。
二.典型例题:【例题1】(19建邺期中)若当x=﹣2时,代数式ax3+bx+1的值为6,则当x=2时,代数式ax3+bx+1的值为 .【分析】根据题意,可先求出﹣8a﹣2b的值,然后把它的值整体代入所求代数式中即可.【解答】解:当x=﹣2时,原式=﹣8a﹣2b+1=﹣(8a+2b)+1=6,8a+2b=﹣5.当x=2时,原式=8a+2b+1=﹣4.故答案为:﹣4.【例题2】(19玄武期中)若多项式2x3﹣8x2+x﹣1与多项式3x3+2mx2﹣5x+3相加后不含二次项,则m的值为 .【分析】先把两式相加,合并同类项得5x3﹣8x2+2mx2﹣4x+2,不含二次项,即2m﹣8=0,即可得m的值.【解答】解:据题意两多项式相加得:5x3﹣8x2+2mx2﹣4x+2,∵相加后结果不含二次项,∴当2m﹣8=0时不含二次项,即m=4.三.练习巩固:1. (18秦淮期中) 已知a﹣2b+1=0,则代数式2a﹣4b﹣1的值为 .2. (18玄武期中)已知3x2﹣x=2,则5﹣2x+6x2的值为 .3. (19鼓楼期中)如果x﹣y=2,m+n=1,那么(y+2m)﹣(x﹣2n)= .4. (19建邺期中)对于代数式(xyz2﹣4yx﹣1)+(﹣3xy+z2yx﹣3)﹣(2xyz2+xy)的值的描述,下列说法正确的是( )A.与x、y、z的取值都有关B.与x的取值有关,而与y、z的取值无关C.与x、y的取值有关,而与z的取值无关D.与x、y、z的取值均无关初⼀数学易错点:整式化简之整体代⼊和“⽆关”与“不含”问题答案与解析1.(18秦淮期中) 已知a﹣2b+1=0,则代数式2a﹣4b﹣1的值为 ﹣3 .【分析】根据a﹣2b+1=0,可得:a﹣2b=﹣1,据此求出代数式2a﹣4b﹣1的值为多少即可.【解答】解:∵a﹣2b+1=0,∴a﹣2b=﹣1,∴2a﹣4b﹣1=2(a﹣2b)﹣1=2×(﹣1)﹣1=﹣2﹣1=﹣3故答案为:﹣3.2. (18玄武期中)已知3x2﹣x=2,则5﹣2x+6x2的值为 9 .【分析】原式变形后,将已知等式代入计算即可求出值.【解答】解:∵3x2﹣x=2,∴原式=5+2(3x2﹣x)=5+4=9,故答案为:93. (19鼓楼期中)如果x﹣y=2,m+n=1,那么(y+2m)﹣(x﹣2n)= 0.【分析】原式去括号整理后,将已知等式代入计算即可求出值.【解答】解:当x﹣y=2,m+n=1时,原式=y+2m﹣x+2n=﹣(x﹣y)+2(m+n)=﹣2+2=0,故答案为:0.4.(19建邺期中)对于代数式(xyz2﹣4yx﹣1)+(﹣3xy+z2yx﹣3)﹣(2xyz2+xy)的值的描述,下列说法正确的是( )A.与x、y、z的取值都有关B.与x的取值有关,而与y、z的取值无关C.与x、y的取值有关,而与z的取值无关D.与x、y、z的取值均无关【分析】原式去括号合并得到最简结果,判断即可.【解答】解:原式=xyz2﹣4yx﹣1﹣3xy+z2yx﹣3﹣2xyz2﹣xy=﹣8xy﹣4,则代数式的值与x、y的取值有关,而与z的取值无关.故选:C.。

解题技巧专题:整式求值的方法类型一:先化简,再代入求值1.先化简,再求值:(1)-3(3x2-2x+1)-3(-2x2-5x),其中x=-1;解:原式=-9x2+6x-3+6x2+15x=-3x2+21x-3.当x=-1时,原式=-3×1-21-3=-27.(2)2(a2-ab)-3(23a2-ab)-5,其中a=-2,b=3.解:原式=2a2-2ab-2a2+3ab-5=ab-5.当a=-2,b=3时,原式=(-2)×3-5=-6-5=-11.2.设A=2x2-3xy+2y,B=4x2-6xy-3x-y.(1)求B-2A;(2)已知x=2,y=3,求B-2A的值.解:(1)B-2A=4x2-6xy-3x-y-2(2x2-3xy+2y)=4x2-6xy-3x-y-4x2+6xy -4y=-3x-5y.(2)当x=2,y=3时,B-2A=-3×2-5×3=-21.类型二:先变型,再整体代入求值3.已知a+2b=5,则3(2a-3b)-4(a-3b+1)+b的值为( C )A.14B.10C.6D.不能确定4.已知xy=1,x+y=12,则多项式y-(xy-4x-3y)的值等于 1 .5.当x=1时,多项式ax3+bx+1的值为5,则当x=-1时,多项式12ax3+12bx+1的值为-1.6.先化简,再求值:(3x2+5x-2)-2(2x2+2x-1)+2x2-5,其中x2+x-3=0.解:原式=x2+x-5.∵x2+x-3=0,∵x2+x=3.∵原式=3-5=-2.类型三:利用“无关”求值和说理7.已知A=2x2+ax-5y+1,B=x2+3x-by-4,且对于任意有理数x,y,式子A-2B的值不变,则(a-13a)-(2b-23b)的值是23.8.老师出了这样一道题:“当a=2019,b=-2020时,计算(2a3-3a2b-2ab2)-(a3-2ab2+b3)+(3a2b-a3+b3)的值.”但在计算过程中,同学甲错把“a=2019”写成“a=-2019”,而同学乙错把“b=-2020”写成“b=-20.20”,可他俩的运算结果都是正确的,请你找出其中的原因,并说明理由.解:原因是该多项式的值与字母a、b的取值无关.理由如下:原式=2a3-3a2b-2ab2-a3+2ab2-b3+3a2b-a3+b3=0,即多项式的值与a、b的取值无关.所以无论a、b取何值,都不会改变运算结果.类型四:与绝对值相关的整式化简求值9.若a≤0,则|a|+a+2等于( B )A.2a+2B.2C.2-2aD.2a-210.已知有理数a、b、c在数轴上的位置如图所示.(1)填空:A、B之间的距离为a-b,B、C之间的距离为b-c,A、C 之间的距离为a-c;(2)化简:|a-1|-|c-b|-|b-1|+|-1-c|.解:由图可得a-1>0,c-b<0,b-1<0,-1-c>0,所以原式=a-1-[-(c-b)]-[-(b-1)]+(-1-c)=a-1+c-b+b-1-1-c =a-3.拓展专题:整式运算中添括号的问题类型一:整式加减中添括号的法则方法点拨:添括号法则:添括号后,①若括号前面的符号为“+”,则括号里的式子符号不变,如:a+b+c=a+(b +c);②若括号前面的符号为“-”,则括号里的式子改变符号,如:a-b-c=a-(b +c).1.下列变形正确的是( A)A.x-y+z=x-(y-z)B.x-y-z=x+(y-z)C.x+y-z=x+(y+z)D.x+y+z=x-(-y+z)2.在等式1-a2+2ab-b2=1-( )中,括号里应填( A)A.a2-2ab+b2B.a2-2ab-b2C.-a2-2ab+b2D.-a2+2ab-b23.对多项式3a+4b-c进行添括号,正确的是( D)A.3a+(4b+c)B.3a-(4b+c)C.3a+4(b-c)D.3a-(-4b+c)4.在括号里填上相应的式子:(1)m-3n-2p+q=m-( );(2)a+2b-c-d=2b-();(3)a-b+c-d=a-()+c.5.按下列要求给多项式-a3+2a2-a+1添括号.(1)使最高次项系数变为正数;(2)把奇次项放在前面是“-”号的括号里,其余的项放在前面是“+”号的括号里.解:(1)根据题意可得-a3+2a2-a+1=-(a3-2a2+a-1).(2)根据题意可得-a3+2a2-a+1=-(a3+a)+(2a2+1).类型二:运用添括号法则化简求值6.已知2x+3y=1,则3-6x-9y的值为( A)A.0B.3C.-3D.47.已知a+b=3,b-c=12,则a+2b-c的值为( A)A.15B.9C.-15D.-98.(1)已知x-2y=5,则5+(3x-2y)-(5x-6y)=;(2)已知a+b=10,ab=-2,则(3a-2b)-(-5b+ab)=.9.(1)已知3x+5y2+3=6,求-3x-4y2+9x+14y2-7的值;解:原式=6x+10y2-7=2(3x+5y2)-7.因为3x+5y2+3=6,所以3x+5y2=3.所以原式=2×3-7=-1.(2)已知x2-xy=-3,2xy-y2=-8,求2x2+4xy-3y2的值;解:原式=2x2-2xy+6xy-3y2=2(x2-xy)+3(2xy-y2).因为x2-xy=-3,2xy-y2=-8,所以原式=2×(-3)+3×(-8)=-30.(3)已知xy=-2,x-y=3,求(-3xy-7y)+[4x-3(xy+y-2x)]的值.解:原式=-3xy-7y+(4x-3xy-3y+6x)=-3xy-7y+4x-3xy-3y+6x=-6xy+10(x-y).当xy=-2,x-y=3时,原式=-6×(-2)+10×3=42.难点探究专题:整式中的规律探索类型一:整式规律探究一、有规律的一列数1.一列数1,4,7,10,13,…,按此规律排列,第n个数是3n-2 .2.按一定规律排的一列数依次为:2,-5,10,-17,26,…,按此规律排列下去,这列数中第n个数(n为正整数)是(-1)n+1.二、有规律的一列单项式3.按一定规律排列的单项式:x3,-x5,x7,-x9,x11,…,第n个单项式是( C)A.(-1)n-1x2n-1B.(-1)n x2n-1C.(-1)n-1x2n+1D.(-1)n x2n+14.按一定规律排列的一列数依次为-22a,55a,-810a,1117a…(a≠0),按此规律排列下去,这列数中的第n个数是312(1)1nnan--+(n为正整数).三、数的循环规律5.如图是钢琴键盘的一部分,若从4开始,依次弹出4,5,6,7,1,4,5,6,7,1,…,按照上述规律弹到第2021个音符是 4 .6.设a n为n4(n为正整数)的末位数,如a1=1,a2=6,a3=1,a4=6.则a1+a2+a3+…+a24+a25=.解析:a1~a10依次为1,6,1,6,5,6,1,6,1,0,a11~a20与a1~a10分别相等,a21~a25与a1~a5分别相等,因此a1+a2+a3+…+a24+a25=(4×6+1×4+5+0)×2+(6×2+1×2+5)=85.7.如图,是一个运算程序示意图.若第一次输入k的值为125,则第2020次输出的结果是.解析:∵第1次输出的结果是25,第2次输出的结果是5,第3次输出的结果是1,第4次输出的结果是5,第5次输出的结果是1,……,∵第2n次输出的结果是5,第(2n+1)次输出的结果是1(n为正整数).∵第2020次输出的结果是5.四、数表中的规律8.如图,下列各图中的三个数之间具有相同规律.依此规律用含m,n的式子表示y,则y=.9.如图,下面每个图形中的四个数都是按相同的规律填写的,根据此规律确定x 的值为.解析:∵左下角数字为偶数,右上角数字为奇数,∵2n=20,m=2n-1.解得n=10,m=19.∵右下角数字:第一个为1=1×2-1,第二个为10=3×4-2,第三个为27=5×6-3,∵第n个为2n(2n-1)-n.∵x=19×20-10=370.故答案为370.10.如图所示的数表是由1开始的连续自然数排列而成的,根据你观察的规律完成下面问题:(1)第8行共有15 个数,最后一个数是64 ;(2)第n行共有2n-1 个数,第一个数是(n-1)2+1 ,最后一个数是n2.类型二:图形规律探究11.(2019·青海中考)如图,将图∵中的菱形剪开得到图∵,图中共有4个菱形;将图∵中的一个菱形剪开得到图∵,图中共有7个菱形……如此剪下去,第5个图中共有13 个菱形,第n个图中共有3n-2 个菱形.12.如图是用棋子摆成的图案:根据图中棋子的排列规律解决下列问题:(1)第4个图中有22 枚棋子,第5个图中有32 枚棋子;(2)猜想第n个图中棋子的数量(用含n的式子表示).解:第n个图中棋子的数量为[n(n+1)+2]枚.易混易错专题:整式的加减易错点一:把“π”当做字母或系数漏掉符号1.在式子-15a3b,33πx,4a2b2-2ab-6,-a,25x y,0中,单项式有( C)A.2个B.3个C.4个D.5个2.单项式-116πa 3b 的系数与次数分别是( D )A.-116,5B.116,5C.116π,4D.-116π,4 3.多项式3a 2b -a 2-2ab +a -1是 次多项式,它的二次项系数之和是 . 4.已知多项式-2m 3n 2-5中,含字母的项的系数为a ,多项式的次数为b ,常数项为c ,则a +b +c = .易错点二:去括号时符号弄错或漏乘 5.下列等式中正确的是( C )A.2(a +1)=2a +1B.-(a +b )=-a +bC.-(a -b )=b -aD.-(3-x )=3+x 6.化简:(1)2(x -3x 2+1)-3(2x 2-x -2);解:原式=(2x -6x 2+2)-(6x 2-3x -6)=2x -6x 2+2-6x 2+3x +6=-12x 2+5x +8.(2)2x 2-215232x x x ⎡⎤⎛⎫--+ ⎪⎢⎥⎝⎭⎣⎦解:原式=2x 2-5x +2(12x -3)-x 2=2x 2-5x +x -6-x 2=x 2-4x -6.易错点三:多项式加减时漏掉括号7.已知A =3x 2-2xy +y 2,B =2x 2+3xy -4y 2,求: (1)A -2B ; (2)2A +B .解:(1)A -2B =(3x 2-2xy +y 2)-2(2x 2+3xy -4y 2)=3x 2-2xy +y 2-4x 2-6xy +8y 2=-x 2-8xy +9y 2.(2)2A +B =2(3x 2-2xy +y 2)+(2x 2+3xy -4y 2)=6x 2-4xy +2y 2+2x 2+3xy -4y 2=8x 2-xy -2y 2.8.已知A 、B 是两个多项式,其中B =-3x 2+x -6,A 与B 的和等于-2x 2-3. (1)求多项式A ;解:(1)根据题意得A =(A +B )-B =-2x 2-3- (-3x 2+x -6)=-2x 2-3+3x 2-x +6=x 2-x +3. (2)当x =-1.5时,求A 的值.(2)当x =-1.5时,A =(-1.5)2-(-1.5)+3=94+32+3=274.易错点四:利用整式的定义求字母时考虑不全面9.若关于x ,y 的多项式y 2+(m -3)xy +2x |m |是三次三项式,则m 的值为( A ) A.-3 B.3 C.±3 D.不确定10.(2019-2020·仁寿县期末)如果关于x 的多项式mx 4+4x 2-12与多项式3x n +5x的次数相同,那么-2n 2+3n -4= .解析:∵关于x的多项式mx4+4x2-12与多项式3x n+5x的次数相同,∵当m≠0时,n=4,故-2n2+3n-4=-2×42+3×4-4=-32+12-4=-24;当m=0时,n=2,故-2n2+3n-4=-2×22+3×2-4=-8+6-4=-6.故答案为-6或-24.11.若(n-1)x|m|-1y2-(n-2)xy2+x2+4是关于x,y的四次三项式,求多项式m n -(m+n)2+2的值.解:因为(n-1)x|m|-1y2-(n-2)xy2+x2+4是关于x,y的四次三项式,所以|m|-1=2,n-2=0.所以m=±3,n=2.当m=3时,m n-(m+n)2+2=32-(3+2)2+2=9-25+2=-14.当m=-3时,m n-(m+n)2+2=(-3)2-(-3+2)2+2=9-1+2=10.综上所述,m n-(m+n)2+2的值为-14或10.。
整式的加减易错题
当涉及整式(多项式)的加减操作时,有一些容易出错的常见题型。
以下是一些可能会引起困惑的易错题:
1. 符号变化错误:例如,将两个负数项相减时,可能会在符号上出错。
记住,减去一个负数等于加上它的相反数。
2. 括号展开错误:在进行多项式加减时,可能需要展开括号。
不小心忽略或错误地展开括号会导致结果不正确。
务必小心检查每一步的括号展开。
3. 项的系数错误:在合并同类项时,需要注意项的系数。
容易在计算系数时出现错误,特别是当项的系数较大或有分数时。
4. 遗漏或重复项:在进行多项式加减时,容易遗漏或重复项。
确保在计算过程中没有遗漏或重复处理任何项。
5. 未按降幂排列:在最后的结果中,多项式通常按照降幂排列。
如果结果的项没有按降幂排列,可能需要重新检查计算过程。
当你做整式的加减题时,务必仔细检查每一步的计算,特别是注意符号、括号展开、项的系数和排序。
反复练习这些题型,多进行反思和纠正错误,有助于提高准确性和处理整式的熟练程度。
整式的加减典型难题题型一化简求值:注意去括号和代入时加括号1、 []{})24(32522222b a ab ab b a ab +--- 其中a=-3 , b= 0.52、李明在计算一个多项式减去2245x x -+时,误认为加上此式,计算出错误结果为221x x -+-,试求出正确答案。
3、已知多项式3(ax 2+2x -1)-(9x 2+6x -7)的值与x 无关,试求5a 2-2(a 2-3a +4)的值。
4、已知A=2x 2+3xy-2x-1, B= -x 2+xy-1, 且3A+6B 的值与x 无关,求y 的值.练习:1、有这样一道题“当22a b ==-,时,求多项式()()22233322a ab b a ab b -----+的值”,马小虎做题时把2a =错抄成2a =-时,王小明没抄错题,但他们做出的结果却都一样,你知道这是怎么回事吗?说明理由。
2、若P=223b ab a ++, Q=223b ab a +-,则代数式()[]Q P P Q P -----2化简后结果是多少?题型二:整体代入,当其中的未知数不方便算出或无法算出是,把其中的未知数部分看做一个整体进行运算;1、已知x 2+x +3的值为7,求2x 2+2x -3的值。
2、化简求值。
(1)3(a +b -c)+8(a -b -c)-7(a +b -c)-4(a -b -c),其中b =2 (2)已知a -b =2,求2(a -b)-a +b +9的值。
3、已知当x=-2时 ,代数式13++bx ax 的值为6,那么当x=2时,代数式13++bx ax = 当x=1时,代数式的值为2005,求x=-1时,代数式 的值. 4.已知3xy x y =+,求2323x xy yx xy y-+-+-的值.练习:1、把()a b +当作一个整体,合并22()5a b +-2()b a ++2()a b +的结果是( )A .2()a b +B .2()a b -+C .22()a b -+D . 22()a b +2、如果代数式2a 2+3a+1的值是6,则代数式6a 2+9a+5的值为( ) A.18 B.16. C.15. D.203、 已知代数式3a 2-2a+6的值为8, 求的值.4、已知32c a b =-,求代数式22523c a b a b c ----的值。
专题2.1 整式加减重难点题型(12大题型)【题型1 代数式的定义及书写】【题型2 列代数式】(包含和差倍/数字/销售/增长率/分段计费问题)【题型3 代数式求值】(包含整体代入法/程序框图)【题型4单项式的系数与次数】【题型5 多项式的项与次数】【题型6 规律探究】(与数有关/与式有关/与图形排列有关的律探索)【题型7 同类项的定义】【题型8 合并同类型】【题型9 添括号与去括号】【题型10 整式的加减】【题型11 整式加减的应用】【题型12 整式的化简求值】(包含化繁为简/整体带入求值)【题型1 代数式的定义及书写】【典例1】(2022秋•沙坪坝区校级期中)下列符合代数式书写要求的是( )A.ab2B.C.ab÷3D.【答案】A【解答】解:A.在代数式中出现的乘号,通常简写“•”或者省略不写,原书写正确,符合题意;B.带分数应写成假分数,原书写错误,不符合题意;C.在代数式中出现的除法运算,一般按照分数的写法来写,原式为,原书写错误,不符合题意;D.x﹣x=x,原书写错误,不符合题意;故选:A.【变式1-1】(2022秋•宁远县期中)下列各式中,不是代数式的是( )A.﹣3B.a2﹣2a C.2x+3=0D.【答案】C【解答】解:A选项,﹣3是代数式,不符合题意;B选项,a2﹣2a是代数式,不符合题意;C选项,2x+3=0是等式,不是代数式,符合题意;D选项,是代数式,不符合题意;故选:C.【变式1-2】(2021秋•定兴县期末)下列对代数式3a﹣b的意义叙述错误的是( )A.a的3倍与b的差B.a的3倍减去bC.a与b的差的3倍D.3与a的积减去b【答案】C【解答】解:代数式3a﹣b的意义正确的叙述是a的3倍与b的差、或a的3倍减去b、或3与a的积减去b,叙述错误的是a与b的差的3倍.故选:C.【典例2】(2021秋•义乌市期末)下列不能表示“2a”的意义的是( )A.2的a倍B.a的2倍C.2个a相加D.2个a相乘【答案】D【解答】解:2个a相乘表示为a2,故选:D.【变式2-1】(2020秋•衢州期末)代数式的意义是( )A.x除以y加3B.y加3除xC.y与3的和除以xD.x除以y与3的和所得的商【答案】D【解答】解:的意义是x除以y与3的和所得的商.故选:D.【变式2-2】(2022秋•庆云县期中)对单项式“0.5a”可以解释为:商品原价为a 元,若按原价的5折出售,这件商品现在的售价是0.5a元,请你对“0.5a”再赋予一个含义: 练习本每本0.5元,小明买了a本,共付款0.5a元 .【答案】练习本每本0.5元,小明买了a本,共付款0.5a元.【解答】解:练习本每本0.5元,小明买了a本,共付款0.5a元,故答案为:练习本每本0.5元,小明买了a本,共付款0.5a元.【变式2-3】(2021秋•朝阳区期末)同一个式子可以表示不同的含义,例如6n 可以表示长为6,宽为n的长方形面积,也可以表示更多的含义,请你给6n 再赋予一个含义 笔记本的单价为每本6元,买n个笔记本的总钱数 .【答案】笔记本的单价为每本6元,买n个笔记本的总钱数.【解答】解:同一个式子可以表示不同的含义,例如6n可以表示长为6,宽为n的长方形面积,也可以表示更多的含义,请你给6n再赋予一个含义:笔记本的单价为每本6元,买n个笔记本的总钱数,故答案为:笔记本的单价为每本6元,买n个笔记本的总钱数.【题型2 列代数式】(包含和差倍/数字/销售/增长率/分段计费问题)(类型一:销售问题)【典例3】(2023•孝义市三模)某商店经销一种品牌的空气炸锅,其中某一型号的空气炸锅的进价为每台m元,商店将进价提高30%后作为零售价销售,一段时间后,商店又按零售价的8折销售,这时该型号空气炸锅的零售价为( )A.m元B.1.3m元C.1.04m元D.0.8m元【答案】C【解答】解:由题意可得,该型号空调的零售价:m(1+30%)×0.8=1.04m(元),故选:C.【变式3-1】(2022秋•南昌县期末)某商品进价m元,商店将价格提高50%作零售价销售,在销售旺季过后,商店以8折的价格开展促销活动,这时一件商品的售价为( )A.1.2m元B.1.5m元C.0.8m元D.m元【答案】A【解答】解:根据题意商品的售价是:m(1+50%)×80%=1.2m(元).故选:A.【变式3-2】(2023•天镇县三模)某服装以单价a元的价格购进一批服装,加价50%进行销售,把最后的两件服装按售价的八折售完,则最后两件服装的售价是 1.2a 元.(用含有a的代数式表示)【答案】1.2a.【解答】解:根据题意,得(1+50%)a×0.8=1.2a(元).故答案为:1.2a.【变式3-3】(2023•桦南县一模)某种商品原价是m元,第一次降价打“九折”,第二次降价每件又减20元,第二次降价后的售价是 (0.9m﹣20) 元.【答案】见试题解答内容【解答】解:根据题意得:第一次降价后的售价是0.9m,第二次降价后的售价是(0.9m﹣20)元.故答案为:(0.9m﹣20).【变式3-4】(2023•和平区校级三模)某种商品进价为a元/件,在销售旺季,商品售价较进价高30%;销售旺季过后,商品又以7折(即原售价的70%)的价格开展促销活动,这时一件该商品的售价为 0.91a 元.【答案】见试题解答内容【解答】解:依题意得,a(1+30%)×70%=0.91a(元).(类型二:数字问题)【典例4】(2022秋•柳州期末)一个两位数,十位上的数字为a,个位上的数字为b,则这个两位数是 10a+b .【答案】见试题解答内容【解答】解:这个两位数是10a+b.【变式4-1】(2023春•海淀区期末)有一个两位数,它的个位上的数为a,十位上的数为b,那么这个两位数可以用含有a,b的式子表示为 10b+a ,如果将它个位和十位上的数对调,使得到的两位数比原来的两位数大,那么a,b的大小关系为 a>b .【答案】10b+a,a>b【解答】解:两位数十位上是b,个位上的数为a,∴这个两位数就是10b+a,将它个位和十位上的数对调,则新的两位数为:10a+b,使得到的两位数比原来的两位数大,即得到的两位数十位上的数比原两位数十位上的数大,∴a>b.故答案为:a>b.【变式4-2】(2023春•南岗区期中)一个两位数的十位上的数字是a,个位上的数字是十位上数字的2倍,则这个两位数是 12a .【答案】12a.【解答】解:十位数字为a,个位上的数字是十位上的数字的2倍,∴个位数字为2a,∴10a+2a=12a.∴两位数为:12a,故答案为:12a.【变式4-3】(2022秋•宛城区校级期末)x表示一个三位数,y表示一个两位数,把x放在y的右边组成一个五位数,则这个五位数可以表示为 1000y+x .【答案】1000y+x.【解答】解:把一个表示三位数的x接在一个表示两位数的y的右边,相当于把y扩大了1000倍,因此此五位数应表示成1000y+x.故答案是:1000y+x.(类型三:增长率问题)【典例5】(2022•蜀山区校级三模)某快递公司受新一次疫情影响,4月份业务量比3月份下降了30%,由于采取了科学的防控措施,5月份疫情明显好转,该快递公司5月份业务量比4月份增长了40%,若设该快递公司3月份业务量为a,则5月份的业务量为( )A.(1﹣30%+40%)a B.(30%+40%)aC.(40%﹣30%)a D.(1﹣30%)(1+40%)a【答案】D【解答】解:∵该快递公司3月份业务量为a,4月份业务量比3月份下降了30%,∴4月份业务量是(1﹣30%)a,∵5月份业务量比4月份增长了40%,∴5月份业务量是(1+40%)(1﹣30%)a,故选:D.【变式5-1】(2022秋•光明区期中)某工厂1月份的产值为500万元,平均每月产值的增长率为x,则该工厂3月份的产值为( )万元.A.500(1+x)B.500(1+x)2C.x2+500x D.500x2+x【答案】B【解答】解:∵该工厂1月份的产值为500万元,平均每月产值的增长率为x,∴该工厂3月份的产值为500(1+x)2万元.故选:B.【变式5-2】(2021秋•西城区校级期中)某厂2020年的生产总值为a万元,2021年的生产总值比2020年增长了20%,那么该厂2021年的生产总值是( )A.20%a万元B.(20%+a)万元C.(1+20%)a万元D.[a+(1+20%)a]万元【答案】C【解答】解:由题意得,2021年的生产总值=(1+20%)a.故选:C.【变式5-3】(2022秋•嘉峪关校级期末)某工厂去年生产了x台机床,今年增长了35%,今年的产量为 (x+35%x) 台.【答案】x(1+35%).【解答】解:增长产量为35%x.∴今年产量为x+35%x=x(1+35%).故答案为:x(1+35%).(类型四:和倍差问题)【典例6】(2021秋•亭湖区期末)用代数式表示“x的2倍与3的差”为( )A.3﹣2x B.2x﹣3C.2(x﹣3)D.2(3﹣x)【答案】B【解答】解:由题意得,x的2倍与3的差表示为:2x﹣3.故选:B.【变式6-1】(2023•淳安县一模)苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )A.(a+b)元B.(3a+2b)元C.5(a+b)元D.(2a+3b)元【答案】D【解答】解:根据题意得:买2千克苹果和3千克香蕉共需(2a+3b)元.故选:D.【变式6-2】(2022秋•江夏区期末)某校七年级1班有学生a人,其中女生人数比男生人数的少3人,则女生的人数为( )A.B.C.D.【答案】B【解答】解:设男生人数为x人,则:x+x﹣3=a,则x=(a+3),所以x﹣3=.故选:B.(类型五:分段计费问题)【典例7】(2022秋•昆都仑区校级期末)某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为( )A.20a元B.(20a+1.2)元C.(17a+3.6)元D.(20a+3.6)元【答案】D【解答】解:∵20>17,∴该用户应缴纳的水费为:17a+(20﹣17)×(a+1.2)=17a+3a+3.6=(20a+3.6)元.故选:D.【变式7-1】(2022秋•如皋市校级期末)某地居民生活用水收费标准:每月用水量不超过10立方米,每立方米a元;超过部分每立方米(a+1.5)元,该地区某用户上月用水量为16立方米,则该用户应缴水费为( )A.10a元B.(16a+24)元C.(10a+9)元D.(16a+9)元【答案】D【解答】解:∵16立方米中,前10立方米单价为a元,后面6立方米单价为(a+1.5)元,∴应缴水费为10a+6(a+1.5)=16a+9(元),故选:D.【变式7-2】(2022秋•高新区期末)某地居民生活用水收费标准:每月用水量不超过20立方米,每立方米a元;超过部分每立方米(a+2)元.该地区某家庭上月用水量为25立方米,则应缴水费( )A.25a元B.(25a+10)元C.(25a+50)元D.(20a+10)元【答案】B【解答】解:20a+(a+2)(25﹣20)=20a+5a+10=(25a+10)(元),故选:B.【变式7-3】(2022秋•卫辉市期末)为鼓励节约用水,某地推行阶梯式水价计费制,标准如下:每月用水不超过17吨的按每吨a元计费,超过17吨而未超过30吨的部分按每吨b元计费,超过30吨的部分按每吨c元计费,某户居民上月用水35吨,应缴水费 (17a+13b+5c) 元.【答案】(17a+13b+5c).【解答】解:由题意可得:17a+13b+(35﹣30)c=(17a+13b+5c)元.故答案为:(17a+13b+5c).【题型3 代数式求值】(包含整体代入法/程序框图)(类型一:整体代入法)【典例8】(2022秋•庐阳区校级期末)如果代数式a2﹣3a+7的值为8,那么代数式7﹣2a2+6a的值为( )A.9B.5C.﹣9D.﹣5【答案】B【解答】解:∵代数式a2﹣3a+7的值为8,∴a2﹣3a+7=8,a2﹣3a=1,则7﹣2a2+6a=7﹣2(a2﹣3a)=7﹣2×1=5,故选:B.【变式8-1】(2022秋•柳州期末)代数式a2+2a+3的值为1,则3a2+6a+4的值是( )A.2B.﹣2C.16D.﹣16【答案】B【解答】解:∵a2+2a+3的值为1,∴a2+2a+3=1,则a2+2a=﹣2,故3a2+6a+4=3(a2+2a)+4=3×(﹣2)+4=﹣6+4=﹣2.故选:B.【变式8-2】(2023•龙江县四模)代数式3x2﹣4x﹣5的值为7,则x2﹣x﹣5的值为( )A.4B.﹣1C.﹣5D.7【答案】B【解答】解:∵3x2﹣4x﹣5的值为7,3x2﹣4x=12,代入x2﹣x﹣5,得(3x2﹣4x)﹣5=4﹣5=﹣1.故选:B.【变式8-3】(2023•雅安)若m2+2m﹣1=0,则2m2+4m﹣3的值是( )A.﹣1B.﹣5C.5D.﹣3【答案】A【解答】解:2m2+4m﹣3=2(m2+2m﹣1)﹣1=0﹣1=﹣1.故选:A.【变式8-4】(2023•姑苏区校级二模)若a2﹣3a+2=0,则1+6a﹣2a2=( )A.5B.﹣5C.3D.﹣3【答案】A【解答】解:由题意知a2﹣3a=﹣2,∴1+6a﹣2a2=﹣2(a2﹣3a)+1=﹣2×(﹣2)+1=5,故选:A.(类型二:图形框图法)【典例9】(2023春•沙坪坝区校级期末)按如图所示的运算程序:若输入x的值是29,则输出结果是( )A.257B.261C.286D.293【答案】A【解答】解:把x=29代入3x﹣1,得3×29﹣1=86,∵86<251,把x=86代入3x﹣1,得3×86﹣1=257,∵257>251,∴输出结果.故选:A.【变式9-1】(2022秋•衡山县期末)按如图所示的运算程序,能使输出y值为5的是( )A.m=2,n=1B.m=2,n=0C.m=2,n=2D.m=3,n=2【答案】C【解答】解:A.当m=2,n=1时,y=2n﹣1=2×1﹣1=1,不符合题意;B.当m=2,n=0时,y=2×0﹣1=﹣1,不符合题意;C.当m=2,n=2时,y=2×2+1=2×2+1=5,符合题意;D.当m=3,n=2时,y=2n﹣1=2×2﹣1=3,不符合题意;故选:C.【变式9-2】(2023春•市南区期末)如图是一个简单的数值运算程序,当输入n 的值为5时,输出的结果为( )A.10B.12C.132D.380【答案】D【解答】解:当n=5时,n2﹣n=52﹣5=20<28.将n=20继续代入n2﹣n=202﹣20=380.380>28,∴输出结果为380.故选:D.【变式9-3】(2023•隆昌市校级三模)按如图所示的程序计算,若开始输入的x 值为﹣2,则最后输出的结果是( )A.8B.64C.120D.128【答案】B【解答】解:因为x=﹣2<0,x+10=8≤50,所以把x=8>0,再次代入得,=64>50,因此输出的结果为64,故选:B.【题型4单项式的系数与次数】【典例10】(2022秋•泗阳县期末)代数式﹣4πxy2的系数与次数分别是( )A.﹣4π,3B.﹣4π,4C.﹣4,3D.﹣4,4【答案】A【解答】解:代数式﹣4πxy2的系数是﹣4π,次数是1+2=3.故选:A.【变式10-1】(2022秋•靖西市期末)单项式﹣3x3y2的系数与次数分别为( )A.3,5B.﹣3,5C.0,5D.1,5【答案】B【解答】解:单项式﹣3x3y2的系数与次数分别为﹣3,5,故选:B.【变式10-2】(2022秋•温州期末)单项式﹣的系数与次数分别是( )A.﹣3,3B.,3C.﹣,2D.﹣,3【答案】D【解答】解:单项式﹣的系数是﹣,次数是3.故选:D.【变式10-3】(2022秋•大连期末)单项式﹣7a3b4c的系数和次数分别是( )A.﹣7,7B.﹣7,8C.7.7D.7,8【答案】B【解答】解:单项式﹣7a3b4c的系数是﹣7,次数是3+4+1=8.故选:B【题型5 多项式的项与次数】【典例11】(2023•高州市一模)多项式a3+2ab+a﹣3的次数和常数项分别是( )A.6,3B.6,﹣3C.3,﹣3D.3,3【答案】C【解答】解:多项式a3+2ab+a﹣3的次数和常数项分别是3,﹣3.故选:C.【变式11-1】(2023春•沙坪坝区校级月考)多项式x2﹣2x﹣3的一次项系数是( )A.﹣2x B.﹣2C.2x D.2【答案】B【解答】解:多项式x2﹣2x﹣3的一次项系数是﹣2,故选:B.【变式11-2】(2022秋•新乡县校级期末)多项式2xy2﹣﹣5的常数项和次数是( )A.﹣5,3B.5,5C.﹣5,5D.5,3【答案】C【解答】解:2xy2﹣﹣5的常数项和次数是﹣5,5,故选:C.【变式11-3】(2022秋•鼓楼区校级期末)下列关于多项式5m2n2﹣2m2n﹣1的说法中,正确的是( )A.它的项数为2B.它的最高次项是﹣2m2nC.它是三次多项式D.它的最高次项系数是5【答案】D【解答】解:5m2n2﹣2m2n﹣1是四次多项式,它的项数为是3,最高次项是5m2n2,它的最高次项系数是5,故A,B,C错误,D选项正确故选:D.【题型6 规律探究】(与数有关/与式有关/与图形排列有关的律探索)(类型一:与数有关的规律问题)【典例11】(2023•岳阳二模)按一定规律排列的一列数依次是、1、、、、…按此规律,这列数中第100个数是( )A.B.C.D.【答案】B【解答】解:由、、、、、、…可得第n个数为.∵n=100,∴第100个数为:故选:B.【变式11-1】(2023•牡丹江模拟)按一定规律排列的一列数依次为3,6,12,24,…,按此规律排列下去,这列数的第7个数是( )A.96B.124C.192D.234【答案】C【解答】解:观察一系列等式得:第(n+1)个数为3×2n,则这列数中的7个数为3×26=192.故选:C.【变式11-2】(2023•丽江二模)按一定规律排列的等式:1=12,1+3=22,1+3+5=32,1+3+5+7=42,……,按此规律1+3+5+7+9+⋯+2023=( )A.10102B.10112C.10122D.20212【答案】C【解答】解:∵1=12,1+3=22,1+3+5=32,1+3+5+7=42,……,按此规律1+3+5+7+9+⋯+2023=10122,故选:C.【变式11-3】(2023•牡丹江一模)按一定规律排列的一列数依次为,,……按此规律排列下去,这列数的第9个数是( )A.B.C.D.【答案】B【解答】解:∵=,=,,……∴第n个数为:,∴第9个数为:.故选:B.(类型二:与式有关的规律问题)【典例12】(2023•五华区校级模拟)按一定规律排列的单项式:2a,5a2,10a3,17a4,…,则第n个单项式是( )A.(n2﹣1)a n B.(n2+1)a n﹣1C.(n2+1)a n D.(n2+1)a n+1【答案】C【解答】解:∵2a=(12+1)a1,5a2=(22+1)a2,10a3=(32+1)a3,…,∴第n个为:(n2+1)a n;故选:C.【变式12-1】(2023•巧家县一模)按一定规律排列的单项式:﹣x2,x4,﹣x6,x8,﹣x10,…第n个单项式是( )A.(﹣1)n x2n B.(﹣1)n﹣1x2n C.(﹣1)n+1x2n D.(﹣1)n x n【答案】A【解答】解:∵﹣x2,x4,﹣x6,x8,﹣x10,…,∴第n个单项式为:(﹣1)n x2n,故选:A.【变式12-2】(2023•红塔区模拟)按一定规律排列的单项式:x2,2x4,4x6,8x8,16x10,32x12,…,第n个单项式是( )A.2n x2n B.2n﹣1x2n C.(2n﹣2)x2n D.n2x2n【答案】B【解答】解:∵x2=21﹣1x1×2,2x4=22﹣1x2×2,4x6=23﹣1x3×2,……,∴第n个单项式是2n﹣1x2n,故选:B.【变式12-3】(2023•红河州二模)按一定规律排列的单项式:3a2,﹣5a4,7a6,﹣9a8,…,第13个单项式为( )A.27a26B.﹣27a26C.25a26D.﹣25a25【答案】A【解答】解:观察这列单项式,可以发现系数的绝对值是从3开始的奇数,可表示为:(﹣1)n+1•(2n+1),字母a的指数为连续的偶数,可表示为:a2n,因此第n个单项式为:(﹣1)n+1•(2n+1)a2n,∴第13个单项式为:27a26,故选:A.(类型三:与图形有关的规律问题)【典例13】(2023春•开州区期末)观察如图所示的一系列图形,它们是按一定规律排列的,依照此规律,第九个图中“〇”的个数为( )A.26B.28C.30D.32【答案】A【解答】解:第一个图中“〇”的个数为:2,第二个图中“〇”的个数为:5=2+3第三个图中“〇”的个数为:8=2+3×2,第四个图中“〇”的个数为:11=2+3×3,……,第n个图中“〇”的个数为:2+3(n﹣1)=3n﹣1,∴当n=9时,3n﹣1=26,即第九个图中“〇”的个数为:26,故选:A.【变式13-1】(2023春•重庆期末)如图,图形是一组按照某种规律摆放而成的图案,则图⑨中圆点的个数是( )A.81B.82C.83D.84【答案】B【解答】解:第1个图形共有空心圆的个数为1×1+1;第2个图形共有空心圆的个数为2×2+1;第3个图形共有空心圆的个数为3×3+1;…;则第n个图形共有实心圆的个数为n2+1,故图⑨中圆点的个数是:92+1=82.故选:B.【变式13-2】(2023春•沙坪坝区校级期末)观察图中用火柴棒摆的三角形图案,图①共用3根火柴棒,图②共用9根火柴棒,图③共用18根火柴棒,按这种方式摆下去,图⑦需要的总火柴棒数是( )A.63B.108C.74D.84【答案】D【解答】解:由题目得,图①的火柴棒数为3;图②的火柴棒数为9;图③的火柴棒数为18;发现图①是1个三角形的火柴棒数,则图②的火柴棒数比图①多加了2个三角形的火柴棒数,图③的火柴棒数比图②多加了3个三角形的火柴棒数;则图④的火柴棒数应比图③多加4个三角形的火柴棒数,为30;进一步发现规律:第n个图形的火柴棒数为3×(1+2+3+…+n)=3×所以图⑦的总火柴数量为故选:D.【变式13-3】(2023春•丰都县期末)如图,古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第7个五边形数是( )A.62B.70C.84D.108【答案】B【解答】解:∵第1个五边形数为1,第2个五边形数为1+4=5,第3个五边形数为1+4+7=12,第4个五边形数为1+4+7+10=22,∴第5个五边形数为1+4+7+10+13=35,第6个五边形数为1+4+7+10+13+16=51,第7个五边形数为1+4+7+10+13+16+19=70.故选:B.【题型7 同类项的定义】【典例14】(2022秋•柳州期末)下列式子中,与单项式4ab是同类项的是( )A.3a2b2B.ab C.2a2b D.2bc【答案】B【解答】解:∵3a2b2,2a2b和2bc都不与4ab是同类项,ab与4ab是同类项,∴选项A,C,D不符合题意,选项B符合题意,故选:B.【变式14-1】(2023•诸暨市模拟)下列每组中的两个代数式,属于同类项的是( )A.7a2b和3ab2B.和﹣2x2yC.x2yz和x2y D.3x2和3y2【答案】B【解答】解:A.7a2b和3ab2,所含字母相同,但相同字母的指数不相同,所以不是同类项,故本选项不合题意;B.和﹣2x2y,所含字母相同且相同字母的指数也相同,是同类项,故本选项符合题意;C.x2yz和x2y,所含字母不尽相同,不是同类项,故本选项不合题意;D.3x2和3y2,所含字母不尽相同,不是同类项,故本选项不合题意;故选:B.【变式14-2】(2023•陇县一模)若单项式﹣2x m y3与y n x2的和仍为单项式,则m n的值为( )A.8B.6C.9D.27【答案】A【解答】解:∵单项式﹣2x m y3与y n x2的和仍是单项式,∴它们是同类项,∴m=2,n=3,则m n=23=8,故选:A.【变式14-3】(2023春•互助县期中)单项式x m﹣1y3与﹣4xy n是同类项,则m n 的值是( )A.3B.1C.8D.6【答案】C【解答】解:∵单项式x m﹣1y3与﹣4xy n是同类项,∴m﹣1=1,n=3,∴m=2,n=3,∴m n=23=8.故选:C.【题型8 合并同类型】【典例15】(2023•乌当区模拟)计算a3+a3的结果为( )A.a3B.2a3C.a6D.2a6【答案】B【解答】解:a3+a3=2a3.故选:B.【变式15】(2022秋•西宁期末)化简:4a2﹣6a2+a2= ﹣a2 .【答案】﹣a2.【解答】解:4a2﹣6a2+a2=(4﹣6+1)a2=﹣a2.故答案为:﹣a2.【题型9 添括号与去括号】【典例16】(2023•海南二模)下列运算中“去括号”正确的是( )A.a+(b﹣c)=a﹣b﹣c B.a﹣(b+c)=a﹣b﹣cC.m﹣2(p﹣q)=m﹣2p+q D.x2﹣(﹣x+y)=x2+x+y【答案】B【解答】解:A、原式=a+b﹣c,错误;B、原式=a﹣b﹣c,正确;C、原式=m﹣2p+2q,错误;D、原式=x2+x﹣y,错误,故选:B.【变式16-1】(2022秋•柳州期末)下面去括号正确的是( )A.a﹣(b+1)=a﹣b﹣1B.2(x+3)=2x+3C.x﹣(y﹣1)=x﹣y﹣1D.﹣3(m﹣n)=﹣3m﹣3n【答案】A【解答】解:A、a﹣(b+1)=a﹣b﹣1,故本选项正确.B、2(x+3)=2x+6,故本选项错误.C、x﹣(y﹣1)=x﹣y+1,故本选项错误.D、﹣3(m﹣n)=﹣3m+3n,故本选项错误.故选:A.【变式16-2】(2022秋•黔江区期末)下列去括号或添括号的变形中,正确的是( )A.2a﹣(3b﹣c)=2a﹣3b﹣c B.3a+2(2b﹣1)=3a+4b﹣1C.m﹣n+a﹣b=m﹣(n+a﹣b)D.a+2b﹣3c=a+(2b﹣3c)【答案】D【解答】解:A、2a﹣(3b﹣c)=2a﹣3b+c,不合题意;B、3a+2(2b﹣1)=3a+4b﹣2,不合题意;C、m﹣n+a﹣b=m﹣(n﹣a+b),不合题意;D、a+2b﹣3c=a+(2b﹣3c),符合题意.故选:D.【变式16-3】(2022秋•叙州区期末)下列各式变形正确的是( )A.﹣(a﹣b)﹣c=﹣a+b+c B.a﹣2(b﹣c)=a﹣2b﹣2cC.a+2(b﹣c)=a+2b﹣c D.a﹣3(b﹣c)=a﹣3b+3c【答案】D【解答】解:A.﹣(a﹣b)﹣c=﹣a+b﹣c,选项A不符合题意;B.a﹣2(b﹣c)=a﹣2b+2c,选项B不符合题意;C.a+2(b﹣c)=a+2b﹣2c,选项C不符合题意;D.a﹣3(b﹣c)=a﹣3b+3c,选项D符合题意;故选:D.【题型10 整式的加减】【典例17】(2023春•南关区校级月考)计算:(1)3(a2﹣ab)﹣5(ab+2a2﹣1);(2)3x2﹣[5x﹣(﹣3)+3x2].【答案】(1)﹣7a2﹣8ab+5;(2)﹣x﹣3.【解答】解:(1)3(a2﹣ab)﹣5(ab+2a2﹣1)=3a2﹣3ab﹣5ab﹣10a2+5=﹣7a2﹣8ab+5;(2)3x2﹣[5x﹣(﹣3)+3x2]=3x2﹣5x+(﹣3)﹣3x2=3x2﹣5x+﹣3﹣3x2=﹣x﹣3.【变式17-1】(2022秋•青神县期末)2(x﹣2y)﹣(2x﹣3y)+3(x﹣y).【答案】3x﹣4y.【解答】解:原式=2x﹣4y﹣2x+3y+3x﹣3y=3x﹣4y.【变式17-2】(2022秋•梁山县期末)计算:(1)(2a﹣b)﹣(2b﹣3a)﹣2(a﹣2b)(2).【答案】见试题解答内容【解答】解:(1)原式=2a﹣b﹣2b+3a﹣2a+4b=3a+b;(2)原式=4x2﹣5xy﹣y2﹣2x2+6xy﹣y2﹣y2=2x2+xy﹣y2.【变式17-3】(2022秋•邹平市期末)化简:(1)5(3a2b﹣ab2)﹣2(ab2+3a2b);(2).【答案】(1)9a2b﹣7ab2(2)5xy2﹣x.【解答】解:(1)5(3a2b﹣ab2)﹣2(ab2+3a2b)=15a2b﹣5ab2﹣2ab2﹣6a2b=9a2b﹣7ab2;(2)=6xy2﹣(2x﹣x+2xy2﹣xy2)=6xy2﹣(x+xy2)=5xy2﹣x.【题型11 整式加减的应用】(类型一:与图形有关的问题)【典例18】(2022秋•张店区期末)已知,两个长方形A和B的周长相等,其各边长如图所示,请求出长方形B的长.【答案】见试题解答内容【解答】解:由题意,得4x+3y+(2x﹣y)﹣(3x﹣2y)=4x+3y+2x﹣y﹣3x+2y =3x+4y,答:长方形B的长为3x+4y.【变式18-1】(2022秋•二道区校级期末)如图,学校要利用专款建一长方形的自行车停车场,其他三面用护栏围起,其中长方形停车场的长为(2a+3b)米,宽比长少(a﹣b)米.(1)用a、b表示长方形停车场的宽;(2)求护栏的总长度;(3)若a=30,b=10,每米护栏造价80元,求建此停车场所需的费用.【答案】(1)(a+4b)米;(2)护栏的长度是:(4a+11b)米;(3)若a=30,b=10,每米护栏造价80元,建此车场所需的费用是18400元.【解答】解:(1)依题意得:(2a+3b)﹣(a﹣b)=2a+3b﹣a+b=(a+4b)米;(2)护栏的长度=2(a+4b)+(2a+3b)=4a+11b;答:护栏的长度是:(4a+11b)米;(3)由(2)知,护栏的长度是4a+11b,则依题意得:(4×30+11×10)×80=18400(元).答:若a=30,b=10,每米护栏造价80元,建此车场所需的费用是18400元.【变式18-2】(2021秋•青岛期末)从一个边长为a的正方形纸片(如图1)上剪去两个相同的小长方形,得到一个美术字“S”的图案(如图2),再将剪下的两个小长方形拼成一个新长方形(如图3).(1)用含有a,b的式子表示新长方形的长是 a﹣b ,宽是 a﹣3b ;(2)若a=8,剪去的1个小长方形的宽为1,求新长方形的周长.【答案】(1)a﹣b,a﹣3b;(2)16.【解答】解:(1)由题意得:新长方形的长为a﹣b,宽为a﹣3b,故答案为:a﹣b,a﹣3b;(2)新长方形的周长=2[(a﹣b)+(a﹣3b)]=4a﹣8b;由题意得:a﹣3b=2,∵a=8,∴b=2,∴当a=8,b=2时,4a﹣8b=16.【变式18-3】(2022秋•二道区校级期末)为帮助农民打通产品销路,某县领导干部进行网络直播带货,为特色农产品代言,为配合云直播,现需搭建一个长方形的直播舞台,已知长方形的长是(3a+2b)米,宽比长的2倍小(a+8b)米.(1)求长方形的周长(用含有a,b的式子表示);(2)当,时,求长方形的长比宽长多少米?【答案】(1)(16a﹣4b)米;(2)0.5米.【解答】(1)解:由题意得,长方形的宽为:2(3a+2b)﹣(a+8b)=6a+4b ﹣a﹣8b=5a﹣4b(米),所以长方形的周长为:2(5a﹣4b+3a+2b)=2(8a﹣2b)=16a﹣4b (米).(2)3a+2b﹣(5a﹣4b)=3a+2b﹣5a+4b=﹣2a+6b,当,时,原式=(米).答:长方形的长比宽长0.5米(类型二:分段计费问题)【典例19】(2022秋•丰南区期中)为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段以达到节水的目的.如下所示是该市自来水收费价格见价目表.价目表每月用水量单价不超出6m3的部分2元/m3超出6m3但不超出10m3的部分4元/m3超出10m3的部分8元/m3注:水费按月结算.(1)填空:若该户居民2月份用水4m3,则应收水费 8 元;(2分)(2)若该户居民3月份用水am3(其中6<a<10),则应收水费多少元?(用a的整式表示并化简)(3)若该户居民4,5月份共用水15m3(5月份用水量超过了4月份),设4月份用水xm3,求该户居民4,5月份共交水费多少元?(用x的整式表示并化简)【答案】见试题解答内容【解答】解:(1)根据题意得:2×4=8(元);(2)根据题意得:4(a﹣6)+6×2=4a﹣12(元);(3)由5月份用水量超过了4月份,得到4月份用水量少于7.5m3,当4月份得用水量少于5m3时,5月份用水量超过10m3,则4,5月份共交水费为2x+8(15﹣x﹣10)+4×4+6×2=﹣6x+68(元);当4月份用水量不低于5m3,但不超过6m3时,5月份用水量不少于9m3,但不超过10m3,则4,5月份交的水费为2x+4(15﹣x﹣6)+6×2=﹣2x+48(元);当4月份用水量超过6m3,但少于7.5m3时,5月份用水量超过7.5m3但少于9m3,则4,5月份交的水费为4(x﹣6)+6×2+4(15﹣x﹣6)+6×2=36(元).【变式19-1】(2023春•农安县期中)为节约用水,某市规定三口之家每月标准用水量为15立方米,超过部分加价收费,假设不超过部分水费为1.5元/立方米,超过部分水费为3元/立方米.(1)如果小明家6月份用水12立方米,则应缴水费多少元?(2)如果小明家某月的用水为m立方米(m>15),那么这个月应缴水费多少元?(用含m的代数式表示)(3)如果小明家某月的用水为20立方米,那么这个月应缴水费多少元?【答案】(1)18元;(2)(3m﹣22.5)元;(3)37.5元.【解答】解:(1)12×1.5=18(元).故应缴水费18元;(2)这个月应缴水费为15×1.5+(m﹣15)×3=(3m﹣22.5)元;(3)3×20﹣22.5=37.5(元).答:这个月应缴水费37.5元.【变式19-2】(2022秋•鲤城区校级期中)为鼓励节约用电,某地用电收费标准规定:如果每月每户用电不超过150度,那么每度电0.5元;如果该月用电超过150度,那么超过部分每度电0.8元.(1)小张家一月份用电120度,那么这个月应缴电费 60 元.(2)如果小张家一个月用电a度(a>150),那么这个月应缴电费多少元?(用含a的式子表示)(3)如果小张家八月份用电215度,那么这个月应缴电费多少元?【答案】(1)60;(2)(0.8a﹣45)元.(3)127元.【解答】解:(1)120×0.5=60(元).答:这个月应缴电费60元.故答案为:60;(2)150×0.5+0.8(a﹣150)=75+0.8a﹣120=(0.8a﹣45)(元).答:如果小张家一个月用电a度(a>150),那么这个月应缴电费(0.8a﹣45)元.(3)当a=215时,0.8a﹣45=0.8×215﹣45=127.答:这个月应缴电费127元.【变式19-3】(2022春•武昌区期中)某市居民使用自来水按如下标准收费(水费按月缴纳):户月用水量单价不超过12m3的部分a元∕m3超过12m3但不超过20m3的部分 1.5a元∕m3超过20m3的部分2a元∕m3(1)当a=2时,某用户一个月用了28m3水,求该用户这个月应缴纳的水费.(2)设某户月用水量为n立方米,当n>20时,则该用户应缴纳的水费 2na ﹣16a 元(用含a、n的整式表示).(3)当a=2时,甲、乙两用户一个月共用水40m3,已知甲用户缴纳的水费超过了24元,设甲用户这个月用水xm3,试求甲、乙两用户一个月共缴纳的水费(用含x的整式表示).【答案】详见解答.【解答】解:(1)2×12+2×1.5×(20﹣12)+2×2×(28﹣20)=24+24+32=80(元).答:该用户这个月应缴纳80元水费.(2)a×12+1.5a×(20﹣12)+2a×(n﹣20)=12a+12a+2na﹣40a=(2na﹣16a)元.故答案为:(2na﹣16a)(3)∵甲用户缴纳的水费超过了24元,∴x>12.①12<x≤20,甲:2×12+3×(x﹣12)=3x﹣12.乙:20≤40﹣x<28.12×2+8×3+4×(40﹣x﹣20)=128﹣4x.共计:3x﹣12+128﹣40x=116﹣x.②20<x≤28,甲:2×12+3×8+4(x﹣20)=4x﹣32.乙:12<40﹣x≤20,2×12+3×(40﹣x﹣12)=108﹣3x.共计:4x﹣32+108﹣3x=x+76.③28<x≤40,甲:2×12+3×8+4×(x﹣20)=4x﹣32.乙:0<40﹣x≤12,2×(40﹣x)=80﹣2x.共计:4x﹣32+80﹣2x=2x+48.答:甲、乙两用户共缴纳的水费:当12<x≤20时,缴水费(116﹣x)元;当20<x≤28时,缴水费(x+76)元;当28<x≤40时,缴水费(2x+48)元;(类型三:方案问题)【典例20】(2022秋•翠屏区期末)某体育用品商场销售某品牌的羽毛球拍和羽毛球,一副羽毛球拍定价150元,一盒羽毛球定价20元.根据市场调查,商场决定开展促销活动,活动期间向客户提供两种优惠方案.方案一:买一副羽毛球拍送一盒羽毛球;方案二:羽毛球拍和羽毛球都按定价的90%付款.现某校要到该商场购买羽毛球拍20副,羽毛球x盒(x>20).(1)用含x的代数式分别表示两种方案需付的款项,方案一: (20x+2600)元 ,方案二: (18x+2700)元 ;(2)当x=30和x=60时,请你分别通过计算说明选用方案一购买还是方案二购买更合算?【答案】(1)(20x+2600)元;(18x+2700)元;(2)答案见解析.【解答】解:方案一需付的款项为:150×20+20(x﹣20)=(20x+2600)元;方案二需付的款项为:(150×20+20x)×90%=(18x+2700)元.故答案为:(20x+2600)元;(18x+2700)元;(2)当x=30时,方案一需付的款项为:20×30+2600=3200(元),方案二需付的款项为:18×30+2700=3240(元),∵3200<3240,∴当x=30时,选用方案一购买更合算;当x=60时,方案一需付的款项为:20×60+2600=3800(元),方案二需付的款项为:18×60+2700=3780(元),∵3780<3800,∴当x=60时,选用方案二购买更合算.【变式20-1】(2022秋•巴中期末)某电器商店销售一种洗衣机和电磁炉,洗衣机每台定价900元,电磁炉每台定价200元.双“十一”期间商店决定开展促销活动,活动期间向客户提供两种优惠方案:方案一:买一台洗衣机送一台电磁炉;方案二:洗衣机和电磁炉都按定价9折出售.现某客户要在该商店购买洗衣机10台,电磁炉x台(x>10).(1)若该客户按方案一、方案二购买,分别需付款多少元?(用含x的式子表示)(2)若x=40,通过计算说明此时按哪种方案购买较为合算?【答案】(1)200x+7000,180x+8100;(2)方案一划算.【解答】解:(1)设方案一付款费用为y1,方案二付款费用为y2,(1)y1=900×10+200(x﹣10)=(200x+7000)(元),y2=900×0.9×10+200×0.9x=(180x+8100)(元),(2)当x=40时,y1=200x+7000=200×40+7000=15000(元),y2=180x+8100=180×40+8100=15300(元);∵15000<15300,∴方案一划算.【变式20-2】(2022秋•朝阳区期末)春暖花开,新学期伊始,某中学为了给学。