第8章：信号处理中常用的正交变换

正 交 变 换1．研究对象：空间中物体的位置变化。

观察空间中的物体，当我们把一个物体从一个地点搬到另一个地点时，物体有什么性质保持不变，有什么东西会起变化。

2． 正交变换的建立搬动物体，除了物体的位置发生变化外，物体的本身属性都保持不变。

用数学的相关知识进行描述之即长度、面积、角度、体积等保持不变。

从测量、计算的角度而言，物体的度量性质不变。

由于长度是各种计算的基础，长度不变将导致角度、面积、体积等不变，即长度不变是本质性的。

用数学语言——变换——描述上述现象，即搬动物体的过程是一个保持长度不变的变换。

定义：保持任两点间距离不变的变换称为正交变换。

3． 正交变换的不变系统直线、线段、单位向量、垂直性、平行性，······。

4． 笛卡尔直角坐标系为了用代数的方法来研究正交变换，我们应该建立一种在正交变换下保持不变的坐标系5． 特例物体位置的变动不外乎移动、转动和翻动（以及它们的组合），它们的数学表示为 （1） 平移 ⎩⎨⎧+='+='00y y y x x x（2） 旋转⎩⎨⎧+='-='θθθθc o s s i n s i n c o s y x y y x x 或 X X ⎪⎪⎭⎫⎝⎛-='θθθθc o s s i n s i n c o s。

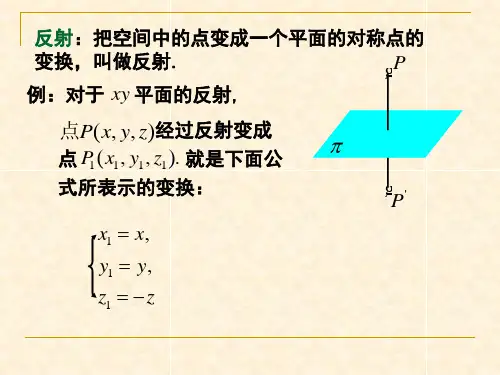
（3） 反射⎩⎨⎧-='='yy xx 或 X X ⎪⎪⎭⎫⎝⎛-='1001 。

问题探索：绕点),(000y x P 6． 正交变换的代数表示M O O O M O ''+'='，另一方面， 21e y e x M O'+'='所以 M O O O e y e x ''+'='+'21（*） 又 2010e y e x O O+='，21e y e x OM+=，根据正交变换的性质知 21e y e x M O '+'=''由向量代数知识可知 22211222211111,e a e a e e a e a e+='+=' 将它们代入（*）可得202221101211222112221111201021)()()()(e y y a x a e x y a a e a e a y e a e a x e y e x e y e x+++++=+++++='+'所以 ⎩⎨⎧++='++='0222101211y y a x a y x y a x a x所以正交变换的代数表示为⎩⎨⎧++='++='232221131211a y a x a y a y a x a x ，其中 0,122211211222212221211=+=+=+a a a a a a a a 。

实数域上正交变换的分类一、正交变换定义1.1 设A是欧氏空间V的一个线性变换,若A保持向量的内积不变,即对于任意的α，βεV都有(Aɑ，Aβ) = (ɑv，β)，则称A为V的正交变换.二、等价条件定理2.1 设A是n维欧氏空间V的一个线性变换,则下列命题等价:1)A是正交变换；2)A保持向量的长度不变,即对于V，|Aα|=|ɑ|；3)A把V的规范正交基变为V的规范正交基；4)A在规范正交基下的矩阵是正交矩阵.⇒2）对于αεV, 由证：1）(Aɑ，Aɑ)=(ɑ，ɑ),即得：|Aɑ|=|ɑ|2）⇒3）设ε1，ε2，…，εn是V的任一规范正交基,记εi+εj=ɑεV.由|Aɑ|=|ɑ|或(Aɑ，Aɑ)=(ɑ,ɑ)得(A(εi+εj)，A(εi+εj))=(εi+εj，εi+εj）而(A(εi+εj)，A(εi+εj))=(Aεi，Aεi)+2(Aεi，Aεj)+(Aεj，Aεj)=(εi ，εi)+2(εi ，εj)+(εj ，εj)(εi+εj,εi+εj ）=(εi ，εi)+2(εi ，εj)+(εj ，εj)故 A ε1，A ε2，…，A εn 是V 的一组规范正交基. 3)⇒4）设ε1，ε2，…，εn 是V的规范正交基,A(ε1，ε2，…，εn)=(A ε1， A ε2，…，A εn)= (ε1，ε2，…，εn)A由3), A ε1，A ε2，…，A εn 是0,(,)(,)1,i j i j i j A A i j εεεε≠⎧∴==⎨=⎩V的规范正交基,故A可看作是由规范正交基ε1，ε2，…，εn到规范正交基Aε1，Aε2，…，Aεn的过渡矩阵,A是正交矩阵.4) 1）设ε1，ε2，…，εn是V 的规范正交基,且A在此基下的矩阵A为正交矩阵.由(Aε1，Aε2，…，Aεn)= (ε1，ε2，…，εn)A,知Aε1，Aε2，…，Aεn也是V的规范正交基,设α=x1ε1+x2ε2+……x nεn,Β=y1ε1+y2ε2+……y nεn,Aɑ=x1Aε1+x2Aε2+…+xnAεnAβ=y1Aε1+y2Aε2+…+ynAεn (Aα,Aβ)= x1y1+x2y2+…+xnyn(α,β)= x1y1+x2y2+…+xnyn 所以 (A α，A β)=(α，β),故A 为正交变换.三、规范正交基到规范正交基的过渡矩阵。

数字信号处理讲义第8章离散傅里叶变换数字信号处理讲义--第8章离散傅里叶变换第8章离散傅里叶变换教学目的1．理解离散傅里叶级数、傅里叶变换的概念和性质，掌握循环卷积的计算方法；2．掌控用线性傅里叶转换同时实现线性卷积的条件和方法。

教学重点与难点重点：1．理解离散傅里叶级数、傅里叶变换的概念和性质，掌握循环卷积的计算方法；2．掌控用线性傅里叶转换同时实现线性卷积的条件和方法。

难点：１．循环卷积的计算方法。

２．线性傅里叶转换同时实现线性卷积的条件与方法。

8.0开场白在前面讨论了序列的傅里叶变换和z变换。

由于数字计算机只能计算有限长离散序列，因此有限长序列在数字信号处理中就显得很重要，当然可以用z变换和傅里叶变换来研究它，但是，这两种变换无法直接利用计算机进行数值计算。

针对序列“有限长”这一特点，可以导出一种更有用的变换：离散傅里叶变换（discretefouriertransform，简写为dft）。

它本身也是有限长序列。

作为有限长序列的一种傅里叶表示法，离散傅里叶变换除了在理论上相当重要之外，而且由于存在有效的快速算法――快速离散傅里叶变换，因而在各种数字信号处理的算法中起着核心作用。

有限长序列的离散傅里叶变换（dft）和周期序列的离散傅里叶级数（dfs）本质上是一样的。

为了讨论离散傅里叶级数与离散傅里叶变换，我们首先来回顾并讨论傅里叶变换的几种可能形式，见图8-1所示。

|x(j?)|x(t)1(a)oo?t－?－x(t)|x(jk??)|(b)otok?t?|x(e?)|x(nt)1/t(c)ntoo－tn点|x(e??)|x(n)aa00pppjjkspon点n(d)－?on点?s??图８-1各种形式的傅里叶变换一个非周期实已连续时间信号xa(t)的傅里叶转换，即为频谱xa(jω)就是一个已连续的非周期函数，这一转换对的示意图见到图8-1(a)。

该转换关系与第1章“已连续时间信号的取样”中所牵涉至的非周期已连续时间信号xa(t)的情况相同。

数字信号处理————信号正交的理解以及复数1.数学解释 正交最早出现于中的。

在三维中，两个向量的如果是零，那么就说这两个向量是正交的。

注： （1）. 在数学中，数量积（dot product; scalar product，也称为点积）是接受在实数R上的两个并返回⼀个实数值的。

它是的标准。

（2）. 向量积，数学中⼜称外积、叉积，物理中称⽮积、叉乘，是⼀种在中向量的。

与不同，它的运算结果是⼀个向量⽽不是⼀个标量。

并且两个向量的叉积与这两个向量和垂直。

例如：三⾓函数系{1,cosx,sinx,cos2x,sin2x,……,cosnx,sinnx,……} 在区间[-π,π]上正交，就是指在三⾓函数系⑴中任何不同的两个函数的乘积在区间[-π,π]上的积分等于0，即 ∫[-π->π]cosnxdx=0 ∫[-π->π]sinnxdx=0 ∫[-π->π]sinkxcosnxdx=0 ∫[-π->π]coskxcosnxdx=0 ∫[-π->π]sinkxsinnxdx=0 (k,n=1,2,3.....,k≠n)2.正交信号的理解 （1）. 定义 正交信号的具有理想冲击函数的形式，为零。

然⽽由知道，这样的理想信号是不存在的。

因此,需要对发射信号进⾏优化设计，使得信号的和尽可能低。

到⽬前为⽌，国际上⼰经提出了⼀些针对MIMO的正交信号设计⽅法 正交信号，也称为复信号，被⽤于数字信号处理的很多领域，⽐如：数字通信系统、雷达系统、⽆线电测向中对到达时间差异的处理、相关脉冲测量系统、天线波束形成的应⽤、信号边带调制器等等。

实际表⽰复数变量使⽤实部和虚部两个分量。

正交信号也⼀样，必须⽤实部和虚部两路信号来表⽰它，两路信号传输会带来⿇烦，实际信号的传输总是⽤实信号，⽽在信号处理中则⽤复信号。

（实部和虚部的称谓是传统的叫法，在我们⽇常应⽤中⼀直被延⽤。

在通信⼯程中分别⽤同相和正交相表⽰。

正交变换数学三
（最新版）
目录
1.引言
2.正交变换的定义和性质
3.正交变换在数学三中的应用
4.结论
正文
1.引言
正交变换是线性代数中的一个重要概念，在数学中有广泛的应用。

在数学三这门课程中，正交变换是一个重要的内容，本文将从正交变换的定义和性质入手，介绍正交变换在数学三中的应用。

2.正交变换的定义和性质
正交变换是指将一个向量空间中的向量映射到另一个向量空间中的
向量，并且保持向量的模长不变，同时也保持向量之间的角度不变。

正交变换具有以下性质:
- 正交变换是线性变换。

- 正交变换保持向量的模长不变。

- 正交变换保持向量之间的角度不变。

- 正交变换的逆变换也是正交变换。

3.正交变换在数学三中的应用
正交变换在数学三中有广泛的应用，下面举几个例子来说明:
- 傅里叶变换：傅里叶变换是一种将时域信号转换为频域信号的方法，
可以将信号分解成不同频率的成分，是信号处理中的重要工具。

- 离散余弦变换：离散余弦变换是一种将离散信号转换为频域信号的方法，常用于图像压缩和信号处理中。

- 正交矩阵：正交矩阵是一种特殊的矩阵，它的转置矩阵和逆矩阵都是它本身，常用于线性变换和矩阵运算中。

4.结论
正交变换是线性代数中的一个重要概念，具有保持向量的模长和角度不变的性质，在数学三中有广泛的应用，如傅里叶变换、离散余弦变换和正交矩阵等。

信号空间：将信号看做空间里的向量内积：（jiang2）内积为0—正交范数：（jiang3）/zh-cn/%E6%AD%A3%E4%BA %A4/jsjy/kc/xhyjs/chap6/chap6_1/chap6_1_1.htm第一讲信号的正交分解把实际的信号分解为信号单元是信号分析和处理中常用的方法。

一方面，信号的分解使我们能了解它的性质与特征，有助于我们从中提取有用的信息，这一点，在信号的傅里叶变换中就已经体现出来了。

另一方面，把信号分解之后，可以按照我们的意愿对它进行改造，对于信号压缩、分析等都有重要的意义。

信号分解的方法有很多。

例如，对一离散信号，我们可把它分解成一组函数的组合，即，式中，。

但这种分解无实用意义，因为的权重即是信号自己。

另一种分解的方法是把N点数据看成是N维空间的一个向量，我们选择该空间的单位基向量作为分解的“基”，也就是按照这种分解方法，各正交向量的权仍是信号自己的各个分量，也无太大意义，但这一分解已经体现了“正交”分解的概念。

一般，我们可把信号看成N维空间中的的一个元素，可以是连续信号，也可以是离散信号。

N可以是有限值也可以是无穷大。

设是由一组向量所张成，即这一组向量可能是线性相关的，也可能是线性独立的。

如果它们线性独立，我们则称它们为空间中的一组“基”。

各自可能是离散的，也可能是连续的，这视而定。

这样，我们可将按这样一组向量作分解，即(6-1-1)式中是分解系数，它们是一组离散值。

因此，上式又称为信号的离散表示（Discrete Representation）。

如果是一组两两互相正交的向量，则（6-1-1）式称为的正交展开（或正交分解）。

分解系数是在各个基向量上的投影。

若N=3，其含意如图6-1-1所示。

图6-1-1 信号的正交分解为求分解系数，我们设想在空间中另有一组向量：，这一组向量和满足：（6-1-2）这样，用和（6-1-1）式两边做内积，我们有，即：(6-1-3a)或(6-1-3b)(6-1-3a)式对应连续时间信号，(6-1-3b)式对应离散时间信号。

讲座2 信号变换基础 --- 线性空间及正交变换的基本理论2.1 前言在电子技术、通信工程、自动控制等领域，怎样描述和分析信号，抽取其特征，这对于信号处理是非常重要的。

这个问题的理论基础是高等代数中的线性空间变换问题。

人们知道，三维空间中的向量一般要用它在正交坐标系的三个分量来描述。

但是，如果适当地旋转坐标轴（进行正交变换），使所讨论的向量与其中一个坐标轴重合，而垂直于其它两个坐标轴，那么，向量就可以只用它在该坐标轴上的投影来描述。

对于平面上的向量也可以作类似的处理。

一般信号看起来很复杂，可视为无限维空间的一个向量。

人们很难从这样的向量获知信号的本质，从而也难以对其进行有效的处理。

所以，对信号进行分析就理所当然地涉及坐标系的变换，即从时域变换到频域或相反。

这种变换就是高等代数中的正交变换。

正交变换具有“能量”不变性（即向量长度不变）。

傅里叶变换是信号处理中常用的正交变换。

它有四种基本形式，即 1．连续时间周期函数的傅里叶级数变换 2．连续时间非周期函数的傅里叶变换 3．离散时间非周期函数的序列傅里叶变换4．离散时间周期序列的序列傅里叶级数变换为了使读者从更宽广的角度领会本书的内容，作者认为非常有必要开设本讲座。

本讲座的任务是帮助读者复习一些先修课程的重要内容。

作者将按以下顺序导出正交变换：线性空间 ---〉线性空间的线性变换 ---〉欧几里德空间 ---〉正交变换2.2 空间n K2.2.1 n 元向量空间人们在解析几何中已经知道，三维几何空间在取定三个互相正交的单位向量1e ，2e和3e ，形成一个Descartes直角坐标系后，任一向量与它在各坐标轴上的投影（图2.2.1），即三个有序实数1ξ，2ξ，3ξ 一一对应：T321),,(ξξξ↔x图2.2.1 三维向量这里，x是由行向量),,(321ξξξ转置而成的列向量，”T ”表示转置。

向量的数乘是指T 321),,(ξξξa a a x a ↔向量还有加法运算。

正交变换设M是对称矩阵， P是正交矩阵， N=P^tMP 称为 M的正交变换。

（正交矩阵的定义为：P.P^t = I）正交变换既是相似变换，也是相合变换。

正交变换不改变M的特征值。

正交变换最初来自于维基百科,这种矩阵元被称为简正坐标.用质量加权坐标表示的分子内部运动的动能,用质量加权坐标表示的分子内部势能,用质量加权坐标表示的分子内部势能,由力常数的数学表达式可以知道fij = fji因而矩阵为一个正交变换通过酉变换可以把矩阵变形成为对角矩阵的形式：。

则有：它的每一个矩阵元都是分子所有质量加权坐标的线性组合，总的矩阵元的数量恰巧等于质量加权坐标的个数，这些矩阵元就被称作简正坐标,而这些变换中分子的势能不变,所以正交变换又称为酉变换.采用OpenCV进行人脸识别一、实现原理本程序的实现方法请参看《face recognition using an embedded HMM》。

二、开发工具1、OpenCV视觉开发库2、MFC三、程序运行1、主界面主界面包括识别区域和结果区域。

如下：2、参数设置（Set Params）u状态数的设置，默认为5个超态，从上到下分别代表前额（3），眼睛（6），鼻子（6），嘴巴（6），下巴（3）u观察向量2D-DCT：包括观察向量大小（OBS），DCT大小和Delta大小u最大迭代次数，默认为80u混合高斯次数，默认为33、人员管理（Per Manage）人员管理界面如下：u添加人员信息：输入人员信息具有Name与NO属性，NO不可重复。

u删除人员信息：在人员列表中选择要删除的人员，然后进行删除，人员信息删除后，包括人员的图片也进行删除，该人员也不在识别范围内。

u添加人员图片：一个人可以多张图片，点击要添加的人员，可以通过此按钮添加图片。

添加前最好在.. \HMM\××文件夹里（××表示该人员名称）。

u删除人员图片：点击要删除的图片，按“Del Image”按钮进行删除，图片删除后只是该图片不在训练的区域。

54. 坐标系中的正交变换如何实现？关键信息项：1、正交变换的定义及基本原理2、常见的正交变换类型3、正交变换的矩阵表示4、实现正交变换的步骤和方法5、应用场景举例6、正交变换的性质和特点1、正交变换的定义及基本原理11 正交变换是一种保持向量长度和内积不变的线性变换。

在数学上，如果一个线性变换 T 满足对于任意向量 x 和 y，有（Tx, Ty) ＝（x, y)，且｜｜Tx|｜＝｜｜x|｜，则称 T 为正交变换。

12 正交变换的基本原理基于向量空间的几何性质。

它在不改变向量空间结构的前提下，对向量进行旋转、反射等操作。

2、常见的正交变换类型21 旋转变换：绕着坐标轴或特定的轴进行旋转。

22 反射变换：关于某个平面或直线进行反射。

3、正交变换的矩阵表示31 任何正交变换都可以用一个正交矩阵来表示。

正交矩阵 Q 满足Q^TQ ＝ QQ^T ＝ I，其中 I 是单位矩阵，Q^T 是 Q 的转置。

32 例如，二维平面中的旋转变换矩阵可以表示为cosθ sinθ; sinθcosθ，其中θ 是旋转角度。

4、实现正交变换的步骤和方法41 确定变换的类型（旋转、反射等）和相关参数（如旋转角度、反射平面等）。

42 根据变换类型和参数构建正交矩阵。

43 对于给定的向量或点，通过矩阵乘法实现变换。

5、应用场景举例51 计算机图形学：用于图形的旋转、缩放、镜像等操作，以实现逼真的视觉效果。

52 物理学：在量子力学、力学系统等领域中，用于描述物体的运动和状态变化。

53 信号处理：如在图像处理中，用于图像的校正、增强等。

6、正交变换的性质和特点61 保持向量长度不变：即经过正交变换后，向量的模长不发生改变。

62 保持向量间的夹角不变：这意味着向量之间的相对位置关系在变换前后保持不变。

63 正交矩阵的行列式值为±1：当行列式值为1 时，对应旋转变换；当行列式值为－1 时，对应反射变换。

总之，正交变换在数学和相关领域中具有重要的地位和广泛的应用。