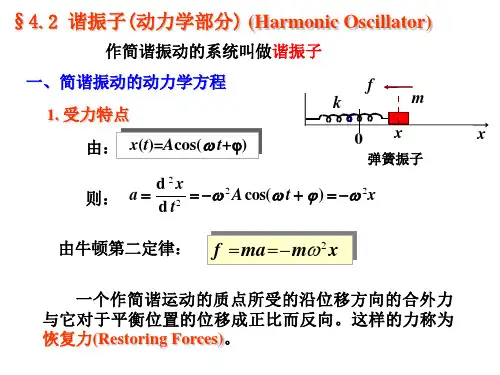
简谐振动的动力学方程为

动的依据） 2.对称性——简谐振动物体具有对平衡位置的对称
性，在关于平衡位置对称的两个位置，动能、势 能相等，位移、回复力、加速度大小相等，方向 相反,速度大小相等，方向可能相同，也可能相 反,振动过程相对平衡位置两侧的最大位移值相等.
3.周期性——简谐运动的物体经过相同时间t=nT(n) 为整数,必回复到原来的状态,经时间t=(2n+1) T2 (n为整数)，则物体所处的位置必与原来的位置 关于平衡位置对称，因此在处理实际问题中，
图2 3.简谐运动的能量
简谐运动过程中动能和势能相互转化，机械能 守恒，振动能量与 振幅 有关， 振幅 越大， 能量越大.
二、简谐运动的两种基本模型
弹簧振子（水 平）
单摆
模型示意图
条件 平衡位置
回复力
忽略弹簧质量、 无摩擦等阻力
细线不可伸长、质量 忽略、无空气等阻力、 摆角很小
弹簧处于原长处
最低点
度方向上的力充当向心力，即F向=F-mgcosθ；摆 球重力在平行于速度方向上的分力充当摆球的回复
力.当单摆做小角度摆动时，由于F回=-mgsinθ= - mg x=-kx，所以单摆的振动近似为简谐运动.
l
3.单摆的周期公式 (1)单摆振动的周期公式T=2π l ,该公式提供了
g
一种测定重力加速度g的方法. (2)l为等效摆长,表示从悬点到摆球重心的距离, 要区分摆长和摆线长，悬点实质为摆球摆动所在
2. 简谐运动的描述 （1）描述简谐运动的物理量 ①位移x：由平衡位置指向振动质点所在位置的 有向线段表示振动位移，是矢量. ②振幅A：振动物体离开平衡位置的最大距离， 是标量，表示振动的强弱. ③周期T和频率f:做简谐运动的物体完成 一次 全振动所需要的时间叫周期，而频率则等于单 位时间内完成 全振动的次数 ；它们是表示振动 快慢的物理量.二者互为倒数关系.

x Acos(t )
(4)
约定(4)式简谐振动的运动学方程
1 简谐振动速度 加速度
v dx A sin(t )
dt
a
d2x dt 2
A 2
cos(t
)
x
x t 图
A
t
x Acost
Hale Waihona Puke vt 图A vv A sint
t
A cos(t )
2
a t 图
a
A 2
t
a A2 cost
A2 cos(t )
2 描述简谐振动的特征量
(1)振幅 A
x Acos(t )
(2)周期、频率、圆频率
弹簧振子 k
m
单 摆 g
l
T 2 m
k
T 2 l
g
1 k 2 m
1 g 2 l
复 摆 mgh T 2 I 1 mgh
I
mgh
2 I
(3) 位相和初位相
x Acos(t 0 )
t 0 — 位相，决定谐振动物体的运动状态 0 是t =0时刻的位相—初位相
1 7
66
3.14s1
A vm 31.4 10cm
3.14
故振动方程为 x 10 cos( t )cm
6
方法2：用旋转矢量法辅助求解。
x Acos(t )
v
A
sin(t
)
vm
cos(t
2
)
vm A 31.4cms1
v的旋转矢量与v轴夹角表示t 时刻相位
t
(4)简谐振动的旋转矢量表示法
t t A
t
t 0
x
o
x

O
2) 由： A
02
2 0
和已知条件：
2
0
x0
b
x0
mg k
0.05
m
b
O' 0
x0
可得：A 0.07 m
x
3)
由
tg 0
0 0
1
和初速度为负值，可知：0 4
4) (t) Acos(t ) 0.07cos(4t 4) (m)
5) E 1 kA2 0.039 (J) 6) 做图略
x0
和速度
0，由：
x0
Acos Asin
0
联立可得：
A
x02
2 0
2
tg1( 0 ) x0
简谐运动实例：
( 1 ) 单摆
准弹性力：
l
1. 细线质量不计 约
ft mg
定 2. <5 以保证sin 由牛顿定律：
m
ft
3. 阻力忽略不计
ft
பைடு நூலகம்
mg
mat
m
l
ml
d2
dt 2
mg
d2g 0
dt2 l
一个作简谐运动的质点所受的沿位移方向的合外力 与它对于平衡位置的位移成正比而反向。这样的力称为 恢复力(Restoring Forces)。
2. 动力学方程 (以水平弹簧振子为例)
由 f ma m d2 x dt2
及 f kx 得
f
k
m
0x
x
弹簧振子
d2 x m d t 2 kx
d 2x dt2
§4.2 谐振子(动力学部分) (Harmonic Oscillator)

m
O
x X
k mg / l
令向下有位移x, 则 f mg k (l x) kx
作谐振动
设振动方程为

x A cos(t 0 )
k m g l 9.8 10rad / s 0.098
由初条件得
A x0 (
2
v0

) 2 0.098m
0 是t =0时刻的位相—初位相
(4)简谐振动的旋转矢量表示法

A
t
t t

t0
o
x
x
x A cos(t )
请看动画……
用旋转矢量图画简谐运动的 x t 图
三 简谐运动的特征
1）
2） 3）
F kx
d2 x 2 x 2 dt
(平衡位置
x0 )
v0 0 arctg ( ) 0, x0
由x0=Acos0=-0.098<0 cos0<0, 取0= 振动方程为：x=9.810-2cos(10t+)m
(2)按题意 t=0 时
m
O
x X
x0=0，v0>0
x0=Acos0=0 , cos0=0 0=/2 ,3/2 v0=-Asin>0 , sin 0 <0, 取0=3/2 x=9.810-2cos(10t+3/2) m
x t 图
x A cos t
x
A
t
v t 图
v A sin t
A cos(t
A

2 )
2
v
t
a t 图
a A 2 cos t

简谐振动的方程
一、简谐振动的动力学方程
1.弹簧振子
l0 k
m
d2x m dt2
F
kx
A o
x
A
k 2
m
d2x k
dt 2
m
x0
d2 dt
x
2
2
x
0
(1)
2 单摆
sin
(ml
2
)
d2
dt 2
M mgl
d2
dt 2
g l
0
(2)
记 2 g x
l
d2x dt 2
2x
0
(1)
O
l
T
mg
mg k
1
1
(m
2kh M
)g
一、简谐振动的动力学方程
小
d2 dt
x
2
2
x
0
结
二、简谐振动的运动学方程
x Acos(t )
t t A
t
t 0 x
o
x
x Acos(t )
旋转矢量法
初始条件确定A 初位相
例:如图m=2×10-2kg,弹簧的静止形变为l=9.8 cm. t=0 时,x0=-9.8cm,v0=0
2 描述简谐振动的特征量
(1)振幅 A
x Acos(t )
(2)周期、频率、圆频率
弹簧振子 k
m
单 摆 g
l
T 2 m
k
T 2 l
g
1 k 2 m
1 g 2 l
复 摆 mgh T 2 I 1 mgh
I
mgh
2 I
(3) 位相和初位相
x A cos(t 0 )

动contents •简谐振动•阻尼振动与受迫振动•振动的合成与分解•振动在介质中的传播•多自由度系统的振动•非线性振动与混沌目录01简谐振动简谐振动的定义与特点定义简谐振动是最基本、最简单的振动形式，指物体在跟偏离平衡位置的位移成正比，并且总是指向平衡位置的回复力的作用下的振动。

特点简谐振动的物体所受的回复力F与物体偏离平衡位置的位移x成正比，且方向始终指向平衡位置；振动过程中，系统的机械能守恒。

动力学方程根据牛顿第二定律，简谐振动的动力学方程可以表示为F=-kx，其中F为回复力，k为比例系数，x为物体偏离平衡位置的位移。

运动学方程简谐振动的运动学方程可以表示为x=Acos(ωt+φ)，其中A为振幅，ω为角频率，t为时间，φ为初相。

势能与动能在简谐振动过程中，系统的势能Ep和动能Ek都在不断变化，但它们的总和保持不变，即机械能守恒。

能量转换在振动过程中，势能和动能之间不断相互转换。

当物体向平衡位置运动时，势能减小、动能增加；当物体远离平衡位置时，势能增加、动能减小。

同方向同频率简谐振动的合成当两个同方向、同频率的简谐振动同时作用于同一物体时，它们的合振动仍然是一个简谐振动，其振幅等于两个分振动振幅的矢量和，其初相等于两个分振动初相的差。

同方向不同频率简谐振动的合成当两个同方向、不同频率的简谐振动同时作用于同一物体时，它们的合振动一般不再是简谐振动，而是比较复杂的周期性振动。

在某些特定条件下（如两个分振动的频率成简单整数比），合振动可能会呈现出一定的规律性。

相互垂直的简谐振动的合成当两个相互垂直的简谐振动同时作用于同一物体时，它们的合振动轨迹一般是一条复杂的曲线。

在某些特定条件下（如两个分振动的频率相同、相位差为90度），合振动轨迹可能会呈现出一定的规律性，如圆形、椭圆形等。

02阻尼振动与受迫振动阻尼振动的定义与分类定义阻尼振动是指振动系统在振动过程中，由于系统内部摩擦或外部介质阻力的存在，使振动幅度逐渐减小，能量逐渐耗散的振动。

大学物理振动和波动 知识点总结1．简谐振动的基本特征（1）简谐振动的运动学方程: cos()x A t ϖϕ=+（2）简谐振动的动力学特征:F kx =-r r 或 2220d x x d t ϖ+= （3）能量特征： 222111222k p E E E mv kx KA =+=+=， k p E E = （4）旋转矢量表示: 做逆时针匀速转动的旋转矢量A r 在x 轴上的投影点的运动可用来表示简谐振动。

旋转矢量的长度A r 等于振动的振幅,旋转矢量的角速度等于谐振动的角频率,旋转矢量在0t =时刻与坐标轴x 的夹角为谐振动的初相。

2．描述简谐振动的三个基本量（1）简谐振动的相位：t ωϕ+，它决定了t 时刻简谐振动的状态；其中：00arctan(/)v x ϕω=-（2）简谐振动的振幅：A ，它取决于振动的能量。

其中：A =（3）简谐振动的角频率：ω，它取决于振动系统本身的性质。

3．简谐振动的合成(1)两个同方向同频率简谐振动的合成:合振动的振幅：A =合振幅最大： 212,0,1,2....k k ϕϕπ-==；合振幅最小：21(21),0,1,2....k k ϕϕπ-=+=（2）不同频率同方向简谐振动的合成：当两个分振动的频率都很大，而两个频率差很小时，产生拍现象，拍频为21ννν∆=-；合振动不再是谐振动，其振动方程为21210(2cos 2)cos 222x A t t ννννππ-+=（3）相互垂直的两个简谐振动的合成：若两个分振动的频率相同，则合成运动的轨迹一般为椭圆；若两个分振动的频率为简单的整数比，则合成运动的轨迹为李萨如图形。

（4）与振动的合成相对应，有振动的分解。

4．阻尼振动与受迫振动、共振：阻尼振动： 220220d x dx x dt dt βϖ++=；受迫振动 220022cos d x dx x f t dt dtβϖϖ++= 共振: 当驱动力的频率为某一特定值时,受迫振动的振幅将达到极大值.5．波的描述（1）机械波产生条件:波源和弹性介质（2）描述机械波的物理量:波长λ、周期T （或频率ν）和波速u ，三者之间关系为：uT λ= u λν=（3）平面简谐波的数学描述：(,)cos[()]xy x t A t uωϕ=±+； 2(,)cos()x y x t A t πωϕλ=±+；(,)cos 2()t x y x t A T πϕλ=±+ 其中，x 前面的±号由波的传播方向决定，波沿x 轴的正(负)向传播，取负(正)号。

g l
dengyonghe1@
例4.3 复摆
M = − m g l sinθ ≈ − m g l θ
据 M =Iβ =I − mg lθ = I d 2θ d 2θ dt
2
o
d 2θ dt
2
得
θ
c
整理得
mg
mgl mgl + θ =0 记 =ω2 I I d t2 d 2θ d t2 + ω 2θ = 0
I T= = 2π mgl ω 2π

单摆？
I = ml 2
T = 2π
l g
dengyonghe1@
LC电路：如图 电路： 电路 当开关K接向 时达到稳定 当开关 接向b时达到稳定， 接向 时达到稳定， 在电容器内储存了能量. 在电容器内储存了能量 当开关K接向 时 当开关 接向c时，由于电容 接向 器内储存了能量，会对LC回 器内储存了能量，会对 回 路放电，电流为i，即： 路放电，电流为 ，
2
F = ma = −mω x
2
在位移方向的合外力与它对平衡位置的位移成正比且反向。 在位移方向的合外力与它对平衡位置的位移成正比且反向。
即：
F = − kx
2
d x m 2 = −kx dt
常系数二阶微分方程
dengyonghe1@
2
d x k + x=0 2 dt m
d x k k 2 + x=0 令ω = 2 m dt m 可以确定方程的解： 由初始条件x(t = o), v(t = 0)可以确定方程的解：
2 E0 A= k
振幅取决于振动的总能量
dengyonghe1@
单摆： 质量集中于小球上， 单摆： 质量集中于小球上， 不计悬线质量。 不计悬线质量。 取逆时针为 θ 张角正向， 张角正向， 以悬点为轴，受力如图。 以悬点为轴，受力如图。 只受到切方向的合外力： 只受到切方向的合外力：

1 T
t T
Ek dt
t
1 kA2 4
E P

1 T
t T

E dt P
t

1 kA2 4
(3) 机械能
E

Ek

Ep

1 kA2 2
简谐振动系统 机械能守恒
(3) 机械能
E

Ek

Ep

1 kA2 2
弹簧振子总的机械能和振幅的平方成正比， 这一结论对其它的简谐振动系统也是正确的， 从能量的角度看振幅不仅反映振动的幅度， 还反映振动的强度
k max
2
k min
P max
2
P min
1 KA2 2
o
EE
P
K
x
E
E E
K
P
t
E 1 kA2 sin 2 ( t )
K
2
E 1 kA2 cos2 ( t )
P
2
E
1 kA2 , E
0
k max
2
k min
E
1 kA2 , E
0
P max
2
P min
Ek
O
l
m o
t 时刻细绳与竖直方向
夹角为θ
忽略空气阻力，
小球受力如图.
小球所受合外力矩为

M M M
T
G
选择逆时针方向为正
●
l
T
o mg
M mgl sin
M 0 T
M mgl sin G
M mgl sin
由转动定律 d 2
M J dt 2

第九章基本知识小结⒈物体在线性回复力F = - kx ，或线性回复力矩τ= - c φ作用下的运动就是简谐振动，其动力学方程为 ,02022=+x dt x d ω（x 表示线位移或角位移）；弹簧振子：ω02=k/m ，单摆：ω02=g/l ，扭摆：ω02=C/I.⒉简谐振动的运动学方程为 x = Acos(ω0t+α)；圆频率、频率、周期是由振动系统本身决定的，ω0=2π/T=2πv ；振幅A 和初相α由初始条件决定。

⒊在简谐振动中，动能和势能互相转换，总机械能保持不变；对于弹簧振子，22021221A m kA E E p k ω==+。

⒋两个简谐振动的合成⒌阻尼振动的动力学方程为 022022=++x dt dx dtx d ωβ。

其运动学方程分三种情况：⑴在弱阻尼状态（β＜ω0），振动的方向变化有周期性，220'),'cos(βωωαωβ-=+=-t Ae x t ，对数减缩 = βT ’.⑵在过阻尼状态（β＞ω0），无周期性，振子单调、缓慢地回到平衡位置。

⑶临界阻尼状态（β=ω0），无周期性，振子单调、迅速地回到平衡位置⒍受迫振动动力学方程 t f x dt dx dt x d ωωβcos202022=++； 其稳定解为 )cos(0ϕω+=t A x ，ω是驱动力的频率，A 0和φ也不是由初始条件决定,222220004)(/ωβωω+-=f A 2202ωωβωϕ--=tg 当2202βωω-=时，发生位移共振。

9.2.1 一刚体可绕水平轴摆动。

已知刚体质量为m ，其重心C 和轴O 间的距离为h ，刚体对转动轴线的转动惯量为I 。

问刚体围绕平衡位置的微小摆动是否是简谐振动？如果是，求固有频率，不计一切阻力。

解：规定转轴正方向垂直纸面向外，忽略一切阻力，则刚体所受力矩τ= - mghsin φ因为是微小摆动，sin φ≈φ,∴τ= - mgh φ，即刚体是在一线性回复力矩作用下在平衡位置附近运动，因而是简谐振动。

动力学中的简谐振动与周期动力学是描述物体运动规律的学科，简谐振动是动力学中一个重要的概念。

本文将介绍简谐振动的基本概念和特点，并讨论简谐振动的周期。

第一部分：简谐振动的基本概念简谐振动是指物体沿着某一直线或围绕某一固定点作来回往复运动的现象。

在简谐振动中，物体的加速度与位移的关系呈线性正比，并且加速度与位移方向相反。

简谐振动的运动方程可以表示为：x = A * cos(ωt + φ)其中，x表示物体的位移，A表示振幅，ω表示角频率，t表示时间，φ表示相位常数。

在简谐振动中，振幅和角频率是常数，而位移和时间的关系为一个正弦函数。

简谐振动还具有以下特点：1. 周期性：简谐振动的运动是周期性的，即物体在一个周期内完成一次完整的往复运动，并且周期相等。

2. 同频率：对于相同的简谐振动，频率相同，即每秒完成的周期数相等。

3. 相位差：不同简谐振动之间可以存在相位差，即两个物体具有相同的角频率，但相对于起始位置存在一定的相位差。

第二部分：简谐振动的周期简谐振动的周期是指物体完成一个完整往复运动所需的时间。

周期与角频率之间存在以下关系：T = 2π/ω其中，T表示周期，ω表示角频率。

通过上述关系可以看出，简谐振动的周期与角频率呈倒数关系，即角频率越大，周期越小，物体的振动就越快。

在简谐振动中，周期是一个重要的物理量，它可以决定物体振动的快慢和频率的高低。

周期的倒数即为频率，频率是指在单位时间内完成振动的次数。

简谐振动的周期也与振幅有关。

通过实验可以发现，当振幅越大时，周期也越大，即物体振幅越大，振动的周期就越长。

第三部分：简谐振动的应用简谐振动在实际生活和科学研究中有着广泛的应用。

以下是一些常见的应用领域：1. 机械工程：简谐振动的研究对于机械工程领域中的结构和机械系统的设计和分析非常重要。

例如，建筑物的自然频率分析和机械系统的振动控制都离不开对简谐振动的研究。

2. 物理学：简谐振动是物理学中一个基础的概念，它不仅在力学中有应用，还在电磁学、波动学等领域起着重要的作用。

振动、波动和光学习题精解第10章 机械振动10.1 要求1 了解 简谐振动的能量；2 理解 旋转矢量法、同方向和同频率简谐振动的合成的规律；3 掌握 简谐振动的各物理量（ϕω,,A ）及各量间的关系、简谐振动的基本特征、建立简谐振动的微分方程、根据初始条件写出一维简谐振动方程、同方向和同频率简谐振动的合成。

10.2 内容摘要1 简谐振动运动学方程)cos(ϕω+=t A x特征量：振幅A ：决定振动的范围和能量；角频率ω：决定振动重复的快慢，频率ωπνπων21,2===T 周期； 初相ϕ：决定起始的时刻的位置和速度。

2 振动的位相 （ϕω+t ）简谐振动在t 时刻的位相；3 简谐振动动力学方程0222=+x dt x d ω 弹性力：kx F -=，Km T m K πω2,==； 4、简谐振动的能量 2222121)(21kA kx dt dx m E E E k p =+=+= 5、受迫振动：是在驱动力作用下的振动。

稳态的受迫振动的频率等于驱动力的频率。

当驱动力的频率等于系统的频率时，发生共振现象，振幅最大。

6、同方向、同频率简谐振动的合成 )cos(111ϕω+=t A x ， )cos(222ϕω+=t A x)cos(21ϕω+=+=t A x x x其中， A =)cos(212212221ϕϕ-++A A A A ， 22112211cos cos sin sin arctan ϕϕϕϕϕA A A A ++= 相位差12ϕϕϕ-=∆起了相当重要的作用（1） 两个谐振的频率相同时，合运动的振幅决定于它们的相位差：同向时 （ 3,2,1,0,2=±=∆k k πϕ），合振动最大，为两者振幅之和； 反向时 合振动最小[ 3,2,1,0,)12(=+±=∆k k πφ]，为两者振幅之差；（2） 两个谐振的频率不相同时，合运动会产生拍现象，拍的频率为两个谐振的频率之差。

6、简谐振动的合成： 简谐振动的合成： 同方向、同频率的简谐振动的合成： 同方向、同频率的简谐振动的合成：
v A2
ϕ2 ϕ ϕ1
v A
v A1
x1
x (t ) = x1 (t ) + x2 (t )
= A cos(ωt + ϕ )
o
合成结果仍为同频率的简谐运动
x2
x
x
A=
2 A12 + A2 + 2 A1 A2 cos( ϕ 2 − ϕ 1 )
2π (r2 − r1 ) = ±2kπ k = 0,1,2,3,.....
λ 相消干涉： 相消干涉：∆ϕ = (ϕ20 − ϕ10 ) − 2π (r2 − r1 ) = ±(2k + 1)π k = 0,1,2,3,..... λ
相位、相位差和初相位的求法： 相位、相位差和初相位的求法：
解析法和 常用方法为解析法 旋转矢量法。 常用方法为解析法和旋转矢量法。 1、由已知的初条件求初相位： 、由已知的初条件求初相位： 已知初位置的大小、正负以及初速度的正负。 ①已知初位置的大小、正负以及初速度的正负。 A [例1]已知某质点振动的初位置 y0 = 且v0 > 0 。 例 已知某质点振动的初位置 2 y = A cos( ω t + ϕ )
A1 sin ϕ 1 + A2 sin ϕ 2 ϕ = arctg A1 cos ϕ 1 + A2 cos ϕ 2
机械波： 二、机械波：
1、产生的条件：波源及弹性媒质。 产生的条件：波源及弹性媒质。 2、描述波的物理量： 、描述波的物理量： 波长: 波传播时, 在同一波线上两个相邻的相位差为2 波长 波传播时 在同一波线上两个相邻的相位差为 π 的 质元之间的距离 （ λ ）。 周期:波前进一个波长的距离所需的时间（ 周期:波前进一个波长的距离所需的时间（T ）。 频率:单位时间内波动传播距离中所包含的完整波长的数目(ν)。 频率:单位时间内波动传播距离中所包含的完整波长的数目 。 波速: 波在介质中的传播速度为波速。（ 。（u 波速 波在介质中的传播速度为波速。（ ） 各物理量间的关系： 各物理量间的关系：

第十五章振动学基础§15-1简谐振动【基本内容】一、简谐振动的动力学描述1、谐振动的受力特征谐振动的动力学定义：振动系统在与位移大小成正比，而方向相反的回复力作用下的运动称为简谐振动。

kxf-=, k为比例系数。

2、简谐振动的微分方程222=+xdtxdωmk=ω3、简谐振动的判据判据一kxf-=动力学判据判据二运动学判据判据三)cos(φω+=tAx运动方程4、简谐振动实例单摆小角度摆动、复摆、扭摆二、简谐振动的运动学描述1、谐振动的数学表达式——运动方程谐振动的运动学定义：位移按余弦规律移随时间变化的运动是谐振动。

)cos(φω+=tAx)cos()sin(2φωωφωω+-=+-=tAatAv2、简谐振动的三个特征量角频率、频率、周期——由振动系统的性质决定。

角频率：mk=ω周期：ωπ2=T频率：T1=ν振幅A ——表示振动物体离开平衡位置的最大距离。

振幅A 和初相ϕ由初始条件决定：⎪⎪⎩⎪⎪⎨⎧-=+=-)(0012202x v tg v x A ωϕω 度ω（1（2（3（4123、谐振动的机械能：2222121ωmA kA E E E p K ==+=弹簧振子的动能和势能按正弦或余弦的平方随时间作周期性变化，其周期为谐振周期的一半；当动能最大时，势能最小；当动能最小时，势能最大；但机械能保持恒定不变。

【典型例题】【例15-1】半径为R 的木球静止浮于水面上时，其体积的一半浸于水中，求： （1）木球振动的微分方程；22222)31(dtxd m g R x x R =--ρπ平衡位置时：ρπ33421R m ⋅=，故 0)31(232222=-+Rx x R g dt x d 此即木球的运动微分方程。

当R x <<时，0322→R x02322=+x R gdtx d 木球作简谐振动g R T R g 3222,23πωπω===【例15-2】 弹簧下挂g m 1000=的法码时，弹簧伸长cm 8。

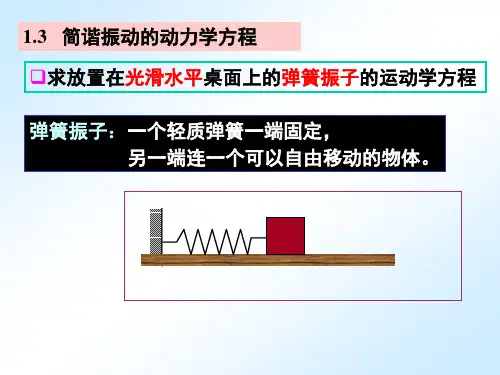
第10章振动与波动一.基本要求1. 掌握简谐振动的基本特征，能建立弹簧振子、单摆作谐振动的微分方程。

2. 掌握振幅、周期、频率、相位等概念的物理意义。

3. 能根据初始条件写出一维谐振动的运动学方程，并能理解其物理意义。

4. 掌握描述谐振动的旋转矢量法，并用以分析和讨论有关的问题。

5. 理解同方向、同频率谐振动的合成规律以及合振幅最大和最小的条件。

6. 理解机械波产生的条件。

7. 掌握描述简谐波的各物理量的物理意义及其相互关系。

8. 了解波的能量传播特征及能流、能流密度等概念。

9. 理解惠更斯原理和波的叠加原理。

掌握波的相干条件。

能用相位差或波程差概念来分析和确定相干波叠加后振幅加强或减弱的条件。

10. 理解驻波形成的条件，了解驻波和行波的区别，了解半波损失。

二. 内容提要1. 简谐振动的动力学特征作谐振动的物体所受到的力为线性回复力，即取系统的平衡位置为坐标原点，则简谐振动的动力学方程（即微分方程）为2. 简谐振动的运动学特征作谐振动的物体的位置坐标x与时间t成余弦（或正弦）函数关系，即由它可导出物体的振动速度)=tAv-ω+ωsin(ϕ物体的振动加速度)=tAa2cos(ϕ-+ωω3. 振幅A 作谐振动的物体的最大位置坐标的绝对值，振幅的大小由初始条件确定，即4. 周期与频率 作谐振动的物体完成一次全振动所需的时间T 称为周期，单位时间内完成的振动次数γ称为频率。

周期与频率互为倒数，即ν=1T 或 T1=ν5. 角频率(也称圆频率）ω 作谐振动的物体在2π秒内完成振动的次数，它与周期、频率的关系为 ωπ=2T 或 πν=ω26. 相位和初相 谐振动方程中（ϕ+ωt ）项称为相位，它决定着作谐振动的物体的状态。

t=0时的相位称为初相，它由谐振动的初始条件决定，即应该注意，由此式算得的ϕ在0~2π范围内有两个可能取值，须根据t=0时刻的速度方向进行合理取舍。

7. 旋转矢量法 作逆时针匀速率转动的矢量，其长度等于谐振动的振幅A ，其角速度等于谐振动的角频率ω，且t=0时，它与x 轴的夹角为谐振动的初相ϕ，t=t时刻它与x 轴的夹角为谐振动的相位ϕω+t 。

简谐振动的特点和动力学描述简谐振动是物体在恢复力作用下沿着某个轴线上做往复振动的一种特殊运动形式。

它具有以下几个特点：1. 平衡位置稳定：简谐振动的平衡位置是物体的稳定位置，当物体偏离平衡位置时，会受到一个恢复力的作用，使得物体趋向于返回平衡位置。

2. 振幅固定：简谐振动的振幅是一个固定值，表示物体在振动过程中离开平衡位置的最大距离。

3. 频率恒定：简谐振动的频率与振动系统本身的性质有关，而与振幅无关。

频率是指单位时间内振动的完整周期数，单位为赫兹（Hz）。

4. 正弦函数描述：简谐振动的运动可用正弦函数来描述。

物体在简谐振动过程中，其位置、速度和加速度随时间的变化都可以用正弦函数表示。

根据简谐振动的特点，在动力学上可以进行如下的描述：1. 动力学方程：对于简谐振动，其动力学方程可以由胡克定律得到。

胡克定律指出，弹性力与物体偏离平衡位置的距离成正比，即恢复力F 与位移x的关系为F = -kx，其中k为弹性系数。

2. 牛顿第二定律：根据牛顿第二定律，物体的加速度与作用力成正比，与物体的质量成反比。

对于简谐振动，可以将牛顿第二定律应用于沿轴线的振动，并根据动力学方程得到加速度与位移之间的关系。

3. 振动的能量：在简谐振动中，物体的能量在势能和动能之间不断转换。

当物体通过平衡位置时，其动能最大，而势能最小；当物体运动到最大位移时，其势能最大，而动能最小。

总能量保持不变。

4. 平衡位置的稳定性：简谐振动的平衡位置是稳定的，当物体偏离平衡位置时，会受到恢复力使其回到平衡位置。

这种稳定性是由弹簧的弹性恢复力所决定的。

综上所述，简谐振动具有稳定平衡位置、固定振幅、恒定频率等特点，并可以通过动力学方程和能量转换进行描述和分析。

研究简谐振动有助于理解振动现象的基本规律，对于很多领域如机械、电子、光学等都有重要的应用价值。

动力学简谐振动的计算方法简谐振动是物理学中重要的概念之一，它在多个领域中都有广泛应用。

本文将介绍动力学简谐振动的计算方法。

一、简谐振动的定义简谐振动是指周期性地以某个平衡位置为中心做正弦或余弦函数形式的振动。

它的特点是振幅恒定，并且振动周期、频率和角频率与振动系统的物理特性有关。

二、简谐振动的描述对于一个简谐振动系统，我们可以用一个带有负号的二次导数的微分方程来描述。

一般而言，动力学简谐振动的微分方程可以表示为：\[m\frac{d^2x}{dt^2} + kx = 0\]其中，m是振动系统的质量，k是系统的弹性常数，x是质点的位移，t是时间。

三、简谐振动的解析解基于上述微分方程，我们可以得到简谐振动的解析解。

解析解形式如下：\[x(t) = A\cos(\omega t + \phi)\]其中，A是振幅，表示振动的最大位移；$\omega$是角频率，与振动周期T的关系为$\omega = \frac{2\pi}{T}$；$\phi$是初相位，表示在t=0时刻的相位角。

四、简谐振动的参数计算1. 振动周期：振动周期T是指振动系统完成一个完整振动所需要的时间。

根据上述关系，可计算出振动周期为：\[T = \frac{2\pi}{\omega}\]2. 频率：振动频率f是指单位时间内振动的次数，与振动周期的倒数成反比。

可通过如下公式计算得到：\[f = \frac{1}{T}\]3. 角频率：角频率$\omega$定义为单位时间内角位移的增量。

可以通过如下公式计算得到：\[\omega = 2\pi f\]4. 振动速度和加速度：振动速度v和振动加速度a分别定义为位移的一阶和二阶导数，可以通过对位移解析解求导得到。

五、简谐振动的能量在简谐振动中，振动系统的能量在势能和动能之间不断转换。

振动系统的总能量E是守恒的，可以表示为：\[E = \frac{1}{2}kA^2\]其中，$\frac{1}{2}kA^2$表示势能，而动能则与质点的速度有关，可以表示为$\frac{1}{2}mv^2$。