简谐振动的方程

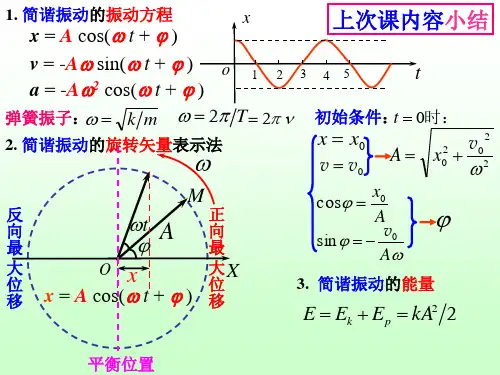
简谐运动方程知识点总结1. 简谐运动的基本特征简谐运动是一种最基本的振动运动，它具有以下几个基本特征：（1）周期性：简谐运动是周期性的，即物体在受力作用下做往复振动，每个周期内物体都会经历相同的振动过程。

（2）恢复力的特性：简谐运动的振动是由一个恢复力（例如弹簧力或重力）驱动的，且恢复力的大小与物体的位移成正比。

（3）运动是否受到阻尼和驱动力的影响：简谐运动通常假设没有阻尼和驱动力的影响，即物体受到的唯一作用力是恢复力。

2. 简谐振动方程的一般形式简谐振动可以用一个二阶微分方程来描述，其一般形式如下：$$m\frac{d^2x}{dt^2}+kx=0$$其中，m为物体的质量，k为弹簧的弹性系数，x为物体的位移，t为时间。

上述方程也可以写成更常见的形式：$$\frac{d^2x}{dt^2}+\frac{k}{m}x=0$$这个二阶微分方程描述了简谐振动系统中物体的加速度与位移之间的关系。

该方程是一个线性齐次微分方程，它的解决方法通常是通过代数方法或微积分方法来求解。

3. 简谐振动方程的解法对于上述的简谐振动方程，可以通过代数或微积分方法来求解。

通常有以下几种解法：（1）代数方法：当简谐振动系统的质量m和弹簧的弹性系数k已知时，可以通过代数方法求解简谐振动方程的解析解。

这种方法通常涉及到代数运算和三角函数的应用，例如正弦函数和余弦函数。

（2）微积分方法：对于更一般的简谐振动问题，可以通过微积分方法来求解简谐振动方程。

这种方法通常涉及到微分方程的解法，例如特征方程法、特解法和叠加原理等。

（3）复数方法：简谐振动方程也可以通过复数方法进行求解。

这种方法通常利用复数的性质和欧拉公式来简化求解过程，从而得到方程的解析解。

4. 简谐振动方程的解析解当求解简谐振动方程时，通常可以得到一组解析解，它们可以用来描述简谐振动系统的振动特性。

一般而言，简谐振动方程的解析解可以分为如下几种情况：（1）无阻尼情况下的简谐振动：当简谐振动系统没有受到阻尼力的作用时，其解析解通常为正弦函数或余弦函数。

振动方程和波动方程振动方程和波动方程是物理学中非常重要的两个方程，它们分别描述了物体在振动和波动时的运动规律。

下面我们将详细介绍这两个方程。

一、振动方程振动是指物体围绕某个平衡位置做小幅度的周期性运动。

例如，弹簧振子、简谐振子等都是典型的振动系统。

振动方程就是用来描述这些系统运动规律的数学公式。

对于简谐振子而言，它的运动可以用如下公式表示：x = A sin(ωt + φ)其中，x表示位移，A表示最大位移（即振幅），ω表示角频率（2πf），t表示时间，φ表示初始相位。

而对于一般的线性简谐系统，其运动可以用如下形式的二阶微分方程来描述：m(d²x/dt²) + kx = 0其中，m为质量，k为弹性系数，x为位移。

这就是典型的简谐振动方程。

通过对这个方程进行求解，我们可以得到物体在不同时间点上的位移、速度和加速度等信息。

二、波动方程波浪是指媒介中沿某一方向传播的能量扰动。

例如，水波、声波、光波等都是典型的波动现象。

而波动方程则是用来描述这些现象的数学公式。

对于一维的机械波而言，它可以用如下形式的偏微分方程来描述：∂²y/∂t² = v²∂²y/∂x²其中，y表示位移，t表示时间，x表示空间位置，v表示波速。

这就是典型的一维波动方程。

通过对这个方程进行求解，我们可以得到物体在不同时间点上的位移分布情况。

对于二维或三维空间中的波动问题，则需要使用更加复杂的偏微分方程进行描述。

例如光学中常见的亥姆霍兹方程：(∇² + k²)n(r) = 0其中，n(r)为介质折射率分布情况，k为波数。

通过对这个方程进行求解，我们可以得到光线在不同介质中传播时的路径和相位变化等信息。

总结：振动方程和波动方程是物理学中非常基础和重要的两个数学工具。

它们能够帮助我们深入理解物体在振动和波动时所表现出来的运动规律，并为我们研究和应用这些现象提供了强有力的数学工具。

简谐振动的运动学方程一、简谐振动的概念和特征简谐振动是指在没有阻力的情况下，一个物体围绕着平衡位置做往复运动的现象。

简谐振动具有以下特征： - 循环性：振动物体围绕平衡位置做往复运动，一次完整的运动称为一个循环。

- 周期性：振动物体完成一个循环所需的时间称为振动的周期，记为T。

- 频率性：振动的频率是指单位时间内完成的循环数，记为f，与周期的倒数成正比。

二、简谐振动的描述简谐振动的运动学方程用来描述振动物体位置随时间的变化关系。

对于单摆、弹簧振子等简谐振动系统，可以根据其运动状态和受力情况建立相应的方程。

2.1 单摆的简谐振动单摆的简谐振动是指将一个质点用一根轻细线连接到固定点上，质点在重力作用下围绕该固定点做往复运动的现象。

单摆的运动学方程可以通过下面的推导得到：•设单摆的质点离开平衡位置的角度为θ，质点到固定点的距离为l。

•考虑到单摆的往复运动，可将角度θ表示为θ = θ0sin(ωt + φ)，其中θ0为最大摆角，ω为角速度，t为时间，φ为相位角。

•根据几何关系可知，质点在水平方向上的位移为l sinθ，根据物体在一维直线运动中的位移与时间的关系，可得到质点在水平方向上的位移与时间的关系方程为x = l sin(θ0sin(ωt + φ))。

2.2 弹簧振子的简谐振动弹簧振子是指将一根具有一定弹性的弹簧的一端固定，另一端挂上质点后产生的简谐振动现象。

弹簧振子的运动学方程可以通过下面的推导得到：•设弹簧振子的质点离开平衡位置的位移为x，弹簧的劲度系数为k，质点的质量为m。

•根据胡克定律可知，弹簧的拉力与位移成正比，即F = -kx。

•根据牛顿第二定律可知，质点所受的合力与加速度成正比，即F = ma。

•将上述两个等式联立可得到弹簧振子的运动学方程为m*d2x/dt2 + kx = 0。

三、求解简谐振动的运动学方程为了求解简谐振动的运动学方程，我们需要确定简谐振动的周期、频率和振幅。

借助初态条件和边界条件，我们可以使用微分方程求解的方法得到简谐振动的解析解。

简谐振子的运动方程简谐振子是物理学中一个重要的概念，它描述了一类具有周期性振动的系统。

无论是在物理学还是其他领域，简谐振子的运动方程都有着广泛的应用。

本文将探讨简谐振子的运动方程及其相关的物理学原理。

简谐振子的运动方程可以用以下形式表示：\[ m\frac{d^2x}{dt^2} + kx = 0 \]其中，m是振子的质量，k是振子的弹性系数，x是振子的位移，t是时间。

这个方程描述了简谐振子在无阻尼和无外力的情况下的运动。

它是一个二阶线性常微分方程，可以通过解方程得到简谐振子的运动规律。

首先，我们可以将上述方程改写为：\[ \frac{d^2x}{dt^2} + \frac{k}{m}x = 0 \]令ω² = k/m，可以得到：\[ \frac{d^2x}{dt^2} + \omega^2x = 0 \]这个方程是一个简单的谐波方程，它描述了简谐振子的运动规律。

根据这个方程，我们可以得到简谐振子的解析解。

假设振子的位移可以表示为x = A*cos(ωt + φ)，其中A是振幅，φ是相位差。

将这个表达式代入上述方程，可以得到：\[ -A\omega^2*cos(ωt + φ) + \omega^2*A*cos(ωt + φ) = 0 \]化简后可得：\[ -A\omega^2*cos(ωt + φ) + A\omega^2*cos(ωt + φ) = 0 \]由此可见，当x = A*cos(ωt + φ)时，振子的运动方程成立。

这个方程说明了简谐振子的位移随时间的变化规律。

简谐振子的运动方程还可以通过其他方法得到。

例如，我们可以利用拉格朗日方程来推导简谐振子的运动方程。

拉格朗日方程是描述物体运动的一种数学工具，它基于能量守恒和最小作用量原理。

对于简谐振子，拉格朗日方程可以表示为：\[ L = T - U \]其中，L是拉格朗日函数，T是振子的动能，U是振子的势能。

对于简谐振子，动能可以表示为：\[ T = \frac{1}{2} m(\frac{dx}{dt})^2 \]势能可以表示为：\[ U = \frac{1}{2} kx^2 \]将动能和势能代入拉格朗日方程，可以得到：\[ \frac{d}{dt}(\frac{\partial L}{\partial(\frac{dx}{dt})}) - \frac{\partial L}{\partial x} = 0 \]化简后可得：\[ m\frac{d^2x}{dt^2} + kx = 0 \]这个方程与我们之前得到的简谐振子的运动方程是一致的。

简谐运动运动方程
简谐运动是一个重要的物理现象，在很多领域都有广泛的应用。

它的运动方程可以用以下公式来表示：x = A sin(ωt + φ)。

其中，x是物体的位移，A是振幅，ω是角速度，t是时间，φ是初相位。

这个公式说明，物体的位移随时间呈正弦变化，形成周期性的运动。

振幅决定了物体的最大位移，角速度则决定了运动的频率。

简谐运动的运动方程可以用不同的形式来表示，比如用余弦函数或复数形式。

但是无论采用何种形式，都必须满足简谐运动的特点，即运动周期为一定值，且每个周期的位移变化是相同的。

简谐运动在机械振动、电磁波、量子力学等领域都有广泛的应用。

在机械振动中，简谐运动可以用来描述弹簧振子、摆锤等物体的运动。

在电磁波中，简谐运动可以用来描述光的振动和声波的传播。

在量子力学中，简谐运动可以用来描述原子的振动和分子的振动。

因此，掌握简谐运动的运动方程对于理解这些物理现象具有重要的意义。

- 1 -。