对灰色关联度计算方法的改进(精)

基于改进灰色关联度的指标体系构建方法摘要：评价指标体系建立的是否合理决定着人们能否对评价对象有个正确的认识。

本文提出一种基于改进灰色关联度的评价指标体系构建方法，该方法首先计算出各因素与系统的关联度，采用德尔菲法对专家打分进行处理，打分结果作为各因素重要性的得分；然后将因素的关联度与重要性得分相结合，排序后筛选出初始指标；最后通过对初选指标之间的相关性分析，求解出有效的指标体系。

比较实验是在真实的数据集上进行的，实验结果证明改进的灰色关联度分析法明显优于主成分分析法。

因此可以认为改进后的方法能够有效的实现指标筛选。

abstract： whether evaluation objects can be understood comprehensively or not depends on a reasonable evaluation index system. in this paper， a novel evaluation index system construction method based on improved grey correlative degree analysis has been proposed. firstly， the correlation between various factors and the system has been calculated， dealing with expert scores based on the delphi method and assigning the results to the importance score of each factor. secondly，the correlative degree has been combined with the importance score and the initial indicators have been screened after sorting. finally， an effective index system has been drawn out through analyzing the correlations of primary indexes.comparison experiment has been conducted on real data sets. the experimental results demonstrate that the improved grey correlation analysis method outperforms the principal component analysis method. it suggests that the proposed method can be applied for achieving effective index screening.关键词：指标体系；指标筛选；灰色关联度；相关性分析key words： evaluation index system；index selection；grey relational degree；correlation analysis中图分类号：f22 文献标识码：a 文章编号：1006-4311（2013）07-0004-040 引言20世纪上半叶，在经历了项目预算、计划项目预算、目标管理预算、零基预算等多个发展阶段后，以美国、澳大利亚和新西兰为代表的oecd国家开始实施绩效预算改革。

灰色关联度分析解法及详细例题解答精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】1.地梭梭生长量与气候因子的关联分析下表为1995年3年梭梭逐月生长量（X0）、月平均气温（X1）、月降水量（X2）、月日照（X3）时数和月平均相对湿度（X4）的原始数据，试排出影响梭梭生长的关联序，并找出主要的影响因子。

灰色系统理论提出了灰色关联度的概念，它是提系统中两个因素关联性大小的量度，关联度的大小直接反映系统中的各因素对目标值的影响程度。

运用灰色关联分析法进行因素分析的一般步骤为：第一步：确定分析数列。

确定反映系统行为特征的参考数列和影响系统行为的比较数列。

反映系统行为特征的数据序列，称为参考数列。

（Y）设参考数列（又称母序列）为Y = {Y（k）|k= 1，2，Λ，n}；影响系统行为的因素组成的数据序列，称比较数列。

（X）比较数列（又称子序列）Xi = {Xi（k）|k= 1,2,Λ,n}，i?= 1，2，Λ，m。

第二步，变量的无量纲化由于系统中各因素列中的数据可能因量纲不同，不便于比较或在比较时难以得到正确的结论。

因此为了保证结果的可靠性，在进行灰色关联度分析时，一般都要进行数据的无量纲化处理。

第三步，计算关联系数。

X0（k）与xi（k）的关联系数记，则，称为分辨系数。

ρ越小，分辨力越大，一般ρ的取值区间为(0,1),具体取值可视情况而定。

当时，分辨力最好，通常取ρ = 0.5。

ξi（k）继比较数列xi的第k个元素与参考数列xo的第k个元素之间的关联系数。

第四步，计算关联度因为关联系数是比较数列与参考数列在各个时刻（即曲线中的各点）的关联程度值，所以它的数不止一个，而信息过于分散不便于进行整体性比较。

因此有必要将各个时刻（即曲线中的各点）的关联系数集中为一个值，即求其平均值，作为比较数列与参考数列间关联程度的数量表示，关联度ri公式如下：第五步，关联度排序关联度按大小排序，如果r1<r2，则参考数列y与比较数列x2更相似。

灰色关联度分析方法模型灰色综合评价主要是依据以下模型：R=Y×W式中，R 为M 个被评价对象的综合评价结果向量；W 为N 个评价指标的权重向量；E 为各指标的评判矩阵，（矩阵略）)(k i ξ为第i 个被评价对象的第K 个指标与第K 个最优指标的关联系数。

根据R 的数值，进行排序。

（1）确定最优指标集设],,[**2*1n j j j F =,式中*k j 为第k 个指标的最优值。

此最优序列的每个指标值可以是诸评价对象的最优值，也可以是评估者公认的最优值。

选定最优指标集后，可构造矩阵D （矩阵略）式中i k j 为第i 个期货公司第k 个指标的原始数值。

（2）指标的规范化处理由于评判指标间通常是有不同的量纲和数量级，故不能直接进行比较，为了保证结果的可靠性，因此需要对原始指标进行规范处理。

设第k 个指标的变化区间为],[21k k j j ,1k j 为第k 个指标在所有被评价对象中的最小值，2k j 为第k 个指标在所有被评价对象中的最大值，则可以用下式将上式中的原始数值变成无量纲值)1,0(∈i k C 。

i k k k i k i kj j j j C --=21，m i ,2,1=，n k ,,2,1 =（矩阵略）（3）计算综合评判结果根据灰色系统理论，将],,,[}{**2*1*n C C C C =作为参考数列，将],,,[}{21i n i i C C C C =作为被比较数列，则用关联分析法分别求得第i 个被评价对象的第k 个指标与第k 个指标最优指标的关联系数，即i k k k i i k k i k k k i i k k k iC C C C C C C C k -+--+-=****i max max max max min min )ρρξ（式中)1,0(∈ρ，一般取5.0=ρ。

这样综合评价结果为：R=ExW若关联度i r 最大，说明}{C 与最优指标}{*C 最接近，即第i 个被评价对象优于其他被评价对象，据此可以排出各被评价对象的优劣次序。

新型灰色关联分析模型的改进与拓展杨文光;吴云洁;王建敏【摘要】为了解决灰色相似关联度与接近关联度存在失准的缺陷, 提出了基于面积的新型灰色关联分析的改进模型.对于具有相同量纲的不同序列数据, 首先利用分段二次Lagrange插值建立它们的逼近函数, 进而对逼近函数进行始点零化操作, 然后分别计算以逼近函数曲线或其始点零化像与t=1, t=n所围图形面积, 最后得到相应序列数据的灰色相似关联度与接近关联度, 并研究了它们的性质.在具体计算所围图形面积时,采用了微元法与梯形法.算例计算结果表明, 本文所提出模型与方法是有效的, 客观反映了序列数据之间的相关性大小, 避免了计算失效的可能.%In order to solve the incorrectness defects of the similitude degree of grey incidence and the close degree of grey incidence, the improvement model of grey relational analysis model was proposed based on the area.For different sequence data with the same dimension, the approximation function was set up by using the piecewise quadratic Lagrange interpolation, and the approximation function was operated by zero starting point operator.Then the area was calculated between t=1, t=n and the approximation function curve or the image of zero starting point of them.Finally, the similitude degree of grey incidence and the close degree of grey incidence were obtained, and their properties were studied.In the concrete calculation around the figure area infinitesimal method could trapezoidal method could be used.The calculation results showed that, the proposed model and method were effective, which objectively reflectedthe correlation between the sizes of sequence data and avoided computing the possibility of failure.【期刊名称】《郑州大学学报（理学版）》【年(卷),期】2017(049)002【总页数】6页(P24-29)【关键词】灰色关联分析;相似性;接近性;分段二次Lagrange插值;梯形求积【作者】杨文光;吴云洁;王建敏【作者单位】华北科技学院基础部河北三河 065201;北京航空航天大学自动化科学与电气工程学院北京 100191;北京航空航天大学自动化科学与电气工程学院北京 100191;中国科学院空间应用工程与技术中心北京 100094【正文语种】中文【中图分类】C931灰色关联分析理论以研究“小样本，贫信息”的数据系列相关性大小为主要内容，为不确定性系统的建模、评价与决策提供了有利工具. 传统灰色关联分析模型是依据比较序列与参考序列的曲线几何相似程度进行度量的. 事实上，关联度大小不仅与曲线相似程度密切相关，也与曲线之间的接近程度紧密联系. 目前，不同学者从几何、积分、分数阶导数、插值等不同角度定义了多种不同的改进型灰色关联分析模型[1-7]. 文献[1]构建了绝对灰色关联度, 该模型满足偶对称性, 且计算相对简便. 文献[2]基于数据序列相似性与相近性视角构建了新型灰色关联分析模型，但该模型对于走势不一致的两组数据会出现灰色关联度为1的情况. 文献[3]指出关联度取值随分辨系数变化而变化，从而造成关联度取值唯一性不满足或关联度不满足对称性等问题. 文献[4]利用光滑性与逼近效果较好的三次样条插值函数逼近序列数据改进了灰色绝对关联度, 提高了逼近精度.文献[5]利用梯形求积法建立了序列数据折线面积基础上的灰色预测模型. 文献[6]采用Caputo型分数阶导数的记忆性改进灰色预测模型. 文献[7]提出了基于改进灰色关联度模型的综合一致性检验方法. 这些工作都促进了灰色系统理论的发展.灰色相似关联度与接近关联度是建立在两组序列数据所围图形面积基础之上的[2, 8]，但当两组序列数据存在振荡情况时表现的并不准确，当一组序列数据在另一组序列数据之上与之下的面积相等时，关联度为1. 本文将利用分段二次Lagrange 插值完成对序列数据的逼近，通过引入绝对值表示所围面积的改进型灰色相似关联度与灰色接近关联度模型.结合微元法与梯形法的计算，客观地反映序列数据的相似性与接近性.1.1 基于面积的灰色相似关联度与接近关联度的定义与计算定义1[2] 设系统第i组与第j组序列数据为Xi=(xi(1),xi(2),…,xi(n)),Xj=(xj(1),xj(2),…,xj(n))，它们的始点零化像分别为((1),(2),…,(n))，((1),(2),…,(n))，其中：i,j表示序列标号；(k)=xi(k)-xi(1),(k)=xj(k)-xj(1)，k=1,2,…,n，且n≥3.定义2 设fi(t)是第i组序列数据Xi的逼近函数, fj(t)是第j组序列数据Xj的逼近函数, t∈[1,n]， fi(t)与fj(t)的始点零化像分别为(t)与(t)，其中：(t)=fi(t)-fi(1)，(t)=fj(t)-fj(1)， fi(t)与fj(t)可以采用拟合或插值的方法对原始序列数据进行逼近. 当使用分段线性Lagrange插值逼近原始序列数据时会出现光滑性较差, 且精度不高的问题, 而三次样条插值又相对较复杂, 故为了简化计算, 提高计算精度, 下面采用分段二次Lagrange插值.定义3[9] 对于如定义1所给的第i组序列数据Xi，任取相邻节点k-1,k,k+1，以[k-1,k+1]作为插值区间构造分段二次Lagrange插值函数，其中：lk-1(t)；lk(t)=-(t-k+1)(t-k-1)；lk+1(t)，k=2,4,6,…，n,且n≥3.根据定义3整理出序列数据Xi,Xj的分段二次Lagrange插值函数的整体形式.当n≥3,且n=2g+1,g∈Z+时,当n≥4,且n=2g,g∈Z+时,其中为Xj在t∈[k-1,k+1]时的分段二次Lagrange插值函数, 插值基函数lk-1(t),lk(t),lk+1(t)定义同上, k=2,4,6,…，n,且n≥3.在得到分段二次Lagrange插值函数fi(t)与fj(t)的基础上,再按照定义2分别对fi(t)与fj(t)进行始点零化像操作后可以获得(t)与(t).定义4 设Δ，Δ，则称为序列数据Xi与Xj基于面积的灰色相似关联度,称为序列数据Xi与Xj基于面积的灰色接近关联度.注：Δsij表示(t)与(t)对应曲线与直线t=1,t=n所围图形的面积, ΔSij表示fi(t)与fj(t)对应曲线与直线t=1,t=n所围图形的面积.对于量纲相同的两组原始序列数据Xi与Xj，基于面积的灰色相似关联度αij可以表征Xi与Xj对应曲线的相似程度, Xi与Xj越相似, fi(t)与fj(t)也就越相似, 则(t)与(t)重合的可能性就越大, Δsij取值越接近于0, αij取值就越接近1.基于面积的灰色接近关联度βij可以表征Xi与Xj对应曲线的接近程度, Xi与Xj越接近, fi(t)与fj(t)也就越接近, 则ΔSij取值越接近于0, βij取值就越接近1.构建的基于面积的灰色相似关联度与接近关联度均充分考虑了原始序列数据在始点零化处理之前与之后各自在平面直角坐标系中所围封闭图形的面积大小的差异性. 对于定义4中的Δsij与ΔSij，用两种近似数值计算方法.1) 微元法其中Δt为采样步长.2) 梯形求积法(简称梯形法)Δ≈ΔΔt+ Δt，其中:Δt为采样步长, m=(n-1)/Δt.证明设Xi与Xj是如定义1所给出的两个不同序列数据, fi(t)与fj(t)是对应的分段二次Lagrange插值函数.a) 当始点零化像恒在的一侧时代入(9)即得公式(7).同理当fi(t)恒在fj(t)的一侧时, 使用梯形求积公式可证明公式(8).b) 当始点零化像与存在除(1,0)外的交点(1+k0Δt,x)时, 则存在某个k=k0，使得(1+k0Δt)=(1+k0Δt)=x，k=0,1,…,m，则其中:Δ为第k个小梯形的面积, k=0,1,…,m; k≠k0,k≠k0-1; m=(n-1)/Δt，Δt为采样步长; Δ,Δ为三角形面积.因为k≠k0,k≠k0-1时,又由=0，可知代入式(10)化简即得公式(7). 同理当fi(t)与fj(t)存在交点时, 使用梯形求积公式亦可证明公式(8).1.2 基于面积的灰色相似关联度与接近关联度的相关性质定理1 基于面积的灰色相似关联度为，与基于面积的灰色接近关联度，都满足邓氏灰色关联公理中的规范性、接近性与偶对称性.证明1) 规范性.显然Δsij≥0,ΔSij≥0，故0<αij≤1,0<βij≤1，当且仅当Δsij=0时，αij=1，ΔSij=0时，βij=1.2) 接近性.由1)可知，显然成立.3) 偶对称性.对于X={Xi,Xj}，显然有，Δsij=Δsji，，ΔSij=ΔSji，故αij=αji，βij=βji.定理2 在平面直角坐标系下, 当始点零化像恒在的一侧时, αij≈εij，当序列数据Xi恒在Xj的一侧时, βij≈ρij. 其中εij，ρij分别为文献[2]所定义的灰色相似关联度与灰色接近关联度,证明当始点零化像恒在的一侧时, 因((t)(t))(t)(t)≈Δsij，故αij≈εij.当序列数据Xi恒在Xj的一侧时, 因(xi(t)-xj(t))(t)-xj(t)≈ΔSij，故βij≈ρij.当始点零化像不恒在的一侧时, αij≠εij,当序列数据Xi不恒在Xj的一侧时, βij≠ρij. 当始点零化像恒在的一侧时, 实际计算中, 由于文献[2]采用了离散点计算, 步长为1, 产生较大误差. 对于存在交点的情况刘氏灰色相似关联度与接近关联度模型存在失准甚至错误.对于非1-时距序列可以采用相应变换转化为1-时距序列, 故假设下面讨论的均是1-时距序列[2], 并且要求序列数据的长度是一致的, 而当序列长度不一致时可以采用分层逐次均值填补空缺[2].例1 设序列数据X1=(x1(1),x1(2),…,x1(7))=(0.91,0.97,0.90,0.93,0.91,0.93,0.95)，X2=(x2(1),x2(2),…,x2(7))=(0.60,0.68,0.61,0.62,0.63,0.64,0.65)，X3=(x3(1),x3(2),…,x3(7))=(0.82,0.86,0.90,0.89,0.88,0.87,0.86)，X1,X2,X3均是1-时距序列, n=7，试求X2,X3与X1三者之间基于面积的灰色相似关联度α12,α13,α23与灰色接近关联度β12,β13,β23，要求给出与文献[2]方法、基于微元法的相似与接近关联度、基于梯形求积法的相似与接近关联度(简称梯形法)的对比结果.解 1) 由于n=7，故首先按照公式(1)，计算X1,X2,X3的分段二次Lagrange插值曲线得f1(t),f2(t),f3(t)，见图1.2) 计算f1(t),f2(t),f3(t)的始点零化像(t),(t),(t)，为了与其他方法进行对比, 也一并算出X1,X2,X3的始点零化像,,得,(t)=fi(t)-fi(1),i=1,2,3.((1),(2),…,(7))=(0,0.06,-0.01,0.02,0,0.02,0.04)，((1),(2),…,(7))=(0,0.08,0.01,0.02,0.03,0.04,0.05)，((1),(2),…,(7))=(0,0.04,0.08,0.07,0.06,0.05,0.04)，其中(t),(t),(t)是f1(t),f2(t),f3(t)的始点零化像, 也是,,的分段二次Lagrange插值曲线,如图2所示.3) 根据微元法与梯形法给定的公式分别计算Δsij,ΔSij.采用微元法由公式(5)计算Δsij，采样步长Δt=0.01,由公式(6)计算ΔSij，得Δs12≈0.104 8，Δs13≈0.266 1，Δs23≈0.215 6，ΔS12≈2.061 6，ΔS13≈0.419 3，ΔS23≈1.642 3.采用梯形求积法由公式(7)计算Δsij，由公式(8)计算ΔSi j，得4) 最后代入公式(3)和(4)计算出基于面积的灰色相似关联度与灰色接近关联度, 结合文献[2]的方法给出对序列数据两两比较的3种结果, 见表1.使用微元法得灰色相似关联度与灰色接近关联度为：使用梯形求积法得灰色相似关联度与灰色接近关联度为α12=0.905 1，α13=0.789 9，α23=0.822 7，β12=0.327 0，β13=0.705 1，β23=0.378 8.上述两种方法的计算结果表明, X1,X2,X3中的X1,X2最相似, X2,X3的相似程度次之, 而X1,X3的相似程度最低; X1,X3最接近, X2,X3的接近程度次之, 而X1,X2的接近程度最低.对于本算例, 三种方法给出的序列数据的相似程度和接近程度的排序是一致的.例2 设序列数据试给出X1,X2基于分段二次Lagrange插值微元法、梯形法与刘氏法的灰色相似关联度与接近关联度.解本算例的计算与上例是一样的, 采用上例相同的4步操作可得X1,X2基于分段二次Lagrange插值微元法、梯形法的结果，见表2. 显然,微元法和梯形法的结果是合理的,而刘氏法的结果是不合理的,因为差异较大数据的关联度是不可能取1的. 原序列数据与分段二次Lagrange插值曲线见图3.建立不同序列数据的分段二次Lagrange插值, 尽可能以一种简单的方式逼近序列数据,基于序列数据被逼近曲线与t=1,t=n所围的图形面积，构建了微元法与梯形法两种计算灰色相似关联度与灰色接近关联度的改进算法, 使得灰色关联度的计算更能反映数据间的几何位置关系. 改进模型克服了原有灰色相似关联度与接近关联度不能客观反映振荡序列相似性与接近性的弊端, 是对原有模型的有效拓展. 通过算例证明了本文所提出的基于面积的两种方法是有效的.当数据较多, 信息包含较多时, 基于分段二次Lagrange插值建立的逼近曲线将具有较高的逼近精度, 随之建立的灰色相似关联度与接近关联度模型也将具有较高的评估精度.【相关文献】[1] LIU S, FANG Z, LIN Y. A new definition for the degree of grey incidence[J]. Grey systems theory and application, 2005, 7(2): 8-18.[2] 刘思峰, 谢乃明, FORREST J. 基于相似性和接近性视角的新型灰色关联分析模型[J]. 系统工程理论与实践, 2010, 30(5): 881-887.[3] 刘勇, 刘思峰, FORREST J. 一种新的灰色绝对关联度模型及其应用[J]. 中国管理科学, 2010, 20(5): 173-177.[4] 陈勇明, 张明. 灰色样条绝对关联度模型[J]. 系统工程理论与实践, 2015, 35(5): 1304-1310.[5] 蒋诗泉, 刘思峰, 刘中侠, 等.基于面积的灰色关联决策模型[J]. 控制与决策, 2015, 30(4): 685-690.[6] 吴利丰, 刘思峰, 姚立根. 含Caputo型分数阶导数的灰色预测模型[J]. 系统工程理论与实践, 2015, 35(5): 1311-1316.[7] 胡玉伟, 马萍, 杨明, 等. 基于改进灰色关联分析的仿真数据综合一致性检验方法[J]. 北京理工大学学报(自然科学版), 2013, 33(7): 711-715.[8] 刘思峰, 杨英杰, 吴利丰, 等. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2014.[9] 施吉林, 张宏伟, 金光日.计算机科学计算[M]. 北京: 高等教育出版社, 2005.。

改进灰色聚类关联分析法的综合评价及应用陈泉 李灿* 朱尚斌 马千里 董菁菁湖南工业大学土木工程学院摘 要： 为权衡关联度值对等级排序的影响， 采用点图分类排序方法对站点进行分类并对其空气质量排序进行优 化调整。

并对其和传统改进灰色聚类评价结果进行了对比分析。

结果表明： 株洲市城区空气质量综合评价等级总 体处于Ⅱ级。

应用基于不同归属等级的关联度值构成的向量来建立点图分类排序方法，对相邻站点进行优化调整， 得到的排序更合理， 符合实际情况。

计算比较株洲市7个空气质量监测点季节及年度的污染状况， 发现改进灰 色聚类关联分析法对污染等级的敏感度更高， 聚类评价结果更合理。

表明改进灰色聚类关联分析法应用于大气环 境质量评价具有重要实际价值。

关键词： 大气质量评价 改进灰色聚类关联法 优化排序Comprehensive Evaluation and Application based onImproved Gray Clustering Association AnalysisCHEN Quan,LI Can*,ZHU Shang­bin,MA Qian­li,DONG Jing­jingSchool of Civil Engineering,Hunan University of TechnologyAbstract: To weigh the impact of correlation degree values on rank ordering,the point map classification method was used to classify the monitoring sites and optimize the air quality order.Finally,the traditional improved grey clustering analysis methods and the comprehensive evaluation level of air quality in Zhuzhou City is in Grade Ⅱ.The improved gray clustering relation analysis method were compared and analyzed.The results show that the point map classification method is established by using the vectors of correlation degree values based on different attribution levels.The optimal adjustment of adjacent stations are made,and the sorting is more reasonable and realistic.And the seasonal and annual pollution status of seven air quality monitoring stations in Zhuzhou City are calculated and compared,it is found that the improved gray clustering correlation analysis method was more sensitive to pollution level.The improved gray clustering correlation analysis have important practical value in atmospheric environment quality evaluation.Keywords:air quality evaluation,improved gray clustering relation analysis method,optimize sorting收稿日期： 2018­1­16通讯作者： 李灿 （1968~）， 女， 博士， 教授； 湖南省株洲市天元区泰山路88号湖南工业大学土木工程学院 （412007）； E­mail:lc19992@ 基金项目： 湖南省自然科学基金（2017JJ4005） 大气环境质量受到多种因素的影响， 评价方法应 能够反映多个因子共同作用于大气环境质量的综合效应， 目前评价方法较多 [1­6]， 均存在不足。

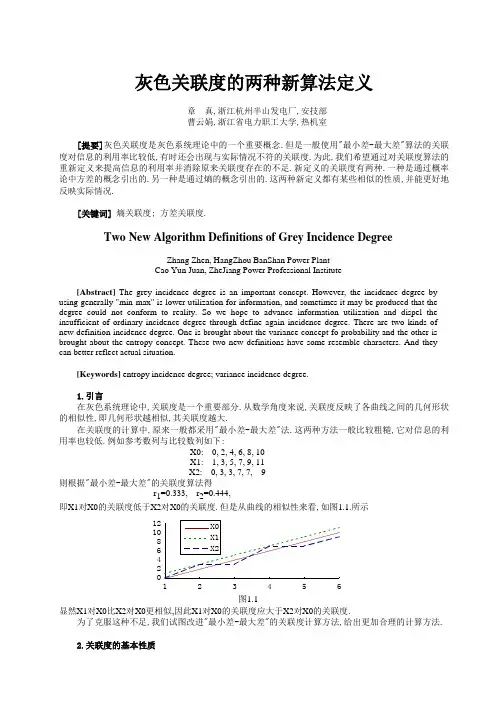
灰色关联度的两种新算法定义章 真,浙江杭州半山发电厂,安技部 曹云娟,浙江省电力职工大学,热机室[提要]灰色关联度是灰色系统理论中的一个重要概念.但是一般使用"最小差-最大差"算法的关联度对信息的利用率比较低,有时还会出现与实际情况不符的关联度.为此,我们希望通过对关联度算法的重新定义来提高信息的利用率并消除原来关联度存在的不足.新定义的关联度有两种.一种是通过概率论中方差的概念引出的.另一种是通过熵的概念引出的.这两种新定义都有某些相似的性质,并能更好地反映实际情况.[关键词] 熵关联度; 方差关联度.Two New Algorithm Definitions of Grey Incidence DegreeZhang Zhen, HangZhou BanShan Power Plant Cao Yun Juan, ZheJiang Power Professional Institute[Abstract] The grey incidence degree is an important concept. However, the incidence degree by using generally "min-max" is lower utilization for information, and sometimes it may be produced that the degree could not conform to reality. So we hope to advance information utilization and dispel the insufficient of ordinary incidence degree through define again incidence degree. There are two kinds of new definition incidence degree. One is brought about the variance concept fo probability and the other is brought about the entropy concept. These two new definitions have some resemble characters. And they can better reflect actual situation.[Keywords] entropy incidence degree; variance incidence degree.1.引言在灰色系统理论中,关联度是一个重要部分.从数学角度来说,关联度反映了各曲线之间的几何形状的相似性,即几何形状越相似,其关联度越大.在关联度的计算中,原来一般都采用"最小差-最大差"法.这两种方法一般比较粗糙,它对信息的利用率也较低.例如参考数列与比较数列如下:X0: 0, 2, 4, 6, 8, 10 X1: 1, 3, 5, 7, 9, 11 X2: 0, 3, 3, 7, 7, 9则根据"最小差-最大差"的关联度算法得r 1=0.333, r 2=0.444,即X1对X0的关联度低于X2对X0的关联度.但是从曲线的相似性来看,如图1.1.所示024*******23456图1.1显然X1对X0比X2对X0更相似,因此X1对X0的关联度应大于X2对X0的关联度.为了克服这种不足,我们试图改进"最小差-最大差"的关联度计算方法,给出更加合理的计算方法.2.关联度的基本性质关联度作为反映曲线形状相似性的一种度量,首先它应与参考曲线的上下平移无关,即如有参考数列与比较数列为:X0: X0(1), X0(2), …, X0(N) Xi: Xi(1), Xi(2), …, Xi(N),其关联度为r i ,则将X0加上(或减去)一个常数CX0+C: X0(1)+C, X0(2)+C, …, X0(N)+C其关联度不应变化,还是应该为r i .这个性质我们称为"平移不变性"..20406080100123456图2.1.平移不变性其次,如果X0(1)-Xi(1)=X0(2)-Xi(2)=…=X0(N)-Xi(N)=常数,则其关联度应最大,即r=1.这个性质我们称为等差最大性.020406080100123456图2.2.等差最大性3.熵型关联度熵是热力学中的一个概念,它反映系统的混乱程度.在热力学中,一个系统在达到热平衡后,即各点的温度相同,则熵最大.这就是说,一个分布在各点都相同时其熵达到最大.为此我们可以定义熵关联度为:定义3.1.设∆∆=m ax (),i ki k , πi i i lk k l ()()(())=++∑∆∆∆∆, H k k i i i k N=-=∑ππ()log ()1.则熵关联度为r H H i i jj=m ax .从定义可以看出,熵关联度是一种相对关联度,关联度中的最大者始终为1.定理3.1.熵关联度满足等差最大性. 证明.显然.对于第1节中的例子,用熵关联度计算得H r 1107781==.,与H r 220458059==.,..由此可见这比较符合实际情况并且与下述方差关联度的值也比较接近.4.方差关联度在概率论中,方差反映了分布曲线的离散程度.如果分布曲线的点越离散,则方差越大.现在我们根据方差的这个特性来定义关联度.定义4.1.设X0: X0(1), X0(2), …, X0(N) Xi: Xi(1), Xi(2), …, Xi(N),则Xi 与X0的方差关联度定义为r i i=+11α∆此处α是分辨系数,∆∆∆i iil Nk NNk Nl =-==∑∑11112(()()),∆i k Xi k X k ()()()=-0.定理4.1.方差关联度满足平移不变性与等差不变性. 证明.(1)设X0经过平移后变成X0+C: X0(1)+C, X0(2)+C, …, X0(N)+C, 则)∆i C +()()()()()∆∆iC i i k X k X k C k C =--=-0,故 ∆∆∆iCiC iC l Nk NNk N l =-==∑∑11121(()()) =---==∑∑11211N k C Nl C iil N k N(()(()))∆∆=-===∑∑11211Nk Nl i il Nk Ni (()())∆∆∆ ,即得r r i Ci = .(2)设差为D ,即∆i k Xi k X k D ()()()=-=0.则∆∆∆i iil Nk Nl Nk NNk Nl ND ND =-=-=====∑∑∑∑11110211211(()())(),故r i i=+=+=111101α∆.对于第1节中的例子,用方差关联度计算得∆1101==,r 与∆2208975069==.,.r ,此处α取0.5.由此可见这比较符合实际情况.5.结束语方差关联度与熵关联度作为两种关联度的新定义各有其特点.熵虽然是一个热力学概念,但是它具有更深刻的信息论意义.因此通过熵定义的关联度较适用于信息不全的埸合.方差是概率论中的一个概念,而概率论本身就是描述不确定性的一门学科.对于灰色系统理论来说,其主要目的也是描述不确定性,不同的是更广义的不确定性,即随机不确定性与模糊不确定性.因此可以肯定方差关联度较适用于随机不确定性占主导地位灰色系统.参考文献[1]邓聚龙,"灰色预测与决策",华中理工大学出版社,1986. 注：《系统工程》98增刊。

改进灰色关联分析法在工程造价评估中的应用我国目前关于建设项目的全生命周期造价评价研究较少，据此通过对建设项目的全生命周期各阶段对造价的影响因素进行分析，构建了造价科学性评价指标体系，并通过对分辨系数ρ和权重的改进，优化了传统的灰色关联分析法，最后结合实际案例验证了该评价体系的适用性和科学性，这对我国未来工程造价控制和管理方面的研究具有重要的现实意义。

标签：改进灰色关联分析法；全生命周期；造价科学性1引言目前我国采用的全过程工程造价管理模式主要关注建设成本的控制，而忽视建设前期和后期的成本控制。

但随着人们对于建筑物整个生命周期的研究发现，建设前期和后期对整个造价的影响同样重要，仅仅关注建设成本的管理不能如实地反映该项目造价的科学性和经济性。

全生命周期工程造价管理在西方发达国家已成为了一种较普遍的管理模式，但在我国的研究和应用还很少。

由于我国大部分的建设项目决算之后的信息资料收集不足，导致在建设项目造价的全生命周期评价方法选择上存在很大的局限性，而灰色关联分析法对样本量的要求较少，且不一定要服从某种典型分布，因此可以用于建设项目造价的评价。

但在计算中，分辨系数ρ没有具体的量化标准，只能根据已知文献取值（一般取0.5），然而ρ的不同取值会导致结果的不同，不当的ρ取值会导致评价结果失真。

基于此，本文改进了传统的灰色关联模型，不但具体量化了ρ的取值，还采用熵值法求出每个指标的权重再与关联系数加权平均得到关联度，根据关联度判断建设项目全生命周期造价的科学性。

最后以达州市区三大房地产项目为例，对改进灰色关联评价模型的适用性进行验证。

2评价指标体系的建立全生命周期造价的科学性需要从各个阶段考虑各种因素，大致可以分为以下几类：（1）建设前期。

项目的可行性研究可以根据大量的数据资料，通过市场调查，掌握市场需求和前景，确定合理的项目方案，使项目达到最优；在项目设计时可以充分利用价值工程和限额设计方法，以实现项目的价值最大化。

第３２卷第１１期２　０　１　４年１　１月水　电　能　源　科　学Ｗａｔｅｒ　Ｒｅｓｏｕｒｃｅｓ　ａｎｄ　ＰｏｗｅｒＶｏｌ．３２Ｎｏ．１１Ｎｏｖ．２　０　１　４文章编号：１０００－７７０９（２０１４）１１－０２０２－０５改进灰色关联度算法在地区能源—经济—环境系统协调关系中的应用黄研利１，何璞玉２，喻小宝２，谭忠富２（１．国网陕西省电力公司营销部，陕西西安７１００４８；２．华北电力大学经济与管理学院，北京１０２２０６）摘要：针对传统灰色关联度算法分析能源—经济—环境系统关系存在的缺陷问题，提出了一种改进的灰色关联度算法，满足了序列的保序效应和算法的规范性，并以某地区能源—经济—环境系统协调性研究为例，利用该算法分别研究了能源与经济、经济与环境和能源与环境等二元系统的协调关系以及能源—经济—环境三元系统的协调关系，并将计算结果与传统算法进行比较。

结果表明，改进的算法合理、可行；影响该地区能源经济环境系统协调性的重要因素是能源消费布局，在该地区范围内推广电能替代政策对能源经济环境系统的协调发展起着至关重要的作用。

关键词：改进灰色关联度算法；能源—经济—环境系统；协调关系；能源布局；电能替代中图分类号：Ｆ２２４．０文献标志码：Ａ收稿日期：２０１４－０８－１８，修回日期：２０１４－１０－０９基金项目：国家自然科学基金项目（７１２７３０９０）作者简介：黄研利（１９７４－），女，高级工程师，研究方向为电力营销和电力经济，Ｅ－ｍａｉｌ：６１０２８０７２９＠ｑｑ．ｃｏｍ通讯作者：谭忠富（１９６４－），男，教授、博导，研究方向为能源经济、电力市场等，Ｅ－ｍａｉｌ：ｔａｎｚｈｏｎｇｆｕ＠ｓｉｎａ．ｃｏｍ１　引言近年来，随着ＰＭ２．５等概念的传播、大部分地区雾霾的加重，人们对环境的重视程度与日俱增，对环境恶化的研究亦越来越多。

在很大程度上，环境的恶化是由于一些能源的使用，而经济发展少不了这些能源消费的支撑，这样似乎形成一个悖论，其实不然，首先最重要的就是厘清能源—经济—环境这一复杂动态系统中三者的关系。

灰色关联分析法原理及解题步骤---------------研究两个因素或两个系统的关联度(即两因素变化大小,方向与速度的相对性)关联程度——曲线间几何形状的差别程度灰色关联分析是通过灰色关联度来分析和确定系统因素间的影响程度或因素对系统主行为的贡献测度的一种方法。

灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密1> 曲线越接近,相应序列之间的关联度就越大,反之就越小 2> 灰色关联度越大，两因素变化态势越一致分析法优点它对样本量的多少和样本有无规律都同样适用,而且计算量小,十分方便,更不会出现量化结果与定性分析结果不符的情况。

灰色系统关联分析的具体计算步骤如下 1》参考数列和比较数列的确定参考数列——反映系统行为特征的数据序列比较数列——影响系统行为的因素组成的数据序列2》无量纲化处理参考数列和比较数列(1) 初值化——矩阵中的每个数均除以第一个数得到的新矩阵(2) 均值化——矩阵中的每个数均除以用矩阵所有元素的平均值得到的新矩阵(3) 区间相对值化3》求参考数列与比较数列的灰色关联系数ξ(Xi) 参考数列X0比较数列X1、X2、X3……………比较数列相对于参考数列在曲线各点的关联系数ξ(i)称为关联系数，其中ρ称为分辨系数，ρ?(0，1)，常取0.5.实数第二级最小差，记为Δmin。

两级最大差，记为Δmax。

为各比较数列Xi曲线上的每一个点与参考数列X0曲线上的每一个点的绝对差值。

记为Δoi(k)。

所以关联系数ξ(Xi)也可简化如下列公式:4》求关联度ri关联系数——比较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值，所以它的数不止一个，而信息过于分散不便于进行整体性比较。

因此有必要将各个时刻(即曲线中的各点)的关联系数集中为一个值，即求其平均值，作为比较数列与参考数列间关联程度的数量表示，关联度ri公式如下:5》排关联序因素间的关联程度，主要是用关联度的大小次序描述，而不仅是关联度的大小。

基于灰关联和模糊规划的产品设计改进方法米传民;夏卫国;强媛【摘要】Considering that the relationship between customer needs ( CNs) and product engineering char-acteristics ( ECs) in House of Quality ( HoQ) model has the characteristics of “small data” and“poor in-formation”, the grey relational analysis is introduced to calculate the importance degree of ECs .Taking in-to account the impact of product development cost , technical realizing difficulties , market competition re-quirements and the actual fuzziness of product development cost restraint on the optimum product design during the process of product design , a fuzzy hybrid integer programming model is established to realize the optimum design level for ECs .Finally, an application to improve the ECs of the intelligent cellphones il-lustrates the effectiveness and practicality of proposed model .%考虑质量屋模型中顾客需求与产品工程特性之间相关关系具有“少数据”、“贫信息”特点，将灰关联分析引入到质量屋模型中求解产品工程特性重要度。