《电路分析》戴维南定理的解析与练习
- 格式:doc
- 大小:354.50 KB
- 文档页数:6

§2-6戴维宁定理内容: 戴维宁定理的定义戴维宁定理的证明应用戴维宁定理的步骤戴维宁定理的意义和注意事项一、戴维南定理内容i a3、数学表述:二、戴维南定理的证明i’a3、最简单等效电路三、应用戴维宁定理的步骤例:电路如图(a)所示,其中x 电流I =2A ,此时电压U 为何值?将虚线所示的两个单口网络N 1和N 2分别用戴维南等效电路代替,到图(b)电路。
V103V 202)1(+=×+×Ω=U gU U 单口N 1的开路电压U oc1可从图(c)电路中求得,列出KVL方程解:将20V电压源用短路代替,得到图(d)电路,再用外加电流源I 计算电压U 的方法求得R o1。
列出KVL方程IU I I gU U )2(322)()1(Ω+=×⎟⎞⎜⎛Ω×++×Ω=求R 01:最后从图(b)电路求得电流I 的表达式为xx x R R R R R U U I +Ω=+Ω+Ω−−−=++−=1V 821)V 5(V 3o2o1oc1oc2当只对电路中某一条支路或几条支路(记为N L )的电压电流感兴趣时,可以将电路分解为两个单口网络N L 与N 1的连接,如图(a)所示。
用戴维南等效电路代替更复杂的含源单口N 1,不会影响单口N L (不必是线性的或电阻性的)中的电压和电流。
代替后的电路[图(b)]规模减小,使电路的分析和计算变得更加简单。
四、意义和注意事项1、意义:2、注意:等效电源的电压方向与开路电压(短路电流)方向一致;当有受控源时,等效内阻可能出现“-”值;受控源支路可单独进行变换;而若控制支路进行变换时,受控源支路必须一起进行变换。
如书p57图(b)到(c)的变换。
习题:p452-3-2,2-3-3p81~832-8,2-14,2-16,。


§3-4 戴维南定理和诺顿定理求图示电路中通过12Ω电阻的电流i 。
将原电路从a、b 处断开,求左端部分的戴维南等效电路。
解:Ω6ΩΩ20Ω20Ω10Ω10V 15Ω5aioc 10201515201020101215155V33u =⨯-⨯++=⨯-⨯=-Ω33.13=30400=30200=2×10+2010×20=eqR将移出的支路与求出的戴维南等效电路进行连接Ω6Ω12ieqR ocu 解(续).eq 560096A612612612i R -=⨯=-⨯+++Ω20Ω20Ω10Ω10Ω5abeq求图示单口网络的戴维南等效电路。
解:开路电压su 11i 1i α2R a eqR 方法1:外加电源法求(αααs 2oc 122s11u R u i R R u R R ==-=-11i 2R 10i a 001i i =-()0eq 21u R αR i ==-()()()0102002021u αi i R αi i R αi R=+=-+=-有缘学习更多+谓ygd3076或关注桃报:奉献教育(店铺)解(续)eqR 方法2:短路电流法求s u 2i 1R 1i α1i 2R sc1s2sc12==+R u i i i i 1sc =i αi ()ssc 11αu i αR =-()()2soc 1eq 2ssc 111R αu u R R αRαu i αR -===--方法3:VCR 确定法解(续)s11u i i R =-s u 11i 1i α2R a +-ui ()12u αi i R =-()2s 211R u αu αR iR =---eqR ocu b求图示电路的诺顿等效电路。
4V 2kΩ3k Ωx 40001u +-xu 解:分别求短路电流和等效电阻。
由于0=x u ,所以mA 8.0=3000+20004=sc i 4V 2k Ω3k Ω4000x u sc-xu +Ωk 10=8.08==sc oc eq i u R 求开路电压oc x oc 40001×2000+4==u u u V 8=ocu eqR sci解:求出BD以左的戴维南等效电路。

第四章电路定理◆重点:1、叠加定理2、戴维南定理和诺顿定理◆难点:1、熟练地运用叠加定理、戴维南定理和诺顿定理分析计算电路。
2、掌握特勒根定理和互易定理,理解这两个定理在路分析中的意义。
4-1 叠加定理网络图论与矩阵论、计算方法等构成电路的计算机辅助分析的基础。
其中网络图论主要讨论电路分析中的拓扑规律性,从而便于电路方程的列写。
4.1.1 几个概念1.线性电路——Linear circuit由线性元件和独立源组成的电路称为线性电路。
2.激励与响应——excitation and response在电路中,独立源为电路的输入,对电路起着“激励”的作用,而其他元件的电压与电流只是激励引起的“响应”。
3.齐次性和可加性——homogeneity property and additivity property“齐次性”又称“比例性”,即激励增大K倍,响应也增大K倍;“可加性”意为激励的和产生的响应等于激励分别产生的响应的和。
“线性”的含义即包含了齐次性和可加性。
齐次性:可加性:4.1.2 叠加定理1.定理内容在线性电阻电路中,任一支路电流(电压)都是电路中各个独立电源单独作用时在该支路产生的电流(电压)之叠加。
此处的“线性电阻电路”,可以包含线性电阻、独立源和线性受控源等元件。
2.定理的应用方法将电路中的各个独立源分别单独列出,此时其他的电源置零——独立电压源用短路线代替,独立电流源用开路代替——分别求取出各独立源单独作用时产生的电流或电压。
计算时,电路中的电阻、受控源元件及其联接结构不变。
4.1.3 关于定理的说明1.只适用于线性电路2.进行叠加时,除去独立源外的所有元件,包含独立源的内阻都不能改变。
3.叠加时应该注意参考方向与叠加时的符号4.功率的计算不能使用叠加定理4.1.4 例题1.已知:电路如图所示–6V+4– 6V +求:X U 及两个独立源和受控源分别产生的功率。
解:根据叠加定理,电路中电压源和电流源分别作用时的电路如图(b )、(c )所示。

学M O O C 中国大学M O O C 中国大学M O O C中国大学学M O O C中国大学M O O C 中国大学M OO C中国大学学M O O C中国大学MO O C中国大学MO O C中国大学学M OO C 中国大学M O O C中国大学MO O C中国大学学M OO C中国大学M O O C 中国大学MO OC中国大学学M OO C 中国大学M O O C 中国大学M OO C中国大学戴维南定理戴维南定理的应用主要内容 CONTENT学M O O C中国大学M O O C 中国大学M O O C中国大学学M O O C中国大学M O O C 中国大学MO OC中国大学学M O O C中国大学MO O C中国大学MO O C中国大学学M OO C 中国大学M O O C中国大学MO O C中国大学学M OOC中国大学M O O C 中国大学MO OC中国大学学M OO C 中国大学M O O C 中国大学MO OC中国大学2、单口网络的描述p 等效电路:= += / −学M O O C中国大学M O O C 中国大学M O O C 中国大学学M O O C中国大学M O O C 中国大学MO OC中国大学学M O O C中国大学MO O C中国大学M O OC中国大学学M OO C 中国大学M O O C中国大学MO O C中国大学学M OO C中国大学M O O C中国大学MO OC中国大学学M OO C 中国大学MO O C中国大学M O OC中国大学例题p 线性单口网络的VCR:ü如果网络内部含有独立源,其VCR 为= +ü如果网络内部不含有独立源,其VCR 为=电路可等效为一个电压源串联一个电阻或VCR 为= +电路可等效为一个电流源并联一个电阻电路可等效为一个电阻学M O O C 中国大学M O O C 中国大学M O O C 中国大学学M O O C中国大学M O O C 中国大学MO OC中国大学学M O O C中国大学M O O C中国大学MO OC中国大学学M O O C中国大学M O O C中国大学MO O C中国大学学M OO C中国大学M O O C 中国大学MO OC中国大学学M OO C中国大学M O O C中国大学MO OC中国大学等效一个线性含源单口网络可以用一个电压源串联电阻的电路来等效。
![戴维南定理_电路分析基础_[共3页]](https://uimg.taocdn.com/05791529910ef12d2bf9e7d6.webp)
第3章 线性电路的基本定理 57
3.2 戴维南定理
电路分析时经常遇到只研究某一支路电压或电流的情况,此时虽然可以使用3.1节的方法求解,但通常都不如用戴维南定理方便。
戴维南定理指出:一个线性含源二端网络N ,对外电路而言,总可以用一个电压源模型等效代替,如图3-6所示。
该电压源的电压U S 等于有源二端网络的开路电压U OC ,其内阻R S 等于网络N 中所有独立源均为零时所得无源网络N 0的等效内阻R ab 、U S 和R S 相串联的模型称为戴维南等效电路。
图3-6
应当指出的是:画戴维南等效电路时,电压源的极性必须与开路电压的极性保持一致。
另外,当等效电阻R ab 不能用电阻串、并联计算时,可用下列两种方法求解。
(1)外加电压法:使网络N 中所有独立源均为零值(受控源不能作同样处理),得一个无源二端网络N 0,然后在N 0两端点上施加电压U ,如图3-7所示,然后计算端点上的电流I ,则 ab s U R R I ==
图3-7。


戴维南定理在电路分析中,往往只需要计算一个网络中某一支路的电流或电压,而其他支路的电流或电压不需求出。
如果用前面介绍方法来进行求解则要把全部电路方程列出以后,才能求解所需支路上的电流或电压,这当然是繁琐的。
能否有一种简便方法,既能求解出所需支路的电流或电压,而又不需建立方程组进行求解。
网络的戴维南定理就满足这样要求。
一、二端网络及其等效电路在电路分析中,可以把互连的一组元件作为一个整体来看待,当这个整体只有两个端钮用以与外部相连接时,则不管它的内部结构如何,称它为二端网络,又因从一端钮流进的电流必然等于另一端钮流出的电流,因而也可称为一端口网络。
如果二端口网络内部没有电源,称之为无源二端网络(如图2-15a);如果内部有电源,称之为有源二端网络(如图2-15b)。
我们常用一个方框代替二端网络,方框中的P代表无源(如图2-15c);A代表有源(如图2-15d)。
从二端网络一端钮流进的电流必然等于另一端钮流出的电流,称为端口电流。
二个端钮之间的电压称为端口电压。
图2-15二端网络对外的作用可用一个简单的等效电路代替。
在§1-3中讨论过串并联电阻电路可以用等效电阻来代替,在§2-2中讨论过电源支路的串并联,它们也可以用一个等效电源来代替。
这些都是特殊类型的二端网络的等效电路,本节将讨论一般线性二端网络的等效电路。
等效电路和它所等效的二端网络对外电路应具有完全相同的影响,即等效电路和它所等效的二端网络应具有完全相同的外特性。
线性无源二端网络可以用一个线性电阻作为等效电路,这个电阻称为该端口的输入电阻,用R0代表。
输入电阻与等效电阻是相等的。
线性有源二端网络的等效电路是一个等效电源支路,它可以用电压源串联支路来表示,也可以用电流源并联支路来表示。
这便是戴维南定理和诺顿定理,统称为等效电源定理。
二、戴维南定理戴维南定理的内容是:含独立源的线性二端电阻网络,对外部而言,都可用电压源电阻串联组合等效代替;该电压源的电压等于网络的开路电压,而电阻等于网络内部所有独立电源作用为零情况下的网络的等效电阻。

电工学实验报告戴维南定理电工学实验报告——戴维南定理一、实验目的1、验证戴维南定理的正确性,加深对该定理的理解。
2、掌握测量有源二端网络等效参数的一般方法。
3、学习使用电路实验仪器进行电路参数的测量和分析。
二、实验原理戴维南定理指出:任何一个线性有源二端网络,对外电路来说,可以用一个电压源和电阻的串联组合来等效替代。
其中,电压源的电压等于有源二端网络的开路电压 Uoc,电阻等于有源二端网络除源(将所有独立电源置零)后的等效电阻 Ro。
三、实验设备与器材1、直流稳压电源2、直流电压表3、直流电流表4、电阻箱5、实验电路板6、连接导线若干四、实验内容与步骤1、按图 1 连接实验电路,其中 RL 为可变电阻,US1 和 US2 为直流稳压电源,R1、R2 为已知电阻。
!实验电路图 1(具体电路图此处省略)2、测量有源二端网络的开路电压 Uoc。
将 RL 开路,用电压表测量有源二端网络 A、B 两端的电压,即为开路电压 Uoc,记录测量值。
3、测量有源二端网络的短路电流 Isc。
将 A、B 两端短路,用电流表测量短路电流 Isc,记录测量值。
4、测量有源二端网络除源后的等效电阻 Ro。
将有源二端网络中的电源 US1 和 US2 置零(即将稳压电源的输出电压调为零),然后用电阻箱测量 A、B 两端间的电阻,即为等效电阻 Ro,记录测量值。
5、构建戴维南等效电路。
根据测量得到的 Uoc 和 Ro,用一个电压源 Uoc 和一个电阻 Ro 串联组成戴维南等效电路,如图 2 所示。
!实验电路图 2(具体电路图此处省略)6、测量等效电路的外特性。
改变负载电阻 RL 的值,测量对应的电流 I 和电压 U,记录数据并绘制 U I 曲线。
五、实验数据记录与处理1、测量有源二端网络的开路电压 Uoc|测量次数|1|2|3|平均值||||||||测量值(V)|_____|_____|_____|_____|2、测量有源二端网络的短路电流 Isc|测量次数|1|2|3|平均值||||||||测量值(A)|_____|_____|_____|_____|3、测量有源二端网络除源后的等效电阻 Ro|测量次数|1|2|3|平均值||||||||测量值(Ω)|_____|_____|_____|_____|4、测量等效电路的外特性|RL(Ω)|_____|_____|_____|_____|_____||I(A)|_____|_____|_____|_____|_____||U(V)|_____|_____|_____|_____|_____|根据测量数据,绘制等效电路的 U I 曲线。
三、应⽤戴维南定理分析第七章习题7-1. 如图7-1(a)所⽰电路求⽹络函数12)(U U j H =ω的幅频特性和相频特性。
图7-1 (a) 图7-1(b)7-2 如图7-2所⽰电路,已知 150=Q ,H L µ310=,pF C 280=,mV U S 11=, kHz f 5401=,mV U S 12=,kHz f 6002=,求两个信号在电路中的电流。
7-3 RLC 串联电路中,外施电源电压,5,50, cos 101mH L R tV u =Ω==ω F C µ5.0= ,(1) 求Q 和0ω;(2) 求输出电压(取⾃电容)在0ω时有效值;(3) 求使输出电压为最⼤时的频率m ω;(4) m ω时输出电压是多少?(5) 绘出幅频特性;(6) 当R 降低到Ω10时重复 (1) 到 (5) 的各项要求。
7-4 电路如图7-3所⽰,1000 , 1.10 ,/ 10 , 1002130Ω=Ω===R R s rad V U S ω, , 10 F C µ=求10, U L 。
图7-37-5如图7-5所⽰电路,已知H 2.01=L ,H 4.02=L ,H 2.0=M ,Ω=k 1R ,F 25.1µ=C ,试求该电路谐振时的⾓频率。
L 212L 同答案:s /rad 1021025.12.011360?=??==-C L 同ω7-6 如图7-6所⽰正弦稳态电路,R = 1k Ω,C = 1µF ,当u S (t) = 10 cos(103t )V 时,u C (t ) = ? 当u S (t) = 10 cos(2×103t )V 时,u C (t ) = ?7-7 ⼀rLC 串联谐振电路,L = 50µH ,C = 200pF ,回路品质因数Q = 50,电源电压U S = 1mV 。
求电路的谐振频率、谐振时的回路电流I 0、电容电压U C0和带宽B 。
电路分析基础实验报告直流电路测量一.实验目的1.通过实验熟悉万用表、面包板的使用方法;2.在线性网络中,验证基尔霍夫定律、叠加定理;3.在线性网络中,验证戴维南定理;4.了解戴维南定理的实际应用。
二.实验仪器万用表 1 台直流稳定电源 1 台面包板 1 块三.预习要求1.认真阅读课本关于直流电路知识相关内容。
2.认真学习微信公众号上直流电路相关课件。
3.复习万用表、直流稳定电源的使用方法。
4.计算实验内容中的表1、2、3、4 中的理论值。
5.请通过查找资料回答以下几个预习问题:(1)请简述基尔霍夫定律KVL、KCL。
KCL:所有进入某节点的电流的总和等于所有离开这节点的电流的总和。
(2)请简述叠加定理。
叠加定理:任一支路的电流(电压)可以看成电路中每一个独立电源单独作用于电路时在该支路产生的电路(或电压)的代数和。
(3)请画出实验中,验证基尔霍夫定律和叠加定理所用电路图并标出电路参数、abd 回路cbd 回路。
(4)请简述戴维南定理。
戴维南定理:含独立电源的线性电阻单口网络N,就端口特性而言,可以等效为一个电压源和电阻串联的单口网络。
(5)验证戴维南定理需要先测量出开路电压UOC和等效电阻RO,本次实验用哪两种方法测量这两个参数?答:①外特性测量法②直接测量法(6)在已经测量出开路电压UOC和等效电阻RO后,如何通过实验验证戴维南定理?答:电压源调到Uoc,串联一个阻值大小为Ro的电阻,再接上电阻箱组成一个回路,调整电阻箱的值,使RL 分别等于1000,800,600,400,200,100,测量URL,然后与外特性测量法的数据相比较,看两个电路的外部特性是否一致。
四.实验原理实验原理见预习内容。
五.实验内容1.将两个电源同时接入电路(12V,6V),验证基尔霍夫定律KVL,根据电路图测量表1 数据,表1 中理论值应在课前预习时计算完。
2. 将两个电源同时接入电路(12V,6V),验证基尔霍夫定理KCL,根据电路图测量表2 数据(电流的测量值可以测量相应电压值后代入欧姆定律求得), 表2 中理论值应在课前预习时计算完。
电路分析戴维南定理与电流计算电路分析是电子工程中非常重要的一部分,它涉及到电路中各个元件的性质和相互关系。
在进行电路分析的过程中,戴维南定理和电流计算是两个基本而关键的概念。
本文将对这两个概念进行详细的介绍和解析。
一、戴维南定理戴维南定理是电路分析中一个非常有用的工具,它可以帮助我们简化复杂的电路,并找到我们所关心的电流或电压数值。
戴维南定理的核心思想是将被测电阻或电源通过一个等效电阻或等效电源替代,从而简化电路的分析过程。
为了更好地理解戴维南定理,我们先来看一个具体的例子。
假设我们有一个包含多个电阻的电路,我们想要计算某一点的电流。
按照戴维南定理,我们可以先将该点与电路中其他分支断开,并用一个电压源来保持该点电势恒定。
接下来,我们需要计算在这个条件下,通过该点的电流。
这个电流即为我们所求的结果。
除了计算电流,戴维南定理也可以用于计算电压。
当我们想要计算电路中某一分支的电压时,可以使用戴维南定理化简电路,并计算在等效电路中的电压值。
二、电流计算电流是电子电路中最基本的物理量之一,它描述了电荷在电路中的流动情况。
在电路分析中,我们常常需要计算电流来确定电路的工作状态和性能。
通常情况下,计算电路中的电流有两种方法:理论计算和实验测量。
理论计算是通过应用基本电路定律和电路分析技巧,结合元件的参数和拓扑结构,来推导出电流的数学表达式。
实验测量则是通过使用电流计或多用表等测量设备,直接测量电路中各个分支的电流值。
在实际应用中,为了确保电流计算的准确性,我们需要注意以下几点:1. 元件参数的准确性:电流计算所依赖的电阻、电容、电感等元件参数应尽可能精确,以避免计算结果的误差。
2. 电路拓扑结构的分析:在进行电流计算之前,需要先了解电路的布置和拓扑结构,分析电路中的节点、支路和回路,以确保计算的有效性。
3. 使用正确的电路定律:在进行电流计算时,需要正确地应用欧姆定律、基尔霍夫定律等电路定律,以确保计算过程的准确性和一致性。
戴维南定理基础练习题(打印版)# 戴维南定理基础练习题## 一、理论回顾戴维南定理(Thevenin's Theorem)是电路理论中的一个重要定理,它提供了一种将复杂电路简化为等效电路的方法。
根据戴维南定理,任何线性双端网络都可以用一个电压源和内阻串联的等效电路来代替。
### 1. 定理内容戴维南定理指出,对于任何线性双端网络,当其两端开路时,等效电压源的电压等于开路电压;当其两端短路时,等效内阻等于短路电流除以开路电压。
### 2. 应用条件- 电路必须是线性的。
- 电路两端可以是任意的两个节点。
## 二、基础练习题### 练习题1:开路电压与短路电流的计算题目描述:给定一个简单的电路,包含一个电压源Vs,一个电阻R1,和一个并联电阻R2。
计算开路电压和短路电流。
电路参数:- Vs = 10V- R1 = 1kΩ- R2 = 2kΩ解答:开路电压等于电压源的电压,即Voc = Vs = 10V。
短路电流Isc可以通过计算总电阻Rt得到:\[ R_t = \frac{R_1 \times R_2}{R_1 + R_2} = \frac{1k\Omega \times 2k\Omega}{1k\Omega + 2k\Omega} = 0.6667k\Omega \]\[ I_{sc} = \frac{V_s}{R_t} = \frac{10V}{0.6667k\Omega}\approx 15.01mA \]### 练习题2:等效电路的构建题目描述:在练习题1的基础上,构建等效电路,并计算当负载电阻RL = 3kΩ时的输出电压。
解答:等效电路由10V的电压源和0.6667kΩ的内阻串联组成。
当连接负载电阻RL时,总电阻为:\[ R_{total} = R_{th} + R_L = 0.6667k\Omega + 3k\Omega = 3.6667kΩ \]输出电压Vout可以通过欧姆定律计算:\[ V_{out} = I_{load} \times R_{total} \]\[ I_{load} = \frac{V_{oc}}{R_{total}} =\frac{10V}{3.6667k\Omega} \approx 2.73mA \]\[ V_{out} = 2.73mA \times 3.6667k\Omega \approx 10V \]### 练习题3:电路参数的调整题目描述:如果将练习题1中的R1改为2kΩ,重新计算开路电压和短路电流。
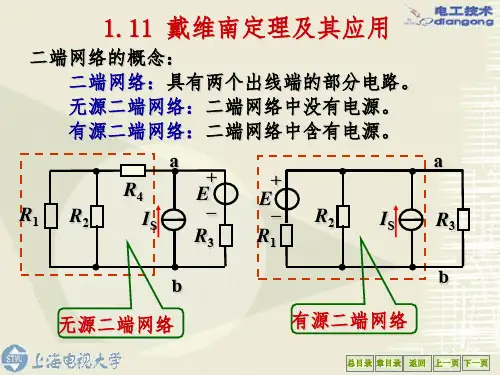
《戴维南定理》习题练习、知识点1、二端(一端口)网络的概念:二端网络:具有向外引出一对端子的电路或网络。
无源二端网络:二端网络中没有独立电源。
有源二端网络:二端网络中含有独立电源。
2、戴维宁(戴维南)定理等效电路的电压 U OC 是有源二端网络的开路电压,即将负载 R L 断开后a 、b 两端之间的电压。
等效电路的电阻 R o 是有源二端网络中所有独立电源均置零(理想电压源用短路代替, 理想电流源用开路代替)后 ,所得到的无源二端网络 a 、b 两端之间的等效电阻。
源端络无二网无源二端网络可 化简为一个电阻匸戴维宁廣匸> |诺顿定理任何一个线性有源二端网络都可以用一个电压为 U oc 的理想电压源和一个电阻 R0串联的等效电路来代替。
如图所示:二、例题:应用戴维南定理解题戴维南定理的解题步骤:1•把电路划分为待求支路和有源二端网络两部分,如图1中的虚线。
2•断开待求支路,形成有源二端网络(要画图),求有源二端网络的开路电压UOC。
3•将有源二端网络内的电源置零,保留其内阻(要画图),求网络的入端等效电阻Rab。
4•画出有源二端网络的等效电压源,其电压源电压US=UOC (此时要注意电源的极性),内阻R0=Rab。
5•将待求支路接到等效电压源上,利用欧姆定律求电流。
【例1】电路如图,已知U仁40V , U2=20V,R仁R2=4」R3=13 ■'?,试用戴维宁定理求电流13。
⑵求等效电阻R0将所有独立电源置零(理想电压源用短路代替,理想电流源用开路代替)例L團解:(1)断开待求支路求开路电压UOC5 -u2R1 R240-204 4-2.5AUOC = U2 + I R2 = 20 +2.5 4 =30V或:UOC = U1 T R1 = 40 T2.5 4UOC也可用叠加原理等其它方法求。
=30V⑶画出等效电路求电流I3U OC _ 30R。
R3 _ 2 13=2AlA R)【例2】用戴维南定理计算图中的支路电流13。
《戴维南定理》习题练习
一、知识点
1、二端(一端口) 网络的概念:
二端网络:具有向外引出一对端子的电路或网络。
无源二端网络:二端网络中没有独立电源。
有源二端网络:二端网络中含有独立电源。
2、戴维宁(戴维南)定理
任何一个线性有源二端网络都可以用一个电压为U OC的理想电压源和一个电阻R0串联的等效电路来代替。
如图所示:
等效电路的电压U OC是有源二端网络的开路电压,即将负载R L断开后 a 、b两端之间的电压。
等效电路的电阻R0是有源二端网络中所有独立电源均置零(理想电压源用短路代替,理想电流源用开路代替)后, 所得到的无源二端网络 a 、b两端之间的等效电阻。
二、例题:应用戴维南定理解题
戴维南定理的解题步骤:
1.把电路划分为待求支路和有源二端网络两部分,如图1中的虚线。
2.断开待求支路,形成有源二端网络(要画图),求有源二端网络的开路电压UOC 。
3.将有源二端网络内的电源置零,保留其内阻(要画图),求网络的入端等效电阻Rab 。
4.画出有源二端网络的等效电压源,其电压源电压US=UOC (此时要注意电源的极性),内阻R0=Rab 。
5.将待求支路接到等效电压源上,利用欧姆定律求电流。
【例1】电路如图,已知U 1=40V ,U 2=20V ,R 1=R 2=4
,R 3=13 ,试用戴维宁定理求电流
I 3。
解:(1) 断开待求支路求开路电压
U OC
U OC = U 2 + I R 2 = 20 + 4 = 30V
或: U OC = U 1 – I R 1 = 40 –
4 = 30V
U OC 也可用叠加原理等其它方法求。
(2) 求等效电阻R 0
将所有独立电源置零(理想电压源用短路代替,理想电流源用开路代替)
A 5.24420
402121
=+-=+-=R R U U I Ω=+⨯=22
1210R R R R R
(3) 画出等效电路求电流I 3
【例2】 用戴维南定理计算图中的支路电流I 3。
解:① 等效电源的电动势E 可由图1-58(b)求得
于是 或
② 等效电源的内阻R O 可由图1-58(c)求得 因此
③ 对a 和b 两端讲,R 1和R 2是并联的,由图1-58(a)可等效于图1-58(d)。
所以
【例3】用戴维南定理求图中5Ω电阻中的电流I ,并画出戴维南等效电路
【例4】试用戴维南定理计算图示电路中6欧电阻中的电流I 。
()
A 21323030OC 3=+=+=R R U I -10V+
【例5】计算图示电路中的电流I。
(用戴维南定理求解)(2A)
【例6】计算图示电路中的电流I。
(用戴维南定理求解)()
【例7】用戴维南定理求下图所示电路中的电流I(2A)
【例8】电路如图所示,R=Ω,试用戴维南定理求电阻R中的电流I。
()
6 3Ω
3Ω
5A
2A
- 20V +
题3图。