三角形的中位线及性质

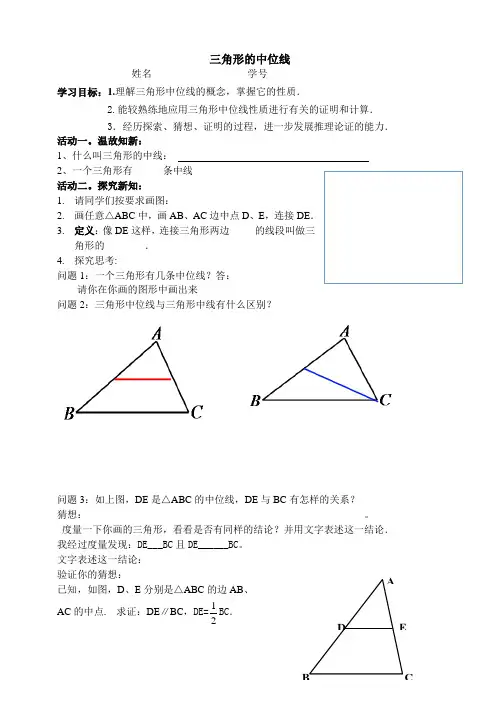
三角形的中位线姓名___________________学号____________________学习目标：1.理解三角形中位线的概念，掌握它的性质．2.能较熟练地应用三角形中位线性质进行有关的证明和计算．3．经历探索、猜想、证明的过程，进一步发展推理论证的能力．活动一。

温故知新：1、什么叫三角形的中线：2、一个三角形有______条中线 活动二。

探究新知：1. 请同学们按要求画图：2. 画任意△ABC 中，画AB 、AC 边中点D 、E ，连接DE ．3. 定义：像DE 这样，连接三角形两边_____的线段叫做三角形的________． 4. 探究思考:问题1：一个三角形有几条中位线？答：__________请你在你画的图形中画出来问题2：三角形中位线与三角形中线有什么区别？问题3：如上图，DE 是△ABC 的中位线，DE 与BC 有怎样的关系？ 猜想：_______________________________________________________。

度量一下你画的三角形，看看是否有同样的结论？并用文字表述这一结论． 我经过度量发现：DE___BC 且DE______BC 。

文字表述这一结论：_______________________________________________ 验证你的猜想： 已知，如图，D 、E 分别是△ABC 的边AB 、 AC 的中点. 求证：DE ∥BC ，DE=21BC ．A B CD E归纳：由此我通过猜想，测量，证明等方式得到三角形中位线定理：即：______________________________________________________。

几何语言：活动三。

运用新知如图，△ABC中，D、E分别是AB、AC中点(1）若DE=5，则BC=_____________ .。

（2）若∠B=65°，则∠ADE=_________。

三角形中位线定理及推论一、三角形中位线定理三角形中位线定理是指在任意三角形中，连接一个顶点与对边中点的线段称为中位线，三条中位线交于一点，且该点与三个顶点的距离相等。

具体表述为：三角形三条中位线的交点与三个顶点的距离相等。

以三角形ABC为例，连接顶点A与边BC的中点D，顶点B与边AC 的中点E，顶点C与边AB的中点F，根据中位线定理可知，中位线AD、BE和CF三条线段交于一点G，并且AG=BG=CG。

中位线定理的证明可以通过向量法或平面几何法进行，这里我们选择平面几何法证明。

证明思路如下：1. 连接顶点A与边BC的中点D，假设点G是中位线AD与中位线BE 的交点；2. 连接顶点B与边AC的中点E；3. 通过顶点C以平行于边AB的直线与中位线AD交于点H；4. 由平行线的性质可知，AH=CH；5. 进一步，由三角形的对应边成比例可得：AH/AD=CH/CF；6. 由于AH=CH，所以AD=CF；7. 同样地，由中位线定理可得：BE=CF；8. 综上所述，AD=BE=CF，即证明了中位线定理。

二、三角形中位线推论基于中位线定理，我们可以得出一些有关三角形的推论。

1. 三角形中位线长度关系推论根据中位线定理，三角形三条中位线的交点与三个顶点的距离相等，即AG=BG=CG。

由此可得，中位线上的点距离顶点的距离是相等的。

进一步推论，三角形中位线的长度满足以下关系：AG=2GD，BG=2GE，CG=2GF。

2. 三角形中位线与三角形面积推论由三角形中位线定理可知，三条中位线交于一点G。

以G为顶点，三边中点分别为D、E、F，连接DG、EG和FG。

我们可以发现，连接G与三角形顶点的线段将三角形分成了六个小三角形，而这些小三角形的面积相等。

因此，我们可以推论得到：三角形中位线所分割的三个小三角形的面积相等。

3. 三角形中位线与三角形高度推论在三角形中，如果我们将中位线作为底边，那么与之对应的高度就是顶点到底边中点的距离。

三角形中的中线与中位线的性质在几何学中，三角形是最基本的多边形之一，由三个边和三个顶点组成。

在三角形中，中线和中位线是两个重要的概念。

本文将探讨这些线段的性质，展示它们在三角形中的重要作用。

一、中线的性质中线是指连接三角形的一个顶点和对应边中点的线段。

在任何三角形中，都存在三条中线，它们相交于一个点，称为三角形的重心。

以下是中线的性质：1. 中心位置：三角形的三条中线的交点即为三角形的重心。

重心将三角形划分为三个面积相等的三角形。

2. 等长性：三角形的三条中线长度相等。

即，连接三角形的一个顶点和对边中点的线段长度相等。

3. 三点共线：三角形的顶点和对边中点以及重心共线。

这意味着无论三角形是等腰、等边还是普通三角形，其中心点都位于三角形内部，并且与三角形的顶点与边具有一定的关系。

二、中位线的性质中位线是指连接三角形的两个顶点中点的线段。

在任何三角形中，存在三条中位线，也具有一些重要的性质。

以下是中位线的性质：1. 中点连线：三角形的三条中位线的交点即为三角形内心。

2. 等长性：三角形的三条中位线长度相等。

即，连接三角形的两个顶点中点的线段长度相等。

3. 平分性：中位线将三角形的面积平分为两部分。

即，三角形内所有通过一个顶点的中位线所对应的两个小三角形面积之和等于大三角形的一半。

三、中线与中位线的关系中线和中位线是三角形中具有重要关系的特殊线段。

以下是它们之间的一些关系：1. 位置关系：三角形的三条中线相交于三角形的重心，而三条中位线相交于三角形的内心。

2. 长度比较：在同一个三角形中，中位线的长度大于中线的长度。

3. 关于重心的性质：连接三角形的一个顶点和对边中点的线段与连接该顶点与三角形的重心的线段之间的比值为2:1。

4. 关于内心的性质：连接三角形的两个顶点中点的线段与连接这两个顶点与三角形的内心的线段之间的比值为1:1。

结论：通过对三角形中的中线与中位线的性质进行分析，我们可以得出以下结论：1. 中线和中位线都是三角形中的重要线段，它们与三角形重心和内心的位置关系密切。

三角形中位线的性质引言在几何学中，三角形是最基本的几何形状之一。

三角形有很多有趣的特性和性质，其中一个重要的性质是中位线。

本文将介绍三角形的中位线的性质，并且通过几何推导和实例演示来解释这些性质。

什么是三角形中位线？首先，我们需要了解中位线的定义。

在三角形ABC中，中位线是从三角形的每个顶点到对应对边的中点的线段。

triangletriangle在上图中，AD、BE和CF是三角形ABC的中位线，其中D、E和F分别是边BC、AC和AB的中点。

第一性质：中位线与边的关系首先，我们来看中位线与边的关系。

我们可以发现，三角形的每条中位线分割对应的边成为两个相等的线段。

证明这一性质，我们以中位线AD为例。

连接点D和B，我们可以得到三角形ADB。

由于D是边BC的中点，根据线段的性质，我们可以得出AD=BD。

同样地，以中位线BE和CF为例，我们可以得出BE=EC和CF=AF。

因此，三角形的每条中位线都能将对应的边分割成两个相等的线段。

第二性质：中位线的交点三角形的中位线是由三个中位线构成的。

我们可以证明这三条中位线相交于一个点，这个点被称为三角形的重心。

我们以中位线AD和BE的交点为例。

我们可以证明这个交点C，是边AB的中点。

连接点C和A，以及点C和B，我们可以得到三角形ACB。

我们知道，BC是中位线，所以C是边AB的中点。

同样地，我们也可以证明中位线AD和CF的交点，以及中位线BE和CF的交点分别是边AC和BC的中点。

因此，中位线的交点是三角形边的中点，也就是三角形的重心。

第三性质：重心的性质重心是一个非常有趣的点，它拥有一些特殊的性质。

首先，重心到三角形的每个顶点的距离相等。

也就是说，重心到顶点的距离是相等的。

我们可以通过几何推导来证明这一性质。

以重心为原点，我们可以使用向量的方法来推导这个等式。

假设三角形的重心是点G，顶点分别是A、B和C。

我们使用向量表示，AG=a，BG=b，CG=c。

根据重心定义，可以得到AG=(2/3)AD，BG=(2/3)BE和CG=(2/3)CF。

第9讲三角形的中位线知识导航1.连接三角形两边中点的线段叫三角形的中位线；2.三角形的中位线性质：三角形的中位线平行且等于第三边的一半；3.一个三角形有三条中位线.【板块一】运用中位线的性质计算与证明方法技巧三角形的中位线平行且等于第三边的一半，给出了中位线与第三边的位置关系和数量关系，为证明两线平行，探求两线段的数量关系提供了依据.题型一利用中位线的性质计算与证明【例1】如图，△ABC中，12AB=，8AC=，AD，AE分别是△ABC的角平分线和中线，过点C作CG⊥AD于点F，交AB于点G，连接EF，则线段EF的长为_______.【例2】如图，点E为□ABCD中DC边的延长线上一点，且CE DC=，连接AE，分别交BC，BD于点F，G，连接AC交BD于点O，连接OF.(1)求证：△ABF≌△ECF；(2)求证：2=.AB OF针对练习11.如图，□ABCD的周长为8，对角线AC，BD交于点M，延长AB到点E，使BE BC=，BN⊥EC于点N，连接MN，求MN的长.2.如图，O 为△ABC 两条中线BF 与CD 的交点，求证：12OD OC =，12OF BO =.【板块二】 构造中位线的方法与技巧方法技巧构造中位线的方法与技巧有：连中点构造中位线，取中点构造中位线，角平分线与垂线组合构造中位线，倍长线段构造中位线，连接第三边构造中位线.题型二 连中点构造中位线【例1】如图，△ABC 和△DCE 都是等腰直角三角形，90ACB DCE ︒∠=∠=，点D ，C ，B 在同一条直线上，点F ，G ，M 分别为AD ，BE ，AB 的中点.(1)求FGM ∠的度数；(2)求FG BD的值.题型三 取中点构造中位线方法技巧三角形的一条边上有中点，可以取另一边的中点，然后连接这两个中点，构造三角形的中位线.【例2】如图1，在△ACB 中，CA CB =，90ACB ︒∠=，点E 在AC 上，EF ⊥AC 交AB 于点F ，连接BE ，D 为AF 的中点，M 为BE 的中点.(1)判断CM 与CD 之间的数量关系，并加以证明；(2)将△AEF 绕点A 旋转任意一锐角，如图2，其他条件不变，（1）中的结论是否仍然成立？请加以证明.题型四 角平分线＋垂线→构造中位线方法技巧角平分线＋垂线，通过延长直角边，可以补全成等腰三角形，形成一边上有中点的情形，与另外的边的中点连线可得到中位线.【例3】(2017徐州改)如图，在△ABC 中，点D ，点E 分别为AB ，AC 的中点，点F 在DE 上，且AF ⊥BF .(1)求证：ABF CBF ∠=∠；(2)若5AB =，8BC =，求EF 的长.【例4】如图，BD ,CE 分别是△ABC 的外角平分线，过点A 作AF ⊥BD 于点F ，AG ⊥CE 于点G ，连接FG . 求证：(1)FG ∥BC ； (2) ()12FG AB BC AC =++.【例5】已知点M 为△ABC 的边BC 的中点，12AB =，18AC =，BD ⊥AD 于点D ，连接DM .(1)如图1，若AD 为△ABC 的角平分线，延长BD 交AC 于点E .①求证：BD DE =；②求MD 的长；(2) 如图2，若AD 为△ABC 的外角平分线，则_______MD =.【例6】如图，在△ABC 中，90ACB ︒∠=，AB 边上的高线CH 与△ABC 的两条内角平分线AM ，BN 分别交于P ，Q 两点，PM ，QN 的中点分别为E ，F .求证：EF ∥AB .【例7】如图，△ABC 和△CDE 都是等腰直角三角形，90ACB CDE ︒∠=∠=，点E 在AC上，M 为BE 的中点.求证：2AE DM =.题型五 倍长线段构造中位线【例8】如图，点P 为△ABC 的边BC 的中点，分别以AB ,AC 为斜边作Rt △ABD 和Rt △ACE ，且BAD CAE ∠=∠.求证：PD PE =.题型六 连接第三边构造中位线方法技巧若图形中存在共顶点的两边上都有中点，可以连接第三边，构造中位线. 【例9】如图，在□ABCD 中，120C ︒∠=，2AB =，4AD =，点H ，G 分别是边CD ，BC 上的动点，连接AH ，HG ，点E 为AH 的中点，点F 为GH 的中点，连接EF .则EF 的最大值与最小值的差为（ ）A ．1 B.31- C.32D.23-【例10】如图，E ，F ，G ，H 分别是AB ，BC ，CD ，DA 的中点，求证：四边形EFGH 是平行四边形.【例11】如图，点B 为线段AC 上一点，分别以AB ，BC 为边AC 的同侧作等边△ABD 和等边△BCE ，点P ，M ，N 分别为AC ，AD ，CE 的中点.(1)求证：PM PN =；(2)求MPN ∠的度数.针对练习21.(课本62页第16题改编)如图，在△ABC 中，M 为BC 的中点，AD 为BAC ∠的平分线，BD ⊥AD 于点D .(1)求证：()12DM AC AB =-； (2)若6AD =，8BD =，2D M =，求AC 的长.2.如图，在△ABC 中，BE ，CF 分别平分ABC ∠，ACB ∠，AG ⊥BE ，AH ⊥CF ，G ，H 为垂足，求证：GH ∥BC .3.如图，点E ，F ，G ，H 分别是四边形ABCD 的边AB ，BC ，CD ，DA 的中点，求证：EG 与HF 互相平分.4.如图，BF 是△ABC 的角平分线，AM ⊥BF 于点M ，CE 平分△ABC 的外角，AN ⊥CE 于点N .(1)求证：MN ∥BC ；(2)若AB c =，AC b =，BC a =，求MN 的长.【板块三】 中位线与动态探究题型七 中位线与路径问题方法技巧中位线的动态图求值，先分别选取运动点的起点，中间某一特殊点，终止点这些特殊位置对应的点，然后由特殊到一般猜想估计运动点的情形，最后验证.【例1】如图，在△ABC 中，90B ︒∠=，60BAC ︒∠=，1AB =，若点E 为BC 上一动点，以AE 为边在AE 右侧作等边△AEF ，连接CF ，点G 为线段CF 的中点，若点E 从点B 出发，沿着BC 方向运动到点C ，则在此过程中，点G 运动的路径长为_________.【例2】如图，()2,0A ，()0,2B ，点P 在线段OA 上运动，BP ⊥PM ，BP PM =，C 为x轴负半轴上一定点，连接CM ，N 为CM 的中点，当点P 从点O 运动至点A 时，点N 运动的路径长为________.针对练习3 .1.如图，已知AB =10，P 是线段AB 上的动点，分别以AP ,PB 为边在线段AB 的同侧作等边△ACP 和等边△PDB ，连接CD,设CD的中点为G,当点P从点A运动到点B时,求点G移动的路径长。

中位线与角的关系中位线是指一个三角形内连接三个顶点与各边中点的线段。

在三角形中，中位线有着重要的几何性质，其中之一是与三角形的内角有着特殊的关系。

一、中位线的定义对于一个三角形ABC，连接顶点A与边BC中点D的线段AD称为三角形ABC的中位线，其中AD为中位线的长度，D为中位线的中点。

二、中位线的性质1. 三角形的三条中位线交于一点对于任意一个三角形ABC，连接顶点A与边BC的中点D，连接顶点B与边AC的中点E，连接顶点C与边AB的中点F，可以证明线段AD、BE和CF三条中位线交于一点G。

这个点G称为三角形ABC的重心，也是三条中位线的交点。

2. 中位线的长度与角在一个三角形中，中位线的长度与三个顶点相应的内角有着特殊的关系：（1）中位线的长度为相应两边长度的一半例如，在三角形ABC中，AD为中位线，AD的长度等于边BC的长度的一半，即AD = BC / 2。

同样地，BE = AC / 2，CF = AB / 2。

（2）中位线与相应两边所夹的角的关系以三角形ABC的边BC为例，AD为中位线，在三角形ABC中，角∠BAD与∠CAD分别为∠BAC的角平分线。

即角∠BAD与角∠CAD的角度相等，且与∠BAC的角度相等。

同样地，以中位线BE和CF为例，可以得到类似的结论。

三、中位线的应用1. 求解三角形的面积由于三角形的三条中位线交于一点，这个点正好是三角形重心。

利用三角形的面积公式S = 1/2 * 底边长度 * 高，可以通过三角形重心到三边的距离来计算三角形的面积。

由于中位线等于相应两边长度的一半，所以可以依靠中位线求解三角形面积的问题。

2. 定位重心知道了一个三角形的三个顶点坐标，可以通过求解三个顶点坐标的中点坐标，得到中位线的交点，从而求解出三角形的重心坐标。

这在几何定位和相关问题的求解中具有重要的应用价值。

总结：中位线是一个三角形内连接顶点与各边中点的线段，具有重要的几何性质。

中位线与三个顶点的内角有着特殊的关系，长度等于相应两边长度的一半，并且与相应的内角角度相等。

三角形的中位线与中心线一、三角形的中位线1.定义：三角形的中位线是从三角形的一个顶点出发，在对面的边上找到中点，然后连接这个中点和顶点的线段。

(1)三角形的中位线平行于第三边。

(2)三角形的中位线等于第三边的一半。

(3)三角形的中位线将对边的夹角平分。

二、三角形的中心线1.定义：三角形的中心线是从三角形的某个顶点出发，延长到对边上的点，使得这个点到三角形其他两个顶点的距离相等。

(1)三角形的中心线将对边的夹角平分。

(2)三角形的中心线将对边的中点连接起来，形成的线段是三角形的中位线。

(3)三角形的三条中心线相交于一点，称为三角形的心。

1.在等边三角形中，中位线和中心线重合，都是三角形的角平分线、中线和高线。

2.在一般三角形中，中位线是中心线的一部分，中心线是延长的中位线。

四、三角形的中位线与中心线在实际应用中的意义1.在建筑设计中，通过测量三角形的中位线和中心线，可以判断建筑物的结构是否稳定。

2.在工程测量中，利用三角形的中位线和中心线可以简化计算，提高测量精度。

3.在解决几何问题时，运用三角形的中位线和中心线可以简化问题，找到解决问题的突破口。

习题及方法：1.习题：在三角形ABC中，D、E、F分别是边AB、BC、AC上的中点，求证：DE平行于BC，且DE等于BC的一半。

答案：根据三角形的中位线性质，D、E分别是边AB、BC的中点，所以DE平行于BC，且DE等于BC的一半。

2.习题：在三角形ABC中，M是边AC上的中点，求证：BM平行于AC。

答案：延长BM到N，使得MN=BM。

由于M是AC的中点，所以AN=NC。

根据等腰三角形的性质，AN平行于BC，且AN=BC。

又因为DE平行于BC，所以DE平行于AN。

又因为DE=BC，所以MN平行于AC，且MN=AC。

根据平行线的性质，BM平行于AC。

3.习题：在等边三角形DEF中，G是边DE的中点，求证：FG平行于DE。

答案：由于DEF是等边三角形，所以DE平行于DF。

三角形中位线在我们学习三角形的众多知识中，三角形中位线是一个非常重要且有趣的概念。

它看似简单，却蕴含着丰富的几何性质和实用价值。

首先，咱们来弄清楚啥是三角形中位线。

三角形中位线，就是连接三角形两边中点的线段。

比如说，在三角形 ABC 中，D 是 AB 的中点，E 是 AC 的中点，那么线段 DE 就是三角形 ABC 的一条中位线。

三角形中位线有几个特别重要的性质。

其中一个关键性质就是：三角形的中位线平行于第三边，并且等于第三边的一半。

这可太有用啦！为啥这么说呢？咱们来想想，如果我们知道了一条中位线的长度，那就能马上算出与之平行的那条边的长度。

反过来，如果我们知道了第三边的长度，也能迅速得出中位线的长度。

比如说，在三角形 ABC 中，DE 是中位线，BC ＝ 10 厘米。

因为中位线等于第三边的一半，所以 DE 的长度就是 5 厘米。

又或者，已知中位线 DE 长 6 厘米，那 BC 的长度就是 12 厘米。

那这个性质是咋证明出来的呢？咱们可以通过构造平行四边形来证明。

连接三角形的一个顶点和中位线的一个端点，比如说连接 CE 。

因为 D 是 AB 的中点，E 是 AC 的中点，所以 AD ＝ BD ，AE ＝ CE 。

这样一来，四边形 BCED 就是一个平行四边形，根据平行四边形的性质，对边平行且相等，就可以得出 DE 平行于 BC 且 DE ＝ 1/2 BC 。

三角形中位线的这些性质在解决很多几何问题中都能派上大用场。

比如在求三角形的边长、角度，或者证明线段之间的关系时，中位线往往能成为解题的关键线索。

咱们来看个实际的例子。

有一个三角形的田地，三边长度分别是 12 米、16 米和 20 米。

现在要在这块田地上修一条平行于最长边的小路，并且这条小路恰好是中位线。

那这条小路的长度是多少呢？因为 20 米是最长边，所以与之平行的中位线连接的是另外两条边的中点。

根据中位线的性质，中位线等于第三边的一半，所以这条中位线的长度就是 10 米。

数学篇数苑纵横三角形中位线的性质是平面几何中的一个重要定理.该定理的结论既包含两线段所在直线的位置关系，又包含两线段之间的数量关系，在解答平面几何问题中有着广泛的应用．在运用三角形中位线的性质解题时，有时需要运用平行关系，有时需要运用倍分关系，可以根据具体情况，按需选用.下面结合例题予以说明.一、三角形中位线的定义和性质三角形中位线的定义：连接三角形两边中点的线段叫做三角形的中位线.三角形有三条边，所以三角形的中位线应该有三条，如图1所示：如果点D 、E 、F 分别是AB 、BC 、CA 的中点，那么线段DE 、EF 、FD 都是三角形的中位线.三角形中位线的性质:三角形的中位线平行于第三边，并且等于第三边的一半.由此不难得到三角形的中位线与第三边的关系：(1)位置关系：三角形的中位线与第三边互相平行，如在图1中，有DF ∥BC ；(2)数量关系：三角形的中位线等于第三边的一半，如在图1中，有DF =12BC.图1二、三角形中位线的性质在解题中的应用中位线的性质在解三角形问题时通常有以下三种用途：第一种是用于三角形的线段长度的计算；第二种是证明线段间的位置关系或由位置关系得出角之间的关系；第三种是求解三角形内线段间的和、差、倍分关系．1.利用三角形中位线的性质证明角相等由于三角形的中位线与三角形第三边之间存在平行的位置关系，因此，在证明两个角相等的时候，就可以借助或构造三角形的中位线，利用两直线平行，同位角及内错角相等来证明.这样既快捷，又简便.例1如图2，四边形ABCD 中，AB =CD ，点E ，F 分别是AD ，BC 的中点，GH ⊥EF 交于点P .延长BA ，FE 相交于点Q ，延长CD 交FE 的延长线于点K ，求证：∠AGH =∠DHG．图2图3分析：如图，连接BD ，作BD 的中点M ，连接EM 、FM ．利用三角形中位线定理证得△MEF 是等腰三角形，则∠EMP =∠FMP ．利用三角形中位线定理、平行线的性质推知∠Q =∠CKF ，由等量代换，证得∠AGH =∠DHG ．证明：如图3，连接BD ，作BD 的中点M ，三角形中位线的性质及其应用探析江西九江卢明23数学篇数苑纵横连接EM 、FM ，∵点E 是AD 的中点，∴ME 是△ADG 的中位线，∴ME ∥AB ，ME ＝12AB ，∴∠AGH ＝∠EMP ，同理可证：MF ∥DC ，MF ＝12DC ，∵AB ＝CD ，∴ME ＝MF ，∴∠MFE ＝∠MEF ，∵∠MFE ＝∠CKF ，∠MEF ＝∠Q ，∴∠Q ＝∠CKF ，∵GH ⊥EF ，∴∠QPG ＝∠KPH ＝90°，∴∠Q +∠AGH ＝90°，∠CKF +∠DHG ＝90°，∴∠AGH ＝∠DHG ．2.利用三角形中位线的性质求线段的长度三角形中位线的长度等于第三边长度的一半.利用好这个性质，可以为我们求解两线段的数量关系提供一个重要的依据.所以当题目中遇到三角形一边的中点，所求的问题涉及求线段的长度时，常将三角形中位线的性质和三角形其他知识结合起来.例2如图4，△ABC 中，M 是BC 的中点，AD 是∠A 的平分线，BD ⊥AD 于D ，AB =12，AC =18，求DM的长．例4图5分析：由于DM 无法直接求出，因此可通过构建三角形来得出与DM 相关联的线段，延长BD 交AC 于E ．AD 是∠BAC 的平分线，那么∠BAD ＝∠CAD ，AD ⊥BE ，又有一条公共边，所以△ABD 和△ADE 全等.那么AB ＝AE ，BD ＝DE ，又有BM ＝MC ，所以DM 是三角形BCE 的中位线，那么DM ＝12CE ，又因为CE ＝AC -AE ＝AC -AB ＝6，因此DM ＝3．解：延长BD 交AC 于E ，如图5，∵BD ⊥AD ，∴∠ADB ＝∠ADE ＝90°，∵AD 是∠A 的平分线，∴∠BAD ＝∠EAD ，在△ABD 与△AED 中ìíîïï∠BAD =∠EAD ,AD =AD ,∠ADB =∠ADE ,∴△ABD ≌△AED （ASA ），∴BD ＝ED ，AE ＝AB ＝12，∴EC ＝AC -AE ＝18-12＝6，∵M 是BC 的中点，∴DM ＝12EC ＝12×6=3．3.利用三角形中位线的性质证明线段的倍分关系三角形的中位线不仅体现了线段之间的位置关系，也体现了线段之间的数量关系．在证明线段的和差倍分等问题中，最重要的是找到线段之间的数量关系，而很多题目是难以直接进行数量转换的，因此需作出正确的辅助线，找出图形中形状、位置或者数量上的联系，借助中间量，将所求线段之间的间接关系转化为直接关系，最终求得答案．例5已知，如图6，在△ABC 中AB =AC ，延长AB 到D ，使BD =AB ，E 为AB 的中点，求证：CD =2CE .图6分析：这是证明线段的倍半问题，证明一24数学篇数苑纵横条线段等于另一条线段的二倍或一半时，常常是先找出短线段二倍长的线段，或者取长线段的一半，设法把线段的倍半问题转化为证明线段相等的问题.这就是通常所说的“加倍”“折半”的方法.方法1：找出CD 的一半，然后证明CD 的一半和CE 相等，取CD 中点F ，证CF =CE .证明：取CD 的中点F ，连接BF ，如图7.图7∴CD =2CF ，∵AB =BD ，∴BF 是△ADC 的一条中位线，BF ∥AC ，BF =12AC ，∴∠2=∠ACB ，∵AB =AC ,∴∠1=∠ACB ，∠1=∠2，∴E 是AB 中点，BE =12AC ，∵BF =12AC ，且AB =AC ，∴BE =BF .在△BCE 和△BCF 中，ìíîïïBE =BF ,∠1=∠2,BC =BC ,∴△BCE ≌△BCF (SAS)，∴CE =CF ，∵CD =CF ，CD =2CF ，∴CD =2CE .方法2：找出CE 的2倍，然后证明CE 的2倍和CD 相等，因此，要延长CE 到F ,使EF =CE ，证CF =CD .证明：延长CE 至F ,使EF =CE ，连接FB ，如图8.图8∴CF =2CE ，∠1=∠2，∵E 为AB 中点，∴AE =BE ，在△AEC 和△BEF 中ìíîïïCE =EF ,∠1=∠2,AE =BE ,∴△AEC ≌△BEF (SAS),∴AC =BF ，∠3=∠F ，∴AC ∥BF ，∠FBC +∠ACB =180°，∵∠CBD +∠ABC =180°，又∵AB =AC ，∴∠ABC =∠ACB ，∴∠FBC =∠DBC ，∵AC =AB ，AB =BC ，AC =BF ，∴BF =BD .在△CBF 和△CBD 中，ìíîïïCB =CB ,∠FBC =∠DBC ,BF =BD ,∴△CBF ≌△CBD (SAS)，∴CD =CF ，CF =2CE ，∴CD =2CE .由以上几例不难看出，当题目有中点这一条件时，应设法寻找另一个“中点”，以构造三角形的中位线，然后利用中位线的性质解题.这是一种常用的解题技巧.25。

三角形中位线的概念1. 概念定义在平面几何中，三角形的中位线是连接三角形的一个顶点与对边中点的线段。

每个顶点都有一条中位线与之对应，因此三角形共有三条中位线。

2. 中位线的构造方法以三角形ABC为例，构造方法如下： - 连接顶点A和边BC的中点M，得到AM； - 连接顶点B和边AC的中点N，得到BN； - 连接顶点C和边AB的中点P，得到CP。

3. 关键概念3.1 中位线长度可以证明，在任意三角形ABC中，每条中位线的长度等于对边长度的一半。

即AM= BM = CN = AN = CP = BP = 0.5 * AB = 0.5 * AC = 0.5 * BC。

这是由于在等腰三角形和全等三角形中，对边长度相等。

3.2 中位线交汇于同一点对于任意一个三角形ABC，它的三条中位线AM、BN、CP交于一点G，这个交点G被称为重心。

重心是指一个物体或几何图形在重力作用下保持平衡时所处的位置。

3.3 重心的性质重心G具有以下性质： - 重心到三角形各顶点的距离满足：AG : GM = BG : GN = CG : GP = 2 : 1。

即重心到顶点的距离是中位线长度的两倍。

- 重心将每条中位线分成两段，其中一段的长度是另一段的两倍。

- 重心所在的中位线被分成1:2的比例。

4. 中位线的重要性4.1 几何性质中位线具有以下几何性质： - 中位线平行于底边。

由于中位线连接对边中点，而对边平行于底边，因此中位线也平行于底边。

- 中位线等于底边长度一半。

根据定义可知，中位线连接顶点和对边中点，长度等于对边长度一半。

- 中位线交汇于同一点。

三条中位线交于重心G。

4.2 划分三角形通过连接三角形顶点和对边的中点，可以将三角形划分为六个小三角形和一个大三角形。

这种划分方式有助于研究和计算各个小三角形的性质。

4.3 计算面积利用中位线可以方便地计算三角形的面积。

根据性质，重心将每条中位线分成两段，其中一段的长度是另一段的两倍。

三角中位线定理的应用中位线的性质：平行与第三边，并且等于第三边的一半。

三角形有三条中位线，最终将三角形分成四个全等三角形。

能够造出三个平行四边形，其中平行四边形的周长恰好等于三角形长两边之和。

中位线与第三边上的中线互相平分。

利用的是平行四边形的对角线互相平分。

三角形的中位线围成的三角形跟原三角形形状一样，周长是原来的一半，面积是原来的1/4，中位线的应用测距，中位线的定义，经过三角形两边中点的连线。

中线指的是一顶点与对边中点的连线。

中线性质，中线将三角形分成面积相等的两部分（等底同高面积相等）知识要点：三角形的中位线平行于三角形第三边，并且等于第三边的一半.1.三角形三条中位线围成的三角形与原三角形在某些数量上的关系（形状一样/相似）⑴.周长关系三角形的三条中位线围成的三角形的周长是原三角形的周长的一半.⑵.三角形的三条中位线围成的三角形的面积是原三角形的面积的41.2.中点四边顺次连结四边形四边中点所构成的四边形，我们把它简称为中点四边形.中点四边形的特殊性主要是看原四边形的对角线的特征，分为下面几种情况：任意四边形的中点四边形是平行四边形。

对角线相等的四边形的中点四边形是菱形；对角线垂直的四边形的中点四边形的是矩形；对角线既相等又垂直的四边形的中点四边形是正方形。

中位线与第三边上的中线互相平分。

利用的是平行四边形的对角线互相平分。

1、已知△ABC 的周长为1，连结△ABC 的三边中点构成第二个三角形， 再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是（）2、如图所示，已知四边形ABCD ，R ，P 分别是DC ，BC 上的点，E ，F 分别是AP ，RP 的中点，当点P 在BC 上从点B 向点C 移动而点R 不动时，那么下列结论成立的是（）A ．线段EF 的长逐渐增大B ．线段EF 的长逐渐减少C ．线段EF 的长不变D ．线段EF 的长不能确定3、如图ABC 中，EF 为三角形的中位线，AD 是BC 边上的中点，点O 为EF 和AD 的交点.求证：EF 和AD 互相平分.4、如图，在四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．四边形EGFH 是平行四边形吗？请证明你的结论．5、如图，在四边形ABCD 中，E 、F 、G 、H 分别是AB 、CD 、AC 、BD 的中点．四边形EGFH 是平行四边形吗？请证明你的结论．6、如图，在四边形ABCD中，点P是对角线BD的中点，点E，F分别是AB，CD的中点，AD＝BC，（1）∠PEF＝35°，则∠PFE的度数．（2）∠CBD=20°，∠ADB=100°，则∠PFE的度数．7、已知：如图，在四边形ABCD中，对角线AC、BD相交于O，且AC＝BD，E、F分别是AB、CD的中点，E、F分别交BD、AC于点G、H．求证：（1）OG＝OH．（2）∠ONM＝∠OMN.8、如图，在四边形ABCD中，已知AB＝CD，点E，F分别为AD，BC的中点，延长BA，CD，分别交射线FE于P，Q两点．求证：∠P＝∠CQF..９、点M为△ABC的边BC的中点，AB＝12，AC＝18，BD⊥AD于点D，连DM.(1)如图1，若AD为∠BAC的平分线，则MD＝；（1）DM∥AC；DM＝21（AC﹣AB）．(2)如图2，若AD为∠BAC的外角平分线，则MD＝．．【变式】如图，在Rt△ABC中，∠ACB＝90°，D为△ABC外一点，使∠DAC＝∠BAC，E为BD的中点．若∠ABC＝60°，则∠ACE＝.１０、如图，△ABC的中线BD、CE相交于点O，F、G分别是OB、OC的中点，线段EF与DG之间有什么关系？为什么？１１、如图，点E F G H、、、分别是CD BC AB DA、、、的中点.求证：四边形EFGH是平行四边形１２、如图，已知在□ABCD中，EF∥BC,分别交AB CD、于E F、两点，DE AF、交于M,CE BF、交于N．求证:1MN AB2=.１３、已知：E为ABCD的边DC的延长线上的一点，且CE DC=,连结AE分别交BC BD、于F G、，对角线AC BD、交于点O.求证：AB2OF=。

三角形的中位线和垂直平分线在几何学中，三角形是最基本的形状之一。

除了三个顶点和三条边外，三角形还有一些特殊的线段，如中位线和垂直平分线。

本文将详细探讨三角形的中位线和垂直平分线，以及它们在三角形性质和应用中的重要作用。

一、中位线中位线是连接三角形两个顶点与对边中点的线段。

三角形的每个顶点都有一条中位线，因此一个三角形有三条中位线。

我们可以将三条中位线交于一点，该点被称为三角形的重心。

重心是三条中位线交点的几何中心，也是三角形的一个重要性质。

三角形的重心有一些特殊的性质。

首先，重心将每条中位线分成两段，其中一段是另一段的两倍。

其次，重心到每个顶点的距离相等，即重心到三个顶点的距离相等。

此外，重心到任意一条边的距离为该边上相应中位线的1/3。

这些性质使得重心成为一些几何问题的关键。

中位线在三角形的平衡性质中也起着重要作用。

当一个三角形悬挂在某一点时，这个点就是重心。

这种平衡性质应用广泛，特别是在工程学和建筑学中。

例如，当设计桥梁或悬挂物体时，需要考虑三角形的平衡性，以确保结构的稳定性。

二、垂直平分线垂直平分线是指将三角形的一条边垂直平分，并延长至另外两条边的线段。

每个三角形的三条边都有一条垂直平分线，因此一个三角形有三条垂直平分线。

三条垂直平分线交于一点，该点被称为三角形的外心。

三角形的外心有一些特殊的性质。

首先，外心到每个顶点的距离相等，即外心到三个顶点的距离相等。

其次，外心到每条边的距离相等，即外心到三条边的距离相等。

此外，外心位于三角形的外接圆上，外接圆是通过三个顶点构造的圆。

垂直平分线和外心在三角形的外接圆性质中起到关键作用。

外接圆的圆心就是三角形的外心，这个点对于许多几何问题和证明是非常重要的。

外心与外接圆的关系使得它们在三角形的求解、证明和构造中发挥着重要作用。

三、三角形的性质和应用中位线和垂直平分线不仅仅是三角形的几何性质，它们还有很多应用。

例如，在计算三角形的面积时，可以利用中位线将三角形划分为三个小三角形，从而简化计算。