rlc串联电路
- 格式:ppt
- 大小:1.65 MB
- 文档页数:3









rlc串联电路方程RLC串联电路是由电阻(R)、电感(L)和电容(C)按照一定的顺序连接在一起形成的电路。
在RLC串联电路中,电感与电容并联,而电阻与电感和电容串联。
在RLC串联电路中,电阻器对电流起阻碍作用,电感器对变化电流起滞后作用,并且当电压或电流在电感器中发生变化时,电流的变化率与电压成正比;电容器对电压起阻碍作用,对变化电压起滞后作用,并且当电压或电流在电容器中发生变化时,电压的变化率与电流成正比。
在RLC串联电路中,可以通过对电路进行分析和求解得到由电压和电流的方程,即RLC串联电路方程。
下面我们对RLC串联电路方程进行推导。
设电流为i(t),电压为v(t),通过电阻器的电压为vR(t),通过电感器的电压为vL(t),通过电容器的电压为vC(t)。
根据基尔霍夫电压定律,电源电压等于电阻器电压、电感器电压和电容器电压之和,即v(t) = vR(t) + vL(t) + vC(t)。
然后,我们分别对电阻器、电感器和电容器进行方程的推导。
1.电阻器方程根据欧姆定律,电阻器的电压与电流成正比,即vR(t) = Ri(t)。
2.电感器方程根据电感器的特性,电流的变化率与电感器的电压成正比,即vL(t) = L(di(t)/dt)。
3.电容器方程根据电容器的特性,电压的变化率与电容器的电流成正比,即vC(t) = (1/C)∫i(t)dt。
在上述三个方程中,分别代入电源电压v(t)的表达式,即可得到RLC串联电路方程。
RLC串联电路的方程为:L(di(t)/dt) + Ri(t) + (1/C)∫i(t)dt = v(t)通过对RLC串联电路方程进行求解,我们可以得到电路中电流和电压随时间的变化规律。
在实际应用中,RLC串联电路方程可以用来分析电路中的电流、电压的变化及相位关系,了解电路的稳定性和工作性能。
同时,RLC串联电路方程也为我们提供了一种设计电路的方法,以满足特定的电流、电压要求。
总结起来,RLC串联电路方程是通过对电阻器、电感器和电容器各自的特性进行分析和推导得到的。

rlc串联谐振电路
RLC串联电路是电子技术中一种重要的线性电路,也叫RLC谐振电路,由电阻R、电感L、电容C三个元件串联而成。
它是一种非线性电子电路,能够形成谐振现象。
RLC串联电路可以用来检测、滤波及放大特定频率的输入信号,工作原理为当输入信号的频率接近RLC电路自身振荡频率时,RLC电路自身发生振荡,造成输入信号强度的增大,从而形成放大效果。
另外,它还可以用于滤波,可以在振荡反馈强度较小的振荡波的频率下,阻挡其他频率的信号,这样,RLC串联电路可用于滤波或波形分离。
RLC串联电路的制作并不复杂,其基本构成为一个非线性的谐振电路,由三个元件构成,只要把电阻、电感和电容按照一定的顺序串联,即可在一定频率段内形成振荡。
RLC串联电路的特点十分显著,可以提高放大器的稳定性和增益,以及抑制噪声,同时还能够抑制高谐振频率的输入信号,以实现信号的检测和滤波。
RLC串联谐振电路也可用于检测和放大一定频率段内的输入信号,具有很高的应用价值。
RLC串联电路在工程实践中有着非常广泛的应用,特别是在调制电路、振荡电路、叫声电路和转换电路中普遍应用,它已经广泛应用于电视、电台和电脑中。
总之,RLC串联谐振电路是一种重要的电子电路,它可以用来放大、检测和滤波某一定频率段的信号,广泛应用于许多工程实践中,具有重要的理论及应用价值。
究竟什么是RLC串联谐振电路
什么是RLC?
相信有过电子基础的人应该都知道什么是RLC,R是电阻、L是电感、C是电容,RLC电路是指在由电阻、电感和电容组成的电路,一般分为两种结构:串联结构和并联结构,RLC的原理应用于电缆串联谐振试验装置,如下图:
RLC串联电路中R、L、C的关系
在电源电压U的作用下,流过电路的电流为I,电路有以下特点。
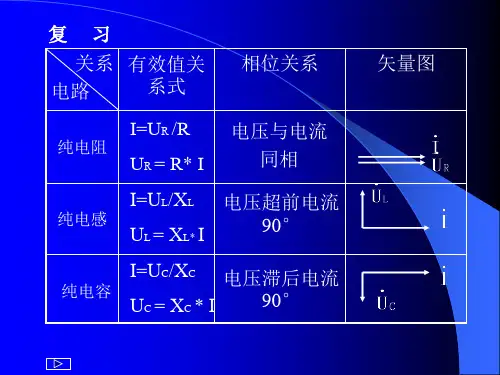
(a)在电阻R两端产生的电压降为UR=IR,其相位与电流相同。
(b)在电感L两端产生的电压降为UL=IXL,在相位上比电流超前90°。
(c)在电容C两端产生的电压降为UC = IXC,在相位上比电流滞后90。
(d)电路的总电压等于各元件上的电压降之和,但因R、L、C的相位不同,此时不能用代数和,而要用矢量和,即U=UR+UL+UC。
RLC串联谐振电路的特点
(1)电路的阻抗最小并呈电阻性;
(2)电路中大电流最大;
(3)容抗等于感抗(XL=XC)时,串联谐振可在电容和电感两端产生高压,即满足谐振条件。
最后,如果您还有更好的建言,可与我们联系,。