知识点一RLC串联电路的电压关系
- 格式:ppt
- 大小:1007.00 KB
- 文档页数:8

8.3 RL和RC串联电路考纲要求:熟练掌握RLC串联正弦交流电路中电流和电压的关系及功率的计算。
教学目的要求:掌握RL、RC串联电路中电压与电流的大小、相位和功率的关系。
教学重点:掌握RL、RC串联电路中电压与电流的大小、相位和功率的关系。
教学难点:掌握RL、RC串联电路中电压与电流的相位关系。
课时安排:3节课型:复习教学过程:【知识点回顾】一、RL串联电路1、电压与电流的相位关系相量图:超前Φ角, <Φ< ,电路呈性。
2、电压与电流的大小关系(1)电压三角形由电压三角形可得:U= Φ= = (2)阻抗三角形由阻抗三角形可得:Z= Φ= =3、相量关系•I=4、功率关系:(1)有功功率P= = (2)无功功率Q= = (3)视在功率S= =功率三角形:5、功率因数 cosΦ= = =二、RC串联电路1、电压与电流的相位关系相量图:超前Φ角, <Φ< ,电路呈性。
2、电压与电流的大小关系(1)电压三角形由电压三角形可得:U= Φ= =(2)阻抗三角形由阻抗三角形可得:Z= Φ= = 3、相量关系•I=4、功率关系:(1)有功功率P= = (2)无功功率Q= = (3)视在功率S= =功率三角形:5、功率因数 cosΦ= = =6、应用(1)超前网络 (2)滞后网络【课前练习】一、判断题1、R-L 串联电路分析相位关系时,I 与U R 相位相同,I 比U L 相位滞后90 O ,故不能直接相加。
( )2、一个实际的电感线圈可以看成是一个RL 的串联电路。
( )3、RL 串联电路中的电压在相位上超前电流90O 。
( )二、选择题1、RL 串联电路中,电阻、电感的电压均为100 V ,则总电压为 ( )A. 200VB.141.4 VC.100VD.150 V2、在RL 串联电路中正确的表达式是 ( ) A. I=L X R U + B .i=22L X R u + C.I=22LX R U + D.i=u /|Z| 3、在日光灯等效电路如图所示,由交流电源供电,如果交流电的频率增大时,则镇流器(线圈)的 ( )A.电感增大 B .电感减小 C .感抗增大 D .感抗减小4、两纯电容串联,Xc1 =4Ω,Xc2 =3Ω.下列结论正确的是( )A .总电容为7FB .总容抗为7ΩC .总容抗为5ΩD .总容抗随交流电频率增大而增大三、填空题1、如图所示,已知u=28.28sin(ωt+45 O )V ,R=4Ω,XL=3Ω,则各电流表,电压表的读数为:A 的读数为: V1的读数为:V2的读数为: V 的读数为:2、当交流电源的频率增加时,R-C 串联电路上端电压和电流的相位差将 。

知识点一RLC串联电路的电压关系RLC串联电路是由电阻(R)、电感(L)和电容(C)依次串联而成的电路。
在RLC串联电路中,电压的关系可以通过分析电流关系得出,并利用欧姆定律和基尔霍夫定律进行推导。
首先,我们来分析电阻对电压的影响。
根据欧姆定律,电阻上的电压与电流成正比,电压等于电流乘以电阻的阻值。
因此,电阻上的电压可以表示为UR=IR*R,其中UR表示电阻上的电压,IR表示电流,R表示电阻的阻值。
接下来,我们来分析电感对电压的影响。
电感是一个具有自感的元件,当电流通过电感时,会在电感上产生自感电压。
自感电压的大小与电感的大小、电流的变化率有关。
利用基尔霍夫电压定律,可以得出电感上的电压表达式为UL=XL*IL,其中UL表示电感上的电压,XL表示电感的自感抗性,IL表示电流。
最后,我们来分析电容对电压的影响。
电容是一个具有电容量的元件,当电容处于充电或放电状态时,会在电容两端产生电压。
电容的电压与电容两端的电荷量和电容量有关。
利用基尔霍夫电压定律,可以得出电容两端的电压表达式为UC = 1/C∫id t,其中UC表示电容两端的电压,C表示电容的电容量,∫idt表示电流对时间的积分。
综上所述,RLC串联电路的总电压可以表示为UT=UR+UL+UC。
根据基尔霍夫电压定律,UT等于电阻上的电压UR、电感上的电压UL和电容两端的电压UC之和。
在以时间为变量的情况下,RLC串联电路的总电压可以用微分方程来描述。
根据欧姆定律和基尔霍夫电压定律,微分方程可以表示为Ld²i/dt² + Rd(di/dt) + 1/C∫idt = V(t),其中L表示电感的电感量,R表示电阻的阻值,C表示电容的电容量,i表示电流,V(t)表示外加电源的电压。
通过求解这个微分方程,可以得出RLC串联电路中电压和电流的关系。
但是由于求解过程比较复杂,具体的推导过程超过了1200字的限制。
总结起来,RLC串联电路的电压关系可以通过分析电流关系,并利用欧姆定律和基尔霍夫电压定律来得出。


课时教案科目电工电子技术与技能第 1 周第课时 2020 年 2 月日课题复习3.3RLC串联电路授课班级教学目标知识与技能目标1、了解RLC串联电路。
2、掌握RL、RLC串联电路电压和阻抗的计算。
3、掌握RL,RLC串联电路功率的计算。
4、掌握RLC串联谐振电路产生的条件4过程与方法目标1.培养学生的理解能力。
2.培养学生解决实际问题的能力。
情感态度与价值观培养学生温故知新的学习习惯,学习适应网络教学模式,培养学生勇于面对挫折的精神重点RL,RLC串联电路的电压和电流的关系以及电路中的功率问题。
难点理解掌握RL,RLC串联电路的功率的计算。
教学方法网络直播,讲授,练习课型复习课教具资源笔记本电脑,手机,腾讯课堂,问卷星,云班课教学实施(仿此格式填写)内容安排时间安排教师活动学生活动设计意图复习导入5min ◆利用腾讯课堂播放PPT回顾总结纯电阻、纯电感和纯电容电路。
◆利用大学慕课播放RLC串联电路的授课视频。
【设备】腾讯课堂通过手机或者是电脑登入腾讯课堂熟悉上课软件一、RLC 串联电路的电压关系由电阻、电感、电容相串联构成的电路称为 RLC 串联电路。
各电压之间的大小关系为:22)(C L R U U U U -+=ZI X X R I U U U U C L C L R =-+=-+=2222)()(R-L-C 串联电路的欧姆定律表达式ZU I =2222)(X R X X R I UZ C L +=-+==阻抗:|Z |称为电路的阻抗,单位:欧姆 电抗:X = XL - XC 叫做电抗二、 R-L-C 串联电路的电压与电流的相位关系阻抗角:Φ 叫做阻抗角,体现了总电压与总电流之间的相位关系R X X R XC L arctan arctan-==ϕ(1)当C L X X >时,X > 0,0>ϕ,电路呈感性。
(2)当C L X X <时,X < 0,0<ϕ,电路呈容性。


文章标题:深度解析rlc串联电路实验中总电压与分电压之间的关系在电路学的学习中,rlc串联电路实验是一个重要的实验课程,通过该实验可以深入理解总电压与分电压之间的关系。
本文将从理论基础、实验操作和数据分析三个方面来全面解析rlc串联电路实验中总电压与分电压之间的关系。
一、理论基础rlc串联电路是由电阻R、电感L和电容C组成的串联电路,其理论模型如下:总电压U=√(UR^2+UL^2+UC^2)其中UR、UL和UC分别代表电阻、电感和电容上的电压。
在交流电路中,电压的大小和相位会随着频率的变化而变化,这就导致了总电压与分电压之间的关系并不是简单的线性关系。
二、实验操作在进行rlc串联电路实验时,首先需要搭建好电路实验装置,并连接好电源和示波器。
通过改变频率和电阻、电感、电容的数值组合,可以获取不同条件下的总电压和各个元件上的分电压。
在实验过程中需要严格控制变量,保证实验数据的准确性和可靠性。
三、数据分析通过实验测量得到的数据,可以绘制出频率与总电压、分电压的关系曲线。
从曲线上可以观察到在不同频率下总电压和分电压的变化规律。
在某些特定频率下,总电压和分电压之间存在共振现象,这时总电压将达到最大值,而分电压之间也会存在一定的相位差。
四、个人观点和理解通过本次实验,我深刻认识到总电压与分电压之间的关系并不是简单的线性关系,而是受到频率、电阻、电感和电容等元件的影响。
在实际工程应用中,了解和掌握好rlc串联电路的特性对于电路设计和故障分析至关重要,因此需要深入学习和理解这一关系。
总结回顾通过以上的理论分析和实验操作,我们深入探讨了rlc串联电路实验中总电压与分电压之间的关系。
通过实验数据的分析,我们发现在不同的频率下,总电压和分电压之间存在着复杂的变化规律,需要通过实验来深入研究和理解。
在未来的学习和工作中,我们需要进一步深化对rlc串联电路的理解,将理论知识应用到实际中,不断提升自己的电路分析和设计能力。



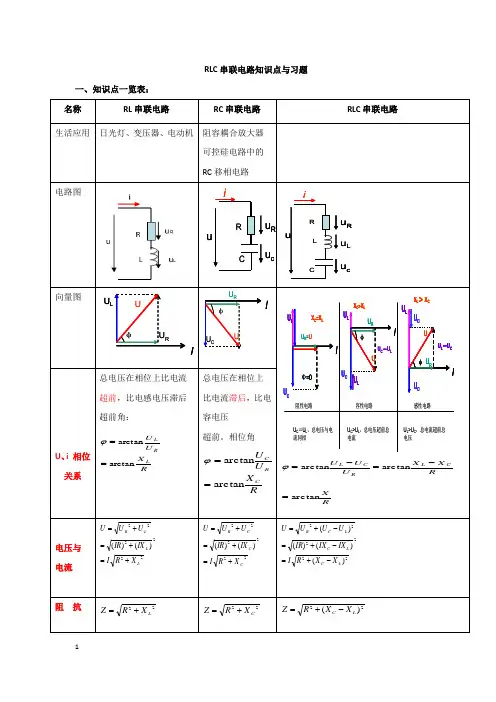
RLC串联电路知识点与习题一、知识点一览表:iuuRuL LRuc C1二、习题:(一)填空题:1. RL串联电路中,()、()和()构成电压三角形。
(用符号表示)2. RL串联电路中,()、()和()构成阻抗三角形。
(用符号表示)3. RL串联电路中,()、()和()构成功率三角形。
(用符号表示)4.在多个元件组成的交流电路中,把总电压和总电流的乘积称做视在功率,用符号。
表示,视在功率的单位符号为。
5. RL串联电路中,既有耗能元件_,又有储能元件,为了反映功率利用率,在工程上,将_功率与_功率的比值称做功率因数,用符号_表示。
6.在RC串联电路中,阻抗三角形由_、_和_,组成,电压三角形由_、_和_组成,功率三角形由_、_和_组成。
7.在RC串联电路中,有功功率_无功功率Q=_,视在功率_.8.在RC串联电路中,已知电阻R= 40Ω,容抗Xc =30Ω,则电路阻抗Z=____,总电压___,电流_ _,如果电压u= 200√2sin (314 t+30°)(V),则电流I=_,电阻上的电压UR= __,电容上的电压UC=_ _,电流i=_ _ ______.9.在RLC串联电路中,已知电阻R=8Ω,感抗XL= 10Ω,容抗Xc=4Ω,则总阻抗z=_,,总电压_电流_,如果电压u= 220√2sin(314t+70°)(V),则电流i=_ A,电阻上的电压UR=_V,电感上的电压UL=_, 电容上的电压Uc=_。
10、把一个RLC串联电路接到u= 200√2sinl 000 t(V) 的交流电源上,已知R=6Ω,L=10mH,C= 500μ,则电路的总阻抗Z=_ __ Ω.电流I=_ A.电路呈_性。
11、如图所示,V1读数为3V,V2读数为4V,则V读二、选择题1.RL串联电路中,下列关系式正确的是( )。
A. Z=R+LB. Z=R+XL C、Z2=R2+XL2D无法判断2.在RL串联电路中,总电压与分电压的关系是()。
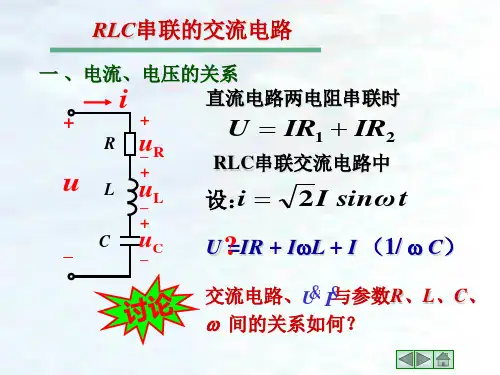
21IRIR U +=交流电路、与参数R 、L 、C 、ω间的关系如何?UI 一、电流、电压的关系U =IR + I ωL + I (1/ ωC )?直流电路两电阻串联时RLC 串联的交流电路设:tωsin I i 2=RLC 串联交流电路中R L CR u +_Lu +_Cu +_u+_itωI i sin 2=设:)90(sin )1(2)90(sin )(2sin 2︒-+︒++=t ωCωI t ωL ωI tωIR u 则1. 瞬时值表达式根据KVL 可得:CL R u u u u ++=⎰++=ti Ct i L iR d 1d d 为同频率正弦量RL CR u +_Lu +_Cu +_u+_i 一、电流、电压的关系RLC 串联的交流电路2. 相量法(1)相量式)[]CLC L X X R IX I X I R I U -+=-++=j )j ()(j CL R U U U U ++=︒∠=0I I设(参考相量))j (CCX I U-= )(j L L X I U =则 R I U R=总电压与总电流的相量关系式RL CR u +_Lu +_Cu +_u+_i()[]CL X X R I U -+=j )C L X X R Z -+=j 令则IU =iu i u IU Z I U I U Z ψψϕψψ-∠=∠=∠∠== Z 的模表示u 、i 的大小关系,辐角(阻抗角)为u 、i 的相位差。
Z 是一个复数,不是相量,上面不能加点。
复阻抗复数形式的欧姆定律注意根据电路参数与电路性质的关系:22)(C L X X R I U Z -+==阻抗模:()C L X X R Z Z -+=∠=j ϕR X X ψψC L i u -=-=arctan ϕ阻抗角:RC ωL ω1arctan -=当X L >X C 时,ϕ>0,u 超前i 电路呈感性当X L < X C 时,ϕ<0,u 滞后i 电路呈容性当X L = X C 时,ϕ=0,u.i 同相电路呈电阻性ϕ由电路参数决定。
串并联电路中电压的规律在电路中,串联和并联是两种常见的连接方式。
当电路中包含多个电阻、电容、电感等元件时,这些元件的连接方式会影响电路中电压的分布。
本文将着重讨论串联和并联电路中电压的规律。
串联电路中电压的规律串联电路是指多个电阻、电容、电感等元件依次连接在一起,形成一个电路。
串联电路中的电压分布规律如下:•在串联电路中,各个元件的电压之和等于电源的电压。
这是因为在串联电路中,电流经过每个元件时,都会产生一定的电压降,而这些电压降的总和等于电源的电压。
•在串联电路中,电压随着电阻值的增加而增加。
这是因为在串联电路中,电流经过每个电阻时都会产生电压降,而电压降正好等于电流乘以电阻值。
并联电路中电压的规律并联电路是指多个电阻、电容、电感等元件并列连接在一起,形成一个电路。
并联电路中的电压分布规律如下:•在并联电路中,各个元件的电压相等。
这是因为在并联电路中,每个元件的两端都连接在同一电位上,因此它们之间不存在电势差。
•在并联电路中,电压不随着电阻值的增加而增加。
这是因为在并联电路中,电阻值越大,电流就越小,而电流减小会导致电压降减小,因此元件两端的电压也随之减小。
串并联电路中电压的规律当电路中既包含串联又包含并联时,它被称为串并联电路。
在串并联电路中,电压的分布规律与串联和并联电路中的规律相结合。
具体来说,当有两个元件并联,再与另一个串联时,可以按照以下规律来计算电压:•并联电路中的所有元件两端电压相等。
•串联电路中的各个元件的电压之和等于上一步骤中得出的并联电路中的电压。
•对于整个电路,电源的电压等于上一步骤中得出的串联电路中的各个元件电压之和。
通过以上规律,可以轻松地计算出串并联电路中各个元件的电压。
需要注意的是,在实际应用中,还需要考虑元件的电阻、电容、电感等实际值以及电源的电压和电流等因素。
起来,串联和并联电路是电路中常见的连接方式,它们的电压分布规律不同。
在串并联电路中,可以按照一定规律来计算各个元件的电压分布,从而为电路的设计和调试提供帮助。
rlc回路的基尔霍夫电压定律1.引言1.1 概述在这篇文章中,我们将探讨基尔霍夫电压定律在RLC回路中的应用。
RLC回路是由电阻、电感和电容元件组成的电路系统,常见于许多电子和电气工程应用中。
基尔霍夫电压定律是描述电路中电压分布的一条重要定律。
根据基尔霍夫电压定律,一个闭合回路中所有电压的代数和等于零。
这意味着在一个电路中,电压的总和必须等于零。
在RLC回路中,电流在电阻、电感和电容之间流动,而基尔霍夫电压定律可以帮助我们理解电压在电路中的分布情况。
通过将基尔霍夫电压定律应用于RLC回路,我们可以推导出电阻、电感和电容之间的电压关系。
了解基尔霍夫电压定律在RLC回路中的应用对于电子和电气工程师非常重要。
它可以帮助我们计算和分析电路中的电压分布,从而更好地理解电路的工作原理。
同时,对于RLC回路的进一步研究和应用,基尔霍夫电压定律也提供了基本的理论基础。
在接下来的文章中,我们将介绍基尔霍夫电压定律的基本概念以及RLC回路的特点,同时探讨基尔霍夫电压定律在RLC回路中的应用。
我们还将总结其在实际电路设计和分析中的重要性,并展望对RLC回路更深入的研究和应用。
希望通过这篇文章的阅读,读者能够更好地理解和应用基尔霍夫电压定律,为电子和电气工程领域的实践工作提供帮助。
1.2 文章结构:本文将按照以下结构进行展开讨论RLC回路的基尔霍夫电压定律的应用和进一步研究。
首先,在引言部分概述了本文所要讨论的话题和背景信息。
随后,给出了文章的目的,即通过对基尔霍夫电压定律在RLC回路中的应用的研究,深入了解并分析其物理原理和实际应用。
在正文部分,我们首先介绍了基尔霍夫电压定律的基本概念,解释了它的真正含义和应用的范围。
通过这个介绍,读者将能够对基尔霍夫电压定律建立起基本的理解和认识。
接下来,我们将重点关注RLC回路的基本概念。
我们将介绍什么是RLC回路,它由哪些元素组成以及各个元素的功能和特点。
了解这些基本概念将为我们对基尔霍夫电压定律在RLC回路中的应用提供必要的背景知识。
RLC串联电路知识点与习题一、知识点一览表:iuuRuL LRuc C1二、习题:(一)填空题:1. RL串联电路中,()、()和()构成电压三角形。
(用符号表示)2. RL串联电路中,()、()和()构成阻抗三角形。
(用符号表示)3. RL串联电路中,()、()和()构成功率三角形。
(用符号表示)4.在多个元件组成的交流电路中,把总电压和总电流的乘积称做视在功率,用符号。
表示,视在功率的单位符号为。
5. RL串联电路中,既有耗能元件_,又有储能元件,为了反映功率利用率,在工程上,将_功率与_功率的比值称做功率因数,用符号_表示。
6.在RC串联电路中,阻抗三角形由_、_和_,组成,电压三角形由_、_和_组成,功率三角形由_、_和_组成。
7.在RC串联电路中,有功功率_无功功率Q=_,视在功率_.8.在RC串联电路中,已知电阻R= 40Ω,容抗Xc =30Ω,则电路阻抗Z=____,总电压___,电流_ _,如果电压u= 200√2sin (314 t+30°)(V),则电流I=_,电阻上的电压UR= __,电容上的电压UC=_ _,电流i=_ _ ______.9.在RLC串联电路中,已知电阻R=8Ω,感抗XL= 10Ω,容抗Xc=4Ω,则总阻抗z=_,,总电压_电流_,如果电压u= 220√2sin(314t+70°)(V),则电流i=_ A,电阻上的电压UR=_V,电感上的电压UL=_, 电容上的电压Uc=_。
10、把一个RLC串联电路接到u= 200√2sinl 000 t(V) 的交流电源上,已知R=6Ω,L=10mH,C= 500μ,则电路的总阻抗Z=_ __ Ω.电流I=_ A.电路呈_性。
11、如图所示,V1读数为3V,V2读数为4V,则V读二、选择题1.RL串联电路中,下列关系式正确的是( )。
A. Z=R+LB. Z=R+XL C、Z2=R2+XL2D无法判断2.在RL串联电路中,总电压与分电压的关系是()。
串联交流电路中总电压与各部分电压的关系在串联交流电路中,总电压与各部分电压之间存在着一定的关系。
要了解它们之间的关系,首先需要了解串联电路的基本原理。
串联电路是将电子元件按照一定的顺序连接起来,电流只有一条路径可走。
在串联电路中,电流通过每个电子元件时会遇到一定的阻抗,这些阻抗会使电压分布在不同的部分电路之间。
在串联交流电路中,电压有一个重要的性质,即总电压等于各部分电压之和。
这是因为在串联电路中,电流是保持不变的,而根据欧姆定律,电压和电流之间的关系是U=IR,其中U代表电压,I代表电流,R代表电阻。
由于电流保持不变,所以总电压等于各部分电压之和。
以一个简单的串联电路为例,假设有一个交流电源和两个电阻器依次连接在电源上。
这个电路可以表示为如下形式:电源----电阻器1----电阻器2。
假设电源的电压为V,电阻器1的阻值为R1,电阻器2的阻值为R2。
那么根据欧姆定律,电阻器1上的电压为U1=IR1,电阻器2上的电压为U2=IR2。
总电压等于电源的电压,即V=U1+U2=IR1+IR2。
从这个简单的例子可以看出,总电压等于各部分电压之和。
当串联电路中有多个电阻器时,只需要将各个电阻器上的电压相加即可得到总电压。
这是因为在串联电路中,电流只有一条路径可走,所以电流通过每个电阻器时所受到的电阻是相同的,因此各个电阻器上的电压之和就等于总电压。
在实际应用中,我们常常会遇到串联电路中的电压分压问题。
电压分压是指在串联电路中,按照一定比例分配电压的过程。
分压器是串联电路中用于实现电压分压的电路。
分压器可以通过调整电阻器的阻值来改变电压分配的比例。
在串联电路中,电压降是指电流通过电阻器时,电压的降低。
电压降等于电阻器的电阻乘以电流,即U=IR。
在串联电路中,电压降的总和等于总电压,即各个电阻器的电压降之和等于总电压。
这也可以作为计算电压分配比例的一个重要依据。
在实际电路中,电压分配的情况会受到许多因素的影响,例如电源的内阻、电路中其他元件的阻抗等。
串联交流电路中总电压与各部分电压的关系在串联交流电路中,总电压是指整个电路中的总电势差,也就是电源提供给电路的电压。
而各部分电压是指电路中各个元件所消耗的电压,也可以理解为电路中各个元件之间的电压差。
我们来看一下串联电路的基本原理。
串联电路是指电路中的元件依次连接在一起,形成一条电流路径。
在串联电路中,电流只有一条路径可以流过,因此电流是恒定的,即各个元件中的电流相等。
根据欧姆定律,电流与电阻成正比,与电压成反比,所以电阻越大,电压越小。
在串联交流电路中,总电压等于各部分电压之和。
这是因为交流电路中的电压是随时间变化的,根据基尔霍夫电压定律,电路中的总电压等于各个元件之间的电压差之和。
具体来说,如果电路中有两个电阻R1和R2,总电压为V0,那么可以得到以下关系式:V0 = V1 + V2。
在实际应用中,我们常常需要根据总电压和各部分电压的关系来进行电路设计和故障排除。
例如,如果我们需要在某个元件上提供固定的电压,我们可以根据总电压和其他元件的电压差来计算出这个元件所需要的电阻值。
又例如,如果我们在电路中测量到了某个元件的电压异常,我们可以通过测量其他元件的电压,来判断是哪个元件出现了问题。
除了上述的基本原理和应用,我们还可以通过一些实例来进一步理解总电压与各部分电压的关系。
例如,假设有一个串联电路,其中包含一个电源和三个电阻。
电源提供的总电压为10V,三个电阻的阻值分别为2Ω、3Ω和5Ω。
根据欧姆定律和串联电路的特性,我们可以计算出各个元件的电流如下:第一个电阻的电流为10V/2Ω=5A;第二个电阻的电流为10V/3Ω≈3.33A;第三个电阻的电流为10V/5Ω=2A。
根据基尔霍夫电压定律,我们可以得到各个元件的电压差如下:第一个电阻的电压差为5A × 2Ω=10V;第二个电阻的电压差为3.33A × 3Ω≈10V;第三个电阻的电压差为2A × 5Ω=10V。
可以看到,总电压等于各部分电压之和,即10V = 10V + 10V。