平行线经典四大模型典型例题及练习

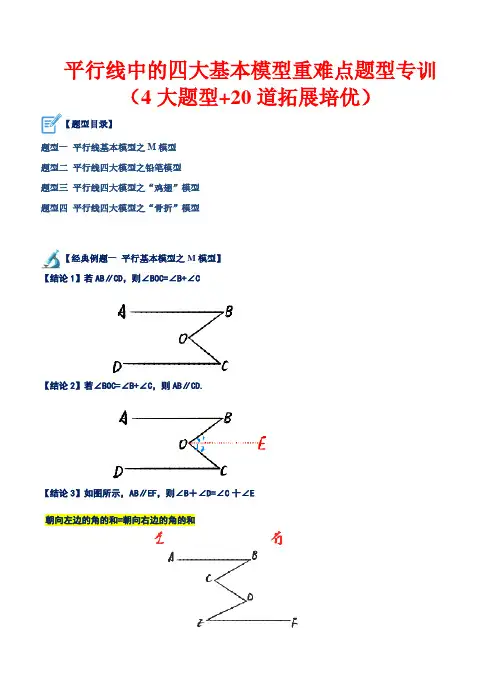
平行线中的四大基本模型重难点题型专训（4大题型+20道拓展培优）【题型目录】题型一平行线基本模型之M模型题型二平行线四大模型之铅笔模型题型三平行线四大模型之“鸡翅”模型题型四平行线四大模型之“骨折”模型【经典例题一平行基本模型之M模型】【结论1】若AB∥CD，则∠B0C=∠B+∠C【结论2】若∠BOC=∠B+∠C，则AB∥CD.【结论3】如图所示，AB∥EF，则∠B＋∠D=∠C十∠E朝向左边的角的和=朝向右边的角的和结论3的模型也称为锯齿模型；锯齿模型的变换解题思路拆分成猪蹄模型和内错角拆分成2个猪蹄模型【例1】（2023春·山东济宁·七年级统考阶段练习）如图所示，如果AB ∥ CD ，则∠α、∠β、∠γ之间的关系为（）A．∠α+∠β+∠γ＝180°B．∠α－∠β+∠γ＝180°C．∠α+∠β－∠γ＝180°D．∠α－∠β－∠γ＝180°[【答案】C【分析】过E作EF∥AB，由平行线的质可得EF∥CD，∠α+∠AEF=180°，∠FED=∠γ，由∠β=∠AEF+∠FED即可得∠α、∠β、∠γ之间的关系．【详解】解：过点E作EF∥AB，∴∠α+∠AEF=180°（两直线平行，同旁内角互补），∵AB∥CD，∴EF∥CD，∴∠FED=∠EDC（两直线平行，内错角相等），∵∠β=∠AEF+∠FED，又∵∠γ=∠EDC，∴∠α+∠β-∠γ=180°，故选：C．【点睛】本题主要考查了平行线的性质，正确作出辅助线是解答此题的关键．【变式训练】 1．（2023上·黑龙江哈尔滨·七年级校考期中）已知：直线AB 与直线CD 内部有一个点P ，连接BP ．(1)如图1，当点E 在直线CD 上，连接PE ，若B PEC P ∠+∠=∠，求证：AB CD ；(2)如图2，当点E 在直线AB 与直线CD 的内部，点H 在直线CD 上，连接EH ，若ABP PEH P EHD ∠+∠=∠+∠，求证：AB CD ；(3)如图3，在（2）的条件下，BG 、EF 分别是ABP ∠、PEH ∠的角平分线，BG 和EF 相交于点G ，EF 和直线AB 相交于点F ，当BP PE ⊥时，若10BFG EHD ∠=∠+︒，36BGE ∠=︒，求EHD ∠的度数．【答案】(1)证明见解析；(2)证明见解析；(3)18︒.【分析】（1）过点P 作PF AB ∥，推出PEC EPF ∠=∠，进而得PF CD ∥，根据平行公理的推论即可得证； （2）分别过点P 和点E 作PF AB ∥，EM CD ，推出PEM FPE ∠=∠，进而得PF EM ∥，根据平行公理的推论即可得证；（3）过点E 作EN AB ∥，同（1）（2）理证明FEH FEN NEH BFE EHD ∠=∠+∠=∠+∠，设EHD α∠=，PBG β∠=，PEG γ∠=，则10BFG α∠=+︒，结合角平分线得2290βγα+=︒+，用含α的式子代替β，γ，代入2290βγα+=︒+即可求解．【详解】（1）证明：如图，过点P 作PF AB ∥，∴B BPF Ð=Ð，∵B PEC BPE BPF EPF ∠+∠=∠=∠+∠，∴PEC EPF ∠=∠，∴PF CD ∥，∴AB CD ∥；（2）证明：如图，分别过点P 和点E 作PF AB ∥，EM CD ，∴ABP BPF ∠=∠，MEH EHD ∠=∠，∵ABP PEH P EHD ∠+∠=∠+∠， 即ABP PEM MEH BPF FPE EHD ∠+∠+∠=∠+∠+∠，∴PEM FPE ∠=∠，∴PF EM ∥，∴EM AB ∥，∴AB CD ∥；（3）如图，过点E 作EN AB ∥，由 (2) 得AB CD ∥，∴EN CD ∥，BFE FEN ∠=∠，NEH EHD ∠=∠，∴FEH FEN NEH BFE EHD ∠=∠+∠=∠+∠，设EHD α∠=，PBG β∠=，PEG γ∠=，则10BFG α∠=+︒，∵ BG 、EF 分别是ABP ∠、PEH ∠的角平分线，∴2ABP β∠=，2PEH γ∠=∵BP PE ⊥，∴90P ∠=︒，由 (2) 得ABP PEH P EHD ∠+∠=∠+∠，∴2290βγα+=︒+，∵FEH FEN NEH BFE EHD ∠=∠+∠=∠+∠，∴10210γααα=+︒+=+︒，∵36BGE ∠=︒，()180FGB BFG FBG ∠=︒−∠+∠，180FGB BGE ∠=︒−∠，∴36BFG FBG BGE ∠+∠=∠=︒，∴1036αβ+︒+=︒，∴26βα=︒−∴()()226221090ααα︒−++︒=︒+，∴18α=︒，即EHD ∠的度数为18︒.【点睛】本题考查平行线的判定与性质，角平分线的定义，三角形的内角和，平角定义等知识，添加辅助线，灵活运用平行公理的推论是解题的关键． 2．（2021下·广东河源·七年级河源市第二中学校考期中）已知直线12l l ∥， A 是l1上的一点，B 是l2上的一点，直线l3和直线l1，l2交于C 和D ，直线CD 上有一点P ．(1)如果P 点在C ，D 之间运动时，问PAC ∠，APB ∠，PBD ∠有怎样的数量关系？请说明理由．(2)若点P 在C ，D 两点的外侧运动时（P 点与C ，D 不重合），试探索PAC ∠，APB ∠，PBD ∠之间的关系又是如何？（请直接写出答案，不需要证明）【答案】(1)PAC PBD APB ∠+∠=∠(2)当点P 在直线1l 上方时，∠−∠=∠PBD PAC APB ；当点P 在直线2l 下方时，∠−∠=∠PAC PBD APB ．【分析】（1）过点P 作1PE l ∥，由“平行于同一条直线的两直线平行”可得出12PE l l ∥∥，再由“两直线平行，内错角相等”得出PAC APE ∠=∠、PBD BPE ∠=∠，再根据角与角的关系即可得出结论；（2）按点P 的两种情况分类讨论：①当点P 在直线1l 上方时；②当点P 在直线2l 下方时，同理（1）可得PAC APE ∠=∠、PBD BPE ∠=∠，再根据角与角的关系即可得出结论．【详解】（1）解：PAC PBD APB ∠+∠=∠．过点P 作1PE l ∥，如图1所示．1PE l ∥，12l l ∥，∴12PE l l ∥∥，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB APE BPE ∠=∠+∠，PAC PBD APB ∴∠+∠=∠．（2）解：结论：当点P 在直线1l 上方时，∠−∠=∠PBD PAC APB ；当点P 在直线2l 下方时，∠−∠=∠PAC PBD APB ．①当点P 在直线1l 上方时，如图2所示．过点P 作1PE l ∥．1PE l ∥，12l l ∥，∴12PE l l ∥∥，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB BPE APE ∠=∠−∠，PBD PAC APB ∴∠−∠=∠．②当点P 在直线2l 下方时，如图3所示．过点P 作1PE l ∥．1PE l ∥，12l l ∥，∴12PE l l ∥∥，PAC APE ∴∠=∠，PBD BPE ∠=∠，APB APE BPE ∠=∠−∠，PAC PBD APB ∴∠−∠=∠．【点睛】本题考查了平行线的性质以及角的计算，解题的关键是根据“两直线平行，内错角相等”找到相等的角．本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质得出相等（或互补）的角是关键．3．（2022下·广东东莞·七年级东莞市光明中学校考期中）阅读下面内容，并解答问题．已知：如图1， AB CD ∥，直线EF 分别交AB ，CD 于点E ，F ．BEF ∠的平分线与DFE ∠的平分线交于点G ．(1)求证：EG FG ⊥；(2)填空，并从下列①、②两题中任选一题说明理由．我选择 题．①在图1的基础上，分别作BEG ∠的平分线与DFG ∠的平分线交于点M ，得到图2，则EMF ∠的度数为 ． ②如图3，AB CD ∥，直线EF 分别交AB ，CD 于点E ，F ．点O 在直线AB ，CD 之间，且在直线EF 右侧，BEO ∠的平分线与DFO ∠的平分线交于点P ，则EOF ∠与EPF ∠满足的数量关系为 ．【答案】(1)见解析(2)①45︒；②结论：2EOF EPF ∠=∠【分析】（1）利用平行线的性质解决问题即可；（2）①利用基本结论EMF BEM MFD ∠=∠+∠求解即可；②利用基本结论EOF BEO DFO ∠=∠+∠，EPF BEP DFP ∠=∠+∠，求解即可．【详解】（1）证明：如图，过G 作GH AB ∥，∥AB CD ，AB GH CD ∴∥∥，BEG EGH DFG FGH ∠∠∠∠∴==，，//AB CD ,180BEF DFE ∴∠+∠=︒， EG 平分BEF ∠，FG 平分DFE ∠，12GEB BEF ∴∠=∠，12GFD DFE ∠=∠，111()90222GEB GFD BEF DFE BEF DFE ∴∠+∠=∠+∠=∠+∠=︒， 90EGF GEB GFD ∴∠=∠+∠=︒，EG FG ∴⊥；（2）解：①如图2中，由题意，90BEG DFG ∠+∠=︒， EM 平分BEG ∠，MF 平分DFG ∠，1()452BEM MFD BEG DFG ∴∠+∠=∠+∠=︒，45EMF BEM MFD ∴∠=∠+∠=︒，故答案为：45︒；②结论：2EOF EPF ∠=∠．理由：如图3中，由题意，EOF BEO DFO ∠=∠+∠，EPF BEP DFP ∠=∠+∠， PE 平分BEO ∠，PF 平分DFO ∠，2BEO BEP ∴∠=∠，2DFO DFP ∠=∠，2EOF EPF ∴∠=∠，故答案为：2EOF EPF ∠=∠．【点睛】本题考查平行线的性质和判定，角平分线的定义，垂直的定义，解题的关键是熟练掌握相关的性质． 4．（2020下·北京西城·七年级北京师大附中校考阶段练习）请阅读小明同学在学习平行线这章知识点时的一段笔记，然后解决问题．小明：老师说在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，今天老师介绍了一个“美味”的模型“猪蹄模型”．即已知：如图1，AB CD ∥，E 为AB 、CD 之间一点，连接AE ，CE 得到AEC ∠．求证：AEC A C ∠=∠+∠小明笔记上写出的证明过程如下:证明：过点E 作EF AB ∥∵1A ∠=∠∵AB CD ∥，EF AB ∥∴EF CD ∥∴2C ∠=∠∴12AEC ∠=∠+∠∴AEC A C ∠=∠+∠请你利用“猪蹄模型”得到的结论或解题方法，完成下面的两个问题．(1)如图，若AB CD ∥，60E ∠=o ，求B C F ∠+∠+∠；(2)如图，AB CD ∥， BE 平分ABG ∠， CF 平分DCG ∠，27G H ∠=∠+，求H ∠．【答案】(1)240(2)51【分析】（1）作EM AB ∥，FN CD ∥，如图，根据平行线的性质得EM AB FN CD ∥∥∥，所以1B ∠=∠，23∠∠=，4180C ∠+∠=，然后利用等量代换计算240B F C ∠+∠+∠=；（2）分别过G 、H 作AB 的平行线MN 和RS ，根据平行线的性质和角平分线的性质可用ABG ∠和DCG ∠分别表示出H ∠和G ∠，从而可找到H ∠和G ∠的关系，结合条件可求得51H ∠=．【详解】（1）作EM AB ∥，FN CD ∥，如图，且AB CD ∥∴EM AB FN CD ∥∥∥∴1B ∠=∠，23∠∠=，4180C ∠+∠=∴1344180B CFE C C BEF C BEF ∠+∠+∠=∠+∠+∠+∠=∠+∠+∠=∠+，∵60BEF ∠=，∴60180240B CFE C ∠+∠+∠=+=；（2）如图，分别过G 、H 作AB 的平行线MN 和RS ，∵BE 平分ABG ∠，CF 平分DCG ∠，∴12ABE ABG ∠=∠，12SHC DCF DCG ∠=∠=∠，∵AB CD ∥∴AB CD RS MN ∥∥∥ ∴12RHB ABE ABG ∠=∠=∠，12SHC DCF DCG ∠=∠=∠，∴180NGB ABG MGC DCG ∠+∠=∠+∠=， ∴()11801802BHC RHB SHC ABG DCG ∠=−∠−∠=−∠+∠， ()()180180180180180BGC NGB MGC ABG DCG ABG DCG ∠=−∠−∠=−−∠−−∠=∠+∠−∴36021801802BGC BHC BHC ∠=−∠−=−∠，∵27BGC BHC ∠=∠+，∴180227BHC BHC −∠=∠+，∴51BHC ∠=．【点睛】本题考查了平行线的性质和判定的应用，能运用平行线的性质和判定进行推理是解此题的关键，注意：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．【经典例题二 平行基本模型之铅笔模型】【结论1】如图所示，AB ∥CD ，则∠B+∠BOC+∠C=360°【结论2】如图所示，∠B+∠BOC+∠C=360°，则AB ∥CD.变异的铅笔头：拐点数n,∠A+...+∠C=180°×（n+1）拐点数：1 拐点数：2 拐点数：n 【例2】（2023下·山东德州·七年级统考期中）如图，AB DE ∥，则下列说法中一定正确的是( )A ．123∠=∠+∠B ．123180∠+∠−∠=︒C ．123270∠+∠+∠=︒D ．12390∠−∠+∠=︒【答案】B 【分析】此题要作辅助线，过点C 作CM AB ∥，则根据平行线的传递性，得CM DE ∥．先利用AB CM ∥，可得1180BCM ∠+∠=︒，即1801BCM ∠=︒−∠，再利用CM DE ∥，可得3DCM ∠=∠，而23BCM ∠−∠=∠，整理可得：123180∠+∠−∠=︒．【详解】解：过点C 作CM AB ∥，AB DE ，CM DE ∴∥，1180BCM ∴∠+∠=︒，3MCD ∠=∠，又BCM BCD MCD ∠=∠−∠，180123∴︒−∠=∠−∠，123180∴∠+∠−∠=︒．故选：B ．【点睛】注意此类题要作的辅助线：构造平行线．根据平行线的性质即可找到三个角之间的关系．【变式训练】 【变式1】（2023下·甘肃白银·七年级校考期中）如图1是一个由齿轮、轴承、托架等元件构成的手动变速箱托架，其主要作用是动力传输．如图2是手动变速箱托架工作时某一时刻的示意图，已知AB CD ，∥CG EF ，150BAG ∠=︒，80AGC ∠=︒，则DEF ∠的度数为（ ）A ．110︒B ．120︒C ．130︒D ．140︒【答案】C 【分析】过点F 作FM CD ∥，则AB CD FM ∥∥，再根据平行线的性质可以求出MFA ∠、EFA Ð，进而可求出EFM ∠，再根据平行线的性质即可求得DEF ∠．【详解】解：如图，过点F 作FM CD ∥，∥AB CD ，AB CD FM ∴∥∥，180DEF EFM ∴∠+∠=︒，180MFA BAG ∠+∠=︒，180********MFA BAG ∴∠=︒−∠=︒−︒=︒．CG EF ∥，80EFA AGC ∴∠=∠=︒．803050EFM EFA MFA ∴∠=∠−∠=︒−︒=︒．180********DEF EFM ∴∠=︒−∠=︒−︒=︒．故选：C ．【点睛】本题考查平行线的性质，结合图形利用平行线的性质进行角的转化和计算是解题关键． 【变式2】（2023下·浙江杭州·七年级统考期末）如图，AB CD ∥，射线FE ，FG 分别与AB ，CD 交于点M ，N ，若3F FND EMB ∠=∠=∠，则F ∠的度数是 ．【答案】108︒/108度【分析】过点F 作FH AB ∥，可得AB FH CD ∥∥，根据平行线的性质结合已知求出23HFN EFN ∠=∠，可得21803EFN EFN ∠+∠=︒，即可求出EFN ∠的度数．【详解】解：如图，过点F 作FH AB ∥，∵AB CD ∥，∴AB FH CD ∥∥，∴EMB EFH ∠=∠，180HFN FND ∠+∠=︒，∵3EFN FND EMB ∠=∠=∠，∴13EFH EFN ∠=∠，∴23HFN EFN ∠=∠， ∴21803EFN EFN ∠+∠=︒，∴108EFN ∠=︒，故答案为：108︒．【点睛】此题考查了平行线的判定与性质，熟记：①两直线平行，同位角相等；②两直线平行，内错角相等；③两直线平行，同旁内角互补是解题的关键． 【变式3】（2023下·内蒙古鄂尔多斯·七年级统考期中）探究题 (1)如下图，AB CD ∥，130PAB ∠=︒，120PCD ∠=︒．求APC ∠度数；(2)如下图，AD BC ∥，点P 在射线OM 上运动，ADP α∠=∠，BCP β∠=∠．①当点P 在A ，B 两点之间运动时，CPD ∠，α∠，∠β之间的数量关系为__________②当点P 在A ，B 两点外侧运动时(点P 与点A ，B ，O 三点不重合)，请写出CPD ∠，α∠，∠β之间的数量关系，并说明理由．【答案】(1)110APC ∠=︒；(2)①CPD αβ∠=∠+∠；②CPD βα∠=∠−∠或CPD αβ∠=∠−∠．【分析】本题考查了平行线的性质和判定的应用，解决问题的关键是作辅助线构造内错角以及同旁内角．（1）过P 作PE AB ∥，构造同旁内角，利用平行线性质，可得110APC ∠=︒；（2）①过P 作PE AD ∥交CD 于E ，推出AD PE BC ∥∥，根据平行线的性质得出DPE α∠=∠，CPE β∠=∠，即可得出答案；②画出图形（分两种情况：点P 在BA 的延长线上，点P 在AB 的延长线上），根据平行线的性质得出DPE α∠=∠，CPE β∠=∠，即可得出答案．【详解】（1）解：过P 作PE AB ∥，∵AB CD ∥，∴PE AB CD ∥∥，∵130PAB ∠=︒，120PCD ∠=︒．∴18050APE PAB ∠=︒−∠=︒，18060CPE PCD ∠=︒−∠=︒，∴5060110APC ∠=︒+︒=︒；（2）解：①CPD αβ∠=∠+∠：如图3，过P 作PE AD ∥交CD 于E ，∵AD BC ∥，∴AD PE BC ∥∥，∴DPE α∠=∠，CPE β∠=∠，∴CPD DPE CPE αβ∠=∠+∠=∠+∠；故答案为：CPD αβ∠=∠+∠；②当P 在AB 延长线时，CPD βα∠=∠−∠；理由：如图4，过P 作PE AD ∥交CD 于E ，∵AD BC ∥，∴AD PE BC ∥∥，∴DPE α∠=∠，CPE β∠=∠，∴CPD CPE DPE βα∠=∠−∠=∠−∠；当P 在BO 之间时，CPD αβ∠=∠−∠．理由：如图5，过P 作PE AD ∥交CD 于E ，∵AD BC ∥，∴AD PE BC ∥∥，∴DPE α∠=∠，CPE β∠=∠，∴CPD DPE CPE αβ∠=∠−∠=∠−∠．CPD αβ∴∠=∠−∠综上所述，CPD ∠，α∠，∠β之间的数量关系为CPD βα∠=∠−∠或CPD αβ∠=∠−∠．【经典例题三 平行基本模型之“鸡翅”模型】【例3】（2023秋·全国·八年级专题练习）①如图1，AB ∥CD ，则360A E C ∠+∠+∠=︒；②如图2，AB ∥CD ，则P A C ∠=∠−∠；③如图3，AB ∥CD ，则1E A ∠=∠+∠；④如图4，直线AB ∥CD ∥ EF ，点O 在直线EF 上，则180αβγ∠−∠+∠=︒．以上结论正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个【答案】B【分析】①过点E 作直线EF ∥AB ，由平行线的性质：两直线平行，同旁内角互补，即可得出结论； ②如图2，先根据三角形外角的性质得出∠1＝∠C+∠P ，再根据两直线平行，内错角相等即可作出判断； ③如图3，过点E 作直线EF ∥AB ，由平行线的性质可得出∠A+∠AEC ﹣∠1＝180°，即得∠AEC ＝180°+∠1﹣∠A ； ④如图4，根据平行线的性质得出∠α＝∠BOF ，∠γ+∠COF ＝180°，再利用角的关系解答即可．【详解】解：①如图1，过点E 作直线EF ∥AB ，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠1＝180°，∠2+∠C＝180°，∴∠A+∠B+∠AEC＝360°，故①错误；②如图2，∵∠1是△CEP的外角，∴∠1＝∠C+∠P，∵AB∥CD，∴∠A＝∠1，即∠P＝∠A﹣∠C，故②正确；③如图3，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠3＝180°，∠1＝∠2，∴∠A+∠AEC﹣∠1＝180°，即∠AEC＝180°+∠1﹣∠A，故③错误；④如图4，∵AB∥EF，∴∠α＝∠BOF，∵CD∥EF，∴∠γ+∠COF＝180°，∵∠BOF＝∠COF+∠β，∴∠COF＝∠α﹣∠β，∴∠γ+∠α﹣∠β＝180°，故④正确；综上结论正确的个数为2，故选：B．【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质，根据题意作出辅助线是解答此题的关键．【变式训练】 1、（2021下·广东东莞·七年级东莞市光明中学校考期中）（1）如图（1）ABCD ，猜想BPD ∠与B D ∠∠、的关系，说出理由．（2）观察图（2），已知AB CD ，猜想图中的BPD ∠与B D ∠∠、的关系，并说明理由．（3）观察图（3）和（4），已知ABCD ，猜想图中的BPD ∠与B D ∠∠、的关系，不需要说明理由．【答案】（1）360B BPD D ∠+∠+∠=︒，理由见解析；（2）BPD B D ∠=∠+∠，理由见解析；（3）图（3）BPD D B ∠=∠−∠，图（4）BPD B D ∠=∠−∠【分析】（1）过点P 作EF AB ∥，得到180B BPE ∠+∠=︒，由ABCD ，EF AB ∥，得到EF CD ，得到180EPD D ∠+∠=︒，由此得到360B BPD D ∠+∠+∠=︒； （2）过点P 作PE AB ，由PE AB CD ∥∥，得到12B D ∠=∠∠=∠，，从而得到结论12BPD B D ∠=∠+∠=∠+∠；（3）由ABCD ，根据两直线平行，内错角相等与三角形外角的性质，即可求得BPD ∠与B D ∠∠、的关系． 【详解】（1）解：猜想360B BPD D ∠+∠+∠=︒．理由：过点P 作EF AB ∥，∴180B BPE ∠+∠=︒，∵AB CD ，EF AB ∥，∴EF CD ，∴180EPD D ∠+∠=︒，∴360B BPE EPD D ∠+∠+∠+∠=︒，∴360B BPD D ∠+∠+∠=︒；（2）BPD B D ∠=∠+∠．理由：如图，过点P 作PEAB ，∵AB CD ，∴PE AB CD ∥∥，∴12B D ∠=∠∠=∠，，∴12BPD B D ∠=∠+∠=∠+∠；（3）如图（3）：BPD D B ∠=∠−∠．理由：∵AB CD ，∴1D ∠=∠，∵1B P ∠=∠+∠，∴D B P ∠=∠+∠，即BPD D B ∠=∠−∠；如图（4）：BPD B D ∠=∠−∠．理由：∵AB CD ，∴1B ∠=∠，∵1D P ∠=∠+∠，∴B D P ∠=∠+∠，即BPD B D ∠=∠−∠．【点睛】此题考查了平行线的性质，平行公理的推论，三角形的外角的性质定理，熟记平行线的性质是解题的关键． 2．（2020下·湖北武汉·七年级校考期中）如图，已知：点A 、C 、B 不在同一条直线，AD BE ∥(1)求证：180B C A ∠+∠−∠=︒：(2)如图②，AQ BQ 、分别为DAC EBC ∠∠、的平分线所在直线，试探究C ∠与AQB ∠的数量关系；(3)如图③，在（2）的前提下，且有AC QB ∥，直线AQ BC 、交于点P ，QP PB ⊥，直接写出=DAC ACB CBE ∠∠∠：： ．【答案】(1)见解析(2)2=180AQB C ∠+∠︒，理由见解析(3)122：：【分析】（1）过点C 作CF AD ∥，则CF BE ∥，根据平行线的性质可得出ACF A ∠=∠、180BCF B ∠=︒−∠，据此可得；（2）过点Q 作QM AD ∥，则QM BE ∥，根据平行线的性质、角平分线的定义可得出1()2AQB CBE CAD ∠=∠−∠，结合（1）的结论可得出2180AQB C ∠+∠=︒；（3）由（2）的结论可得出12CAD CBE ∠=∠①，由QP PB ⊥可得出180CAD CBE ∠+∠=︒②，联立①②可求出CAD CBE ∠∠、的度数，再结合（ 1）的结论可得出ACB ∠的度数，将其代入DAC ACB CBE ∠∠∠：：中可求出结论．【详解】（1）在图①中，过点C 作CF AD ∥，则CF BE ∥．∵CF AD BE ∥∥，∴180ACF A BCF B ∠=∠∠+∠=︒，，∴180180ACB B A ACF BCF B A A A ∠+∠−∠=∠+∠+∠−∠=∠+︒−∠=︒．（2）在图2中，过点Q 作QM AD ∥，则QM BE ∥．∵QM AD QM BE ∥，∥，∴AQM NAD BQM EBQ ∠=∠∠=∠，．∵AQ 平分CAD ∠，BQ 平分CBE ∠， ∴11,22NAD CAD EBQ CBE ∠=∠∠=∠， ∴1()2AQB BQM AQM CBE CAD ∠=∠−∠=∠−∠． ∵180()1802C CBE CAD AQB ︒︒∠=−∠−∠=−∠，∴2180AQB C ∠+∠=︒．（3）∵AC QB ∥， ∴11,22AQB CAP CAD ACP PBQ CBE ∠=∠=∠∠=∠=∠， ∴11801802ACB ACP CBE ∠=︒−∠=︒−∠．∵2180AQB ACB ∠+∠=︒， ∴1.2CAD CBE ∠=∠．又∵QP PB ⊥，∴90CAP ACP ∠+∠=︒，即180CAD CBE ∠+∠=︒，∴60120CAD CBE ∠=︒∠=︒，，∴180120()ACB CBE CAD ∠=︒−∠−∠=︒，∴60120120122DAC ACB CBE ∠∠∠=︒︒︒=：：：：：：， 故答案为：122：：． 【点睛】本题主要考查平行线的的判定与性质，解题的关键是熟练掌握平行线的性质、添加辅助线构建平行线． 3．（2021上·八年级课时练习）（1）已知：如图（a ），直线DE AB ∥．求证：ABC CDE BCD ∠+∠=∠； （2）如图（b ），如果点C 在AB 与ED 之外，其他条件不变，那么会有什么结果？你还能就本题作出什么新的猜想？ 【答案】（1）见解析；（2）当点C 在AB 与ED 之外时，ABC CDE BCD ∠−∠=∠，见解析【分析】（1）由题意首先过点C 作CF ∥AB ，由直线AB ∥ED ，可得AB ∥CF ∥DE ，然后由两直线平行，内错角相等，即可证得∠ABC+∠CDE=∠BCD ；（2）根据题意首先由两直线平行，内错角相等，可得∠ABC=∠BFD ，然后根据三角形外角的性质即可证得∠ABC -∠CDE=∠BCD ．【详解】解：（1）证明：过点C 作CF ∥AB ，∵AB ∥ED ，∴AB ∥ED ∥CF ，∴∠BCF=∠ABC ，∠DCF=∠EDC ，∴∠ABC+∠CDE=∠BCD ；（2）结论：∠ABC -∠CDE=∠BCD ，证明：如图：∵AB ∥ED ，∴∠ABC=∠BFD ，在△DFC 中，∠BFD=∠BCD+∠CDE ，∴∠ABC=∠BCD+∠CDE ，∴∠ABC -∠CDE=∠BCD ．若点C 在直线AB 与DE 之间，猜想360ABC BCD CDE ︒∠+∠+∠=,∵AB ∥ED ∥CF ，∴180,180,ABC BCF CDE DCF ︒︒∠+∠=∠+∠=∴360ABC BCD CDE ABC BCF DCF CDE ︒∠+∠+∠=∠+∠+∠+∠=.【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质是解答本题的关键，注意掌握辅助线的作法．4．（2021下·浙江·七年级期末）已知//AM CN ，点B 为平面内一点，AB BC ⊥于B ．（1）如图1，点B 在两条平行线外，则A ∠与C ∠之间的数量关系为______；（2）点B 在两条平行线之间，过点B 作BD AM ⊥于点D ．①如图2，说明ABD C ∠=∠成立的理由；②如图3，BF 平分DBC ∠交DM 于点,F BE 平分ABD ∠交DM 于点E ．若180,3FCB NCF BFC DBE ∠∠∠∠+=︒=，求EBC ∠的度数．【答案】（1）∠A+∠C=90°；（2）①见解析；②105°【分析】（1）根据平行线的性质以及直角三角形的性质进行证明即可；（2）①过点B 作BG ∥DM ，根据平行线找角的联系即可求解；②先过点B 作BG ∥DM ，根据角平分线的定义，得出∠ABF=∠GBF ，再设∠DBE=α，∠ABF=β，根据∠CBF+∠BFC+∠BCF=180°，可得2α+β+3α+3α+β=180°，根据AB ⊥BC ，可得β+β+2α=90°，最后解方程组即可得到∠ABE=15°，进而得出∠EBC=∠ABE+∠ABC=15°+90°=105°．【详解】解：（1）如图1，AM 与BC 的交点记作点O ，∵AM ∥CN ，∴∠C=∠AOB ，∵AB ⊥BC ，∴∠A+∠AOB=90°，∴∠A+∠C=90°；（2）①如图2，过点B作BG∥DM，∵BD⊥AM，∴DB⊥BG，∴∠DBG=90°，∴∠ABD+∠ABG=90°，∵AB⊥BC，∴∠CBG+∠ABG=90°，∴∠ABD=∠CBG，∵AM∥CN，BG∥DM，//,BG CN∴∠C=∠CBG，∠ABD=∠C；②如图3，过点B作BG∥DM，∵BF平分∠DBC，BE平分∠ABD，∴∠DBF=∠CBF，∠DBE=∠ABE，由（2）知∠ABD=∠CBG，∴∠ABF=∠GBF，设∠DBE=α，∠ABF=β，则∠ABE=α，∠ABD=2α=∠CBG，∠GBF=∠AFB=β，∠BFC=3∠DBE=3α，∴∠AFC=3α+β，∵∠AFC+∠NCF=180°，∠FCB+∠NCF=180°，∴∠FCB=∠AFC=3α+β，△BCF中，由∠CBF+∠BFC+∠BCF=180°得：2α+β+3α+3α+β=180°，∵AB⊥BC，∴β+β+2α=90°，∴α=15°，∴∠ABE=15°，∴∠EBC=∠ABE+∠ABC=15°+90°=105°．【点睛】本题主要考查了平行线的性质的运用，解决问题的关键是作平行线构造内错角，运用等角的余角（补角）相等进行推导．余角和补角计算的应用，常常与等式的性质、等量代换相关联．解题时注意方程思想的运用．【经典例题四平行基本模型之“骨折”模型】【例4】（2023·全国·九年级专题练习）如图所示，AB∥CD，∠E＝37°，∠C＝20°，则∠EAB的度数为__________．【答案】57°【分析】根据三角形内角和180°以及平行线的性质：1、如果两直线平行，那么它们的同位角相等；2、如果两直线平行，那么它们的同旁内角互补；3、如果两直线平行，那么它们的内错角相等，据此计算即可．【详解】解：设AE、CD交于点F，∵∠E ＝37°，∠C ＝ 20°，∴∠CFE=180°-37°-20°=123°，∴∠AFD=123°，∵AB ∥CD ，∴∠AFD+∠EAB=180°，∴∠EAB=180°-123°=57°，故答案为：57°．【点睛】本题主要考查三角形内角和定理以及平行线的性质，熟知平行的性质是解题的关键．【变式训练】【变式1】（2023春·湖北黄冈·七年级校考期中）如图，已知//AB DE ，∠ABC =80°，∠CDE =140°，则∠BCD =_____．【答案】40︒【分析】延长ED 交BC 于M ，根据两直线平行，内错角相等证明∠BMD=∠ABC ，再求解CMD ∠，再利用三角形的外角的性质可得答案．【详解】解：延长ED 交BC 于M ，∵//AB DE ，∴∠BMD=∠ABC=80°，∴180100CMD BMD ∠=︒−∠=︒；又∵∠CDE=∠CMD+∠C ，∴14010040BCD CDE CMD ∠=∠−∠=︒−︒=︒．故答案是：40°【点睛】本题考查了平行线的性质．三角形的外角的性质，邻补角的定义，掌握以上知识是解题的关键．【变式2】（2023春·江苏盐城·七年级景山中学校考阶段练习）如图，若//AB CD ，则∠1+∠3-∠2的度数为______【答案】180°【分析】延长EA 交CD 于点F ，则有∠2+∠EFC=∠3，然后根据//AB CD 可得∠1=∠EFD ，最后根据领补角及等量代换可求解．【详解】解：延长EA 交CD 于点F ，如图所示：//AB CD ，∴∠1=∠EFD ，∠2+∠EFC=∠3，∴32EFC ∠=∠−∠，+180EFC EFD ∠∠=︒，∴132180∠+∠−∠=︒；故答案为180°．【点睛】本题主要考查三角形外角的性质及平行线的性质，熟练掌握三角形外角的性质及平行线的性质是解题的关键．【变式3】（2023春·全国·七年级专题练习）（1）如图，AB //CD ，CF 平分∠DCE ，若∠DCF =30°，∠E =20°，求∠ABE 的度数；（2）如图，AB//CD，∠EBF=2∠ABF，CF平分∠DCE，若∠F的2倍与∠E的补角的和为190°，求∠ABE的度数．（3）如图，P为（2）中射线BE上一点，G是CD上任一点，PQ平分∠BPG，GN//PQ，GM平分∠DGP，若∠B＝30°，求∠MGN的度数．【答案】（1）∠ABE=40°；（2）∠ABE=30°；（3）∠MGN=15°．【分析】（1）过E作EM∥AB，根据平行线的判定与性质和角平分线的定义解答即可；（2）过E作EM∥AB，过F作FN∥AB，根据平行线的判定与性质，角平分线的定义以及解一元一次方程解答即可；（3）过P作PL∥AB，根据平行线的判定与性质，三角形的内角和定理，三角形的一个外角等于与它不相邻的两个内角的和的性质，角平分线的定义解答即可．【详解】解：（1）过E作EM∥AB，∵AB∥CD，∴CD∥EM∥AB，∴∠ABE＝∠BEM，∠DCE＝∠CEM，∵CF平分∠DCE，∴∠DCE＝2∠DCF，∵∠DCF＝30°，∴∠DCE＝60°，∴∠CEM＝60°，又∵∠CEB＝20°，∴∠BEM＝∠CEM﹣∠CEB＝40°，∴∠ABE＝40°；（2）过E作EM∥AB，过F作FN∥AB，∵∠EBF＝2∠ABF，∴设∠ABF＝x，∠EBF＝2x，则∠ABE＝3x，∵CF平分∠DCE，∴设∠DCF＝∠ECF＝y，则∠DCE＝2y，∵AB∥CD，∴EM∥AB∥CD，∴∠DCE＝∠CEM＝2y，∠BEM＝∠ABE＝3x，∴∠CEB＝∠CEM﹣∠BEM＝2y﹣3x，同理∠CFB＝y﹣x，∵2∠CFB+（180°﹣∠CEB）＝190°，∴2（y﹣x）+180°﹣（2y﹣3x）＝190°，∴x＝10°，∴∠ABE＝3x＝30°；（3）过P作PL∥AB，∵GM平分∠DGP，∴设∠DGM＝∠PGM＝y，则∠DGP＝2y，∵PQ平分∠BPG，∴设∠BPQ＝∠GPQ＝x，则∠BPG＝2x，∵PQ∥GN，∴∠PGN＝∠GPQ＝x，∵AB∥CD，∴PL∥AB∥CD，∴∠GPL＝∠DGP＝2y，∠BPL＝∠ABP＝30°，∵∠BPL＝∠GPL﹣∠BPG，∴30°＝2y﹣2x，∴y﹣x＝15°，∵∠MGN＝∠PGM﹣∠PGN＝y﹣x，∴∠MGN＝15°．【点睛】此题考查平行线的判定与性质，角平分线的定义，三角形的内角和定理，解题关键在于作辅助线和掌握判定定理．【拓展培优】1．（2023下·安徽·九年级专题练习）如图，已知：AB EF∥．在证明该结论∥，B E∠=∠，求证：BC DE时，需添加辅助线，则以下关于辅助线的作法不正确的是（）A ．延长BC 交FE 的延长线于点GB ．连接BEC ．分别作BCD ∠，CDE ∠的平分线CG ，DHD ．过点C 作CG AB ∥（点G 在点C 左侧），过点D 作DH EF ∥（点H 在点D 左侧）【答案】C【分析】根据平行线的性质与判定逐一判断即可．【详解】解：A 、如图，∵AB EF ∥，∴B G ∠=∠，∵B DEF ∠=∠，∴G DEF =∠∠，∴BC DE ∥，故此选项不符合题意；B 、如图，∵AB EF ∥，∴ABE FEB ∠=∠，∵ABC FED ∠=∠，∴CBE DEB ∠=∠，∴BC DE ∥，故此选项不符合题意；C 、如图，由CG 平分BCD ∠，DH 平分CDE ∠，没有条件说明BCD ∠与CDE ∠相等，也没有条件说明CG 与DH 平行，∴此辅助线的作法不能说明BC 与DE 平行，故此选项符合题意；D 、如图，延长BC 交DH 于点M ，∵AB EF ∥，CG AB ∥，DH EF ∥，∴AB CG DH EF ∥∥∥，∴B BMD ∠=∠，MDE E ∠=∠，∵B E ∠=∠，∴BMD MDE ∠=∠，∴BC DE ∥，故此选项不符合题意．故选：C ．【点睛】本题考查平行线的判定和性质，角平分线的定义，平行公理的推论．掌握平行线的判定和性质是解题的关键． 2．（2023下·山东菏泽·七年级统考期末）图1是男子竞技体操项目双杠的静止动作，图2是其俯视示意图，已知a b ∥，若AB 与BC 的夹角为100︒，150∠=︒，则2∠的度数为（ ）A ．100︒B ．120︒C ．125︒D ．130︒【答案】D 【分析】过点B 作BD a ∥，则BD b ∥，利用平行线的性质，进行求解即可．【详解】解：如图，过点B 作BD a ∥，∵a b ，∴BD b ∥，∴150ABD ∠=∠=︒，2180CBD ∠+∠=︒，∵100ABC ∠=︒，∴1005050CBD ∠=︒−︒=︒，∴218050130︒︒=∠=−︒．故选：D ．【点睛】本题考查平行线的判定和性质．解题的关键是构造平行线．3．（2021下·湖北武汉·七年级武汉外国语学校（武汉实验外国语学校）校考期中）如图，直线AB CD EF ∥∥，且40B ∠=︒，125C ∠=︒，则(CGB ∠= )A ．10︒B ．15︒C ．20︒D ．25︒【答案】B【分析】根据平行线的性质得出40BGF B ∠=∠=︒，180C CGF ∠+∠=︒，求出55CGF ∠=︒，即可得出答案．【详解】解：∵AB CD EF ∥∥，40B ∠=︒，125C ∠=︒，40BGF B ∴∠=∠=︒，18055CGF C ∠=︒−∠=︒，15CGB CGF BGF ∴∠=∠−∠=︒．故选：B ．【点睛】本题考查了平行线的性质的应用，主要考查学生的推理能力和计算能力． 4．（2023下·甘肃白银·八年级统考期末）如图，ABC 为等边三角形，AP CQ ∥．若20BAP ∠=︒，则1∠=（）A ．80︒B ．40︒C ．60︒D ．70︒【答案】B【分析】过点B 作BE CQ ，可得AP CQ BE ，用平行线性质求解即可．【详解】解：过点B 作BE CQ ，如图，∵AP CQ ∥，∴AP CQ BE ，∴20BAP ABE ∠=∠=︒，∵ABC 为等边三角形，∴60ABC ∠=︒，∴40CBE ABC ABE ∠∠=−∠=︒，∵BE CQ ，∴140CBE ∠=∠=︒，故选：B ．【点睛】本题考查平行线的判定与性质，正确作出辅助线是关键． 5．（2023下·浙江绍兴·七年级统考期末）如图，AB CD ∥，AE 平分BAN ∠，AE 的反向延长线交CDN ∠的平分线于点M ，则M ∠与N ∠的数量关系是（ ）A ．2M N ∠=∠B ．3M N ∠=∠C ．180M N ∠+∠=︒D ．2180M N ∠+∠=︒【答案】D 【分析】先利用角平分线的定义得到12BAE BAN ∠=∠，12CDM CDN ∠=∠，过M 作MF AB ∥，过N 作NH AB ∥，再利用平行线的判定与性质得到12FME BAE BAN ∠=∠=∠，BAN ANH ∠=∠，12FMD CDM CDN ∠=∠=∠，180CDN HND ∠+∠=︒，经过角度之间的运算得到180CDN BAN AND ∠−∠=︒−∠，()11802DMA AND ∠=︒−∠，即2180DMA AND ∠+∠=︒可求解．【详解】解：∵AE 平分BAN ∠，DM 平分CDN ∠，∴12BAE BAN ∠=∠，12CDM CDN ∠=∠，过M 作MF AB ∥，过N 作NH AB ∥，则12FME BAE BAN ∠=∠=∠，BAN ANH ∠=∠，∵AB CD ∥，∴MF CD ∥，NH CD ∥，∴12FMD CDM CDN ∠=∠=∠，180CDN HND ∠+∠=︒， ∴180AND ANH HND BAN CDN ∠=∠+∠=∠+︒−∠，即180CDN BAN AND ∠−∠=︒−∠，又∵DMA FMD FME ∠=∠−∠()12CDN BAN =∠−∠()11802AND =︒−∠，∴2180DMA AND ∠+∠=︒，即2180M N ∠+∠=︒，故选：D ．【点睛】本题考查角平分线的定义、平行线的判定与性质、角的运算，添加平行线，利用平行线的性质探究角之间的关系是解答的关键． 6．（2023下·辽宁沈阳·七年级统考期中）如图，AD BC ∥，CAD ∠和CBD ∠的平分线相交于点P ．请写出C ∠、D ∠、P ∠的数量关系 ．【答案】2P C D ∠=∠+∠【分析】作PG AD ∥，则PG AD BC ∥∥，根据平行线的性质可得APB DAP CBP ∠=∠+∠，结合角平分线定义可得1122APB DAC CBD ∠=∠+，再根据AD BC ∥推出DAC C ∠=∠，D CBD ∠=∠，即可得出2P C D ∠=∠+∠．【详解】解：如图，作PG AD ∥，AD BC ∥，∴PG AD BC ∥∥，PG AD ∥，∴DAP APG ∠=∠，PG BC ∥，∴CBP BPG ∠=∠，∴APB APG BPG DAP CBP ∠=∠+∠=∠+∠，CAD ∠和CBD ∠的平分线相交于点P ．∴12DAP DAC ∠=∠，12CBP CBD ∠=∠， ∴1122APB DAC CBD ∠=∠+，∴2APB DAC CBD ∠=∠+∠，AD BC ∥，∴DAC C ∠=∠，D CBD ∠=∠，∴2APB C D ∠=∠+∠，即2P C D ∠=∠+∠．故答案为：2P C D ∠=∠+∠．【点睛】本题考查平行线的判定与性质，角平分线的定义，角的和差关系等，解题的关键是熟练掌握平行线的性质． 7．（2023下·浙江·七年级校联考期中）如图，图1是一盏可折叠台灯，图2为其平面示意图，底座AO OE ⊥点O ，支架AB ，BC 为固定支撑杆，BAO ∠是CBA ∠的两倍，灯体CD 可绕点C 旋转调节，现把灯体CD 从水平位置旋转到CD '位置（如图 2中虚线所示），此时，灯体CD '所在的直线恰好垂直支架AB ，且120BCD DCD '∠−∠=︒，则DCD '∠= ．【答案】40︒/40度【分析】延长OA 交CD 于点F ，延长D C '交AB 于G ，可得90AGC AFC ∠=∠=︒，可得DCD GAF '∠=∠，在四边形ABCF 中，利用四边形内角和为360︒列出等式计算即可．【详解】解：延长OA 交CD 于点F ，延长D C '交AB 于G ，如图．CD OE ∥，AO OE ⊥，OA CD ∴⊥，AO OE ⊥Q ，D C AB '⊥，90AGC AFC ∴∠=∠=︒，180GCF GAF ∴∠+∠=︒，180DCD GCF '∠+∠=︒Q ，DCD GAF '∴∠=∠，180180BAO GAF DCD '∴∠=︒−∠=︒−∠，∵BAO ∠是CBA ∠的两倍，()11802CBA DCD '∴∠=︒−∠∵120BCD DCD '∠−∠=︒，120BCD DCD '∴∠=∠+︒，在四边形ABCF 中，360GAF CBA BCD AFC ∠+∠+∠+∠=︒，()1180120903602DCD DCD DCD '∴∠'+︒−∠+∠'+︒+︒=︒，解得40DCD '∠=︒．故答案为：40︒．【点睛】此题考查平行线的性质，四边形的内角和定理，一元一次方程的应用，利用图形性质建立方程求解是解题关键．8．（2023下·湖北·七年级黄石市有色中学校联考期末）如图，直线AB CD ∥，直线EF 与AB ，CD 分别交于点E ，F ，AEF ∠与CFE ∠的角平分线交于点P ，延长FP 交AB 于点G ，过点G 作GQ FG ⊥交直线EF 于点Q ，连接PQ ，点M 是QG 延长线上的一点，且PQM QPM ∠=∠，若PN 平分FPM ∠交CD 于点N ，则NPQ ∠的度数为 ．【答案】135︒/135度【分析】根据平行线的性质求出180AEF CFE ∠+∠=︒，根据角平分线定义求出90PEF PFE ∠+∠=︒，求出90EPF ∠=︒，求出GQ EP ∥，根据平行线的性质求出PQM QPE ∠=∠，再求出答案即可．【详解】设PQM QPM x ∠=∠=︒，∵PN 平分MPF ∠，∴MPN FPN ∠=∠，设MPN FPN y ∠=∠=︒，∵AEF ∠与CFE ∠的角平分线交于点P ，∴12PEF AEF ∠=∠，12EFP CFE ∠=∠，∵AB CD ∥，∴180AEF CFE ∠+∠=︒，∴1180902PEF PFE ∠+∠=⨯︒=︒，∴()1801809090EPF PEF PFE ∠=︒−∠+∠=︒−︒=︒，∵GQ PF ⊥，∴90QGP =︒∠，∴QGP EPF ∠=∠，∴GQ EP ∥，∴PQM QPE x ∠=∠=︒，∵360QPE QPM FPN NPM EPF ∠+∠+∠+∠+∠=︒，∴90360x x y y ++++=，∴135x y +=，即135QPM NPM ∠+∠=︒，∴135NPQ QPM NPM ∠=∠+∠=︒．故答案为：135︒．【点睛】本题考查了平行线的性质，角平分线的定义，三角形的内角和定理等知识点，能综合运用知识点进行推理是解此题的关键． 9．（2023下·四川成都·七年级统考期末）如图，直线AE CF ，ABC ∠ 的平分线BD 交直线CF 于点D ，若2260A BCF ∠=︒∠=︒，，则D ∠的度数为 ． 【答案】19︒/19度【分析】过点B 作B G C F ∥，利用平行线的性质求得22,60ABG CBG ∠=︒∠=︒，从而得到82ABC ∠=︒，再运用角平分线的性质得到1412CBD ABC ∠=∠=︒，继而求出19DBG ∠=︒，最后利用平行线的性质得到19D DBG ∠=∠=︒．【详解】过点B 作B G C F ∥，∵B G C F ∥，AE CF ，∴BG CF AE ∥∥∴,A ABG CBG BCF ∠=∠∠=∠，又∵2260A BCF ∠=︒∠=︒，，∴22,60A ABG CBG BCF ∠=∠=︒∠=∠=︒，∴82ABC ABG CBG ∠=∠+∠=︒，又∵BD 是ABC ∠ 的平分线， ∴1412CBD ABC ∠=∠=︒， ∴19DBG CBG CBD ∠=∠−∠=︒，又∵B G C F ∥，∴19D DBG ∠=∠=︒．【点睛】本题考查角平分线的定义，平分线的性质等知识，掌握平行线的性质是解题的关键． 10．（2023下·湖北武汉·七年级统考期末）如图，80AEC ∠=︒，在AEC ∠的两边上分别过点A 和点C 向同方向作射线AB 和CD ，且ABCD ，若EAB ∠和ECD ∠的角平分线所在的直线交于点P （P 与C 不重合），则APC ∠的大小为 ． 【答案】40︒【分析】根据题意作图，过点E 作EF AB ∥，过点P 作PQ AB ∥，利用平行线的性质可得80ECD EAB AEC ∠−∠=∠=︒，PCD PAB APC ∠−∠=∠，再结合角平分线即可求得答案．【详解】解：根据题意作图，过点E 作EF AB ∥，过点P 作PQ AB ∥，∵AB CD ，∴AB CD EF PQ ∥∥∥，∵EF AB ∥，EF CD ，∴180EAB AEC CEF ∠+∠+∠=︒，180CEF ECD ∠+∠=︒，∴EAB AEC ECD ∠+∠=∠，即80ECD EAB AEC ∠−∠=∠=︒，∵PQ AB ∥，PQ CD ∥，∴180PAB APC CPQ ∠+∠+∠=︒，180CPQ PCD ∠+∠=︒，∴PAB APC PCD ∠+∠=∠，即PCD PAB APC ∠−∠=∠，又∵点P 为EAB ∠和ECD ∠的角平分线所在的直线的交点， ∴12PAB EAB ∠=∠，12PCD ECD ∠=∠， ∴11140222APC PCD PAB ECD EAB AEC ∠=∠−∠=∠−∠=∠=︒，故答案案为：40︒．【点睛】本题考查平行线的性质，角平分线的定义，掌握平行线的性质是解决问题的关键． 11．（2023下·七年级课时练习）如图，AB ∥CD ，ME 平分∠AMF ，NF 平分∠CNE ，EN ，MF 交于点O ． (1)若∠AMF ＝50°，∠CNE ＝40°，分别求∠MEN ，∠MFN 的度数；(2)若图中∠MEN ＋60°＝2∠MFN ，求∠AMF 的度数；(3)探究∠MEN ，∠MFN 与∠MON 之间的数量关系．【答案】(1)∠MEN ＝65°，∠MFN ＝70°(2)∠AMF ＝40°(3)32MEN MFN MON ∠+∠=∠，理由见解析【详解】（1）分别过点E ，F 作AB 的平行线，则它们同时也与CD 平行，则有∠MEN ＝∠AME ＋∠CNE ，∠MFN ＝∠AMF ＋∠CNF ．由∠AMF ＝50°，∠CNE ＝40°，ME 平分∠AMF ，NF 平分∠CNE ，得∠AME ＝25°，∠CNF ＝20°，∴∠MEN ＝65°，∠MFN ＝70°．（2）由（1）可知，∠MEN ＝∠AME ＋∠CNE ，∠MFN ＝∠AMF ＋∠CNF ，则有∠AME ＋∠CNE ＋60°＝2∠AMF ＋2∠CNF ．又2∠CNF ＝∠CNE ，2∠AME ＝∠AMF ． ∴3602AMF ∠=︒，故∠AMF ＝40°．（3）过点O 作AB 的平行线，则它同时也与CD 平行，易证∠MON ＝∠AMF ＋∠CNE ．∵∠MEN ＝∠AME ＋∠CNE ，∠MFN ＝∠AMF ＋∠CNF ， ∴32MEN MFN ∠+∠=（∠AMF ＋∠CNE ）． ∴32MEN MFN MON ∠+∠=∠． 12．（2023上·浙江·八年级专题练习）已知，如图，AB 与CD 交于点O (1)如图1，若A B ∠∠＝，求证：A C B D ∠+∠∠+∠＝(2)如图2，若A B ∠≠∠，（1）中的结论是否仍然成立？请判断并证明你的结论（注：不能用三角形内角和定理）(3)如图3，若65B ∠︒＝，25C ∠︒＝，AP 平分BAC ∠，DP 平分BDC ∠，请你（2）中结论求出P ∠的度数，请直接写出结果P ∠= ．【答案】(1)见解析(2)仍然成立，证明见解析(3)45︒【分析】本题考查了平行线的性质、三角形内角和定理的综合运用，掌握三角形内角和180︒是解题的关键．（1）依据平行线的性质，即可得到C D ∠∠＝，依据等式基本性质得到A C B D ∠+∠∠+∠＝；。

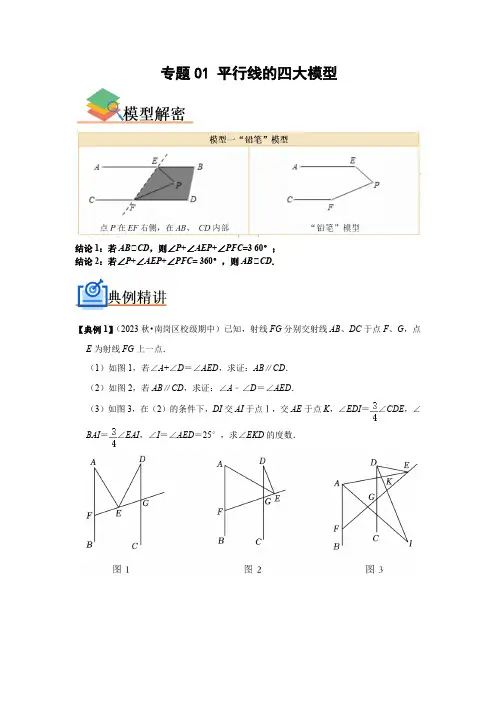
专题01 平行线的四大模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=3 60°；结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.【典例1】（2023秋•南岗区校级期中）已知，射线FG分别交射线AB、DC于点F、G，点E为射线FG上一点．（1）如图1，若∠A+∠D＝∠AED，求证：AB∥CD．（2）如图2，若AB∥CD，求证：∠A﹣∠D＝∠AED．（3）如图3，在（2）的条件下，DI交AI于点Ⅰ，交AE于点K，∠EDI＝∠CDE，∠BAI＝∠EAI，∠I＝∠AED＝25°，求∠EKD的度数．【变式1-1】（2022秋•古县期末）如图：按虚线剪去长方形纸片的相邻两个角，并使∠1＝1 50°，AB⊥BC，则∠2的度数为（）A．100°B．110°C．120°D．130°【变式1-2】（2023•金安区一模）如图，已知a∥b，∠1＝45°，∠2＝125°，则∠ABC的度数为（）A．100°B．105°C．115°D．125°【变式1-3】（2023秋•北碚区期末）如图，AB∥CD，点E是直线AB，CD之间一点．（1）如图1，求证：∠B+∠D+∠E＝360°；（2）如图2，若∠B＝120°，∠BED，∠CDE的平分线相交于点F．求∠DFE的度数；（3）如图3，若∠D＝α，∠EBF＝4∠ABF，∠BEF＝4∠DEF．请直接写出∠BFE的度数（用含α的代数式表示）．【变式1-4】（2023秋•重庆期末）已知，MN∥PQ，直线AB交MN于点A，交PQ于点B，点C在线段AB上，过C作射线CE、CF分别交直线MN、PQ于点E、F．（1）如图1，当CE⊥CF时，求∠AEC+∠BFC的度数；（2）如图2，若∠MEC和∠PFT的角平分线交于点G，求∠ECF和∠G的数量关系；（3）如图3，在（2）的基础上，当CE⊥CF，且∠ABP＝60°，∠ACE＝20°时，射线FT绕点F以5°每秒的速度顺时针旋转，设运动时间为t秒，当射线FG与△AEC的一边互相平行时，请直接写出t的值．模型二“猪蹄”模型（模型）点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；结论2：若∠P=∠AEP+∠CFP，则AB∥CD.【典例2】（2023春•邵阳县期末）如图，直线AB∥CD，连接EF，直线AB，CD及线段EF把平面分成①②③④四个部分，规定：线上各点不属于任何部分．当动点G落在某个部分时，连接GE，GF，构成∠EGF，∠GEB，∠GFD三个角．（1）当动点G落在第③部分时，如图一，试说明：∠EGF，∠GEB，∠GFD三者的关系；（2）当动点G落在第②部分时，如图二，思考（1）中三者关系是否仍然成立若不成立，说明理由．【变式2-1】（2023•盘锦）如图，直线AB∥CD，将一个含60°角的直角三角尺EGF按图中方式放置，点E在AB上，边GF，EF分别交CD于点H，K，若∠BEF＝64°，则∠GHC等于（）A．44°B．34°C．24°D．14°【变式2-2】（2023•大石桥市校级三模）如图，直线a∥b，等边△ABC的顶点C在直线b 上，∠1＝28°，则∠2的度数为（）A．36°B．24°C．28°D．32°【变式2-3】（2023春•浏阳市期末）（1）感知与探究：如图①，直线AB∥CD，过点E作E F∥AB．请直接写出∠B，∠D，∠BED之间的数量关系：；（2）应用与拓展：如图②，直线AB∥CD．若∠B＝23°，∠G＝35°，∠D＝25°，借助第（1）问中的结论，求∠BEG+∠GFD的度数；（3）方法与实践：如图③，直线AB∥CD．若∠E＝∠B＝60°，∠F＝85°，则∠D＝度．【变式2-4】（2023春•霸州市期中）如图1，AB∥CD，∠P AB＝135°，∠PCD＝125°，求∠APC度数．小明的思路是：过P作PE∥AB，如图2，通过平行线性质来求∠APC．（1）按小明的思路，易求得∠APC的度数为；请说明理由；（2）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠A DP＝∠α，∠BCP＝∠β，则∠CPD、∠α、∠β之间有何数量关系？请说明理由；（3）在（2）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．【变式2-5】（2023春•南漳县期中）如图1，点A是直线HD上一点，C是直线GE上一点，B是直线HD、GE之间的一点．∠HAB+∠BCG＝∠ABC．（1）求证：AD∥CE；（2）如图2，作∠BCF＝∠BCG，CF与∠BAH的角平分线交于点F，若α+β＝50°，求∠B+∠F的度数；（3）如图3，CR平分∠BCG，BN平分∠ABC，BM∥CR，已知∠BAH＝40°，试探究∠NBM的值，若不变求其值，若变化说明理由．结论1：若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.【典例3】（2023春•中山区期末）如图，∠ABE+∠BED＝∠CDE．（1）如图1，求证AB∥CD；（2）如图2，点P在AB上，∠CDP＝∠EDP，BF平分∠ABE，交PD于点F，探究∠BFP，∠BED的数量关系，并证明你的结论；（3）在（2）的条件下，如图3，PQ交ED延长线于点Q，∠DPQ＝2∠APQ，∠PQD ＝80°，求∠CDE的度数．【变式3-1】（2023春•伊通县期末）如图1，线段CD是由线段AB平移得到的．分别连接B D，AC．直线BE⊥AC于点E，延长DC与BE相交于点F．点P是射线FD上的一个动点，点P不与点F、点C、点D重合．连接BP，EP．（1）线段AC，BD的关系是；（2）如图1，当点P在线段FC上运动时，∠DBP，∠CEP，∠BPE之间的数量关系是；（3）如图2，当点P在线段CD上运动时，∠DBP，∠CEP，∠BPE之间的数量关系是否发生变化？若发生变化请写出它们的关系，并证明；若没有发生变化，请说明理由；（4）如图3，当点P在点D上方运动时，请直接写出∠DBP，∠CEP，∠BPE之间的数量关系：．【变式3-2】（2023春•大足区期末）已知直线AB∥CD，E为平面内一点，连接EB、EC．（1）如图1，已知∠B＝32°，∠C＝120°，求∠BEC的度数；（2）如图2，判断∠ABE、∠BEC、∠DCE之间的数量关系为；（3）如图3，BE⊥CE，BF平分∠ABE，若，求∠BFC的度数．【变式3-3】（2023春•吴兴区期中）已知：AB∥CD，E、G是AB上的点，F、H是CD上的点，∠1＝∠2．（1）如图1，求证：EF∥GH；（2）如图2，过F点作FM⊥GH交GH延长线于点M，作∠BEF、∠DFM的角平分线交于点N，EN交GH于点P，求证：∠N＝45°；（3）如图3，在（2）的条件下，作∠AGH的角平分线交CD于点Q，若3∠FEN＝4∠HFM，直接写出的值．1．（2023•五华区校级模拟）如图，点B在△CDE的边EC的延长线上，AB∥CD，若∠B ＝50°，∠E＝30°，则∠D的度数为（）A．15°B．20°C．30°D．50°2．（2023•西峡县三模）如图是一款手推车的平面示意图，其中AB∥CD，∠1＝30°，∠2＝70°，则∠3的度数为（）A．120°B．130°C．140°D．150°3.（2023春•西塞山区期中）如图，AB与HN交于点E，点G在直线CD上，GF交AB于点M，∠FMA＝∠FGC，∠FEN＝2∠NEB，∠FGH＝2∠HGC，下列四个结论：①AB∥CD；②∠EHG＝2∠EFM；③∠EHG+∠EFM＝90°；④3∠EHG﹣∠EFM＝180°．其中正确的结论是（）A．①②③B．②④C．①②④D．①④4．（2023春•德城区期末）已知M，N分别是长方形纸条ABCD边AB，CD上两点（AM＞DN），如图1所示，沿M，N所在直线进行第一次折叠，点A，D的对应点分别为点E，F，EM交CD于点P；如图2所示，继续沿PM进行第二次折叠，点B，C的对应点分别为点G，H，若∠1＝∠2，则∠CPM的度数为（）A．74°B．72°C．70°D．68°5．（2023•西城区二模）如图，直线AB∥CD，直线EF分别交AB，CD于点E，F，∠BEF 的平分线交CD点G，若∠BEF＝116°，则∠EGC的大小是（）A．116°B．74°C．64°D．58°6．（2023•佛山二模）如图，把正方形ABCD沿EF折叠，点A的对应点为点A′，点B的对应点为点B′，若∠1＝40°，则∠AEF的度数是（）A．100°B．110°C．115°D．120°7．（2023秋•长春期末）如图，AB∥CD，点E、F分别在直线AB、CD上，点P是AB、C D之间的一个动点．【感知】如图①，当点P在线段EF左侧时，若∠AEP＝50°，∠PFC＝70°，求∠EPF 的度数．分析：从图形上看，由于没有一条直线截AB与CD，所以无法直接运用平行线的性质，这时需要构造出“两条直线被第三条直线所截”的基本图形，过点P作PG∥AB，根据两条直线都和第三条直线平行，那么这两条直线也互相平行，可知PG∥CD，进而求出∠EPF的度数．【探究】如图②，当点P在线段EF右侧时，∠AEP、∠EPF、∠PFC之间的数量关系为．8．（2023春•天元区校级期末）如图，AQ∥BP，AB⊥BP，E、C、D分别是线段AQ、AB、BP上的点，且满足EC⊥CD．EF是∠GEC的角平分线与BP交于点F，在EQ上截一点G，连接GF，令GF＝FE．（1）如图1，若∠AEC＝40°，求∠CDB的度数．（2）如图1，连接GP，若GP∥EF，H是线段FP上的一点（FH＜HP），连接GH，使得2∠GHP＝3∠AEC，求∠FGH和∠CDB的数量关系．（3）如图2，在（2）的条件下，过点Q作QM⊥GP，垂足为M．N是线段GP上的一点，且满足∠QNM＝∠GEF．求∠GQN和∠CEF的数量关系．9．（2023春•安化县期末）在课后学习中，小红探究平行线中的线段与角的数量关系，如图，直线AB∥CD，点N在直线CD上，点P在直线AB上，点M为平面上任意一点，连接MP，MN，PN．（1）如图1，点M在直线CD上，PM平分∠APN，试说明∠PMN＝∠MPN；（2）如图2，点M在直线AB，CD之间，∠PMN＝70°，∠MNC＝30°，求∠APM的度数；（3）如图3，∠APM和∠MNC的平分线交于点Q，∠PQN与∠PMN有何数量关系？并说明理由．10．（2023春•海阳市期末）如图，AM∥BN，∠A＝40°，点P是射线AM上一动点（不与点A重合），BC，BD分别平分∠ABP和∠PBN，交射线AM于C，D两点．（1）求∠CBD的度数；（2）当点P运动到使∠ACB＝∠ABD时，求∠ABC的度数；（3）当点P运动时，∠APB与∠ADB的度数之比是否随之发生变化？若不变，求出∠A PB与∠ADB的度数之比；若变化，请说明变化规律．11．（2023春•大同期末）综合与探究已知直线AB∥CD，直线EF分别与AB，CD交于点G，H（0°＜∠EHD＜90°）．将一把含30°角的直角三角尺PMN按如图1所示的方式放置，使点N，M分别在直线AB，CD上，且在直线EF的右侧．（1）填空：∠PNB+∠PMD＝∠MPN．（填“＞”“＜”或“＝”）（2）若∠MNG的平分线NO交直线CD于点O．①如图2，当NO∥PM∥EF时，求∠EHD的度数；②如图3，若将三角尺PMN沿直线BA向左移动，保持PM∥EF（点N不与点G重合），点N，M分别在直线AB、CD上，请直接写出∠MON和∠EHD之间的数量关系．12．（2023春•安阳期末）【学习新知】射到平面镜上的光线（入射光线）和反射后的光线（反射光线）与平面镜所夹的角相等．如图1，AB是平面镜，若入射光线与水平镜面的夹角为∠1，反射光线与水平镜面的夹角为∠2，则∠1＝∠2．（1）【初步应用】生活中我们可以运用“激光”和两块相交的平面镜进行测距．如图2当一束“激光”DO 1射到平面镜AB上，被平面镜AB反射到平面镜BC上，又被平面镜BC反射后得到反射光线O2E，回答下列问题：①当DO1∥EO2∠AO1D＝30°（即∠1＝30°）时，求∠O1O2E的度数；②当∠B＝90°时，任何射到平面镜AB上的光线DO1经过平面镜AB和BC的两次反射后，入射光线与反射光线总是平行的．请你根据所学知识及新知说明理由．（提示：三角形的内角和等于180°）（2）【拓展探究】如图3，有三块平面镜AB，BC，CD，入射光线EO1经过三次反射，得到反射光线O3F 已知∠1＝∠6＝35°，若要使EO1∥O3F，请直接写出∠B的度数；13．（2023春•宜都市期中）已知，直线AB∥CD，点E、F分别在直线AB、CD上，点P 是直线AB与CD外一点，连接PE、PF．（1）如图1，若∠AEP＝45°，∠DFP＝105°，求∠EPF的度数；（2）如图2，过点E作∠AEP的角平分线EM交FP的延长线于点M，∠DFP的角平分线FN交EM的反向延长线交于点N，若∠M与3∠N互补，试探索直线EP与直线FN 的位置关系，并说明理由；（3）若点P在直线AB的上方且不在直线EF上，作∠DFP的角平分线FN交∠AEP的角平分线EM所在直线于点N，请直接写出∠EPF与∠ENF的数量关系．14．（2022秋•香坊区期末）已知：直线AB、CR被直线UV所截，直线UV交直线AB于点B，交直线CR于点D，∠ABU+∠CDV＝180°．（1）如图1，求证：AB∥CD；（2）如图2，BE∥DF，∠MEB＝∠ABE+5°，∠FDR＝35°，求∠MEB的度数；（3）如图3，在（2）的条件下，点N在直线AB上，分别连接EN、ED，MG∥EN，连接ME，∠GME＝∠GEM，∠EBD＝2∠NEG，EB平分∠DEN，MH⊥UV于点H，若∠E DC＝∠CDB，求∠GMH的度数．。

平行线的判定及性质一、【基础知识精讲】1、平行线的判定（1）平行公理：经过直线外一点，有且只有一条直线与已知直线平行. （2）平行公理的推论：平行于同一条直线的两条直线. （3）在同一平面内，垂直于同一条直线的两条直线. （4）同位角相等，两直线平行. （5）内错角相等，两直线平行.（6）同旁内角互补，两直线平行.3、平行线的性质（1）两直线平行，同位角相等. （2）两直线平行，内错角相等.（3）两直线平行，同旁内角互补.二、【例题精讲】专题一：余角、补角、对顶角与三线八角例题1：∠A的余角与∠A的补角互为补角，那么2∠A是（）A．直角 B.锐角 C.钝角 D.以上三种都有可能【活学活用1】如图2-79中，下列判断正确的是（）A.4对同位角，2对内错角，4对同旁内角B.4对同位角，2对内错角，2对同旁内角C.6对同位角，4对内错角，4对同旁内角D.6对同位角，4对内错角，2对同旁内角【活学活用2】如图2-82，下列说法中错误的是( )A.∠3和∠5是同位角B.∠4和∠5是同旁内角C.∠2和∠4是对顶角D.∠1和∠2是同位角【活学活用3】如图,直线AB与CD交于点O,OE⊥AB于O,图中∠1与∠2的关系是（）A.对顶角B.互余C.互补D相等例题2：如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30°，那么这两个角分别是_______.【活学活用4】如图，∠AOC +∠DOE +∠BOF = .专题二：平行线的判定例题3：如图，已知∠EFB+∠ADC=180°，且∠1=∠2，试说明DG ∥AB.1 2A BCDF E G【活学活用】1、长方体的每一对棱相互平行，那么这样的平行棱共有 ( )A ．9对B ．16对 C.18对 D ．以上答案都不对2、已知:如图2-96,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ，∠1=∠2,求证：DO ⊥AB.3、如图2-97,已知：∠1=∠2=，∠3=∠4，∠5=∠6.求证:AD ∥BC.4、如图2—101，若要能使AB ∥ED ，∠B 、∠C 、∠D 应满足什么条件?ABCDOE F5、同一平面内有四条直线a 、b 、c 、d ，若a ∥b ，a ⊥c ，b ⊥d ，则c 、d 的位置关系为（ ） A.互相垂直 B ．互相平行 C.相交 D ．没有确定关系专题三：平行线的性质1、如图，110,ABC ACB BO ∠+∠=、CO 分别平分ABC ∠和,ACB EF ∠过点O 与BC 平行，则BOC ∠= . 2、如图，AB //CD ，BC //DE ，则∠B+∠D = .3、如图，直线AB 与CD 相交于点O ，OB 平分∠DOE .若60DOE ∠=，则∠AOC 的度数是 .4、 如图，175,2120,375∠=∠=∠=，则4∠= .13 425、如图，//AB CD ，直线EF 分别交AB 、CD 于E 、F ，ED 平分BEF ∠，若172∠=，则2∠= .【例题讲解】例1：如图，已知：AD ∥BC, ∠AEF=∠B,求证：AD ∥EF 。

平行线四大模型1、平行线的判定根据平行线的定义，如果平面内的两条直线不相交，就可以判断这两条直线平行，但是，由于直线无限延伸，检验它们是否相交有困难，所以难以直接根据定义来判断两条直线是否平行，这就需要更简单易行的判定方法来判定两直线平行．判定方法1：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．简称：同位角相等，两直线平行．判定方法2：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简称：内错角相等，两直线平行，判定方法3：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行．简称：同旁内角互补，两直线平行，如上图：若已知∠1=∠2，则AB∥CD（同位角相等，两直线平行）；若已知∠1=∠3，则AB∥CD（内错角相等，两直线平行）；若已知∠1+∠4=180°，则AB∥CD（同旁内角互补，两直线平行）．另有平行公理推论也能证明两直线平行：平行公理推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．2、平行线的性质利用同位角相等，或者内错角相等，或者同旁内角互补，可以判定两条直线平行．反过来，如果已知两条直线平行，当它们被第三条直线所截，得到的同位角、内错角、同旁内角也有相应的数量关系，这就是平行线的性质．性质1：两条平行线被第三条直线所截，同位角相等．简称：两直线平行，同位角相等性质2：两条平行线被第三条直线所截，内错角相等.简称：两直线平行，内错角相等性质3：两条平行线被第三条直线所截，同旁内角互补．简称：两直线平行，同旁内角互补平移3.平移是指在平面内，将一个图形沿着某个方向移动一定的距离，这样的图形运动叫做图形的平移（translation），简称平移。

4.平移的性质经过平移，对应线段平行（或共线）且相等，对应角相等，对应点所连接的线段平行且相等；平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形)。

（1）图形平移前后的形状和大小没有变化，只是位置发生变化;（2）图形平移后，对应点连成的线段平行且相等（或在同一直线上）（3）多次平移相当于一次平移。

专题03 平行线四大模型（能力提升）1．将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置，如果∠CDE ＝40°，那么∠BAF的大小为（）A．25°B．20°C．15°D．10°【答案】D【解答】解：由题意知：∠CAB＝60°，∠C＝90°．∵∠CDE＝40°，∴∠CED＝50°．∵DE∥AF，∴∠F AE＝∠CED＝50°．∴∠BAF＝∠CAB﹣F AE＝60°﹣50°＝10°．故选：D．2．如图，l1∥l2，将一副直角三角板作如下摆放，图中点A、B、C在同一直线上，∠1＝80°，则∠2的度数为（）A．100°B．120°C．130°D．150°【答案】C【解答】解：如图，过点A作AD∥l1，∵l1∥l2，∴AD∥l2，∴∠FNA+∠NAD＝180°，∵AD∥l1，∴∠EMA+∠MAD＝180°，∴∠EMA+∠MAD+∠DAN+∠ANF＝180°+180°＝360°，∵∠EMA＝∠EMC+∠CMA＝80°+60°＝140°，∠MAD+∠DAN＝90°，∴∠FNA＝360°﹣140°﹣90°＝130°，即∠2＝130°，故选：C．3．如图，AB与HN交于点E，点G在直线CD上，GF交AB于点M，∠FMA＝∠FGC，∠FEN＝2∠NEB，∠FGH＝2∠HGC，下列四个结论：①AB∥CD；②∠EHG＝2∠EFM；③∠EHG+∠EFM＝90°；④3∠EHG﹣∠EFM＝180°．其中正确的结论是（）A．①②③B．②④C．①②④D．①④【答案】D【解答】解：∵∠FMA＝∠FGC∴AB∥CD∴①正确；过点F作FP∥AB，HQ∥AB，∵AB∥CD，∴FP∥AB∥HQ∥CD，设∠NEB＝x，∠HGC＝y，则∠FEN＝2x，∠FGH＝2y∴∠EHG＝∠EHQ+∠GHQ＝∠AEH+∠HGC＝∠NEB+∠HGC＝x+y，∠EFM＝∠BEF﹣∠FME＝∠BEF﹣∠AMG＝∠BEF﹣（180°﹣∠FGC）＝x+2x﹣（180°﹣y﹣y）＝3x+3y﹣180°，∴2∠EFM＝6x+6y﹣360°，∴∠EHG≠2∠EFM∴②错误；∴∠EHG+∠EFM＝x+y+3x+3y﹣180°＝4x+4y﹣180°≠90°，∴③错误；∴3∠EHG﹣∠EFM＝3（x+y）﹣（3x+3y﹣180°）＝180°，∴④正确．综上所述，正确答案为①④．故选：D．4．如图，AB∥EF，∠C＝90°，则α、β、γ的关系为（）A．β＝α+γB．α+β﹣γ＝90°C．α+β+γ＝180°D．β+γ﹣α＝90°【答案】B【解答】解：延长DC交AB于G，延长CD交EF于H．直角△BGC中，∠1＝90°﹣α；△EHD中，∠2＝β﹣γ，∵AB∥EF，∴∠1＝∠2，∴90°﹣α＝β﹣γ，即α+β﹣γ＝90°．故选：B．5．如图，AB∥EF，∠C＝90°，则α、β、y的关系是（）A．β+γ﹣α＝90°B．α+β+γ＝180°C．α+β﹣γ＝90°D．β＝α+γ【答案】C【解答】解：如图，过点C、D分别作AB的平行线CG、DH，∵AB∥EF，∴AB∥CG∥DH∥EF，∴∠1＝∠α，∠2＝∠3，∠4＝∠γ，∵∠2＝90°﹣∠1＝90°﹣∠α，∠3＝∠β﹣∠4＝∠β﹣∠γ，∴90°﹣∠α＝∠β﹣∠γ，∴α+β﹣γ＝90°．故选：C．6．如图，AB∥CD，EMNF是直线AB、CD间的一条折线．若∠1＝40°，∠2＝60°，∠3＝70°，则∠4的度数为（）A．55°B．50°C．40°D．30°【答案】B【解答】解：如图2，过M作OM∥AB，PN∥AB，∵AB∥CD，∴AB∥OM∥PN∥CD，∴∠1＝∠EMO，∠4＝∠PNF，∠OMN＝∠PNM，∴∠EMN﹣∠MNF＝（∠1+∠MNP）﹣（∠MNP+∠4）＝∠1﹣∠4，∴60°﹣70°＝40°﹣∠4，∴∠4＝50°．故选：B．7．为了落实“双减”政策，促进学生健康成长，各学校积极推行“5+2”模式，立足学生的认知成长规律，满足学生多样化的需求，打造特色突出、切实可行的体育锻炼内容．晋中市的某学校将“抖空竹”引入阳光体育一小时活动，如图1是一位同学抖空竹时的一个瞬间，小丽把它抽象成图2的数学问题：已知AB∥CD，∠EAB＝80°，∠ECD＝110°，则∠E的度数是30°．【答案】30°【解答】解：延长DC交AE于点F，∵AB∥CD，∴∠EFC＝∠A＝80°，由外角的性质得，∠DCE＝∠E+∠EFC，∴∠E＝110°﹣80°＝30°．故答案为：30°．8．如图，直线PQ∥MN，直角三角尺ABC的∠BAC＝30°，∠ACB＝90°．（1）若把三角尺按图甲方式放置，则∠MAC+∠PBC＝90°；（2）若把三角尺按图乙方式放置，点D，E，F是三角尺的边与平行线的交点，若∠AEN ＝∠A，求∠BDF的值；（3）如图丙，三角尺的直角顶点C始终在两条平行线之间，点G在线段CD上，连接EG，适当转动三角尺，使得CE恰好平分∠MEG，求的值．【解答】解：（1）延长BC交MN于点D，∵PQ∥MN，∴∠PBC＝∠ADC，∵∠ACB是△ACD的一个外角，∴∠ACB＝∠ADC+∠MAC，∴∠ACB＝∠PBC+∠MAC＝90°，故答案为：90；（2）∵∠AEN＝∠A，∠BAC＝30°，∴∠AEN＝∠A＝30°，∴∠CEM＝∠AEN＝30°，利用（1）的结论可得：∠ACB＝∠PDC+∠MEC，∴∠PDC＝∠ACB﹣∠MEC＝60°，∴∠BDF＝∠PDC＝60°，∴∠BDF的度数为60°；（3）∵CE平分∠MEG，∴∠CEM＝∠CEG，设∠CEM＝∠CEG＝x，∴∠GEN＝180°﹣∠CEM﹣∠CEG＝180°﹣2x，利用（1）的结论可得：∠ACB＝∠PDC+∠MEC，∴∠PDC＝∠ACB﹣∠MEC＝90°﹣x，∴∠BDF＝∠PDC＝90°﹣x，∴＝＝2，∴的值为2．9．如图，AB∥CD，点E为两直线之间的一点．（1）如图1，若∠BAE＝35°，∠DCE＝20°，则∠AEC＝；（2）如图2，试说明，∠BAE+∠AEC+∠ECD＝360°；（3）①如图3，若∠BAE的平分线与∠DCE的平分线相交于点F，判断∠AEC与∠AFC 的数量关系，并说明理由；②如图4，若设∠E＝m，∠BAF＝∠F AE，∠DCF＝∠FCE，请直接用含m、n的代数式表示∠F的度数．【解答】解：（1）55°如图所示，过点E作EF∥AB，∵AB∥CD∴AB∥CD∥EF，∴∠BAE＝∠1，∠ECD＝∠2，∴∠AEC＝∠1+∠2＝∠BAE+∠ECD＝35°+20°＝55°，故答案为55°．（2）如图所示，过点E作EG∥AB，∵AB∥CD∴AB∥CD∥EG，∴∠A+∠1＝180°，∠C+∠2＝180°，∴∠A+∠1+∠2+∠C＝360°，即∠BAE+∠AEC+∠ECD＝360°．（3）①2∠AFC+∠AEC＝360°，理由如下：由（1）可得，∠AFC＝∠BAF+∠DCF，∵AF平分∠BAE，CF平分∠DCE，∴∠BAE＝2∠BAF，∠DCE＝2∠DCF，∴∠BAE+∠DCE＝2∠AFC，由（2）可知，∠BAE+∠AEC+∠DCE＝360°，∴2∠AFC+∠AEC＝360°．②由①知∠F+∠F AE+∠E+∠FCE＝360°，∵∠BAF＝∠F AE，∠DCF＝∠FCE，∠BAF+∠DCF＝∠F，∴∠F＝（∠F AE+∠FCE），∴∠F AE+∠FCE＝n∠F，∴∠F+∠E+n∠F＝360°，∴（n+1）∠F＝360°﹣∠E＝360°﹣m，∴∠F＝．10．已知AM∥CN，点B在直线AM、CN之间，AB⊥BC于点B．（1）如图1，请直接写出∠A和∠C之间的数量关系：．（2）如图2，∠A和∠C满足怎样的数量关系？请说明理由．（3）如图3，AE平分∠MAB，CH平分∠NCB，AE与CH交于点G，则∠AGH的度数为45°．【解答】解：（1））过点B作BE∥AM，如图，∵BE∥AM，∴∠A＝∠ABE．∵BE∥AM，AM∥CN，∴BE∥CN．∴∠C＝∠CBE．∵AB⊥BC，∴∠ABC＝90°．∴∠A+∠C＝∠ABE+∠CBE＝∠ABC＝90°．故答案为：∠A+∠C＝90°；（2）∠A和∠C满足：∠C﹣∠A＝90°．理由：过点B作BE∥AM，如图，∵BE∥AM，∴∠A＝∠ABE．∵BE∥AM，AM∥CN，∴BE∥CN．∴∠C+∠CBE＝180°．∴∠CBE＝180°﹣∠C．∵AB⊥BC，∴∠ABC＝90°．∴∠ABE+∠CBE＝90°．∴∠A+180°﹣∠C＝90°．∴∠C﹣∠A＝90°．（3）设CH与AB交于点F，如图，∵AE平分∠MAB，∴∠GAF＝∠MAB．∵CH平分∠NCB，∴∠BCF＝∠BCN．∵∠B＝90°，∴∠BFC＝90°﹣∠BCF．∵∠AFG＝∠BFC，∴∠AFG＝90°﹣∠BCF．∵∠AGH＝∠GAF+∠AFG，∴∠AGH＝∠MAB+90°﹣∠BCN＝90°﹣（∠BCN﹣∠MAB）．由（2）知：∠BCN﹣∠MAB＝90°，∴∠AGH＝90°﹣45°＝45°．故答案为：45°．11．已知直线EF分别与直线AB，CD相交于点G，M，并且∠AGE+∠CHF＝180°．（1）如图1，求证：AB∥CD；（2）如图2，点M在直线AB，CD之间，连接GM，HM，求证：∠M＝∠AGM+∠CHM；（3）如图3，在（2）的条件下，若射线GH恰好是∠BGM的平分线，在MH的延长线上取点N，连接GN，若∠N＝∠AGM，则∠M、∠N、∠FGN的数量关系是（直接写答案）．【解答】（1）证明：∵∠AGE＝∠BGF，∠CHF＝∠EHD，又∠AGE+∠CHF＝180°，∴∠BGF+∠EHD＝180°，∴AB∥CD；（2）证明：过点M作MK∥CD，则∠KMH＝∠CHM，又AB∥CD；∴AB∥MK；∴∠AGM＝∠GMK，∵∠GMH＝∠AGM+∠KMH∴∠GMH＝∠AGM+∠CHM．（3）解：如图3，令∠AGM＝2α，∠CHM＝β，则∠N＝2α，∠M＝2α+β，∵射线GF是∠BGM的平分线，∴∠FGM＝∠BGM＝（180°−∠AGM）＝90°−α，∴∠AGH＝∠AGM+∠FGM＝2α+90°﹣α＝90°+α，∵∠GMH＝∠N+∠FGN，∴2α+β＝2α+∠FGN，∴∠FGN＝2β，∴∠M＝2α+β＝∠N+∠FGN，即：∠M＝∠N+∠FGN．12．问题情境我们知道，“两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补”，所以在某些探究性问题中通过“构造平行线”可以起到转化的作用．已知三角板ABC中，∠BAC＝60°，∠B＝30°，∠C＝90°，长方形DEFG中，DE∥GF．问题初探（1）如图（1），若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M，AB⊥DE于点N，求∠EMC的度数．分析：过点C作CH∥GF．则有CH∥DE，从而得∠CAF＝∠HCA，∠EMC＝∠MCH，从而可以求得∠EMC的度数．由分析得，请你直接写出：∠CAF的度数为，∠EMC的度数为．类比再探（2）若将三角板ABC按图（2）所示方式摆放（AB与DE不垂直），请你猜想写∠CAF 与∠EMC的数量关系，并说明理由．（3）请你总结（1），（2）解决问题的思路，在图（3）中探究∠BAG与∠BMD的数量关系？并说明理由．【解答】解：（1）由题可得，∠CAF＝∠BAF﹣∠BAC＝90°﹣60°＝30°，∠EMC＝∠BCH＝90°﹣30°＝60°；故答案为：30°，60°；（2）∠EMC+∠CAF＝90°，理由：证明：如图，过C作CH∥GF，则∠CAF＝∠ACH，∵DE∥GF，CH∥GF，∴CH∥DE，∴∠EMC＝∠HCM，∴∠EMC+∠CAF＝∠MCH+∠ACH＝∠ACB＝90°；（3）∠BAG﹣∠BMD＝30°，理由：证明：如图，过B作BK∥GF，则∠BAG＝∠KBA，∵BK∥GF，DE∥GF，∴BK∥DE，∴∠BMD＝∠KBM，∴∠BAG﹣∠BMD＝∠ABK﹣∠KBM＝∠ABC＝30°．13．已知AB∥CD，直线EF与AB、CD分别交于点E、F，点G为落在直线AB和直线CD 之间的一个动点．（1）如图1，点G恰为∠BEF和∠DFE的角平分线的交点，则∠EGF＝；（2）若点G恰为∠BEF和∠DFE的三等分线的交点，有如下结论：①∠EGF一定为钝角；②∠EGF可能为60°；③若∠EGF为直角，则EF⊥CD．其中正确结论的序号为．（3）进一步探索，若EF⊥CD，且点G不在线段EF上，记∠AEG＝α，∠CFG＝β，EM 为∠AEG最接近EG的n等分线，FN是∠CFG最接近CF的n等分线（其中n≥2）．直线EM、FN交于点P n，是否存在某一正整数n，使得∠EP n F＝90°？说明理由．【解答】解：（1）∵AB∥CD，∴∠BEF+∠DFE＝180°，∵点G恰为∠BEF和∠DFE的角平分线的交点，∴∠FEG+∠EFG＝×180°＝90°，∴∠EGF＝180°﹣90°＝90°．故答案为：90°．（2）若点G恰为∠BEF和∠DFE的三等分线的交点，∴∠FEG+∠EFG＝×180°或者∠FEG+∠EFG＝×180°，∠FEG+∠EFG＝60°或∠FEG+∠EFG＝120°，∴∠EGF＝180°﹣60°＝120°或∠EGF＝180°﹣120°＝60°，∴①错误，②正确，当∠EGF为直角，只有∠BEF+∠DFE＝90°或∠BEF+∠DFE＝90°，不妨假设∠BEF+∠DFE＝90°，∴∠BEF+∠DFE＝90°，∴（∠BEF﹣∠DFE）+（∠DFE﹣∠BEF）＝0，∴∠BEF＝∠DFE，∵∠BEF+∠DFE＝180°，∴∠BEF＝∠DFE＝90°，∴EF⊥CD，故③正确．故答案为：②③．（3）不存在某一整数n，使得∠EP n F＝90°，理由如下：∵EM为∠AEG最接近EG的n等分线，FN是∠CFG最接近CF的n等分线（其中n≥2），∴∠AEM＝α，∠CFM＝β．①当点G在EF的左侧，此时α＜90°，β＜90°，P n必在EF的左侧，如图2所示，过点P n作P n Q∥AB，∵AB∥CD，∴P n Q∥CD，∴∠EP n F＝∠EPnQ+∠FP n Q＝∠AEM+∠CFN＝α+β＜×90°+×90°＜90°，②当点G在右侧，此时α＞90°，β＞90°．若α＜90°，则P n在EF的左侧，如图3中，同理可得∠EP n F＝α+β＞90°．若α＝90°，则P n与F重合，不存在∠EP n F，舍弃．若α＞90°，则P n在EF的右侧，如图4中，过点P n作P n Q∥AB，∵AB∥CD，∴P n Q∥CD，∴∠EP n F＝∠EP n Q﹣∠FP n Q＝∠BEM+∠CFN＝（180°﹣α）﹣β，∵α＞90°，β＞0，∴（180°﹣α）﹣β＜90°，即∠EP n F＜90°，综上所述，不存在某一整数n，使得∠EP n F＝90°．。

平行线四大模型(完整版+培优)平行线四大模型模型一：铅笔模型当点P在EF右侧，在AB、CD内部时，有以下结论：1.若AB∥CD，则∠P+∠AEP+∠PFC=360°；2.若∠P+∠AEP+∠PFC=360°，则AB∥CD.模型二：猪蹄模型当点P在EF左侧，在AB、CD内部时，有以下结论：1.若AB∥CD，则∠P=∠AEP+∠CFP；2.若∠P=∠AEP+∠CFP，则AB∥CD.模型三：臭脚模型当点P在AB、CD之间时，有以下结论：1.若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；2.若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.模型四：骨折模型当点P在EF右侧，在AB、CD外部时，有以下结论：1.若AB∥CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；2.若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.当点P在EF左侧，在AB、CD外部时，有以下结论：1.若AB∥CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；2.若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.应用：例1：1.∠l+∠2+∠3=180°；2.∠E=110°；3.∠BCD=40°；4.∠P=70°.练：1.∠EAB的度数为17°；2.∠C=30°；3.∠P=30°+n×20°.例2：BF、DF分别平分∠ABC、∠XXX，则∠C、∠F的关系为∠ABF=∠XXX∠XXX.练：1.∠XXX∠BDE；2.当n=2时，∠C=∠F；3.∠C=n×∠F.1.如图，已知AB∥CD，BE平分∠ABC，DE平分∠ADC，要证明∠E=2(∠A+∠C)。

2.如图，已知AB∥DE，BF、DF分别平分∠ABC、∠XXX，要求出∠C、∠F的关系。

专题01平行线（四种模型）专项训练题型一：M 模型（锯齿形） 题型二：笔尖型题型三：“鸡翅”型 题型四：“骨折”型模型一：M 模型如图，若 AB // CD ，你能确定∠B 、∠D 与∠BED 的大小关系吗？解：∠B ＋∠D ＝∠DEB ．理由如下：过点E 作 EF // AB又 ∵ AB//CD ．∴ EF//CD ．∴ ∠D =∠DEF ．∠B=∠BEF ．∴∠B ＋∠D ＝∠BEF ＋∠DEF ＝∠DEB即∠B ＋∠D ＝∠DEB ．一．选择题（共3小题）1．（2023春•临淄区期末）如图，//AB EF ，90C Ð=°，则a 、b 和g 的关系是( )A ．b a g =+B ．180a b g ++=°C ．90a b g +-=°D ．180b g a +-=°【分析】此题可以构造辅助线，利用三角形的外角的性质以及平行线的性质建立角之间的关系．【解答】解：延长DC 交AB 与G ，延长CD 交EF 于H ．在直角BGC D 中，190a Ð=°-；EHD D 中，2b g Ð=-，//AB EF Q ，12\Ð=Ð，90a b g \°-=-，即90a b g +-=°．故选：C ．【点评】本题考查的是平行线的性质，根据题意作出辅助线是解答此题的关键．2．（2023春•天宁区校级期中）如图，//AB CD ，EMNF 是直线AB 、CD 间的一条折线．若140Ð=°，260Ð=°，370Ð=°，则4Ð的度数为( )A ．55°B ．50°C ．40°D ．30°【分析】过M 作//OM AB ，//PN AB ，根据平行线的性质得到1EMO Ð=Ð，4PNF Ð=Ð，OMN PNM Ð=Ð，由角的和差得到(1)(4)14EMN MNF MNP MNP Ð-Ð=Ð+Ð-Ð+Ð=Ð-Ð，代入数据即可得到结论．【解答】解：如图2，过M 作//OM AB ，//PN AB ，//AB CD Q ，//////AB OM PN CD \，1EMO \Ð=Ð，4PNF Ð=Ð，OMN PNM Ð=Ð，(1)(4)14EMN MNF MNP MNP \Ð-Ð=Ð+Ð-Ð+Ð=Ð-Ð，6070404\°-°=°-Ð，450\Ð=°．故选：B ．【点评】本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键．3．（2022春•海安市校级月考）如图，//AB EF ，90C Ð=°，则a 、b 、g 的关系为( )A ．b a g =+B ．90a b g +-=°C ．180a b g ++=°D ．90b g a +-=°【分析】此题可以构造辅助线，利用三角形的外角的性质以及平行线的性质建立角之间的关系．【解答】解：延长DC 交AB 于G ，延长CD 交EF 于H ．直角BGC D 中，190a Ð=°-；EHD D 中，2b g Ð=-，//AB EF Q ，12\Ð=Ð，90a b g \°-=-，即90a b g +-=°．故选：B ．【点评】此题主要考查了三角形的外角的性质以及平行线的性质，解题的关键是通过作辅助线，构造了三角形以及由平行线构成的内错角．二．解答题（共6小题）4．（2023春•仪征市期末）如图1，已知线段AB 、线段CD 被直线l 所截于点A 、点C ，150Ð=°，2Ð的度数是1Ð的3倍少20°．（1）求证：//AB CD ；（2）如图2，连接BD ，AB 沿BD 方向平移得到EF ，点F 在BD 上，点G 是BD 上的一点，连接AG 、EG ，30BAG Ð=°，20FEG Ð=°，求AGE Ð的度数；（3）如图3，点M 是线段BD 上一点，点N 是射线CD 上一点，CAM Ð度数为k ，AMN Ð度数为m ，MND Ð度数为n ，请直接写出k 、m 、n 之间的数量关系．（本题的角均小于180)°【分析】（1）根据已知先求得1Ð的邻补角BAC Ð的度数，得到2BAC Ð=Ð即可得结论；（2）过G 作//GQ AB ，利用平行线的性质定理和平行公理的推论即可；（3）利用平行线的性质定理和平行公理的推论即可．【解答】证明：（1）150Ð=°Q ，2Ð的度数是1Ð的3倍少20°，23120130\Ð=Ð-°=°，180250ACD \Ð=°-Ð=°，12\Ð=Ð，//AB CD \；（2）过G 作//GQ AB ，30AGQ BAG \Ð=Ð=°，//AB EF Q ，//GQ EF \，20GEF EGQ \Ð=Ð=°，50AGE AGQ EGQ \Ð=Ð+Ð=°；（3）//AB CD Q ，与（2）同理可得：AMN MAB MND Ð=Ð+Ð，AMN m Ð=Q ，MND n Ð=，m n MAB \=+Ð，150Ð=°Q ，CAM k Ð=，180118050BAM CAM k \Ð=°-Ð-Ð=°-°-，130m n k \=+°-，即130m n k -+=°．【点评】本题考查了平行线的性质定理及平行公理的推论，理解题意是解决问题的关键．5．（2022春•赣榆区期末）已知：如图，//AB CD ，BFE FEC Ð=Ð．求证：ABF DCE Ð=Ð．（1）下面是小明同学的推理过程，请按先后顺序填写空格：解：连接BC ．BFE FEC Ð=ÐQ （已知），\　BF　// （内错角相等，两直线平行）．\Ð=Ð )，FBC ECB(AB CDQ（已知），//\Ð=Ð（两直线平行，内错角相等）ABC DCB\Ð-Ð=Ð- ( )，ABC FBC DCB即ABF DCEÐ=Ð．（2）试用其他方法进行推理，并书写证明过程．【分析】（1）连接BC，根据已知，得出//AB CDÐ=Ð，再根据//BF CE，根据平行线的性质得到FBC ECB得出ABC DCBÐ-Ð=Ð-Ð即可得出答案；Ð=Ð，进而得出ABC FBC DCB ECBÐ=Ð，再利用等量代换可得H DCE （2）延长BF交DC的延长线于H，根据平行线的性质可得ABF HÐ=Ð，进而可判定//Ð=Ð．BH CE，然后可得BFE FEC【解答】（1）解：连接BC．BFE FECQ（已知），Ð=ÐBF CE\（内错角相等，两直线平行）．//FBC ECB\Ð=Ð两直线平行，内错角相等），(Q（已知），//AB CD\Ð=Ð（两直线平行，内错角相等）ABC DCBABC FBC DCB ECB\Ð-Ð=Ð-Ð等式的基本性质），(即ABF DCEÐ=Ð．故答案为：BF，CE；两直线平行，内错角相等；ECBÐ；等式的基本性质．（2）证明：延长BF交DC的延长线于H，Q，AB CD//\Ð=Ð，ABF HABF DCE Ð=ÐQ ．H DCE \Ð=Ð，//BH CE \，BFE FEC \Ð=Ð．【点评】本题考查了平行线的判定和性质，熟练应用判定定理和性质定理是解题的关键，平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．6．（2023春•天宁区校级期中）已知：如图，180ABE CEB Ð+Ð=°，12Ð=Ð，求证：M N Ð=Ð．【分析】首先证明//AB CD ，再根据平行线的性质得出ABE DEB Ð=Ð，然后结合已知条件可得到MBE NEB Ð=Ð，进而可判定//BM EN ，据此可得出结论．【解答】证明：180ABE CEB Ð+Ð=°Q ，//AB CD \，ABE DEB \Ð=Ð，即：12MBE NEB Ð+Ð=Ð+Ð，又12Ð=ÐQ ，MBE NEB \Ð=Ð，//BM EN \，M N \Ð=Ð．【点评】此题主要考查了平行线的判定和性质，解答此题的关键是准确识图，熟练掌握平行线的判定及性质：两直线平行Û同位角相等，两直线平行Û内错角相等，两直线平行Û同旁内角互补．7．（2023春•崇川区期中）如图1，已知直线EF 与直线AB 交于点E ，与直线CD 交于点F ，EM 平分AEF Ð交直线CD 于点M ，且FEM FME Ð=Ð．（1）试判断直线AB 与CD 的位置关系，并说明理由；（2）点G 是射线MD 上的一个动点（不与点M ，F 重合），EH 平分FEG Ð交直线CD 于点H ，过点H 作//HN EM 交直线AB 于点N ．设EHN a Ð=，EGF b Ð=．①如图2，当点G 在点F 的右侧，且50a =°时，求b 的值；②当点G 在运动过程中，a 和b 之间有怎样的数量关系？请写出你的猜想，并加以证明．【分析】（1）由EM 平分AEF Ð，得到AEM FEM Ð=Ð，又FEM FME Ð=Ð，所以AEM FME Ð=Ð，证得//AB CD ．（2）①由EH 平分FEG Ð，EM 平分AFE Ð，得到12HEM HEF FEM AEG Ð=Ð+Ð=Ð，由//HN EM ，//AB CD 可得，HEM EHN a Ð=Ð=，GEB EGF b =Ð=，即可得到结果．②当点G 在点F 的左侧时，由EM 平分AEF Ð，EH 平分FEH Ð，得到12HEM HEF FEM AEG Ð=Ð+Ð=Ð，由//AB CD ，//HN EM ，得到AEG b Ð=，HEM a Ð=，从而得到结果．【解答】解（1）如图1，//AB CD ，理由如下：EM Q 平分AEF Ð，AEM FEM \Ð=Ð，FEM FME Ð=ÐQ ，AEM FME \Ð=Ð，//AB CD \．（2）①如图2，EH Q 平分FEG Ð，12HEF FEG \Ð=Ð，EM Q 平分AFE Ð，12FEM AEF \Ð=Ð，12HEM HEF FEM AEG \Ð=Ð+Ð=Ð，//HN EM Q ，HEM EHN a \Ð=Ð=，//AB CD Q ，GEB EGF b \Ð=Ð=，1(180)2a b \=°-，180218025080b a \=°-=°-´°=°．②a 和b 之间的数量关系为2b a =或1802b a =°-．理由如下：当点G 在点F 的右侧时，由①得1802b a =°-，当点G 在点F 的左侧时，如图3，EM Q 平分AEF Ð，2AEF FEM \Ð=Ð，EH Q 平分FEH Ð，2GEF HEF \Ð=Ð，222AEG AEF GEF FEM HEF HEM \Ð=Ð-Ð=Ð-Ð=Ð，//AB CD Q ，AEG b \Ð=，//HN EM Q ，HEM a \Ð=，2b a \=，综上得，a 和b 之间的数量关系为2b a =或1802b a =°-．【点评】本题主要考查了平行线的判定与性质，角平分线的定义，熟练运用平行线的判定与性质是解题关键．8．（2023春•海安市期末）如图，在ABC D 中，ACB BAC Ð=Ð．过点A 作//MN BC ．（1）判断AC 是否平分BAN Ð，并说明理由；（2）如图2，点D 是射线CB 上一动点（不与点B ，C 重合），AE 平分BAD Ð交射线BC 于E ，过点E 作EF AC ^于F ．①当点D 在点B 左侧时，若20AEF Ð=°，求ADB Ð的度数；②点D 在运动过程中，AEF Ð和ADB Ð之间有怎样的数量关系？请写出你的猜想，并说明理由．【分析】（1）根据//MN BC 得ACB CAN Ð=Ð，结合已知条件得证；（2）①在直角三角形AFE 中，20AEF Ð=°，则9070EAF EAF Ð=°-Ð=°，根据19020702EAF BAC BAE DAE CAN DAN Ð=Ð+Ð=°-°=°=Ð+Ð=Ð，从而求出140DAN Ð=°，即可求出ADB Ð；②分两种情况进行讨论，当点D 在点B 左侧时和点D 在点B 右侧时，数形结合即可解答．【解答】解：（1）AC 平分BAN Ð，//MN BC Q ，ACB CAN \Ð=Ð，ACB BAC Ð=ÐQ ．BAC CAN \Ð=Ð，AC \平分BAN Ð，（2）EF AC ^Q ，9070EAF EAF \Ð=°-Ð=°，AC Q 、AE 是角平分线，DAE BAE \Ð=Ð，BAC CAN Ð=Ð，19020702EAF BAC BAE DAE CAN DAN \Ð=Ð+Ð=°-°=°=Ð+Ð=Ð，140DAN \Ð=°，40ADB \Ð=°．②设AEF a Ð=，EF AC ^Q ，90EAF a \Ð=°-，如图2，当点D 在点B 左侧时，由（1）知12NAC BAC BAN Ð=Ð=Ð，AE Q 平分BAD Ð交射线BC 于E ，12DAE BAE BAD \Ð=Ð=Ð，又1111()902222EAF BAE BAC BAD BAN BAD BAN DAN a Ð=Ð+Ð=Ð+Ð=Ð+Ð=Ð=°-Q ，1802DAN a \Ð=°-，//MN BC Q ，180ADB DAN \Ð+Ð=°，180180(1802)2ADB DAN a a \Ð=°-Ð=°-°-=，2ADB AEF \Ð=Ð；当点D 在点B 右侧时，如图：AC Q 、AE 是角平分线，12DAE BAE BAD \Ð=Ð=Ð，12BAC CAN BAN Ð=Ð=Ð，1111()902222EAF BAC BAE BAN BAD BAN BAD DAN a Ð=Ð-Ð=Ð-Ð=Ð-Ð=Ð=°-Q ，1802DAN a \Ð=°-，//MN BC Q ，1802ADB DAN a \Ð=Ð=°-，1802ADB AEF \Ð=°-Ð．综上，2ADB AEF Ð=Ð或1802AEF °-Ð．【点评】本题主要考查了平行线的性质与判定，角平分线的定义的运用，解决问题的关键是掌握两直线平行内错角相等，两直线平行同旁内角，利用角的和差关系进行推理论证．9．（2023春•姜堰区期末）已知12//l l ，李想同学将ABC D 放置在这两条平行线上展开探究，其中ABC D 三边与两条平行线分别交于点D 、E 、F 、G ．（1）【特例探究】如图1，90C Ð=°．①CED CGF Ð+Ð=　270　度；②若CED Ð与CGF Ð的角平分线相交于点P ，则EPG Ð= 度；（2）【一般探索】如图2，C a Ð=，EPG b Ð=．①若13DEP CED Ð=Ð，13FGP CGF Ð=Ð，求a 与b 的关系；②若1DEP CED n Ð=Ð，1(2FGP CGF n nÐ=Ð…且n 为整数），直接写出a 与b 的关系 ；（3）【拓展应用】如图3，CED Ð与CGF Ð的角平分线相交于点1P ，1PED Ð与1PGF Ð的角平分线相交于点2P ，2P ED Ð与2P GF Ð的角平分线相交于点3P ；¼，以此类推，则2023360C EP G°-ÐÐ的值是多少？（直接写出结果）【分析】（1）①作1//CM l 根据平行线的性质可得180CED ECM Ð+Ð=°，_180CGF GCM Ð+Ð=°两式相加即可得360CED CGF C Ð+Ð=°-Ð；②由①知：360CED CGF C Ð+Ð=°-Ð，再根据平行线的性质以及角平分线的定义即可得：1()2EPG CED CGF Ð=Ð+Ð化简整理即可；（2）①13DEP CED Ð=Ð，13FGP CGF Ð=Ð时，结合（1）中的结论和平行线的性质，可得a 与b 之间的关系；②类似于前面的证明，结合平行线的性质和角平分线的定义即可得结论；（3）根据角平分线的定义和平行线的性质找到规律即可得结论．【解答】解：（1）①作1//CM l，180CED ECM \Ð+Ð=°，2l Q //1l ，2//CM l \，_180CGF GCM \Ð+Ð=°，360CED ECM CGF GCM \Ð+Ð+Ð+Ð=°，90ECG ECM CGF Ð=Ð+Ð=°Q ，_90360CED CGF \Ð+Ð+°=°，270CED CGF \Ð+Ð=°，故答案为270°；②CED ÐQ 与CGF Ð的角平分线相交于点P ，2CED CEP \Ð=Ð，2CGF CGP Ð=Ð，由①知：270CED CGF Ð+Ð=°，22270CEP CGP \Ð+Ð=°，135CEP CGP \Ð+Ð=°，360CEP CGP EPG ECG Ð+Ð+Ð+Ð=°Q ，135EPF \Ð=°；（2）21//l l Q ，ECG a Ð=，由（1）①知360CED CGF ECF Ð+Ð+Ð=°，360360CED CGF ECG a \Ð+Ð=°-Ð=°-，由（1）②知若13DEP CED Ð=Ð，13FGP CGF Ð=Ð，\23CED CEP Ð=Ð，23CGF CGP Ð=Ð，2222()(360)3333CEP CGP CED CGF CED CGF a \Ð+Ð=Ð+Ð=Ð+Ð=°-，360CEP CGP EPG ECG Ð+Ð+Ð+Ð=°Q ，\2(360)3603a b a °-++=°，整理得：3360a b +=°；②若1DEP CED n Ð=Ð，1(2FGP CGF n nÐ=Ð…且n 为整数）时，由①同理可得a 与b 的关系：360n a b +=°；（3）通过前面的证明易得360360CED CGF C a Ð+Ð=°-Ð=°-，当CED Ð与CGF Ð的角平分线相交于点1P ，1PED Ð与1PGF Ð的角平分线相交于点2P ，2P ED Ð与2P GF Ð的角平分线相交于点3P ；¼，以此类推，则111111()()(360)222EPG CED CGF CED CGF a Ð=Ð+ÐÐ+Ð=°-，222111()())(360)422EP G CED CGF CED CGF a Ð=Ð+Ð=Ð+Ð==°-，333111()())(360)822EP G CED CGF CED CGF a Ð=Ð+Ð=Ð+Ð=°-，444111()())(360)1622EP G CED CGF CED CGF a Ð=Ð+Ð=Ð+Ð=°-，551(360)2EP G a Ð=°-，.....．1(360)2n nEP G a Ð=°-，当2023n =时，202320231(360)2EP G a Ð=°-，\20232023202336036021(360)2C EP G a a °-а-==а-，【点评】本题考查了平行线的性质，以及角平分线的定理，灵活运用所学知识找到规律是解决问题的关键．模型二、笔尖型如图，AB // CD ，探索∠B 、∠D 与∠DEB 的大小关系 ？解：∠B ＋∠D ＋∠DEB ＝360°．理由如下：过点E 作 EF // AB．又∵AB//CD．∴EF//CD．∴∠B+∠BEF＝180°．∠D+∠DEF＝180°．∴∠B＋∠D+∠DEB＝∠B＋∠D+∠BEF＋∠DEF ＝360°．即∠B＋∠D＋∠DEB＝360°．一．选择题（共3小题）1．（2022春•海陵区期末）如图//a b，M、N分别在a、b上，P为两平行线间一点，那么Ð+Ð+Ð= )123(A．180°B．270°C．360°D．540°【分析】首先过点P作//PA a，构造三条平行线，然后利用两直线平行，同旁内角互补进行做题．【解答】解：过点P作//a b PA，PA a，则////Ð+Ð=°，1180NPA\Ð+Ð=°，3180MPA\Ð+Ð+Ð=°．123360故选：C．【点评】两直线平行时，应该想到它们的性质，由两直线平行的关系得到角之间的数量关系，从而达到解决问题的目的．2．（2023春•沭阳县期末）如图，把一块含有30°角的直角三角板的两个顶点放在直尺的对边上．如果137Ð=°，那么2Ð的度数是( )A．30°B．25°C．23°D．37°【分析】根据平行线的性质，两直线平行，内错角相等，进而可以得出答案．【解答】解：如图，Q直尺的两条边平行，137Ð=°，\Ð=Ð=°，1337Q直角三角板的一个角为30°，\Ð+Ð=°，2360\Ð=°-°=°，2603723故选：C．【点评】本题主要考查了平行线的性质，注意隐含条件，直尺的两条对边平行和直角三角板的一个锐角是30°是解题的关键．3．（2023春•东台市月考）某小区车库门口的“曲臂直杆道闸”（如图）可抽象为如图所示模型．已知AB 垂直于水平地面AE．当车牌被自动识别后，曲臂直杆道闸的BC段将绕点B缓慢向上抬高，CD段则一直保持水平状态上升（即CD与AE始终平行），在该运动过程中ABC BCDÐ+Ð的度数始终等于( )度A．360B．180C．250D．270【分析】过点B作//Ð+Ð=°，从而可C CBGBG AE，利用平行线的性质可得180BAE ABGÐ+Ð=°，180得360BAEÐ=°，最后进行计算即可解答．Ð+Ð+Ð=°，然后根据垂直定义可得90BAE ABC BCD【解答】解：过点B作//BG AE，BAE ABG\Ð+Ð=°，180AE CDQ，//\，BG CD//\Ð+Ð=°，180C CBG\Ð+Ð+Ð+Ð=°，BAE ABG CBG C360BAE ABC BCD\Ð+Ð+Ð=°，360^Q，BA AE\Ð=°，90BAE\Ð+Ð=°-Ð=°，ABC BCD BAE360270故选：D．【点评】本题考查了平行线的性质，熟练掌握铅笔模型是解题的关键．二．填空题（共3小题）4．（2022春•崇川区校级月考）如图，直线//Ð=°，则3Ð=　78　度，Ð=°，250a b，128Ð+Ð+Ð= 度．345【分析】过3Ð的顶点作已知直线的平行线，充分运用平行线的性质，不难发现：312Ð=Ð+Ð，Ð+Ð+Ð=°345360【解答】解：如图所示：过3Ð的顶点作//c a，a bQ，//\，a b c////Ð=Ð，16\Ð=Ð，72又367Ð=Ð+Ð，\Ð=Ð+Ð=°；31278又4675180Ð+Ð=Ð+Ð=°\Ð+Ð+Ð=°．345360【点评】注意此类题中常见的辅助线：构造已知直线的平行线．根据平行线的性质发现并证明：312Ð=Ð+Ð；345360Ð+Ð+Ð=°．5．（2022春•淮安期末）如图，//Ð和AB CD，E、F分别是AB、CD上的点，EH、FH分别是AEGÐ=　125　°．GÐ=°，则HCFGÐ的角平分线．若110【分析】过点G作//CD GM，Ð+Ð=°，再结合已知可得// GM AB，根据平行线的性质可得180AEG EGM然后利用平行线的性质可得180Ð+Ð=°，再利用角平分线的定AEG CFGÐ+Ð=°，从而可得250CFG MGF义可得125Ð+Ð=°，最后利用四边形的内角和定理进行计算即可解答．HEG GFH【解答】解：过点G作//GM AB，\Ð+Ð=°，AEG EGM180Q，//AB CD//CD GM \，180CFG MGF \Ð+Ð=°，360AEG EGM CFG MGF \Ð+Ð+Ð+Ð=°，110EGF EGM MGF Ð=Ð+Ð=°Q ，360250AEG CFG EGF \Ð+Ð=°-Ð=°，EH Q 、FH 分别是AEG Ð和CFG Ð的角平分线，12HEG AEG \Ð=Ð，12GFH CFG Ð=Ð，1112522HEG GFH AEG CFG \Ð+Ð=Ð+Ð=°，360125H HEG HFG EGF \Ð=°-Ð-Ð-Ð=°，故答案为：125．【点评】本题考查了平行线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．6．（2023春•邗江区期中）将一副三角板如图1所示摆放，30BAC Ð=°，45E Ð=°，直线//GH MN ，现将三角板ABC 绕点A 以每秒1°的速度顺时针旋转，同时三角板DEF 绕点D 以每秒3°的速度顺时针旋转，如图2，设时间为t 秒，当0120t ……时，若边BC 与三角板DEF 的一条直角边（边DE ，)DF 平行，则所有满足条件的t 的值为 15或105或60　．【分析】先根据题意画出旋转后的图形，由已知条件，利用平行线的旋转，求出旋转角之间的关系，列出方程解答即可．【解答】解：由题意得：30HAC BAH BAC t Ð=Ð+Ð=°+°，3FDM t Ð=°，（1）当//BC DE 时，如图所示：延长AC 交MN 于点P ，①DE 在MN 上方，//DE BC Q ，DE DF ^，AC BC ^，//AP DF \，FDM MPA \Ð=Ð，//MN GH Q ，MPA HAC \Ð=Ð，FDM HAC \Ð=Ð，即330t t =+，15t =；②1DE 在MN 下方时，1(3180)F DP t Ð=-°，1//DE BC Q ，11DE DF ^，AC BC ^，1//AP DF \，1F DM MPA \Ð=Ð，//MN GH Q ，MPA HAC \Ð=Ð，1F DM HAC \Ð=Ð，即318030t t -=+，解之得：105t =；如图：当//BC DF 时，延长AC 交MN 于点I ，①DF 在MN 上方，(1803)FDN t Ð=-度，//DF BC Q ，AC BC ^，//AI DE \，90FDN MIA \Ð+Ð=°，//MN GH Q ，MIA HAC \Ð=Ð，90FDN HAC \Ð+Ð=°，即18033090t t -++=，解之得：60t =；②DF 在MN 下方，2(1803)F DN t Ð=-度，2//DF BC Q ，AC BC ^，22ED DF ^，2//AC DE \，2AIM MDE \Ð=Ð，//MN GH Q ，MIA HAC \Ð=Ð，2E DM HAC \Ð=Ð，即318030t t -=+，解之得：105t =，综上可知：所有满足条件的t 的值为：15或105或60，故答案为：15或105或60．【点评】本题主要考查了平行线的性质，解题关键是根据题意，画出旋转后的图形．三．解答题（共3小题）7．（2022春•海州区校级期中）如图，在ABC D 中，点D 、E 分别在AB 、BC 上，且//DE AC ，12Ð=Ð．求证：//AF BC ．【分析】根据平行线的性质得出1C Ð=Ð，求出2C Ð=Ð，根据平行线的判定得出即可．【解答】证明：//DE AC Q ，1C \Ð=Ð，12Ð=ÐQ ，2C \Ð=Ð，//AF BC \．【点评】本题考查了平行线的判定和性质，熟练应用判定定理和性质定理是解题的关键，平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．8．（2023春•盐都区期中）如图，在ABC D 中，点D 、E 分别在AB 、BC 上，//AF BC ，12Ð=Ð，求证：//DE AC ．【分析】由两直线平行内错角相等得到1C Ð=Ð，再根据同位角相等两直线平行可解题．【解答】证明：//AF BC Q ，1C \Ð=Ð，12Ð=ÐQ ，2C \Ð=Ð，//DE AC \．【点评】本题考查平行线的判定与性质，是重要考点，掌握相关知识是解题关键．9．（2022春•亭湖区校级月考）如图，已知1BDC Ð=Ð，23180Ð+Ð=°．（1）AD 与EC 平行吗？试说明理由．（2）若DA 平分BDC Ð，DA FA ^于点A ，182Ð=°，试求FAB Ð的度数．【分析】（1）直接利用平行线的判定与性质得出//AB CD ，进而得出3180ADC Ð+Ð=°，即可得出答案；（2）利用角平分线的定义结合平行线的性质得出2Ð，即可得出答案．【解答】（1）解：AD 与EC 平行，理由如下：1BDC Ð=ÐQ ，//AB CD \（同位角相等，两直线平行），2ADC \Ð=Ð（两直线平行，内错角相等），23180Ð+Ð=°Q ，3180ADC \Ð+Ð=°（等量代换），//AD CE \（同旁内角互补，两直线平行）；（2）解：1BDC Ð=ÐQ ，182Ð=°，82BDC \Ð=°，DA Q 平分BDC Ð，1412ADC BDC \Ð=Ð=°（角平分线定义），241ADC \Ð=Ð=°（已证），又DA FA ^Q ，90FAD \Ð=°（垂直定义），2904149FAB FAD \Ð=Ð-Ð=°-°=°．【点评】此题主要考查了平行线的判定与性质，正确得出90AEC FAD Ð=Ð=°是解题关键．模型三、“鸡翅”型如图，已知AB//CD ，试猜想∠A 、∠E 、∠C 的关系，并说明理由．解：∠AEC=∠A-∠C,理由如下：过点E 作 EF // AB又 ∵AB//CD ．∴EF//CD ．∴∠A+∠FEA=180°，∠C+∠FEC=180°∴ ∠AEC ＝ ∠FEC- ∠FEA= 180°- ∠C –(180°-∠A)=∠A-∠C即：∠AEC=∠A-∠C一、单选题1．（2021下·湖南株洲·七年级统考期末）①如图1，AB ∥CD ，则360A E C Ð+Ð+Ð=°；②如图2，AB ∥CD ，则P A C Ð=Ð-Ð；③如图3，AB ∥CD ，则1E A Ð=Ð+Ð；④如图4，直线AB ∥CD ∥ EF ，点O 在直线EF 上，则180a b g Ð-Ð+Ð=°．以上结论正确的个数是（ ）A．1个B．2个C．3个D．4个【答案】C【分析】①过点E作直线EF∥AB，由平行线的性质：两直线平行，同旁内角互补，即可得出结论；②如图2，先根据三角形外角的性质得出∠1＝∠C+∠P，再根据两直线平行，内错角相等即可作出判断；③如图3，过点E作直线EF∥AB，由平行线的性质可得出∠A+∠AEC﹣∠1＝180°，即得∠AEC＝180°+∠1﹣∠A；④如图4，根据平行线的性质得出∠α＝∠BOF，∠γ+∠COF＝180°，再利用角的关系解答即可．【详解】解：①如图1，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A+∠1＝180°，∠2+∠C＝180°，∴∠A+∠1+∠2+∠C＝360°，∴∠A+∠AEC+∠C=360°，故①正确；②如图2，∵∠1是△CEP的外角，∴∠1＝∠C+∠P，∵AB∥CD，∴∠A＝∠1，即∠P＝∠A﹣∠C，故②正确；③如图3，过点E作直线EF∥AB，∵AB∥CD，∴AB∥CD∥EF，∴∠A +∠3＝180°，∠1＝∠2，∴∠A +∠AEC ﹣∠1＝180°，即∠AEC ＝180°+∠1﹣∠A ，故③错误；④如图4，∵AB ∥EF ，∴∠α＝∠BOF ，∵CD ∥EF ，∴∠γ+∠COF ＝180°，∵∠BOF ＝∠COF +∠β，∴∠COF ＝∠α﹣∠β，∴∠γ+∠α﹣∠β＝180°，故④正确；综上结论正确的个数为3，故选：C ．【点睛】本题考查的是平行线的性质及三角形外角的性质，熟练掌握平行线的性质，根据题意作出辅助线是解答此题的关键．二、解答题2．（2021下·浙江台州·七年级统考期末）如图，已知AD AB ^于点A ，AE ∥CD 交BC 于点E ，且EF AB ^于点F ．求证：12C Ð=Ð+Ð．证明：∵AD AB ^于点A ，EF AB ^于点F ，（已知）∴90DAB EFB Ð=Ð=°．（垂直的定义）∴AD ∥EF ，（ ）∴__________1=Ð（ ）∵AE ∥CD ，（已知）∴C Ð=________．（两直线平行，同位角相等）∵2AEB AEF Ð=Ð+Ð，∴12C Ð=Ð+Ð．（等量代换）【答案】见解析Q 1PE l ∥，12l l ∥，\12PE l l ∥∥，PAC APE \Ð=Ð，PBD BPE Ð=Ð，APB APE BPE Ð=Ð+ÐQ ，PAC PBD APB \Ð+Ð=Ð．（2）解：结论：当点P 在直线1l 上方时，Ð-Ð=ÐPBD PAC APB ；当点P 在直线2l 下方时，Ð-Ð=ÐPAC PBD APB ．①当点P 在直线1l 上方时，如图2所示．过点P 作1PE l ∥．Q 1PE l ∥，12l l ∥，\12PE l l ∥∥，PAC APE \Ð=Ð，PBD BPE Ð=Ð，APB BPE APE Ð=Ð-ÐQ ，PBD PAC APB \Ð-Ð=Ð．②当点P 在直线2l 下方时，如图3所示．过点P 作1PE l ∥．Q 1PE l ∥，12l l ∥，\12PE l l ∥∥，PAC APE \Ð=Ð，PBD BPE Ð=Ð，APB APE BPE Ð=Ð-ÐQ ，PAC PBD APB \Ð-Ð=Ð．【点睛】本题考查了平行线的性质以及角的计算，解题的关键是根据“两直线平行，内错角相等”找到相等的角．本题属于基础题，难度不大，解决该题型题目时，根据平行线的性质得出相等（或互补）的角是关键．4．（2021下·广东东莞·七年级东莞市光明中学校考期中）（1）如图（1）AB CD P ，猜想BPD Ð与B D ÐÐ、的关系，说出理由．（2）观察图（2），已知AB CD P ，猜想图中的BPD Ð与B D ÐÐ、的关系，并说明理由．（3）观察图（3）和（4），已知AB CD P ，猜想图中的BPD Ð与B D ÐÐ、的关系，不需要说明理由．【答案】（1）360B BPD D Ð+Ð+Ð=°，理由见解析；（2）BPD B D Ð=Ð+Ð，理由见解析；（3）图（3）BPD D B Ð=Ð-Ð，图（4）BPD B DÐ=Ð-Ð【分析】（1）过点P 作EF AB ∥，得到180B BPE Ð+Ð=°，由AB CD P ，EF AB ∥，得到EF CD P ，得到180EPD D Ð+Ð=°，由此得到360B BPD D Ð+Ð+Ð=°；（2）过点P 作PE AB P ，由PE AB CD ∥∥，得到12B D Ð=ÐÐ=Ð，，从而得到结论12BPD B D Ð=Ð+Ð=Ð+Ð；（3）由AB CD P ，根据两直线平行，内错角相等与三角形外角的性质，即可求得BPD Ð与B D ÐÐ、的关系．【详解】（1）解：猜想360B BPD D Ð+Ð+Ð=°．理由：过点P 作EF AB ∥，∴180B BPE Ð+Ð=°，∵AB CD P ，EF AB ∥，∴EF CD P ，∴180EPD D Ð+Ð=°，∴360B BPE EPD D Ð+Ð+Ð+Ð=°，∴360B BPD D Ð+Ð+Ð=°；（2）BPD B D Ð=Ð+Ð．理由：如图，过点P 作PE AB P ，∵AB CD P ，∴PE AB CD ∥∥，∴12B D Ð=ÐÐ=Ð，，∴12BPD B D Ð=Ð+Ð=Ð+Ð；（3）如图（3）：BPD D B Ð=Ð-Ð．理由：∵AB CD P ，∴1D Ð=Ð，∵1B P Ð=Ð+Ð，∴D B P Ð=Ð+Ð，即BPD D B Ð=Ð-Ð；如图（4）：BPD B D Ð=Ð-Ð．理由：∵AB CD P ，∴1B Ð=Ð，∵1D P Ð=Ð+Ð，∴B D P Ð=Ð+Ð，即BPD B D Ð=Ð-Ð．【点睛】此题考查了平行线的性质，平行公理的推论，三角形的外角的性质定理，熟记平行线的性质是解题的关键．5．（2021下·浙江·七年级期末）已知//AM CN ，点B 为平面内一点，AB BC ^于B ．（1）如图1，点B 在两条平行线外，则A Ð与C Ð之间的数量关系为______；（2）点B 在两条平行线之间，过点B 作BD AM ^于点D ．①如图2，说明ABD C Ð=Ð成立的理由；②如图3，BF 平分DBC Ð交DM 于点,F BE 平分ABD Ð交DM 于点E ．若180,3FCB NCF BFC DBE ÐÐÐÐ+=°=，求EBC Ð的度数．【答案】（1）∠A +∠C =90°；（2）①见解析；②105°【分析】（1）根据平行线的性质以及直角三角形的性质进行证明即可；（2）①过点B 作BG ∥DM ，根据平行线找角的联系即可求解；②先过点B 作BG ∥DM ，根据角平分线的定义，得出∠ABF =∠GBF ，再设∠DBE =α，∠ABF =β，根据∠CBF +∠BFC +∠BCF =180°，可得2α+β+3α+3α+β=180°，根据AB ⊥BC ，可得β+β+2α=90°，最后解方程组即可得到∠ABE =15°，进而得出∠EBC =∠ABE +∠ABC =15°+90°=105°．【详解】解：（1）如图1，AM 与BC 的交点记作点O ，∵AM ∥CN ，∴∠C =∠AOB ，∵AB ⊥BC ，∴∠A +∠AOB =90°，∴∠A +∠C =90°；（2）①如图2，过点B 作BG ∥DM ，∵BD⊥AM，∴DB⊥BG，∴∠DBG=90°，∴∠ABD+∠ABG=90°，∵AB⊥BC，∴∠CBG+∠ABG=90°，∴∠ABD=∠CBG，∵AM∥CN，BG∥DM，BG CN\//,∴∠C=∠CBG，∠ABD=∠C；②如图3，过点B作BG∥DM，∵BF平分∠DBC，BE平分∠ABD，∴∠DBF=∠CBF，∠DBE=∠ABE，由（2）知∠ABD=∠CBG，∴∠ABF=∠GBF，设∠DBE=α，∠ABF=β，则∠ABE=α，∠ABD=2α=∠CBG，∠GBF=∠AFB=β，∠BFC=3∠DBE=3α，∴∠AFC =3α+β，∵∠AFC +∠NCF =180°，∠FCB +∠NCF =180°，∴∠FCB =∠AFC =3α+β，△BCF 中，由∠CBF +∠BFC +∠BCF =180°得：2α+β+3α+3α+β=180°，∵AB ⊥BC ，∴β+β+2α=90°，∴α=15°，∴∠ABE =15°，∴∠EBC =∠ABE +∠ABC =15°+90°=105°．【点睛】本题主要考查了平行线的性质的运用，解决问题的关键是作平行线构造内错角，运用等角的余角（补角）相等进行推导．余角和补角计算的应用，常常与等式的性质、等量代换相关联．解题时注意方程思想的运用．6．（2021下·福建厦门·七年级厦门市第十一中学校考期中）已知，//AE BD ，A D Ð=Ð．（1）如图1，求证：//AB CD ；（2）如图2，作BAE Ð的平分线交CD 于点F ，点G 为AB 上一点，连接FG ，若CFG Ð的平分线交线段AG 于点H ，连接AC ，若ACE BAC BGM Ð=Ð+Ð，过点H 作HM FH ^交FG 的延长线于点M ，且3518E AFH Ð-Ð=°，求EAF GMH Ð+Ð的度数．【答案】（1）见解析；（2）72°【分析】（1）根据平行线的性质得出180A B Ð+Ð=°，再根据等量代换可得180B D Ð+Ð=°，最后根据平行线的判定即可得证；（2）过点E 作//EP CD ，延长DC 至Q ，过点M 作//MN AB ，根据平行线的性质及等量代换可得出ECQ BGM DFG Ð=Ð=Ð，再根据平角的含义得出ECF CFG Ð=Ð，然后根据平行线的性质及角平分线的定义可推出,BHF CFH CFA FAB Ð=ÐÐ=Ð；设,FAB CFH a b Ð=Ð=，根据角的和差可得出2AEC AFH Ð=Ð，结合已知条件35180AEC AFH Ð-Ð=°可求得18AFH Ð=°，最后根据垂线的含义及平行线的性质，即可得出答案．AFH CFH CFA CFH FABÐ=Ð-Ð=Ð-ÐQ AFH b a \Ð=-，BHF CFH bÐ=Ð=222ECF AFH AEC EAB AFH AEC b\Ð+Ð=Ð+Ð+Ð=Ð+22ECF AFH E BHF\Ð+Ð=Ð+Ð2AEC AFH\Ð=Ð35180AEC AFH Ð-Ð=°Q 18AFH \Ð=°FH HM^Q 90FHM \Ð=°90GHM b\Ð=°-180CFM NMF Ð+Ð=°Q 90HMB HMN b\Ð=Ð=°-EAF FABÐ=ÐQ 18EAF CFA CFH AFH b \Ð=Ð=Ð-Ð=-°189072EAF GMH b b \Ð+Ð=-°+°-=°72EAF GMH \Ð+Ð=°．【点睛】本题考查了平行线的判定及性质，角平分线的定义，能灵活根据平行线的性质和判定进行推理是解此题的关键．模型四、“骨折模型”如图，已知BC//DE ，试猜想∠A 、∠B 、∠D 的关系，并说明理由．解：∠BAD=∠D-∠B ,理由如下：过点A 作 AG // BC又 ∵CB//DE ．∴AG//DE∴∠GAB+∠B=180°，∠GAD+∠D=180°∴ ∠BAD ＝ ∠GAB- ∠GAD=180°-∠B–(180°-∠D)=∠D-∠B即：∠BAD=∠D-∠B注：平行线四大模型大题不可直接使用，必须证明后再用，选择填空满足条件即可直接用！【答案】60°【分析】过点B作BD∥2CBDÐ=Ð，进而可得Ð【详解】解：如图，过点Q Rt ABC△中，30AÐ=°，\9060ABC AÐ=°-Ð=°．Q BD EF∥，\1ABDÐ=Ð．【答案】40°/40度∥【分析】过C作CF ABÐ=°即可得到答案；CDE140【点睛】本题考查平行线的判定与性质，解题的关键是作出辅助线，根据平行线性质得到角度关系．二、解答题4．（2021·全国·九年级专题练习）已知AB //CD ，求证：∠B ＝∠E ＋∠D【答案】见解析【分析】过点E 作EF ∥CD ，根据平行线的性质即可得出∠B =∠BOD ，根据平行线的性质即可得出∠BOD =∠BEF 、∠D =∠DEF ，结合角之间的关系即可得出结论．【详解】证明：过点E 作EF ∥CD ，如图∵AB ∥CD ，∴∠B =∠BOD ，∵EF ∥CD （辅助线），∴∠BOD =∠BEF （两直线平行，同位角相等）；∠D =∠DEF （两直线平行，内错角相等）；∴∠BEF =∠BED +∠DEF =∠BED +∠D （等量代换），∴∠BOD=∠E +∠D （等量代换）， 即∠B =∠E +∠D ．【点睛】本题考查了平行线的性质以及角的计算，解题的关键是根据平行线的性质找出相等或互补的角．5．（2021下·山西晋中·七年级统考期中）综合与探究【问题情境】王老师组织同学们开展了探究三角之间数量关系的数学活动（1）如图1，//EF MN ，点A 、B 分别为直线EF 、MN 上的一点，点P 为平行线间一点，请直接写出PAF Ð、PBN Ð和APB Ð之间的数量关系；【问题迁移】（2）如图2，射线OM 与射线ON 交于点O ，直线//m n ，直线m 分别交OM 、ON 于点A 、D ，直线n 分别交OM 、ON 于点B 、C ，点P 在射线OM 上运动，①当点P 在A 、B （不与A 、B 重合）两点之间运动时，设ADP a Ð=Ð，BCP b Ð=Ð．则CPD Ð，a Ð，Ðb 之间有何数量关系？请说明理由．②若点P 不在线段AB 上运动时（点P 与点A 、B 、O 三点都不重合），请你画出满足条件的所有图形并直接写出CPD Ð，a Ð，Ðb 之间的数量关系．【答案】（1）360PAF PBN APB Ð+Ð+Ð=°；（2）①CPD a b Ð=Ð+Ð，理由见解析；②图见解析，CPD b a Ð=Ð-Ð或CPD a bÐ=Ð-Ð【分析】（1）作PQ ∥EF ，由平行线的性质，即可得到答案；（2）①过P 作//PE AD 交CD 于E ，由平行线的性质，得到DPE a Ð=Ð，CPE b Ð=Ð，即可得到答案；②根据题意，可对点P 进行分类讨论：当点P 在BA 延长线时；当P 在BO 之间时；与①同理，利用平行线的性质，即可求出答案．【详解】解：（1）作PQ ∥EF ，如图：∵//EF MN ，∴////EF MN PQ ，∴180PAF APQ Ð+Ð=°，180PBN BPQ Ð+Ð=°，∵APB APQ BPQÐ=Ð+Ð∴360PAF PBN APB Ð+Ð+Ð=°；（2）①CPD a b Ð=Ð+Ð；理由如下：如图，过P 作//PE AD 交CD 于E ，∵//AD BC ，∴////AD PE BC ，∴DPE a Ð=Ð，CPE b Ð=Ð，∴CPD DPE CPE a b Ð=Ð+Ð=Ð+Ð；②当点P 在BA 延长线时，如备用图1：∵PE ∥AD ∥BC ，∴∠EPC=b ，∠EPD =a ，∴CPD b a Ð=Ð-Ð；当P 在BO 之间时，如备用图2：∵PE ∥AD ∥BC ，∴∠EPD =a ，∠CPE =b ，∴CPD a b Ð=Ð-Ð．【点睛】本题考查了平行线的性质，解题的关键是熟练掌握两直线平行同旁内角互补，两直线平行内错角。

初中平行线模型整理——全面完整版（模型总结+精选例题+优化练习）第一部分 模型总结一、平行线模型：1）a//b,AC.BC 分别为∠BAD. ∠ABE 的角平分线, 则∠ACB=90 总结：两直线平行，一对同旁内角的角平分线互相垂直2）直线CF//BG ，OE 平分∠AOF ，PH 平分∠APG ，则OE//PH ，总结：两直线平行，一对同位角的角平分线互相平行3）直线CF//BG ，OE 平分∠COP ，PH 平分∠APG，则OE//PH总结：两直线平行，一对内错角的角平分线互相平行二、平行线拐点模型1）如图，线段AB//ED ，则∠B=∠C+∠D2） 如图，线段AB//EF 则∠F=∠C+∠B3）如图，线段AB//EF 则∠C=∠F+∠B总结：以上（1）（2）（3）可总结为，图中最大的角等于零两个角之和bF JF J E D E F B E F4）已知：如图，AA1∥BA3，则有∠B1＋∠B2=∠A1＋∠A2＋∠A3（即向左凸出的角的和等于向右凸出的角的和）5）如图1，线段AB//EF则∠F+∠C+∠B=360图1如图2，线段AB//CD，则∠F+∠E+∠B+∠FD=540图2总结：综合图1和图2，则每增加一个拐点，就增加了180度，即当有n个顶点时，内角和为（n-1）180第二部分精选例题例1已知：如图，AB∥CD，∠1＝∠2．求证：BE∥CF．例2 ．如图，直线AB.CD被EF所截，∠1 =∠2，∠CNF =∠BME。

求证：AB∥CD，MP∥NQ．例3．如图3，已知∠ABE +∠DEB = 180°，∠1 =∠2，求证：∠F =∠G．ABECFA BEFA A1A2A3B1B2B（练习1）F2A BC DQE1PMN1A CBFG例4．如图4，∠ABD 和∠BDC 的平分线交于E ，BE 交CD 于点F ，∠1 +∠2 = 90°．求证：（1）AB∥CD； （2）∠2 +∠3 = 90°．第三部分 优化练习1．如图，已知AD ∥BC ，BD 平分ABC ∠，A ∠：ABC ∠＝2：1，则ADB ∠的度数是多少？ 分析：对象：ADB ∠的度数 角度：（1）AD ∥BC （2）BD 平分ABC ∠ （3）A ∠：ABC ∠＝2：1 2．如图，EF ∥BC ，DF ∥AB ，图中与A ∠相等的角有那些？ 3．已知一个角的余角为︒40，那么这个角的补角是 ； 4、A ∠与B ∠互为补角，如果︒=∠37A ，则B ∠的度数为 度；5、如图21∠=∠，︒∠=∠1253，则2∠＝ ；6、如图，︒=∠701，︒=∠502，则C ∠＝ 时，AB ∥CD ；7、若FDE A ∠=∠，则互相平行的直线是 ；8、如图，若a MN =，b NP =，则MP ＝ ，MP MN 22+＝ ；1 2 3 第3题第1题A B C DM N P第8题A B CD E FG第2题 A E C B D F 第4题1 2A E BC DC图4 12 3AB DF9、下列选项中正确的是（）。

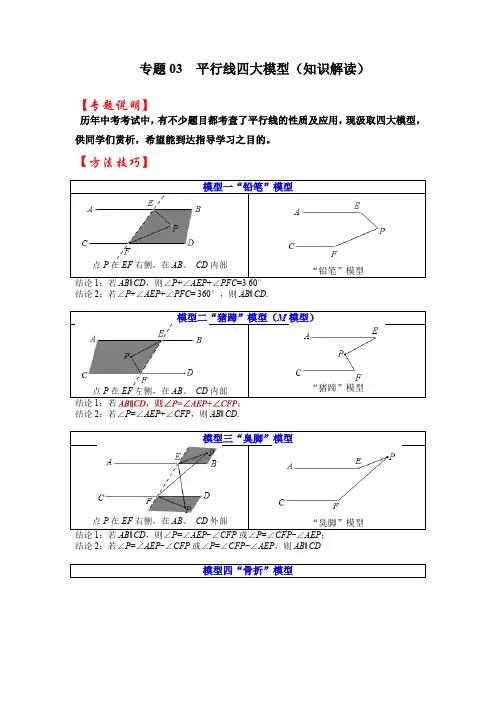
专题03 平行线四大模型（知识解读）【专题说明】历年中考考试中，有不少题目都考查了平行线的性质及应用，现汲取四大模型，供同学们赏析，希望能到达指导学习之目的。

【方法技巧】模型一“铅笔”模型点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=3 60°结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.模型二“猪蹄”模型（M模型）点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；结论2：若∠P=∠AEP+∠CFP，则AB∥CD.模型三“臭脚”模型点P在EF右侧，在AB、CD外部“臭脚”模型结论1：若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD模型四“骨折”模型点P在EF左侧，在AB、CD外部·“骨折”模型结论1：若AB∥CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.【典例分析】【模型1 “铅笔”模型】【典例1】如图，直线a∥b，点M、N分别在直线a、b上，P为两平行线间一点，那么∠1+∠2+∠3等于（ ）A．360°B．300°C．270°D．180°【答案】A【解答】解：如图，过点P作PA∥a，则a∥b∥PA，∴∠3+∠NPA＝180°，∠1+∠MPA＝180°，∴∠1+∠2+∠3＝180°+180°＝360°．故选：A．【变式1-1】把一块等腰直角三角尺和直尺按如图所示的方式放置，若∠1＝32°，则∠2的度数为（ ）A．20°B．18°C．15°D．13°【答案】D【解答】解：如图，过点O作OP∥AB，则OP∥AB∥CD，∴∠1＝∠3，∠2＝∠4，∵∠3+∠4＝45°，∴∠1+∠2＝45°，∴∠2＝45°﹣∠1＝45°﹣32°＝13°．故选：D．【典例2】问题情境：（1）如图1，AB∥CD，∠BAP＝120°，∠PCD＝130°，求∠APC的度数．（提示：如图2，过P作PE∥AB）问题迁移：（2）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP ＝α，∠PCB＝β，α、β、∠DPC之间有何数量关系？请说明理由；（3）在（2）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出α、β、∠DPC之间的数量关系．（提示：三角形内角和为180°）【解答】解：（1）∵AB∥CD，∠PAB＝120°，∠PCD＝130°，∴∠PAB+∠APE＝180°，∠EPC+∠C＝180°，∴∠APE＝180°﹣120°＝60°，∠EPC＝180°﹣130°＝50°，∴∠APC＝∠APE+∠EPC＝60°+50°＝110°；（2）∠CPD＝∠α+∠β，理由如下：如图3，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠DPE+∠CPE＝∠α+∠β；（3）①当P在OA延长线时，∠CPD＝∠β﹣∠α；②当P在AB延长线时，∠CPD＝∠α﹣∠β，①当P在OA延长线时，∠CPD＝∠β﹣∠α；理由：如图4，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠CPE﹣∠DPE＝∠β﹣∠α；②当P在AB延长线时，∠CPD＝∠α﹣∠β，理由：如图5，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α＝∠DPE，∠β＝∠CPE，∴∠CPD＝∠DPE﹣∠CPE＝∠α﹣∠β．【变式2-1】已知，AB∥CD，试解决下列问题：（1）如图1，∠1+∠2＝ ；（2）如图2，∠1+∠2+∠3＝ ；（3）如图3，∠1+∠2+∠3+∠4＝ ；（4）如图4，试探究∠1+∠2+∠3+∠4+…+∠n＝ ．【解答】解：（1）∵AB∥CD，∴∠1+∠2＝180°（两直线平行，同旁内角互补）；（2）过点E作一条直线EF∥AB，∵AB∥CD，∴CD∥EF，∴∠1+∠AEF＝180°，∠FEC+∠3＝180°，∴∠1+∠2+∠3＝360°；（3）过点E、F作EG、FH平行于AB，∵AB∥CD，∴AB∥EG∥FH∥CD，∴∠1+∠AEG＝180°，∠GEF+∠EFH＝180°，∠HFC+∠4＝180°；∴∠1+∠2+∠3+∠4＝540°；（4）根据上述规律，显然作（n﹣2）条辅助线，运用（n﹣1）次两条直线平行，同旁内角互补．即可得到n个角的和是180°（n﹣1）．【变式2-2】如图，已知BQ∥GE，AF∥DE，∠1＝50°．（1）求∠AFG的度数；（2）若AQ平分∠FAC，交BC于点Q，且∠Q＝15°，求∠ACB的度数．【解答】解：（1）∵BQ∥GE，∠1＝50°，∴∠E＝∠1＝50°，∵AF∥DE，∴∠AFG＝∠E＝50°；（2）过点A作AM∥BQ，由（1）得∠AFG＝∠E＝50°，∵BQ∥GE，∴AM∥BQ∥GE，∴∠FAM＝∠AFG＝50°，∠MAQ＝∠Q＝15°，∴∠FAQ＝∠FAM+∠MAQ＝65°，∵AQ平分∠FAC，∴∠QAC＝∠FAQ＝65°，∴∠MAC＝∠QAC+∠MAQ＝80°，∵AM∥BQ，∴∠ACB＝∠MAC＝80°．【模型2 “猪蹄”模型（M模型）】【典例3】【问题背景】同学们，观察小猪的猪蹄，你会发现一个熟悉的几何图形，我们就把这个图形的形象称为“猪蹄模型”，猪蹄模型中蕴含着角的数量关系．【问题解决】（1）如图1，AB∥CD，E为AB、CD之间一点，连接AE、CE．若∠A＝42°，∠C＝28°．则∠AEC＝　．【问题探究】（2）如图2，AB∥CD，线段AD与线段BC交于点E，∠A＝36°，∠C＝54°，EF平分∠BED，求∠BEF的度数．【问题拓展】（3）如图3．AB∥CD，线段AD与线段BC相交于点G，∠BCD＝56°，∠GDE＝20°，过点D作DF∥CB交直线AB于点F，AE平分∠BAD，DG平分∠CDF，求∠AED的度数．【解答】解：（1）延长CE交AB于点F，∵AB∥CD，∴∠AFC＝∠C＝28°，∵∠AEC是△AEF的一个外角，∴∠AEC＝∠A+∠AFC＝∠A+∠C＝70°，故答案为：70°；（2）利用（1）的结论可得：∠AEC＝∠A+∠C＝36°+54°＝90°，∴∠AEC＝∠BED＝90°，∵EF平分∠BED，∴∠BEF＝∠BED＝45°，∴∠BEF的度数为45°；（3）∵BC∥DF，∴∠CDF＝180°﹣∠BCD＝124°，∵DG平分∠CDF，∴∠CDG＝∠CDF＝62°，∵AB∥CD，∴∠BAG＝∠CDG＝62°，∵AE平分∠BAD，∴∠BAE＝∠BAD＝31°，∵∠GDE＝20°，∴∠EDH＝180°﹣∠CDG﹣∠GDE＝98°，利用（1）的结论可得：∠AED＝∠BAE+∠EDH＝31°+98°＝129°，∴∠AED的度数为129°．。

专题03 平行线四大模型（专项训练）1．将一副三角板按图中方式叠放，则角α等于（）A．30°B．45°C．60°D．75°【答案】D【解答】解：如图，根据两直线平行，内错角相等，∴∠1＝45°，根据三角形的一个外角等于与它不相邻的两个内角的和，∴∠α＝∠1+30°＝75°．故选：D．2．如图，直线a∥b，直线c分别交a，b于点A，C，∠BAC的平分线交直线b于点D，若∠1＝55°，则∠2的度数是（）A．50°B．70°C．80°D．110°【答案】B【解答】解：∵AD平分∠BAC，∴∠BAD＝∠CAD，∵a∥b，∠1＝55°，∴∠BAD＝∠CAD＝55°，∴∠2＝180°﹣55°﹣55°＝70°．故选：B．3．如图，a∥b，M、N分别在a，b上，P为两平行线间一点，那么∠1+∠2+∠3＝（）A．180°B．360°C．270°D．540°【答案】B【解答】解：过点P作P A∥a，∵a∥b，P A∥a，∴a∥b∥P A，∴∠1+∠MP A＝180°，∠3+∠APN＝180°，∴∠1+∠MP A+∠3+∠APN＝180°+180°＝360°，∴∠1+∠2+∠3＝360°．故选：B．4．把一块直尺与一块直角三角板如图放置，若∠1＝38°，则∠2的度数为．【答案】128°【解答】解：如图，∵∠1＝∠3＝38°，∴∠2＝90°+∠3＝90°+38°＝128°．故答案为：128°．5．如图，是赛车跑道的一段示意图，其中AB∥DE，测得∠B＝140°，∠D＝120°，则∠C的度数为度．【答案】100【解答】解：如图所示：过点C作CF∥AB．∵AB∥DE，∴DE∥CF；∴∠BCF＝180°﹣∠B＝40°，∠DCF＝180°﹣∠D＝60°；∴∠C＝∠BCF+∠DCF＝100°．故答案为：100．6．问题情境（1）如图①，已知∠B+∠E+∠D＝360°，试探究直线AB与CD有怎样的位置关系？并说明理由．小明给出下面正确的解法：直线AB与CD的位置关系是AB∥CD．理由如下：过点E作EF∥AB（如图②所示），所以∠B+∠BEF＝180°（依据1），因为∠B+∠BED+∠D＝360°（已知），所以∠B+∠BEF+∠FED+∠D＝360°，所以∠FED+∠D＝180°，所以EF∥CD（依据2），因为EF∥AB，所以AB∥CD（依据3）．交流反思上述解答过程中的“依据1”，“依据2”，“依据3”分别指什么？“依据1”：，“依据2”：，“依据3”：，类比探究（2）如图，当∠B、∠E、∠F、∠D满足条件时，有AB ∥CD．拓展延伸（3）如图，当∠B、∠E、∠F、∠D满足条件时，有AB∥CD．【解答】解：（1）“依据1”：两直线平行，同旁内角互补，“依据2”：同旁内角互补，两直线平行，“依据3”：平行于同一条直线的两直线平行，故答案为：两直线平行，同旁内角互补；同旁内角互补，两直线平行；平行于同一条直线的两直线平行，（2）如图，当∠B、∠BEF、∠EFD、∠D满足条件∠B+∠BEF+∠EFD+∠D＝540°时，有AB∥CD．理由：过点E、F分别作GE∥HF∥CD．则∠GEF+∠EFH＝180°，∠HFD+∠CDF＝180°，∴∠GEF+∠EFD+∠FDC＝360°；又∵∠B+∠BEF+∠EFD+∠D＝540°，∴∠B+∠BEG＝180°，∴AB∥GE，∴AB∥CD；故答案为：∠B+∠BEF+∠EFD+∠D＝540°；（3）如图，当∠B、∠BEF、∠EFD、∠D满足条件∠B+∠BEF+∠D＝180°+∠EFD时，有AB∥CD．理由：过点E、F分别作GE∥FH∥CD．则∠GEF＝∠EFH，∠D＝∠HFD，∵∠B+∠BEF+∠D＝180°+∠EFD，即∠B+∠BEG+∠GEF+∠D＝180°+∠EFH+∠HFD，∴∠B+∠BEG＝180°，∴AB∥GE，∴AB∥CD，故答案为：∠B+∠BEF+∠D＝180°+∠EFD．7．如图，a∥b，将一个等腰直角三角板放置到如图所示位置．若∠1＝15°，则∠2的大小是（）A．20°B．25°C．30°D．45°【答案】C【解答】解：如图：过点B作BC∥b，∴∠1＝∠CBD＝15°，∵△ABD是等腰直角三角形，∴∠ABD＝45°，∴∠ABC＝∠ABD﹣∠CBD＝30°，∵a∥b，∴a∥BC，∴∠2＝∠ABC＝30°，故选：C．8．将长方形纸条按如图方式折叠，折痕为DE，点A，B的对应点分别为A′，B′，若∠α＝∠β﹣20°，则∠β的度数为（）A．50°B．60°C．70°D．80【答案】C【解答】解：如图：延长EB′交AF于点G，∵四边形ABHF是矩形，∴∠B＝90°，AF∥BH，由折叠得：∠B＝∠A′B′E＝90°，∠BEB′＝2∠BED＝2∠β，∴∠CB′G＝180°﹣∠A′B′E＝90°，∵AF∥BH，∴∠FGB′＝∠BEB′＝2∠β，∵∠FGB′是△CGB′的一个外角，∴∠FGB′＝∠GCB′+∠CB′G，∴2∠β＝∠α+90°，∵∠α＝∠β﹣20°，∴2∠β＝∠β﹣20°+90°，∴∠β＝70°，故选：C．9．如图，AB∥DE，∠ABC＝80°，∠CDE＝140°，则∠BCD的度数为（）A．30°B．40°C．60°D．80°【答案】B【解答】解：反向延长DE交BC于M，如图：∵AB∥DE，∴∠BMD＝∠ABC＝80°，∴∠CMD＝180°﹣∠BMD＝100°；又∵∠CDE＝∠CMD+∠C，∴∠BCD＝∠CDE﹣∠CMD＝140°﹣100°＝40°．故选：B．10．如图，将直尺与30角的三角尺叠放在一起，若∠2＝50°，则∠1的大小是（）A．40°B．50°C．70°D．80°【答案】C【解答】解：如图：由题意得，∠3＝60°，∵∠2＝50°，AB∥CD，∴∠4＝∠2＝50°，∴∠1＝180°﹣60°﹣50°＝70°，故选：C．11．如图，一副三角板叠放在一起，使直角顶点重合于点O，AB∥OC，DC与OA交于点E，则∠DEO的度数为（）A．85°B．75°C．70°D．60°【答案】B【解答】解：过点E作EF∥CO，∴∠AEF＝∠A＝30°，∵AB∥CO，∴EF∥CO，∴∠FEC＝∠C＝45°，∴∠AEC＝∠AEF+∠FEC＝75°，∴∠DEO＝∠AEC＝75°，故选：B．12．如图，船C在观测站A的北偏东35°方向上，在观测站B的北偏西20°方向上，那么∠ACB＝（）度．A．20°B．35°C．55°D．60°【答案】C【解答】解：如图：过点C作CF∥AD，由题意得：∠DAC＝35°，∠CBE＝20°，AD∥EB，∴CF∥EB，∴∠FCB＝∠CBE＝20°，∵CF∥AD，∴∠ACF＝∠DAC＝35°，∴∠ACB＝∠ACF+∠FCB＝55°，故选：C．13．如图，AB∥CD，将一副直角三角板作如下摆放，∠GEF＝60°，∠MNP＝45°．下列结论：①GE∥MP；②∠EFN＝150°；③∠BEF＝65°；④∠AEG＝35°，其中正确的个数是（）A．1B．2C．3D．4【答案】B【解答】解：①由题意得：∠G＝∠MPN＝90°，∴GE∥MP，故①正确；②由题意得∠EFG＝30°，∴∠EFN＝180°﹣∠EFG＝150°，故②正确；③过点F作FH∥AB，如图，∵AB∥CD，∴∠BEF+∠EFH＝180°，FH∥CD，∴∠HFN＝∠MNP＝45°，∴∠EFH＝∠EFN﹣∠HFN＝105°，∴∠BEF＝180°﹣∠EFH＝75°，故③错误；④∵∠GEF＝60°，∠BEF＝75°，∴∠AEG＝180°﹣∠GEF﹣∠BEF＝45°，故④错误．综上所述，正确的有2个．故选：B．14．已知l1∥l2，一个含有30°角的三角尺按照如图所示的位置摆放，若∠1＝65°，则∠2＝度．【答案】25【解答】解：如图，过直角顶点作l3∥l1，∵l1∥l2，∴l1∥l2∥l3，∴∠1＝∠3，∠2＝∠4，∴∠1+∠2＝∠3+∠4＝90°，∵∠1＝65°，∴∠2＝25°．故答案为：25．15.如图，AB∥CD，点E，F分别是AB，CD上的点，点M位于AB与CD之间且在EF的右侧．（1）若∠M＝90°，则∠AEM+∠CFM＝；（2）若∠M＝n°，∠BEM与∠DFM的角平分线交于点N，则∠N的度数为．（用含n的式子表示）【答案】270°n°．【解答】解：（1）过点M作MP∥AB，∵AB∥CD，∴AB∥CD∥MP，∴∠1＝∠MEB，∠2＝∠MFD，∵∠M＝∠1+∠2＝90°，∴∠MEB+∠MFD＝90°，∵∠AEM+∠MEB+∠CFM+∠MFD＝180°+180°＝360°，∴∠AEM+∠CFM＝360°﹣90°＝270°．故答案为：270°；（2）过点N作NQ∥AB，∵AB∥CD，∴AB∥CD∥NQ，∴∠3＝∠NEB，∠4＝∠NFD，∴∠NEB+∠NFD＝∠3+∠4＝∠ENF，∵∠BEM与∠DFM的角平分找交于点N，∵∠NEB＝∠MEB，∠DFN＝MFD，∴∠3+∠4＝∠BEN+∠DFN＝（∠MEB+∠MFD），由（1）得，∠MEB+∠MFD＝∠EMF，∴∠ENF＝∠EMF＝n°．故答案为：n°．16．小明同学遇到这样一个问题：如图①，已知：AB∥CD，E为AB、CD之间一点，连接BE，ED，得到∠BED．求证：∠BED＝∠B+∠D．小亮帮助小明给出了该问的证明．证明：过点E作EF∥AB，则有∠BEF＝∠B．∵AB∥CD，∴EF∥CD，∴∠FED＝∠D，∴∠BED＝∠BEF+∠FED＝∠B+∠D．请你参考小亮的思考问题的方法，解决问题：直线l1∥l2，直线EF和直线l1、l2分别交于C、D两点，点A、B分别在直线l1、l2上，猜想：如图②，若点P在线段CD上，∠P AC＝15°，∠PBD＝40°，求∠APB的度数．拓展：如图③，若点P在直线EF上，连接P A、PB（BD＜AC），直接写出∠P AC、∠APB、∠PBD之间的数量关系．【解答】解：猜想：如图1，过点P作PH∥AC，则∠P AC＝∠APH，∵l1∥l2，∴BD∥PH，∴∠PBD＝∠BPH，∴∠APB＝∠APH+∠BPH＝∠P AC+∠PBD，∵∠P AC＝15°，∠PBD＝40°，∴∠APB＝15°+40°＝55°．拓展：①如图1，当点P在线段CD上时，由猜想可知，∠APB＝∠P AC+∠PBD；②如图2，当点P在射线DP上时，过点P作PH∥AC，则∠P AC＝∠APH，∵l1∥l2，∴BD∥PH，∴∠PBD＝∠BPH，∴∠APB＝∠APH﹣∠BPH＝∠P AC﹣∠PBD；③如图3，当点P在射线CE上时，过点P作PH∥AC，则∠P AC＝∠APH，∵l1∥l2，∴BD∥PH，∴∠PBD＝∠BPH，∴∠APB＝∠BPH﹣∠APH＝∠PBD﹣∠P AC；综上所述，∠P AC、∠APB、∠PBD之间的数量关系为∠APB＝∠P AC+∠PBD或∠APB ＝∠P AC﹣∠PBD或∠APB＝∠PBD﹣∠P AC．17．如图1，AB∥CD，EOF是直线AB、CD间的一条折线．（1）试证明：∠O＝∠BEO+∠DFO．（2）如果将折一次改为折二次，如图2，则∠BEO、∠O、∠P、∠PFC之间会满足怎样的数量关系，证明你的结论．【解答】（1）证明：作OM∥AB，如图1，∴∠1＝∠BEO，∵AB∥CD，∴OM∥CD，∴∠2＝∠DFO，∴∠1+∠2＝∠BEO+∠DFO，即：∠O＝∠BEO+∠DFO．（2）解：∠O+∠PFC＝∠BEO+∠P．理由如下：作OM∥AB，PN∥CD，如图2，∵AB∥CD，∴OM∥PN∥AB∥CD，∴∠1＝∠BEO，∠2＝∠3，∠4＝∠PFC，∴∠1+∠2+∠PFC＝∠BEO+∠3+∠4，∴∠O+∠PFC＝∠BEO+∠P．18．如图，AB∥CD，点E为AB上方一点，FB、CG分别为∠EFG、∠ECD的角平分线，若∠E+2∠G＝210°，则∠EFG的度数为（）A．140°B．150°C．130°D．160°【答案】A【解答】解：过G作GM∥AB，∴∠2＝∠5，∵AB∥CD，∴MG∥CD，∴∠6＝∠4，∴∠G＝∠5+∠6＝∠2+∠4，∵FB、CG分别为∠EFG，∠ECD的角平分线，∴∠1＝∠2＝∠EFG，∠3＝∠4＝∠ECD，∴∠E+∠EFG+∠ECD＝210°，∵AB∥CD，∴∠ENB＝∠ECD，∴∠E+∠EFG+∠ENB＝210°，∵∠1＝∠E+∠ENB，∴∠1+∠EFG＝∠1+∠1+∠2＝210°，∴3∠1＝210°，∴∠1＝70°，∴∠EFG＝2×70°＝140°．故选：A．19．如图，AB∥EF，∠C＝90°，则α、β和γ的关系是（）A．β＝α+γB．α+β+γ＝180°C．α+β﹣γ＝90°D．β+γ﹣α＝180°【答案】C【解答】解：延长DC交AB与G，延长CD交EF于H．在直角△BGC中，∠1＝90°﹣α；△EHD中，∠2＝β﹣γ，∵AB∥EF，∴∠1＝∠2，∴90°﹣α＝β﹣γ，即α+β﹣γ＝90°．故选：C．20．某小区车库门口的“曲臂直杆道闸”（如图）可抽象为如右图所示模型．已知AB垂直于水平地面AE．当车牌被自动识别后，曲臂直杆道闸的BC段将绕点B缓慢向上抬高，CD段则一直保持水平状态上升（即CD与AE始终平行），在该运动过程中∠ABC+∠BCD的度数始终等于（）度A．360B．180C．250D．270【答案】D【解答】解：过点B作BG∥AE，∴∠BAE+∠ABG＝180°，∵AE∥CD，∴BG∥CD，∴∠C+∠CBG＝180°，∴∠BAE+∠ABG+∠CBG+∠C＝360°，∴∠BAE+∠ABC+∠BCD＝360°，∵BA⊥AE，∴∠BAE＝90°，∴∠ABC+∠BCD＝360°﹣∠BAE＝270°，故选：D．。

七年级数学下册《平行线的经典模型》平行线的经典模型题型一、平行加拐点——“M”模型例1：如图，AB∥CD，求∠BAP、∠APC、∠PCD的关系式，并加以证明。

解：根据平行线的性质，得到PE∥AB，因此∠1＝∠BAP。

又因为AB∥CD，PE∥AB，所以PE∥CD，因此∠2＝∠PCD。

所以∠1＋∠2＝∠BAP＋∠PCD，即∠APC＝∠BAP＋∠PCD。

练一练】1、如图，BA∥DE，∠B＝30°，∠D＝40°，则∠C的度数是（）。

A、10°B、35°C、70°D、80°2、如图，AB∥DE，则∠1、∠2、∠3关系是（）。

A、∠3＞∠1＋∠2B、∠2＝∠3－∠1C、∠3＝∠1＋∠2D、无法确定3、如图，AB∥CD，∠BED＝90°，则∠1与∠2之间的数量关系是（）。

A、∠2＝2∠1B、∠2－∠1＝90°C、∠1＋∠2＝180°D、无法确定4、如图，已知AB∥CD∥EF，GC⊥CF，∠B＝60°，∠EFC＝45°，求∠BCG的度数。

5、如图，一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上，如果∠1＝25°，那么∠2的度数是（）。

A、130°B、105°C、115°D、125°6、将一个直角三角板和一把直尺按如图所示放置，若∠α＝43°，则∠β＝？例2：已知如图，AB∥CD∥EF，点M、N、P分别在AB、CD、EF上，NQ平分∠___。

1）若∠AMN＝50°，∠EPN＝70°，求∠MNP，∠DNQ的度数；2）若∠AMN＝x度，∠EPN＝y度，请直接写出∠DNQ的度数（用含x，y的代数式表示）；3）试探究：∠___与∠___，∠___之间的数量关系，并说明理由。

练一练】如图，已知AB∥MP∥CD，MN平分∠AMD，∠A＝40°，∠D＝50°，求∠NMP的度数。

七下专题：平行线四大模型知识导航一、平行线的定义1、定义：在同一平面内，不相交的两条直线叫做平行线，直线a与直线b互相平行，记作a∥b．2、在同一平面内，两条直线的位置关系只有两种：(1)相交；(2)平行．这里，我们把重合的两直线看成一条直线．【注】初中不涉及到重合．二、平行公理及推论平行公理：经过直线外一点，有且只有一条直这条直线平行．推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．三、行线的判定判定1：同位角相等，两直线平行．判定2：内错角相等，两直线平行．判定3：同旁内角互补，两直线平行．四、平行线的性质性质1：两直线平行，同位角相等．性质2：两直线平行，内错角相等．性质3：两直线平行，同旁内角互补．五、两条平行线间的距离同时垂直于两条平行线，并且夹在这两条平行线间的线段的长度叫做这两条平行线的距离，平行线间的距离处处相等．如图2，EF的长度就是AB和CD这两条平行线的距离题型一基础巩固例1（1）（二中广雅）如图，已知AB∥CD，CB平分∠ACD，且∠A:∠ACD＝3:1，则∠B的度数为．（2）（武昌七校七下期中）如图，已知AB平行CD，能判断BE平行CF的条件是（）A．∠1＝∠3B．∠2＝∠4C．∠1＝∠4D．∠1＝∠2（3）如图AF∥CD，BC平分∠ACD，交AF于点B，点E在CD上，BD平分∠EBF，交CE的延长线于点D，且BD⊥BC，下列结论：①BC平分∠ABE；②AC∥BE；③∠BCD＋∠CDB＝90°；④∠DBF＝2＝S△ABD．∠ABC；⑤S△BCEA．2个B．3个C．4个D．5个练1（1）两条直线被第三条直线所截，那么内错角之间的大小关系是（）A．相等B．互补C．不相等D．无法确定（2）（二中广雅七下期中）如图，∠1＝∠2，且∠3＝105°，则∠4的度数为（）A．75°B．62°C．82°D．108°(3)(武昌七校七下期中)完成下面的推理填空：如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2＋∠3＝180°，求证：∠GDC＝∠B．证明:∵AD⊥BC，EF⊥BC(已知)，∴∠ADB＝＝90°(垂直的定义)，∴AD∥EF()∴（），又∠2＋∠3＝180°(已知)，∵∠1＝∠3(同角的补角相等)，∴∥（），∴∠GDC＝∠B()．模块二四大模型之“铅笔”“猪蹄”模型知识导航四大模型之模型一：“铅笔”模型点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P＋∠AEP＋∠PFC＝360°；结论2：若∠P＋∠AEP＋∠PFC＝360°，则AB∥CD．四大模型之模型二：“猪蹄”模型点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P＝∠AEP＋∠PFC；结论2：若∠P＝∠AEP＋∠PFC，则AB∥CD．题型一“铅笔”与“猪蹄”的证明例2（1）若AE∥CF，求证：∠P＋∠AEP＋∠PFC＝360°．（2）若AE∥CF，求证：∠P＝∠AEP＋∠PFC．（2）若∠P＝∠AEP＋∠PFC，求证：AE∥CF．题型二“铅笔”“猪蹄”基础应用例3（1）（七一月考）已知EF∥MN，一直角三角板如图放置，∠ACB＝90°．①如图1，若∠1＝60°，则∠2＝度；②如图2，若∠1＝∠B－20°，则∠2＝度．练2（1）若∠P＋∠AEP＋∠PFC＝360°，求证：AE∥CF；．练3（1）如图，已知直线a∥b，∠1＝40°，∠2＝60°，则∠3等于（）A．100°B．60°C．40°D．20°（2）如图，a∥b，M、N分别在a，b上，P为两平行线间一点，那么∠1＋∠2＋∠3＝．巅峰突破已知：如图，AF∥CD，求证：∠A＋∠C＋∠E＝∠B＋∠D＋∠F．（2）（武昌区七下期中）如图，已知a∥b，∠1＝100°，∠2＝140°，则∠3＝模块三四大模型之“臭脚”“骨折”模型知识导航四大模型之模型三：“臭脚”模型点P在EF右侧，在AB、CD外部“臭脚”模型结论1：若AB∥CD，则∠P＝∠AEP－∠CFP或∠P＝∠CFP－∠AEP；结论2：若∠P＝∠AEP－∠CFP或∠P＝∠CFP－∠AEP，则AB∥CD．四大模型之模型三：“骨折”模型点P在EF左侧，在AB、CD外部“骨折”模型结论1：若AB∥CD，则∠P＝∠CFP－∠AEP或∠P＝∠AEP－∠CFP；结论2：若∠P＝∠CFP－∠AEP或∠P＝∠AEP－∠CFP，则AB∥CD．题型一“臭脚”与“骨折”的证明例4（1）若AE∥CF，求证：∠P＝∠AEP－∠CFP．（2）若AE∥CF，求证：∠P＝∠CFP－∠AEP．练4（1）若∠P＝∠AEP－∠CFP，则AE∥CF．（2）若∠P＝∠CFP－∠AEP，求证：AE∥CF．题型二“臭脚”“骨折”基础应用例5（梅苑中学七下期中）已知直线AB∥CD，E是直线AB的上方一点，连接AE、EC ①如图1，求证：∠AEC＋∠EAB＝∠ECD；②如图2，AF平分∠BAE，CF平分∠DCE，且∠AFC比∠AEC的32倍少40°，直接写出∠AEC的度数．练5（1）如图，已知直线AB∥CD，∠C＝115°，∠A＝25°，则∠E＝（）A．70°B．80°C．90°D．100°（2）如图，已知a∥b，∠3＝50°，则∠1＋∠2＝．例6★★如图，AC∥DE，∠EFG＝∠A＋∠E，试判断AB和FG的位置关系，井说明你的理由．练6如图，AB∥EF，∠B＝50°，∠C＝20°，∠E＝130°，求证：BC∥DE．总结归纳所有的四大模型解决方法都是：转折角处画平行线（拐点＋平行）“铅笔”模型“猪蹄”模型“骨折”模型“臭脚”模型典题示例已知∠B＝25°，∠BCD＝45°，∠CDE＝30°，∠E＝10°，求证：AB∥EF．【考点】“铅笔”“猪蹄”模型结合配套作业平行线四大模型（一）1．如图，∠1＝∠2，且∠3＝108°，则∠4的度数为（）A．72°B．62°C．82°D．80°2．下列说法中，正确的有（）①两点之间，线段最短；②在同一平面内，过一点有且只有一条直线与已知直线平行；③平行于同一直线的两条直线互相平行A．0个B．1个C．2个D．3个3．如图，l1∥l2，∠1＝120°，∠2＝100°，则∠3＝．4．如图，射线AC∥BD，∠A＝70°，∠B＝40°，则∠P＝．第4题图第5题图5．（武珞路七下期中）如图，直线AB、CD、EF被直线GF所截，∠1＝70°，∠2＝110°，∠3＝70°，求证：AB∥CD证明：∵∠1＝70°，∠3＝70°（已知）∴∠1＝∠3（）∴∥（）∵∠2＝110°，∠3＝70°（已知）∴＋＝180°（等式性质）∴∥（）∴AB∥CD．；请证明．②在图2中，∠BMF 、∠F 、∠FND 的数量关系为；请证明．7.如图，已知180EFC BDC ︒∠+∠=，DEF B ∠=∠．（1）试判断DE 与BC 的位置关系，并说明理由．（2）若DE 平分ADC ∠，3BDC B ∠=∠，求EFC ∠的度数．6．（武昌区七下期末）如图，直线AB ∥CD ，①在图1中，∠BME 、∠E 、∠END 的数量关系为9.如图（1）所示是一根木尺折断后的情形，你可能注意过，木尺折断后的断口一般是参差不齐的，那么请你深入考虑一下其中所包含的一类数学问题，我们不妨取名叫“木尺断口问题”．（1）如图（2）所示，已知//AB CD ，请问B Ð，D ∠，E ∠有何关系并说明理由；（2）如图（3）所示，已知//AB CD ，请问B Ð，E ∠，D ∠又有何关系并说明理由；（3）如图（4）所示，已知//AB CD ，请问E G +∠∠与B F D ++∠∠∠有何关系并说明理由8.如图1，AB ∥CD ，∠PAB =130°，∠PCD =120°，求∠APC 的度数．小明的思路是：过P 作PE ∥AB ，通过平行线性质来求∠APC ．（1）按小明的思路，求∠APC 的度数；（2）如图2，AB ∥CD ，点P 在射线OM 上运动，记∠PAB =α，∠PCD =β当点P 在B 、D 两点之间运动时，问∠APC 与α、β之间有何数量关系？请说明理由；（3）在（2）的条件下，如果点P 在B 、D 两点外侧运动时（点P 与点O 、B 、D 三点不重合），请直接写出∠APC 与α、β之间的数量关系．（2）如图，当点G 在AB 上方时，且90EGF ︒∠=，求证：90︒∠-∠=BEG DFG；（3）如图，在（2）的条件下，过点E 作直线HK 交直线CD 于K ，FT 平分DFG ∠交HK 于点T ，延长GE 、FT 交于点R ，若ERT TEB ∠=∠，请你判断FR 与HK 的位置关系，并证明．（不可以直接用三角形内角和180°）10、已知AB //CD ，点E 、F 分别在AB 、CD 上，点G 为平面内一点，连接EG 、FG ．（1）如图，当点G 在AB 、CD 之间时，请直接写出∠AEG 、∠CFG 与∠G 之间的数量关系__________．。

专题2.3 平行线四大模型专项训练（40道）【北师大版】考卷信息：本套训练卷共40题，题型针对性较高，覆盖面广，选题有深度，涵盖了平行线四大模型的综合问题的所有类型！【模型1 “铅笔”模型】1．（2022·湖南·永州市剑桥学校七年级阶段练习）如图所示，l1∥l2，∠1＝105°，∠2＝140°，则∠3的度数为( )A．55°B．60°C．65°D．70°2．（2022·贵州六盘水·七年级期中）如图所示，若AB∥EF，用含α、β、γ的式子表示x，应为（）A．α+β+γB．β+γ−αC．180°−α−γ+βD．180°+α+β−γ3．（2022·甘肃·北京师范大学庆阳实验学校七年级期中）如图，如果AB∥CD，那么∠B＋∠F＋∠E＋∠D＝___°．4．（2022·全国·七年级专题练习）如图所示，AB//CD，∠ABE与∠CDE的角平分线相较于点F，∠E=80°，求∠BFD的度数.5．（2022·全国·七年级专题练习）已知如图所示，AB//CD，∠ABE=3∠DCE，∠DCE=28°，求∠E的度数.6．（2022·全国·七年级）(1)问题情景：如图1，AB//CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．小明想到一种方法，但是没有解答完：如图2，过P作PE//AB，∴∠APE+∠PAB=180°，∴∠APE=180°-∠PAB=180°-130°=50°∵AB//CD，∴PE//CD．……请你帮助小明完成剩余的解答．(2)问题迁移：请你依据小明的解题思路，解答下面的问题：如图3，AD//BC，当点P在A、B两点之间时，∠ADP=∠α，∠BCP=∠β，则∠CPD，∠α，∠β之间有何数量关系？请说明理由．7．（2022·全国·七年级专题练习）如图1，四边形MNBD为一张长方形纸片．（1）如图2，将长方形纸片剪两刀，剪出三个角（∠BAE、∠AEC、∠ECD），则∠BAE+∠AEC+∠ECD= __________°．（2）如图3，将长方形纸片剪三刀，剪出四个角（∠BAE、∠AEF、∠EFC、∠FCD），则∠BAE+∠AEF+∠EFC+∠FCD=__________°．（3）如图4，将长方形纸片剪四刀，剪出五个角（∠BAE、∠AEF、∠EFG、∠FGC、∠GCD），则∠BAE+∠AEF+∠EFG+∠FGC+∠GCD=___________°．（4）根据前面探索出的规律，将本题按照上述剪法剪n刀，剪出(n+1)个角，那么这(n+1)个角的和是____________°．8．（2022·安徽合肥·七年级期末）问题情景：如图1，AB∥CD，∠PAB＝140°，∠PCD＝135°，求∠APC的度数．（1）丽丽同学看过图形后立即口答出：∠APC＝85°，请补全她的推理依据．如图2，过点P作PE∥AB，因为AB∥CD，所以PE∥CD．（）所以∠A+∠APE＝180°，∠C+∠CPE＝180°．（）因为∠PAB＝140°，∠PCD＝135°，所以∠APE＝40°，∠CPE＝45°，∠APC＝∠APE+∠CPE＝85°．问题迁移：（2）如图3，AD∥BC，当点P在A、B两点之间运动时，∠ADP＝∠α，∠BCP＝∠β，求∠CPD与∠α、∠β之间有什么数量关系？请说明理由．（3）在（2）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请直接写出∠CPD与∠α、∠β之间的数量关系．【模型2 “猪蹄”模型】9．（2022·全国·七年级）如图所示，直角三角板的60°角压在一组平行线上，AB∥CD，∠ABE=40°，则∠EDC=______度．10．（2022·河南平顶山·八年级期末）如图：(1)如图1，AB∥CD，∠ABE=45°，∠CDE=21°，直接写出∠BED的度数．(2)如图2，AB∥CD，点E为直线AB，CD间的一点，BF平分∠ABE，DF平分∠CDE，写出∠BED与∠F之间的关系并说明理由．(3)如图3，AB与CD相交于点G，点E为∠BGD内一点，BF平分∠ABE，DF平分∠CDE，若∠BGD=60°，∠BFD=95°，直接写出∠BED的度数．11．（2022·江苏常州·七年级期中）问题情境：如图①，直线AB∥CD，点E，F分别在直线AB，CD上．(1)猜想：若∠1=130°，∠2=150°，试猜想∠P=______°；(2)探究：在图①中探究∠1，∠2，∠P之间的数量关系，并证明你的结论；(3)拓展：将图①变为图②，若∠1+∠2=325°，∠EPG=75°，求∠PGF的度数．12．（2022·山东聊城·七年级阶段练习）已知直线AB//CD，EF是截线，点M在直线AB、CD之间．(1)如图1，连接GM，HM．求证：∠M＝∠AGM＋∠CHM；(2)如图2，在∠GHC的角平分线上取两点M、Q，使得∠AGM＝∠HGQ．试判断∠M与∠GQH之间的数量关系，并说明理由．13．（2022·广东韶关·七年级期中）如图1，点A、B分别在直线GH、MN上，∠GAC=∠NBD，∠C=∠D.（1）求证：GH//MN；（提示：可延长AC交MN于点P进行证明）（2）如图2，AE平分∠GAC，DE平分∠BDC，若∠AED=∠GAC，求∠GAC与∠ACD之间的数量关系；∠GAC，若∠AKB=∠ACD，（3）在（2）的条件下，如图3，BF平分∠DBM，点K在射线BF上，∠KAG=13直接写出∠GAC的度数．14．（2022·全国·九年级专题练习）如图所示，已知AB//CD，BE平分∠ABC，DE平分∠ADC，求证：∠E=12(∠A+∠C)15．（2022·浙江工业大学附属实验学校七年级期中）已知AB//CD．（1）如图1，E为AB，CD之间一点，连接BE，DE，得到∠BED．求证：∠BED＝∠B+∠D；（2）如图，连接AD，BC，BF平分∠ABC，DF平分∠ADC，且BF，DF所在的直线交于点F．①如图2，当点B在点A的左侧时，若∠ABC＝50°，∠ADC＝60°，求∠BFD的度数．②如图3，当点B在点A的右侧时，设∠ABC＝α，∠ADC＝β，请你求出∠BFD的度数．（用含有α，β的式子表示）16．（2022·全国·七年级）如图1，AB//CD，E是AB，CD之间的一点．(1)判定∠BAE，∠CDE与∠AED之间的数量关系，并证明你的结论；(2)如图2，若∠BAE，∠CDE的角平分线交于点F，直接写出∠AFD与∠AED之间的数量关系；(3)将图2中的射线DC沿DE翻折交AF于点G得图3，若∠AGD的余角等于2∠E的补角，求∠BAE的大小．17．（2022·广东·高州市第一中学附属实验中学七年级阶段练习）如图1，已知AB∥CD，∠B＝30°，∠D＝120°；(1)若∠E＝60°，则∠F＝；(2)请探索∠E与∠F之间满足的数量关系？说明理由；(3)如图2，已知EP平分∠BEF，FG平分∠EFD，反向延长FG交EP于点P，求∠P的度数．18．（2022·河南·商丘市第十六中学七年级期中）已知AB∥CD，线段EF分别与AB，CD相交于点E，F．（1）请在横线上填上合适的内容，完成下面的解答：如图1，当点P在线段EF上时，已知∠A＝35°，∠C＝62°，求∠APC的度数；解：过点P作直线PH∥AB，所以∠A＝∠APH，依据是 ；因为AB∥CD，PH∥AB，所以PH∥CD，依据是 ；所以∠C＝（ ），所以∠APC＝（ ）+（ ）＝∠A+∠C＝97°．（2）当点P，Q在线段EF上移动时（不包括E，F两点）：①如图2，∠APQ+∠PQC＝∠A+∠C+180°成立吗？请说明理由；②如图3，∠APM＝2∠MPQ，∠CQM＝2∠MQP，∠M+∠MPQ+∠PQM＝180°，请直接写出∠M，∠A与∠C的数量关系．19．（2022·湖北武汉·七年级期末）如图1，点A在直线MN上，点B在直线ST上，点C在MN，ST之间，且满足∠MAC+∠ACB+∠SBC=360°．（1）证明：MN//ST；（2）如图2，若∠ACB=60°，AD//CB，点E在线段BC上，连接AE，且∠DAE=2∠CBT，试判断∠CAE与∠CAN的数量关系，并说明理由；（n为大于等于2的整数），点E在线段BC上，连接AE，若∠MAE=n∠CBT，则（3）如图3，若∠ACB=180°n∠CAE:∠CAN=______．20．（2022·重庆江北·七年级期末）如图1，AB//CD，点E、F分别在AB、CD上，点O在直线AB、CD之间，且∠EOF=100°．（1）求∠BEO+∠OFD的值；（2）如图2，直线MN分别交∠BEO、∠OFC的角平分线于点M、N，直接写出∠EMN−∠FNM的值；（3）如图3，EG在∠AEO内，∠AEG=m∠OEG；FH在∠DFO内，∠DFH=m∠OFH，直线MN分别交EG、FH 分别于点M、N，且∠FMN−∠ENM=50°，直接写出m的值．21．（2022·黑龙江哈尔滨·七年级期末）已知，AB∥CD，点E在CD上，点G，F在AB上，点H在AB，CD之间，连接FE，EH，HG，∠AGH＝∠FED，FE⊥HE，垂足为E．（1）如图1，求证：HG⊥HE；（2）如图2，GM平分∠HGB，EM平分∠HED，GM，EM交于点M，求证：∠GHE＝2∠GME；（3）如图3，在（2）的条件下，FK平分∠AFE交CD于点K，若∠KFE：∠MGH＝13：5，求∠HED的度数．22.（2022·广西柳州·七年级期中）已知直线a∥b，直线EF分别与直线a，b相交于点E，F，点A，B分别在直线a，b上，且在直线EF的左侧，点P是直线EF上一动点（不与点E，F重合），设∠PAE＝∠1，∠APB ＝∠2，∠PBF＝∠3．(1)如图1，当点P在线段EF上运动时，试说明∠1＋∠3＝∠2；(2)当点P在线段EF外运动时有两种情况．①如图2写出∠1，∠2，∠3之间的关系并给出证明；②如图3所示，猜想∠1，∠2，∠3之间的关系（不要求证明）．【模型3 “臭脚”模型】23．（2022·全国·八年级课时练习）（1）已知：如图（a），直线DE∥AB．求证：∠ABC+∠CDE=∠BCD；（2）如图（b），如果点C在AB与ED之外，其他条件不变，那么会有什么结果？你还能就本题作出什么新的猜想？24．（2022·全国·七年级）已知，AE//BD，∠A=∠D．（1）如图1，求证：AB//CD；（2）如图2，作∠BAE的平分线交CD于点F，点G为AB上一点，连接FG，若∠CFG的平分线交线段AG于点H，连接AC，若∠ACE=∠BAC+∠BGM，过点H作HM⊥FH交FG的延长线于点M，且3∠E−5∠AFH=18°，求∠EAF+∠GMH的度数．25．（2022·广东·东莞市光明中学七年级期中）（1）如图（1）AB∥CD，猜想∠BPD与∠B、∠D的关系，说出理由．（2）观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，并说明理由．（3）观察图（3）和（4），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，不需要说明理由．26．（2022·浙江台州·七年级期末）如图，已知AD⊥AB于点A，AE∥CD交BC于点E，且EF⊥AB于点F．求证：∠C=∠1+∠2．证明：∵AD⊥AB于点A，EF⊥AB于点F，（已知）∴∠DAB=∠EFB=90°．（垂直的定义）∴AD∥EF，（）∴__________=∠1（）∵AE∥CD，（已知）∴∠C=________．（两直线平行，同位角相等）∵∠AEB=∠AEF+∠2，∴∠C=∠1+∠2．（等量代换）27．（2022·广东珠海·七年级期中）已知AM//CN，点B为平面内一点，AB⊥BC于B．（1）如图1，点B在两条平行线外，则∠A与∠C之间的数量关系为______；（2）点B在两条平行线之间，过点B作BD⊥AM于点D．①如图2，说明∠ABD=∠C成立的理由；②如图3，BF平分∠DBC交DM于点F,BE平分∠ABD交DM于点E．若∠FCB+∠NCF=180°,∠BFC=3∠DBE，求∠EBC的度数．28．（2022·湖南·新田县云梯学校七年级阶段练习）①如图1，AB∥CD，则∠A+∠E+∠C=360°；②如图2，AB∥CD，则∠P=∠A−∠C；③如图3，AB∥CD，则∠E=∠A+∠1；④如图4，直线AB∥CD∥EF，点O在直线EF上，则∠α−∠β+∠γ=180°．以上结论正确的个数是（）A．1个B．2个C．3个D．4个【模型4 “铅笔”模型】29．（2022·福建·浦城县教师进修学校八年级期中）如图，直线MA∥NB，∠A=70°，∠B=40°，则∠P=___________度．30．（2022·江苏·景山中学七年级阶段练习）如图，若AB//CD，则∠1+∠3-∠2的度数为______31．（2022·湖北·浠水县兰溪镇兰溪初级中学七年级期中）如图，已知AB//DE，∠ABC=80°，∠CDE=140°，则∠BCD=_____．32．（2022·全国·九年级专题练习）如图所示，AB∥CD，∠E＝37°，∠C＝20°，则∠EAB的度数为__________．33．（2022·全国·七年级）如图，如果AB∥EF，EF∥CD，则∠1，∠2，∠3的关系式__________．34．（2022·全国·九年级专题练习）已知AB//CD，求证：∠B＝∠E＋∠D35．（2022·浙江·七年级期中）为更好地理清平行线与相关角的关系，小明爸爸为他准备了四根细直木条AB、BC，CD、DE，做成折线ABCDE，如图1，且在折点B、C、D处均可自由转出．（1）如图2，小明将折线调节成∠B=50°,∠C=75°,∠D=25°，判别AB是否平行于ED，并说明理由；（2）如图3，若∠C=∠D=25°，调整线段AB、BC使得AB//CD，求出此时∠B的度数，要求画出图形，并写出计算过程．（3）若∠C=85°,∠D=25°,AB//DE，求出此时∠B的度数，要求画出图形，直接写出度数，不要求计算过程．36．（2022·山西晋中·七年级期中）综合与探究【问题情境】王老师组织同学们开展了探究三角之间数量关系的数学活动（1）如图1，EF//MN，点A、B分别为直线EF、MN上的一点，点P为平行线间一点，请直接写出∠PAF、∠PBN和∠APB之间的数量关系；【问题迁移】（2）如图2，射线OM与射线ON交于点O，直线m//n，直线m分别交OM、ON于点A、D，直线n分别交OM、ON于点B、C，点P在射线OM上运动，①当点P在A、B（不与A、B重合）两点之间运动时，设∠ADP=∠α，∠BCP=∠β．则∠CPD，∠α，∠β之间有何数量关系？请说明理由．②若点P不在线段AB上运动时（点P与点A、B、O三点都不重合），请你画出满足条件的所有图形并直接写出∠CPD，∠α，∠β之间的数量关系．37．（2022·湖北武汉·七年级阶段练习）如图1，MN∥PQ，点C、B分别在直线MN、PQ上，点A在直线MN、PQ之间．（1）求证：∠CAB＝∠MCA+∠PBA；（2）如图2，CD∥AB，点E在PQ上，∠ECN＝∠CAB，求证：∠MCA＝∠DCE；（3）如图3，BF平分∠ABP，CG平分∠ACN，AF∥CG．若∠CAB＝60°，求∠AFB的度数．38．（2022·全国·七年级专题练习）（1）如图，AB//CD，CF平分∠DCE，若∠DCF=30°，∠E=20°，求∠ABE 的度数；（2）如图，AB//CD，∠EBF=2∠ABF，CF平分∠DCE，若∠F的2倍与∠E的补角的和为190°，求∠ABE的度数．（3）如图，P为（2）中射线BE上一点，G是CD上任一点，PQ平分∠BPG，GN//PQ，GM平分∠DGP，若∠B＝30°，求∠MGN的度数．39．（2022·江苏·扬州中学教育集团树人学校七年级阶段练习）已知直线AB∥CD，P为平面内一点，连接PA、PD．（1）如图1，已知∠A＝50°，∠D＝150°，求∠APD的度数；（2）如图2，判断∠PAB、∠CDP、∠APD之间的数量关系为 ．∠PAB＝∠APD，求∠AND的度数．（3）如图3，在（2）的条件下，AP⊥PD，DN平分∠PDC，若∠PAN+1240．（2022·浙江杭州·七年级期中）已知，AB∥CD．点M在AB上，点N在CD上．（1）如图1中，∠BME、∠E、∠END的数量关系为：　；（不需要证明）如图2中，∠BMF、∠F、∠FND的数量关系为：　；（不需要证明）（2）如图3中，NE平分∠FND，MB平分∠FME，且2∠E＋∠F＝180°，求∠FME的度数；（3）如图4中，∠BME＝60°，EF平分∠MEN，NP平分∠END，且EQ∥NP，则∠FEQ的大小是否发生变化，若变化，请说明理由，若不变化，求出∠FEQ的度数．。

平行线相关模型模型一、拐角模型：图 1 图 2 图3已知：如图1，AB∥CD，则有∠BED=∠B+∠D证法一：如图2，过点E作EF∥AB，∴∠B=∠BEF，∵AB∥CD，∴EF∥CD，∴∠D=∠DEF，∵∠BED=∠BEF+∠DEF，∴∠BED=∠B+∠D证法二：如图3，延长BE交CD于点G（或延长DE交AB于点G），∵AB∥CD，∴∠B=∠EGD，由三角形外角定理，可得∠BED=∠EGD+∠D，∴∠BED=∠B+∠D【注意】证法一中不要忽略对EF∥CD的证明.例题1：如图，直线AB∥CD，∠C=44°，∠E为直角，则∠1等于（）A.132°B.134°C.136°D.138°例题2：如图，已知HD//GE,∠DAB=120°如图1.若∠BCG=20°，求∠B的度数如图2，∠BCG=∠BCF，AF平分∠BAH，∠BCG=20°，则∠F的度数是．如图3，P是AB上一点，Q是GE上一点，PN平分∠APQ,QN平分∠PQE，探究∠HAP与∠N的数量关系，并说明理由巩固练习：1、如图，AB∥CD，用含∠1，∠2，∠3的式子表示∠4为（）A.∠1+∠2-∠3B.∠1+∠3-∠2C.180°+∠3-∠1-∠2D.∠2+∠3-∠1-180°2.已知，直线AB∥DC，点P为平面上一点，连接AP与CP．（1）如图1，点P在直线AB、CD之间，当∠BAP=60°，∠DCP=20°时，求∠APC．（2）如图2，点P在直线AB、CD之间，∠BAP与∠DCP的角平分线相交于点K，写出∠AKC 与∠APC之间的数量关系，并说明理由．（3）如图3，点P落在CD外，∠BAP与∠DCP的角平分线相交于点K，∠AKC与∠APC有何数量关系？并说明理由．模型二、铅笔模型图 1 图 2 图3已知：如图1，AB∥CD，则∠B+∠BED+∠D=360°.证法一：如图2，过点E作EF∥AB，∴∠B+∠BEF=180°，∵AB∥CD，∴EF∥CD，∴∠D+∠FED=180°，∴∠B+∠BEF+∠FED+∠D=360°，即∠B+∠BED+∠D=360°.证法二：如图3，延长AB和DE交于点G，（或延长BE和CD），∴∠ABE+∠EBG=180°，∵AB∥CD，∴∠G+∠D=180°.由三角形的外角定理，得∠BED=∠G+∠EBG，∴∠ABE+∠BED+∠D=∠ABE+∠EBG+∠G+∠D=360°.例题1：如图，已知AE // CF ,∠P +∠AEP +∠PFC = _____________.例题2：已知：直线EF分别与直线AB，CD相交于点F，E，EM平∠FED，AB∥CD，H，P分别为直线AB和线段EF上的点．（1）如图1，HM平分∠BHP，若HP⊥EF，求∠M的度数．（2）如图2，EN平分∠HEF交AB于点N，NQ⊥EM于点Q，当H在直线AB上运动（不与点F重合）时，探究∠FHE与∠ENQ的关系，并证明你的结论．2、如图，AB⊥BC，AE平分∠BAD交BC于E，AE⊥DE，∠l+∠2= 90°，M、N分别是BA、CD的延长线上的点，∠EAM和∠EDN的平分线相交于点F则∠F的度数为（）．A.120°B.135°C.145°D.150度模型三、臭脚模型图1 图2已知：如图1，AB∥CD，则∠ABE=∠D+∠E.证明：如图2，延长EB交CD于点F（或延长AB与DE相交），∵AB∥CD，∴∠ABE=∠CFE，∵∠CFE=∠D+∠E，∴∠ABE=∠D+∠E.例题1：如图，已知AE∥CF，试求出∠P，∠AEP和∠CFP的数量关系.例题2：如图，AB∥CD，∠B=30°，∠O=∠C．则∠C=__________ .巩固练习：1、如图，已知AB∥DE，∠ABC=80°，∠CDE =140°，则∠BCD=___________.模型四：骨折模型已知：如图，AB∥CD，则有∠B=∠D+∠E.证明：∵AB∥CD，∴∠B=∠BFD，∵∠BFD=∠D+∠E，∴∠B=∠D+∠E.例题1：已知直线AB∥CD，直线EF与AB、CD分别交于点M、N，点P在直线CD上，点Q是直线EF上一动点。