中考数学几何模型专题13平行线之猪脚模型(M模型)(老师版)知识点+例题

初一下学期，平行线拐角模型之猪蹄、臭脚、骨折模型，模型解题平行线拐角模型除铅笔模型外，本章介绍拐角模型剩下的三个模型：猪蹄模型、臭脚模型和骨折模型，以及利用这三个模型进行解题。

01“猪蹄”模型该模型类似英文字母“M”，我们称之为M模型，也类似猪蹄，又称之为“猪蹄”模型。

满足的条件为：点P在直线BC的左侧，在直线AB与直线CD的内部。

结论为：若AB∥CD，则∠P=∠B+∠C。

证明的方法与上一篇“铅笔”模型类似，我们提供一种思路进行验证。

02“臭脚”模型“臭脚”模型需要满足的条件为：点P在直线BC的右侧，在直线AB、CD外部。

结论为：∠P=∠ABP-∠DCP或∠P=∠DCP-∠ABP。

要证明这个结论，需要用到的知识点有：平行线的性质与三角形的外角等于两个不相邻的内角和。

当然，也可以利用作平行线的方法来进行证明。

03“骨折”模型“骨折”模型需满足的条件：点P在直线BC左侧，在直线AB与直线CD外部。

结论为：∠P=∠DCP-∠ABP。

证明的方法与前三种模型类似，这边不再重复证明，可以作任意一边的平行线为辅助线，也可以利用平行线的性质与三角形的外角等于两个不相邻的内角和来进行证明。

04模型应用例题1：（2019秋金凤区校级期末）如图1，已知AB∥CD，∠B=30°，∠D=120°；（1）若∠E=60°，则∠F=______°；（2）请探索∠E与∠F之间满足的数量关系？说明理由；（3）如图2，已知EP平分∠BEF，FG平分∠EFD，反向延长FG交EP于点P，求∠P的度数．例题2：（2019春梁园区期末）如图1，AB∥CD，点E是直线AB、CD之间的一点，连接EA、EC．（1）探究猜想：①若∠A=20°，∠C=50°，则∠AEC=______．②若∠A=25°，∠C=40°，则∠AEC= ______．③猜想图1中∠EAB、∠ECD、∠AEC的关系，并证明你的结论．（2）拓展应用：如图2，AB∥CD，线段MN把ABCD这个封闭区域分为I、Ⅱ两部分（不含边界），点E是位于这两个区域内的任意一点，请直接写出∠EMB、∠END、∠MEN的关系.在利用模型解题前，我们首先要知道这些模型的基本结构，以及证明的过程（这是关键），不单单是记住结论，因为题目千变万化，但是又万变不离其宗，解题的思路是类似的。

平行线间的“拐点”问题福建省仙游县第二中学（351200）　陈国权［摘　要］平行线间的“拐点”问题，可以分为“猪脚”模型、“铅笔头”模型、“锯齿”模型、“臭脚”模型等，文章结合几则典例，探讨平行线间的“拐点”问题的求解方法，以提高学生灵活运用几何定理的能力，发展学生的核心素养。

［关键词］平行线；拐点；模型［中图分类号］G633.6［文献标识码］A［文章编号］ 1674-6058（2023）23-0022-03平行线间的“拐点”问题，可以分为以下几个类型：“猪脚”模型、“铅笔头”模型、“锯齿”模型、“臭脚”模型，下面笔者结合几则典例，逐一分析探讨。

类型一、平行线间的“猪脚”模型如图1乙所示，这个几何图形因为与猪脚相像，我们形象地称之为“猪脚”模型。

“猪脚”模型中蕴含着角之间的特殊关系，即∠AEC=∠A+∠C。

如何证明呢？因为在两条平行线间是折线相连，不是直线连接，所以不能直接应用平行线的性质解答，它们之间需要一个“桥梁”将两者联系起来，常用的联系方式就是在“拐点”处作平行线，如图2所示，作EG∥AB。

因为AB∥CD，所以EG∥AB∥CD，根据“两直线平行，内错角相等”得∠A=∠AEG，∠C=∠CEG，因为∠AEC=∠AEG+∠CEG，所以∠AEC=∠A+∠C（等量代换）。

甲乙图1 图2实际上对于“猪脚”模型，还可以进一步扩展，如图3所示，AB∥CD，在AB与CD之间有P1、P2、P3三点，顺次连接B、P1、P2、P3、D。

如图4所示，分别过P1、P2、P3作直线AB的平行线P1E，P2F，P3G，∵AB∥CD，∴AB∥P1E∥P2F∥P3G。

由平行线的性质可得 ∠1=∠B①，∠2+∠3=180°②，∠4+∠5=180°③，∠6=∠D④，①+②+③+④得，∠BP1P2+∠P1P2P3+∠P2P3D=180°+180°+∠B+∠D=360°+∠B+∠D。

三角形中的倒角模型-平行线+拐点模型近年来各地中考中常出现一些几何倒角模型，该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。

平行线+拐点模型在初中数学几何模块中属于基础工具类问题，也是学生必须掌握的一块内容，熟悉这些模型可以快速得到角的关系，求出所需的角。

本专题就平行线+拐点模型(猪蹄模型(M型)、铅笔头模型、牛角模型、羊角模型、“5”字模型)进行梳理及对应试题分析，方便掌握。

拐点(平行线)模型的核心是一组平行线与一个点，然后把点与两条线分别连起来，就构成了拐点模型，这个点叫做拐点，两条线的夹角叫做拐角。

通用解法：见拐点作平行线；基本思路：和差拆分与等角转化。

模型1：猪蹄模型(M型)【模型解读】图1图2图3如图1，①已知：AM∥BN，结论：∠APB=∠A+∠B；②已知：∠APB=∠A+∠B，结论：AM∥BN.如图2，已知：AM∥BN，结论：∠P1+∠P3=∠A+∠B+∠P2.如图3，已知：AM∥BN，结论：∠P1+∠P3+...+∠P2n+1=∠A+∠B+∠P2+...+∠P2n.1(2022·河南洛阳·统考二模)如图，AB∥CD，∠ABM=30°，∠CDM=45°，则∠BMD的度数为()A.105°B.90°C.75°D.70°2(2023春·安徽蚌埠·九年级校联考期中)太阳灶、卫星信号接收锅、探照灯及其他很多灯具都与抛物线有关．如图，从点O照射到抛物线上的光线OB，OC反射后沿着与PO平行的方向射出，已知图中∠ABO =46°，∠OCD=88°，则∠BOC的度数为()A.116°B.124°C.134°D.135°3(2023春·四川泸州·七年级校考期末)如图所示，若AB∥EF，用含α、β、γ的式子表示x，应为()A.α+β+γB.β+γ-αC.180°-α-γ+βD.180°+α+β-γ4(2023·广东深圳·校联考模拟预测)北京冬奥会掀起了滑雪的热潮，谷爱凌的励志故事也激励着我们青少年，很多同学纷纷来到滑雪场，想亲身感受一下奥运健儿在赛场上风驰电掣的感觉，但是第一次走进滑雪场的你，如果不想体验人仰马翻的感觉，学会正确的滑雪姿势是最重要的，正确的滑雪姿势是上身挺直略前倾，与小腿平行，使脚的根部处于微微受力的状态，如图所示，AB ∥CD ，当人脚与地面的夹角∠CDE =60°时，求出此时上身AB 与水平线的夹角∠BAF 的度数为()A.60°B.45°C.50°D.55°5(2023春·河南驻马店·九年级专题练习)已知AB ∥CD ，∠EAF =13∠EAB ，∠ECF =13∠ECD ，若∠E =66°，则∠F 为()A.23°B.33°C.44°D.46°6(2022·浙江七年级期中)如图(1)所示是一根木尺折断后的情形，你可能注意过，木尺折断后的断口一般是参差不齐的，那么请你深入考虑一下其中所包含的一类数学问题，我们不妨取名叫“木尺断口问题”．(1)如图(2)所示，已知AB ⎳CD ，请问∠B ，∠D ，∠E 有何关系并说明理由；(2)如图(3)所示，已知AB ⎳CD ，请问∠B ，∠E ，∠D 又有何关系并说明理由；(3)如图(4)所示，已知AB ⎳CD ，请问∠E +∠G 与∠B +∠F +∠D 有何关系并说明理由．模型2：铅笔头模型图1图2图3如图1，①已知：AM∥BN，结论：∠1+∠2+∠3=360°；②已知：∠1+∠2+∠3=360°，结论：AM∥BN.如图2，已知：AM∥BN，结论：∠1+∠2+∠3+∠4=540°如图3，已知：AM∥BN，结论：∠1+∠2+⋯+∠n=(n-1)180°.7(2023·广东·统考二模)如图所示，已知AB∥EF，那么∠BAC+∠ACE+∠CEF=()A.180°B.270°C.360°D.540°8(2023·山西吕梁·校联考模拟预测)如图，这是路政工程车的工作示意图，工作篮底部与支撑平台平行.若∠1=32°，∠2=62°，则∠3的度数为()A.118°B.148°C.150°D.162°9(2023·河南三门峡·校联考一模)如图，图1是某小区车库门口的“曲臂直杆道闸”，可抽象为图2所示的数学图形．已知CD垂直地面上的直线DF于点D，当车牌被自动识别后，曲臂直杆道闸的BC段将绕点C 缓慢向上抬高，AB段则一直保持水平状态上升(即AB始终平行于DF)．在该运动过程中，当∠ABC=112°时，∠BCD的度数是()A.112°B.138°C.158°D.128°10(2023春·新疆·七年级校考阶段练习)如图，如果AB∥CD，那么∠B+∠F+∠E+∠D=°．11(2022春·河北保定·七年级校考期中)如图，已知A1B∥A n C，则∠A1+∠A2+∠A3=，则∠A1+∠A2 +⋅⋅⋅+∠A n等于(用含n的式子表示)．模型3：牛角模型图1图2如图1，已知：AB∥DE，结论：α=β-γ.如图2，已知：AB∥DE，结论：α=β+γ-180°.12(2023·安徽滁州·校联考二模)如图，若AB∥CD，则()A.∠1=∠2+∠3B.∠1+∠3=∠2C.∠1+∠2+∠3=180°D.∠1-∠2+∠3=180°13(2023·江苏·七年级假期作业)如图，若AB ⎳CD ，则∠1+∠3-∠2的度数为14(2022·湖北洪山·七年级期中)如图，已知AB ∥CD ，P 为直线AB ，CD 外一点，BF 平分∠ABP ，DE 平分∠CDP ，BF 的反向延长线交DE 于点E ，若∠FED =a ，试用a 表示∠P 为．15(2023春·广东深圳·九年级校校考期中)已知直线AB ∥CD ，点P 为直线AB ，CD 所确定的平面内的一点，(1)问题提出：如图1，∠A =120°，∠C =130°．求∠APC 的度数：(2)问题迁移：如图2，写出∠APC ，∠A ，∠C 之间的数量关系，并说明理由：(3)问题应用：如图3，∠EAH :∠HAB =1:3，∠ECH =20°，∠DCH =60°，求∠H ∠E的值．16(2023·余干县八年级期末)已知直线AB ∥CD ，(1)如图1，直接写出∠BME 、∠E 、∠END 的数量关系为；(2)如图2，∠BME 与∠CNE 的角平分线所在的直线相交于点P ，试探究∠P 与∠E 之间的数量关系，并证明你的结论；(3)如图3，∠ABM =1n ∠MBE ，∠CDN =1n∠NDE ，直线MB 、ND 交于点F ，则∠F=．∠E模型4：羊角模型图1图2如图1，已知：AB∥DE，结论：α=γ-β.如图2，已知：AB∥DE，结论：α+β+γ=180°.17(2023春·上海·七年级专题练习)如图所示，AB∥CD，∠E=37°，∠C=20°，则∠EAB的度数为．18(2022·江苏七年级期中)如图所示，已知AB∥CD，∠A=50°，∠C=∠E．则∠C等于()A.20°B.25°C.30°D.40°19(2023春·浙江·七年级专题练习)已知AB⎳CD，求证：∠B=∠E+∠D20(2023·河南·统考三模)如图，已知AB∥DE，∠ABC=150°，∠CDE=75°，则∠BCD的度数为()A.55°B.60°C.45°D.50°21(2023·河北沧州·校考模拟预测)如图，∠A=58°，∠D=122°，∠1=3∠2，∠2=25°，点P是BC上一点．(1)∠DFE的度数为；(2)若∠BFP=50°．则CE与PF(填“平行”或“不平行”)．模型5：蛇形模型(“5”字模型)基本模型：如图，AB∥CD，结论：∠1+∠3-∠2=180°.图1图2如图1，已知：AB∥DE，结论：α=β+180°-γ.如图2，已知：AB∥DE，结论：α=γ+180°-β.22(2023·四川广元·统考三模)珠江流域某江段江水流向经过B、C、D三点，拐弯后与原来方向相同，如图，若∠ABC=120°，∠BCD=80°，则∠CDE等于()A.50°B.40°C.30°D.20°23(2023·湖南长沙·九年级校联考期中)如图，若AB∥CD，∠α=65°，∠γ=25°，则∠β的度数是()A.115°B.130°C.140°D.150°24(2023·河南周口·校联考三模)如图，AB∥EF，∠B=100°，∠CDE=25°，则∠BCD的度数是()A.125°B.75°C.95°D.105°25(2023·陕西西安·校考模拟预测)如图，AB∥CD，CD∥EF，CE平分∠BCD，若∠ABC=58°，则∠CEF 的度数为()A.131°B.141°C.151°D.161°26(2023·江西·九年级校考阶段练习)如图∠BAC=10°，∠ACD=125°，CD⊥EF于点D，将AB绕点A 逆时针旋转α，使AB∥EF，则α的最小值为．课后专项训练1(2023·山东临沂·统考二模)如图，a∥b,∠1=45°，则∠2的度数为()A.105°B.125°C.135°D.145°2(2023春·安徽·九年级专题练习)如图，已知：AB∥EF，∠B=∠E，求证：BC∥DE．在证明该结论时，需添加辅助线，则以下关于辅助线的作法不正确的是()A.延长BC交FE的延长线于点GB.连接BEC.分别作∠BCD，∠CDE的平分线CG，DHD.过点C作CG∥AB(点G在点C左侧)，过点D作DH∥EF(点H在点D左侧)3(2023·浙江台州·统考一模)如图是路政工程车的工作示意图，工作篮底部与支撑平台平行．若∠1= 30°，∠2=50°，则∠3的度数为( )．A.130°B.140°C.150°D.160°4(2023·江苏·八年级假期作业)如图，两直线AB、CD平行，则∠1+∠2+∠3+∠4+∠5+∠6=( )．A.630°B.720°C.800°D.900°5(2023·辽宁抚顺·统考三模)如图，若AB∥CD∥EF，∠1=15°，∠2=60°，那么∠BCE=()A.120°B.125°C.130°D.135°6(2022·安徽芜湖·七年级期中)如图，AB ∥CD ，BF ,DF 分别平分∠ABE 和∠CDE ，BF ∥DE ，∠F 与∠ABE 互补，则∠F 的度数为A.30°B.35°C.36°D.45°7(2023·内蒙古呼伦贝尔·统考三模)如图是一款手推车的平面示意图，其中AB ∥CD ，∠1=24°，∠3=148°，则∠2的度数为()A.56B.66C.98D.1048(2023春·重庆江津·七年级校联考期中)如图，AB ⎳CD ，∠ABE =12∠EBF ，∠DCE =13∠ECF ，设∠ABE =α，∠E =β，∠F =γ，则α，β，γ的数量关系是()A.4β-α+γ=360°B.3β-α+γ=360°C.4β-α-γ=360°D.3β-2α-γ=360°9(2022·江苏七年级期末)如图，AB ∥CD ，则∠1+∠3-∠2的度数等于．10(2023·湖南长沙·校联考二模)如图所示，AB∥DE，∠1=130°，∠2=36°，则∠3=度．11(2022·四川成都·七年级期末)已知直线AB∥DE，射线BF、DG分别平分∠ABC，∠EDC，两射线反向延长线交于点H，请写出∠H，∠C之间的数量关系：．12(2022·黑龙江·七年级月考)如图，AB⎳CD，E是CD上的点，过点E作EF⎳DP，若∠PEF=∠PEH，EG平分∠DEH，∠B=152°，∠PEG=65°，则∠BPD=．13(2023·浙江·九年级专题练习)如图，已知AB∥DE，∠BCD=30°，∠CDE=138°，求∠ABC的度数．14(2023春·重庆南岸·九年级校考期中)在数学课上老师提出了如下问题：如图，∠B=160°，当∠A与∠D满足什么关系时，BC∥DE?小明认为∠D-∠A=20°时BC∥DE，他解答这个问题的思路和步骤如下，请根据小明的思路完成下面的作图与填空：15(2023春·河北廊坊·七年级校考阶段练习)(1)如图(1)AB∥CD，猜想∠BPD与∠B、∠D的关系，说出理由．(2)观察图(2)，已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，并说明理由．(3)观察图(3)和(4)，已知AB∥CD，猜想图中的∠BPD与∠B、∠D的关系，不需要说明理由．16(2023秋·广东江门·八年级校考阶段练习)(1)如图①，如果AB∥CD，求证：∠APC=∠A+∠C．(2)如图②，AB∥CD，根据上面的推理方法，直接写出∠A+∠P+∠Q+∠C=．(3)如图③，AB∥CD，若∠ABP=x，∠BPQ=y，∠PQC=z，∠QCD=m，则m=(用x、y、z表示)．17(2023春·山东淄博·九年级校考期中)如图，AB∥CD，点E为两直线之间的一点．(1)如图1，若∠BAE=30°，∠DCE=20°，则∠AEC=；如图1，若∠BAE=α，∠DCE=β，则∠AEC=；(2)如图2，试说明，∠BAE+∠AEC+∠ECD=360°；(3)如图3，若∠BAE的平分线与∠DCE的平分线相交于点F，判断∠AEC与∠AFC的数量关系，并说明理由．18(2022·湖南株洲市八年级期末)已知直线a∥b，直线EF分别与直线a，b相交于点E，F，点A，B分别在直线a，b上，且在直线EF的左侧，点P是直线EF上一动点(不与点E，F重合)，设∠PAE=∠1，∠APB=∠2，∠PBF=∠3．(1)如图1，当点P在线段EF上运动时，试说明∠1+∠3=∠2；(提示：过点P作PM∥a)(2)当点P在线段EF外运动时有两种情况，①如图2写出∠1，∠2，∠3之间的关系并给出证明．②如图3所示，猜想∠1，∠2，∠3之间的关系(不要求证明)．19(2023·内蒙古鄂尔多斯·七年级校考期中)问题探究：如下面四个图形中，AB∥CD．(1)分别说出图1、图2、图3、图4中，∠1与∠2、∠3三者之间的关系．(2)请你从中任选一个加以说明理由．解决问题：(3)如图5所示的是一探照灯灯碗的纵剖面，从位于O点的灯泡发出两束光线OB、OC经灯碗反射后平行射出．如果∠ABO=57°，∠DCO=44°，那么∠BOC=°．20(2023春·湖北黄冈·七年级校考期中)如图，已知：点A、C、B不在同一条直线，AD∥BE(1)求证：∠B+∠C-∠A=180°：(2)如图②，AQ、BQ分别为∠DAC、∠EBC的平分线所在直线，试探究∠C与∠AQB的数量关系；(3)如图③，在(2)的前提下，且有AC∥QB，直线AQ、BC交于点P，QP⊥PB，直接写出∠DAC：∠ACB：∠CBE=．21(2023春·广东·七年级专题练习)(1)如图1，AB∥CD，∠ABE=45°，∠CDE=21°，直接写出∠BED 的度数．(2)如图2，AB∥CD，点E为直线AB,CD间的一点，BF平分∠ABE，DF平分∠CDE，写出∠BED与∠F之间的关系并说明理由．(3)如图3，AB与CD相交于点G，点E为∠BGD内一点，BF平分∠ABE，DF平分∠CDE，若∠BGD=60°，∠BFD=95°，直接写出∠BED的度数．22(2023春·福建三明·七年级校考期中)探索：小明在研究数学问题：已知AB⎳CD，AB和CD都不经过点P，探索∠P与∠A、∠C的数量关系．发现：在图1中，∠APC=∠A+∠C；如图5小明是这样证明的：过点Р作PQ⎳AB∴∠APQ=∠A∵PQ⎳AB，AB⎳CD．∴PQ⎳CD∴∠CPQ=∠C∴∠APQ+∠CPQ=∠A+∠C即∠APC=∠A+∠C(1)为小明的证明填上推理的依据；(2)理解：①在图2中，∠P与∠A、∠C的数量关系为；②在图3中，若∠A=30°，∠C=70°，则∠P的度数为；(3)拓展：在图4中，探究∠P与∠A、∠C的数量关系，并说明理由．23(2023春·山东·七年级专题练习)如图1，直线AB⎳CD，点P在两平行线之间，点E在AB上，点F 在CD上，连接PE，PF．(1)若∠PEB=60°，∠PFD=50°，请求出∠EPF．(请写出必要的步骤，并说明理由)(2)如图2，若点P，Q在直线AB与CD之间时，∠1=30°，∠2=40°，∠3=70°，请求出∠4=．(不需说明理由，请直接写出答案)(3)如图3，在图1的基础上，作P1E平分∠PEB，P1F平分∠PFD，若设∠PEB=x°，∠PFD=y°，则∠P1= (用含x，y的式子表示)．若P2E平分∠P1EB，P2F平分∠P1FD，可得∠P2；P3E平分∠P2EB，P3F平分∠P2 FD，可得∠P3⋯，依次平分下去，则∠Pn=．(用含x，y的式子表示)三角形中的倒角模型-平行线+拐点模型近年来各地中考中常出现一些几何倒角模型，该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。

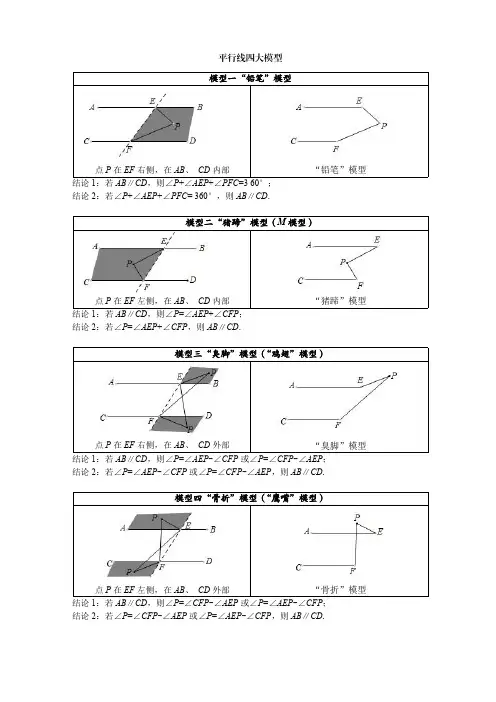
平行线之子弹模型解题策略基本模型：ACEFP结论1：若AB⎳CD，则∠P+∠AEP+∠PFC=360o;结论2：若∠P+∠AEP+∠PFC=360o，则AB⎳CD.拓展1：A CEFP结论1：若AB⎳CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB⎳CD.拓展2：A CE FPQ结论1：若AB⎳CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB⎳CD.经典例题1.(2022春•长沙期中)问题情境我们知道，“两条平行线被第三条直线所截，同位角相等，内错角相等，同旁内角互补”，所以在某些探究性问题中通过“构造平行线”可以起到转化的作用．已知三角板ABC中，∠BAC=60°，∠B=30°，∠C=90°，长方形DEFG中，DE∥GF．问题初探(1)如图(1)，若将三角板ABC的顶点A放在长方形的边GF上，BC与DE相交于点M，AB⊥DE于点N，求∠EMC的度数．分析：过点C作CH∥GF．则有CH∥DE，从而得∠CAF=∠HCA，∠EMC=∠MCH，从而可以求得∠EMC的度数．由分析得，请你直接写出：∠CAF的度数为30°，∠EMC的度数为60°．类比再探(2)若将三角板ABC按图(2)所示方式摆放(AB与DE不垂直)，请你猜想写∠CAF与∠EMC的数量关系，并说明理由．(3)请你总结(1)，(2)解决问题的思路，在图(3)中探究∠BAG与∠BMD的数量关系？并说明理由．【分析】(1)过点C作CH∥GF，则CH∥DE，这样就将∠CAF转化为∠HCA，∠EMC转化为∠MCH，从而可以求得∠EMC的度数；(2)过C作CH∥GF，依据平行线的性质，即可得到内错角相等，进而得出∠EMC+∠CAF=∠MCH+∠ACH=∠ACB=90°；(3)过B作BK∥GF，依据平行线的性质，即可得到内错角相等，进而得出∠BAG-∠BMD=∠ABK-∠KBM=∠ABC=30°．【解答】解：(1)由题可得，∠CAF=∠BAF-∠BAC=90°-60°=30°，∠EMC=∠BCH=90°-30°=60°；故答案为：30°，60°；(2)∠EMC+∠CAF=90°，理由：证明：如图，过C作CH∥GF，则∠CAF=∠ACH，∵DE∥GF，CH∥GF，∴CH∥DE，∴∠EMC=∠HCM，∴∠EMC+∠CAF=∠MCH+∠ACH=∠ACB=90°；(3)∠BAG-∠BMD=30°，理由：证明：如图，过B作BK∥GF，则∠BAG=∠KBA，∵BK∥GF，DE∥GF，∴BK∥DE，∴∠BMD=∠KBM，∴∠BAG-∠BMD=∠ABK-∠KBM=∠ABC=30°．2.(2022春•莆田期末)李想是一位善于思考的学生，在一次数学活动课上，他将一块含有60°的直角三角板摆放在一组平行线上展开探究．已知直线EF∥GH，直角三角板ABC中，∠ACB=90°，∠CAB=60°，点C为直线EF上一定点．将直角三角板ABC绕点C转动，当点A在直线GH上时，点B也恰好在直线GH上．(1)如图1，求∠ECB的度数；(2)如图2，若点A在直线EF上方，点B在GH下方，BC与GH交于点Q，作∠ACE的角平分线并反向延长与∠CQH的角平分线交于点O．在直角三角板ABC绕点C转动的过程中，∠O的度数是否保持不变？若不变，求出∠O的度数；否则，请说明理由；(3)如图3，直角三角板ABC绕点C转动，若点A在直线EF，GH之间(不含EF，GH上)，点B在GH下方，AB，BC分别与GH交于点P，Q．设∠FCB=n°，是否存在正整数m和n，使得∠APH= m∠FCB，若存在，请求出m和n的值；若不存在，请说明理由．【分析】(1)根据两直线平行内错角相等，求得∠ECA，然后求得∠ECB．(2)过点O作EF的平行线，利用平行线的性质、角平分线的定义，得出∠O始终为∠ACB的一半，即45°，从而得出∠O的度数始终不变．(3)根据四边形的内角和360°及平行线的性质得出关于m和n的关系式，根据题意得出m的范围，在范围内找到m和n都是正整数的所有可能的情况．【解答】解：(1)∵EF∥GH，∴∠ECA=∠CAB=60°，∴∠ECB=∠ACB+∠ECA=90°+60°=150°．(2)∠O的度数保持不变．理由如下：过点O作OP∥EF，∵EF∥GH，∴EF∥OP∥GH，∴∠COP=∠FCO，∠POQ=∠OQH，∠ECQ=∠CQH，∵CD平分∠ACE，OQ平分∠CQH，∴∠DCE=12∠ACE，∠OQH=12∠CQH=12∠ECB，∴∠POQ=∠ECB，∵∠DCE=∠FCO，∴∠COP=∠DCE=12∠ACE，∴∠COQ=∠COP+∠POQ=12∠ACE+12∠ECB=12(∠ACE+∠ECB)=12∠ACB=12×90°=45°．∴∠O的度数保持不变，始终是45°．(3)存在．理由如下：∵∠ACB=90°，∠A=60°，∴∠APQ+∠CQP=360°-∠ACB-∠A =360°-90°-60°=210°，∵EF∥GH，∴∠FCB=∠CQP=n°，∴∠APQ+∠CQP=∠APQ+n°=210°，∵∠APH=m∠FCB，∴∠APH=mn°，∴mn°+n°=210°，由此得出，n=210m+1，∵点A在直线EF，GH之间(不含EF，GH上)，点B在GH下方，∴30°<n°<90°，即mn°<180°，m，n是正整数，∴当m=1时，n=2102=105，不符合题意，舍去；当m=2时，n=2103=70，符合题意；当m=3时，n=1052不是正整数，舍去；当m=4时，n=2105=42，符合题意；当m=5时，n=35，符合题意；当m=6时，n=2107=30，不符合题意，舍去．综上所得，m=2，n=70，或m=4，n=42，或m=5，n=35．3.(2022春•宜春期末)问题：已知线段AB∥CD，在AB、CD间取一点P(点P不在直线AC上)，连接PA、PC，试探索∠APC与∠A、∠C之间的关系．(1)端点A、C同向：如图1，点P在直线AC右侧时，∠APC-(∠A+∠C)=　0　度；如图2，点P在直线AC左侧时，∠APC+(∠A+∠C)=　360　度；(2)端点A、C反向：如图3，点P在直线AC右侧时，∠APC与∠A-∠C有怎样的等量关系？写出结论并证明；如图4，点P在直线AC左侧时，∠APC-(∠A-∠C)=　180　度．【分析】(1)过点P作PE∥AB，分别利用猪脚模型，铅笔模型即可解答；(2)过点P作PE∥CD，利用平行线的性质，以及角的和差关系进行计算即可解答．【解答】解：(1)如图：过点P作PE∥AB，∴∠A=∠APE，∵AB∥CD，∴PE∥CD，∴∠C=∠EPC，∵∠APC=∠APE+∠EPC，∴∠APC=∠A+∠C，∴∠APC-(∠A+∠C)=0度，故答案为：0；如图：过点P作PE∥AB，∴∠A+∠APE=180°，∵AB∥CD，∴PE∥CD，∴∠C+∠EPC=180°，∴∠A+∠APE+∠C+∠EPC=360°，∴∠APC+∠A+∠C=360°，∴∠APC+(∠A+∠C)=360度，故答案为：360；(2)∠APC+∠A-∠C=180°，证明：过点P作PE∥CD，∴∠C=∠EPC，∵AB∥CD，∴PE∥AB，∴∠A+∠APE=180°，∴∠A+∠APC-∠EPC=180°，∴∠A+∠APC-∠C=180°，∴∠APC+∠A-∠C=180°；如图：过点P作PE∥AB，∴∠A=∠APE，∵AB∥CD，∴PE∥CD，∴∠C+∠EPC=180°，∴∠C+∠APC-∠APE=180°，∴∠C+∠APC-∠A=180°，∴∠APC-(∠A-∠C)=180°，故答案为：180．4.(2022春•佛山月考)问题情境：(1)如图1，AB∥CD，∠BAP=120°，∠PCD=130°，求∠APC的度数．(提示：如图2，过P作PE∥AB)问题迁移：(2)如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP=α，∠PCB=β，α、β、∠DPC之间有何数量关系？请说明理由；(3)在(2)的条件下，如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合)，请你直接写出α、β、∠DPC之间的数量关系．(提示：三角形内角和为180°)【分析】(1)过P作作PE∥AB，然后利用平行线的性质可以解决问题；(2)过P作作PE∥AB，然后利用平行线的性质可以解决问题；(3)有两种情况：当P在AB延长线和当P在OA延长线，都是通过作平行线利用平行线的性质解决问题．【解答】解：(1)∵AB∥CD，∠PAB=120°，∠PCD=130°，∴∠PAB+∠APE=180°，∠EPC+∠C=180°，∴∠APE=180°-120°=60°，∠EPC=180°-130°=50°，∴∠APC=∠APE+∠EPC=60°+50°=110°；(2)∠CPD=∠α+∠β，理由如下：如图3，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠DPE+∠CPE=∠α+∠β；(3)①当P在OA延长线时，∠CPD=∠β-∠α；②当P在AB延长线时，∠CPD=∠α-∠β，①当P在OA延长线时，∠CPD=∠β-∠α；理由：如图4，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠CPE-∠DPE=∠β-∠α；②当P在AB延长线时，∠CPD=∠α-∠β，理由：如图5，过P作PE∥AD交CD于E，∵AD∥BC，∴AD∥PE∥BC，∴∠α=∠DPE，∠β=∠CPE，∴∠CPD=∠DPE-∠CPE=∠α-∠β．培优训练一、选择题1.(2022春•交口县期末)某小区车库门口的“曲臂直杆道闸”(如图)可抽象为如右图所示模型．已知AB垂直于水平地面AE．当车牌被自动识别后，曲臂直杆道闸的BC段将绕点B缓慢向上抬高，CD段则一直保持水平状态上升(即CD与AE始终平行)，在该运动过程中∠ABC+∠BCD的度数始终等于()度A.360B.180C.250D.270【分析】过点B作BG∥AE，利用平行线的性质可得∠BAE+∠ABG=180°，∠C+∠CBG=180°，从而可得∠BAE+∠ABC+∠BCD=360°，然后根据垂直定义可得∠BAE=90°，最后进行计算即可解答．【解答】解：过点B作BG∥AE，∴∠BAE+∠ABG=180°，∵AE∥CD，∴BG∥CD，∴∠C+∠CBG=180°，∴∠BAE+∠ABG+∠CBG+∠C=360°，∴∠BAE+∠ABC+∠BCD=360°，∵BA⊥AE，∴∠BAE=90°，∴∠ABC+∠BCD=360°-∠BAE=270°，故选：D．2.(2022春•陆河县期末)①如图1，AB∥CD，则∠A+∠E+∠C=180°；②如图2，AB∥CD，则∠A=∠P+∠C；③如图3，AB∥CD，则∠A+∠E=180°+∠1；④如图4，AB∥CD∥EF，则∠α+∠r= 180°+∠β以上结论正确的是()A.①③④B.①②④C.②③④D.①②③【分析】①过点E作EF∥AB，根据平行线的性质可得∠A+∠AEF=180°，∠C+∠CEF=180°，从而可得∠A+∠AEC+∠C=360°，即可判断；②设CD与AP交于点G，先利用三角形的外角可得∠DGP=∠C+∠P，再利用平行线的性质可得∠A=∠DGP，然后根据等量代换即可判断；③延长AE交CD于点H，根据平行线的性质可得∠A+∠EHC=180°，然后利用三角形的外角可得∠EHC=∠AEC-∠1，然后进行计算即可判断；④利用平行线的性质可得∠COE=∠γ，从而可得∠BOE=∠γ-∠β，再利用平行线的性质可得∠α+∠BOE=180°，然后进行计算即可解答．【解答】解：①如图：过点E作EF∥AB，∴∠A+∠AEF=180°，∵AB∥CD，∴CD∥EF，∴∠C+∠CEF=180°，∴∠A+∠AEF+∠CEF+∠C=360°，∴∠A+∠AEC+∠C=360°，故①不正确；②如图：设CD与AP交于点G，∵∠DGP是△CPG的一个外角，∴∠DGP=∠C+∠P，∵AB∥CD，∴∠A=∠DGP，∴∠A=∠C+∠P，故②正确；③如图：延长AE交CD于点H，∵AB∥CD，∴∠A+∠EHC=180°，∵∠AEC是△EHC的一个外角，∴∠EHC=∠AEC-∠1，∴∠A+∠AEC-∠1=180°，∴∠A+∠AEC=180°+∠1，故③正确；④∵CD∥EF，∴∠COE=∠γ，∵∠BOE=∠COE-∠β，∴∠BOE=∠γ-∠β，∵AB∥EF，∴∠α+∠BOE=180°，∴∠α+∠γ-∠β=180°，∴∠α+∠r=180°+∠β，故④正确；所以，以上结论正确的是②③④，故选：C．3.(2022春•西湖区校级期中)如图，AB∥CD，点E为AB上方一点，FB、CG分别为∠EFG、∠ECD的角平分线，若∠E+2∠G=210°，则∠EFG的度数为()A.140°B.150°C.130°D.160°【分析】过G作GM∥AB，根据平行线的性质可得∠2=∠5，∠6=∠4，进而可得∠FGH=∠2+∠4，再利用平行线的性质进行等量代换可得3∠1=210°，求出∠1的度数，然后可得答案．【解答】解：过G作GM∥AB，∴∠2=∠5，∵AB∥CD，∴MG∥CD，∴∠6=∠4，∴∠G=∠5+∠6=∠2+∠4，∵FB、CG分别为∠EFG，∠ECD的角平分线，∴∠1=∠2=12∠EFG，∠3=∠4=12∠ECD，∴∠E+∠EFG+∠ECD=210°，∵AB∥CD，∴∠ENB=∠ECD，∴∠E+∠EFG+∠ENB=210°，∵∠1=∠E+∠ENB，∴∠1+∠EFG=∠1+∠1+∠2=210°，∴3∠1=210°，∴∠1=70°，∴∠EFG=2×70°=140°．故选：A．4.(2022春•林州市期末)如图，AB∥EF，∠C=90°，则α、β和γ的关系是()A.β=α+γB.α+β+γ=180°C.α+β-γ=90°D.β+γ-α=180°【分析】此题可以构造辅助线，利用三角形的外角的性质以及平行线的性质建立角之间的关系．【解答】解：延长DC交AB与G，延长CD交EF于H．在直角△BGC中，∠1=90°-α；△EHD中，∠2=β-γ，∵AB∥EF，∴∠1=∠2，∴90°-α=β-γ，即α+β-γ=90°．故选：C．5.(2021春•硚口区月考)如图，AB与HN交于点E，点G在直线CD上，GF交AB于点M，∠FMA=∠FGC，∠FEN=2∠NEB，∠FGH=2∠HGC，下列四个结论：①AB∥CD；②∠EHG=2∠EFM；③∠EHG+∠EFM=90°；④3∠EHG-∠EFM=180°．其中正确的结论是()A.①②③B.②④C.①②④D.①④【分析】过点F作FP∥AB，HQ∥AB，设∠NEB=x，∠HGC=y，利用猪脚模型、锯齿模型表示出∠EHG、∠EFM，即可分析出答案．【解答】解：∵∠FMA=∠FGC∴AB∥CD∴①正确；过点F作FP∥AB，HQ∥AB，∵AB∥CD，∴FP∥AB∥HQ∥CD，设∠NEB=x，∠HGC=y，则∠FEN=2x，∠FGH=2y∴∠EHG=∠EHQ+∠GHQ=∠AEH+∠HGC=∠NEB+∠HGC=x+y，∠EFM=∠BEF-∠FME=∠BEF-∠AMG=∠BEF-(180°-∠FGC)=x+2x-(180°-y-y)=3x +3y-180°，∴2∠EFM=6x+6y-360°，∴∠EHG≠2∠EFM∴②错误；∴∠EHG+∠EFM=x+y+3x+3y-180°=4x+4y-180°≠90°，∴③错误；∴3∠EHG-∠EFM=3(x+y)-(3x+3y-180°)=180°，∴④正确．综上所述，正确答案为①④．故选：D．6.(2022春•左权县期中)为了落实“双减”政策，促进学生健康成长，各学校积极推行“5+2”模式，立足学生的认知成长规律，满足学生多样化的需求，打造特色突出、切实可行的体育锻炼内容．晋中市的某学校将“抖空竹”引入阳光体育一小时活动，如图1是一位同学抖空竹时的一个瞬间，小丽把它抽象成图2的数学问题：已知AB∥CD，∠EAB=80°，∠ECD=110°，则∠E的度数是　30°　．【分析】延长DC交AE于点F，根据两直线平行，同位角相等可得∠EFC=80°，再根据三角形外角的性质可得∠E的度数．【解答】解：延长DC交AE于点F，∵AB∥CD，∴∠EFC=∠A=80°，由外角的性质得，∠DCE=∠E+∠EFC，∴∠E=110°-80°=30°．故答案为：30°．7.(2022春•九江期末)为了提醒司机不要疲劳驾驶，高速公路上安装了如图1所示的激光灯，图2是激光位于初始位置时的平面示意图，其中P，Q是直线MN上的两个发射点，∠APQ=∠BQP=60°，现激光PA绕点P以每秒3度的速度逆时针旋转，同时激光QB绕点Q以每秒2度的速度顺时针旋转，设旋转时间为t秒(0≤t≤40)，当PA∥QB时，t的值为　12　．【分析】根据当PA∥QB时，∠APQ+∠BQP=180°建立等式即可求解．【解答】解：设旋转时间为t秒后，PA∥QB，由题意得：60°+3°×t+60°+2°×t=180°，5°×t=60°，解得：t=12．故答案为：12．8.(2017春•南岸区期末)如图，AB∥CD，∠1=30°，∠2=50°，∠3=60°，则∠4=　140°　．【分析】过E作EM∥AB，过F作FN∥AB，求出AB∥EM∥FN∥CD，根据平行线的性质得出∠1=∠AEM，∠MEF=∠EFN，∠4+∠NFC=180°，再求出答案即可．【解答】解：过E作EM∥AB，过F作FN∥AB，∵AB∥CD，∴AB∥EM∥FN∥CD，∴∠1=∠AEM，∠MEF=∠EFN，∠4+∠NFC=180°，∵∠1=30°，∠AEF=50°，∠EFC=60°，∴∠AEM=30°，∴∠EFN=∠MEF=50°-30°=20°，∴∠NFC=60°-20°=40°，∴∠4=180°-40°=140°，故答案为：140°．9.(2022•南京模拟)如图，AB ∥CD ，AF 平分∠CAB ，CF 平分∠ACD ．(1)∠B +∠E +∠D =　360°　；(2)∠AFC =　90°　．【分析】(1)由两直线平行同旁内角互补可得：∠CAB +∠ACD =180°，再由五边形内角和540°，进行计算即可解答；(2)由角平分线的性质，解得∠FAC =12∠BAC ，∠FCA =12∠ACD ，根据两直线平行同旁内角互补解得∠CAB +∠ACD =180°，最后由三角形内角和180°解答．【解答】解：(1)∵AB ∥CD ，∴∠CAB +∠ACD =180°，∵五边形的内角和为(5-2)×180°=540°，∴∠B +∠E +∠D =540°-(∠CAB +∠ACD )=360°，故答案为：360°；(2)∵AB ∥CD ，∴∠CAB +∠ACD =180°，∵AF 平分∠CAB ，CF 平分∠ACD ，∴∠FAC =12∠BAC ，∠FCA =12∠ACD ，∴∠FAC +∠FCA =12∠BAC +∠ACD =12×180°=90°，∴∠AFC =180°-(∠FAC +∠FCA )=90°，故答案为：90°．10.(2022春•临沭县期中)如图，AB ∥CD ，将一副直角三角板作如下摆放，∠GEF =60°，∠MNP =45°．下列结论：①GE ∥MP ；②∠EFN =150°；③∠BEF =75°；④∠AEG =∠PMN ．其中正确的是　①②③④　．【分析】①由题意得∠G =∠MPN =∠MPG =90°，利用内错角相等，两直线平行即可判定GE ∥MP ；②由题意得∠EFG=30°，利用邻补角即可求出∠EFN的度数；③过点F作FH⊥AB，可得FH∥CD，从而得到∠HFN=∠MNP=45°，可求得∠EFN=105°，再利用平行线的性质即可求出∠BEF；④利用角的计算可求出∠AEG=45°，从而可判断．【解答】解：①∵∠G=∠MPN=∠MPG=90°，∴GE∥MP，故①正确；②∵∠EFG=30°，∴∠EFN=180°-30°=150°，故②正确；③过点F作FH∥AB，如图，∵AB∥CD，∴FH∥CD，∴∠HFN=∠MNP=45°，∴∠EFN=150°-45°=105°，∵FH∥AB，∴∠BEF=180°-105°=75°；故③正确；④∵∠GEF=60°，∠BEF=75°，∴∠AEG=180°-60°-75°=45°，∴∠AEG=∠PMN=45°，故④正确．故答案为：①②③④．11.(2022春•大安市期末)如图，在△ABC中，点D、E分别在AB、BC上，且DE∥AC，∠1=∠2．求证：AF∥BC．【分析】根据平行线的性质得出∠1=∠C，求出∠C=∠2，根据平行线的判定得出即可．【解答】证明：∵DE∥AC，∴∠1=∠C，∵∠1=∠2，∴∠C =∠2，∴AF ∥BC ．12.(2022春•随州期末)已知AB ∥CD ，点M 在射线AB ，CD 之间．(1)如图1，若∠BAM =150°，∠AMC =90°，小聪同学过点M 作MH ∥AB ，利用平行线的性质，求得∠MCD =　120　度；(2)如图2，请写出你发现的∠BAM ，∠AMC ，∠MCD 之间的数量关系，并证明你的结论；(3)如图3，MN 平分∠AMC 交AB 于点N ，CE 平分∠MCD 交AB 于点E ，MF ∥CE 交AB 于点F ，试猜想∠FMN 与∠BAM 的数量关系，并说明理由．【分析】(1)根据平行线的性质可得∠A +∠AMH =180°，∠C +∠CMH =180°，从而可得∠A +∠C +∠AMC =360°，然后进行计算即可解答；(2)过点M 作MH ∥AB ，然后利用平行线中的铅笔模型，即可解答．(3)根据角平分线的定义可得∠NMC =12∠AMC ，∠MCE =12∠MCD ，再利用平行线的性质可得∠FMC 180°-12∠MCD ，然后利用(2)的结论可得∠AMC +∠MCD =360°-∠A ，最后根据角的和差关系，进行计算即可解答．【解答】解：(1)∵MH ∥AB ，∴∠A +∠AMH =180°，∵AB ∥CD ，∴MH ∥CD ，∴∠C +∠CMH =180°，∴∠A +∠AMH +∠C +∠CMH =360°，∴∠A +∠C +∠AMC =360°，∵∠BAM =150°，∠AMC =90°，∴∠MCD =360°-∠BAM -∠AMC =120°，故答案为：120；(2)∠BAM +∠AMC +∠MCD =360°，证明：过点M 作MH ∥AB ，MH ∥AB ，∴∠A+∠AMH=180°，∵AB∥CD，∴MH∥CD，∴∠C+∠CMH=180°，∴∠A+∠AMH+∠C+∠CMH=360°，∴∠BAM+∠AMC+∠MCD=360°；(3)∠FMN=12∠BAM，理由：∵MN平分∠AMC，CE平分∠MCD，∴∠NMC=12∠AMC，∠MCE=12∠MCD，∵MF∥CE，∴∠FMC=180°-∠MCE=180°-12∠MCD，由(2)得：∠BAM+∠AMC+∠MCD=360°，∴∠AMC+∠MCD=360°-∠A，∵∠FMN=∠FMC-∠NMC，∴∠FMN=180°-12∠MCD-12∠AMC=180°-12(∠MCD+∠AMC)=180°-12(360°-∠A)=180°-180°+12∠A，=12∠A，∴∠FMN=12∠BAM．13.(2022春•甘井子区期末)已知直线EF分别与直线AB，CD相交于点G，M，并且∠AGE+∠CHF=180°．(1)如图1，求证：AB∥CD；(2)如图2，点M在直线AB，CD之间，连接GM，HM，求证：∠M=∠AGM+∠CHM；(3)如图3，在(2)的条件下，若射线GH恰好是∠BGM的平分线，在MH的延长线上取点N，连接GN，若∠N=∠AGM，则∠M、∠N、∠FGN的数量关系是　∠M=∠N+12∠FGN　(直接写答案)．【分析】(1)根据已知条件和对顶角相等即可证明；(2)过点M作MR∥AB，可得AB∥CD∥MR．进而可以求解；(3)令∠AGM=2α，∠CHM=β，则∠N=2α，∠M=2α+β，可得∠FGN=2β，进而可得结论．【解答】(1)证明：∵∠AGE=∠BGF，∠CHF=∠EHD，又∠AGE+∠CHF=180°，∴∠BGF+∠EHD=180°，∴AB∥CD；(2)证明：过点M作MK∥CD，则∠KMH=∠CHM，又AB∥CD；∴AB∥MK；∴∠AGM=∠GMK，∵∠GMH=∠AGM+∠KMH∴∠GMH=∠AGM+∠CHM．(3)解：如图3，令∠AGM=2α，∠CHM=β，则∠N=2α，∠M=2α+β，∵射线GF是∠BGM的平分线，∴∠FGM=12∠BGM=12(180°-∠AGM)=90°-α，∴∠AGH=∠AGM+∠FGM=2α+90°-α=90°+α，∵∠GMH=∠N+12∠FGN，∴2α+β=2α+12∠FGN，∴∠FGN=2β，∴∠M=2α+β=∠N+12∠FGN，即：∠M=∠N+12∠FGN．14.(2022春•宾阳县期末)如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG交于点H，∠C=∠EFG，∠CED=∠GHD．(1)求证：AB∥CD；(2)若∠EHF=70°，∠D=50°，求∠AEM的度数．【分析】(1)根据同位角相等两直线平行，可证CE∥GF，进而利用平行线的性质和判定证明；(2)根据对顶角相等可求∠DHG，根据三角形外角的性质可求∠CGF，根据平行线的性质可得∠C，∠AEC，再根据邻补角的定义可求∠AEM的度数．【解答】(1)证明：∵∠CED=∠GHD，∴CE∥GF，∴∠CEF+∠EFG=180°，∵∠C=∠EFG，∴∠CEF+∠C=180°，∴AB∥CD；(2)解：∵∠DHG=∠EHF=70°，∠D=50°，∴∠CGF=70°+50°=120°，∵CE∥GF，∴∠C+∠CGF=180°，∴∠C=180°-120°=60°，∵AB∥CD，∴∠AEC=∠C=60°，∴∠AEM=180°-∠AEC=180°-60°=120°．15.(2022春•江岸区期中)如图1，直线GH分别交直线AB、CD于点E、F(点F在点E左侧)，动点M、N不在AB、CD、GH上，若∠1=∠2，EM平分∠AEF，∠HFN=2∠DFN，连MN．(1)求证：AB∥CD；(2)如图2所示，点M、N停在图2位置，且∠M=∠N+70°，求∠AEM度数；(3)如图3，点M在GH左侧，点N在CD下方运动，请直接写出∠M、∠N、∠AEF三个角之间存在的数量关系　∠M-∠N=16∠AEF+60°或∠M+∠N=16∠AEF+60°　．(M、F、N三点不共线)【分析】(1)根据同位角相等两直线平行，即可证明．(2)设MN与GH交于点K，在△FNK和□EMK中，根据三角形内角和为180°，可得∠M+∠MEK=∠N+∠NFK，令∠AEM=a，由已知条件及平行线的性质，可得∠M+a=∠N+60°-2a+2a，进而可3得a的值．(3)根据点M在直线CD上方与下方进行分类讨论，再利用角的和差关系以及三角形的外角即可得出三个角之间的数量关系．【解答】解：(1)证明：∵AB与GH相交，∴∠1=∠3，∵∠1=∠2，∴∠2=∠3，∴AB∥CD．(2)设MN与GH交于点K，在△FNK和△EMK中，∵∠M+∠MEK+∠MKE=180°，∠N+∠NFK+∠NKF=180°，∠MKE=∠NKF，∴∠M+∠MEK=∠N+∠NFK，∵EM平分∠AEF，∴∠AEM=∠MEF，∵AB∥CD，∴∠AEF=∠DFG，令∠AEM=a，则∠DFG=2a，∴∠HFD=180°-2a，即∠HFN+∠DFN=180°-2a，∵∠HFN=2∠DFN，∴∠DFN=60°-2a3，∴∠M+a=∠N+60°-2a+2a，3∵∠M=∠N+70°，∴可得a=30°，∴∠AEM=30°．(3)①如图2，∠AEF=2a，∠M=13a+60°+∠N，∴∠M-∠N=16∠AEF+60°．②如图3．∵∠AEF=∠EFD=2a，∠MEF=∠AEM=a，∠DFN=60°-2a3，根据三角形外角的定义，可得∠EFD+∠DFN=∠M+∠N+∠MEF，即2a+60°-2a3=∠M+∠N+a，∴∠M+∠N=13a+60°，∴∠M+∠N=16∠AEF+60°．故答案为：∠M-∠N=16∠AEF+60°或∠M+∠N=16∠AEF+60°．16.(2022春•宁阳县期末)如图，AB∥CD，点E为两直线之间的一点．(1)如图1，若∠BAE=35°，∠DCE=20°，则∠AEC=　55°　；(2)如图2，试说明，∠BAE+∠AEC+∠ECD=360°；(3)①如图3，若∠BAE的平分线与∠DCE的平分线相交于点F，判断∠AEC与∠AFC的数量关系，并说明理由；②如图4，若设∠E=m，∠BAF=1n∠FAE，∠DCF=1n∠FCE，请直接用含m、n的代数式表示∠F的度数．【分析】(1)过点E作平行线，利用平行的性质求解；(2)过点E作平行线，利用平行的性质求解；(3)利用(1)(2)中的结论进行等量代换求解．【解答】解：(1)55°如图所示，过点E作EF∥AB，∵AB∥CD∴AB∥CD∥EF，∴∠BAE=∠1，∠ECD=∠2，∴∠AEC=∠1+∠2=∠BAE+∠ECD=35°+20°=55°，故答案为55°．(2)如图所示，过点E作EG∥AB，∵AB∥CD∴AB∥CD∥EG，∴∠A+∠1=180°，∠C+∠2=180°，∴∠A+∠1+∠2+∠C=360°，即∠BAE+∠AEC+∠ECD=360°．(3)①2∠AFC+∠AEC=360°，理由如下：由(1)可得，∠AFC=∠BAF+∠DCF，∵AF平分∠BAE，CF平分∠DCE，∴∠BAE=2∠BAF，∠DCE=2∠DCF，∴∠BAE+∠DCE=2∠AFC，由(2)可知，∠BAE+∠AEC+∠DCE=360°，∴2∠AFC+∠AEC=360°．②由①知∠F+∠FAE+∠E+∠FCE=360°，∵∠BAF=1n ∠FAE，∠DCF=1n∠FCE，∠BAF+∠DCF=∠F，∴∠F=1n(∠FAE+∠FCE)，∴∠FAE+∠FCE=n∠F，∴∠F+∠E+n∠F=360°，∴(n+1)∠F=360°-∠E=360°-m，∴∠F=360°-mn+1．17.(2021秋•香坊区期末)已知：直线AB、CR被直线UV所截，直线UV交直线AB于点B，交直线CR于点D，∠ABU+∠CDV=180°．(1)如图1，求证：AB∥CD；(2)如图2，BE∥DF，∠MEB=∠ABE+5°，∠FDR=35°，求∠MEB的度数；(3)如图3，在(2)的条件下，点N在直线AB上，分别连接EN、ED，MG∥EN，连接ME，∠GME=∠GEM，∠EBD=2∠NEG，EB平分∠DEN，MH⊥UV于点H，若∠EDC=17∠CDB，求∠GMH的度数．【分析】(1)利用平行线的判定定理即可证得结论；(2)利用平行线的性质及角的和差关系即可得出答案；(3)设∠MEN=α，可得出：∠NEG=2α，∠BEN=2α+40°，∠EBD=2∠NEG=4α，∠ABD=35°+4α，由EB平分∠DEN，可得：∠BED=∠BEN=α+40°，∠DEM=α+80°，再根据AB∥CD，∠EDC=1 7∠CDB，可得：∠BDE=67(145°-4α)，再根据三角形内角和定理建立方程可求得：α=10°，进而可得出答案．【解答】(1)证明：如图1，∵∠ABU+∠CDV=180°，∠ABU+∠ABV=180°，∴∠ABV=∠CDV，∴AB∥CD；(2)解：如图2，由(1)知：AB∥CD，∴∠ABD=∠BDR，∵BE∥DF，∴∠EBD=∠DBF，∴∠ABD-∠EBD=∠BDR-∠DBF，∴∠ABE=∠FDR=35°，∴∠MEB=∠ABE+5°=40°；(3)如图3，设∠MEN=α，∵MG∥EN，∴∠GME=∠MEN=α，∵∠GME=∠GEM=α，∴∠NEG=2α，∠BEN=2α+40°，∴∠EBD=2∠NEG=4α，∴∠ABD =∠ABE +∠EBD =35°+4α，∵EB 平分∠DEN ，∴∠BED =∠BEN =α+40°，∴∠DEM =α+80°，∵AB ∥CD ，∴∠CDB =180°-∠ABD =180°-(35°+4α)=145°-4α，∵∠EDC =17∠CDB ，∴∠BDE =67∠CDB =67(145°-4α)，∵∠EBD +∠BED +∠BDE =180°，∴4α+(α+40°)+67(145°-4α)=180°，解得：α=10°，∴∠BDE =67(145°-4α)=67(145°-4×10°)=90°，∠DEM =α+80°=10°+80°=90°，∵MH ⊥UV ，∴∠MHD =90°，∴∠EMH =360°-∠MHD -∠BDE -∠DEM =360°-90°-90°-90°=90°，∴∠GMH =∠EMH -∠GME =90°-10°=80°．18.(2021春•白云区期末)在四边形ABCD 中，AB ∥CD ，CF 平分∠DCE ．(1)如图1，点E 在四边形ABCD 内部，BF 平分∠ABE ，若∠BEC =150°，求∠BFC 的度数；(2)如图2，点E 在四边形ABCD 外部，BF 平分∠ABE ，∠BEC 和∠BFC 有怎样的等量关系？请证明你的结论；(3)如图3，点E 在四边形ABCD 内部，点M 在AB 的延长线上，∠MBE 的平分线交CF 反向延长线于点N ，∠BEC 和∠BNC 有怎样的等量关系？请直接写出你的结论．【分析】本题需要平行线的性质及对顶角相等，还要有多边形的内角和定理．(1)属于平行线里的锯齿模型：∠BFC =∠ABF +∠DCF ．(2)属于平行线里的外凸模型：∠ABE +∠DCE +∠BEC =360°．(3)利用平行线的性质和三角形的外角定理求解．【解答】解：(1)由平行线的性质可知：∠ABE+∠DCE=∠BEC=150°①①÷2及角平分线的定义得：∠ABF+∠DCF=75°∴∠BFC=∠ABF+∠DCF=75°．(2)由平行线的性质可知：∠ABE+∠DCE+∠BEC=360°①①÷2及角平分线的性质得：∠ABF+∠DCF+12∠BEC=180°．∵∠ABF+∠DCF=∠BFC．∴∠BFC+12∠BEC=180°．(3)延长DC交BN于G，则∠BEC=180°-2∠MBN+2∠FCD①而∠MBN=∠BGC=∠BNC+∠FCD②由①②及角平分线的定义可得：2∠BNC+∠BEC=180°．19.(2022春•凤泉区校级期末)如图，已知AB∥CD，E、F分别在AB、CD上，点G在AB、CD之间，连接GE、GF．(1)当∠BEG=40°，EP平分∠BEG，FP平分∠DFG时：①如图1，若EG⊥FG，则∠P的度数为　45°　；②如图2，在CD的下方有一点Q，EG平分∠BEQ，FD平分∠GFQ，求∠Q+2∠P的度数；(2)如图3，在AB的上方有一点O，若FO平分∠GFC．线段GE的延长线平分∠OEA，则当∠EOF+∠EGF=100°时，请直接写出∠OEA与∠OFC的数量关系．【分析】(1)①②根据平行线的性质，以及角平分线的定义即可求解；(2)过点O作OT∥AB，则OT∥CD，设∠OFC=∠OFG=β，∠OEH=∠HEA=α，∠G=∠BEG+∠GFD=α+180°-2β，根据平行线的性质求得α+β=80°，进而根据3∠OEA-∠OFC=3β-(β-2a)=2β+2α-160°即可求解．【解答】解：(1)①如图，分别过点G，P作GN∥AB，PM∥AB，∴∠BEG=∠EGN，∵AB∥CD，∴∠NGF=∠GFD，∴∠EGF=∠BEG+∠GFD，同理可得∠EPF=∠BEP+∠PFD，∵EG⊥FG，∴∠EGF=90°，∵EP平分∠BEG，FP平分∠DFG；∴∠BEP=12∠BEG，∠PFD=12∠GFD，∴∠EPF=12(∠BEG+∠GFD)=12∠EGF=45°，故答案为：45°；②如图，过点Q作QR∥CD，∵∠BEG=40°，∵EG恰好平分∠BEQ，FD恰好平分∠GFQ，∠GEQ=∠BEG=40°，∠GFD=∠QFD，设∠GFD=∠QFD=α，∵QR∥CD，AB∥CD，∴∠EQR=180°-∠QEB=180°-2∠QEG=100°，∵CD∥QR，∴∠DFQ+∠FQR=180°，∴α+∠FQR=180°，∴α+∠FQE=80°，∴∠FQE=80°-α，由①可知∠G=2∠P=∠BEG+∠GFD=40°+α，∴∠FQE+2∠P=80°-α+40°+α=120°；(2)3∠OEA-∠OFC=160°．∵在AB的上方有一点O，若FO平分∠GFC，线段GE的延长线平分∠OEA，设H为线段GE的延长线上一点，∴∠OFC=∠OFG，∠OEH=∠HEA，设∠OFC=∠OFG=β，∠OEH=∠HEA=α，如图，过点O作OT∥AB，则OT∥CD，∴∠TOF=∠OFC=β，∠TOE=∠OEA=2α，∴∠EOF=β-2α，∵∠HEA=∠BEG=a，∠GFD=180°-2β，由(1)可知∠G=∠BEG+∠GFD=α+180°-2β，∵∠EOF+∠EGF=100°，∴β-2α+α+180°-2β=100°，∴α+β=80°，∵∠ÓFC=β-2a，∠OEA=β，∴3∠OEA-∠OFC=3β-(β-2α)=2β+2α=160°，即3∠OEA-∠OFC=160°．20.(2022•南京模拟)已知AB∥CD，直线EF与AB、CD分别交于点E、F，点G为落在直线AB和直线CD之间的一个动点．(1)如图1，点G恰为∠BEF和∠DFE的角平分线的交点，则∠EGF=　90°　；(2)若点G恰为∠BEF和∠DFE的三等分线的交点，有如下结论：①∠EGF一定为钝角；②∠EGF可能为60°；③若∠EGF为直角，则EF⊥CD．其中正确结论的序号为　②③　．(3)进一步探索，若EF⊥CD，且点G不在线段EF上，记∠AEG=α，∠CFG=β，EM为∠AEG最接近EG的n等分线，FN是∠CFG最接近CF的n等分线(其中n≥2)．直线EM、FN交于点P n，是否存在某一正整数n，使得∠EP n F=90°？说明理由．【分析】(1)根据平行线的性质定理，两直线平行同旁内角互补，以及三角形内角和定理来完成．(2)根据平行线的性质定理，两直线平行同旁内角互补，以及三角形内角和定理，另外角的等分来判断．(3)按题意添加辅助线，画出相应的EM、FN、点P n，再根据平行线的性质定理，两直线平行同旁内角互补，以及三角形内角和定理、角的n等分，通过分类别讨论推测出n是否存在，存在的值．【解答】解：(1)∵AB∥CD，∴∠BEF+∠DFE=180°，∵点G恰为∠BEF和∠DFE的角平分线的交点，∴∠FEG+∠EFG=1×180°=90°，2∴∠EGF=180°-90°=90°．故答案为：90°．(2)若点G 恰为∠BEF 和∠DFE 的三等分线的交点，∴∠FEG +∠EFG =13×180°或者∠FEG +∠EFG =23×180°，∠FEG +∠EFG =60°或∠FEG +∠EFG =120°，∴∠EGF =180°-60°=120°或∠EGF =180°-120°=60°，∴①错误，②正确，当∠EGF 为直角，只有13∠BEF +23∠DFE =90°或23∠BEF +13∠DFE =90°，不妨假设13∠BEF +23∠DFE =90°，∴23∠BEF +13∠DFE =90°，∴13(∠BEF -∠DFE )+23(∠DFE -∠BEF )=0，∴∠BEF =∠DFE ，∵∠BEF +∠DFE =180°，∴∠BEF =∠DFE =90°，∴EF ⊥CD ，故③正确．故答案为：②③．(3)不存在某一整数n ，使得∠EP n F =90°，理由如下：∵EM 为∠AEG 最接近EG 的n 等分线，FN 是∠CFG 最接近CF 的n 等分线(其中n ≥2)，∴∠AEM =n -1n α，∠CFM =1nβ．①当点G 在EF 的左侧，此时α<90°，β<90°，P n 必在EF 的左侧，如图2所示，过点P n 作P n Q ∥AB ，∵AB ∥CD ，∴P n Q ∥CD ，∴∠EP n F =∠EPnQ +∠FP n Q =∠AEM +∠CFN =n -1n α+1n β<n -1n ×90°+1n×90°<90°，②当点G 在右侧，此时α>90°，β>90°．若n -1nα<90°，则P n 在EF 的左侧，如图3中，同理可得∠EP n F =n -1n α+1nβ>90°．若n -1nα=90°，则P n 与F 重合，不存在∠EP n F ，舍弃．若n -1n α>90°，则P n 在EF 的右侧，如图4中，过点P n作P n Q∥AB，∵AB∥CD，∴P n Q∥CD，∴∠EP n F=∠EP n Q-∠FP n Q=∠BEM+∠CFN=(180°-n-1nα)-1nβ，∵n-1n α>90°，1nβ>0，∴(180°-n-1n α)-1nβ<90°，即∠EP n F<90°，综上所述，不存在某一整数n，使得∠EP n F=90°．21.(2022春•坪山区校级期中)【问题情境】：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．小明的思路是：过P作PE∥AB，通过平行线的性质来求∠APC的度数．(1)按小明的思路，求∠APC的度数；(2)【问题迁移】如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；(3)【问题应用】在(2)的条件下，如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合)，请直接写出∠APC与α、β之间的数量关系．【分析】(1)利用平行线的性质，分别同得∠APE，∠CPE的度数，相加即可；(2)利用平行线的性质，和(1)辅导线的作法，推理即可；(3)利用平行线的性质，分情况直接写出数量关系即可．【解答】解：(1)过点P作PE∥AB，∵AB∥CD，∴AB∥CD∥PE，∴∠BAP+∠APE=180°，∠DCP+∠CPE=180°，∴∠BAP+∠APE+∠DCP+∠CPE=360°，即∠BAP+∠APC+∠DCP=360°，∵∠BAP=130°，∠DCP=120°，∴∠APC=360°-130°-120°=110°；故答案为：110°．(2)如图，过P点作PE∥CD∥AB，∴∠CPE=∠PCD，∠EPA=∠PAB，∴∠APC=∠CPE+∠EPA=∠PCD+∠PAB，∵∠PAB=α，∠PCD=β∴∠APC=α+β故答案为：∠APC=α+β．(3)如图所示，①过点P作PE∥AB，∵AB∥CD，∴∠PCD=∠EPC，∠EPA=∠PAB，∴∠PCD=∠EPC=∠APC+∠EPA=∠APC+∠PAB，∵∠PAB=α，∠PCD=β，∴∠APC=β-α．②如图所示，过点P作PE∥AB，∵AB∥CD，∴∠PAB=∠EPA，∠EPC=∠PCD，∴∠APC=∠EPA-∠EPC=∠PAB-∠PCD，又∵∠PAB=α，∠PCD=β，∴∠APC=α-β故答案为：①∠APC=β-α，②∠APC=α-β．。

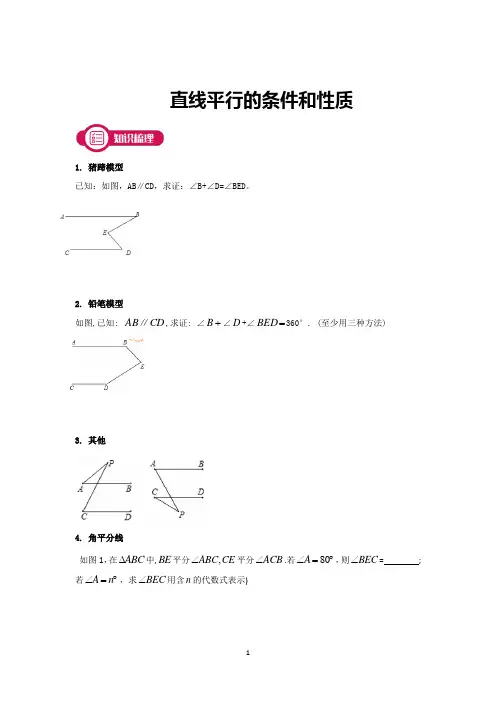
直线平行的条件和性质1. 猪蹄模型已知：如图，AB ∥CD ，求证：∠B+∠D=∠BED 。

2. 铅笔模型如图,已知: CD AB ∥,求证: ∠+B ∠D +∠=BED 360°. (至少用三种方法)3. 其他4. 角平分线如图1，在ABC ∆中,BE 平分,ABC CE ∠平分ACB ∠.若80A ∠=︒，则BEC ∠= ;若A n ∠=︒，求BEC ∠用含n 的代数式表示)如图3，在ABC ∆中，BO 平分外角,CBD CO ∠平分外角BCE ∠.若A n ∠=︒，求BOC ∠.如图5，在ABC ∆中，BE 平分ABC ∠, CE 平分外角ACM ∠.若A n ∠=︒，求BEC ∠.5. “8”字形 如图b 所示的“”字型，其也存在着一个等式：1+2=3+4∠∠∠∠，请证明；6. “A ”字型如图a 所示的“”字型，我们可称其为“A 字型”或“塔形”，其存在一个等式：1+2=3+4∠∠∠∠，请证明；7. 燕尾形如图c所示，其也存在着如下等式：D A B C∠=∠+∠+∠，请证明一．考点：平行线的性质，角度的计算与证明．二．重难点：常见的几种两条直线平行的结论1．两条平行线被第三条直线所截，一组同位角的角平分线平行；2．两条平行线被第三条直线所截，一组内错角的角平分线平行；3．两条平行线被第三条直线所截，一组同旁内角的角平分线垂直．三．易错点：1．性质是由图形的“位置关系”决定“数量关系”；2．两条平行线之间的距离其实可看成点到直线的距离．题型一：猪蹄模型例1. 如图，直线a∥b，直角三角形ABC的顶点B在直线a上，∠C=90°，∠β=55°，则∠α的度数为（）A． 15° B． 25° C． 35° D． 55°题型二：铅笔模型∠+∠+∠+∠=（）例2. 如图，AB∥CD，A E F CA ． 180°B ． 360°C ． 540°D ． 720°题型三：铅笔、猪蹄模型综合压轴例3. 某学习小组发现一个结论：已知直线a ∥b ，若直线c ∥a ，则c ∥b ．他们发现这个结论运用很广，请你利用这个结论解决以下问题：已知直线AB ∥CD ，点E 在AB 、CD 之间，点P 、Q 分别在直线AB 、CD 上，连接PE 、EQ ． （1）如图1，运用上述结论，探究∠PEQ 与∠APE +∠CQE 之间的数量关系，并说明理由； （2）如图2，PF 平分∠BPE ，QF 平分∠EQD ，当∠PEQ ＝140°时，求出∠PFQ 的度数； （3）如图3，若点E 在CD 的下方，PF 平分∠BPE ，QH 平分∠EQD ，QH 的反向延长线交PF 于点F ．当∠PEQ ＝70°时，请求出∠PFQ 的度数．题型三：其他例4. （周练）如图，已知AB ∥CD ，则∠A 、∠C 、∠P 的关系为.FE DCBA练习1. 如图，若AB∥CD，则α、β、γ之间的关系为．题型四：翻折例5. 如图所示，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置，若∠EFB=65°，则∠AED′等于______例6. 如图，将四边形纸片ABCD沿MN折叠，点A、D分别落在点A1、D1处．若∠1＋∠2＝140°，则∠B＋∠C＝°．题型五：角平分线例7. 如图，在△ABC中，∠ABC与∠ACB的平分线交于点O．（1）如图1，已知∠ABC＝40°，∠ACB＝60°，求∠BOC的度数．（2）如图2，已知∠A＝90°，求∠BOC的度数．（3）如图1，设∠A＝m°，求∠BOC的度数．例8. 如图13, 1BA 和1CA 分别是ABC ∆的内角平分线和外角平分线，2BA 是1A BD ∠的角平分线，2CA 是1A CD ∠的角平分线，3BA 是2A BD ∠的角平分线，3CA 是2A CD ∠的角平分线，若A α∠=，则2018A ∠为 .1. 如图，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F 的度数为（ ）A ．180°B ．360°C ．540°D ．720°2. 如图，将ABC ∆纸片沿DE 折叠，使点A 落在点'A 处，且'A B 平分ABC ∠，'A C 平分ACB ∠，若'110BA C ∠=︒，则12∠+∠的度数为（ ） A. 80° B. 90° C. 100° D. 110°3. 如图，将矩形纸带ABCD ，沿EF 折叠后，C 、D 两点分别落在C ′、D ′的位置，经测量得∠EFB=65°，则∠AED ′的度数是（ ）A ． 65°B ． 55°C ． 50°D ． 25°4. 如图，已知30B ∠=︒，55BCD ∠=︒，45CDE ∠=︒，20E ∠=︒，求证：AB ∥CD ．AFBC ED3.5. 如图，已知AB ∥DE ，BF ，EF 分别平分∠ABC 与∠CED ，若140BCE ∠=︒，求BFE ∠的度数．1. 如图，ABCDE 是封闭折线，则∠A 十∠B ＋∠C ＋∠D ＋∠E 为_______度．2. 如图，△ABE 和△ACD 是△ABC 分别沿着AB ，AC 边翻折180°形成的，若∠BAC ＝150°，则∠θ的度数是_______．3. 如图，在△ABC 中，∠C ＝90°．若BD ∥AE ，∠DBC ＝20°，则∠CAE 的度数是A ．40°B ．60°C ．70°D ．80° 4. 如图，把矩形沿对折后使两部分重合，若，则=（ ）A ．110°B ．115°C ．120°D ．130°A BCD E1.如图所示，将△ABC沿着DE翻折，若∠1+∠2=80°，则∠B=____度．2. 如图，若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED=70o，则∠BFD=________．3. 将一张长方形纸片如图所示折叠后，再展开．如果∠1=55o，那么∠2等于( )A．55o B．60o C．65o D．70o4. 问题情境：如图1，AB∥CD，∠PAB＝130°，∠PCD＝120°．求∠APC度数．小明的思路是：如图2，过P作PE∥AB，通过平行线性质，可得∠APC＝50°+60°＝110°．问题迁移：（1）如图3，AD∥BC，点P在射线OM上运动，当点P在A、B两点之间运动时，∠ADP ＝∠α，∠BCP＝∠β．∠CPD、∠α、∠β之间有何数量关系？请说明理由；（2）在（1）的条件下，如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD、∠α、∠β间的数量关系．5. 在△ABC中，∠A＝40°（1）如图1，若两内角∠ABC、∠ACB的角平分线交于点P，则∠P＝，∠A与∠P 之间的数量关系是．为什么有这样的关系？请证明它；（2）如图2，若内角∠ABC、外角∠ACE的角平分线交于点P，则∠P＝，∠A与∠P 之间的数量关系是；（3）如图3，若两外角∠EBC、∠FCB的角平分线交于点P，则∠P＝，∠A与∠P 之间的数量关系是．6. 【探究发现】如图1，在△ABC中，点P是内角∠ABC和外角∠ACD的角平分线的交点，试猜想∠P与∠A 之间的数量关系，并证明你的猜想．【迁移拓展】如图2，在△ABC中，点P是内角∠ABC和外角∠ACD的n等分线的交点，即∠PBC＝∠ABC，∠PCD＝∠ACD，试猜想∠P与∠A之间的数量关系，并证明你的猜想．【应用创新】已知，如图3，AD、BE相交于点C，∠ABC、∠CDE、∠ACE的角平分线交于点P，∠A＝35°，∠E＝25°，则∠BPD＝．。

七年级下册数学猪蹄模型知识点在七年级下学期的数学教学中，猪蹄模型是一个重要的知识点。

猪蹄模型是一种图形模型，其形状类似于猪蹄，用于辅助学生理解和解决数学问题。

本文将详细介绍猪蹄模型的定义、构造方法、使用场景以及使用技巧。

一、猪蹄模型定义猪蹄模型是一种三维图形模型，其外形类似于猪蹄子，由两个半球和一个圆柱组成。

具体来说，猪蹄模型可以由一个半径为r的半球和一个底面半径为r、高为2r的圆柱组成。

通常情况下，猪蹄模型也可能由两个大小相等或不相等的半球和一个圆柱组成。

二、猪蹄模型构造方法猪蹄模型的构造方法分为两种，一种是手工制作，另一种是使用计算机软件进行模拟建模。

手工制作方法：1. 准备所需材料，包括圆规、铅笔、剪刀、卡纸等。

2. 画出圆柱的底面圆，直径为2r。

3. 用圆规在半径为r的底面圆上画出一个半径为r的圆，然后沿着这个圆割下一段，形成半圆形。

4. 将卡纸用胶水粘在半球和圆柱上，最后组合在一起即可。

计算机模拟方法：1. 打开计算机三维建模软件，选中立方体工具。

2. 将左侧工具栏中的“拉伸”工具调整为圆柱形状。

3. 输入底面圆的半径和圆柱高度，确定圆柱形状。

4. 在左侧工具栏中选择“布尔运算”工具，选择圆柱和两个半球进行布尔运算，即可生成猪蹄模型。

三、猪蹄模型的使用场景猪蹄模型是一种三维模型，适用于多种数学问题的解决。

常见的使用场景如下：1.体积求解。

将圆柱和半球分别看作一份，再将两份组合起来即可求出题目中所要求的物体的体积。

例如：一个直径为12cm的圆球铁块，用铁球和铁圆柱组成，高度为8cm，求该铁块的重量。

2. 表面积求解。

将圆柱和半球的表面积分别计算，再将两者求和就可以得到猪蹄模型的表面积。

例如：一个底面半径为4cm，高为10cm的圆锥体，用猪蹄模型来近似表示，确定猪蹄模型的底部半径为4cm，则该猪蹄模型的表面积是多少？四、猪蹄模型的使用技巧使用猪蹄模型时需要注意以下几点：1.注意模型的比例关系。

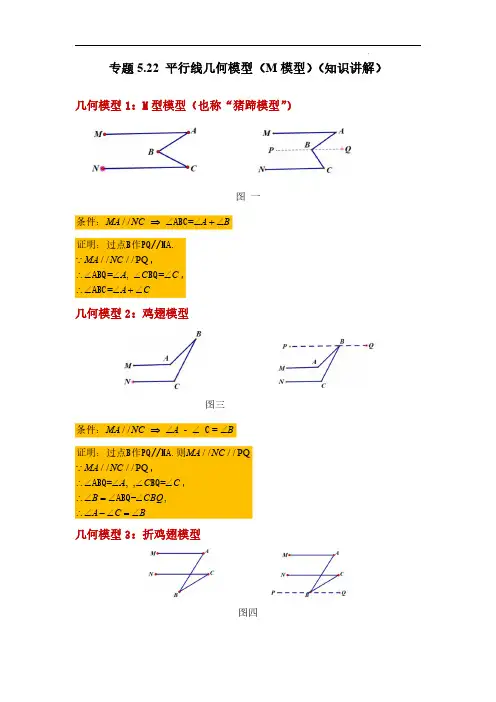
专题5.22平行线几何模型（M模型）（知识讲解）几何模型1：M型模型（也称“猪蹄模型”）图一//=MA NC A B⇒∠∠+∠条件：ABC////PQ=,==MA NCA C CA C∴∠∠∠∠∴∠∠+∠证明：过点B作PQ//MA.，ABQ BQ，ABC几何模型2：鸡翅模型图三//-=MA NC A B⇒∠∠∠条件：C////PQ////PQ,,,MA NCMA NCA C CB CBQA C B∴∠∠∠∠∴∠=∠∠∴∠-∠=∠证明：过点B作PQ//MA.则，ABQ=BQ=，ABQ-几何模型3：折鸡翅模型图四//MA NC A B⇒∠=∠+∠条件：C ////PQ////PQ ,,,MA NC MA NC A C C ABC CBQ A ACB C∴∠∠∠∠∴∠=∠∠∴∠==∠+∠ 证明：过点B作PQ//MA.则，ABQ=BQ =，ABQ-几何模型4：多个M 型模型12121//......n n MA NB P P P A Q Q Q B-⇒∠+∠++∠=∠+∠+∠++∠条件：【典型例题】类型一、平行线几何模型➽➼猪蹄模型➻➸求解✬✬证明1．请阅读小明同学在学习平行线这章知识点时的一段笔记，然后解决问题．小明：老师说在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，今天老师介绍了一个“美味”的模型“猪蹄模型”．即已知：如图1，AB CD ∥，E 为AB 、CD 之间一点，连接AE ，CE 得到AEC ∠．求证：AEC A C∠=∠+∠小明笔记上写出的证明过程如下:证明：过点E 作EF AB∥∵1A∠=∠∵AB CD ∥，EF AB∥∴EF CD∥∴2C∠=∠∴12AEC ∠=∠+∠∴AEC A C∠=∠+∠请你利用“猪蹄模型”得到的结论或解题方法，完成下面的两个问题．(1)如图，若AB CD ∥，60E ∠=o ，求B C F ∠+∠+∠；(2)如图，AB CD ∥，BE 平分ABG ∠，CF 平分DCG ∠，27G H ∠=∠+ ，求H ∠．【答案】(1)240 ；(2)51【分析】（1）作EM AB ∥，FN CD ∥，如图，根据平行线的性质得EM AB FN CD ∥∥∥，所以1B ∠=∠，23∠∠=，4180C ∠+∠= ，然后利用等量代换计算240B F C ∠+∠+∠= ；（2）分别过G 、H 作AB 的平行线MN 和RS ，根据平行线的性质和角平分线的性质可用ABG ∠和DCG ∠分别表示出H ∠和G ∠，从而可找到H ∠和G ∠的关系，结合条件可求得51H ∠= ．解：（1）作EM AB ∥，FN CD ∥，如图，且AB CD ∥180∴180227BHC BHC -∠=∠+ ，∴51BHC ∠= ．【点拨】本题考查了平行线的性质和判定的应用，能运用平行线的性质和判定进行推理是解此题的关键，注意：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．举一反三：【变式】阅读下面内容，并解答问题．已知：如图1，AB CD ，直线EF 分别交AB ，CD 于点E ，F ．BEF ∠的平分线与DFE ∠的平分线交于点G ．(1)求证：EG FG ⊥；(2)填空，并从下列①、②两题中任选一题说明理由．我选择题．①在图1的基础上，分别作BEG ∠的平分线与DFG ∠的平分线交于点M ，得到图2，则EMF ∠的度数为．②如图3，AB CD ，直线EF 分别交AB ，CD 于点E ，F ．点O 在直线AB ，CD 之间，且在直线EF 右侧，BEO ∠的平分线与DFO ∠的平分线交于点P ，则EOF ∠与EPF ∠满足的数量关系为．【答案】(1)见解析；(2)①45︒；②结论：2EOF EPF ∠=∠【分析】（1）利用平行线的性质解决问题即可；（2）①利用基本结论EMF BEM MFD ∠=∠+∠求解即可；②利用基本结论EOF BEO DFO ∠=∠+∠，EPF BEP DFP ∠=∠+∠，求解即可．（1）证明：如图，过G 作GH AB ，AB CD ，AB GH CD ∴ ，BEG EGH DFG FGH ∠∠∠∠∴==，，180BEF DFE ∴∠+∠=EG 平分BEF ∠，FG 12GEB BEF ∴∠=∠，12GEB GFD ∴∠+∠=∠在EFG ∆中，GEF ∠+∠EGF GEB GFD ∴∠=∠+∠EG FG ∴⊥；）解：①如图2中，由题意，EM 平分BEG ∠，MF 1(2BEM MFD ∴∠+∠=∠EMF BEM MFD ∴∠=∠+∠故答案为：45︒；结论：2EOF EPF ∠=∠理由：如图3中，由题意，PE 平分BEO ∠，PF 2BEO BEP ∴∠=∠，DFO ∠类型二、平行线几何模型➽➼鸡翅模型➻➸求解✬✬证明2．已知直线12l l ∥，3l 和1l ，2l 分别交于C ，D 点，点A ，B 分别在线1l ，2l 上，且位于3l 的左侧，点P 在直线3l 上，且不和点C ，D 重合．(1)如图1，有一动点P 在线段CD 之间运动时，求证：12APB ∠=∠+∠；(2)如图2，当动点P 在C 点之上运动时，猜想APB ∠、1∠、2∠有何数量关系，并说明理由．【答案】(1)证明见解析；(2)21APB ∠=∠+∠，理由见解析．【分析】()1过点P 作1//PE l ，根据12l l //可知2//PE l ，故可得出1APE ∠=∠，2.BPE ∠=∠再由APB APE BPE ∠=∠+∠即可得出结论；()2过P 作//PE AC ，依据12l l //，可得//PE BD ，进而得到2BPE ∠=∠，1APE ∠=∠，再根据BPE APE APB ∠=∠+∠，即可得出21APB ∠=∠+∠．（1）证明：如图1，过点P 作1//PE l ，12//l l ，2//PE l ∴，1APE ∴∠=∠，2BPE ∠=∠．又APB APE BPE ∠=∠+∠ ，12APB ∴∠=∠+∠；（2）解：21APB ∠=∠+∠．理由如下：如图2，过P 作//PE AC ，12//l l ，//PE BD ∴，2BPE ∴∠=∠，1APE ∠=∠，BPE APE APB ∠=∠+∠ ，21APB ∴∠=∠+∠．【点拨】本题考查的是平行线的性质，根据题意作出辅助线，构造出平行线是解答此题的关键．举一反三：【变式】【原题】已知直线AB ∥CD ，点P 为平行线AB ，CD 之间的一点，如图1，若∠ABP =50°，∠CDP =60°，BE 平分∠ABP ，DE 平分∠CDP ．(1)则∠P =______，∠E =______．(2)【探究】如图2，当点P 在直线AB 的上方时，若∠ABP =α，∠CDP =β，∠ABP 和∠CDP 的平分线交于点1E ，∠ABE 1与1CDE ∠的角平分线交于点2E ，∠ABE 2与∠CDE 2的角平分线交于点3E ，…以此类推，求∠E 2的度数，并猜想∠E n 的度数．(3)【变式】如图3，∠ABP 的角平分线的反向延长线和∠CDP 的补角的角平分线交于点E ，试直接写出∠P 与∠E 的数量关系．类型三、平行线几何模型➽➼多个M型模型➻➸求解✬✬证明3．探究：(1)如图①，已知AB CD，图中∠1，∠2，∠3之间有什么关系？(2)如图②，已知AB CD，图中∠1，∠2，∠3，∠4之间有什么关系？(3)如图③，已知AB CD，请直接写出图中∠1，∠2，∠3，∠4，∠5之间的关系；【答案】(1)∠1＋∠3＝∠2；(2)∠1＋∠3＝∠2＋∠4；(3)∠1＋∠3＋∠5＝∠2＋∠4．【分析】（1）过点E作EM∥AB，根据平行线的性质及角的和差求解即可；（2）过点F作NF∥AB，结合（1）并根据平行线的性质及角的和差求解即可；（3）过点G作GM∥AB，结合（2）并根据平行线的性质及角的和差求解即可．（1）解：如图①，过点E作EM∥AB，∵AB∥CD，∴AB∥CD∥EM，∴∠1＝∠NEM，∠3＝∠MEF，∴∠1＋∠3＝∠NEM＋∠MEF，即∠1＋∠3＝∠2；（2）如图②，过点F作NF∥AB，∵AB∥CD，∴AB ∥CD ∥FN ，∴∠4＝∠NFH ，由（1）知，∠1＋∠EFN ＝∠2，∴∠1＋∠EFN ＋∠NFH ＝∠2＋∠4，即∠1＋∠3＝∠2＋∠4；（3）如图③，过点G 作GM ∥AB ，∵AB ∥CD ，∴AB ∥CD ∥GM ，∴∠5＝∠MGN ，由（2）得，∠1＋∠3＝∠2＋∠FGM ，∴∠1＋∠3＋∠5＝∠2＋∠FGM ＋∠MGN ，即∠1＋∠3＋∠5＝∠2＋∠4．【点拨】此题考查了平行线的性质，熟记两直线平行，内错角相等是解题的关键．举一反三：【变式】【发现】如图，已知AB ∥CD ，直线AB ，CD 被EF 所截．若EM ，FN 分别平分∠AEF 和∠DFE ，判断EM 与FN 之间的位置关系，并证明你的结论；【变式】如图，已知180AEF EFC ∠+∠=︒，∠M ＝∠N ，求证∠1＝∠2；【拓展】如图，AB ∥CD ，∠1＝∠2，求证∠M ＝∠N ．∵AB∥CD，∴∠1＝∠EPD．∵∠1＝∠2，【点拨】本题考查平行线的性质和判定，熟练掌握平行线的性质和判定是解题的关键．类型四、平行线几何模型➽➼综合模型➻➸求解✬✬证明4．根据下列叙述填依据．(1)已知如图1，AB CD ∥，求∠B +∠BFD +∠D 的度数．解：过点F 作FE AB∥所以∠B +∠BFE =180°（）因为AB CD ∥、FE AB ∥（已知）所以（）所以∠D +∠DFE =180°（）所以∠B +∠BFE +∠D =∠B +∠BFE +∠EFD +∠D =360°(2)根据以上解答进行探索．如图（2）（3）AB EF 、∠D 与∠B 、∠F 有何数量关系（请选其中一个简要证明）备用图：(3)如图（4）AB EF ，∠C =90°，∠α与∠β、∠γ有何数量关系（直接写出结果，不需要说明理由）【答案】(1)两直线平行，同旁内角互补；FE CD ∥，平行于同一直线的两直线平行；两直线平行，同旁内角互补；(2)见解析；(3)90αβγ∠+∠-∠=︒【分析】（1）过点F 作FE AB ∥，得到∠B +∠BFE =180°，再根据AB CD 、FE AB ∥得到FE CD ∥，∠D +∠DFE =180°，最后利用角度的和差即可得出答案；（2）类比问题（1）的解题方法即可得解；（3）类比问题（1）的解题方法即可得解．（1）解：过点F 作FE AB ∥，如图，∴∠B +∠BFE =180°（两直线平行，同旁内角相等），∵AB CD ∥、FE AB ∥（已知）∴FE CD ∥（平行于同一直线的两直线平行），∴∠D +∠DFE =180°（两直线平行，同旁内角互补），∴∠B +∠BFE +∠D =∠B +∠BFE +∠EFD +∠D =360°；故答案为：两直线平行，同旁内角互补；FE CD ∥，平行于同一直线的两直线平行；两直线平行，同旁内角互补；（2）解：选图（2），∠D 与∠B 、∠F 的数量关系为：∠BDF +∠B =∠F ；理由如下：过点D 作DC//AB ，∴∠B =∠BDC ，∵AB EF ∥，DC AB ∥，∴DC EF ∥，∴∠CDF =∠F ，∴∠BDF +∠BDC =∠F ，即∠BDF +∠B =∠F ；选图（3），∠D 与∠B 、∠F 的数量关系：∠BDF +∠B =∠F过点D 作DC AB ∥，∴∠B =∠BDC ，∵AB EF ∥，DC AB ∥，∴DC EF ∥，∴∠CDF =∠F ，∴∠BDF +∠BDC =∠F ，即∠BDF +∠B =∠F∠BDF +∠B =∠F ；（3）解：90αβγ∠+∠-∠=︒如图（4）所示，过点C 作MC AB ∥，过D 作DN EF ∥，∴BCM α∠=∠，NDE g Ð=Ð，∵AB CM ∥，EF AB ∥，DN EF∥∴AB EF CM DN ∥∥∥，∴CDN MCD Ð=Ð，∵90MCD BCM Ð+Ð=°，CDN NDE b Ð=Ð+Ð，∴90αβγ∠+∠-∠=︒．【点拨】本题考查根据平行线的性质探究角的关系和平行线公理推论的运用，熟练掌握平行线的性质和平行线公理推论的运用是解题的关键．举一反三：【变式】已知：AB ∥EF ，在平面内任意选取一点C ．利用平行线的性质，探究∠B 、∠F、∠C满足的数量关系．(1)将探究∠B、∠C、∠F之间的数量关系填写下表：(2)请选择其中一个图形进行说明理由．图（2）∠F-∠B=∠C图（3）∠B-∠F=∠C图（4）∠B+∠F+∠C=360°图（5）∠B-∠F=∠C图（6）∠F-∠B=∠C（2）解：图（1）∠C与∠B、∠F之间的数量关系是：∠B+∠F=∠C．理由：过点C作CG∥AB，∴∠BCG=∠B，∵AB∥EF，∴CG∥EF，∴∠GCF=∠F，∴∠BCG+∠GCF=∠B+∠F，∴∠B+∠F=∠BCF；图（2）∠C与∠B、∠F之间的数量关系是：∠F-∠B=∠C．理由：过点C作CG∥AB，∴∠BCG=∠B，∵AB∥EF，∴CG∥EF，∴∠GCF=∠F，∴∠GCF-∠BCG=∠F-∠B，∴∠F-∠B=∠BCF；图（3）∠C与∠B、∠F之间的数量关系是：∠B-∠F=∠C．理由：过点C作CG∥AB，∴∠BCG=∠B，∵AB∥EF，∴CG∥EF，∴∠GCF=∠F，∴∠BCG-∠GCF=∠B-∠F，∴∠B-∠F=∠BCF；图（4）∠C与∠B、∠F之间的数量关系是：∠B+∠F+∠C=360°．理由：过点C作CG∥AB，∴∠BCG+∠B=180°，∵AB∥EF，∴CG∥EF，∴∠GCF+∠F=180°，∴∠BCG+∠B+∠GCF+∠F=180°+180°，∴∠B+∠F+∠BCF=360°；图（5）∠C与∠B、∠F之间的数量关系是：∠B-∠F=∠C．理由：过点C作CG∥AB，∴∠BCG=∠B，∵AB∥EF，∴CG∥EF，∴∠GCF=∠F，∴∠BCG-∠GCF=∠B-∠F，∴∠B-∠F=∠BCF；图（6）∠C与∠B、∠F之间的数量关系是：∠F-∠B=∠C．理由：过点C作CG∥AB，∴∠BCG=∠B，∵AB∥EF，∴CG∥EF，∴∠GCF=∠F，∴∠GCF-∠BCG=∠F-∠B，∴∠F-∠B=∠BCF；【点拨】本题考查平行线的判定和性质，解题的关键是学会添加常用辅助线，构造平行线解决问题．。

数学中平行线的猪蹄模型典型例题In mathematics, the猪蹄 model for parallel lines is a classic example that illustrates the properties of parallel lines and their intersection with other lines. This model, named after its resemblance to the shape of a pig's trotter, effectively demonstrates concepts such as angle relationships and line segments.在数学中，平行线的猪蹄模型是一个经典例子，它展示了平行线的性质以及它们与其他线的交点。

这个模型因其形状类似于猪蹄而得名，有效地演示了角度关系和线段等概念。

Consider the following scenario: We have two parallel lines, labeled Line A and Line B. A transversal line, Line C, intersects both Line A and Line B, forming a series of angles. The猪蹄 model helps us visualize and understand the relationships between these angles.考虑以下情况：我们有两条平行线，分别标记为线A和线B。

一条横截线，即线C，与线A和线B相交，形成一系列角度。

猪蹄模型有助于我们可视化并理解这些角度之间的关系。

One key aspect of the猪蹄 model is that alternate interior angles are equal. This means that the angles formed between Line A and Line C on one side, and between Line B and Line C on the other side, are equal to each other. This property is fundamental in understanding and applying the concept of parallel lines.猪蹄模型的一个关键方面是交替内角相等。