鲁教版(五四制)数学七年级下册 10.1 全等三角形 同步习题和答案

鲁教版（五四制）七年级数学下册第十章三角形的有关证明综合测试考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，在△ABC中，∠BAC＝90°，AB=AC，AD是经过A点的一条直线，且B、C在AD的两侧，BD⊥AD于D，CE⊥AD于E，交AB于点F，CE=10，BD＝4，则DE的长为（）A．6 B．5 C．4 D．82、如图，点E在等边△ABC的边BC上，BE＝4，射线CD⊥BC，垂足为点C，点P是射线CD上一动点，点F是线段AB上一动点，当EP+FP的值最小时，BF＝5，则AB的长为（）A．7 B．8 C．9 D．103、如图，在△ABC 中，∠BAC ＞90°，D 为BC 的中点，点E 在AC 上，将△CDE 沿DE 折叠，使得点C 恰好落在BA 的延长线上的点F 处，连接AD 、CF ，则图中所有的等腰三角形的个数为（ ）A ．1B ．2C ．3D ．44、在Rt ABC 与Rt DEF △中，90B E ∠=∠=︒，①AB DE =，AC DF =；②BC EF =，C F ∠=∠；③AB DE =，BC EF =；④A D ∠=∠，C F ∠=∠；⑤AC DF =，C F ∠=∠；能判断这两个三角形全等的有（ ）A ．1组B ．2组C ．3组D ．4组5、如图，矩形ABCD 中，对角线AC 、BD 相交于点O ，若AB ＝2，∠AOB ＝60°，则AC 的长度为（ ）A ．2B ．3C ．4D ．66、如图，AD 是△ABC 中∠BAC 的角平分线，DE ⊥AB 于点E ，S △ABC ＝7，DE ＝2，AB ＝4，则AC 长是（ ）A ．3B ．4C ．5D ．67、已知ABC 的周长是16，且AB AC =，又AD BC ⊥，D 为垂足，若ABD △的周长是12，则AD 的长为（ ）A ．7B ．6C ．5D ．48、如图所示，在等边三角形ABC中，D为AC边的中点，E为边BC延长线上一点，BD＝DE，DF⊥BE垂足为点F．下列结论：①AD＝CE；②CE+CD＝AB；③∠BDE＝120°；④CF：BF＝1：3；⑤S△CDE＝1 6S△ABE．其中正确的有（）A．2个B．3个C．4个D．5个9、如图，△ABC是等边三角形，点E是AC的中点，过点E作EF⊥AB于点F，延长BC交EF的反向延长线于点D，若EF=1，则DF的长为（）A．2 B．2.5 C．3 D．3.510、△BDE和△FGH是两个全等的等边三角形，将它们按如图的方式放置在等边三角形ABC内．若BC ＝5，则五边形DECHF的周长为（）A．8 B．10 C．11 D．12第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、等腰三角形的两边长分别为2和4，则这个三角形的周长为______．2、如图，在△ABC 中，AD 平分∠BAC ，DE ⊥AB 于点E ，S △ABC ＝15，DE ＝3，AB ＝6，则AC 长是___．3、如图，四边形ABCD 中，90A ∠=︒，3AD =，连接BD ，BD CD ⊥，垂足为D ，ADB C ∠=∠，点P 是边BC 上的一动点，则DP 的最小值是______．4、已知△ABC 中，AB =5， BC =8， BC 边上的中线AD =3，则AC =__________________．5、在△ABC 中，AD 是BC 边上的中线，AD ⊥AB ，如果AC =5，AD =2，那么AB 的长是________．三、解答题（5小题，每小题10分，共计50分）1、如图AB ∥CD ，∠B ＝∠D ，AE ＝CF ，求证：△ABF ≌△CDE ．2、如图，在Rt△ABC中，∠C＝90°，∠CAB的平分线交BC于点D，又DE是AB的垂直平分线，垂足为E．(1)求∠CAD的大小；(2)若BC＝3，求DE的长．3、如图，在Rt△ABC中，∠BAC＝60°，AD、BE分别是∠BAC与∠ABC的平分线，并交于点H．(1)若DC＝2，则AD＝；(2)∠AHB的度数．4、如图①，在△ABC中，∠B＝45°，∠C＝30°，过点A作直线AC的垂线交BC于点D．(1)求∠BAD 的度数；(2)若AC ＝AB 的长；(3)如图②，过点A 作∠DAC 的角平分线交BC 于点P ，点D 关于直线AP 的对称点为E ，试探究线段CE 与BD 之间的数量关系，并对结论给予证明．5、如图，在△ABC 中，AB AC =，AD 为BC 边上的中线，E 为AC 上一点，且AE AD =，50BAD ∠=︒，求∠CDE 的度数．-参考答案-一、单选题1、A【解析】【分析】根据∠BAC ＝90°得到∠BAD +∠CAD ＝90°，由于CE ⊥AD 于E ，于是得到∠ACE +∠CAE ＝90°，根据余角的性质得到∠BAD ＝∠ACE ，推出△ABD ≌△CAE ，根据全等三角形的性质即可得到结论．【详解】解：∵∠BAC ＝90°，∴∠BAD +∠CAD ＝90°，∵CE ⊥AD 于E ，∴∠ACE +∠CAE ＝90°，∴∠BAD ＝∠ACE ，在△ABD 与△CAE 中，90D AEC BAD ACE AB AC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩， ∴△ABD ≌△CAE （AAS ），∴AE ＝BD ＝4，AD ＝CE ＝10，∴DE ＝AD ﹣AE ＝6．故选：A ．【点睛】本题考查全等三角形的判定与性质，解题的关键是利用余角的性质得到∠BAD ＝∠ACE ．2、A【解析】【分析】作E 点关于CD 的对称点E '，过E '作E 'F ⊥AB 交于点F ，交CD 于点P ，连接PE ，此时EP +FP 的值最小，由题意可得∠FE 'B =30°，则BE '=2BF ，再由BF =5，BE =4，可得10=2CE +4，解得CE =3，可求BC =7．【详解】解：作E 点关于CD 的对称点E '，过E '作E 'F ⊥AB 交于点F ，交CD 于点P ，连接PE ，∴PE=PE'，∴EP+FP=PE'+PF≥E'F，此时EP+FP的值最小，∵△ABC是正三角形，∴∠B=60°，∵E'F⊥AB，∴∠FE'B=30°，∴BE'=2BF，∵BF=5，BE=4，∴E'B=10，∵CE=CE'，∴10=2CE+BE=2CE+4，∴CE=3，∴BC=7，故选：A．【点睛】本题考查轴对称求最短距离，熟练掌握轴对称求最短距离的方法，等边三角形的性质，直角三角形的性质是解题的关键．【解析】【分析】由折叠的性质可得CD=DF，EF=EC，结合D为BC的中点可得BD=CD=DF，可得△BDF，△CDF，△EFC是等腰三角形，再由等腰三角形的性质和余角的性质可得∠FAE=∠AFE，可得EF=EA可说明△AEF是等腰三角形．【详解】解：如图：∵D为BC的中点，∴BD=CD，∵将△CDE沿DE折叠，∴CD=DF，EF=EC，∴BD=CD=DF，∴△BDF，△CDF，△EFC是等腰三角形，∴EF=EC，∴∠EFC=∠ECF，∴∠FAE=∠AFE，∴EF=AE，∴△AEF是等腰三角形，∴图中所有的等腰三角形的个数为4．故选D．【点睛】本题主要考查了翻折变换、等腰三角形的判定和性质等知识点，熟练运用折叠的性质是解答本题的关键．【解析】【分析】根据三角形的判定定理对各选项一一分析判定即可．【详解】解：①AB DE =，AC DF =；在Rt△ABC 和Rt△DEF 中，AB DE AC DF =⎧⎨=⎩， ∴Rt△ABC ≌Rt△DEF （HL ），故①正确；②BC EF =，C F ∠=∠；在△ABC 和△DEF 中，C F BC EF B E ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABC ≌△DEF （ASA ），故②正确；③AB DE =，BC EF =在△ABC 和△DEF 中，AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩， ∴△ABC ≌△DEF （SAS ），故③正确；④A D ∠=∠，C F ∠=∠，90B E ∠=∠=︒；没有边对应相等，故④不正确；⑤AC DF =，C F ∠=∠在△ABC 和△DEF 中，C B E F AC DF ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ABC ≌△DEF （AAS ），故⑤正确；故选D ．【点睛】本题考查三角形全等判定，掌握三角形全等判定定理是解题关键．5、C【解析】【分析】由矩形的性质得OA ＝OB ＝OC ＝OD ，继而证明△ABC 为等边三角形，解得∠ACB ＝30°，最后根据含30°角的直角三角形的性质：30°角所对的直角边等于斜边的一半解题．【详解】解：∵矩形ABCD为矩形，∴OA＝OB＝OC＝OD，∠ABC＝90°，∵∠AOB＝60°，∴△ABC为等边三角形，∴∠BAC＝60°，∴∠ACB＝30°，∵AB＝2，∴AC＝2AB＝4．故选：C．【点睛】本题考查矩形的性质、含30°角的直角三角形的性质、等边三角形的判定与性质等知识，是重要考点，掌握相关知识是解题关键．6、A【解析】【分析】过D作DF⊥AC于F，由角平分线的性质可得2==，进而根据S△ADB＋S△ADC＝7，利用三角形DE EF面积公式即可求得AC的长【详解】解：如图，过D作DF⊥AC于F，∵AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，DE＝2，∴DE＝DF＝2，∵S△ABC＝7，∴S△ADB＋S△ADC＝7，∴1122AB DE AC DF⨯⨯+⨯⨯＝7，∴1142222AC⨯⨯+⨯⨯＝7，解得：AC＝3，故选：A．【点睛】本题考查了角平分线的性质，掌握角平分线的性质是解题的关键．7、D【解析】【分析】根据三线合一推出BD＝DC，再根据两个三角形的周长进而得出AD的长．【详解】解：∵AB=AC，且AD⊥BC，∴BD=DC=12BC，∵AB+BC+AC=2AB+2BD=16，∴AB+BD=8，∴AB+BD+AD=8+AD=12，解得AD=4．故选：D．【点睛】本题考查了等腰三角形的性质，做题时应该将已知和所求联系起来，对已知进行灵活运用，从而推出所求．8、D【解析】【分析】首先证明∠CDE＝∠CED＝30°，可知①②③正确，再证明BC＝3CF，可得④正确，证明BC＝2CE，可得⑤正确．【详解】解：∵△ABC是等边三角形，AD＝DC，∴BD⊥AC，BD平分∠ABC，∵∠ABC＝∠ACB＝60°，∴∠DBC＝30°，∵DB＝DE，∴∠DBC＝∠DEC＝30°，∵∠ACB＝∠CDE+∠CED，∴∠CDE＝∠CED＝30°，∴CD＝CE＝AD，故①正确，∵AB＝AC＝2CD，CD＝CE，∴AB＝CD+CE，故②正确，∵∠BDC＝90°，∠CDE＝30°，∴∠BDE＝∠BDC+∠CDE＝120°，故③正确，∵DF⊥CB，∴∠CDF＝30°，∴CD＝2CF，BC＝2CD，∴BC＝4CF，∴BF＝3CF，故④正确，∵BC＝2CE，∴S△BCD＝2S△DEC，∵AD＝DC，∴S△ABD＝S△CBD＝2S△CDE，S△ADC＝S△CDE，∴S△ABE＝6S△CDE，故⑤正确．故选：D【点睛】本题主要考查了等边三角形的性质，等腰三角形的判定和性质，熟练掌握等边三角形的性质，等腰三角形的判定和性质是解题的关键．9、C【解析】【分析】由△ABC是等边三角形，点E是AC的中点，得∠ABC=60°，∠ABE=30°，根据EF⊥AB，得∠D=30°，得到BE=DE，在Rt△BEF中，求得BE=2EF=2，即可得答案．【详解】解：连接BE，∵△ABC是等边三角形，点E是AC的中点，∴∠ABC=60°，∠ABE=∠CBE=30°，∵EF⊥AB，∴∠D=90°-∠ABC=30°，即∠D=∠CBE=30°，∴BE=DE，在Rt△BEF中，EF=1，∴BE=2EF=2，∴BE=DE=2，∴DF=EF+DE=3，故选：C．【点睛】本题考查等边三角形的性质及应用，解题的关键是证明BE=DE，从而用含30度角的直角三角形的性质解决问题．10、B【解析】【分析】证明△AFH≌△CHG（AAS），得出AF=CH．由题意可知BE=FH，则得出五边形DECHF的周长=AB+BC，则可得出答案．【详解】解：∵△GFH 为等边三角形，∴FH =GH ，∠FHG =60°，∴∠AHF +∠GHC =120°，∵△ABC 为等边三角形，∴AB =BC =AC =5，∠ACB =∠A =60°，∵∠AHF =180°-∠FHG -∠GHC =120°-∠GHC ，∠HGC =180°-∠C -∠GHC =120°-∠GHC ，∴∠AHF =∠HGC ，在△AFH 和△CHG 中A C AHF HGC FH GH ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△AFH ≌△CHG （AAS ），∴AF =CH ．∵△BDE 和△FGH 是两个全等的等边三角形，∴BE =FH ，∴五边形DECHF 的周长=DE +CE +CH +FH +DF =BD +CE +AF +BE +DF ，=(BD +DF +AF )+(CE +BE )，=AB +BC =10．故选：B ．【点睛】本题考查了全等三角形的判定与性质，等边三角形的性质，熟练掌握全等三角形的判定方法是解题的关键．二、填空题1、10【解析】【分析】分2是腰长与底边两种情况讨论求解．【详解】解：①2是腰长时，三角形的三边分别为2、2、4，∵2+2=4，∴不能组成三角形；②2是底边时，三角形的三边分别为2、4、4，能组成三角形，周长=2+4+4=10，综上所述，三角形的周长为10．故答案为：10．【点睛】本题考查了等腰三角形的性质，难点在于要分情况讨论并利用三角形的三边关系判断是否能组成三角形．2、4【解析】【分析】作DF AC ⊥于F ，先利用角平分线的性质得到3DF DE ==，再根据ABD ACD ABC S S S +=△△△即可得．【详解】解：如图，作DF AC ⊥于F ，AD 平分BAC ∠，,,3DE AB DF AC DE ⊥⊥=，3DF DE ∴==，15,6ABD ACD ABCS S S AB +===， 116331522AC ∴⨯⨯+⨯=， 解得4AC =，故答案为：4．【点睛】本题考查了角平分线的性质定理，熟练掌握角平分线的性质定理是解题关键．3、3【解析】【分析】根据垂线段最短，确定DP ⊥BC 时，DP 最短，结合已知，得到∠ABD =∠CBD ，利用角的平分线的性质定理，得到DP =DA ．【详解】如图，过点D 作DP ⊥BC ，垂足为P ，则此时的DP 最短，∵∠ADB =∠C ，∠A =∠BDC =90°，∴∠ABD =∠CBD ，∵DP ⊥BC ，DA ⊥BA ，∴AD =DP =3，故答案为：3．【点睛】本题考查了垂线段最短，角的平分线即经过角的顶点的射线把角分成相等的两个的角；角的平分线的性质，余角的性质，熟练掌握垂线段最短，角的平分线的性质定理是解题的关键．4、5【解析】【分析】先利用勾股定理的逆定理证明90,ADB ∠=︒ 再利用线段的垂直平分线的定义与性质可得答案.【详解】解：如图，BC =8， BC 边上的中线AD =3， 14,2BD CD BC5,AB =222223425,BD AD AB90,,ADB AD BC5.AC AB 故答案为：5【点睛】本题考查的是勾股定理分逆定理的应用，三角形的中线的定义，线段的垂直平分线的定义与性质，证明90ADB ∠=︒是解题的关键.5、3【解析】【分析】过点C 作CE ∥AB 交AD 延长线于E ，先证△ABD ≌△ECD （AAS ），求出AE =2AD =4，在Rt△AEC 中，3CE ===即可．【详解】解：过点C 作CE ∥AB 交AD 延长线于E ，∵AD 是BC 边上的中线，∴BD =CD ，∵AD ⊥AB ，CE ∥AB ，∴AD ⊥CE ，∠ABD =∠ECD ，∴∠E =90°，在△ABD 和△ECD 中ADB EDC ABD ECD BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ABD ≌△ECD （AAS ），∴AB =EC ，AD =ED =2，∴AE =2AD =4，在Rt△AEC中，3CE ===，∴AB =CE =3．故答案为：3．【点睛】本题考查中线性质，平行线性质，三角形全等判定与性质，勾股定理，掌握中线性质，平行线性质，三角形全等判定与性质，勾股定理，关键是利用辅助线构造三角形全等．三、解答题1、见解析【解析】【分析】根据平行线的性质得到A C ∠=∠，根据线段的和差得到AF CE =，结合B D ∠=∠，即可利用AAS 证明ABF CDE ∆≅∆．【详解】证明：//AB CD ，A C ∴∠=∠，AE CF =，AE EF CF EF ∴+=+，即AF CE =，在ABF ∆和CDE ∆中，B D AC AF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()ABF CDE AAS ∴∆≅∆．【点睛】此题考查了平行线的性质、全等三角形的判定，解题关键是熟记全等三角形的判定定理．2、 (1)30°(2)1【解析】【分析】（1）先说明△ABD 是等腰三角形，再根据三角形的内角和即可得出答案；（2）设DC 的长为y ，根据直角三角形的性质列出关于y 方程，解出y 即可．(1)解：∵DE是AB的垂直平分线，∴AD=BD，∴∠B=∠EAD，又∵AD是∠CAB的平分线，∴∠CAD=∠EAD，设∠CAD=x，则3x=90°，∴x=30°，∴∠CAD=30°；(2)∵AD是∠CAB的平分线，DC⊥AC，DE⊥AB，∴DC=DE，设DC=y，则DE=y，BD=3-y，又∵∠B=30°，∴y=32y，解得y=1，∴DE=1．【点睛】本题主要考查中垂线的性质和角平分线的性质，关键是要牢记垂直平分线的性质和角平分线的性质．3、 (1)4(2)135°【解析】【分析】（1）根据角平分线的定义得到∠CAD=30°，根据含30°角的直角三角形的性质计算即可；（2）根据角平分线的定义分别求出∠DA B、∠EBA，根据三角形内角和定理计算，得到答案．【小题1】解：∵AD平分∠BAC，∠BAC=60°，∴∠CAD=12∠BAC=30°，在Rt△ACD中，∠CAD=30°，DC=2，∴AD=2CD=2×2=4，故答案为：4；【小题2】在Rt△ABC中，∠BAC=60°，则∠ABC=30°，∵AD、BE分别是∠BAC与∠ABC的平分线，∴∠DAB=12∠CAB=30°，∠EBA=12∠ABC=15°，∴∠AHB=180°-∠DAB-∠EBA=180°-30°-15°=135°．【点睛】本题考查的是直角三角形的性质、三角形内角和定理、角平分线的定义，掌握含30°角的直角三角形的性质是解题的关键．4、(1)15°(2)2(3)CE=2BD【解析】【分析】（1）利用三角形内角和定理求出∠BAC=105°，再由∠DAC=90°，即可得出答案；AC（2）作AF⊥BC于F，由含30°角的直角三角形的性质得AF=12得AF=BF，从而求出AB的长；（3）作AF⊥BC于F，设DF=x，则AD=2x，AF，AC=，则BD=BF-DF-x，由点D关于直线AP的对称点为E，得AE=AD=2x，可表示出CE的长，从而得出结论．(1)解：∵∠B=45°，∠C=30°，∴∠BAC=180°-∠B-∠C=180°-45°-30°=105°，∵AD⊥AC，∴∠DAC=90°，∴∠BAD=∠BAC-∠DAC=105°-90°=15°；(2)作AF⊥BC于F，∵∠C=30°，AC∴AF=12∵∠ABF=45°，∴AF=BF∴AB AF；(3)CE=2BD，理由如下：作AF⊥BC于F，∵∠DAF+∠CAF=90°，∠CAF+∠C=90°，∴∠DAF=∠C=30°，设DF=x，则AD=2x，AF，AC=，∵BF=AF，∴BD=BF-DF-x，∵点D关于直线AP的对称点为E，∴AE=AD=2x，∴CE=AC-AE=-2x，∴CE=2BD．【点睛】本题是几何变换综合题，主要考查了含30°角的直角三角形的性质，等腰直角三角形的判定与性质，三角形内角和定理等知识，用x的代数式表示各线段长，从而发现线段之间的数量关系是解题的关键．5、25°【解析】【分析】由题意知AD BC ⊥，50CAD BAD ∠=∠=︒，根据等边对等角，三角形内角和定理求出ADE ∠的值，进而可求出CDE ∠的值．【详解】解：∵AB AC =，AD 是中线，50BAD ∠=︒∴AD BC ⊥，50CAD BAD ∠=∠=︒∵AE AD = ∴18050652ADE ︒-︒∠==︒ ∴25CDE ADC ADE ∠=∠-∠=︒∴CDE ∠的值为25°．【点睛】本题考查了等腰三角形的性质，三角形的内角和定理．解题的关键在于熟练掌握等腰三角形的性质．。

鲁教版（五四制）七年级数学下册第十章三角形的有关证明专项测试考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、下列命题：①等腰三角形是轴对称图形；②到线段两端距离相等的点在这条线段的垂直平分线上；③两点之间线段最短；④两边分别相等且其中一边的对角也相等的两个三角形全等．其中假命题的个数是（）A．1个B．2个C．3个D．4个2、下列命题为真命题的是（）A．同位角相等B．三角形的外角等于两个内角的和C．相等的角是对顶角D．全等三角形的对应角相等3、如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE的和最小时，∠ECP的度数是（）A．30°B．45°C．60°D．90°4、如图，在△ABC 中，AB BC =，AD BC ⊥于点D ，CE 平分∠ACB 交AB 于点E ，交AD 于点P ．若B x ∠=︒，则∠APE 的度数为（ ）A ．90x -B ．3454x +C ．1452x +D ．1454x + 5、下列命题是假命题的是（ ）A ．若0a <，则11a a +<-B ．若0a =，0b =，则0ab =C ．三角形的重心是这个三角形的三条角平分线的交点D ．等腰三角形顶角的平分线、底边上的中线、底边上的高相互重合6、如图，在△ABC 中，∠B ＝90°，AD 平分∠BAC ，交BC 于点D ，BC ＝8cm ，BD ：CD ＝3：4，则点D 到AC 的距离为（ ）cm ．A ．3B ．4C ．327D ．2477、如图，在ABC 中，∠C =90°，分别以A 、B 为圆心画弧，所画的弧交于两点，再连接该两点所在直线交BC 于点D ，连接AD ．若BD =2，则AD 的长为（ ）A B C．1 D．28、如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S△ABC＝7，DE＝2，AB＝4，则AC长是（）A．3 B．4 C．5 D．69、罗同学学习了全等三角形后，利用全等三角形绘制出了下面系列图案，第（1）个图案由2个全等三角形组成，第（2）个图案由4个全等三角形组成，第（3）个图案由7个全等三角形组成，第（4）个图案由12个全等三角形组成，则第（6）个图案中全等三角形的个数为（）A．25 B．38 C．70 D．13510、如图，在△ABC中，∠C＝90°，D，E是AC上两点，且AE＝DE，BD平分∠EBC，那么下列说法中不正确的是（）A．BE是△ABD的中线B．BD是△BCE的角平分线C．∠1＝∠2＝∠3D．S△AEB＝S△EDB第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，已知∠1＝∠2，要判定△ABD ≌△ACD ，请你添加一个条件是 _____．（写出一个即可）2、如图，AC AD =，BC BD =，请写出一个正确的结论 __．3、如图，在△ABC 中，BC ＝8，AC 的中垂线交BC 于点E ，则△ADE 的周长等于_____．4、如图，ABC 中，AB ＝AC ＝BC ＝10，点D 、E 、F 分别在边BC 、AB 和AC 上，AE ＝6，当以B 、D 、E 为顶点的三角形与以C 、D 、F 为顶点的三角形全等时，BD ＝______．5、如图，在ABC 中，AB ＝AC ，∠BAC ＝120°，AB 的垂直平分线交AB 点E ，交BC 于点F ，若BF ＝2，则BC 的长为_____．三、解答题（5小题，每小题10分，共计50分）1、如图，在ABC 中，11AB AC ==，120BAC ∠=︒，AD 是ABC 的中线，AE 是ADB △的角平分线，DF AB ∥交AE 的延长线于点F ，求DF 的长．2、如图，在平面直角坐标系中，(1,3)A -，(2,4)B ，连接AB ．(1)画线段11A B ，使得线段11A B 与线段AB 关于y 轴对称，写出1A 、1B 的坐标：1A ，1B ；(2)写出一个点C 的坐标，使ABC ∆成为等腰三角形，(C ， )；(3)已知点C 在坐标轴上，且满足ABC ∆是等腰三角形，则所有符合条件的C 点有 个．3、如图，CD 是经过BCA ∠顶点C 的一条直线，CA CB =，E ，F 分别是直线CD 上的两点，且BEC CFA α∠=∠=.(1)若直线CD 经过BCA ∠的内部，且点E ，F 在射线CD 上（点E 靠近点C ）；①如图1，若90BCA ∠=︒，90α=︒，则BE ________CF ；（填“>”“<”或“=”）②如图2，若090BCA ︒<∠<︒，请添加一个关于α与BCA ∠数量关系的条件，使①中的结论仍然成立，并说明理由；(2)如图3，若直线CD 经过BCA ∠的外部，BCA α=∠，请提出关于EF ，BE ，AF 这三条线段的数量关系的合理猜想，并说明理由.4、在①C F ∠=∠，②A E ∠=∠，③DF CB =这三个条件中选择其中一个，补充在下面的问题中，并完成问题的解答．问题：如图，点A 、D 、B 、E 在同一条直线上，AD BE =，ADF CBE ∠=∠，若______，求证：FE AC =．（注：如果选择多个条件分别作答，按第一个解答计分．）5、如图，在平面直角坐标系中，直线y ＝kx ＋b 与x 轴、y 轴分别交于点A （3，0）、点B （0，2），以线段AB 为直角边在第一象限内作等腰直角三角形ABC ，∠BAC ＝90°．(1)求直线y＝kx＋b的解析式；(2)求出△ABC的面积；(3)若P（1，m）为坐标系中的一个动点，连接PA，PB．当△ABC与△ABP面积相等时，求m的值．-参考答案-一、单选题1、A【解析】【分析】根据轴对称的定义和等腰三角形的性质，可判断①；根据线段垂直平分线的性质，可判断②；根据两点之间线段最短是一个公理，可判断③；根据三角形全等的判定条件，可判断④，由此即可选择．【详解】等腰三角形是轴对称图形，故①是真命题；到线段两端距离相等的点在这条线段的垂直平分线上，故②是真命题；两点之间线段最短，故③是真命题；两边分别相等且其中一边的对角也相等的两个三角形不一定全等，故④为假命题．故选A．【点睛】本题考查判断命题真假．掌握正确的命题就是真命题，错误的命题就是假命题是解答本题的关键．2、D【解析】【分析】由平行线的性质可判断A，由三角形的外角的性质可判断B，由对顶角的定义可判断C，由全等三角形的性质可判断D，从而可得答案.【详解】解：两直线平行，同位角相等，故A不符合题意；三角形的外角等于和它不相邻的两个内角的和，故B不符合题意；相等的角不一定是对顶角，故C不符合题意；全等三角形的对应角相等，是真命题，故D符合题意；故选D【点睛】本题考查的是平行线的性质，三角形的外角的性质，对顶角的定义，全等三角形的性质，命题真假的判断，掌握“判断真假命题的方法”是解本题的关键.3、A【解析】【分析】连接BE，则BE的长度即为PE与PC和的最小值．再利用等边三角形的性质可得∠PBC=∠PCB=30°，即可解决问题．【详解】解：如图，连接BE，与AD交于点P，此时PE+PC最小，∵△ABC是等边三角形，AD⊥BC，∴PC=PB，∴PE+PC=PB+PE≥BE，即BE就是PE+PC的最小值，∵△ABC是等边三角形，∴∠BCE=60°，∵BA=BC，AE=EC，∴BE⊥AC，∴∠BEC=90°，∴∠EBC=30°，∵PB=PC，∴∠PCB=∠PBC=30°，∴∠ECP=30°，故选：A．【点睛】本题考查的是最短线路问题及等边三角形的性质，熟知两点之间线段最短是解答此题的关键．4、D【解析】【分析】先根据等腰三角形的性质得∠ACB=12（180°-x）=90°-12x，由角平分线的定义得到∠ACE=∠BCE=45°-14x，再根据三角形高的定义得到∠ADC=90°，则可根据三角形内角和计算出∠DPC=45°+x，然后利用对顶角相等∠APE的度数．【详解】解：∵AB=BC，∴∠ACB=12（180°-x）=90°-12x，∵CE平分∠ACB交AB于点E，∴∠ACE=∠BCE=45°-14x，∵AD⊥BC于点D，∴∠ADC=90°，∴∠DPC=45°+14x，∴∠APE=45°+14x．故选：D．【点睛】本题考查了等腰三角形的性质和三角形内角和定理．熟练掌握等腰三角形的性质和三角形内角和定理是解题的关键．5、C【解析】【分析】根据不等式的性质可判定A选项，根据有理数乘法运算可判定B选项，根据重心的定义可判定C选项，根据等腰三角形三线合一的性质可判定D选项．【详解】解：A.由a＜0，则-a＞0，即a＜-a，再根据不等式的性质即可判定A选项是真命题；B.根据两个有理数相乘，若一个为0，则积为零，可判定B选项是真命题；C. 三角形的重心是这个三角形的三条中线的交点，可判定C选项是假命题；D.根据等腰三角形“三线合一”的性质可判定D选项是真命题．故答案为C．【点睛】本题主要考查了不等式的性质、有理数的除法运算、重心的定义、等腰三角形的性质以及命题真假的判定，灵活应用所学知识成为解答本题的关键．6、D【解析】【分析】由条件可先求得BD的长，再根据角平分线的性质可知D到AC的距离等于BD，可得到答案．【详解】解：∵BC=8cm，BD：CD=3：4，cm，∴BD=247∵AD平分∠BAC，∠B=90°，∴D到AC的距离等于BD，∴D点到线段AC的距离为24cm，7故选：D．【点睛】本题主要考查角平分线的性质，掌握角平分线上的点到角两边的距离相等是解题的关键．7、D【解析】【分析】如图，根据画图过程可得直线ED是线段AB的垂直平分线，根据线段垂直平分线的性质即可求解．【详解】解：如图，由画图过程得：直线ED是线段AB的垂直平分线，∴AD=BD=2，故选：D．【点睛】本题考查尺规作图-作线段垂直平分线、线段垂直平分线的性质，熟练掌握线段垂直平分线的性质，能得到直线ED是线段AB的垂直平分线是解答的关键．8、A【解析】【分析】过D作DF⊥AC于F，由角平分线的性质可得2DE EF==，进而根据S△ADB＋S△ADC＝7，利用三角形面积公式即可求得AC的长【详解】解：如图，过D作DF⊥AC于F，∵AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，DE＝2，∴DE＝DF＝2，∵S△ABC＝7，∴S△ADB＋S△ADC＝7，∴1122AB DE AC DF⨯⨯+⨯⨯＝7，∴1142222AC⨯⨯+⨯⨯＝7，解得：AC ＝3，故选：A ．【点睛】本题考查了角平分线的性质，掌握角平分线的性质是解题的关键．9、B【解析】【分析】仔细观察图形，发现第n 个图形有12n n -+个三角形，根据规律求解即可．【详解】解：观察发现：第一个图形有112+=个全等三角形；第二个图形有224+=个全等三角形；第三个图形有2327+=个全等三角形；第四个图形有34212+=个全等三角形；⋯第n 个图形有12n n -+个全等三角形；当6n =时，1526238n n -+=+=（个)．故选：B ．【点睛】本题考查了全等的定义，图形类规律题，正确找到规律是解题的关键．对于找规律的题目首先应找出哪些部分发生了变化，按照什么规律变化的．10、C【解析】【分析】根据三角形中线、角平分线的定义逐项判断即可求解．【详解】解：A、∵AE＝DE，∴BE是△ABD的中线，故本选项不符合题意；B、∵BD平分∠EBC，∴BD是△BCE的角平分线，故本选项不符合题意；C、∵BD平分∠EBC，∴∠2＝∠3，但不能推出∠2、∠3和∠1相等，故本选项符合题意；D、∵S△AEB＝12×AE×BC，S△EDB＝12×DE×BC，AE＝DE，∴S△AEB＝S△EDB，故本选项不符合题意；故选：C【点睛】本题主要考查了三角形中线、角平分线的定义，熟练掌握三角形中，连接一个顶点和它的对边的中点的线段叫做三角形的中线；三角形的一个角的平分线与这个角的对边相交，连接这个角的顶点和交点的线段叫三角形的角平分线是解题的关键．二、填空题1、AB=AC或∠B=∠C或∠ADB=∠ADC【解析】【分析】判断△ABD≌△ACD，已知的条件是：∠1=∠2，AD=AD，根据全等三角形的判定定理即可确定．【详解】解：判断△ABD ≌△ACD ，已知的条件是：∠1=∠2，AD =AD ，因而根据SAS ，可以添加条件：AB =AC ；根据AAS ，可以添加条件：∠B =∠C ；根据ASA 可以添加∠ADB =∠AD C ．故答案是：AB =AC 或∠B =∠C 或∠ADB =∠AD C ．【点睛】本题考查了全等三角形的判定，正确理解判定方法是关键．2、ACB ADB ∆≅∆（答案不唯一）【解析】【分析】利用SSS 证明ACB ADB ∆≅∆即可．【详解】解：ACB ADB ∆≅∆，在ACB ∆和ADB ∆中，AC AD BC BD AB AB =⎧⎪=⎨⎪=⎩， ∴()ACB ADB SSS ∆≅∆，∴CAB DAB ∠=∠，ACB ADB ∠=∠，ABD ABC ∠=∠，故答案为：ACB ADB ∆≅∆（答案不唯一）．【点睛】本题考查全等三角形的判定和性质，关键是根据SSS 证明ACB ∆和ADB ∆全等解答．3、8【解析】【分析】根据线段的垂直平分线的性质得到DA=DB，EA=EC，根据三角形的周长公式计算即可．【详解】解：∵AB的中垂线交BC于D，AC的中垂线交BC于E，∴DA=DB，EA=EC，则△ADE的周长=AD+DE+AE=BD+DE+EC=BC=8，故答案为8．【点睛】此题主要考查线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段的两个端点的距离相等．4、6或5##5或6【解析】【分析】设BD＝x，则CD＝10−x，BE＝4，由于∠B＝∠C＝60°，利用三角形全等的判定方法，当BE＝CD，BD ＝CF时，△BED≌△CDF，当BE＝CF，BD＝CD时，△BED≌△CFD，从而得到对应的BD的长．【详解】解：设BD＝x，则CD＝10−x，∵AE＝6，∴BE＝AB−AE＝10−6＝4，∵AB＝AC＝BC，∴∠B＝∠C＝60°，∴当BE ＝CD ，BD ＝CF 时，△BED ≌△CDF ，即CD ＝4，BD ＝CF ＝6；当BE ＝CF ，BD ＝CD 时，△BED ≌△CFD ，即BD ＝CD ＝5，CF ＝BE ＝4，综上所述，BD 的长为6或5．故答案为：6或5．【点睛】本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法是解决问题的关键． 5、6【解析】【分析】如图，连接,AF 求解30,B C 证明90,2,FAC AF 再利用含30的直角三角形的性质可得答案.【详解】解：如图，连接,AF AB ＝AC ，∠BAC ＝120°，30,B C ∴∠=∠=︒EF 是AB 的垂直平分线，BF ＝2，2,30,FB FA FAB B 90,FAC BAC BAF24,CF AFBC BF CF24 6.故答案为：6【点睛】本题考查的是等腰三角形的判定与性质，线段垂直平分线的性质，含30的直角三角形的性质，熟悉等腰三角形与含30的直角三角形的性质是解本题的关键.三、解答题1、5.5【解析】【分析】根据等腰三角形三线合一的性质可得到AD⊥BC，∠BAD=∠CAD，从而可得到∠BAD=60°，∠ADB=90°，再根据角平分线的性质即可得到∠DAE=∠EAB=30°，从而可推出AD=DF，根据直角三角形30度角的性质即可求得AD的长，即得到了DF的长．【详解】解：∵△ABC是等腰三角形，D为底边的中点，∴AD⊥BC，∠BAD=∠CAD，∵∠BAC=120°，∴∠BAD=60°，∠ADB=90°，∵AE是∠BAD的角平分线，∴∠DAE=∠EAB=30°．∵DF//AB，∴∠F=∠BAE=30°．∴∠DAF=∠F=30°，∴AD =DF ．∵AB =11，∠B =30°， ∴1111 5.522AD AB ==⨯=， ∴DF =5.5【点睛】本题考查了含30°角的直角三角形，等腰三角形的判定与性质，平行线的性质等知识点，能求出AD =DF 是解此题的关键．2、 (1)见解析，(1,3)；(2,4)-；(2)(3,1)；(3)7【解析】【分析】（1）依据线段A 1B 1与线段AB 关于y 轴对称，即可得到线段A 1B 1，并得到A 1、B 1的坐标；（2）利用等腰三角形的定义，并结合轴对称的性质，找到一点C 即可；（3）依据点C 在坐标轴上，且△ABC 是等腰△ABC ，即可得出所有符合条件的C 点．(1)解：如图所示，线段11A B 即为所求，1(1,3)A 、1(2,4)B -；-；故答案为：(1,3)；(2,4)(2)C；解：如图所示，使ABC∆成为等腰三角形，点(3,1)故答案为：(3,1)；(3)解：如图所示，分别以点A、B为圆心，AB长为半径作圆，与坐标轴相交，得到5个交点，过两圆交点画直线与坐标轴相交，得到2个交点，则点C在坐标轴上，且满足ΔABC是等腰三角形的C点有7个．【点睛】本题考查了作图-轴对称变换，几何图形都可看作是由点组成，解题的关键是我们在画一个图形的轴对称图形时，也是先从确定一些特殊的对称点开始的．3、 (1)①=，②180BCA α+∠=︒，见解析(2)EF BE AF =+，见解析【解析】【分析】（1）①证明△BCE ≌△CAF 即可得到BE =CF ；②添加180BCA α+∠=︒，和（1）类似，证明△BCE ≌△CAF 即可得到BE =CF ；（2）根据AAS 证明BCE CAF ≌△△得BE CF =，CE AF =，从而可得结论．(1)∵90BEC CFA α∠=∠==︒，∴90BCE CBE ∠+∠=︒.又∵90BCA BCE ACF ∠=∠+∠=︒，∴CBE ACF ∠=∠.在BCE 和CAF 中，BEC CFA CBE ACF CB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()BCE CAF AAS ≌，∴BE CF =.故答案为：=②180BCA α+∠=︒.理由如下：∵BEC CFA α∠=∠=，∴180180BEF BEC α∠=︒-∠=︒-.又∵BEF CBE BCE ∠=∠+∠，∴180CBE BCE α∠+∠=︒-.又∵180BCA α+∠=︒，∴180BCA CBE BCE α∠=︒-=∠+∠.又∵BCA BCE ACF ∠=∠+∠，∴CBE ACF ∠=∠.在BCE 和CAF 中，CBE ACF BEC CFA CB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()BCE CAF AAS ≌，∴BE CF =.(2)EF BE AF =+.理由如下：∵BCA α∠=，∴180180BCE ACF BCA α∠+∠=︒-∠=︒-.又∵BEC α∠=，∴180180CBE BCE BEC α∠+∠=︒-∠=︒-.∴CBE ACF ∠=∠.在BCE 和CAF 中，CBE ACF BEC CFA CB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴()BCE CAF AAS ≌，∴BE CF =，CE AF =，∴EF CE CF AF BE =+=+，即EF BE AF =+.【点睛】本题考查全等三角形的判定和性质、熟练掌握全等三角形的判定是解决问题的关键．4、∠A =∠E （答案不唯一）【解析】【分析】由“ASA ”可证△ABC ≌△EDF ，可得EF =AC ．【详解】解：若∠A =∠E ，∵AD =BE ，∴AB =DE ，∵∠ADF =∠CBE ，∴∠FDE =∠CBA ，在△ABC 和△EDF 中，A E AB DECBA FDE ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ABC ≌△EDF （ASA ），∴EF =AC ．故答案为：∠A =∠E （答案不唯一）．【点睛】本题考查了全等三角形的判定和性质，证明三角形全等是解题的关键．5、 (1)y ＝－23x ＋2 (2)132(3)173或－3 【解析】【分析】（1）根据,A B 的坐标待定系数法求一次函数解析式即可；（2）由勾股定理得：AB 2＝OA 2＋OB 2＝13，根据△ABC 为等腰直角三角形，S △ABC ＝12AB 2，即可求出△ABC 的面积；（3）过点P 作PH ∥y 轴交AB 于点H ，由直线AB 的表达式得，点H （1，43），根据△ABP 面积＝12×PH ×（xP －xB ）=132，解绝对值方程求解即可． (1) 解：直线y ＝kx ＋b 与x 轴、y 轴分别交于点A （3，0）、点B （0，2），则032k bb=+⎧⎨=⎩，解得232kb⎧=-⎪⎨⎪=⎩，故直线l的表达式为：y＝－23x＋2；(2)在Rt△ABC中，由勾股定理得：AB2＝OA2＋OB2＝32＋22＝13，∵△ABC为等腰直角三角形，∴S△ABC＝12AB2＝132；(3)过点P作PH∥y轴交AB于点H，由直线AB的表达式得，点H（1，43），P（1，m）PH∴=|m－43|∵△ABC与△ABP面积相等，∴△ABP面积＝12×PH×（xP－xB）＝12×|m－43|×3＝132；解得m＝－3或17 3故当△ABC与△ABP面积相等时，m的值为173或－3【点睛】本题考查了一次函数综合，待定系数法求一次函数解析式，等腰三角形的性质，坐标与图形，数形结合是解题的关键．．。

鲁教版数学七年级下册 10.1 全等三角形同步习题及答案一、选择题：1.利用尺规作图不能作出唯一三角形的是( )A.已知三边B.已知两边及夹角C.已知两角及夹边D.已知两边及其中一边的对角2.如图所示,已知AB∥CD,A,E,F,D在一条直线上,AB=CD,AE=FD,则图中的全等三角形有( )A.1对B.2对C.3对D.0对3.要测量河两岸相对的两点A,B间的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明ΔEDC≌ΔABC,得ED=AB,因此测出ED的长就是AB的长,判定ΔEDC≌ΔABC最恰当的理由是( )A.边角边B.角边角C.边边边D.边边角4.如图所示,在ΔABC中,AB=AC,∠ABC,∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①ΔBCD≌ΔCBE;②ΔBAD≌ΔBCD;③ΔBDA≌ΔCEA;④ΔBOE≌ΔCOD;⑤ΔACE≌ΔBCE.上述结论一定正确的是(提示:等腰三角形的两底角相等;在三角形中,两个相等的角所对的边相等) ( )A.①②③B.②③④C.①③⑤D.①③④5.如图所示,在ΔABC和ΔADE中:①AB=AD;②AC=AE;③BC=DE;④∠C=∠E;⑤∠B=∠ADE.下列四个选项分别以其中三个为条件，剩下两个为结论，则其中错误的是（）A．若①②③成立，则④⑤成立B．若①②④成立，则③⑤成立C．若①③⑤成立，则②④成立D．若②④⑤成立，则①③成立6.如图，点P是∠AOB平分线上一点，PD⊥OB，垂足为D，若PD=2，则点P到边OA 的距离是（）A. 1B. 2C. √3D. 47.下列四个命题中,真命题是( )A.若一个角的两边分别平行于另一个角的两边,则这两个角相等B.如果两个角的和是180°,那么这两个角是邻补角C.在同一平面内,平行于同一条直线的两条直线互相平行D.在同一平面内,垂直于同一条直线的两条直线互相垂直8.如图所示,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得ΔABC≌ΔADC,这样就有∠QAE=∠PAE,则说明这两个三角形全等的依据是( )A.SASB.ASAC.AASD.SSS二、填空题：1.如图所示,在正方形ABCD中,如果AF=BE,那么∠AOD的度数是.2.如图所示,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°.从中选取两个作为条件,使得命题“如果, ,那么AB∥EF”是一个真命题,并证明你的结论.(填序号)3.根据下列解题过程填空.(1)如图1所示,已知直线EF与AB,CD都相交,且AB∥CD,试说明∠1=∠2的理由.解:∵AB∥CD(已知),∴∠2=∠3( ),∵∠1=∠3( ),∴∠1=∠2( ).(2)如图2所示,已知ΔAOC≌ΔBOD,试说明AC∥BD成立的理由.解:∵ΔAOC≌ΔBOD,∴∠A= ( ),∴AC∥BD( ).4.如图所示,PA=PB,PC是ΔPAB的中线,∠A=55°,求∠B的度数.解:∵PC是AB边上的中线,∴AC= (中线的定义),在中,∴≌( )∴∠A=∠B( ).∵∠A=55°(已知),∴∠B=55°( ).5.如图所示,如果AB=AC, ,根据“SAS”,即可判定ΔABD≌ΔACE.6.如图所示,已知∠CAE=∠DAB,AC=AD.给出下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能判定ΔABC≌ΔAED的条件为.(注:把你认为正确的答案序号都填上)7.如图，△ABC中，∠C=90°，∠BAC的平分线交BC于点D，若CD=4，则点D到AB的距离是________．8.如图所示,已知线段a,c(a<c),求作:直角三角形ABC,使∠C=90°,AC=c,BC=a,作法:(1)作∠MCN=90°;(2)以C为圆心, 为半径画弧,交射线CM于点B;(3)以C为圆心, 为半径画弧,交射线CN于点A;(4)连接,ΔABC就是所求.三、解答题：1.如图所示,有一座小山,现要在小山A,B的两端开一条隧道,施工队要知道A,B两端的距离,但A,B间的距离不能直接测量,请你用已学过的知识按以下要求设计测量方案:(1)画出测量图;(2)写出测量方案;(3)写出推理过程.2.如图所示,广场上有两根旗杆AC,DF都垂直于地面放置.已知太阳光线AB与DE是平行的,经过测量这两根旗杆在太阳光下的影子BC与EF一样长,那么这两根旗杆的高度相等吗?说说你的理由.3.已知:∠α,∠β,线段a,求作:ΔABC,使∠B=∠α,∠C=∠β,BC=a(不写作法,保留作图痕迹).4.如图，点E，F在BC上，BE=CF，AB=DC，∠B=∠C，求证：AF=DE .5.已知：四边形ABCD．求作：点P，使∠PCB=∠B，且点P到边AD和CD的距离相等．6．已知：如图，在△ABC中，DE、DF是△ABC的中位线，连接EF、AD，其交点为O．求证：（1）△CDE≌△DBF；（2）OA=OD．7．如图，在△ABC中，已知AB=AC，AD平分∠BAC，点M，N分别在AB，AC边上，AM=2MB，AN=2NC．求证：DM=DN．8.如图所示,已知四边形ABCD和四边形DEFG都是正方形,连接AE,CG.请猜想AE与CG有什么数量关系,并证明你的猜想.9.如图所示,在ΔABC和ΔDAE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证ΔABD≌ΔAEC.10.如图所示,在四边形ABCD中,AB=AD,CB=CD.求证∠B=∠D.参考答案一、选择题：1-5 DCBDB 6-8 BCD二、填空题：1.90°2.解:(本题答案不唯一)可选①④.如果∠1=∠E,∠B+∠2=180°,那么CD∥EF,AB∥CD,∴AB ∥EF.3.(1)两直线平行,同位角相等对顶角相等等量代换(2)∠B 全等三角形的对应角相等内错角相等,两直线平行4.BC ΔACP和ΔBCP ΔACP ΔBCP SSS 全等三角形的对应角相等等量代换.5.AD=AE6.①③④.7. 48. a c AB(解析:作∠MCN=90°,在射线CM上截取BC=a,以C为圆心,c的长为半径画弧,交射线CN于点A,连接AB,ΔABC就是所求.)三、解答题：1.解:(1)如图所示.(2)①找个能同时看见A点和B点的C点,然后连接AC并延长到D,使AC=DC;②连接BC并延长到E,使BC=EC,测量DE的长度,即为A,B间的距离.(3)在ΔACB和ΔDCE中,∴ΔACB≌ΔDCE(SAS),∴AB=DE.2.解:两根旗杆的高度相等.理由如下:∵太阳光线AB与DE是平行的,∴∠B=∠E,∵两根旗杆都垂直于地面放置,∴∠C=∠F=90°,∵两根旗杆在太阳光下的影子一样长,∴BC=EF,在ΔABC和ΔDEF中,∴ΔABC≌ΔDEF(ASA),∴AC=DF,即两根旗杆的高度相等.3.解:如图所示,ΔABC即为所求.4.证明：∵ BE =CF ，∴ BE +EF =CF +EF ，即 BF =CE ，在 ΔABF 和 ΔDCE 中，⎪⎩⎪⎨⎧=∠=∠=CE BF C B DCAB∴ ΔABF ≌ ΔDCE (SAS) ∴ AF =DE 5. 解： 作法：①作∠ADC 的平分线DE ，②过C 作CP ∥AB ，交DE 于点P ， 则点P 就是所求作的点；6.证明：（1）∵DE 、DF 是△ABC 的中位线， ∴DF=CE ，DF ∥CE ，DB=DC ． ∵DF ∥CE ， ∴∠C=∠BDF ． 在△CDE 和△DBF 中，∴△CDE ≌△DBF （SAS ）；（2）∵DE 、DF 是△ABC 的中位线， ∴DF=AE ，DF ∥AE ，∴四边形DEAF 是平行四边形， ∵EF 与AD 交于O 点， ∴AO=OD7.证明：∵AM=2MB ，AN=2NC ，AB=AC ， ∴AM=AN ，∵AB=AC ，AD 平分∠BAC ， ∴∠MAD=∠NAD ， 在△AMD 与△AND 中，，∴△AMD ≌△AND （SAS ）， ∴DM=DN ．8.解:猜想:AE=CG,证明如下:∵四边形ABCD 和四边形DEFG 都是正方形,∴CD=AD,∠ADC=∠GDE=90°,GD=ED,∴∠CDG=∠ADE,在ΔCDG 与ΔADE 中, ∴ΔCDG ≌ΔADE(SAS),∴AE=CG. 9.证明:∵∠BAC=∠DAE,∴∠BAC-∠BAE=∠DAE-∠BAE, 即∠BAD=∠CAE, 在ΔABD 和ΔAEC 中, ∴ΔABD ≌ΔAEC(SAS).10证明:连接AC,在ΔABC 和ΔADC 中,∵⎪⎩⎪⎨⎧===DC BC AC AC ADAB )(公共边 ∴ΔABC ≌ΔADC ∴∠B=∠D.。

鲁教版七年级数学下册第10章10.1全等三角形测试题（含答案）一．选择题（共10小题）1．（2015春•普陀区期末）下列说法正确的是（）A．两个等边三角形一定全等B．腰对应相等的两个等腰三角形全等C．形状相同的两个三角形全等D．全等三角形的面积一定相等2．（2014秋•博野县期末）下列说法正确的是（）A．形状相同的两个三角形全等B．面积相等的两个三角形全等C．完全重合的两个三角形全等D．所有的等边三角形全等3．（2015春•孟津县期末）如图，△ABC≌△DEF，∠A=50°，∠C=30°，则∠E的度数为（）A．30°B．50°C．60°D． 100°（3题图）（4题图）（5题图）（6题图）4．（2015春•太康县期末）如图：若△ABE≌△ACF，且AB=5，AE=2，则EC的长为（）A．2 B．3 C．5 D． 2.5 5．（2015•宁波）如图，▱ABCD中，E，F是对角线BD上的两点，如果添加一个条件，使△ABE≌△CDF，则添加的条件不能为（）A．BE=DF B．BF=DE C．AE=CF D．∠1=∠2 6．（2015•六盘水）如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（）A．∠A=∠D B．AB=DC C．∠ACB=∠DBC D． AC=BD 7．（2015•杭州模拟）用直尺和圆规作已知角的平分线的示意图如右，则说明∠CAD=∠DAB 的依据是（）A．SSS B．SAS C．ASA D． AAS（7题图）（8题图）（9题图）（10题图）8．（2015•泰安）如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（）A．4个B．3个C．2个D． 1个9．（2015•宜昌）如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（）A．1个B．2个C．3个D． 4个10．（2016•贵阳模拟）如图，每个小正方形的边长都相等，A、B、C是小正方形的顶点，则∠ABC的度数为（）A．30°B．45°C．60°D． 90°二．填空题（共5小题）11．（2015•南昌）如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有对全等三角形．（11题图）（12题图）（13题图）（14题图）12．（2015•齐齐哈尔）如图，点B、A、D、E在同一直线上，BD=AE，BC∥EF，要使△ABC≌△DEF，则只需添加一个适当的条件是．（只填一个即可）13．（2015•娄底）如图，已知AB=BC，要使△ABD≌△CBD，还需添加一个条件，你添加的条件是．（只需写一个，不添加辅助线）14．（2015•贵港）如图，在正方形ABCD的外侧，作等边三角形CDE，连接AE，BE，则∠AEB的度数为．15．（2015•盐亭县模拟）如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，则∠APE 的度数是度．（15题图）（16题图）（17题图）三．解答题（共5小题）16．（2015•晋江市一模）如图，AB∥CD，AB=CD，点E、F在AD上，且AE=DF．求证：△ABE≌△DCF．17．（2015春•安岳县期末）如图，已知△ABC≌△DEB，点E在AB上，DE与AC相交于点F，若DE=7，BC=4，∠D=35°，∠C=60°（1）求线段AE的长．（2）求∠DFA的度数．18．（2015•温州）如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE=DF，∠A=∠D．（1）求证：AB=CD．（2）若AB=CF，∠B=30°，求∠D的度数．19．（2015•泸州）如图，AC=AE，∠1=∠2，AB=AD．求证：BC=DE．20．（2015•通辽）如图，四边形ABCD中，E点在AD上，其中∠BAE=∠BCE=∠ACD=90°，且BC=CE，求证：△ABC与△DEC全等．鲁教版七年级数学下册第10章10.1全等三角形测试题参考答案一．选择题（共10小题）1．D．2．C．3．D．4．B．5．C．6．D．7．A．8．A．9．C．10．B．二．填空题（共5小题）11．312．BC=EF或∠BAC=∠EDF．13．∠ABD=∠CBD或AD=CD．14．30°．15．60三．解答题（共5小题）16．证明：∵AB∥CD，∴∠A=∠D，在△ABE和△DCF中∴△ABE≌△DCF（SAS）．17．解：（1）∵△ABC≌△DEB，∴AB=DE=7，BE=BC=4，∴AE=AB﹣BE=7﹣4=3；（2）∵△ABC≌△DEB，∴∠A=∠D=35°，∠DBE=∠C=60°，∴∠DFA=∠A+∠AEF=∠A+∠D+∠DBE=130°．18．证明：（1）∵AB∥CD，∴∠B=∠C，在△ABE和△CDF中，，∴△ABE≌△CDF（AAS），∴AB=CD；（2）∵△ABE≌△CDF，∴AB=CD，BE=CF，∵AB=CF，∠B=30°，∴AB=BE，∴△ABE是等腰三角形，∴∠D=．19．证明：∵∠1=∠2，∴∠CAB=∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS），∴BC=DE．20．解：∵∠BCE=∠ACD=90°，∴∠3+∠4=∠4+∠5，∴∠3=∠5，在△ACD中，∠ACD=90°，∴∠2+∠D=90°，∵∠BAE=∠1+∠2=90°，∴∠1=∠D，在△ABC和△DEC中，，∴△ABC≌△DEC（AAS）．。

鲁教版（五四制）七年级数学下册第十章综合测试卷一、选择题(每题3分，共36分)1．若等腰三角形的顶角为40°，则它的底角度数为()A．40°B．50°C．60°D．70°2．在△ABC中，∠A，∠B，∠C的对边分别是a，b，c，下列条件中，不能判定△ABC 是直角三角形的是()A．∠A∶∠B∶∠C＝1∶2∶3 B．∠A＋∠B＝90°C．a∶b∶c＝2∶3∶4 D．b2＝a2－c23．下列命题的逆命题是真命题的是()A．若a＞0，b＞0，则a＋b＞0 B．直角都相等C．两直线平行，同位角相等D．若a＝b，则|a|＝|b|4．如图，∠C＝∠D＝90°，添加一个条件，可用“HL”判定Rt△ABC与Rt△ABD全等．以下给出的条件适合的是()A．AC＝AD B．∠ABC＝∠BADC．∠ABC＝∠ABD D．∠BAC＝∠BAD5．【2022·大庆】下列说法不正确的是()A．有两个角是锐角的三角形是直角或钝角三角形B．有两条边上的高相等的三角形是等腰三角形C．有两个角互余的三角形是直角三角形D．底和腰相等的等腰三角形是等边三角形6．如图，在△ABC中，∠ACB＝90°，∠A＝30°，CD⊥AB，垂足为D，则BD AD 的值为()A．12B．25C．13D．147．如图，直线l上有三个正方形a，b，c，若正方形a，c的面积分别为5和11，则正方形b的边长为()A．55 B．16 C．6 D．48．有A，B，C三个社区(不在同一直线上)，现准备修建一座公园，使该公园到三个社区的距离相等，那么公园应建在()A．△ABC三条角平分线的交点处B．△ABC三条中线的交点处C．△ABC三条高线所在直线的交点处D．△ABC三边垂直平分线的交点处9．如图，在△ABC中，AB＝AC，∠A＝120°，BC＝6 cm，AB的垂直平分线交BC 于点M，交AB于点E，AC的垂直平分线交BC于点N，交AC于点F，则MN 的长为()A．4 cm B．3 cm C．2 cm D．1 cm10．如图，已知点E，C，D在同一直线上，△ABC≌△DEF，CD是∠ACB的平分线，已知∠D＝22°，∠CGD＝92°，则∠E的度数是()A．26°B．22°C．34°D．30°11．如图，在等边三角形ABC中，AD是BC边上的高，且AD＝4，E是AB边的中点，点P在AD上运动，则PB＋PE的最小值是()A．6 B．5 C．4 D．312．如图，在锐角三角形ABC中，AB＝AC，点D，E分别在边AB，AC上，连接BE，CD.下列命题中，假命题．．．是()A．若CD＝BE，则∠DCB＝∠EBCB．若∠DCB＝∠EBC，则CD＝BEC．若BD＝CE，则∠DCB＝∠EBCD．若∠DCB＝∠EBC，则BD＝CE二、填空题(每题3分，共18分)13．用反证法证明一个三角形中不能有两个角是直角，第一步是假设这个三角形中_____________．“两直线平行，内错角相等”的逆命题是___________________．14．如图，在△ABC中，AB＝AC＝BC＝4，AD平分∠BAC，E是AC的中点，则DE的长为________．15．如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AC＝3，AD是△ABC的角平分线，点P在AB上，且PD＝PB，则PD＝________．16．【2023·重庆】如图，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D为BC上一点，连接AD.过点B作BE⊥AD于点E，过点C作CF⊥AD交AD的延长线于点F.若BE＝4，CF＝1，则EF的长度为________．17．【新考法】如图，依据尺规作图的痕迹，∠α的度数为________°.18．如图，已知∠MON＝30°，点A1，A2，A3，…在射线ON上，点B1，B2，B3，…在射线OM上，△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，若OA1＝1，则△A6B6A7的边长为________．三、解答题(23题10分，24，25题每题12分，其余每题8分，共66分)19．如图，点A，D，B，E在一条直线上，AD＝BE，AC＝DF，AC∥DF.求证：BC＝EF.20．如图，在△ABC中，已知AB＝5，BC＝7.(1)尺规作图：作AC的垂直平分线DE，与AC交于点D，与BC交于点E，连接AE.(2)求△ABE的周长．21．如图，在Rt△ABC中，∠C＝90°，AB＝13，AC＝5，AD平分∠CAB交CB于点D，求CD的长．22．【2023·苏州】如图，在△ABC中，AB＝AC，AD为△ABC的角平分线．以点A 为圆心，AD长为半径画弧，与AB，AC分别交于点E，F，连接DE，DF.(1)求证：△ADE≌△ADF.(2)若∠BAC＝80°，求∠BDE的度数．23．如图，在Rt△ACB中，∠ACB＝90°，CM＝BM，点E在线段AM上，EF⊥AC 于点F，连接CE.已知∠A＝50°，∠ACE＝30°.(1)求∠ECM的度数．(2)求证：CE＝CM.(3)若AB＝4，求线段FC的长．24．如图①，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C＝90°，∠B＝∠E＝30°.操作发现：如图②，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB 边上时：(1)猜想线段DE与AC的位置关系是__________，并加以证明．(2)设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是__________，并加以证明．25．如图，在平面直角坐标系中，已知点A(0，2)，△AOB为等边三角形，P是x 轴负半轴上一个动点(不与原点O重合)，以线段AP为一边在其右侧作等边三角形APQ.(1)求点B的坐标．(2)连接BQ，在点P运动的过程中，∠ABQ的大小是否发生改变？若不改变，求出其大小；若改变，请说明理由．(3)连接OQ，当OQ∥AB时，求点P的坐标．答案一、1．D2．C 【点拨】A ．∵∠A ︰∠B ︰∠C ＝1︰2︰3，∴∠A ＋∠B ＝∠C .又∵∠A ＋∠B ＋∠C ＝180°， ∴∠C ＝90°.∴△ABC 是直角三角形；B ．∵∠A ＋∠B ＝90°，∴∠C ＝180°－90°＝90°.∴△ABC 是直角三角形；C ．设a ＝2x ，b ＝3x ，c ＝4x .∵a 2＋b 2＝4x 2＋9x 2＝13x 2，c 2＝16x 2，∴a 2＋b 2≠c 2.∴△ABC 不是直角三角形；D ．∵b 2＝a 2－c 2，∴b 2＋ c 2＝a 2.∴△ABC 是直角三角形． 3．C 4．A 5．A 6．C7．D 【点拨】由题意可知∠CAB ＝∠BED ＝90°，∠CBD ＝90°，CB ＝BD ，∴∠ACB ＝∠EBD ＝90°－∠ABC .在△ABC 和△EDB 中，⎩⎨⎧∠ACB ＝∠EBD ，∠CAB ＝∠BED ，CB ＝BD ，∴△ABC ≌△EDB (AAS)．∴AB ＝ED . ∵正方形a ，c 的面积分别为5和11， ∴AC 2＝5，AB 2＝DE 2＝11. ∴BC ＝AC 2＋AB 2＝5＋11＝4， 即正方形b 的边长为4. 8．D 9．C10．A 【点拨】∵∠D ＝22°，∠CGD ＝92°，∴∠DCG ＝180°－∠D －∠CGD ＝66°. ∵CD 是∠ACB 的平分线， ∴∠ACB ＝2∠DCG ＝132°.∵△ABC ≌△DEF ，∴∠F ＝∠ACB ＝132°. ∴∠E ＝180°－∠D －∠F ＝180°－22°－132°＝26°. 11．C12．A 【点拨】∵AB ＝AC ，∴∠ABC ＝∠ACB .若CD ＝BE ，又∵BC ＝CB ，∴△BCD 与△CBE 满足“SSA”的关系，无法证明全等， 因此无法得出∠DCB ＝∠EBC ，故A 是假命题． 若∠DCB ＝∠EBC ，∴∠ACD ＝∠ABE .在△ABE 和△ACD 中，⎩⎨⎧∠ABE ＝∠ACD ，AB ＝AC ，∠A ＝∠A ，∴△ABE ≌△ACD ()ASA ， ∴CD ＝BE .故B 是真命题． 若BD ＝CE ，则AD ＝AE ，在△ABE 和△ACD 中，⎩⎨⎧AB ＝AC ，∠A ＝∠A AE ＝AD ，，∴△ABE ≌△ACD ()SAS ，∴∠ACD ＝∠ABE . 又∵∠ABC ＝∠ACB ，∴∠DCB ＝∠EBC ，故C 是真命题． 若∠DCB ＝∠EBC ，则在△DBC 和△ECB 中，⎩⎨⎧∠ABC ＝∠ACB ，BC ＝BC ，∠DCB ＝∠EBC ，∴△DBC ≌△ECB ()ASA ， ∴BD ＝CE ，故D 是真命题.二、13．有两个角是直角；内错角相等，两直线平行 14．215．2 【点拨】∵∠C ＝90°，∠B ＝30°，AC ＝3，∴∠CAB ＝60°，AB ＝2AC ＝6. ∵AD 是△ABC 的角平分线，∴∠DAB ＝12∠CAB ＝30°.∵PD ＝PB ， ∴∠PDB ＝∠B ＝30°. ∴∠APD ＝∠B ＋∠PDB ＝60°.∴∠ADP ＝180°－∠APD －∠DAB ＝90°. ∴AP ＝2PD .∵AP ＋BP ＝AB ，∴2PD ＋PD ＝6. ∴PD ＝2.16．3 【点拨】∵∠BAC ＝90°，∴∠EAB ＋∠EAC ＝90°.∵BE ⊥AD ，CF ⊥AD ，∴∠AEB ＝∠AFC ＝90°. ∴∠ACF ＋∠EAC ＝90°.∴∠ACF ＝∠BAE .在△AFC 和△BEA 中，⎩⎨⎧∠CF A ＝∠AEB ，∠ACF ＝∠BAE ，AC ＝AB ，∴△AFC ≌△BEA ()AAS . ∴AF ＝BE ＝4，AE ＝CF ＝1. ∴EF ＝AF －AE ＝4－1＝3. 17．6018．32 【点拨】∵△A 1B 1A 2是等边三角形，∴A 1B 1＝A 2B 1，∠A 1B 1A 2＝∠B 1A 1A 2＝∠A 1A 2B 1＝60°. ∴∠OA 1B 1＝120°.∵∠MON ＝30°， ∴∠OB 1A 1＝180°－120°－30°＝30°. ∴OA 1＝A 1B 1＝A 2B 1＝1.又∵∠A 1B 1A 2＝60°， ∴∠A 2B 1B 2＝180°－60°－30°＝90°. ∵△A 2B 2A 3是等边三角形， ∴∠B 2A 2A 3＝60°.∴∠B 1A 2B 2＝60°. ∴∠B 1B 2A 2＝90°－∠B 1A 2B 2＝30°. ∴A 2B 2＝2B 1A 2＝2.同理得出B 3A 3＝2B 2A 3＝2A 2B 2， ∴B 3A 3＝4B 1A 2＝4.以此类推，A 6B 6＝32B 1A 2＝32.三、19．【证明】∵AD ＝BE ，∴AD ＋BD ＝BE ＋BD ，即AB ＝DE .∵AC ∥DF ，∴∠A ＝∠EDF .在△ABC 与△DEF 中，⎩⎨⎧AB ＝DE ，∠A ＝∠EDF ，AC ＝DF ，∴△ABC ≌△DEF (SAS)． ∴BC ＝EF . 20．【解】(1)如图．(2)∵DE 垂直平分AC ， ∴AE ＝EC .∴AB ＋BE ＋AE ＝AB ＋BE ＋EC ＝AB ＋BC . ∵AB ＝5，BC ＝7，∴AB ＋BE ＋AE ＝5＋7＝12， 即△ABE 的周长为12.21．【解】过点D 作DE ⊥AB 于点E .∵AD 平分∠CAB ，∠C ＝90°，DE ⊥AB ， ∴CD ＝ED .在Rt △ACD 和Rt △AED 中，⎩⎨⎧CD ＝ED ，AD ＝AD ，∴Rt △ACD ≌Rt △AED (HL)．∴AE ＝AC ＝5. ∴BE ＝AB －AE ＝13－5＝8.在Rt △ACB 中，BC ＝AB 2－AC 2＝132－52＝12. 设CD ＝ED ＝x ，则BD ＝12－x ， 在Rt △DEB 中，BD 2＝ED 2＋BE 2， ∴(12－x )2＝x 2＋82，解得x ＝103. ∴CD ＝103.22．(1)【证明】∵AD 是△ABC 的角平分线，∴∠BAD ＝∠CAD . 由作图知AE ＝AF .在△ADE 和△ADF 中，⎩⎨⎧AE ＝AF ，∠EAD ＝∠F AD ，AD ＝AD ，∴△ADE ≌△ADF (SAS)．(2)【解】∵∠BAC ＝80°，AD 为△ABC 的角平分线，∴∠EAD ＝12∠BAC ＝40°.由作图知AE ＝AD .∴∠AED ＝∠ADE .∴∠ADE ＝12×(180°－40°)＝70°.∵AB ＝AC ，AD 为△ABC 的角平分线，∴AD ⊥BC .∴∠ADB ＝90°.∴∠BDE ＝90°－∠ADE ＝20°.23．(1)【解】∵∠ACB ＝90°，∠A ＝50°，∴∠ABC ＝40°.∵∠ACE ＝30°，∴∠ECB ＝90°－30°＝60°.∵CM ＝BM ，∴∠MCB ＝∠ABC ＝40°.∴∠ECM ＝∠ECB －∠MCB ＝60°－40°＝20°.(2)【证明】∵EF ⊥AC ，∴∠AFE ＝∠CFE ＝90°.∵∠A ＝50°，∠ACE ＝30°，∴∠AEF ＝90°－∠A ＝40°，∠CEF ＝90°－∠ACE ＝60°.∴∠CEM ＝180°－∠AEF －∠CEF ＝80°.∵∠MCB ＝∠B ＝40°，∴∠CMA ＝∠MCB ＋∠B ＝80°.∴∠CMA ＝∠CEM .∴CE ＝CM .(3)【解】∵∠A ＝50°，∠CMA ＝80°，∴∠ACM ＝180°－∠A －∠CMA ＝50°.∴∠A ＝∠ACM .∴AM ＝CM ＝BM ＝CE ＝12AB ＝2.在Rt △EFC 中，∠EFC ＝90°，∠ECF ＝30°，∴EF ＝12CE ＝1.∴FC＝CE2－EF2＝ 3.24．(1)DE∥AC【证明】∵△DEC绕点C旋转，点D恰好落在AB边上，∴AC＝CD.∵在△ABC中，∠ACB＝90°，∠B＝30°，∴∠BAC＝90°－∠B＝90°－30°＝60°.∴△ACD是等边三角形．∴∠ACD＝60°.∵∠CDE＝∠BAC＝60°，∴∠ACD＝∠CDE.∴DE∥AC.(2)S1＝S2【证明】由(1)知△ACD是等边三角形，∴AC＝AD.∵∠B＝30°，∠ACB＝90°，∴AD＝AC＝12AB.∴BD＝AD.∴S△BDC＝S△ADC.又∵DE∥AC，∴S△ADC＝S△AEC.∴S△BDC＝S△AEC，即S1＝S2.25．【解】(1)如图，过点B作BC⊥x轴于点C.∵A(0，2)，∴OA＝2.∵△AOB为等边三角形，∴∠AOB＝60°，OB＝OA＝2.∴∠BOC＝30°.又∵∠OCB＝90°，∴BC＝12OB＝1，∴OC＝OB2－BC2＝ 3.∴点B的坐标为(3，1)．(2)∠ABQ的大小始终不变．∵△APQ ，△AOB 均为等边三角形，∴AP ＝AQ ，AO ＝AB ，∠P AQ ＝∠OAB ＝60°.∴∠P AQ －∠OAQ ＝∠OAB －∠OAQ ，即∠P AO ＝∠QAB .在△APO 与△AQB 中，⎩⎨⎧AP ＝AQ ，∠P AO ＝∠QAB ，AO ＝AB ，∴△APO ≌△AQB (SAS)．∴∠ABQ ＝∠AOP ＝90°.(3)∵△ABO 是等边三角形，∴∠ABO ＝60°.∵AB ∥OQ ，∠ABQ ＝90°，∴∠BQO ＝180°－∠ABQ ＝90°，∠BOQ ＝∠ABO ＝60°.∴∠OBQ ＝30°. 又∵OB ＝2，∴OQ ＝12OB ＝1.∴BQ ＝OB 2－OQ 2＝ 3.由(2)可知△APO ≌△AQB ，∴OP ＝BQ ＝ 3.∴点P 的坐标为(－3，0)．。

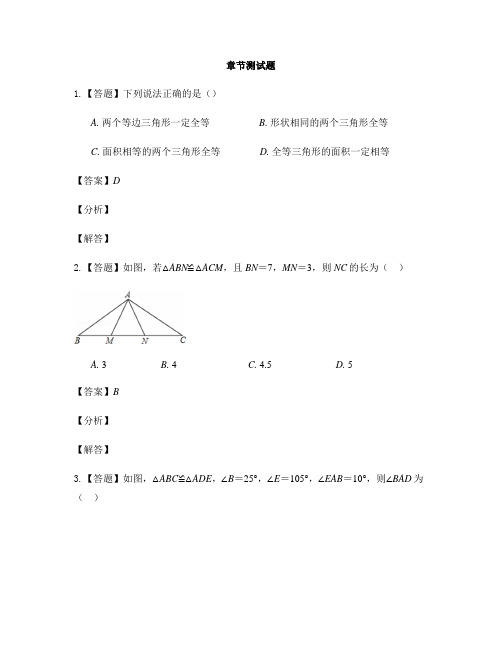
章节测试题1.【答题】下列说法正确的是（）A. 两个等边三角形一定全等B. 形状相同的两个三角形全等C. 面积相等的两个三角形全等D. 全等三角形的面积一定相等【答案】D【分析】【解答】2.【答题】如图，若△ABN≌△ACM，且BN＝7，MN＝3，则NC的长为（）A. 3B. 4C. 4.5D. 5【答案】B【分析】【解答】3.【答题】如图，△ABC≌△ADE，∠B＝25°，∠E＝105°，∠EAB＝10°，则∠BAD为（）A. 50°B. 60°C. 80°D. 120°【答案】B【分析】【解答】4.【答题】如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（）A. ∠B＝∠CB. BE＝CDC. BD＝CED. AD＝AE【答案】B【分析】【解答】5.【答题】如图，在△ABC中，AD⊥BC于点D，BE⊥AC于点E，AD与BE相交于点F，若BF＝AC，∠CAD＝25°，则∠ABE的度数为（）A. 30°B. 15°C. 25°D. 20°【答案】D【分析】【解答】6.【答题】若等腰三角形的两边长分别是3和10，则它的周长是（）A. 16B. 23C. 16或23D. 13【答案】B【分析】【解答】7.【答题】如图，在4×4方格中，以AB为一边，第三个顶点也在格点上的等腰三角形可以作出（）A. 7个B. 6个C. 4个D. 3个【答案】A【分析】【解答】8.【答题】如图所示，△ABC是等边三角形，且BD＝CE，∠1＝15°，则∠2的度数为（）A. 15°B. 30°C. 45°D. 60°【答案】D【分析】【解答】9.【答题】如图，在△ABC中，∠C＝90°，∠A＝30°，BD为△ABC的角平分线，若AC＝12，则在△ABD中AB边上的高为（）A. 3B. 4C. 5D. 6【答案】B【分析】【解答】10.【答题】如图在△ABC中，BC＝8，AB、AC的垂直平分线与BC分别交于E、F 两点，则△AEF的周长为（）A. 2B. 4C. 8D. 不能确定【答案】C【分析】【解答】11.【答题】如图，在△ABC中，∠C＝90°，∠A的平分线交BC于D，AC＝4cm，DC＝3cm，则点D到斜边AB的距离为______cm．【答案】3【分析】【解答】12.【答题】如图，BE与CD交于点A，且∠C＝∠D．添加一个条件：______，使得△ABC≌△AED．【答案】答案不唯一，但必须是一组对应边，如：AC＝AD【分析】【解答】13.【答题】如图，在△ABC中，DE是AB的垂直平分线，且分别交AB，AC于点D和E，∠A＝50°，∠C＝60°，则∠EBC等于______度．【答案】20【分析】【解答】14.【答题】在下列结论中：①有三个角是60°的三角形是等边三角形；②有一个外角是120°的等腰三角形是等边三角形；③有一个角是60°，且是轴对称的三角形是等边三角形；④有一腰上的高也是这腰上的中线的等腰三角形是等边三角形．其中正确的是______．【答案】①②③④【分析】【解答】15.【答题】如图，在△ABC中，∠ABC和∠ACB的平分线相交于点F，过F作DE∥BC，交AB于点D，交A于点E．若BD＝3，DE＝5，则线段EC的长为______．【答案】2【分析】【解答】16.【答题】如图，△ABC中，∠ACB＝90°，∠A＝30°，AB＝4，若CD是高，则BD＝______．【答案】1【分析】【解答】17.【题文】已知△ABC，利用直尺和圆规，根据下列要求作图（保留作图痕迹，不要求写作法），并根据要求填空：（1）作∠ABC的平分线BD交AC于点D；（2）作线段BD的垂直平分线交AB于点E，交BC于点F．【答案】（每题4分，本题共8分）【分析】【解答】18.【题文】如图，已知∠A＝∠D＝90°，E、F在线段BC上，DE与AF交于点O，且AB＝CD，BE＝CF．求证：（1）Rt△ABF≌Rt△DCE；（2）OE＝OF．【答案】（本题共8分）证明：（1）∵BE＝CF，∴BE+EF＝CF+EF，即BF＝CE，……………2分在Rt△ABF和Rt△DCE中，，……………5分∴Rt△ABF≌Rt△DCE（HL）；……………6分（2）∵Rt△ABF≌Rt△DCE（已证），∴∠AFB＝∠DEC，……………7分∴OE＝OF．……………8分【分析】【解答】19.【题文】如图，已知：△ABC中，AB＝AC，BD和CE分别是∠ABC和∠ACB的角平分线，且相交于O点．（1）试说明△OBC是等腰三角形；（2）连接OA，试判断直线OA与线段BC的位置关系，并说明理由．【答案】（本题共10分）解：（1）∵在△ABC中，AB＝AC，∴∠ABC＝∠BCA；……………1分∵BD、CE分别平分∠ABC、∠BCA，∴∠OBC＝∠BCO；……………3分∴OB＝OC，……………4分∴△OBC为等腰三角形．……………5分（2）AO⊥BC……………6分证明如下：在△AOB与△AOC中．∵，∴△AOB≌△AOC（SSS）；……………8分∴∠BAO＝∠CAO；……………9分∴AO⊥BC．……………10分【分析】【解答】20.【题文】如图，△ABC和△EBD中，∠ABC＝∠DBE＝90°，AB＝CB，BE＝BD，连接AE，CD，AE与CD交于点M，AE与BC交于点N．（1）求证：AE＝CD；（2）求证：AE⊥CD；【答案】（本题共10分）（1）证明：∵∠ABC＝∠DBE，∴∠ABC+∠CBE＝∠DBE+∠CBE，即∠ABE＝∠CBD，……………2分在△ABE和△CBD中，，∴△ABE≌△CBD，……………5分∴AE＝CD．……………6分（2）∵△ABE≌△CBD，∴∠BAE＝∠BCD，……………7分∵∠NMC＝180°-∠BCD-∠CNM，∠ABC＝180°-∠BAE-∠ANB，又∠CNM＝∠ABC，∵∠ABC＝90°，……………8分∴∠NMC＝90°，……………9分∴AE⊥CD．……………10分【分析】【解答】。

《全等三角形》自主学习任务单（5）评测练习课题全等三角形课型新授课学习目标1．会根据基本事实证明“AAS”定理．2．灵活运用基本事实和定理判定两个三角形全等．3．对推理证明的要求进一步熟练和提高．目标分解达成目标设计学习形式评价方式预告时间预测一温故知新|知识储备及衔接填空：1．如图，已知△ABC≌△DEF，则可以得到如下结论：．2．如图，（1）如果AB=DE，∠B=∠E，∠A=∠D，则证明△ABC≌△DEF，用到的方法是：；（2）如果AB=DE，∠B=∠E，BC=EF，则证明△ABC≌△DEF，用到的方法是：；（3）如果AB=DE，∠B=∠E，，则证明△ABC≌△DEF，用到的方法是：AAS；（4）如果AB=DE，AC=DF，，则证明△ABC≌△DEF，用到的方法是：SSS．独立思考完成——个别交流答案及知识点．5分钟二、小试锋芒|掌握定理的证明1．用符号语言表示另外两个基本事实：（1）∵∴△ABC≌△A'B'C'（SAS ）（2）∵∴△ABC≌△A'B'C'（ASA ）2．证明命题：两角分别相等且其中一组等角的对边相等的两个三角形全等．符号语言：独立思考——师引领步骤——独立完成——集体展示交流思路．1分钟三思维独立思考完成，第7分钟ACBDFEACBA’C’B’DAB COEBCDAO加油站|巩固判定方法1．如图，线段AB与CD相交于点O．判断下面的命题是否正确，并说明理由．如果AC=BD，AO=DO，那么△AOC≌△DOB．2．已知，如图，AE和CD相交于点O ，∠ADO=∠CEO=90O．要证明△AOD≌△COE ，只需再添加一个条件= ，依据是；或= ，依据是；或= ，依据是．1题个别交流，3题同桌交流，统计掌握情况．四、宝剑锋从磨砺出|灵活运用知识如图，已知AO=DO，∠C=∠B，请你设计本题的问题并给出严谨的证明．个体思考，尝试——学生小组交流，补充——教师引领总结．1分钟五、思维加油站|综合运用1．已知：如图，在四边形ABCD中，AC平分∠BAD，AB=AD．求证：AC平分∠BCD．第一、二两题在独立思考的基础上小组交流，第3题学生小组合作交流探索．8分钟DABCODABC2．已知：如图，AC=BC，AC⊥BC，过点C任意画一条与AB不平行的直线a，分别过点A、B向直线a作垂线，垂足分别是E、F．求证：EF=AE+BF．3．变式：（快手园地）已知：如图，若过点C的直线a与AB交于点D，其余条件不变，请你在图中画出图形，探索此时A E，BF，EF 之间的数量关系并证明．盘点收获1．你认为自己这节课的参与程度怎么样？（1）非常积极（2）一般（3）不积极，原因是什么？2．你认为自己这节课在知识和习惯方面最大的收获是什么？在解题方法和解题思路方面最大的收获是什么？3．在解决问题的过程中，你有什么要提醒大家注意的地方？同桌交流——班级交流5分钟作业布置1．必做：课本随堂练习1、2知识技能12．选作：已知：如图，线段AB与CD相交于点O ，AC=BD，AB=DC．求证：△AOC≌△DOB．AaE BCFaDABCEFBCDAO当堂检测：1．如图，线段AB 与CD 相交于点O ，已知AC =BD ，AB =DC ． 求证：△AOC ≌△DOB ．2．（选作）延长CA 与BD 交于点E ，如果EB=EC ，AC=DB ，试说明C B ∠=∠.D A BC O EBC D A O。

鲁教版七年级下册数学三角形的有关证明单元测试题（含答案）一、选择题（共20小题；共80分）1. 等腰三角形的一条边长为，另一边长为，则它的周长为A. B. 或 C. D.2. 下列命题的逆命题是假命题的是A. 两直线平行，同旁内角互补B. 直角三角形的两个锐角互余C. 全等三角形的对应角相等D. 直角三角形两条直角边的平方和等于斜边的平方3. 如图，四边形中，垂直平分，垂足为，下列结论不一定成立的是A. B. 平分C. D.4. 如图，在中，，平分，，，那么点到的距离是A. B. C. D.5. 已知、、是三角形的三边长，如果满足，则三角形的形状是A. 底与边不相等的等腰三角形B. 等边三角形C. 钝角三角形D. 直角三角形6. 如图，在与中，已有条件，还需要添加两个条件才能使．不能添加的一组条件是A. ，B. ，C. ，D. ，7. 如图，，，则不一定能使的条件是A. B. C. D.8. 如图，在中，，，是的角平分线，，垂足为，，则A. B. C. D.9. 如图，在中，，，边的垂直平分线交于点，交于点，，则的长为A. B. C. D.10. 如图，等腰的周长为，底边，的垂直平分线交于点，交于点，则的周长为A. B. C. D.11. 用直尺和圆规作一个角的平分线的示意图如图所示，则能说明的依据是A.B.C.D. 角平分线上的点到角两边距离相等12. 如图，在中，，，，则的长是A. B. C. D.13. 如图，在中，，，，那么等于A. B. C. D.14. 如图，在中，，垂直平分斜边，交于，是垂足，连接，若，则的长是A. B. C. D.15. 如图是的角平分线，，垂足为，交的延长线于点，若恰好平分，．给出下列四个结论：①；②；③；④．其中正确的结论共有个A. B. C. D.16. 如图，长方体的长为，宽为，高为，点离点的距离为，一只蚂蚁如果要沿着长方体的表面从点爬到点，需要爬行的最短距离是A. B. C. D.17. 如图，在中，，以顶点为圆心，适当长为半径画弧，分别交，于点，，再分别以点，为圆心，大于的长为半径画弧，两弧交于点，作射线交边于点，若，，则的面积是A. B. C. D.18. 如图，在，，，的中垂线交于，为垂足，若，则等于A.19. 如图，坐标平面内一点，为原点，是轴上的一个动点，如果以点，，为顶点的三角形是等腰三角形，那么符合条件的动点的个数为A. B. C. D.20. 如图，在不等边中，，垂足为，，垂足为，且，在上，，下列结论：①；②；③．其中正确的是A. ①②③B. ①②C. ②③D. ①二、填空题（共5小题；共25分）21. 如图所示，，，请你添加一个适当的条件，使．（只需添加一个即可）22. 如图，中，的垂直平分线交于点．若，则的周长为．23. 如图，已知等边中，，与相交于点，则的度数是度．24. 如图，在中，，平分，则度，图中有个等腰三角形．25. 如图所示，在长方形中，，．将此长方形沿折叠，使点落在点处，且与相交于点，则．三、解答题（共4小题；共45分）26. 如图，在和中，点，，，在同一直线上，且，，．求证：．27. 有一块形状为四边形的钢板，量得它的各边长度为，，，，．求这块钢板的面积．28. 已知：如图，在中，，，的垂直平分线交于，交于，．求的度数和边的长．29. 如图，是等边三角形，是边上的一点，以为边作等边三角形，使点，在直线的同侧，连接．求证：．答案第一部分1. C2. C3. C4. B5. D【解析】，，，．解得：，，．．是直角三角形．6. D7. A8. C9. C10. A11. A 【解析】由作图可知，．又，（）．．12. D13. C 【解析】设．，，，．，，．，，，即等于．14. A 【解析】因为垂直平分，所以，所以，所以，所以，所以．15. A【解析】过点作交于点．是的角平分线，恰好平分，，．．可证．，，．可证，．，，．16. B17. B18. C 【解析】连接 .是线段的垂直平分线，，，...，．19. C 【解析】如图：①为等腰三角形底边，符合条件的动点有一个；②为等腰三角形一条腰，符合条件的动点有三个．综上所述，符合条件的点的个数共个．20. B第二部分21. 或或等（写出一个即可）．23.24. ，【解析】，，．平分，，．、、是等腰三角形．25.【解析】设的长为，则 .，，，即 .解得 ..第三部分26. ，，即．在与中，（），知识像烛光，能照亮一个人，也能照亮无数的人。

鲁教版（五四制）七年级数学下册第十章三角形的有关证明同步练习考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、下列命题中，假命题是（）A．三角形三条边的垂直平分线的交点到三角形三个顶点的距离相等B．三角形三个内角的平分线的交点到三角形三条边的距离相等C．两腰对应相等的两个等腰三角形全等D．一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等2、如图，在平面直角坐标系中xOy中，已知点A的坐标是（0，2），以OA为边在右侧作等边三角形OAA1，过点A1作x轴的垂线，垂足为点O1，以O1A1为边在右侧作等边三角形O1A1A2，再过点A2作x轴的垂线，垂足为点O2，以O2A2为边在右侧作等边三角形O2A2A3，……，按此规律继续作下去，得到等边三角形O2020A2020A2021，则点A2023的纵坐标为（）A ．（12）2021B ．（12）2022C ．（12）2023D ．（12）2024 3、下列语句中，为真命题的是（ ）A ．过直线外一点有且只有一条直线与已知直线平行B ．有理数与数轴上的点一一对应C ．三角形的一个外角大于任何一个内角D ．两边和其中一边的对角相等的两个三角形全等4、如图，90ACB ∠=︒，AC BC =，AD CE ⊥，BE CE ⊥，垂足分别是点D 、E ，7cm AD =，3cm BE =，则DE 的长是（ ）A ．3cmB ．3.5cmC ．4cmD ．4.5cm5、如图，ABC 中，分别以A 、B 为圆心，以大于12AB 的长为半径画圆弧，两弧交于点D 、E ，直线DE 与AB 边交于点F ，与AC 边交于点G ，连接BG ，若AC ＝8，BC ＝3，则GBC 的周长为（ ）A．5 B．8 C．11 D．136、等腰三角形的顶角为80°，则其底角的度数是（）A．100°B．80°C．50°D．40°7、等腰三角形的两条边长分别为3和7，则这个等腰三角形的周长是（）A．10 B．13 C．17 D．13或178、如图，在△ABC中，AB的垂直平分线DE与边AB，AC分别交于点D，E.已知△ABC与△BCE的周长分别为16cm和10cm，则AD的长为（）A．3cm B．4cm C．5cm D．6cm9、有下列说法：①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线；②等腰三角形一腰上的高与底边的夹角与顶角互余；③等腰三角形顶角的平分线是它的对称轴, ④等腰三角形两腰上的中线相等，其中正确的说法有（）个．A．1 B．2 C．3 D．410、如图，在用直尺和圆规作一个角等于已知角中，判定△O'C'D'≌△OCD 的依据是（）A．SAS B．SSS C．AAS D．A SA第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图所示的是正方形网格，则∠MDC﹣∠MAB=____°（点A，B，C，D，M．网格线交点）．2、点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP，则当△PMN 的周长的最小时∠MPN=___，△PMN的周长最小值为___．AB的长为半径作3、如图，Rt△ABC中，∠C=100°，∠B=30°，分别以点A和点B为圆心，大于12弧，两弧相交于M、N两点，作直线MN，交BC于点D，连接AD，则∠CAD的度数是________．4、如图是单位长度为1的正方形网格，则123∠+∠+∠=______°．5、在ABC 中，AB AC =，AB 的垂直平分线与AC 所在直线相交所得的锐角为42°，则B ∠=______．三、解答题（5小题，每小题10分，共计50分）1、如图，△ACB 和△DCE 都是等腰直角三角形，∠ACB =∠DCE =90°．AC =41， DE =18， 将△DCE 绕着顶点 C 旋转，连接 AD ，BE ．(1)求证：△ACD ≌△BCE ；(2)在△DCE 的旋转过程中，探求：点 A ，D ，E 在同一直线上时，AE 的长．2、在△ABC 中，∠A =60°，BD ，CE 是△ABC 的两条角平分线，且BD ，CE 交于点F ．(1)用等式表示BE，BC，CD这三条线段之间的数量关系，并证明你的结论．(2)当∠ABC=_____°时，BF=CA．3、如图，在平面直角坐标系中，直线y＝kx＋b与x轴、y轴分别交于点A（3，0）、点B（0，2），以线段AB为直角边在第一象限内作等腰直角三角形ABC，∠BAC＝90°．(1)求直线y＝kx＋b的解析式；(2)求出△ABC的面积；(3)若P（1，m）为坐标系中的一个动点，连接PA，PB．当△ABC与△ABP面积相等时，求m的值．4、如图，在等腰△ABC中，BA=BC，AD平分∠BAC，DE∥AC，求证：∠ADB=3∠EDA．5、如图，在ABC 中，30BAC ∠=︒，AB 边的垂直平分线分别交AB 于点E ，交AC 于点F ，点D 在EF 上，且BD CD =，G 是AC 的中点，连接DG ．(1)求证：DG AC ⊥；(2)判断BCD △是否是等边三角形，并说明理由．-参考答案-一、单选题1、C【解析】【分析】由线段的垂直平分线的性质可判断A ，由三角形的角平分线的性质可判定B ，由SAS 判定两个三角形全等可判断C ，由HL 判定两个直角三角形全等可判断D ，从而可得答案.【详解】解：三角形三条边的垂直平分线的交点到三角形三个顶点的距离相等，是真命题，故A 不符合题意； 三角形三个内角的平分线的交点到三角形三条边的距离相等，是真命题，故B 不符合题意； 两腰对应相等的两个等腰三角形不一定全等，因为两腰的夹角不一定相等，故C 符合题意； 如图，90,,,,,C N AD MF AB MN BD DC NF FG,Rt ADB Rt MFN≌,BD FN则,BC NG,Rt ACB Rt MGN≌一条直角边和另一条直角边上的中线对应相等的两个直角三角形全等，是真命题，故D不符合题意；故选C【点睛】本题考查的是线段垂直平分线的性质，角平分线的性质，全等三角形的判定与性质，掌握“判定命题真假的方法”是解本题的关键.2、B【解析】【分析】根据30°角所对的直角边等于斜边的一半得出O1A1=12OA1=1，O2A2=12O1A2=（12）1，O3A3=12O2A3=（12）2，即点A1的纵坐标为1；点A2的纵坐标为（12），点A3的纵坐标为（12）2，以此类推，从中得出规律，即可求出答案．【详解】解：∵三角形OAA1是等边三角形，∴OA1=OA=2，∠AOA1=60°，∴∠O1OA1=30°．在直角△O1OA1中，∵∠OO1A1=90°，∠O1OA1=30°，∴O1A1=12OA1=1，即点A1的纵坐标为1，同理，O2A2=12O1A2=（12）1，O3A3=12O2A3=（12）2，即点A2的纵坐标为（12）1，点A3的纵坐标为（12）2，…∴点A2023的纵坐标为（12）2022．故选：B．【点睛】此题考查了规律型：点的坐标，等边三角形的性质，解答此题的关键是通过认真分析，根据30°角所对的直角边等于斜边的一半，从中发现规律．3、A【解析】【分析】利用平行线的判定、有理数的性质、三角形的外角的性质及全等三角形的判定方法分别判断后即可确定正确的选项．【详解】解：A、过直线外一点有且只有一条直线与已知直线平行，正确，是真命题，符合题意；B、实数与数轴上的点一一对应，故原命题错误，是假命题，不符合题意；C、三角形的一个外角大于任何一个不相邻的内角，故原命题错误，是假命题，不符合题意；D、两边及其夹角对应相等的两个三角形全等，故原命题错误，是假命题，不符合题意．故选：A．【点睛】本题考查了命题与定理的知识，解题的关键是了解平行线的判定、有理数的性质、三角形的外角的性质及全等三角形的判定方法，难度不大．4、C【解析】【分析】根据AAS 即可证明△CEB ≌△ADC ，再利用全等三角形的性质即可求解．【详解】解：∵BE ⊥CE ，AD ⊥CE ，∴∠E ＝∠ADC ＝90°，∴∠EBC ＋∠BCE ＝90°．∵∠BCE ＋∠ACD ＝90°，∴∠EBC ＝∠DCA ．在△CEB 和△ADC 中，E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△CEB ≌△ADC （AAS ），7cm AD =，3cm BE =，∴BE ＝DC ＝3 cm ，CE ＝AD ＝7cm ，∴DE ＝EC −CD ＝7−3＝4 cm,故选：C ．【点睛】本题考查了全等三角形的判定与性质，正确寻找全等三角形全等的条件是解题的关键．5、C【解析】【分析】根据作图得知DE 是AB 的垂直平分线，得出AG =BG ，3811GBC C BC CG BG BC CG AG BC AC ∆=++=++=+=+=即可．【详解】解：根据作图得知DE 是AB 的垂直平分线，∴AG =BG ，∴3811GBC C BC CG BG BC CG AG BC AC ∆=++=++=+=+=．故选C ．【点睛】本题考查尺规作图，线段垂直平分线的性质，三角形周长，掌握尺规作图，线段垂直平分线的性质，三角形周长是解题关键．6、C【解析】【分析】根据等腰三角形两底角相等即可得解．【详解】解：∵等腰三角形的顶角为80°， ∴它的底角度数为12（180°-80°）=50°．故选：C ．【点睛】本题考查了等腰三角形两底角相等的性质，关键是根据等腰三角形的性质解答．7、C【解析】【分析】因为等腰三角形的两边为3和7，但已知中没有点明底边和腰，所以有两种情况，需要分类讨论，还要注意利用三角形三边关系考虑各情况能否构成三角形．【详解】解：当3为底时，其它两边都为7，3、7、7可以构成三角形，周长为17；当3为腰时，其它两边为3和7，∵3+3=6＜7，所以不能构成三角形，故舍去，∴答案只有17．故选：C．【点睛】本题考查了等腰三角形的性质；对于底和腰不等的等腰三角形，若条件中没有明确哪边是底哪边是腰时，应在符合三角形三边关系的前提下分类讨论．8、A【解析】【分析】根据线段的垂直平分线的性质得到EA=EB，根据三角形的周长公式计算即可．【详解】解：∵DE是AB的垂直平分线，∴EA=EB，AD=BD=12 AB，∵△BCE的周长是10，∴BC+BE+EC=10，即AC+BC=10，∵△ABC的周长是16，∴AB+AC+BC=16，∴AB=16-10=6，∴AD=12AB=12×6=3（cm）．故选：A．【点睛】本题考查的是等腰三角形的定义，线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．9、B【解析】【分析】根据轴对称的性质，轴对称图形的概念，等腰三角形的性质判断即可．【详解】解：①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线，说法正确；②等腰三角形一腰上的高与底边的夹角与底角互余，原说法错误；③等腰三角形的顶角平分线在它的对称轴上，原说法错误；④等腰三角形两腰上的中线相等，说法正确．综上，正确的有①④，共2个，故选：B【点睛】本题考查了对称的性质及等腰三角形的性质，掌握轴对称的性质，轴对称图形的概念，等腰三角形的性质是解题的关键．10、B【解析】【分析】利用基本作图得到OC=OD=O′C′=O′D′，CD=C′D′，然后根据全等三角形的判定方法进行判断．【详解】解：由作法得OC=OD=O′C′=O′D′，CD=C′D′，‘根据“SSS”可判断△O′C′D′≌△OCD．故选：B．【点睛】本题考查了作图-复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了全等三角形的判定．二、填空题1、45【解析】【分析】如图，连接ME、DE，可知∠MAB=∠EDF，∠MDC﹣∠MAB=∠MDC﹣∠EDF=∠EDM，勾股定理计算得到△EMD是等腰直角三角形，进而求出角的值．【详解】解：如图，连接ME、DE可知∠MAB=∠EDF∴∠MDC﹣∠MAB=∠MDC﹣∠EDF=∠EDMMD DE=∵ME∴ME=MD，ME2+MD2=DE2∴△EMD是等腰直角三角形∴∠MDE=45°即∠MDC﹣∠MAB=45°故答案为：45．【点睛】本题考查了勾股定理，等腰三角形．解题的关键在于找出角度之间的数量关系．2、90°##90度 6【解析】【分析】作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．根据对称的性质可以证得：△COD是等腰直角三角形，据此即可求解．【详解】解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．∵P、C关于OA对称，∴∠COP=2∠AOP，OC=OP，同理，∠DOP=2∠BOP，OP=OD，∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．∴△COD是等腰直角三角形，∴∠OCD=∠ODC=45°，∵∠OPM=∠OCM=45°，∠OPN=∠ODN=45°，∴∠MPN=∠OPM+∠OPN=90°，则CD OC．故答案为：90°，6．【点睛】本题考查了对称的性质，正确作出图形，理解△PMN周长最小的条件是解题的关键．3、20°##20度【解析】【分析】由题意根据∠CAB=180°-∠C-∠B和垂直平分线性质，求出∠CAB，∠DAB进而依据∠CAD=∠CAB-∠DAB求出即可．【详解】解：∵∠C=100°，∠B=30°，∴∠CAB=180°-∠C-∠B=180°-100°-30°=50°，由作图可知，MN垂直平分线段AB，∴DA=DB，∴∠DAB=∠B=30°，∴∠CAD=∠CAB-∠DAB=50°-30°=20°.故答案为：20°．【点睛】本题考查作图-基本作图，三角形内角和定理，线段的垂直平分线的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．4、135【解析】【分析】∠=︒，进而即可求如图，证明ABC≌AEF可得1390∠+∠=︒，根据等腰直角三角形的性质可得245得答案．【详解】解：如图，在ABC 与AEF 中AB AE B E BC FE =⎧⎪∠=∠⎨⎪=⎩∴ABC ≌AEF∴4=3∠∠1490∠+∠=︒1390∴∠+∠=︒245∴∠=︒123135∴∠+∠+∠=︒故答案为：135【点睛】本题考查了全等三角形的性质与判定，等腰直角三角形的性质，掌握全等三角形的性质与判定是解题的关键．5、66°或24°##24°或66°【解析】【分析】分两种情况讨论，画出符合题意的图形，再结合三角形的内角和定理与等腰三角形的性质可得答案.AB AC ADE DH是AB的垂直平分线，解：如图，由题意得：,42,B C DHA,90,DAH B C904248,1B DAH24,2AB AC ADE DH是AB的垂直平分线，如图，由题意得：,42,,42,ABC ACB ADH1A B904248,1804866,2B综上：24B∠=︒或66.故答案为：24︒或66.︒【点睛】本题考查的是线段垂直平分线的定义，等腰三角形的性质，掌握“等边对等角”是解本题的关键.1、 (1)见解析(2)AE 的长为49或31【解析】【分析】（1）根据△ACB 和△DCE 都是等腰直角三角形，∠ACB =∠DCE =90°．得出∠ACD =∠BCE ， 再证△ACD ≌△BCE （SAS ）即可；（2）过点C 作CF ⊥DE 于F ，根据△CDE 为等腰直角三角形，CF ⊥DE ，求出DE =DF =EF =1118922DE =⨯=，分两种情况，点E 在AD 延长线上，在Rt△ACF 中，根据勾股定理AF=40=，点E 在AD 上利用线段和差求出AE 即可．(1)证明：∵△ACB 和△DCE 都是等腰直角三角形，∠ACB =∠DCE =90°．∴AC =BC ，DC =EC ，∠ACD +∠DCB =∠DCB +∠BCE ，∴∠ACD =∠BCE ，在△ACD 和△BCE 中，AC BC ACD BCE DC EC =⎧⎪∠=∠⎨⎪=⎩， ∴△ACD ≌△BCE （SAS ），(2)解：过点C 作CF ⊥DE 于F ，∵△CDE 为等腰直角三角形，CF ⊥DE ，∴DE=DF=EF=11189 22DE=⨯=，分两种情况点E在AD延长线上，在Rt△ACF中，根据勾股定理AF40，∴AE=AF+EF=40+9=49；点E在AD上，在Rt△ACF中，根据勾股定理AF40，∴AE=AF-EF=40-9=31；∴点A，D，E 在同一直线上时，AE 的长为49或31．【点睛】本题考查等腰直角三角形性质，三角形全等判定，图形旋转性质，勾股定理，线段和差，掌握等腰直角三角形性质，三角形全等判定，图形旋转性质，勾股定理，线段和差是解题关键．2、 (1)BE＋CD＝BC，理由见解析；(2)40【解析】【分析】（1）利用角平分线得出∠EBF＝∠MBF，进而得出△BEF≌△BMF，求出∠BFM，即可判断出∠CFM＝∠CFD，即可判断出△FCM≌△FCD，即可得出结论；（2）先求出相关角的度数，进而判断出BG＝CE，进而判断出△BGF≌△CEA，即可得出结论．(1)解：BE＋CD＝BC，理由如下：在BC上取一点M，使BM＝BE，∵BD，CE是△ABC的两条角平分线，∴∠FBC＝12∠ABC，∠BCF＝12∠ACB，在△ABC中，∠A＋∠ABC＋∠ACB＝180°，∵∠A＝60°，∴∠ABC＋∠ACB＝180°−∠A＝120°，∴∠BFC＝180°−（∠CBF＋∠BCF）＝180°−12（∠ABC＋∠ACB）＝120°，∴∠BFE ＝60°，∴∠CFD ＝∠BFE ＝60°，∵BD 是∠ABC 的平分线，∴∠EBF ＝∠MBF ，在△BEF 和△BMF 中，BE BM EBF MBF BF BF =⎧⎪∠=∠⎨⎪=⎩， ∴△BEF ≌△BMF （SAS ），∴∠BFE ＝∠BFM ＝60°，∴∠CFM ＝∠BFC −∠BFM ＝60°，∴∠CFM ＝∠CFD ＝60°，∵CE 是∠ACB 的平分线，∴∠FCM ＝∠FCD ，在△FCM 和△FCD 中，CFM CFD CF CFFCM FCD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△FCM ≌△FCD （ASA ），∴CM ＝CD ，∴BC ＝CM ＋BM ＝CD ＋BE ；(2)解：当∠ABC ＝40°时，BF ＝CA ，理由如下：在△ABC 中，∠A ＝60°，∠ABC ＝40°，∴∠ACB ＝80°，∵BD ，CE 是△ABC 的两条角平分线，∴∠ABD ＝∠CBD ＝12∠ABC ＝20°，∠BCE ＝∠ACE ＝12∠ACB ＝40°，∴∠AEC ＝∠ABC ＋∠BCE ＝80°，∠ABC ＝∠BCE ，∴BE ＝CE ，在△ABC 的边AB 左侧作∠ABG ＝20°，交CE 的延长线于G ，∴∠FBG ＝∠ABD ＋∠ABG ＝40°＝∠ACE ．∵∠AEC ＝80°，∴∠BEG ＝80°，∴∠G ＝180°−∠ABG −∠BEG ＝80°＝∠BEG ＝∠AEC ，∴BG ＝BE ，∴BG ＝CE ，在△BGF 和△CEA 中，4080FBG ACE BG CEBGF AEC ∠=∠=︒⎧⎪=⎨⎪∠=∠=︒⎩， ∴△BGF ≌△CEA （ASA ），∴BF ＝AC ．故答案为：40．【点睛】主要考查了角平分线的定义，三角形内角和定理，全等三角形的判定和性质，解本题的关键是（1）判断出∠CFM＝∠CFD，（2）作出辅助线，判断出BG＝CE．3、 (1)y＝－23x＋2(2)13 2(3)173或－3【解析】【分析】（1）根据,A B的坐标待定系数法求一次函数解析式即可；（2）由勾股定理得：AB2＝OA2＋OB2＝13，根据△ABC为等腰直角三角形，S△ABC＝12AB2，即可求出△ABC的面积；（3）过点P作PH∥y轴交AB于点H，由直线AB的表达式得，点H（1，43），根据△ABP面积＝12×PH×（xP－xB）=132，解绝对值方程求解即可．(1)解：直线y＝kx＋b与x轴、y轴分别交于点A（3，0）、点B（0，2），则032k bb=+⎧⎨=⎩，解得232kb⎧=-⎪⎨⎪=⎩，故直线l的表达式为：y＝－23x＋2；(2)在Rt△ABC中，由勾股定理得：AB2＝OA2＋OB2＝32＋22＝13，∵△ABC为等腰直角三角形，∴S△ABC＝12AB2＝132；(3)过点P作PH∥y轴交AB于点H，由直线AB的表达式得，点H（1，43），P（1，m）PH∴=|m－43|∵△ABC与△ABP面积相等，∴△ABP面积＝12×PH×（xP－xB）＝12×|m－43|×3＝132；解得m＝－3或17 3故当△ABC与△ABP面积相等时，m的值为173或－3【点睛】本题考查了一次函数综合，待定系数法求一次函数解析式，等腰三角形的性质，坐标与图形，数形结合是解题的关键．．4、见解析【分析】根据等腰三角形的性质得到∠BAC=∠BCA，根据平行线的性质得到∠BED=∠BAC，∠BDE=∠C，根据角平分线的定义得到∠EAD=∠DAC，于是得到结论．【详解】证明：∵BA=BC，∴∠BAC=∠BCA，∵DE∥AC，∴∠BED=∠BAC，∠BDE=∠C，∴∠BED=∠BDE，∵AD平分∠BAC，∴∠EAD=∠DAC，∵DE∥AC，∴∠ADE=∠DAC，∴∠EAD=∠ADE，∴∠BED=∠EAD+∠ADE=2∠ADE，∴∠BDE=∠BED=2∠ADE，∴∠ADB=3∠EDA．【点睛】本题考查了等腰三角形的判定和性质，平行线的性质，角平分线的定义，熟练掌握等腰三角形的判定和性质定理是解题的关键．5、 (1)见解析△是等边三角形，理由见解析(2)BCD【分析】（1）连接AD ，先证明ACD △是等腰三角形，再根据三线合一即可证明；（2）先求得30BAC ∠=︒，再得到120DBC DCB ∠+∠=︒，故可得到60DBC DCB ∠=∠=︒，即可证明．(1)解：连接AD ，∵EF 是AB 的垂直平分线，点D 在EF 上，∴AD BD =．又∵BD CD =，∴AD CD =，∴ACD △是等腰三角形．∵G 是AC 的中点，∴DG AC ⊥．(2)BCD △是等边三角形，理由如下：∵BD CD AD ==，∴ABD BAD ∠=∠，ACD CAD ∠=∠，∵30BAC BAD CAD ABD ACD ∠=∠+∠=∠+∠=︒，∴()180120DBC DCB BAC ABD ACD ∠+∠=︒-∠-∠+∠=︒，∴60DBC DCB ∠=∠=︒，∴BCD △是等边三角形．【点睛】此题主要考查等腰三角形与等边三角形的判定与性质，解题的关键是熟知垂直平分线的性质、等腰三角形的性质定理．。

鲁教版数学七年级下册10.1全等三角形 习题及答案一、单选题1．如图，△ABD ≌△CDB ，下面四个结论中，不正确的是( )A ．△ABD 和△CDB 的面积相等 B ．△ABD 和△CDB 的周长相等C ．∠A ＋∠ABD ＝∠C ＋∠CBD D ．AD ∥BC ，且AD ＝BC2.如图，ABC R t ∆沿直角边BC 所在的直线向右平移得到DEF ∆，下列结论中错误的是（ ）A.△ABC ≌△DEFB. ︒=∠90DEFC.DF AC =D.CF EC =3.如图，将矩形纸片ABCD 沿对角线BD 折叠一次，则图中全等三角形有（ ）A.2对B. 3对C. 4对D.5对4．如图，已知AB ＝DC ，AD ＝BC ，E ，F 是DB 上两点且BF ＝DE ，若∠AEB ＝100°，∠ADB ＝30°，则∠BCF ＝( )A ．150°B ．40°C ．80°D ．70°5.如图，∠B=∠E=90°，AB=DE ，AC=DF ，则△ABC ≌△DEF 的理由是（ ）A.SASB.ASAC.AASD.HL6.如图，在四边形ABCD 中，E 是BC 边的中点，连接DE 并延长，交AB 的延长线于F 点，AB ＝BF.添加一个条件，使四边形ABCD 是平行四边形．你认为下面四个条件中可选择的是( )A、AD＝BCB、CD＝BFC、∠A＝∠CD、∠F＝∠CDE 7．如图所示，△ABD≌△CDB，下面四个结论中，不正确的是（）A.△ABD和△CDB的面积相等 B.△ABD和△CDB的周长相等C.∠A+∠ABD＝∠C+∠CBDD.AD∥BC，且AD＝BCACB8．如图所示，BE⊥AC于点D，且AD＝CD，BD＝ED，若∠ABC＝54°，则∠E＝（）A.25°B.27°C.30°D.45°A BCDEF129.如图，在△ABC和△AED中，已知∠1＝∠2，AC＝AD，添加一个条件后，仍然不能证明△ABC≌△AED，这个条件是（）A．AB＝AE B．BC＝ED C．∠C＝∠D D．∠B＝∠E10.如图，AD是△ABC的角平分线，DE⊥AB于E，已知△ABC的面积为28．AC＝6，DE＝4，则AB的长为（）A．6 B．8 C．4 D．1011.如图，在△ABC中，点E在边AC上，D E是AB的垂直平分线，△ABC的周长为19，△BCE 的周长为12，则线段AB的长为（）A ．9B ．8C ．7D ．612.如图，已知AB ＝AC ＝BD ，则∠1与∠2的关系是（ ）A ．3∠1﹣∠2＝180°B ．2∠1+∠2＝180°C ．∠1+3∠2＝180°D ．∠1＝2∠2二、填空题13.如图为6个边长相等的正方形的组合图形，则∠1+∠3=________ ．14. 已知ABC DEF ∆∆≌，AC AB =，且ABC ∆的周长为22cm ，BC=4cm ，则DEF ∆的边=DE cm .15. 在△ABC 中，∠C=90°，BC=4cm ，∠BAC 的平分线交B C 于D ，且BD ︰DC=5︰3，则D 到AB 的距离为_____________.16．如图，已知△ABC 中，∠ABC ，∠ACB 的角平分线交于点O ，连接AO 并延长交BC 于D ，OH ⊥BC 于H ，若∠BAC ＝60°，OH ＝5 cm ，则∠BAD ＝_____________，点O 到AB 的距离为____________ cm.17．△ABC ≌△BAD ，A 和B ，C 和D 是对应顶点，如果AB=8cm ，BD=•6cm ，AD=5cm ，则BC=________cm ．18．已知，如图，AD=AC ，BD=BC ，O 为AB 上一点，那么，图中共有 对全等三角形．三、解答题19.如图，已知∠AOB=20°．（1）若射线OC⊥OA，射线OD⊥OB，请你在图中画出所有符合要求的图形；（2）请根据（1）所画出的图形，求∠COD的度数．20．如图，AB＝DC，AD＝BC，DE＝BF.求证：BE＝DF.21. 在ABC∆中，︒=∠90ACB，BCAC=，直线MN经过点C，且MNAD⊥于D，MNBE⊥于E.(1)当直线MN绕点C旋转到图1的位置时，求证：①ADC∆≌CEB∆；②BEADDE+=；(2)当直线MN绕点C旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.22．已知：如图，在直线MN上求作一点P，使点P到∠AOB两边的距离相等（要求写出作法，并保留作图痕迹，写出结论）ONMBA23．（8分）已知： BE ⊥CD ，BE ＝DE ，BC ＝DA ，求证：△BEC ≌△DAE24．已知：如图，AB=AC ，BD ⊥AC ，CE ⊥AB ，垂足分别为D 、E ，BD 、CE 相交于点F ，求证：BE =CD ．25.如图，点C 、E 分别在直线AB 、DF 上，小华想知道∠ACE 和∠DEC 是否互补，但是他没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连结CF ，再找出CF 的中点O ，然后连结EO 并延长EO 和直线AB 相交于点B ，经过测量，他发现EO ＝BO ，因此他得出结论：∠ACE 和∠DEC 互补，而且他还发现BC ＝EF ．小华的想法对吗？为什么？26.如图，已知CA ＝CD ，CB ＝CE ，∠ACB ＝∠DCE ，试说明△ACE ≌△DCB 的理由．27. 如图，四边形ABCD 中，E 点在AD 上，其中∠BAE ＝∠BCE ＝∠ACD ＝90°，且BC ＝CE ，求证：△ABC ≌△DEC ．BF AA CB D E F28.如图，在△ABC中，∠C＝90°，D、E分别为AC、AB上的点，且AD＝BD，AE＝BC，DE＝DC，求证：DE⊥AB．29.如图，在△ABC和△ABD中，∠BAC＝∠ABD＝90°，点E为AD边上的一点，且AC＝AE，连接CE交AB于点G，过点A作AF⊥AD交CE于点F．（1）求证：△AGE≌△AFC；（2）若AB＝AC，求证：AD＝AF+BD．30.△ABC中，AB＝AC，∠A＝40°，D、E分别是AB，AC上的不动点．且BD+CE＝BC，点P 是BC上的一动点．（1）当PC＝CE时（如图1），求∠DPE的度数；（2）若PC＝BD时（如图2），求∠DPE的度数还会与（1）的结果相同吗？若相同，请写出求解过程；若不相同，请说明理由．31.已知：如图，O为△ABC的∠BAC的角平分线上一点，∠1＝∠2，求证：△ABC是等腰三角形．32.如图，在等边△ABC中，∠ABC与∠ACB的平分线相交于点O，且OD∥AB，OE∥AC （1）试判定△ODE的形状，并说明你的理由；（2）若BC＝10，求△ODE的周长．33.如图，A、B、C三点在同一直线上，分别以AB、BC为边，在直线AC的同侧作等边△ABD 和等边△BCE，连接AE交BD于点M，连接CD交BE于点N，连接MN得△BMN．（1）求证：△ABE≌△DBC．（2）试判断△BMN的形状，并说明理由．参考答案一、单选题1-5 CDDDD 6-10 DCBBB 11-12 CA二、填空题13、 90°14. 915. 5.116． 30° 517． 518. 3三、解答题19、解：（1）如图1、如图2，OC （或OC ′）、OD （或OD ′）为所作；（2）如图1，∵OC ⊥OA ，OD ⊥OB ，∴∠BOD=∠AOC=90°，∴∠COD=360°﹣90°﹣90°﹣20°=160°，∠COD ′=∠BOC ﹣∠AOC=90°+20°﹣90°=20°，如图2，同理可得∠COD=160°，∠COD ′=20°，∴∠COD=20°或160°．（2）如图1，由于OC ⊥OA ，OD ⊥OB ，则∠BOD=∠AOC=90°，于是利用周角的定义可计算出∠COD=160°，利用∠COD ′=∠BOC ﹣∠AOC 可得到∠COD ′=20°，如图2，同理可得∠COD=160°，∠COD ′=20°．20. 解：连接BD.∵AD ＝BC ，AB ＝CD ，BD ＝BD ，∴△ABD ≌△CDB(SSS)，∴∠ADB ＝∠DBC ，∴180°－∠ADB ＝180°－∠DBC ，∴∠BDE ＝∠DBF ，易证△BDE ≌△DBF(SAS)，∴BE ＝DF21.（1）证明①︒=∠+∠90BCE ACD Θ︒=∠+∠90ACD DAC BCE DAC ∠=∠∴ 又︒=∠=∠=90,BEC ADC BC AC CEB ADC ∆∆∴≌.②CEB ADC ∆∆≌ΘCE AD BE CD ==∴，BE AD CD CE DE +=+=∴.（2）CEB ADC ∆∆≌成立，BE AD DE +=不成立，此时应有BE AD DE -=.22．作∠BOA 的平分线交MN 于P 点，就是所求做的点。