平面及其方程

平面及其方程说课稿人教版一、说课背景本次说课的内容选自人教版高中数学教材第五章“空间几何”，主要围绕平面及其方程的概念、性质和求解方法进行讲解。

本章节是空间解析几何的基础，对于培养学生的空间想象能力和逻辑推理能力具有重要意义。

二、教学目标1. 知识与技能目标：使学生理解平面的基本概念，掌握平面方程的推导过程及其应用。

2. 过程与方法目标：通过实例演示和练习，培养学生运用平面方程解决实际问题的能力。

3. 情感态度与价值观目标：激发学生对空间几何的兴趣，培养学生的探索精神和团队合作意识。

三、教学重点与难点1. 教学重点：平面的基本性质，平面方程的推导和应用。

2. 教学难点：平面方程的推导过程，以及如何利用平面方程解决实际问题。

四、教学方法与手段1. 教学方法：采用启发式教学法和探究式学习法，通过问题引导学生自主思考和探索。

2. 教学手段：运用多媒体课件展示平面图形，利用几何画板软件动态演示平面方程的推导过程。

五、教学过程1. 引入新课- 通过回顾上节课的立体几何知识，引出平面几何的概念。

- 通过实际问题（如：如何确定一个平面）激发学生的学习兴趣。

2. 概念讲解- 定义平面：平面是没有厚度的二维几何体，由无限多个点组成。

- 介绍平面的基本性质：平面内任意两点确定一条直线，平面与直线的关系等。

3. 平面方程的推导- 介绍平面方程的一般形式：Ax + By + Cz + D = 0。

- 通过实例演示如何从三个不在一条直线上的已知点推导出平面方程。

- 讲解法向量的概念及其在平面方程中的作用。

4. 平面方程的应用- 通过例题讲解如何求解平面与直线的交点问题。

- 探讨平面方程在实际生活中的应用，如建筑设计、工程测量等。

5. 课堂练习- 设计针对性练习题，让学生巩固平面方程的推导和应用。

- 分组讨论，鼓励学生相互合作，共同解决问题。

6. 课堂小结- 总结平面及其方程的主要内容。

- 强调平面方程在解决实际问题中的重要性。

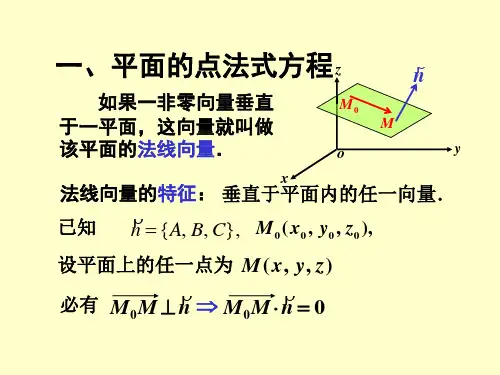
§7.5平面及其方程一、平面的点法式方程法线向量：如果一非零向量垂直于一平面 .这向量就叫做该平面的法线向量.容易知道 '平面上的任一向量均与该平面的法线向量垂直.唯一确定平面的条件 ：当平面口上一点M o (X 0 J0 Z0)和它的一个法线向量 n^A^B *C)为已知时、平面n 的位置就完全确定了 .平面方程的建立：设M(x.y.z)是平面□上的任一点.那么向量M ^M 必与平面n 的法线向量n 垂直、即它们的数量积等于零 ：由于Tn 球A*BC)* M 0M =(x —X 0, y —y 。

, Z —Z 0).所以A(XF 0)+B(y-y 0)弋(z-Z 0)=0 .n 上任一点M 的坐标 心工所满足的方程.、如果M (x 、y .Z)不在平面r 上、那么向量M^M 与法线向量n 不垂直、从而…即不在平面□上的点M 的坐标X y .Z 不满足此方程. 由此可知、方程A(x-X 0)+B(y-y 0)P(z-Z 0)n 就是平面□的方程.而平面口就是平面方程的图 形.由于方程A (X%)怕(y-y 0)4c (z-Z 0)=0是由平面L ［上的一点M 0(X 0、y 0、Z 0)及它的一个法线向量 n=(AB 、C)确定的、所以此方程叫做平面的点法式方程.例1求过点(2Q)且以 ^(K-2. 3)为法线向量的平面的方程.解根据平面的点法式方程 '得所求平面的方程为(x-2)-2(yt3)t3z=0 * x-2y+3z£n .M 1(2 H ⑷、M 2(—1 \3 L 2)和M 3(0 ,2①的平面的方程.T因为 M 1M 2 =(—3,4, -6)、M 1M 3=(-2,3, —1)、 所以T T in= M 1M^M 1M^ -3-2这就是平面 反过来T n M 0M =0即例2求过三点 解我们可以用 T TM i M 2X M 1M 3作为平面的法线向量k-6 =14 + 9j-k . -1根据平面的点法式方程、得所求平面的方程为14(x-2)H(y+1)-(z -4H0 . 14x49y_ z_15』. 二、平面的一般方程由于平面的点法式方程是 x.y 的一次方程.而任一平面都可以用它上面的一点及它的法线 向量来确定 '所以任一平面都可以用三元一次方程来表示.反过来、设有三元一次方程Ax +By 4Cz 4D =0.我们任取满足该方程的一组数 x o .y o .z ^即Ax o +By o 4Cz o +D =0 .把上述两等式相减 '得A(x£o )+B(y-y o )兀(z-z o )=O 、这正是通过点 M o (x o.y oQ )且以nNA 、BQ 为法线向量的平面方程 .由于方程Ax +By 4Cz *DO与方程A(x 必)+B(y-y o )七(Z-z o ) =o同解*所以任一三元一次方程Ax 也y P z +O n 的图形总是一个平面.方程Ax 4By M z +D =o 称为平面的一般方程，其中 心z 的系数就是该平面的一个法线向量n 的坐标‘即nNA'B .0).例如 '方程3x -4y +z -9=0表示一个平面 小=(3\*訂)是这平面的一个法线向量 .讨论：考察下列特殊的平面方程 .指出法线向量与坐标面、 坐标轴的关系 '平面通过的特殊点或线.Ax +By f z ^o ；By 七Z 也 n^Ax ^z P^o r Ax +By +D P ； Cz +D P 'Ax PO By +D P . 提示： 平面过原点.n =(o *B Q).法线向量垂直于 n =(A 、o rC).法线向量垂直于 n =(A *B *o ).法线向量垂直于 n=(o *o *C)、法线向量垂直于 n=(A .o ,o b 法线向量垂直于 n=(o 占,o b 法线向量垂直于例3求通过x 轴和点(4L 1)的平面的方程.解 平面通过x 轴、一方面表明它的法线向量垂直于 点、即DP .因此可设这平面的方程为By 弋z^o .x 轴*平面平行于 y 轴、平面平行于 z 轴、平面平行于x 轴和y 轴，平面平行于 y 轴和z 轴r 平面平行于 x 轴和z 轴r 平面平行于 xOy 平面.yOz 平面. zOx 平面.X 轴、即AR ；另一方面表明 它必通过原又因为这平面通过点(4 *-3 *7) *所以有—BB-Cn 、或 C 」B .将其代入所设方程并除以B （B 如）、便得所求的平面方程为y ；z=0.例4设一平面与X 、y 、z 轴的交点依次为 P （a *0 * 0）、Q （0、b *0）、R （0 , 0、c ）三点、求这平面的 方程（其中乂&?€）.解 j a ^D =0, f bB +D =0, pc +D=0,A=-D 、B=-D r C=—D a b c 将其代入所设方程、得 -Dx-Dy-Dz+D =0 、 a b c X +上也=1 . a b c '上述方程叫做平面的截距式方程 *而a 、b 、c 依次叫做平面在 X 、y 、z 轴上的截距.三、两平面的夹角两平面的夹角：两平面的法线向量的夹角（通常指锐角）称为两平面的夹角.设平面n 1和rb 的法线向量分别为 n 1N A 1占1 C ）和n 2=（A 2旧2、C 2）、那么平面n 1和rb 的夹角e 、―AAA_A应是（n 1, n 2）和（Til , n 2）F —g ,改）两者中的锐角、因此、cos 日^cosg ,匹）！.按两向量夹角余弦的坐标表示式.平面n 1和rt 的夹角e 可由来确定.从两向量垂直、平行的充分必要条件立即推得下列结论平面口 1和巧垂直相当于A1A2怕辰 QC2=0； 平面□ 1和n 2平行或重合相当于 A =BL -C!.A ， B, C 2例5求两平面 x-yPz-6=0和2x 为七-5=0的夹角. 解 n 1=（A 1 启1 Q1）=（1、一1 *2）、n 2m A 2、B 2Q2）=（2*1 * 1）.c 1c2l_ I1'2■ (-1)'T ■ 2…I| Jcos g _lAie 日口2 "T A 2+ Bfg 2叔2 +B ：七："712+(-1)2七2722+12+12~^设所求平面的方程为Ax+By4Cz*HD=0.P （a *0 *0）、Q （0 *b *0）、R （0 ,0 ,c ）都在这平面上*所以点P 、Q 、R 的坐标都满足所设方程*即 因为点 有由此得IAA2+B 1B 2+C 1C 2IAco眄cosg,讣府魯Y A 呢W|1X2 +(-1)X1 +2咒1||AA 2+B ,B 2pi C 2|所以*所求夹角为,4,例6 一平面通过两点 M 1(1」和M 2(o 」#)且垂直于平面 x+y+z=o 、求它的方程.解 方法一：已知从点M 1到点M 2的向量为 山勻/卫、-?)、平面x+y+z=o 的法线向量为n 2=(1、 1 J). 设所求平面的法线向量为n^A 、B 、C).因为点M 1(1、1、1)和M 2(o1)在所求平面上、所以n 丄n 仁即从—2C=o 、A 亠2C . 又因为所求平面垂直于平面 x^^zT*所以n 丄m*即A+B4C=o*B=C. 于是由点法式方程*所求平面为-2CZ)£(y —1)兀(Z —1)0 即 2x —y-z=o.方法二：从点M 1到点M 2的向量为n 1 =(-1 e *-2) *平面x+y+z=o 的法线向量为“2=(1* 1 , 1). 设所求平面的法线向量因为所以所求平面方程为2(x-1)-(y-1)-(z-1)0 2x-y-z=0 .例7设P o (x o ,y o ,z o )是平面Ax+By 兀z 也=0外一点、求P o 到这平面的距离. 解 设e n 是平面上的单位法线向量.在平面上任取一点 P 1(X 1 $1 *Z 1)*则P o 到这平面的距离为|A(X o^i )+B(y o-y i )七(z o^i )|扌是示：en^7A ^B ^(A, B, C)' 活o =(xo —x 1,yo —y 1,zo —z1)、例8求点(2 J J )到平面x +y -z +1 =0的距离.解 d JAxp^y o 弋zo^DI 」仝2丁X 1—(—1門+1| _ 3 —E _J A 2 + B 2 弋2 j 12+12+(—1)273 ' n 可取为npc n2 .i:-J o 1J A 2 +B 2+C 2JAx o 怕y oy z o-(Ax1HBy 1 七Z 1)| J A 2 +B 2 七2JAx^怕yo +Czo +D|Td 斗RP oen 1 =j 12+12+(_1)2。

平面及其方程平面的点法式方程平面的一般方程两平面的夹角平面的点法式方程法线向量: 与平面垂直的非零向量.n即有A (x -x 0)+B (y -y 0)+C (z -z 0)=0 设M 0(x 0,y 0,z 0)是平面П上的已知点, n =(A ,B ,C )是平面П的法线向量,M (x ,y ,z )是平面П上的任一点, 则有n •0M M =0.由于n =(A ,B ,C ) ,0M M =( x -x 0,y -y 0,z -z 0),称为平面的点法式方程.O∏zyxM nM例求过点(2,-3,0)且以n=(1,-2,3)为法线向量的平面方程. 解代入平面的点法式方程得:(x-2)-2(y+3)+3(z-0)=0⇒x-2y+3z-8=0例 求过三点M 1(2,-1,4)、M 2(-1,3,-2)、M 3(0,2,3)的平面方程.解 由于n ∥12M M ×13M M =132643----kj i =14i +9j -k则所求平面方程为⇒ 14(x -2)+9(y +1)-(z -4)=0⇒ 14x +9y -z -15=01M2M 3M ∏n平面的一般方程平面的点法式方程A (x -x 0)+B (y -y 0)+C (z -z 0)=0设有三元一次方程Ax +By +Cz+D =0任取满足方程的一组数000,,x y z 即0000Ax By Cz D +++=两式相减，得A x x B y y C z z 000()()()0-+-+-=是x 、y 、z 的一次方程平面的一般方程为Ax+By+Cz+D=0其中n=(A,B,C)为法向量各种特殊情形D=0,平面Ax+By+Cz=0经过原点;D=0,平面Ax+By+Cz=0经过原点; A=0,平面By+Cz+D=0平行于x轴; B=0,平面Ax+Cz+D=0平行于y轴; C=0,平面Ax+By+D=0平行于z轴;A=B=0,平面Cz+D=0平行于xoy平面; A=C=0,平面By+D=0平行于xoz平面; B=C=0,平面Ax+D=0平行于yoz平面.例求通过x轴和点(4,-3,-1)的平面方程.解平面经过x轴,则平面经过原点, ⇒D=0;平面经过x轴,则法向量在x轴上的投影为0 ⇒A=0;故可设平面方程为: By+Cz=0,又平面经过点(4,-3,-1), ⇒-3B-C=0,或C=-3B.代入有y-3z=0.和R (0,0,c )三点,求此平面的方程.(其中a ≠0,b ≠0,c ≠0)解 设平面方程为 Ax +By +Cz +D =0代入P (a ,0,0)、Q (0,b ,0)和R (0,0,c )得 A =-D a , B =-D b , C =-Dc, 代入方程并消去D 得平面方程: (,0,0)a (0,,0)b (0,0,)c x yz O和R (0,0,c )三点,求此平面的方程.(其中a ≠0,b ≠0,c ≠0)解 代入方程并消去D 得平面方程:1x y za b c++=此方程称为平面的截距式方程, a ,b ,c 依次称为平面在x ,y ,z 轴上的截距.两平面的夹角两平面的夹角: 两平面的法线向量的夹角(通常指锐角).设平面П1和П2的法线向量依次为:n 1=(A 1,B 1,C 1) n 2=(A 2,B 2,C 2)则平面П1和П2的夹角θ为(12,n n ∧)和π-(12,n n ∧)中的锐角,⇒ cos θ=|cos(12,n n ∧)|,⇒222222212121212121cos CB AC B A C C B B A A ++∙++++=θθθ1n 2n 1∏2∏两平面垂直、平行的充分必要条件平面П1和П2垂直⇔ A 1A 2+B 1B 2+C 1C 1=0 2∏1∏1∏2∏2n 1n 1n2n 平面П1和П2平行⇔ 12A A =12B B =12C C设平面П1和П2的法线向量依次为:n 1=(A 1,B 1,C 1) n 2=(A 2,B 2,C 2)例 求两平面x -y +2z -6=0和2x +y +z -5=0的夹角.解n 1=(1,-1,2) n 2=(2,1,1)⇒ cos θ=222222|12(1)121|1(1)2211⨯+-⨯+⨯+-+++=21⇒ θ=π3例一平面通过两点M1(1,1,1)和M2(0,1,-1)且垂直于平面x+y+z=0,求它的方程.解设所求平面的一个法向量为n={A,B,C}.由n⊥M M=(-1,0,-2) ⇒-A-2C=012由n⊥(1,1,1) ⇒A+B+C=0 ⇒A=-2C,B=C, 代入点法式方程:A(x-1)+B(y-1)+C(z-1)=0消去C得所求方程为:2x-y-z=0例 设P 0(x 0,y 0,z 0)是平面Ax +By +Cz +D =0外一点,求P 0到这平面的距离.解 在平面上任取一点P 1(x 1,y 1,z 1),并作法向量 n ={A ,B ,C }. 则所求距离:d =│Prj n 10P P │.又设e n 为与n 方向一致的单位向量, 则有Prj n 10P P = Prj e n 10P P =10P P •e nn1P 0P θ∏则有Prj n 10P P = 10P P •e n而 e n =(222CB A A++,222C B A B ++,222CB A C++) 10P P =(x 0-x 1,y 0-y 1,z 0-z 1)由于Ax 1+By 1+Cz 1+D =0,所以Prj n 10P P =222000CB A DCz By Ax +++++n1P 0P θ∏点到平面的距离 222000CB A DCz By Ax d +++++=例 求点(2,1,1)到平面x +y -z +1=0的距离解 d =222|1211111|11(1)⨯+⨯-⨯+++-=3平面及其方程1.掌握平面的点法式、一般式、截距式方程,会根据相应条件求平面的方程.2.掌握两平面夹角的概念与求法，掌握两平面平行、垂直的充分必要条件.3.掌握点到平面的距离公式，会求点到平面的距离.。

第四节 平面及其方程平面和直线是空间最简单的几何图形，本节和下节将以向量为工具讨论平面与直线的方程 一 平面的点法式方程• 与平面垂直的非零向量称为该平面的法向量。

显然，平面的法向量有无穷多个，而且平面上的任一向量都与该平面的法向量垂直。

• 由立体几何知道，过空间一点可以作而已只能作一个垂直于一条已知直线的平面。

下面我们利用这个结论来建立平面的方程。

• 设平面 π 过点M0(x0,y0,z0)，n=（A ，B ，C ）是平面 π 的法向量（图8-17）。

现在来建立平面 的方程。

• 在平面上 π 任取一点M （x,y,z ）.则点M 在平面 上的充要条件是0M M n⊥即00M M n ⋅=• 因为 0000{,,}M M x x y y z z =---=（x-x0,y-y0,z-z0）,n=(A,B,C),所以有(0)(0)(0)0A x xB y yC z z -+-+-=• 该方程称为平面 π 的点法式方程。

• 例1 求过点（2,1,1）且垂直于向量i+2j+3k 的平面方程。

• 解 显然，我们可以取已知向量i+2j+3k 作为所求平面的法向量n ，又因为平面过点（2,1,1）,所以由公式即可得该平面方程为 • （x-2）+2(y-1)+3(z-1)=0 • 即x+2y+3z-7=0• 例2 求过点M1(1,2,-1)、M2（2,3,1）且和平面x-y+z+1=0垂直的平面方程。

• 解 因为点12,M M 所在平面上（图8-18），所以向量M1M2=（1，1，2）在该平面上。

又因为与平面x-y+z+1=0垂直，而已知平面的法向量n1=(1,-1,1),故可取平面的法向量1211 1 23-21 -1 1i j k n M M n i j k =⨯==+• 由于该平面过点M1(1,2,-1)，因此由平面的点法式方程知道3（x-1）+（y-2）-2(z+1)=0，即3x+y-2z-7=0为所求的平面方程 平面的一般方程• 将方程A(x-x0)+B(y-y0)+C(z-z0)=0展开得• Ax+By+Cz+(-Ax0-By0-Cz0)=0,这是x 、y 、z 的一次方程，所以平面可用x 、y 、z 的一次方程来表示，反之，任意的x 、y 、z 的一次方程 • Ax+By+Cz+D=0 （ a ） • 是否都表示平面呢（式中A 、B 、C 不全为零）？方程是一个含有三个未知数的方程，所以有无穷多组解，设x0、y0、z0是其中一组解，则由 • Ax0+By0+Cz0+D=0 ( b )• a-b 得A(x-x0)+B(y-y0)+C(z-z0)=0,• 它表示过点（x0,y0,z0）,且以n=（A,B,C ）为法向量的平面。