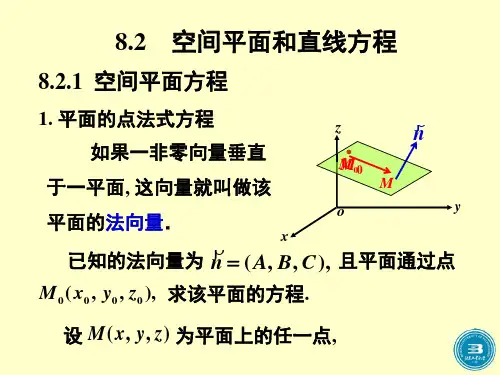
空间平面方程

空间平面方程的求法1、 用参数方程题目的已知条件是给出平面所经过的一个定点以及平面的两个方位矢量，有的题型是要求把所给的方程形式化为参数方程或者把已知的参数方程化为一般方程.①矢量式参数方程 错误!=错误! + t 1错误!+t 2错误!其中错误!=｛X 1,Y 1，Z 1｝， 错误!={X 2，Y 2，Z 2｝②坐标式参数方程⎪⎩⎪⎨⎧++=++=++=221102*********Zt Z t z z Y t Y t y y X t X t x x例1、 写出下面的参数方程:通过点)1,3,2(A 并平行于)1,0,3(),3,1,2(21-=-=v v解：所求的参数方程为⎪⎩⎪⎨⎧vu z u y vu x -+=-=++=313322例2、证明矢量},,{Z Y X v =平行于平面0=+++D Cz By Ax 的充要条件为：0=++CZ BY AX证明:不妨设0=+++D Cz By Ax 中的0≠A ,把这平面的方程化为参数式:,,,v z u y v A C u A B A D x ==---=所以平面的两方位矢量是}0,1,{A B -与}1,0,{A C-,从而知},,{Z Y X v =与已知平面共面的充要条件为v与}0,1,{A B -，}1,0,{A C-共面,或 01001=--AC A BZYX ,即0=++CZ BY AX 。

如果在直角坐标系下,那么由于平面的法矢量为},,{C B A n =,所以v平行于平面的充要条件为0=⋅v n，即0=++CZ BY AX 。

2、 用点位式方程题目会给出平面的两个方位矢量的坐标以及平面上的一个已知点。

222111000Z Y X Z Y X z z y y x x ---=03、用三点式方程题目的条件是平面上的三个已知点。

131313121212111z z y y x x z z y y x x z z y y x x ---------=0 例3、已知三角形顶点为),2,2,2(),1,1,2(),0,7,0(C B A --求平行于三角形ABC 所在的平面且与它相距为2个单位的平面方程.解：由已知，得02921627=+z y x， 所以三角形ABC 所在的平面方程为014623=-+-z y x 。

空间直线与平面的方程空间中的任意一条直线和任意一个平面都可以通过方程来描述。

直线和平面的方程可以用于解决和分析几何问题，例如求直线与平面的交点、直线和平面的距离等。

本文将介绍空间直线与平面的方程的基本概念和求解方法。

一、空间直线的方程在空间中，直线可以由一个点和一个方向向量确定。

一个点可以用坐标表示，方向向量可以用直线上两点之间的向量表示。

假设已知直线上一点为P(x0, y0, z0)，方向向量为v(a, b, c)，则直线的参数方程可以表示为：x = x0 + aty = y0 + btz = z0 + ct其中t为参数，表示直线上的任意一点。

直线的对称方程可表示为：(x - x0)/a = (y - y0)/b = (z - z0)/c通过参数方程和对称方程，我们可以得到空间中直线的方程。

二、空间平面的方程在空间中，平面可以由一个点和一个法向量确定。

一个点可以用坐标表示，法向量可以用平面上两个不共线向量的向量积表示。

假设已知平面上一点为P(x0, y0, z0)，法向量为n(a, b, c)，则平面的方程可以表示为：ax + by + cz + d = 0其中d = -(ax0 + by0 + cz0)。

平面的点法向式方程可表示为：(n·r) + d = 0其中r为平面上的任意一点。

通过方程和点法向式方程，我们可以得到空间中平面的方程。

三、直线与平面的方程在空间中，直线和平面的方程可以用来描述直线和平面的位置关系。

我们可以通过求解直线和平面的交点来得到它们的方程。

假设直线的方程为：x = x0 + aty = y0 + btz = z0 + ct平面的方程为：ax + by + cz + d = 0将直线的方程代入平面的方程，可以得到直线与平面的交点。

解方程组即可求解交点的坐标。

四、实例应用现在我们通过一个实例来应用空间直线和平面的方程。

假设已知直线L上一点为A(1, 2, 3)，方向向量为v(2, 1, -1)；平面P 经过点B(2, -1, 4)，法向量为n(1, -2, 3)。

§2−3 空間中的平面方程式(甲)空間中平面方程式(1)[回顧坐標平面上的直線]：(a)平面坐標系中，只要知道斜率m與點(x0,y0)就可以確定直線的位置，因此可以求出直線的方程式y−y0=m(x−x0) (點斜式)。

(b)考慮平面上的直線L：2x+3y+6=0，P(3,−4)為L上的任意點，我們曾定義直線L的法向量→n=(2,3)，設R(x,y)為L上的一點，根據法向量的定義，可知→n→n=0⇒(x−3,y+4)⋅(2,3)=0⇒2x+3y+6=0。

(2)平面的法線與法向量：平面的法線：若一直線L垂直於平面E，則稱此直線為平面E的法線。

平面的法向量：若直線L為平面E的法線，則直線L的一個方向向量就稱為平面E的一個法向量。

法向量的特性：(a)一個平面的法向量會是唯一嗎？NO！(b)若任取平面E上的兩個相異點A、B→n。

(3)如何求平面的方程式：(a)點法式：若平面E法向量→n=(a,b,c)且過點A(x,y0,z0)，則平面E的方程式為a(x−x0)+b(y−y0)+c(z−z0)=0。

[證明]：在平面E上任取一點P其坐標為(x,y,z)→n所以(x−x0,y−y0,z−z0)⋅(a,b,c)=0⇒a(x−x0)+b(y−y0)+c(z−z0)=0反過來說滿足方程式a(x−x0)+b(y−y0)+c(z−z0)=0的解Q(x,y,z)→n⇒Q落在平面E上。

(b)一般式：將方程式a(x−x0)+b(y−y0)+c(z−z0)=0 化簡可得ax+by+cz+d=0的方程式。

我們將ax+by+cz+d=0稱為一般式。

一般式ax+by+cz+d=0的法向量為→n=(a,b,c)[證明]：設A(m ,n ,l )、B(p ,q ,r )在平面ax +by +cz +d =0上， (a ,b ,c )=(p −m ,q −n ,r −l )⋅(a ,b ,c ) =a (p −m )+b (q −n )+c (r −l ) =ap +bq +cr −(am +bn +cl ) =d −d =0→n 因此ax +by +cz +d =0的法向量為→n =(a ,b ,c )。

空间直角坐标系的平面方程空间直角坐标系是三维空间中最常用的坐标系之一，它由三个相互垂直的坐标轴组成，分别为x轴、y轴和z轴。

通过这三个坐标轴，我们可以在三维空间中精准地描述一个点的位置。

而平面方程则是通过坐标系中的点来描述平面的方程。

在空间直角坐标系中，平面方程的一般形式可表示为Ax + By + Cz + D = 0，其中A、B、C和D为实数常数。

这个方程描述了空间中所有满足该方程的点所构成的平面。

要确定一个平面的方程，我们需要知道平面上的一点以及平面的法向量。

法向量是垂直于平面的向量，它的方向决定了平面的朝向。

根据平面上的一点和法向量，我们可以使用向量的点积来得到平面的方程。

假设平面上有一点P(x0, y0, z0)，而平面的法向量为n(A, B, C)。

则从平面上任意一点Q(x, y, z)到点P的向量可以表示为向量PQ = <x-x0, y-y0, z-z0>。

根据向量PQ和法向量n的点积关系，有：<n, PQ> = 0展开得到：A(x - x0) + B(y - y0) + C(z - z0) = 0整理上式可得平面的方程：Ax + By + Cz - (Ax0 + By0 + Cz0) = 0这就是空间直角坐标系中平面的方程。

在该方程中，A、B、C分别对应平面的法向量的分量，而Ax0 + By0 + Cz0则是平面上任意一点的坐标乘以法向量的分量之和。

需要注意的是，如果A、B、C不全为0，则平面可以看作是一个无限大的平面。

如果A、B、C中有一个为0，那么平面将退化为一个平行于其他两个坐标轴的平面。

除了一般形式的平面方程，我们还可以根据不同的信息形式推导出不同的平面方程。

例如，如果已知平面上的三个点P1(x1, y1, z1)、P2(x2, y2, z2)和P3(x3, y3,z3)，我们可以通过求解这些点确定的向量所构成的矩阵的行列式来得到平面的方程。

另外，如果已知平面的法向量n以及平面上的一点P0，则可以使用法向量和点的坐标来得到平面的方程。

空间直线与平面的方程与性质空间中直线和平面是几何学中重要的概念，它们在解决问题和分析空间关系时起到了关键作用。

本文将介绍空间直线和平面的方程与性质，并探讨它们在几何学中的应用。

一、空间直线的方程与性质空间直线可以由其上两点的坐标表示，我们可以通过已知直线上两点的坐标，来确定直线的方程。

设直线上两点为A(x₁, y₁, z₁)和B(x₂, y₂, z₂)，则直线的方程可以表示为：(x - x₁) / (x₂ - x₁) = (y - y₁) / (y₂ - y₁) = (z - z₁) / (z₂ - z₁)直线的方程可以表示为等比关系，该关系描述了直线上各点的坐标之间的比值关系。

利用这个方程，我们可以求出直线上其他任意一点的坐标。

空间直线还有一些重要的性质：1. 直线的斜率：直线的斜率定义为直线上两个不同点的纵坐标之差除以水平坐标之差。

在三维空间中，直线的斜率无穷大或者不存在时，我们说直线是垂直于坐标面的。

2. 直线的方向向量：直线的方向向量定义为直线上两个不同点的坐标之差。

利用方向向量，我们可以描述直线的走向和方向。

3. 直线与平面的关系：直线与平面可以相交，也可以平行或重合。

我们可以利用空间向量的知识，通过直线的方向向量和平面的法向量来判断直线与平面的关系。

二、空间平面的方程与性质空间平面可以由其上三点的坐标表示，我们可以通过已知平面上三点的坐标，来确定平面的方程。

设平面上三点为A(x₁, y₁, z₁)，B(x₂, y₂, z₂)，C(x₃, y₃, z₃)，则平面的方程可以表示为：| x - x₁, y - y₁, z - z₁ || x₂ - x₁, y₂ - y₁, z₂ - z₁ || x₃ - x₁, y₃ - y₁, z₃ - z₁ | = 0平面的方程可以表示为一个线性方程组的形式，该线性方程组描述了平面上所有点的坐标满足的条件。

利用平面的方程，我们可以求出平面上其他任意一点的坐标。