数学实验(概率部分)第二组

数学实验: 概率统计F实验一,实验目的: 运用数学软件解决概率统计问题二,实验工具: WPS软件, SPSSS软件三,实验要求:1、写出相应软件命令及具体操作截图。

2、给出结果的截图并给出相应统计结论。

3、以实验报告的形式上交，实验报告的格式自己设计。

1、已知某地某品种10头成年母水牛的体高（cm）为：137，133，130，128，127，119，136，132，128，130。

求出均值、标准差、极差、中位数、变异系数及95%置信区间。

（30分）2、某食品企业厂生产瓶装矿泉水，其自动装罐机在正常工作状态时每罐净容量（单位为ml）具正态分布，且均值为500。

某日随机抽查了10瓶水，得结果如下：505，512，497，493，508，515，502，495，490，510，问罐装机该日工作是否正常？（30分）3、分别测定了10只大耳白家兔、11只青紫蓝家兔在停食18小时后正常血糖值如下表，已知其服从正态分布，问该两个品种家兔的正常血糖值是否有显著差异？（单位：kg）（40分）大耳白57 120 101 137 119 117 104 73 53 68青紫蓝89 36 82 50 39 32 57 82 96 31 88 四,实验内容:1、已知某地某品种10头成年母水牛的体高（cm）为：137，133，130，128，127，119，136，132，128，130。

求出均值、标准差、极差、中位数、变异系数及95%置信区间。

使用软件: WPS软件(1)数据输入:(2)计算均值: =AVERAGE(A2,A3,A4,A5,A6,A7,A8,A9,A10,A11)放入C2(3)计算标准差:=STDEV(A2,A3,A4,A5,A6,A7,A8,A9,A10,A11)放入D2(4)计算极差:=MAX(A2:A11)-MIN(A2:A11)放入E2(5)计算中位数:=MEDIAN(A2,A3,A4,A5,A6,A7,A8,A9,A10,A11) F2(6)计算变异系数:=D2/C2 G2(7)自由度: 9 H2(8)自信度：0.95 J2(9)计算t分布双侧分位数：=TINV(0.05,9) I2(10)抽样平均误差：=D2/SQRT(10) K2(11)允许误差：=I2*K2 L2(12)自信下限：=C2-L2 H5(13)自信上限：=C2+L2 I5实验结果：2、某食品企业厂生产瓶装矿泉水，其自动装罐机在正常工作状态时每罐净容量（单位为ml）具正态分布，且均值为500。

数学实验概率论与数理统计分册习题第1章古典概率2．碰运气能否通过英语四级考试大学英语四级考试是全面检验大学生英语水平的一种综合考试,具有一定难度。

这种考试包括听力、语法结构、阅读理解、写作等。

除写作占15分外,其余85道为单项选择题,每道题附有A、B、C、D四个选项。

这种考试方法使个别学生产生碰运气和侥幸心理,那么,靠运气能通过英语四级考试吗?解：假设学生作文得满分，即15分，85道选择题每道题都靠蒙，即每道题做对的概率为1/4，得60分则通过考试。

则该同学通过考试的概率为：P=4540 45851344C⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭>> nchoosek(85,40)*(1/4)^45*(3/4)^40ans =2.3448e-008即：82.344810-⨯由此可见，即使该同学作文满分，靠运气通过考试的概率也是如此的低，所以可以认为靠运气不能通过英语四级考试。

3.在区域H＝{(x，y)| (x，y)∈Q，x2+y2≤1}，Q＝{(x，y) |0≤x≤1，0≤y≤1}上考虑计算二重积分（利用Monte-carlo法）：⎰⎰++=HdxdyyxyxI) sin(解：积分区域如右图所示：>> n = 10000; % 模拟次数x = rand(n,1); % 点的x坐标y = rand(n,1); % 点的y坐标m = sum(sin(x+y)./(x+y) & x.^2 + y.^2 <= 1); Vn = m/n % 落到所求面积内的点的频率，即概率的模拟值Vn =0.7891第2章 随机变量及其分布4．公共汽车车门的高度是按成年男子与车门碰头的机会在0.01以下的标准来设计的。

根据统计资料，成年男子的身高X 服从均值为168厘米，方差为7厘米的正态分布，那么车门的高度应该至少设计为多少厘米？解：>> norminv(0.99, 168, 7)ans =184.2844则车门的高度应该至少设计为184.3厘米5．某研究中心有同类型仪器300台，各仪器工作相互独立，而且发生故障的概率均为0.01，通常一台仪器的故障由一人即可排除。

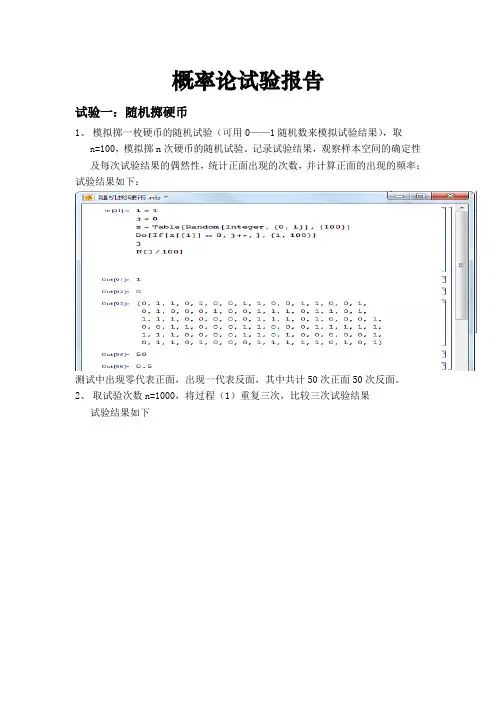
概率论试验报告试验一：随机掷硬币1、模拟掷一枚硬币的随机试验（可用0——1随机数来模拟试验结果），取n=100，模拟掷n次硬币的随机试验。

记录试验结果，观察样本空间的确定性及每次试验结果的偶然性，统计正面出现的次数，并计算正面的出现的频率；试验结果如下：测试中出现零代表正面，出现一代表反面，其中共计50次正面50次反面。

2、取试验次数n=1000，将过程（1）重复三次，比较三次试验结果试验结果如下3、三次结果分别是0.501,0.503,0.521 。

这充分说明模拟情况接近真实情况，频率接近概率0.5。

试验二：高尔顿钉板试验1、自高尔顿钉板上端放一个小球, 任其自由下落. 在其下落过程中，当小球碰到钉子时从左边落下的概率为p , 从右边落下的概率为,1p -碰到下一排钉子又是如此, 最后落到底板中的某一格子. 因此任意放入一球, 则此球落入哪个格子事先难以确定. 设横排共有20=m 排钉子, 下面进行模拟实验:(1) 取,5.0=p 自板上端放入一个小球, 观察小球落下的位置; 将该实验重复作5次, 观察5次实验结果的共性及每次实验结果的偶然性;(2) 分别取,85.0,5.0,15.0=p 自板上端放入n 个小球, 取,5000=n 观察n 个小球落下后呈现的曲线我们分析可知，这是一个经典的古典概型试验问题2、具体程序：3、我们分析实验结果可知，若小球碰钉子后从两边落下的概率发生变化, 则高尔顿钉板实验中小球落入各个格子的频数发生变化, 从而频率也相应地发生变化. 而且, 当,5.0p曲线峰值的格子位置向右偏; 当><p曲线峰值的格子位置向左偏。

,5.0试验三：抽签试验1、我们做模拟实验，用1-10的随机整数来模拟实验结果。

在1-10十个随机数中，假设10代表抽到大王，将这十个数进行全排，10出现在哪个位置，就代表该位置上的人摸到大王。

每次随机排列1-10共10个数，10所在的位置随机变化，分别输出模拟实验10次, 100次,1000次的结果, 将实验结果进行统计分析, 给出分析结果。

人教版九年级数学上册第二十五章概率初步《25.1随机事件与概率》第2课时教案一. 教材分析本节课的主要内容是随机事件与概率的初步概念。

学生需要了解随机事件的定义，以及如何用概率来描述事件的可能发生性。

教材通过大量的实例来帮助学生理解概率的概念，并培养学生的实际应用能力。

二. 学情分析九年级的学生已经具备了一定的逻辑思维能力和抽象思维能力，对于一些基本的概念和原理能够理解和掌握。

但是，由于概率是一个相对抽象的概念，对于一些学生来说，理解起来可能会有难度。

因此，在教学过程中，需要通过大量的实例和实际操作来帮助学生理解和掌握概率的概念。

三. 教学目标1.了解随机事件的定义，理解必然事件、不可能事件和不确定事件的概念。

2.掌握概率的基本计算方法，能够计算简单事件的概率。

3.能够运用概率的知识解决实际问题。

四. 教学重难点1.随机事件的定义和分类。

2.概率的计算方法。

3.概率在实际问题中的应用。

五. 教学方法1.采用问题驱动的教学方法，通过提出问题，引导学生思考和探索，培养学生的思维能力。

2.使用多媒体教学，通过动画和实例的展示，帮助学生直观地理解概率的概念。

3.采用分组讨论的教学方法，让学生通过合作和交流，共同解决问题，培养学生的团队协作能力。

六. 教学准备1.多媒体教学设备。

2.教学课件和教学素材。

3.分组讨论的准备。

七. 教学过程1.导入（5分钟）通过一个简单的实例，如抛硬币实验，引导学生思考事件的可能发生性，并引入随机事件的定义。

2.呈现（10分钟）介绍必然事件、不可能事件和不确定事件的概念，并通过实例进行解释和展示。

3.操练（10分钟）让学生进行一些简单的概率计算练习，如抛硬币实验的概率计算，以及一些简单的实际问题的概率计算。

4.巩固（10分钟）通过一些实际问题，让学生运用概率的知识进行解决，巩固所学的知识。

5.拓展（10分钟）引导学生思考概率在实际生活中的应用，如彩票、赌博等，让学生了解概率在生活中的重要性。

可能性课标要求1.知道简单的随机事件，能列出简单的随机事件中所有可能发生的结果。

2.明确随机事件发生的可能性是有大小的，能对一些简单随机事件发生的可能性大小做出判断。

3.能判断游戏是否公平，并能设计简单公平的游戏规则。

考点1 现象发生的结果1.选择。

（1）某足球评论员预测世界杯德国队有80%的机会战胜意大利队。

与横线部分最接近的意思是（）。

A.德国队肯定会赢得这场比赛B.德国队肯定会输这场比赛C.假如这两支球队进行10场比赛，德国队会赢8场左右D.假如这两支球队进行了10场比赛，德国队恰好会赢8场（2）盒子里有大小相同的三个红球和三个绿球，从中任意摸出两个球，以下说法错误的是（）。

A.可能摸出两个红球B.可能摸出一个红球和一个绿球C.可能摸出两个绿球D.一定摸到一个红球和一个绿球2.袋子中装有红、白两种颜色的球，这些球除颜色外完全相同。

两组同学通过摸球估计袋中两种颜色球的多少。

他们每次摸之前都把球摇匀，摸后再把球放回去，摇匀后再摸。

（1）第一组摸了5次，结果是“红、白、红、红、白”，他们估计袋子中红球多。

他们估计得结果可能是真的吗（在你认为正确的后面画“√”）？可能（）不可能（）（2）第二组摸了120次，结果是98次白球，22次红球，他们估计袋子中白球多。

他们估计得结果可能是真的吗（在你认为正确的后面画“√”）？可能（）不可能（）（3）你认为哪个组的实验估测方法更科学，为什么？考点2 可能性的大小及比较3. 判断。

（1）盒子里有99个红球和一个绿球，摸到绿球的可能性是 。

（ ）（2）连续抛一枚硬币10次，其中7次正面朝上，3次反面朝上，那么再抛一次正面朝上的可能性大。

（ ）（3）小芳和小红做“石头、剪子、布”的游戏，两人获胜的可能性相等。

（ ）4. 选择。

（1）下面每一个转盘中，任意转动指针，停留在涂色区域的可能性最大的是（ ）。

（2）盒子里有大小、材质完全相同的红球、黄球、绿球各5个。

小芳每次摸出一个球，然后放回再摸，前三次摸球的情况如下表：小芳第4次摸球下面说法正确的是（ ）。

出版社，2015 年 8 月.
参 [3] 郑一,戚云松,陈倩华,陈健. 光盘：概率论与数理统计教案、作业册与
考
试卷考题及答案、数学实验视频. 大连理工大学出版社，2015 年 8
文
月.
献 [4] 王玉敏,郑一,林强. 概率论与数理统计教学实验教材. 中国科学技术
出版社，2007 年 7 月.
联系方式：zhengone@
k
讲评 这两条性质常用来判断一个数列{pk}是否是某个离散型随机变量 的概率分布, 或者确定概率分布中的待定参数. 只有 pk同时满足上述两条性质, 数列{pk}才能作为某个离散型随机变量的分布律.
2. 伯努利概型 在 n 重伯努利试验中, 事件 A 恰好发生 k 次的概率为
P{X=k}= Cnk pk qnk , k 0,1, 2, n . 讲评 n 重伯努利试验是一种很重要的数学模型. 它有广泛的应用, 是研 究与应用最多的模型之一. 3. 分布函数 设 X 是一个随机变量(包括离散型及非离散型). x 是任意实数, 定义
《概率论与数理统计》教案 第二章习题课 郑一，戚云松，陈倩华，陈健 编著 大连理工大学出版社出版
第 80 页
题
第二章 随机变量及其概率分布内容习题课
目
课时：2
与
课
时
(1) 熟练计算离散型随机变量及其概率分布问题；
教 (2) 熟练计算连续型随机变量及其概率密度问题； 学 (3) 熟练计算随机变量的分布函数； 目 (4) 熟练计算随机变量函数的概率分布问题。 的
(4) 若 f (x) 在点 x 处连续, 则有 ′F x ( ) = f ( ) x ; (5) 对连续型随机变量 x，总有P{X =a} =0 < ∞ − ,a ∞+ <. 讲评 性质(1)和(2)是连续型随机变量的概率密度 f (x) 必须具有的特性, 常用来检查某一函数 f (x) 是否是连续型随机变量的概率密度. 性质(3)和(4)是 由概率密度的定义导出的性质. 性质(3)和(4)表明：随机变量 X 落在区间 (a,b] 内的概率等于曲线 y f (x) 与 x=a, x=b 及 x 轴所围成的曲边梯形的面积. 性质 (5)表明：对于连续型随机变量 X , 总有

Ｄ ［ ＝ ａ ｄ ｍ［ ｔｇｒ ０１１ ｏｒ Ｒ ｎ ｏ Ｉ ｅ ｅ， ，１ ｅ ｎ ｛ ；
Ｉ［ ：ｒ３ ； ｎ２ ＝＝ Ｏ 】
ｎ ＯБайду номын сангаас０ ＝ｌ ０ ０；
（ 输入初始数据与模拟次数 ）
Ｉ［］ Ｄ ［ ＝ ａ ｌ［ａｄ ｍ Ｉｔｇｒ ｌ ６ ｝｛ｌｒ ；ｂ ａ／ ｎｏ； ｎ３： ｏａ Ｔ ｂｅＲ ｏ ［ ｅｅ， ， ５１ｄ ，｝ｂ ＝ａ／ ｉｎ ＝ ａ ｎ ｎ ｛ ３ ， ｛ｌ Ｕ ｓ【：ｔ ｅｇｈｂ ｌｒ１ １ｉ ，｝ ｓ］ＩＬ ｎ ｔ［ｂ＜，， ，， ｎ】 ． ［ ０ ｛ｌ ｅ＝ ａｌ［ ［，，，１ ｃ Ｔ ｂｅ ｓｉ（１ ］ ｓ ］ｉ ｎ ； （ 编 程 计算 ｝ ） Ｉ［］ ｐ ．ｌｓ ｎ４： ：Ｐｕ＠＠ｃ ／ ： ｃ／ Ｎ （ 要求 概率 的近似值 ）
关键词概率论与数理统计数学实验mathematica高校理科研究487科技信息in7quantileaa1095用另外一种方式计算上005分out7196751in8randomaa11生成一个参数为11服从的分布的随机数out8136576in9sss1tablerandomaa1110000生成10000个参数为11服从的分布的随机数in10gaphics加载图形包in11histogramsss1绘制直方图graphics例2student氏t分布in1clearnn16清除变量的赋值in2aa2studenttdistributionn产生一个服从参数为16的t分布的随机变量in3f2xevaluatepdfaa2x定义其概率密度函数in4plotf2xx66绘制概率密度函数的图形out4graphicsin5plotg2xx66绘制分布函数的图形out5graphicsin6findrootg2x095x13计算上005分位点out6x174588in7f2xdx验证上005分位点out700500003in8quantileaa2095用另外一种方式计算上005分out8174588in9randomaa2生成一个参数为16服从的t分布的随机数out9139094in10sss2tablerandomaa210000生成10000个参数为16服从的t分布的随机数in11graphics加载图形包in12histogramsss2绘制直方图out12gsphics例3f分布in1clearnmn16m19清除变量赋值输入参数值in2aa3fratiodistributionnm生成服从f1619分布的随机变量in3f3xevaluatepdfaa3x定义其概率密度函数in4plotf3xx09绘制概率密度函数的图形out4graphicsin5g3xevaluatecdfaa3xin6plotg3xx09绘制分布函数的图形out6graphicsin7findrootg3x095x9计算上005分位点out7x298897in8f3xdx验证上005分位点out800451076in9quantileaa3095用另外一种方式计算上005分位out9298897in10randomaa3生成一个服从f1619分布的随机数out10109471in11tablerandomaa310生成10个服从f161

X Y
1.9
0.8
1.1
0.1
0.1
4.4 5.5 1.6 4.6 3.4
0.7 -1.6 -0.2 -1.2 -0.1 3.4 3.7 0.8 0.0 2.0
试就下列两种情况分析这两种药物的疗效有无显示性的差异。 （ α = 0.05 ） 。 ① X 与 Y 的方差相同；② X 与 Y 的方差不同。 （7） 、 已知某一试验， 其温度服从正态分布， 现在测量了温度的五个值为： 1250， 1265，1245，1260，1275。问是否可以认为 µ = 1277 （8） 、其它教材上的题目或自己感兴趣的题目。 （ α = 0.05 ） 。 ？
A =[16 25 19 20 25 33 24 23 20 24 25 17 15 21 22 26 15 23 22
20 14 16 11 14 28 18 13 27 31 25 24 16 19 23 26 17 14 30 21 18 16 18 19 20 22 19 22 18 26 26 13 21 13 11 19 23 18 24 28 13 11 25 15 17 18 22 16 13 12 13 11 09 15 18 21 15 12 17 13 14 12 16 10 08 23 18 11 16 28 13 21 22 12 08 15 21 18 16 16
实验四、样本的统计与计算 实验目的： 熟练使用 matlab 对样本进行基本统计，包括样本的位置统计、分散性统计、样 本中心矩、分布的形状统计。求样本均值、中位数、样本方差，偏度、峰度、 样本分位数和其它数字特征，并能做出频率直方图和经验分布函数。 实验内容： 来自总体的样本观察值如下，计算样本的样本均值、中位数、样本方差、极差, 偏度、峰度、画出频率直方图，经验分布函数图。

1 4 1 4 1 4 1 × （ ） 2 × … （ ） n × 5 5 5 5 5 5 5
14、某射手有５发子弹，每射一发的命中率都是０．７，如果命中目标便停止射击，不中目 标就一直射击到子弹用完为止，试求命中目标所用的子弹数Ｘ的分布律． 解： ｘ １ ２ ３ ４ ５ p 0.7 0.3× ０．７＝０．２１ ０．３ 2 × ０．７＝０．０６３ ０．３ 3 × ０．７＝０．０１８９ ０．３ 4 × ０．７＝０．００５６７
1 2
1 1 1 4 2 4
4、 ８件正品２件次品中随机的抽出３件，所抽出的次品数为Ｘ，试写出Ｘ的分布律
−i 解：令 ｘ＝ｉ， ｉ＝０，１，２， 则 Ｐ（ｘ＝ｉ）＝Ｃ i2 Ｃ 3 8
故 Ｘ ０ １ ２ p
0...................x ≤ 1 0.2...............1 < x ≤ 2 所以 Ｆ（ｘ）＝ 0 . 6 .......... ..... 2 < x ≤ 3 1..................3 < x
(2 ) D=[1,2.5], P(X ∈ D)=P(1 ≤ X ≤ 2.5 ) =P( X ≤ 2.5 )－P(X<1) =P(X=2.5)+P(X<2.5)－P(X<1) =0+F(2.5) －F(1) =0+0.6+0=0.6 ５． 从装有 3 个红球和 1 个白球的口袋中任意取出 2 个球，若以 X 表示其中的红球数，以 Y 表示其中的白球数，试求(X，Y)的分布函数。 解：（Ｘ，Ｙ）的分布律为： Ｐ（Ｘ＝１，Ｙ＝１）＝
6、 某射手的命中率为０．６，相互独立地射击４次，求命中目标的次数Ｘ的分布律 解： 此为二项分布 Ｐ（ｘ＝ｉ）＝Ｃ i4 ０．６ｉ （１－０．６）４－ｉ （ｉ＝０，１，２，３，４）

北师大版数学九年级上册《2 用频率估计概率》教案2一. 教材分析《北师大版数学九年级上册》中的《2 用频率估计概率》是学生在学习了概率的基本概念之后，进一步利用频率来估计事件的概率。

通过本节课的学习，学生能够理解频率与概率之间的关系，学会如何利用频率来估计事件的概率，并能够运用这一方法解决实际问题。

二. 学情分析九年级的学生已经具备了一定的概率基础知识，对于频率和概率的概念有一定的了解。

但是，学生对于如何利用频率来估计概率，以及如何运用这一方法解决实际问题，可能还存在一定的困难。

因此，在教学过程中，需要引导学生通过实际操作，理解频率与概率之间的关系，掌握利用频率来估计概率的方法。

三. 教学目标1.理解频率与概率之间的关系，掌握利用频率来估计概率的方法。

2.能够运用频率估计概率的方法解决实际问题。

3.培养学生的动手操作能力，提高学生运用数学知识解决实际问题的能力。

四. 教学重难点1.教学重点：频率与概率之间的关系，利用频率来估计概率的方法。

2.教学难点：如何引导学生通过实际操作，理解频率与概率之间的关系，掌握利用频率来估计概率的方法。

五. 教学方法1.采用问题驱动的教学方法，引导学生通过实际操作，理解频率与概率之间的关系，掌握利用频率来估计概率的方法。

2.利用多媒体教学，展示实验过程，帮助学生直观地理解频率与概率之间的关系。

3.采用小组合作学习的方式，培养学生的团队合作精神，提高学生的动手操作能力。

六. 教学准备1.多媒体教学设备。

2.实验材料：如骰子、卡片等。

3.教学课件。

七. 教学过程1.导入（5分钟）利用多媒体展示实验过程，引导学生思考：频率与概率之间的关系是什么？2.呈现（10分钟）呈现一组实验数据，引导学生通过实际操作，理解频率与概率之间的关系。

3.操练（10分钟）学生分组进行实验，利用频率来估计事件的概率。

教师巡回指导，解答学生的疑问。

4.巩固（10分钟）学生汇报实验结果，教师总结频率与概率之间的关系，强调利用频率来估计概率的方法。

2
第1章 古典概型
从 17 世纪到 19 世纪，贝努利、隶莫弗、拉普拉斯、高斯、 普阿松、切贝谢夫、马尔可夫等著名数学家都对概率论的发 展做出了杰出的贡献。为概率论确定严密的理论基础的是数 学家柯尔莫哥洛夫。1933 年，他发表了著名的《概率论的基 本概念》，用公理化结构，明确定义了概率论中的基本概念， 成为了概率论发展史上的一个里程碑，为以后的概率论的迅 速发展奠定了基础。
(2)至少有 2 个一级品的概率？
（1）>> p1=nchoosek(32,20)*nchoosek(18,10)/nchoosek(50,30)
运行结果：
p1 =
0.2096
（2）
>> p2=1-(nchoosek(32,30)+nchoosek(18,1)*nchoosek(32,29))/nchoosek(50,30)
常见分布的概率密度、分布函数生成
【实验内容】 1. 事件 A 在每次试验中发生的概率是 0.3，计算 （1）在 10 次试验中 A 恰 好发生 6 次的概率； （2）生成事件 A 发生次数的概率分布； （3）在 10 次试验中 A 最多发生 6 次的概率； （4）设事件 A 发生次数为 X，且 X 的分布函数为 F(x)，求 F(6.1)；又 已知 F（x）=0.345，求 x。
27
3425371 5496764
随机数的生成
2．产生 7 个服从参数为 6 的泊松分布的随机数。
>> poissrnd(6,1,7) 运行结果为：
ans =
1.6449
24
2. 1 验证性实验
实验二 随机数的生成
【实验目的】 1．掌握常见分布的随机数产生的有关命令 2．掌握利用随机数进行随机模拟的方法 【实验要求】 掌握常见分布的随机数产生命令，如 binornd，normrnd 等

《概率的简单应用》作业设计方案（第一课时）一、作业目标本作业旨在通过实践操作和理论应用，使学生能够：1. 理解概率的基本概念和计算方法；2. 掌握概率在生活中的简单应用；3. 培养学生的逻辑思维能力和解决问题的能力。

二、作业内容作业内容主要包括以下几个方面：1. 理论复习：要求学生复习概率的基本概念，如事件、概率的定义及计算方法等。

2. 实践操作：设计几个简单的概率实验，如抛硬币、掷骰子等，让学生亲自操作并记录实验结果，计算事件的概率。

3. 情景应用：设计实际生活场景，让学生运用所学概率知识解决实际问题。

例如，设计一个抽奖活动，让学生计算中奖的概率；或者设计一个彩票购买策略，让学生分析购买不同类型彩票的中奖概率。

4. 作业题目：布置一定量的习题，包括选择题、计算题和应用题，以巩固学生对概率知识的理解和应用能力。

三、作业要求1. 实践操作部分：学生需亲自进行实验操作，并准确记录实验数据和结果。

2. 情景应用部分：学生需根据所给情景，运用所学知识进行分析和计算，提出自己的见解和解决方案。

3. 作业题目部分：学生需独立完成作业题目，注意审题，理解题意，运用所学知识进行解答。

同时，要求学生书写规范，步骤清晰，答案准确。

4. 作业提交时，需附上实验记录和解题过程，以便教师了解学生的思考过程和解题方法。

四、作业评价教师将根据以下标准对学生的作业进行评价：1. 实践操作部分：是否亲自进行实验操作，实验数据是否准确，实验结果是否符合理论预期。

2. 情景应用部分：是否能够运用所学知识进行分析和计算，提出的见解和解决方案是否合理。

3. 作业题目部分：是否独立完成作业题目，答案是否准确，步骤是否清晰，书写是否规范。

4. 综合表现：学生是否认真对待作业，是否有独立思考和解决问题的能力。

五、作业反馈教师将对每位学生的作业进行认真批改，指出错误和不足，并提供详细的解题思路和解题方法。

同时，教师将根据学生的作业情况，进行针对性的辅导和指导，帮助学生更好地掌握概率知识。

第一讲Ⅰ 授课题目第二章 随机变量及其分布§1 随机变量 §2 离散型随机变量及其分布律 Ⅱ 教学目的与要求1、深刻理解随机变量的意义，熟练掌握用随机变量表示随机试验的结果；2、离散型随机变量的分布律及其表示；3、熟记两点分布、二项分布、泊松分布的分布律或密度函数及性质。

教学方法：发现式为主，讲授式为辅，讲练案结合 Ⅲ 教学重点与难点重点：掌握离散型随机变量及其分布律，如何用分布律求任何事件的概率。

难点：随机变量的概念及离散型随机变量的分布。

Ⅳ 讲授内容： 一、 引言在随机试验中，人们除对某些特定事件发生的概率感兴趣外，往往还关心某个与随机试验的结果相联系的变量. 由于这一变量的取值依赖于随机试验结果，因而被称为随机变量. 与普通的变量不同，对于随机变量，人们无法事先预知其确切取值，但可以研究其取值的统计规律性. 本章将介绍两类随机变量及描述随机变量统计规律性的分布. 二、§1 随机变量 1、随机变量概念的引入为全面研究随机试验的结果, 揭示随机现象的统计规律性, 需将随机试验的结果数量化，即把随机试验的结果与实数对应起来.1. 在有些随机试验中, 试验的结果本身就由数量来表示.2. 在另一些随机试验中, 试验结果看起来与数量无关,但可以指定一个数量来表示之. 例1 在将一枚硬币抛掷三次, 观察正面H 、反面T 出现情况的试验中, 其样本空间};,,,,,,,{TTT TTH THT HTT THH HTH HHT HHH S =记每次试验出现正面H 的总次数为随机变量X , 则X 作为样本空间S 上的函数定义为1112223XTTTTTH THT HTT THH HTH HHT HHH e例2在抛掷一枚硬币进行打赌时, 若规定出现正面时抛掷者赢1元钱, 出现反面时输1元钱, 则其样本空间为=S {正面, 反面},记赢钱数为随机变量X , 则X 作为样本空间S 的实值函数定义为⎩⎨⎧=-==.,1,,1)(反面正面e e e X例3 在测试灯泡寿命的试验中, 每一个灯泡的实际使用寿命可能是),0[+∞中任何一个实数, 若用X 表示灯泡的寿命（小时），则X 是定义在样本空间}0|{≥=t t S 上的函数，即t t X X ==)(，是随机变量. 2、随机变量的定义定义 设随机试验的样本空间为{}=S e ,()e X X =是定义在样本空间S 上的实值单值函数，称)(e X X =为随机变量.随机变量与高等数学中函数的比较:(1) 它们都是实值函数,但前者在试验前只知道它可能取值的范围,而不能预先肯定它将取哪个值; (2) 因试验结果的出现具有一定的概率,故前者取每个值和每个确定范围内的值也有一定的概率.如 例1中易见, 使X 取值为})2({2=X 的样本点构成的子集为},,,{THH HTH HHT A =故 ,8/3)(}2{===A P X P 类似地，有.2/1},,,{}1{==≤TTT TTH THT HTT P X P3、引入随机变量的意义随机变量的引入,使得随机试验中的各种事件可通过随机变量的关系式表达出来.由此可见,随机事件这个概念实际上是包容在随机变量这个更广的概念内.也可以说,随机事件是从静态的观点来研究随机现象,而随机变量则以动态的观点来研究之.其关系类似高等数学中常量与变量的关系.随机变量概念的产生是概率论发展史上的重大事件. 引入随机变量后,对随机现象统计规律的研究,就由对事件及事件概率的研究转化为随机变量及其取值规律的研究,使人们可利用数学分析的方法对随机试验的结果进行广泛而深入的研究.随机变量因其取值方式不同, 通常分为离散型和非离散型两类. 而非非离散型随机变量中最重要的是连续型随机变量. 今后，我们主要讨论离散型随机变量和连续型随机变量. 三、 §2 离散型随机变量及其分布律 1、离散型随机变量及其概率分布有些随机变量的取值是有有限个或可列无限多个，称此随机变量为离散型随机变量。

概率统计实验指导书理学院实验中心数学专业实验室编写2009.12实验二 统计分析1 引1. 问题：湖中有鱼，其数不知。

现在请你想一个办法，能将湖中的鱼数大致估计出来。

2. 分析：有两种方法。

[方法一] 设湖中有N 条鱼。

先捕出r 条鱼，做上记号后放回湖中（设记号不会消失）。

让湖中的鱼充分混合后，再从湖中捕出s 条鱼，设其中有T 条鱼标有记号，则T 是随机变量，且服从超几何分布{}(0)t s tr N rsNC C P T t t r C --==≤≤。

应用极大似然估计思想，寻找N,使{}P T t =达到最大，得sr N t ⎡⎤=⎢⎥⎣⎦。

于是取sr N t ⎡⎤=⎢⎥⎣⎦作为湖中鱼数的一种估计，其中[]x 表示不超过x 的最大整数。

[方法二] 用矩估计法.因为T 服从超几何分布，其数学期望是()srE T N=，此即捕s 条鱼得到有标记的鱼的总体平均数。

而现在只捕一次，出现t 条有标记的鱼。

由矩估计法，令总体一阶原点矩等于样本一阶原点矩，即srt N =，也得sr N t ⎡⎤=⎢⎥⎣⎦。

3. 问题的解决：由上面的分析，要想估计出湖中的鱼数，首先需要取到样本数据，然后利用样本数据，采用统计中的点估计法对总体进行估计，其属于统计分析中的一部分。

本节重点进行与统计分析相关的实验。

2 实验目的1、利用常用的统计量描述样本数据的集中和分散程度，并对总体特征进行归纳和分析。

2. 学习用MATLAB 对总体均值、方差进行估计。

3. 学习用MATLAB 处理假设检验的相关问题。

4. 解决“引”中的实际问题。

3 实验内容1.使用MATLAB 对样本数据进行处理MATLAB 提供了若干对数据进行统计分析的命令，这些命令作用到一个矩阵上会对各列分别作用，得到一个行向量，现将这些命令列举如下：max 最大分量； mean 平均值； std 标准差； sum 分量和； product 分量积； cumsum 元素累和； min 最小分量； median 中位数； sort 按不增次序排序； hist 直方图； diff 差分函数； cumprod 元素累计积此外，命令corrcoef计算相关系数矩阵，格式为R=corrcoef(X),X为输入矩阵，它的行元素为观测值，列元素为变量，返回相关系数矩阵R，矩阵R的元素为R(i,j);命令cov计算协方差矩阵，格式为C=cov(X)，X若为单个向量，cov(X)返回包含方差的标量；X若为矩阵，X的每一列表示一个变量而行元素为观测值。

三、教学重难点和教学设想
（一）教学重难点
1.重点：理解频率的概念，掌握利用频率估计概率的方法。
2.难点：运用频率稳定性定理，从大量重复实验中总结出事件发生的概率。
（二）教学设想
1.创设情境，导入新课
通过生活中的实例，如彩票中奖概率、天气预报准确性等，引出频率估计概率的概念，激发学生学习兴趣。
2.自主探究，合作交流
学生分组讨论后，我会让每组代表分享他们的实验方案和讨论成果，其他组的学生进行评价和补充。
（四）课堂练习
为了巩固所学知识，我会设计以下课堂练习：
1.请学生完成教材上的练习题，运用频率估计概率。
2.结合生活中的实例，让学生自己设计实验，利用频率估计概率。
在学生完成练习题的过程中，我会巡回指导，及时解答他们的问题，帮助他们掌握频率估计概率的方法。
四、教学内容与个与学生生活密切相关的实例来导入新课。例如，我会询问学生：“大家有没有听说过彩票？有没有想过中奖的概率是多少？”通过这个问题，引导学生思考概率的实际意义。接着，我会拿出事先准备好的彩票，告诉学生：“根据统计数据，这种彩票的中奖概率是1%。那么，我们如何通过实验来估计这个概率呢？”这样，就很自然地引出了频率估计概率的概念。
分组进行实验或调查，收集数据，引导学生运用频率来估计概率。在此过程中，教师巡回指导，帮助学生解决遇到的问题。
3.总结规律，提炼方法
通过分析实验结果，引导学生发现频率稳定性定理，并运用定理来估计事件的概率。
4.案例分析，巩固应用
结合实际问题，让学生运用所学知识解决问题，提高学生的应用能力。
5.课堂小结，反馈评价
九年级数学上册高效课堂（人教版）25.3用频率估计概率（第2课时）教学设计
一、教学目标

解： (1 )由概率的意义可得，n＋n 2＝13，解得 n＝1， 检验，n＝1 是原方程的根，且符合题意， ∴n 的值为 1.
(2)用列表法表示所有可能出现的结果情况如下：
第1球 第2球
黑1
黑2
白
黑1
黑 1 黑 1 黑 2 黑 1 白黑 1
黑2
黑 1 黑 2 黑 2 黑 2 白黑 2
白
黑 1 白 黑 2 白 白白
(1)从π的小数部分随机取出一个数字，估计数字是 6 的概率为________； (2)某校进行校园文化建设，拟从以上 4 位科学家的画像中随机选用 2 幅， 求其中有一幅是祖冲之的概率．(用画树状图或列表方法求解)
解：(1)110.
(2)画树状图如图所示：
∵共有 12 种等可能的结果，其中有一幅是祖冲之的画像有 6 种情况． ∴P(其中有一幅是祖冲之)＝162＝12.
重难点：用列表法或画树状图法求概率 (2021·盐城)圆周率π是无限不循环小数．历史上，祖冲之、刘徽、
韦达、欧拉等数学家都对π有过深入的研究．目前，超级计算机已计算 出π的小数部分超过 31.4 万亿位．有学者发现，随着π小数部分位数的 增加，0～9 这 10 个数字出现的频率趋于稳定接近相同．
解：(1)抽取的学生人数为：60÷0.6＝100(人)，∴c＝100， ∴a＝100－60－10－5＝25，b＝10÷100＝0.1， 故答案为：25；0.1；100.
(2)补全条形统计图所示．
(3)估计测试成绩等级在合格以上(包括合格)的学生约有人数为： 1 600×(0.6＋0.25＋0.1)＝1 520(人)． (4)画树状图如图．
所得数据绘制成如下不完整的统计图表：
等级 频数(人数) 频率

一、实验目的1. 了解概率数学的基本概念和原理。

2. 掌握概率数学在现实生活中的应用。

3. 培养学生的实验操作能力和数据分析能力。

二、实验内容1. 抛掷硬币实验2. 抛掷骰子实验3. 箱子抽球实验4. 概率计算与应用三、实验器材1. 硬币一枚2. 骰子一个3. 箱子一个4. 球若干5. 记录表四、实验步骤1. 抛掷硬币实验（1）将硬币抛掷10次，记录正面朝上和反面朝上的次数。

（2）计算正面朝上和反面朝上的概率。

（3）分析实验结果，验证概率理论。

2. 抛掷骰子实验（1）将骰子抛掷10次，记录每个面出现的次数。

（2）计算每个面出现的概率。

（3）分析实验结果，验证概率理论。

3. 箱子抽球实验（1）将不同颜色的球放入箱子中，共5个球，其中红球2个，蓝球2个，黄球1个。

（2）从箱子中随机抽取球，记录抽取结果。

（3）计算每种颜色球被抽中的概率。

（4）分析实验结果，验证概率理论。

4. 概率计算与应用（1）根据实验结果，计算每种情况的概率。

（2）分析概率在现实生活中的应用，如彩票、保险等。

五、实验结果与分析1. 抛掷硬币实验实验结果显示，正面朝上的次数为5次，反面朝上的次数为5次。

计算概率为：P(正面朝上) = 5/10 = 0.5P(反面朝上) = 5/10 = 0.5实验结果与概率理论相符。

2. 抛掷骰子实验实验结果显示，每个面出现的次数如下：1面1次，2面1次，3面1次，4面1次，5面1次，6面1次。

计算概率为：P(1面) = 1/10 = 0.1P(2面) = 1/10 = 0.1P(3面) = 1/10 = 0.1P(4面) = 1/10 = 0.1P(5面) = 1/10 = 0.1P(6面) = 1/10 = 0.1实验结果与概率理论相符。

3. 箱子抽球实验实验结果显示，红球被抽中的次数为2次，蓝球被抽中的次数为2次，黄球被抽中的次数为1次。

计算概率为：P(红球) = 2/5 = 0.4P(蓝球) = 2/5 = 0.4P(黄球) = 1/5 = 0.2实验结果与概率理论相符。