第4章 平面一般力系

第四章平面一般力系平面一般力系是静力学的重点。

前面讨论的平面汇交力系和平面力偶系是平面一般力系的特殊情况，它们为学习本章打下基础。

平面一般力系的平衡问题在工程中经常遇到，又是学习材料力学、结构力学部分的基础。

因此，切实掌握好本章内容是学好本课程的关键。

一、内容提要（一）平面一般力系向任一点的简化1. 简化依据力的平移定理当一个力平行移动时，必须附加一个力偶才能与原力等效，附加力偶的力偶矩等于原力对新作用点的矩。

2. 简化方法与初始结果3.简化的最后结果或者是一个力，或者是一个力偶，或者平衡。

熟悉平衡方程各种形式的目的，主要用来求解平衡问题的未知量。

在求解单个物体和物体系统的平衡问题中，首先要确实掌握单个物体的平衡问题。

解决好单个物体平衡问题的关键，在于对物体进行受力分析，正确地画出受力图。

求解物体系统的平衡问题，就是计算出物体系统的内、外约束反力。

解决问题的关键在于恰当地选取研究对象，一般有两种选取的方法：1．先取整个物体系统作为研究对象，求得某些未知量；再取其中某部分物体（一个物体或几个物体的组合）作为研究对象，求出其他未知量。

2．先取某部分物体作为研究对象，再取其他部分物体或整体作为研究对象，逐步求得所有的未知量。

不论取整个物体系统或是系统中某一部分作为研究对象，都可根据研究对象所受的力系的类别列出相应的平衡方程去求解未知量。

（四）考虑摩擦时物体的平衡问题学习这一部分内容时，必须掌握摩擦力的特点。

摩擦力的特点以其大小和方向两方面反映。

摩擦力的大小随主动力的变化而变化，但又不能随主动力的增大而无限度地增大。

根据两物体间相对滑动或相对滑动趋势的不同情况，摩擦力的大小有以下几种可能。

1、当一个物体相对另一个物体静止且没有滑动的趋势时，两物体间不产生摩擦力。

2、当一个物体相对于另一个物体有滑动趋势，但仍保持静止时，两物体间产生静摩擦力，摩擦力的大小由平衡条件确定。

3、当一个物体相对于另一个物体即将滑动而处于临界平衡状态时，两物体间的静摩擦力达到最大值F max=fF N。

平面一般力系我们生活在一个相对独立的系统之中，宇宙万物有机地联系在一起，形成了一个整体。

然而这种整体性并非是“固定不变”的，也有破碎的时候，例如发生于地球的小行星撞击。

面对这样的事件，唯一可以采取的态度就是竭尽全力去防止或减缓其危害。

我们知道平面力系是由两个大小相等方向相反的分量构成，所以，我们需要建立一个坐标系，用它来表示这两个分量之间的关系，这样做的好处是可以避免复杂的几何图形计算，提高运算速度，并且这种关系也适合用代数式进行表达，从而使问题更加简单化。

我们把坐标系叫做原点O，并称x轴与y轴分别为x轴与y轴，这就是我们通常所说的x， y轴。

一般情况下，将物体放置在坐标系内，只要其所在的平面保持水平，那么这个物体受到的力都将沿着x轴或y轴方向作用。

如果物体处在某个坐标系内的任意位置，只要它所在的平面不与坐标系原点重合，它受到的力都将沿着x轴或y轴方向作用。

----摘自教科书正文----摘自教科书正文，的确，因为考虑问题方便，物理学家们都普遍认为建立坐标系是有必要的。

但是，我们看到，这样一来，很多物理问题的实质被掩盖住了。

事实上，这些研究工作并没有带来多少实际应用价值，因为真正的难题都隐藏在坐标系里面，而人们却往往错误地认为找出坐标系才是解决问题的根本。

真正值得注意的问题是，为什么坐标系的选择会直接影响物理问题的解决呢？从力学的角度来讲，对于理想化的物体而言，其运动状态和力都是与坐标系的选择无关的，比如一个物体静止在坐标系内，不管在其哪一个位置，对于受力的分析，仅仅需要分析其质心在哪个坐标系内就可以了。

----摘自教科书正文，显然这是不可能的。

可是，既然坐标系是如此重要，为什么还会有那么多的力学家为了追求坐标系的完美而忽视了其他更为基本的力学规律呢？是什么阻碍了科学家们对这个问题的思考呢？一言以蔽之，就是人们对物体的运动状态还没有给予足够的重视，尽管这个问题已经成为物理学的主流研究方向之一。

一旦我们开始研究物体在空间内的运动，或者当物体随着时间的推移而发生变化时，坐标系所带来的麻烦将成倍增长。

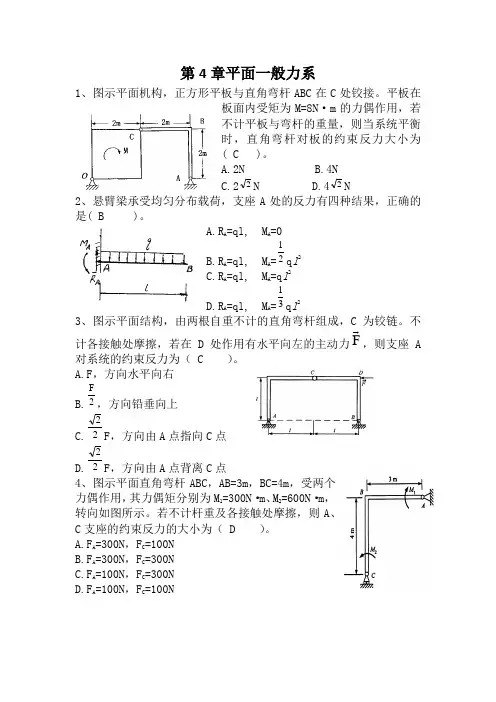
第4章平面一般力系1、图示平面机构，正方形平板与直角弯杆ABC 在C 处铰接。

平板在板面内受矩为M=8N ·m 的力偶作用，若不计平板与弯杆的重量，则当系统平衡时，直角弯杆对板的约束反力大小为( C )。

A.2N B.4N C.2N D.4N 2、悬臂梁承受均匀分布载荷，支座A 处的反力有四种结果，正确的是( B )。

A.R A =ql, M A =0B.R A =ql, M A =q l 2C.R A =ql, M A =q l 2D.R A =ql, M A =q l 23、图示平面结构，由两根自重不计的直角弯杆组成，C 为铰链。

不计各接触处摩擦，若在D处作用有水平向左的主动力，则支座A对系统的约束反力为（ C ）。

A.F ，方向水平向右B.，方向铅垂向上C.F ，方向由A 点指向C 点D.F ，方向由A 点背离C 点4、图示平面直角弯杆ABC ，AB=3m ，BC=4m ，受两个力偶作用，其力偶矩分别为M 1=300N ·m 、M 2=600N ·m ，转向如图所示。

若不计杆重及各接触处摩擦，则A 、C 支座的约束反力的大小为（D ）。

A.F A =300N ，F C =100NB.F A =300N ，F C =300NC.F A =100N ，F C =300ND.F A =100N ，F C =100N222131F 2F22225、力系向某点平移的结果，可以得到( D )。

A.一个主矢量B.一个主矩C.一个合力D.一个主矢量和一个主矩6、平面一般力系向一点O简化结果，得到一个主矢量R′和一个主矩m0，下列四种情况，属于平衡的应是( B )。

A.R′≠0 m0=0B.R′=0 m0=0C.R′≠0 m0≠0D.R′=0 m0≠07、以下有关刚体的四种说法，正确的是( D )。

A.处于平衡的物体都可视为刚体B.变形小的物体都可视为刚体C.自由飞行的物体都可视为刚体D.在外力作用下，大小和形状看作不变的物体是刚体8、力的作用线都相互平行的平面力系称（D ）力系。