第七章从动件规律与凸轮廓线
- 格式:doc
- 大小:1.14 MB
- 文档页数:11



凸轮轮廓及其综合1. 凸轮机构从动件的位移凸轮是把一种运动转化为另一种运动的装置。
凸轮的廓线和从动件一起实现运动形式的转换。
凸轮通常是为定轴转动,凸轮旋转运动可被转化成摆动、直线运动或是两者的结合。
凸轮机构设计的内容之一是凸轮廓线的设计。
定义一个凸轮基圆r b 作为最小的圆周半径。
从动件的运动方程如下:L(ϕ)=r b +s(ϕ)设凸轮的推程运动角和回程运动角均为β,从动件的运动规律均为正弦加速度运动规律,则有:s(ϕ)=h(βϕ-π21sin(2πϕ/β)) 0≤ϕ≤β s(ϕ)=h -h(ββϕ--π21sin(2π(ϕ-β/β)) β≤ϕ≤2β s(ϕ)=0 2β≤ϕ≤2π上式是从动件的位移,h 是从动件的最大位移,并且0≤β≤π。
如果假设凸轮的旋转速度ω=d ϕ/dt 是个常量,则速度υ、加速度a 和瞬时加速度j (加速度对时间求异)分别如下:速度:υ(ϕ)=βωh (1-cos(2πϕ/β)) 0≤ϕ≤β υ(ϕ)=-βωh (1-cos(2π(ϕ-β)/β) β≤ϕ≤2β υ(ϕ)=0 2β≤ϕ≤2π加速度:a(ϕ)=222βπωhsin(2πϕ/β)) 0≤ϕ≤βa(ϕ)=-222βπωhsin(2π(ϕ-β)/β) β≤ϕ≤2βa(ϕ)=0 2β≤ϕ≤2π瞬时加速度:j(ϕ)=3324βωπhcos(2πϕ/β)) 0≤ϕ≤βj(ϕ)=-3324βωπhcos(2π(ϕ-β)/β) β≤ϕ≤2βj(ϕ)=0 2β≤ϕ≤2π定义无量纲位移S=s/h 、无量纲速度V=υ/ωh 、无量纲加速度A=a/h ω3和无量纲瞬时加速度J=j/h ω3。
若β=60°,则如下程序可以对以上各个量进行计算。
beta=60*pi/180;phi=linspace(0,beta,40);phi2=[beta+phi];ph=[phi phi2]*180/pi ;arg=2*pi*phi/beta ;arg2=2*pi*(phi2-beta)/beta ;s=[phi/beta-sin(arg)/2/pi 1-(arg2-sin(arg2))/2/pi];v=[(1-cos(arg))/beta-(1-cos(arg2))/beta];a=[2*pi/beta^2*sin(arg)2*pi/beta^2*sin(arg2)];j=[4*pi^2/beta^3*cos(arg)4*pi^2/beta^3*cos(arg2)]:subplot(2,2,1)plot(ph,s,ˊK ˊ)xlabel(ˊCam angle(degrees)ˊ)ylabel(ˊDisplacement(S)ˊ)g=axis ;g(2)=120;axis(g)subplot(2,2,2)plot(ph,v,ˊk ˊ,[0 120],[0 0],ˊk--ˊ)xlabel(ˊCam angle(degrees)ˊ)ylabel(ˊVelocity(V)ˊ)g=axis ;g(2)=120;axis(g)subplot(2,2,3)plot(ph,a,ˊk ˊ,[0 120],[0 0],ˊk--ˊ)xlabel(ˊCam angle(degrees)ˊ)ylabel(ˊAcceleration(A)ˊ)g=axis;g(2)=120;axis(g)subplot(2,2,4)plot(ph,j,ˊkˊ,[0 120],[0 0],ˊk--ˊ)xlabel(ˊCam angle(degrees)ˊ)ylabel(ˊJerk(J)ˊ)g=axis;g(2)=120;axis(g)2 平底盘形从动作参考下图得到如下关系:在(x,y)坐标系中,凸轮轮廓的坐标为Rx和Ry,刀具的坐标为Cx和Cy:Rx=Rcos( θ+ϕ) Ry=Rsin( θ+ϕ)C x=Ccos( γ+ϕ) C y=Ccos( γ+ϕ)其中, R=θcos L θ=arctan ⎪⎪⎭⎫ ⎝⎛ϕd dL L 1 c=γγcos c L + γ=arctan ⎪⎪⎭⎫ ⎝⎛+c L d dL γϕ/ r c 是刀具的半径,且dL/d ϕ=V(ϕ)/ω。

说出凸轮机构从动件常用运动规律1. 引言1.1 概述凸轮机构是一种常见的运动传动装置,通过凸轮和从动件的配合实现不同运动规律的转换。
凸轮机构被广泛应用于各种机械设备中,如汽车发动机、工业机械等领域。
了解凸轮机构从动件的常用运动规律对于理解其工作原理以及设计和优化具有重要意义。
本文将重点介绍凸轮机构从动件常用的三种运动规律,即正圆运动规律、椭圆运动规律和抛物线运动规律。
通过详细讲解每种运动规律的原理和特点,结合相关的应用案例,旨在帮助读者全面了解这些常见的凸轮机构从动件运动规律。
1.2 文章结构本文分为五个部分进行阐述。
首先,在引言部分对凸轮机构进行了概述,并说明了文章内容和结构。
接下来,在第二部分中简要介绍了凸轮机构的定义与分类以及基本组成部分,同时列举了该装置在各个应用领域中的实际应用。
然后,在第三部分中简要描述了凸轮机构从动件常用的三种运动规律,即正圆运动规律、椭圆运动规律和抛物线运动规律。
在第四部分中,将分别对这些从动件的常用运动规律进行详细解析,并通过实际应用案例加深理解。
最后,在结论与展望部分总结文章的主要内容,并对未来凸轮机构研究方向进行展望。
1.3 目的本文旨在介绍凸轮机构从动件常用的运动规律,包括正圆、椭圆和抛物线三种类型。
通过阐述每一种运动规律的原理和特点,读者能够对凸轮机构从动件的工作原理有更深入的理解,并能够应用于具体的工程设计和优化中。
同时,通过引入实际案例,希望读者能够更好地理解这些运动规律在实际中的应用价值。
2. 凸轮机构简介:2.1 定义与分类:凸轮机构是一种常见的机械传动装置,由凸轮和从动件组成。
凸轮是一个具有非圆周运动的特殊零件,通过转动或移动凸轮使得从动件产生特定的运动规律。
根据凸轮曲线形状和运动规律的不同,凸轮机构可以分为三类主要类型:正圆轨迹型、椭圆轨迹型和抛物线轨迹型。
2.2 基本组成部分:典型的凸轮机构包括凸轮、滑块、连接杆、曲柄等组成部分。
其中,凸轮为核心部件,其曲线形状决定了从动件的运动规律。

凸轮机构中常用的从动件运动规律
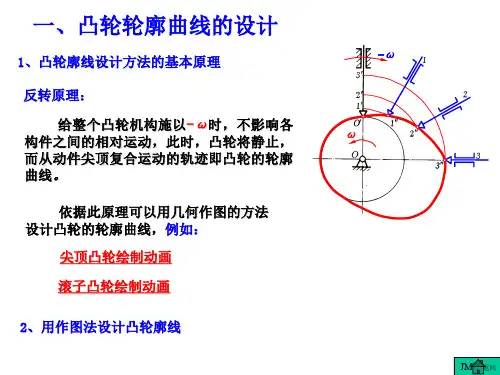
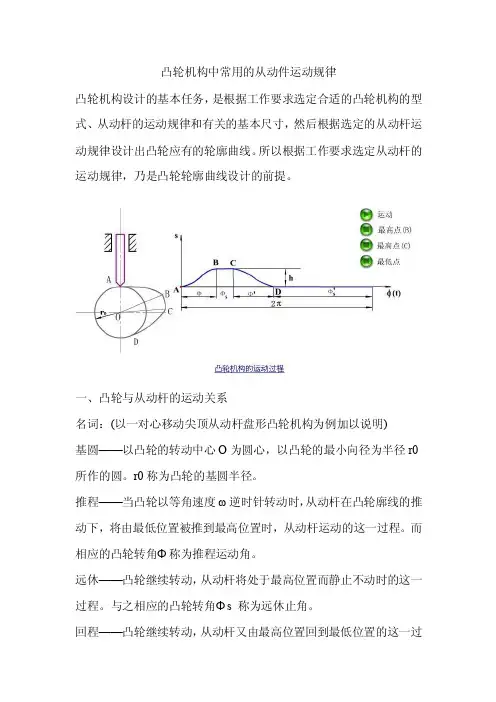
凸轮机构设计的基本任务,是根据工作要求选定合适的凸轮机构的型式、从动杆的运动规律和有关的基本尺寸,然后根据选定的从动杆运动规律设计出凸轮应有的轮廓曲线。
所以根据工作要求选定从动杆的运动规律,乃是凸轮轮廓曲线设计的前提。
一、凸轮与从动杆的运动关系
名词:(以一对心移动尖顶从动杆盘形凸轮机构为例加以说明)
基圆——以凸轮的转动中心O为圆心,以凸轮的最小向径为半径r0所作的圆。
r0称为凸轮的基圆半径。
推程——当凸轮以等角速度ω逆时针转动时,从动杆在凸轮廓线的推动下,将由最低位置被推到最高位置时,从动杆运动的这一过程。
而相应的凸轮转角Φ称为推程运动角。
远休——凸轮继续转动,从动杆将处于最高位置而静止不动时的这一过程。
与之相应的凸轮转角Φs 称为远休止角。
回程——凸轮继续转动,从动杆又由最高位置回到最低位置的这一过
程。
相应的凸轮转角Φ'称为回程运动角。
近休——当凸轮转过角Φs'时,从动杆与凸轮廓线上向径最小的一段圆弧接触,而将处在最低位置静止不动的这一过程。
Φs'称为近休止角。
行程——从动杆在推程或回程中移动的距离h 。
位移线图——描述位移s与凸轮转角φ之间关系的图形。
二、从动件的常用运动规律
所谓从动杆的运动规律是指从动杆在运动时,其位移s、速度v 和加速度a 随时间t变化的规律。
又因凸轮一般为等速运动,即其转角φ与时间t成正比,所以从动杆的运动规律更常表示为从动杆的运动参数随凸轮转角φ变化的规律。

033凸轮廓线设计讲解凸轮轮廓线设计是机械设计中的一项重要内容,它关系到机械运动的性能和精度。
凸轮是一种圆柱体,其轮廓线可以是各种形状,根据具体的机械要求选择合适的轮廓线形状,可以实现各种不同的运动轨迹和作用。
凸轮的主要作用是将一个旋转的运动转换为直线运动或者其他非旋转运动。
其中,凸轮的轮廓线起着关键作用,通过合理的轮廓线设计,可以实现复杂的运动曲线,满足机械系统对于速度、加速度、位置和时间的要求。
凸轮的轮廓线设计需要综合考虑以下几个因素:1.运动要求:根据机械系统的工作要求,确定凸轮的运动参数,如旋转速度、加速度、运动角度等。
这些参数将直接影响到凸轮的轮廓线形状。
2.减速段、稳定段和加速段的划分:根据机械系统的工作要求,将凸轮的运动轨迹分为减速段、稳定段和加速段,以控制运动的速度和加速度。
3.凸轮的基本轮廓线形状:凸轮的基本轮廓线可以是圆弧、椭圆、折线等形状。
根据实际需要选择合适的轮廓线形状,以满足机械系统的运动要求。
4.凸轮的修形:凸轮的轮廓线形状常常需要进行修形,以满足更高的运动精度和要求。
修形常常通过添加或减去一些小的尺寸来实现,比如在圆弧上添加挤压或切割。
5.轮廓线的光滑度:凸轮的轮廓线要求光滑过渡,以减少运动中的冲击和振动。
因此,在设计中需要注意轮廓线的连续性和光滑度。
6.运动的匀速性:在设计凸轮轮廓线时,需要注意运动的匀速性,尽量减少速度的突变和波动,保证运动的稳定性。
凸轮轮廓线设计的目的是实现机械系统的预期功能和性能,因此,为了提高设计效率和准确度,通常采用计算机辅助设计软件来进行轮廓线设计。
在设计过程中,可以通过分析和仿真来验证设计的合理性,以及对于不同的设计要求,可以通过调整轮廓线形状来满足要求。
简而言之,凸轮轮廓线设计是机械设计中的重要内容,需要综合考虑运动要求、轮廓线形状、修形、连续性和光滑度等因素。
通过合理设计的凸轮轮廓线,可以实现复杂的运动曲线,满足机械系统对于速度、加速度、位置和时间的要求。

凸轮机构工作过程和从动件运动规律凸轮机构是一种常见的传动装置,主要用于将转动的轴向运动转变为具有特定规律的径向或直线运动。
它由凸轮、从动件和固定件组成。
在凸轮机构中,凸轮是主动件,从动件是被动件。
凸轮可以是一个圆柱体、椭圆体或者一个不规则形状。
在工作过程中,凸轮通过旋转或者来回运动,驱动从动件进行规律的运动。
凸轮的外形决定了从动件运动的规律,可以实现各种复杂的运动轨迹。
从动件通常是由连杆、滑块等组成的。
其运动规律受到凸轮形状、连接件长度等因素的影响。
常见的凸轮运动规律有以下几种:1.简谐运动:当凸轮的形状为圆形或者椭圆形时,从动件的运动规律呈现出简谐振动的特点,运动轨迹为直线或者椭圆。
2.往复运动:当凸轮的形状为沿轴向的不规则形状时,从动件的运动呈现出往复运动的特点。
这种往复运动可以是直线运动,也可以是曲线运动,具体取决于凸轮的形状。
3.非往复运动:有些凸轮机构的从动件的运动规律是非往复的,从动件的运动轨迹可以是圆弧、摆线等。
这种运动规律可以实现复杂的曲线运动,并广泛应用于工业生产中的各种机械装置中。
凸轮机构的工作过程一般可以分为以下几个步骤:1.凸轮旋转或者运动:凸轮通过外力的作用,开始旋转或者运动。
2.凸轮对从动件的驱动:当凸轮旋转或者运动时,凸轮表面的凸点或者凹槽与从动件的连接件接触,通过摩擦力或者其他力的作用,将动力传递给从动件。
3.从动件的运动:从动件根据凸轮的形状和运动轨迹,进行规律的运动。
从动件可以是连杆、滑块等,在凸轮的作用下,完成各种不同的运动方式。
4.固定件的作用:固定件用于支撑和固定凸轮和从动件,保证凸轮机构的稳定运行。
固定件可以是机架、底座等。
凸轮机构的工作过程和从动件的运动规律是通过优化凸轮形状和连接件长度来实现的。
只有在合理设计和优化的情况下,凸轮机构才能实现稳定可靠的工作,并满足特定的运动要求。
总之,凸轮机构的工作过程主要包括凸轮的运动和从动件的运动,依靠凸轮的形状和运动规律来实现不同的运动效果。
凸轮从动件基本运动规律曲线凸轮从动件基本运动规律曲线一、引言在机械学中,凸轮从动件是一种常见的机械传动装置,它通过凸轮的曲线运动驱动从动件做往复或者旋转运动。
而凸轮的曲线运动规律被称为凸轮从动件的基本运动规律曲线。
本文将深入探讨凸轮从动件的基本运动规律曲线,包括其定义、分类、特点、应用等方面,以便读者更深入地理解凸轮从动件的原理和运动规律。
二、基本概念1. 凸轮从动件凸轮从动件是一种机械传动装置,通过凸轮的曲线运动来驱动从动件做往复或者旋转运动。
它广泛应用于各种机械设备中,如汽车发动机、工业机械等。
凸轮从动件由凸轮和从动件两部分组成,其中凸轮的曲线运动是其基本运动规律曲线的核心。
2. 基本运动规律曲线凸轮从动件的基本运动规律曲线是指凸轮上的曲线运动规律,它决定了从动件的运动方式和特点。
基本运动规律曲线一般包括圆形、椭圆形、抛物线形、正弦曲线形等多种类型,每种类型都具有不同的特点和适用范围。
三、基本运动规律曲线的分类1. 圆形曲线圆形曲线是凸轮上最简单的一种曲线形状,其路径为圆形。
该曲线形状适用于一些简单的往复运动装置,如滚笼机构、飞机起落架等。
2. 椭圆形曲线椭圆形曲线是凸轮上的椭圆形状路径,其优点是在往复运动中有较长时间的停顿和加速阶段,适用于一些要求动作平稳的设备,如自动售货机的货道推板装置。
3. 抛物线形曲线抛物线形曲线是凸轮上的抛物线状路径,其路径具有很好的加减速性能,适用于一些要求动作快速的装置,如车床进给机构、拉床加工机床等。
4. 正弦曲线形曲线正弦曲线形曲线是凸轮上的正弦曲线状路径,其路径具有周期性的特点,适用于一些需要周期性往复运动的装置,如自动打字机的纸张进给机构。
四、基本运动规律曲线的特点1. 稳定性不同类型的基本运动规律曲线具有不同的稳定性特点,圆形曲线和椭圆形曲线具有较好的稳定性,而抛物线形曲线和正弦曲线形曲线的稳定性较差。
2. 加减速性抛物线形曲线和正弦曲线形曲线具有较好的加减速性能,而圆形曲线和椭圆形曲线的加减速性能较差。
凸轮从动件基本运动规律 (有关凸轮机构的部分讲义)1. 多项式类运动规律多项式运动规律的一般形式:其中,(1) 一次多项式运动规律(等速运动规律) a. 通式:b. 推程阶段边界条件:带入通式,可解出:c. 回程阶段边界条件:。
带入通式,可解出:Osv图1 等速运动规律(2) 二次多项式运动规律(等加速等减速运动规律) a. 通式:其中,b. 推程前半阶段(等加速阶段)边界条件:带入通式,可解出:;推程后半阶段(等减速阶段)边界条件:带入通式,可解出:;c. 回程前半阶段(等加速阶段)边界条件:带入通式,可解出:;回程后半阶段(等减速阶段)边界条件:带入通式,可解出:;Os图2 等加速等减速运动规律(3) 五次多项式运动规律 a.通式:其中,b. 推程阶段边界条件:带入通式,可解出:;c. 回程阶段边界条件:带入通式,可解出:;Os图3 五次多项式运动规律2. 三角函数类运动规律(1) 简谐运动规律(余弦加速度运动规律) a.通式:其中,b. 推程阶段边界条件:带入通式,可解出:; k=c. 回程阶段边界条件:带入通式,可解出:; k=Os图 4 简谐运动规律(2) 摆线运动规律(正弦加速度运动规律) a.通式:其中,b. 推程阶段边界条件:带入通式,可解出:; k=c. 回程阶段边界条件:带入通式,可解出:; k=Os图5 摆线运动规律有关简谐运动简谐运动(或简谐振动、谐振)既是最基本也是最简单的一种机械振动。
当某物体进行简谐运动时,物体所受的力跟位移成正比,并且力总是指向平衡位置。
有关摆线摆线(Cycloid ):当一个圆沿一条直线运动时,圆边界上一定点所形成的轨迹。
摆线时最速降线问题的解。
1. 摆线研究历史摆线的研究最初开始于Nicholas of Cusa ,之后梅森 (MarinMersenne) 也有针对摆线的研究。
1599年伽利略为摆线命名。
1634年G.P. de Roberval 指出摆线下方的面积是生成它的圆面积的三倍。
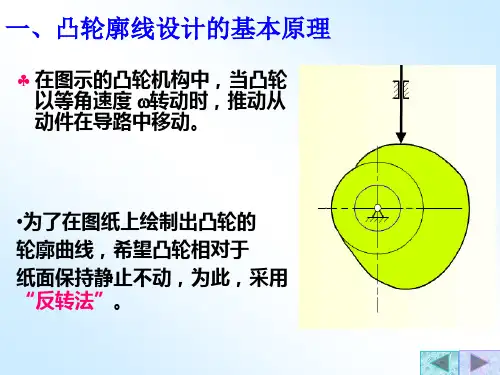
理论轮廓决定运动规律
凸轮机构从动件的运动规律是由凸轮的轮廓决定的。
凸轮是一个具有曲线轮廓或凹槽的构件,一般为主动件,作等速回转运动或往复直线运动。
凸轮从动件的运动规律取决于凸轮的轮廓线或凹槽的形状,凸轮可将连续的旋转运动转化为往复的直线运动,可以实现复杂的运动规律。
理论轮廓线和实际廓线是等距线,从动件的运动规律是由理论廓线决定的,滚子与实际廓线的接触点并不一定总与直动从动件的轨迹重合,所以滚子从动件要按照理论轮廓线画压力角。
理论廓线上任意一点的法向方向上与工作廓线相差一个滚子半径.凸轮机构是由凸轮,从动件和机架三个基本构件组成的高副机构。
凸轮是一个具有曲线轮廓或凹槽的构件,一般为主动件,作等速回转运动或往复直线运动。
与凸轮轮廓接触,并传递动力和实现预定的运动规律的构件,一般做往复直线运动或摆动,称为从动件。
凸轮机构在应用中的基本特点在于能使从动件获得较复杂的运动规律。
因为从动件的运动规律取决于凸轮轮廓曲线,所以在应用时,只要根据从动件的运动规律来设计凸轮的轮廓曲线就可以了。
凸轮机构广泛应用于各种自动机械、仪器和操纵控制装置。
凸轮机构之所以得到如此广泛的应用,主要是由于凸轮机构可以实现各种复杂的运动要求,而且结构简单、紧凑。
凸轮从动件基本运动规律
(有关凸轮机构的部分讲义)
1. 多项式类运动规律
多项式运动规律的一般形式:
其中,
(1) 一次多项式运动规律(等速运动规律) a. 通式:
b. 推程阶段边界条件:
带入通式,可解出:
c. 回程阶段边界条件:。
带入通式,可解出:
O
s φ
B
A
Φ
Φ‘
h
v
O
φ
O
φ
a ∞
∞
-∞
图1 等速运动规律
(2) 二次多项式运动规律(等加速等减速运动规律)
a. 通式:
其中,
b. 推程前半阶段(等加速阶段)边界条件:
带入通式,可解出:
;
推程后半阶段(等减速阶段)边界条件:
带入通式,可解出:
;
c. 回程前半阶段(等加速阶段)边界条件:
带入通式,可解出:
;
回程后半阶段(等减速阶段)边界条件:
带入通式,可解出:
;
O
s
φ
B
A
Φ
Φ‘
Φ/2h/2
v
φ
a
φ
图2 等加速等减速运动规律
(3) 五次多项式运动规律 a.通式:
其中,
b. 推程阶段边界条件:
带入通式,可解出:
;
c. 回程阶段边界条件:
带入通式,可解出:
;
O
s φ
B
A
Φ
Φ‘
h
O
v
φ
O
a
φ
图3 五次多项式运动规律
2. 三角函数类运动规律
(1) 简谐运动规律(余弦加速度运动规律) a.通式:
其中,
b. 推程阶段边界条件:
带入通式,可解出:
; k=
c. 回程阶段边界条件:
带入通式,可解出:
; k=
O
s φ
B
A
Φ
Φ‘
h
O
v
φ
O
a
φ
图4 简谐运动规律
(2) 摆线运动规律(正弦加速度运动规律) a.通式:
其中,
b. 推程阶段边界条件:
带入通式,可解出:
; k=
c. 回程阶段边界条件:
带入通式,可解出:
; k=
O
s φ
B
A
Φ
Φ‘
v
φ
a
φ
图5 摆线运动规律
有关简谐运动
简谐运动(或简谐振动、谐振)既是最基本也是最简单的一种机械振动。
当某物体进行简谐运动时,物体所受的力跟位移成正比,并且力总是指向平衡位置。
有关摆线
摆线(Cycloid ):当一个圆沿一条直线运动时,圆边界上一定点所形成的轨迹。
摆线时最速降线问题的解。
1. 摆线研究历史
摆线的研究最初开始于Nicholas of Cusa ,之后梅森 (Marin Mersenne) 也有针对摆线的研究。
1599年伽利略为摆线命名。
1634年G.P. de Roberval 指出摆线下方的面积是生成它的圆面积的三倍。
1658年克里斯多佛·雷恩也向人们指出摆线的长度是生成它的圆直径的四倍。
在这一时期,伴随着许多发现,也出现了众多有关发现权的争议,甚至抹杀他人工作的现象,而因此摆线也被人们称作“几何学中的海伦”(The Helen of Geometers)。
2. 最速降线问题
在重力作用且忽略摩擦力的情况下,一个质点在一点A 以速率为零开始,沿某条曲线,去到一点不高于A 的B ,怎样的曲线能令所需的时间最短呢?这就是最速降线问题,又称最短时间问题、最速落径问题。
这条线段就是摆线,可以用
变分学求证。
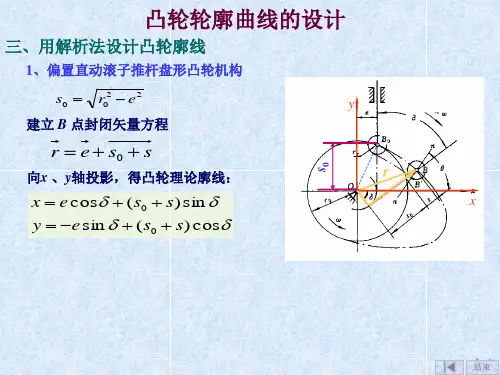
凸轮轮廓曲线的设计
一、尖顶直动从动件凸轮轮廓曲线
s r r +=0
又:θj re r = (蓝色)
)(000ϕ-=j e r r , )2(000000
ϕπ
θ-==j j e r e r r
)2(ϕπ
-=j se s 00cos r e =θ, 0102
cos
ϕπθ-==-r e
)2
()
(002
ϕπ
ϕϕ
θπ---+=j j j se
e
r re
尖顶直动从动件凸轮的实际廓线:
θcos =x )cos()cos(2020ϕϕϕπ
π-+--=s r ϕϕϕsin )sin(00s r ++=
θsin =y )sin()sin(2020ϕϕϕπ
π-+--=s r ϕϕϕcos )cos(
00s r ++=
二、滚子直动从动件凸轮轮廓曲线
对于滚子从动件凸轮机构,可将尖顶从动件的凸轮廓线看成理论廓线,滚子从动件凸轮
的实际廓线是圆心位于理论廓线上的一系列滚子圆簇的包络线,包络线有两条,分别对应于外凸轮和内凸轮的实际廓线。
(参见课本P123)
⎪⎩⎪⎨⎧=∂∂=0),,(0),,(λλ
λy x F y x F 包络原理:上式是曲线簇,下式为包络条件。
2
22)()(r r y Y x X =++- => ⎪⎩
⎪⎨⎧=∂∂=-++-=0
),,(0
)()(),,(222ϕϕϕY X F r y Y x X Y X F r
实际廓线:⎪⎪⎪⎪⎪
⎩
⎪
⎪⎪⎪⎪⎨⎧
+=+±=2222)()()()(ϕϕϕϕϕϕd dy
d dx d dx
r
y Y d dy d dx d dy r x X r r
上面一组符号,内包络,外凸轮; 下面一组符号,外包络,内凸轮; X ,Y 为包络线的坐标
三、平底直动从动件凸轮轮廓曲线
方法一:
b s r r ++=0
)0()(02
)(ϕϕθ
π--++=j j j be e
s r re
(红色)
∵ϕ
ω
d ds
v
OP b =
== (P :为瞬心)
θcos =x )cos()cos()(20ϕϕϕπ-+
-+=d ds s r ϕϕ
ϕcos sin )(0d ds
s r ++= θsin =y )sin()sin()(20ϕϕϕπ-+-+=d ds s r ϕϕ
ϕsin cos )(0d ds s r -+=
方法二:包络线法
平底直线方程:
q px y +=q xtg +-=)(ϕπq x tg +⋅-=ϕ
B ''的坐标:
)(002)(ϕπ-''+=+=j B e s r s r r
∴)cos()(20ϕπ-+=''s r x B ϕsin )(0s r += )sin()(20ϕπ-+=''s r y B ϕcos )(0s r += 带入平底直线方程,得 ϕ
cos 0s
r q +=
∴平底直线簇:ϕ
ϕϕϕcos )
(sin cos 00s r x s r x tg y ++-=++
⋅-= ∴⎪⎩⎪⎨⎧=-+-==∂∂=+-+=0
cos sin 00
)(sin cos ),,(0ϕϕϕϕ
ϕϕϕd ds x y F s r x y y x F
∴ ϕϕ
ϕcos sin )(0d ds
s r x +
+= ϕϕ
ϕsin cos )(0d ds
s r y -+= 与方法一的结果相同。
四、尖顶--滚子摆动从动件凸轮轮廓曲线
l a r +=
)2
3(
)
(02
ψϕψπ
ϕθπ
----+=j j j le
ae
re (红色)
θcos =x )23cos(
)cos(02ψϕψπ
ϕπ---+-=l a )sin(sin 0ψϕψϕ++-=l a θsin =y )2
3sin()sin(02
ψϕψπ
ϕπ---+-=l a )cos(cos 0ψϕψϕ++-=l a 理论廓线: )sin(sin 0ψϕψϕ++-=l a x
)cos(cos 0ψϕψϕ++-=l a y al
r l a 2cos 2
221
0-+=-ψ
实际廓线: 2
22)()(r r y Y x X =++-
⎪⎩
⎪⎨⎧=∂∂=0
0),,(ϕϕF Y X F
与直动滚子从动件的形式相同,(ϕd dy ,ϕ
d dx
不同)。
五、平底摆动从动件凸轮轮廓曲线
b l a r ++=
)23()(02)(ψϕψπϕθπ-----+=j j j e b l ae re (红色)
θcos =x )2
3cos(
)()cos(02ψϕψπϕπ----+-=b l a θsin =y )23sin()()sin(02ψϕψπϕπ----+-=b l a )sin()(sin 0ψϕψϕ++--=b l a x
)cos(
)(cos 0ψϕψϕ++--=b l a y AP OP ⋅=⋅ψω (P :为瞬心) => ϕ
ψd d a
AP +=1
a AP OP =+ )cos(0ψψ+=AP AB
AB l b -= ϕψψψψd d a a AB l b ++-
=-=1)cos(cos 00。