七桥问题和一笔画

七桥问题与一笔画的通解（论文拟稿）在柯尼斯堡的一个公园里，有七座桥将一条河上的两座岛和两岸相连接。

当时有人提出了这么一个问题：如何一次性不重复不遗漏走完七座桥。

后来，数学家欧拉将它变成了一个一笔画问题（如图）。

从欧拉的简化图来看，似乎我们无论如何，也不能一笔画完图形。

但是，这是为什么呢?在这个图中，有ABCD 4个点，有五条线汇聚到A点，三条线汇聚到B,C,D 点，我们可以把这种有奇数条线（3条及以上）汇聚的点称为奇点，作为对应，把有偶数条线（4条及以上）汇聚的点称为偶点。

那么，我们不难发现，在任意封闭图形中，奇点的个数一定是偶数。

因为一条线定连接两个点（或重合），若存在奇数个奇点，则此图形定不符合封闭图形定义。

从一个奇点来看，若要一笔画成，则此奇点定是起笔点或停笔点。

起笔点，停笔点只有两个，所以说，奇点为两个或没有奇点的封闭图形可以一笔画。

回来看七桥问题，图中有四个奇点，以任意两个作为起笔点和落笔点，则还有两个奇点无法连接。

故七桥问题无解。

从上面总结出以下结论：■⒈凡是由偶点组成的连通图，一定可以一笔画成。

画时可以把任一偶点为起点，最后一定能以这个点为终点画完此图。

■⒉凡是只有两个奇点的连通图(其余都为偶点)，一定可以一笔画成。

画时必须把一个奇点为起点，另一个奇点为终点。

■⒊其他情况的图都不能一笔画出。

(奇点数除以二便可算出此图需几笔画成。

)我们可以把得到的结论推广到所有一笔画解法存在问题，如汉字“田”，我们观察到，它有四个奇点，故不可以一笔画。

而汉字“日”，只有两个奇点，则可以一笔画。

早在1736年，欧拉在交给彼得堡科学院的《哥尼斯堡7座桥》的论文报告中，就阐述了这种方法，也为后来的数学新分支--拓扑学的建立奠定了基础。

从这里我们可以看出，伟大的创造一开始可能并不像我们想象的那么高深莫测，仔细观察生活，我们也会有了不起的发现。

七桥问题和一笔画18世纪时，欧洲有一个风景秀丽的小城哥尼斯堡，那里有七座桥。

如图1所示：河中的小岛A与河的左岸B、右岸C各有两座桥相连结，河中两支流间的陆地D与A、B、C各有一座桥相连结。

当时哥尼斯堡的居民中流传着一道难题：一个人怎样才能一次走遍七座桥，每座桥只走过一次，最后回到出发点？大家都试图找出问题的答案，但是谁也解决不了这个问题。

图 1 图 2七桥问题引起了著名数学家欧拉（17071783）的关注。

他把具体七桥布局化归为图2所示的简单图形，于是，七桥问题就变成一个一笔画问题：怎样才能从A、B、C、D中的某一点出发，一笔画出这个简单图形（即笔不离开纸，而且a、b、c、d、e、f、g各条线只画一次不准重复），并且最后返回起点？欧拉经过研究得出的结论是：图2是不能一笔画出的图形。

这就是说，七桥问题是无解的。

这个结论是如何产生呢？请看下面的分析。

如果我们从某点出发，一笔画出了某个图形，到某一点终止，那么除起点和终点外，画笔每经过一个点一次，总有画进该点的一条线和画出该点的一条线，因此就有两条线与该点相连结。

如果画笔经过一个n次，那么就有2n条线与该点相连结。

因此，这个图形中除起点与终点外的各点，都与偶数条线相连。

如果起点和终点重合，那么这个点也与偶数条线相连；如果起点和终点是不同的两个点，那么这两个点部是与奇数条线相连的点。

综上所述，一笔画出的图形中的各点或者都是与偶数条线相连的点，或者其中只有两个点与奇数条线相连。

图2中的A点与5条线相连结，B、C、D各点各与3条线相连结，图中有4个与奇数条线相连的点，所以不论是否要求起点与终点重合，都不能一笔画出这个图形。

1736年，欧拉在圣彼得堡科学院作了一次学术报告。

在报告中，他证明了上述结论。

后来他又给出了鉴别任一图形能否一笔画出的准则，即欧拉定理。

为了介绍这个定理，我们先来看下面的预备知识：由有限条线组成的图形叫做网络，其中每条线都要求有两个不同的端点。

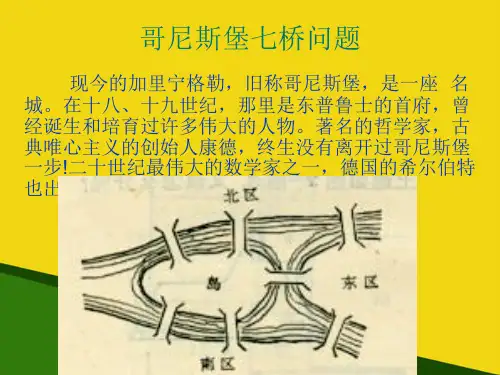
七桥问题与一笔画18世纪时，风景秀丽的欧洲小城哥尼期堡中有一条河，河的中间有两个小岛，河两岸与两岛之间共建有七座桥（图1）当时小城的居民中流传着一道难题：一个人怎样才能不重复地走过所有的七座桥，再回到出发点？这就是数学史上著名的“七桥问题”，为了解决这个问题，我们首先学习一下“一笔画”吧。

把一个图形用笔描绘一遍，笔不能离开图面，已经描过的地方不可以重复，这个图形叫做一笔画。

如图2，由A点出发先走向B点，从B点先描出圆，回到B点后，再描全矩形，这就是一个一笔画。

但图3就不是一个一笔画。

图的顶点可分为两类，奇点和偶点从某点出发的边的条数是奇数时，这样的点叫做奇点（如图3中A、B、C、D）；从某点出发的边的条数是偶数时，这样的点叫偶点（如图2中A、B）由例3我们知道并非所有的图形均可一笔画出，通过研究发现有以下三条规律。

1.凡是仅由偶点组成的图形，一定可以一笔画出，画时可以任意偶点为起点，最后仍回到这点。

2.凡是只有两个奇顶点和任意个偶顶点组成的图形，也可以一笔画出，画时必须以一个奇顶点为起点，而以另一个奇顶点为终点。

3.如果图形中的奇顶点多于两个，那么这个图就不可能一笔画出。

掌握这些结论后，我们就可以顺利的解决七桥问题，首先把被河流隔开的四块区域缩写为A、B、C、D四个点，这样七桥问题就变成了四个点间由七条线相连所成的图（图4）。

因为本图有四个奇点（A、B、C、D），所以一个人不可能不重复地走过所有的七座桥而再回到出发点，这就是著名数学家欧拉研究后得出的结论。

欧拉用他的智慧，把七桥问题变成了一个与位置关系有关的问题，这也为许多现实生活中的七桥问题找到解决的途径。

下面我们来看看它的重要运用。

例1，图5中的线段代表林中小路，在B点A、B两处各有一人，他们约定以相同的速度同时从各自所在的位置出发，走遍林中的每一条小路，最后到达C点，在哪个点出发的人最先到达C点。

分析：从A点出发的人先到。

原因是图中只有A、C两个奇点，由规律可知：从A出发的人可以不重复地走完每一条小路后终止在奇点C；B是偶点，从B点出发不可能不重复地走完每一条小路，他要到达C点，必须在某段小路上重复走一次，从B点出发的人到达C的行程比从A点出发的人更长。

七桥问题——一笔画
18世纪东普鲁士的哥尼斯堡城，有一条河穿过，河上下有两个小岛，有七座桥把两个岛与河岸联系起来（如下图一）。

有人提出一个问题：一个步行者怎样才能不重复，不遗漏地一次走完七座桥，最后回到出发点。

这个问题提出后在很长一段时间内很多人进行了研究都没有研究出答案。

后来大数学家欧拉把它转化成一个几何问题——一笔画问题，使问题得到了解决。

（如下图二）
图一图二
问题的答案如何呢？让我们先来了解三个新概念。

①有奇数条边相连的点叫奇点。

②有偶数条边相连的点叫偶点。

③一笔画指：1、下笔后笔尖不能离开纸。

2、每条线都只能画一次而不能重复。

结论：
课堂练习
1、一辆洒水车要给
再回到出发点？
2、甲乙两个邮递员去送信，两人同时出发以同样的速度走遍所有的街道，甲从A点出发，乙从B点出发，最后都回到邮局（C点）。

如果要选择最短的线路，谁先回到邮局？。