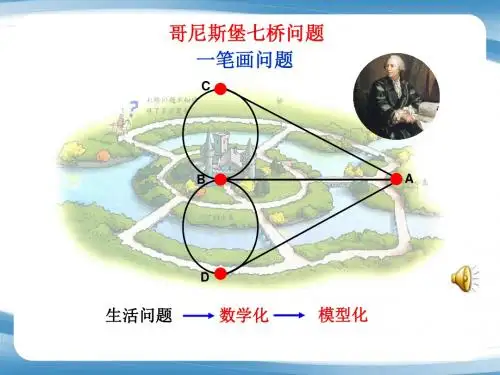
哥城景致迷人,碧波荡漾的普累格河,横贯 其境。在河的中心有一座美丽的小岛。普河的两 条支流,环绕其旁汇成大河,把全城分为下图所 示的四个区域:岛区(A),东区(B),南区(C)和北 区(D)。
著名的哥尼斯堡大学,傍倚于两条支流 的河旁,使这一秀色怡人的区域,又增添了 几分庄重的韵味!有七座桥横跨普累格河及 其支流,其中五座把河岸和河心岛连接起来 。这一别致的桥群,古往今来,吸引了众多 的游人来此散步。
早在十八世纪以前,当地的居民便热衷 于以下有趣的问题:能不能设计一次散步, 使得七座桥中的每一座都走过一次,而且只 走过一次? 这便是著名的哥尼斯堡七桥问题。
如果有兴趣,完全可以照样子画一张地图 ,亲自尝试尝试。不过,要告诉大家的是,想把 所有的可能线路都试过一遍是极为困难的!因 7 P 为各种可能的线路有 7 =5040种。要想一一试 过,真是谈何容易。正因为如此,七桥问题的 解答便众说纷纭:有人在屡遭失败之后,倾向 于否定满足条件的解答的存在;另一些人则认 为,巧妙的答案是存在的,只是人们尚未发现 而已,这在人类智慧所未及的领域,是很常见 的事!
● ● ●
②有偶数条边相连的点叫偶点。如:
● ●
●
③一笔画指:1、下笔后笔尖不能离开纸。 2、每条线都只能画一次而不能重复。
总结规律
①可以一笔画成的图形,与偶点个数无关, 与奇点个数有关。也就是说,凡是图形中没 有奇点的(奇点个数为 0 ),可选任一个点做 起点,且一笔画后可以回到出发点。
②若奇点个数为2,可选其中一个奇点做起点, 而终点一定是另一个奇点,即一笔画后不可以 回到出发点。 ③凡是图形中有2个以上奇点的,不能完成一 笔画。
想不到轰动一时的哥尼斯堡七桥 问题,竟然与孩子们的游戏,想用一 笔画画出“串”字和“田”字这类问 题一样。