七桥问题与一笔画
- 格式：ppt
- 大小：1.73 MB
- 文档页数：21
下载文档原格式
合集下载
七桥问题与一笔画教案
七桥问题与一笔画广西玉林市陆川县万丈初中陈勇欢所用教材人教版七年级上册第三章P121-122教学任务分析教学流程安排课前准备教学过程一、展示问题引入新课18世纪时风景秀丽的小城哥尼斯堡中有一条河，河的中间有两个小岛，河的两岸与两岛之间共建有七座桥（如图），当时小城的居民中流传着一道难题：一个人怎样才能不重复地走过所有七座桥，再回到出发点？这就是数学史上著名的七桥问题，你愿意试一试吗？二、分析：数学家欧拉知道了七桥问题他用四个点A 、B 、C 、D 分别表示小岛和岸，用七条线段表示七座桥（如图）于是问题就成为如何“一笔画”出图中的图形？A 岛D 岸B 岛C 岸● 点A 、B 表示岛点C 。
D 表示岸 ▎线表示桥通过故事的形式把问题引出来，一方面激发学生的学习兴趣，另一方面也可以让学生感受到他们今天探讨的课题就是当年困扰千百人的问题，这样可以增进学生的求知欲。
接着让学生通过对七座桥的观察，在图上试走等活动，留给学生一个悬念，为后面的探究活动埋下伏笔，同时也把学生的求知欲望推上了一个高潮。
欧拉利用了几何的抽象化和理想化来观察生活，建立了准确的数学模型，七年级数学开始讲点、线、面，这些几何概念是从现实中抽象化和理想化而来，在欧拉的眼中，在地图上一个城市是一个点。
岛和陆地抽象成点，桥抽象成线，直线是笔直的，生活中没有完全精确的笔直线，这是理想化了，正因为数学的这种抽象，才使数学具问题的答案如何呢？让我们先来了解三个新概念。
①有奇数条边相连的点叫奇点。
如：●●●②有偶数条边相连的点叫偶点。
如：●●③一笔画指：1、下笔后笔尖不能离开纸。
2、每条线都只能画一次而不能重复。
三、活动探究下列图形中。
请找出每个图的奇点个数，偶点个数。
试一试哪些可以一笔画出，请填●●●●●●让学生充分理解这三个概念为下面探究规律做准备。
教师重点关注：①学生能否理解一笔画②能否勇于克服数学活动中的困难，有学好数学的信心。
老师发给学生每人一份探究的图形与表格然后，学生动手、填表，教师参与学生活动，并在投影仪上展示学生的作品对于图①②③④⑤⑥⑨有什么共同的⑺⑻●●ABCCCBOBCDF用你发现的规律，说一说七桥问题的答案？①凡是“一笔画”，一定有一个“起点”，一个“终点”，还有一些“过路点”。
哥尼斯堡七桥问题与一笔画课件
02
在18世纪，人们开始对图论进行 研究，探索图的结构和性质，其 中哥尼斯堡七桥问题成为了图论 研究的重要问题之一。
哥尼斯堡七桥问题的起源
哥尼斯堡七桥问题起源于18世纪初，当时有一位名叫欧拉的 人，他是一位数学家和工程师，对图论进行了深入研究。
欧拉在研究哥尼斯堡的桥梁和河流时，提出了一个问题：是 否存在一条路径，能够遍历哥尼斯堡的所有桥梁，每座桥只 过一次？这就是著名的哥尼斯堡七桥问题。
哥尼斯堡七桥问题对一笔画问题的影响
哥尼斯堡七桥问题的解决推动了数学领域的发展，它证明了不存在一条遍历七座 桥的路径，每座桥只过一次，最后回到开始的地方。
这个问题的解决对于一笔画问题的研究具有重要意义，它揭示了一笔画问题的复 杂性和多样性，也促使数学家们深入研究一笔画问题的性质和规律。
一笔画问题在哥尼斯堡七桥问题中的应用
哥尼斯堡七桥问题是一笔画问题的经典案例，它探讨的是从哥尼斯堡的一个地方开 始，能否遍历城市的七座桥，每座桥只过一次，最后回到开始的地方。
一笔画问题则是一个更广泛的几何问题，研究的是在一个连通图上，是否存在一条 路径能够遍历所有的边，每条边只过一次。
哥尼斯堡七桥问题实际上是几何图形的一笔画问题，它为后续一笔画问题的研究提 供了基础。
哥尼斯堡七桥问题的历史意义
哥尼斯堡七桥问题的解决标志着图论 的诞生，成为图论发展史上的一个里 程碑。
该问题的解决为后续的图论研究提供 了基础和指导，推动了数学和图论的 发展。
02 一笔画问题概述
一笔画问题的定义
一笔画问题，也称为欧拉路径问题，是图论中的一个经典 问题。它主要探讨的是在一个给定的图形中，是否存在一 条路径，使得这条路径能够遍历图形的每一条边且只遍历 一次。
地图导航
在18世纪，人们开始对图论进行 研究，探索图的结构和性质，其 中哥尼斯堡七桥问题成为了图论 研究的重要问题之一。
哥尼斯堡七桥问题的起源
哥尼斯堡七桥问题起源于18世纪初，当时有一位名叫欧拉的 人，他是一位数学家和工程师，对图论进行了深入研究。
欧拉在研究哥尼斯堡的桥梁和河流时，提出了一个问题：是 否存在一条路径，能够遍历哥尼斯堡的所有桥梁，每座桥只 过一次？这就是著名的哥尼斯堡七桥问题。
哥尼斯堡七桥问题对一笔画问题的影响
哥尼斯堡七桥问题的解决推动了数学领域的发展，它证明了不存在一条遍历七座 桥的路径，每座桥只过一次，最后回到开始的地方。
这个问题的解决对于一笔画问题的研究具有重要意义，它揭示了一笔画问题的复 杂性和多样性，也促使数学家们深入研究一笔画问题的性质和规律。
一笔画问题在哥尼斯堡七桥问题中的应用
哥尼斯堡七桥问题是一笔画问题的经典案例，它探讨的是从哥尼斯堡的一个地方开 始，能否遍历城市的七座桥，每座桥只过一次，最后回到开始的地方。
一笔画问题则是一个更广泛的几何问题，研究的是在一个连通图上，是否存在一条 路径能够遍历所有的边，每条边只过一次。
哥尼斯堡七桥问题实际上是几何图形的一笔画问题，它为后续一笔画问题的研究提 供了基础。
哥尼斯堡七桥问题的历史意义
哥尼斯堡七桥问题的解决标志着图论 的诞生，成为图论发展史上的一个里 程碑。
该问题的解决为后续的图论研究提供 了基础和指导，推动了数学和图论的 发展。
02 一笔画问题概述
一笔画问题的定义
一笔画问题，也称为欧拉路径问题，是图论中的一个经典 问题。它主要探讨的是在一个给定的图形中，是否存在一 条路径，使得这条路径能够遍历图形的每一条边且只遍历 一次。
地图导航
小升初数学专项题第七讲 一笔画与七桥问题_通用版
小升初数学专项题第七讲一笔画与七桥问题_通用版第七讲一笔画与七桥问题【知识梳理】1.一笔画是指能够一笔画成的图形。
2.把和一条、三条、五条等奇数条线相连的点叫做奇点，把和两条、四条、六条等偶数条线相连的点叫做偶点，这样图形中要么是奇点，要么是偶点。
3.有2个奇点或0个奇点（全部是偶点）连通图能够一笔画成，否则不能一笔画成。
4.七桥问题可以转化成一笔画问题解决。
【典例精讲1】一笔画就是笔不离纸，笔画不重复，一笔画出一个图形．你能用一笔画出下列图形吗？思路分析：能够一笔画成的图形，首先必须要相连，结果不相连就一定不能一笔画成，能否一笔画成，关键在于判别奇点、偶点的个数：只有偶点，可以一笔画，并且可以以任意一点作为起点；只有两个奇点，可以一笔画，但必须以这两个奇点分别作为起点和终点；奇点超过两个，则不能一笔画。
解答：观察图形可知（1）第一个图形全是偶点，所以能一笔画出；（2）第二个图形是2个奇点，剩下的都是偶点，所以能一笔画出。
小结：解决这类问题首先要看是不是连通图，其次看奇点或偶点的个数，由偶点组成的，或只有两个奇点的连通图才能一笔画成。
【举一反三】1、下面这些图形，哪个能一笔画？哪个不能一笔画？2.“九点连线”是一道著名的数学题，你能用一笔画4条连续的直线段，把图中所有的9个点都连起来吗？请你在下图画出来。
【典例精讲2】在一个城市中有七座桥和四个区域：能不能一次走遍所有的七座桥，而每座桥只准经过一次？思路分析：用“1、2、3、4、5、6、7”表示七座桥，它们连接着A、B、C、D 四个区域（如图所示），这样一来，七座桥的问题，就转变为一个一笔画问题，即能不能一笔从头到尾不重复地画出这个图形．解答：图中有4个奇点和一个偶点，奇点个数不是2个，因为C、D、E都是奇数点。
【答案】：：（1）不能不重复地走一次穿过每扇门。
（2）当关闭C和D之间的门；或关闭D和E之间的门；或关闭E通向过道的门时，可一次通过．（用A、B、C、D、E五个点表示五个房间，F点表示过道，用线把两个点连起来，于是走的路线就简化成一笔画问题。
七桥问题与一笔画教学设计
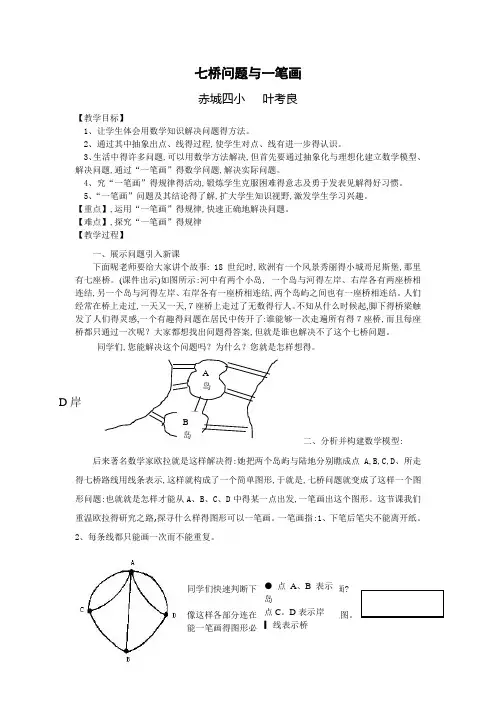
七桥问题与一笔画赤城四小 叶考良【教学目标】1、让学生体会用数学知识解决问题得方法。
2、通过其中抽象出点、线得过程,使学生对点、线有进一步得认识。
3、生活中得许多问题,可以用数学方法解决,但首先要通过抽象化与理想化建立数学模型、解决问题,通过“一笔画”得数学问题,解决实际问题。
4、究“一笔画”得规律得活动,锻炼学生克服困难得意志及勇于发表见解得好习惯。
5、“一笔画”问题及其结论得了解,扩大学生知识视野,激发学生学习兴趣。
【重点】,运用“一笔画”得规律,快速正确地解决问题。
【难点】,探究“一笔画”得规律 【教学过程】一、展示问题引入新课下面呢老师要给大家讲个故事: 18世纪时,欧洲有一个风景秀丽得小城哥尼斯堡,那里有七座桥。
(课件出示)如图所示:河中有两个小岛, 一个岛与河得左岸、右岸各有两座桥相连结,另一个岛与河得左岸、右岸各有一座桥相连结,两个岛屿之间也有一座桥相连结。
人们经常在桥上走过,一天又一天,７座桥上走过了无数得行人。
不知从什么时候起,脚下得桥梁触发了人们得灵感,一个有趣得问题在居民中传开了:谁能够一次走遍所有得７座桥,而且每座桥都只通过一次呢？大家都想找出问题得答案,但就是谁也解决不了这个七桥问题。
同学们,您能解决这个问题吗？为什么？您就是怎样想得。
二、分析并构建数学模型:后来著名数学家欧拉就是这样解决得:她把两个岛屿与陆地分别瞧成点A,B,C,D 、所走得七桥路线用线条表示,这样就构成了一个简单图形,于就是,七桥问题就变成了这样一个图形问题:也就就是怎样才能从A 、B 、C 、D 中得某一点出发,一笔画出这个图形。
这节课我们重温欧拉得研究之路,探寻什么样得图形可以一笔画。
一笔画指:1、下笔后笔尖不能离开纸。
2、每条线都只能画一次而不能重复。
同学们快速判断下面哪些图形能够一笔画?像这样各部分连在一起得图形,叫做连通图。
能一笔画得图形必须就是连通图。
A 岛D 岸B 岛C● 点A 、B 表示岛 点C 。
七桥问题与一笔画
Ｅ、 Ｆ， ０ 个 奇 点 。可 以一 笔
（ Ｃ点 ） ， 如图ｌ １ ． 如 果 要 选 择 最
二
Ｄ
个偶 点 ： Ａ、 Ｂ、 Ｄ、 Ｆ， ２ 个奇点 ： Ｃ、 ， 可 以 一
笔 画成 ． 图７ 中有２ 个 偶点 ： ４、 Ｃ， ２ 个奇 点 ：
Ｂ、 Ｄ， 可 以 一 笔 画 成 ．图 ８ 中有 １ 个偶 点 ： Ｄ。 ４ 个奇点 ： Ａ、 、 Ｃ、 Ｄ， 不 能 一 笔 画 成 ．再
找 几 个 图形 试 一 试 ， 你 能 发 现什 么 规 律 吗 ？
【 规律 】
① 可 以 一 笔 画 成 的 图形 ． 与 偶 点 个 数
无关 ， 与奇点个 数有关 ． 也 就是说 ， 凡 是 图
短 的线 路 ， 谁 先 回到 邮 局 ？
ｃ
形 中没 有 奇 点 的 （ 奇 点 个数 为０ ） ， 可 选 任 一
个点做起点 ． 且 一 笔 画后 可 以 回到 出 发 点 ．
７ ２
Ｅ Ｆ
图 １ １
Ｔ １ ｎ ｔ ｅ 慧 ｌ ｌ ｉ ｇ 散 ｅ ｎ 掌 ｔ ｍ ａ ｔ ｈ ｅ ｍ ａ ｔ ｉ ｃ ｓ
条线都只能画一次而不能重复． 图５ 一图 ８ 四个 图 形 中 。 你 能 找 出图５ 一
图８ 的 每 个 图形 中 奇 点 和 偶 点 的 个 数 吗 ？ 请 你 试 一 试 其 中 哪些 可 以一 笔 画 出 ？
Ｅ
超
店
图 ５
图６
７
图 ８
【 分析 】 图５ 中有６ 个偶 点 ： Ａ、 Ｂ、 ｃ、 Ｄ、
看几 个一 笔 画 的问题 ．
先 让 我 们 来 了解 三 个 新 概 念 ．
（ Ｃ点 ） ， 如图ｌ １ ． 如 果 要 选 择 最
二
Ｄ
个偶 点 ： Ａ、 Ｂ、 Ｄ、 Ｆ， ２ 个奇点 ： Ｃ、 ， 可 以 一
笔 画成 ． 图７ 中有２ 个 偶点 ： ４、 Ｃ， ２ 个奇 点 ：
Ｂ、 Ｄ， 可 以 一 笔 画 成 ．图 ８ 中有 １ 个偶 点 ： Ｄ。 ４ 个奇点 ： Ａ、 、 Ｃ、 Ｄ， 不 能 一 笔 画 成 ．再
找 几 个 图形 试 一 试 ， 你 能 发 现什 么 规 律 吗 ？
【 规律 】
① 可 以 一 笔 画 成 的 图形 ． 与 偶 点 个 数
无关 ， 与奇点个 数有关 ． 也 就是说 ， 凡 是 图
短 的线 路 ， 谁 先 回到 邮 局 ？
ｃ
形 中没 有 奇 点 的 （ 奇 点 个数 为０ ） ， 可 选 任 一
个点做起点 ． 且 一 笔 画后 可 以 回到 出 发 点 ．
７ ２
Ｅ Ｆ
图 １ １
Ｔ １ ｎ ｔ ｅ 慧 ｌ ｌ ｉ ｇ 散 ｅ ｎ 掌 ｔ ｍ ａ ｔ ｈ ｅ ｍ ａ ｔ ｉ ｃ ｓ
条线都只能画一次而不能重复． 图５ 一图 ８ 四个 图 形 中 。 你 能 找 出图５ 一
图８ 的 每 个 图形 中 奇 点 和 偶 点 的 个 数 吗 ？ 请 你 试 一 试 其 中 哪些 可 以一 笔 画 出 ？
Ｅ
超
店
图 ５
图６
７
图 ８
【 分析 】 图５ 中有６ 个偶 点 ： Ａ、 Ｂ、 ｃ、 Ｄ、
看几 个一 笔 画 的问题 ．
先 让 我 们 来 了解 三 个 新 概 念 ．
七桥问题和一笔画
七桥问题和一笔画18世纪时，欧洲有一个风景秀丽的小城哥尼斯堡，那里有七座桥。
如图1所示：河中的小岛A与河的左岸B、右岸C各有两座桥相连结，河中两支流间的陆地D与A、B、C各有一座桥相连结。
当时哥尼斯堡的居民中流传着一道难题：一个人怎样才能一次走遍七座桥，每座桥只走过一次，最后回到出发点？大家都试图找出问题的答案，但是谁也解决不了这个问题。
图 1 图 2七桥问题引起了著名数学家欧拉（17071783）的关注。
他把具体七桥布局化归为图2所示的简单图形，于是，七桥问题就变成一个一笔画问题：怎样才能从A、B、C、D中的某一点出发，一笔画出这个简单图形（即笔不离开纸，而且a、b、c、d、e、f、g各条线只画一次不准重复），并且最后返回起点？欧拉经过研究得出的结论是：图2是不能一笔画出的图形。
这就是说，七桥问题是无解的。
这个结论是如何产生呢？请看下面的分析。
如果我们从某点出发，一笔画出了某个图形，到某一点终止，那么除起点和终点外，画笔每经过一个点一次，总有画进该点的一条线和画出该点的一条线，因此就有两条线与该点相连结。
如果画笔经过一个n次，那么就有2n条线与该点相连结。
因此，这个图形中除起点与终点外的各点，都与偶数条线相连。
如果起点和终点重合，那么这个点也与偶数条线相连；如果起点和终点是不同的两个点，那么这两个点部是与奇数条线相连的点。
综上所述，一笔画出的图形中的各点或者都是与偶数条线相连的点，或者其中只有两个点与奇数条线相连。
图2中的A点与5条线相连结，B、C、D各点各与3条线相连结，图中有4个与奇数条线相连的点，所以不论是否要求起点与终点重合，都不能一笔画出这个图形。
1736年，欧拉在圣彼得堡科学院作了一次学术报告。
在报告中，他证明了上述结论。
后来他又给出了鉴别任一图形能否一笔画出的准则，即欧拉定理。
为了介绍这个定理，我们先来看下面的预备知识：由有限条线组成的图形叫做网络，其中每条线都要求有两个不同的端点。
中国邮递员问题
管梅谷
管梅谷教授。 上海市人。1957年毕业于华 东师范大学数学系。历任 山东师范大学讲师、副教 授、教授、校长，中国运 筹学会第一、二届常务理 事，山东省数学学会第四 届副理事长，山东省运筹 学会第一届副理事长，山 东省世界语协会理事长。 是第六届全国政协委员。 从事运筹学及其应用的研 究，对最短投递路线问题 的研究取得成果。所提模 型在国外称为中国投递问 题。
求解。
推广的中国邮递员问题： 混合图的中国邮递员问题，有各种限制 的中国邮递员问题，动态网络的中国邮 递员问题。 其他相关问题-旅行售货员（TSP）问题， 灾清巡视路线。
谢谢!
v1 2 5 v2 5 9 v3 v4 图2 3 v8
4
3
v7
6
v9 4 4 4
v6
4
v5
这样就得到初始方案.在这个图中，没有奇点， 故称它为欧拉图。对应于这个可行方案，重复 边总权为51。
思考
这样的可行方案是不是只有一种呢？ 在确定一个可行方案后，怎么判断这个方案是 否为最优方案？ 若不是最优方案，如何调整这个方案？
欧拉图及求欧拉回路的算法
欧拉行迹—含所有边恰好一次的行迹 欧拉回路—含所有边恰好一次的回路 欧拉图—存在欧拉回路的图
设G是连通图, 下列命题等价: (1) G是欧拉图. (2) 每个顶点的度数都是偶数. (3) G是两两无公共边的圈的并.
欧拉图及求欧拉回路的算法
求欧拉回路的算法(Fleury算法，1921年) 算法思想: “过河拆桥,尽量不走独木桥”. 即若已选定迹 Wi v0e1v1e2 eivi , 从 G Wi 中选 取下一条边 ei 1 使得ei 1 与 vi 相关联, 且ei 1 不是 G Wi 的桥, 除非无边可选.
七桥问题与一笔画
故事发生在18世纪的哥尼斯堡城.流经那里的一条 河中有两个小岛，还有七座桥把这两个小岛与河岸 联系起来，
那里风景优美，游人众多.在这美丽的地方， 人们议论着一个有趣的问题：一个游人怎样 才能不重复地一次走遍七座桥，最后又回到 出发点呢？
直到1836年，瑞士著名的数学家欧拉才证明了这个 问题的不可能性。
课后作业
请你观察生活，设计一个运 用“一笔画”的数学知识来解 决的实际问题。并与同伴交流。
●B
图⑴
A●
图⑵ 图⑶
●A
B●
●C
E●
●D
A
●●
图⑷
图1
活动探究 下列图形中。请找出每个图的奇点个数，偶点个数。试一试哪 些可以一笔画出，请填表，从中你能发现什么规律？
奇点个数 偶点个数 能否一笔画
●B
图⑴
2
0
能
A●
●A
图⑵
B●
●C
2
3
能
E●
●D
A
●●
图⑶
0
1
能
图⑷
图1
0
5
能
奇点个数 偶点个数 能否一笔画
①有奇数条边相连的点叫奇点。如：
●
●
●
②有偶数条边相连的点叫偶点。如：
●●●源自③一笔画指：1、下笔后笔尖不能离开纸。 2、每条线都只能画一次而不能重复。 不能遗漏。
活动探究 下列图形中。请找出每个图的奇点个数，偶点个数。试一试哪 些可以一笔画出，请填表，从中你能发现什么规律？
奇点个数 偶点个数 能否一笔画
用你发现的规律，说一说七桥问题的答案？
由于七桥问题中的四个点都是奇点，因此可 以判断它是无法一笔画出来的 ，也就是说 根本不存在能不重复走遍七座桥的路线！
那里风景优美，游人众多.在这美丽的地方， 人们议论着一个有趣的问题：一个游人怎样 才能不重复地一次走遍七座桥，最后又回到 出发点呢？
直到1836年，瑞士著名的数学家欧拉才证明了这个 问题的不可能性。
课后作业
请你观察生活，设计一个运 用“一笔画”的数学知识来解 决的实际问题。并与同伴交流。
●B
图⑴
A●
图⑵ 图⑶
●A
B●
●C
E●
●D
A
●●
图⑷
图1
活动探究 下列图形中。请找出每个图的奇点个数，偶点个数。试一试哪 些可以一笔画出，请填表，从中你能发现什么规律？
奇点个数 偶点个数 能否一笔画
●B
图⑴
2
0
能
A●
●A
图⑵
B●
●C
2
3
能
E●
●D
A
●●
图⑶
0
1
能
图⑷
图1
0
5
能
奇点个数 偶点个数 能否一笔画
①有奇数条边相连的点叫奇点。如：
●
●
●
②有偶数条边相连的点叫偶点。如：
●●●源自③一笔画指：1、下笔后笔尖不能离开纸。 2、每条线都只能画一次而不能重复。 不能遗漏。
活动探究 下列图形中。请找出每个图的奇点个数，偶点个数。试一试哪 些可以一笔画出，请填表，从中你能发现什么规律？
奇点个数 偶点个数 能否一笔画
用你发现的规律，说一说七桥问题的答案？
由于七桥问题中的四个点都是奇点，因此可 以判断它是无法一笔画出来的 ，也就是说 根本不存在能不重复走遍七座桥的路线！
一笔画(七桥问题)
能否一笔画是由图的奇、偶点的数目来决定的。 能否一笔画是由图的奇、偶点的数目来决定的。那么什么 叫奇、偶点呢？与奇数（单数）条边相连的点叫做奇点； 叫奇、偶点呢？与奇数（单数）条边相连的点叫做奇点； 与偶数（双数）条边相连的点叫做偶点。如下图中的① 与偶数（双数）条边相连的点叫做偶点。如下图中的①、 为奇点， 为偶点。 ④为奇点，②、③为偶点。
以下网络中哪一个是可以遍历的(即 一笔而不重复地画成)？
拓扑学起源于公元 年一个著名问题—— 拓扑学起源于公元1736年一个著名问题 起源于公元 年一个著名问题 哥尼斯堡七桥问题——的解决． 哥尼斯堡七桥问题 的解决
哥尼斯堡是位于普累格河上的一座城市， 哥尼斯堡是位于普累格河上的一座城市，它 包含两个岛屿及连接它们的七座桥． 包含两个岛屿及连接它们的七座桥．该河流 经城区的这两个岛． 经城区的这两个岛．岛与河岸之间架有六座 另一座桥则连接着两个岛． 桥，另一座桥则连接着两个岛．星期天散步 已成为当地居民的一种习惯， 已成为当地居民的一种习惯，但试图走过这 样的七座桥， 样的七座桥，而且每桥只走过一次却从来没 有成功过．但直至引起瑞士数学家欧拉 有成功过．但直至引起瑞士数学家欧拉 (Leonhard Euler，1707—1783)注意之前， 注意之前， ， 注意之前 没有人能够解决这个问题 ．
一笔画------七桥问题 一笔画------七桥问题
一笔画----------七桥问题 一笔画----------七桥问题
请你做下面的游戏： 请你做下面的游戏：一笔画出图中 的 图形来。 规则：笔不离开纸面， 图形来。 规则：笔不离开纸面，每根 线都只能画一次。 线都只能画一次。这就是古老的民间 游戏——一笔画。 你能画出来吗？ 一笔画。 游戏 一笔画 你能画出来吗？
Konigsberg七桥问题一笔画问题
Konigsberg 七橋問題(一筆畫問題)當Euler在1736年訪問Konigsberg,Prussia(now Kaliningrad Russia)時，他發現當地的市民正從事一項非常有趣的消遣活動。
Konigsberg城中有一條名叫Pregel這項有趣的消遣活動是在星期六作一次走過所有七座橋的散步，每座橋只能經過一次，而且起點與終點必須是同一地點。
Euler把每一塊陸地考慮成一個點，連接兩塊陸地的橋以線表示，便得如下的圖形Euler後來推論出此種走法是不可能的。
他的論點是這樣的，除了起點以外，每一次當一個人由一座橋進入一塊陸地(或點)時，他(或她)同時也由另一座橋離開此點。
所以每行經一點時，計算兩座橋(或線)，從起點離開的線與最後回到始點的線亦計算兩座橋，因此每一個陸地與其他陸地連接的橋數必為偶數。
我們從Konigsberg七橋所成之圖形中，沒有一點含有偶數條數，因此上述的任務是不可能實現的。
Eulerian graphs 歐拉圖形一條途徑v0e1e2v2………..e k v k稱為Euler walk(歐拉走路)如果沒有邊(edge)是重複的，此處v i表頂點，e i表邊。
若一個圖形G中，v0e1v1e2v2……………e k v k行經每一邊恰好一次，且v0=v k（起點=終點），則稱此途徑為Euler tour（歐拉路徑）。
例：從下右圖中找出一歐拉路徑一.筆劃問題問題：有一商人欲推銷某一商品，該商人在下圖中每一地點，A，B，...，J都希望去推銷該商品，但為了達到最低成本故希望不要重複行走已走過的路徑以減低車費成本，問該商人應如何行走？Eulerian graphs 歐拉圖形一條路徑V0e1V1e2V2…..e k V k稱為Euler walk (歐拉走路)如果沒有邊(edge)是重複的，此處V1表頂點，e1表邊。
若一個圖形Ｇ中，V0e1V1e2V2…..e k V k行徑每一邊恰好一次且( 起點=終點)，則稱此途徑為Euler tour (歐拉路徑)。
七桥问题与一笔画
七桥问题与一笔画18世纪时，风景秀丽的欧洲小城哥尼期堡中有一条河，河的中间有两个小岛，河两岸与两岛之间共建有七座桥（图1）当时小城的居民中流传着一道难题：一个人怎样才能不重复地走过所有的七座桥，再回到出发点？这就是数学史上著名的“七桥问题”，为了解决这个问题，我们首先学习一下“一笔画”吧。
把一个图形用笔描绘一遍，笔不能离开图面，已经描过的地方不可以重复，这个图形叫做一笔画。
如图2，由A点出发先走向B点，从B点先描出圆，回到B点后，再描全矩形，这就是一个一笔画。
但图3就不是一个一笔画。
图的顶点可分为两类，奇点和偶点从某点出发的边的条数是奇数时，这样的点叫做奇点（如图3中A、B、C、D）；从某点出发的边的条数是偶数时，这样的点叫偶点（如图2中A、B）由例3我们知道并非所有的图形均可一笔画出，通过研究发现有以下三条规律。
1.凡是仅由偶点组成的图形，一定可以一笔画出，画时可以任意偶点为起点，最后仍回到这点。
2.凡是只有两个奇顶点和任意个偶顶点组成的图形，也可以一笔画出，画时必须以一个奇顶点为起点，而以另一个奇顶点为终点。
3.如果图形中的奇顶点多于两个，那么这个图就不可能一笔画出。
掌握这些结论后，我们就可以顺利的解决七桥问题，首先把被河流隔开的四块区域缩写为A、B、C、D四个点，这样七桥问题就变成了四个点间由七条线相连所成的图（图4）。
因为本图有四个奇点（A、B、C、D），所以一个人不可能不重复地走过所有的七座桥而再回到出发点，这就是著名数学家欧拉研究后得出的结论。
欧拉用他的智慧，把七桥问题变成了一个与位置关系有关的问题，这也为许多现实生活中的七桥问题找到解决的途径。
下面我们来看看它的重要运用。
例1，图5中的线段代表林中小路，在B点A、B两处各有一人，他们约定以相同的速度同时从各自所在的位置出发，走遍林中的每一条小路，最后到达C点，在哪个点出发的人最先到达C点。
分析：从A点出发的人先到。
原因是图中只有A、C两个奇点，由规律可知：从A出发的人可以不重复地走完每一条小路后终止在奇点C；B是偶点，从B点出发不可能不重复地走完每一条小路，他要到达C点，必须在某段小路上重复走一次，从B点出发的人到达C的行程比从A点出发的人更长。
一笔画欧拉定理
一笔画欧拉定理一笔画欧拉定理：连接世界的线条一笔画欧拉定理，也被称为欧拉路径定理或七桥问题，是数学中一项经典的问题。
该问题的核心是，是否可能通过一个图中的每条边恰好经过一次，且不重复，最终回到起点。
这个问题源于18世纪瑞士的柯尼斯堡市，柯尼斯堡市由七座桥连接着两岸，人们思考着如何能够一次性地经过每座桥一次。
欧拉定理的解决，引领了图论的发展，并为后世的研究提供了重要的启示。
它不仅仅是一项数学问题，更是一种思维方式，代表着人类对于连接和探索的渴望。
首先，让我们来了解一下欧拉定理的基本概念。
在图论中，图是由节点（也称为顶点）和边组成的一种抽象结构。
一笔画问题中，节点表示地点，而边则表示连接这些地点的路径。
而所谓“一笔画”，就是通过一条线条将所有的节点连接起来，而且每个节点只经过一次。
欧拉定理告诉我们，一个图能够一笔画的条件是：只有零个或两个节点的度数是奇数，其余节点的度数都是偶数。
度数是指与一个节点相连的边的数量。
这个定理的证明是基于欧拉路径的存在性以及其特点的推导。
那么，为什么欧拉定理如此重要呢？首先，欧拉定理为图论提供了一个重要的研究基础。
图论是一门研究节点和边之间关系的数学学科，它在计算机科学、电子工程、通信网络等领域有广泛的应用。
欧拉定理为图论的发展提供了一个重要的起点，为后续的研究奠定了基础。
其次，欧拉定理的解决也启发了人们对于连接和探索的思考。
在欧拉定理的背后，我们看到了人类对于连接世界的渴望。
人类历史上，无论是地理探险、交通建设还是互联网的发展，都在不断地寻求连接的方式。
欧拉定理的解决，让我们明白了连接并不仅仅是一种物理的行为，更是一种思维方式和哲学观念。
欧拉定理还启发了我们对于问题解决的思考方式。
在解决欧拉路径问题时，我们需要不断地观察、分析和推理，找到一种满足条件的解决方案。
这种思考方式在现实生活中同样适用，我们可以借鉴欧拉定理的思想，通过观察、分析和推理来解决各种复杂的问题。
此外，欧拉定理的应用也不仅仅局限于数学领域。
哥尼斯堡七桥问题与一笔画
笔 画出 的 图首 先 必 须是 连通 图 ．但 是否 所 有 的连 通 图都可 以一 笔 画 出呢 ？ 有 关 这 个 问题 的讨 论 ，要 追溯 到 两百 多
年 前 的 一 个 著 名 问 题 —— 哥 尼 斯 堡 七 桥 问
题． 十八世纪 ， 东普鲁 士哥尼斯堡城（ 今 俄 罗 斯加 里 宁格 勒 ） 有一 条 河 叫普莱 格 尔河 ， 它 有 两个 支流 ， 在 城 市 的 中心汇 成大 河 ， 中间是 岛 区， 河 上 有 ７座桥 ， 将 河 中的两 个 岛和河 岸 连
图 ｌ
图 ２
图 ３
如 果 你 画 出来 了 ，那 么 请你 再 看 图 ２能 不能一 笔 画 出来？
一
这个问题看起来似乎并不难 ，但人们始
虽然你动了脑筋 ，但我相信你肯定不能 终 没 有 能找 到 答 案 ． 最后 ， 问题 被 提 到 了大 数
笔 画 出图 ２ １这 就是 一笔 画 问题 ， 它 是一 种 学 家 欧拉 那 里 ．欧 拉 以 深邃 的洞 察力 很 快 证
是奇 点 ， 共有 四个 ， 所 以这个 图肯定 不 能 一笔 画成． 欧拉对“ 七桥问题” 的 研 究 是 图论 研 究
在 图 中添 上一 条线 段 ， 使它 能一 笔画 成 ．
的开始 ，同时也为拓扑学的研究提供 了一个
初级 例 子 ．
【 例题 赏析 】 图 中添加 最 少 的线段 ，将 其 改成 一 笔 画 的 图
参考路 线 ： ４ － １ ＿ ２ － ５ — ８ 一 － ９ － ６ － １ ０ － １ １ － ７ － ４ — ３ ．
点为终点； （ ４ ） 奇点个数超过两个的图形 ， 一定
不能 一笔 画 出 ．
现在 对 照七 桥 问题 的 图 ，所有 的顶 点都
年 前 的 一 个 著 名 问 题 —— 哥 尼 斯 堡 七 桥 问
题． 十八世纪 ， 东普鲁 士哥尼斯堡城（ 今 俄 罗 斯加 里 宁格 勒 ） 有一 条 河 叫普莱 格 尔河 ， 它 有 两个 支流 ， 在 城 市 的 中心汇 成大 河 ， 中间是 岛 区， 河 上 有 ７座桥 ， 将 河 中的两 个 岛和河 岸 连
图 ｌ
图 ２
图 ３
如 果 你 画 出来 了 ，那 么 请你 再 看 图 ２能 不能一 笔 画 出来？
一
这个问题看起来似乎并不难 ，但人们始
虽然你动了脑筋 ，但我相信你肯定不能 终 没 有 能找 到 答 案 ． 最后 ， 问题 被 提 到 了大 数
笔 画 出图 ２ １这 就是 一笔 画 问题 ， 它 是一 种 学 家 欧拉 那 里 ．欧 拉 以 深邃 的洞 察力 很 快 证
是奇 点 ， 共有 四个 ， 所 以这个 图肯定 不 能 一笔 画成． 欧拉对“ 七桥问题” 的 研 究 是 图论 研 究
在 图 中添 上一 条线 段 ， 使它 能一 笔画 成 ．
的开始 ，同时也为拓扑学的研究提供 了一个
初级 例 子 ．
【 例题 赏析 】 图 中添加 最 少 的线段 ，将 其 改成 一 笔 画 的 图
参考路 线 ： ４ － １ ＿ ２ － ５ — ８ 一 － ９ － ６ － １ ０ － １ １ － ７ － ４ — ３ ．
点为终点； （ ４ ） 奇点个数超过两个的图形 ， 一定
不能 一笔 画 出 ．
现在 对 照七 桥 问题 的 图 ，所有 的顶 点都
一笔画与七桥问题
一笔画与七桥问题贵州省道真自治县旧城中学 张帮洪 (邮编:563509)一笔画就是笔尖在不离开纸面的情况下,一次性画完某个封闭的图形。
你能一笔画出下列图形吗?有的图形可以一笔画完,有的却不能,如何来判定一个图形是否为一笔画图形呢?对这一问题的研究还得追溯到十六世纪三十年代。
在哥尼斯堡,即现在苏联加里宁格勒，布勒格尔河横贯其境。
这条河有两条支流，中间汇合成大河，从而把该地区划分成A 、B 、C 、D 四块。
在这四块土地上，有七座桥梁相连接，如图（图（1） 人们成年累月的来往于此。
于是有人就提出：能否一次走遍这七座桥，既不走重复又不走遗漏？这就是有名的“七桥问题”。
1736年，大数学家欧拉(公元1707—1783年)对七桥问题着手研究，并在彼德堡科学院作了一次有趣的报告。
把这一问题归结为如图（2）所示的一笔画问题，并得出一次性走完七桥是不可能的结论。
原因在于A、B、C、D四个点都分出 D了奇数条叉道，奇数条叉道的点不 B可能是一笔画中的“过路点”（即不是图（2）起点，已不是终点），。
因为“过路点”必须是偶数条叉道的交点，因此A、B、C、D四点必为起点或终点，但一笔画图形中只能有一个起点和一个终点（终点和起点可能为合在一起），故七桥问题得以解决。
最后欧拉给了一笔画问题的判定方法：如果把线图中偶数条线的交叉点叫偶点，把奇数条线的交叉点叫奇点，那么，（1）线图中奇点个数不多于2个，这个图就是一笔画图形，否则就不是一笔画图形。
（2）若没有奇点，则始点与终点重合，若有两个奇点，则始点与终点不重合，还必须从一个奇点画起，另一个奇点必须是终点。
（3）奇点数目总是成双出现的。
一笔画问题与七桥问题的解决，为解决最短邮路和规划问题提供了理论依据，为拓朴学的研究奠定了基础。
因此欧拉对哥尼斯堡七桥问题的研究，成了拓朴学研究的先驱。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
6、下图是某展览厅的平面图，它由五个展室组 成，任两展室之间都有门相通，整个展览厅还有 一个进口和一个出口，问游人能否一次不重复地 穿过所有的门，并且从入口进，从出口出？
BCDຫໍສະໝຸດ EFAE ●
●G F ● D●
C●
●
●A
B
4、下图是一个公园的平面图.要使游客走遍每 条路而不重复，问出入口应设在哪里？
GF
I
H
J
E CD
K
A
B
C
5、 甲乙两个邮递员去送信，两人同时出发以 同样的速度走遍所有的街道，甲从A点出发， 乙从B点出发，最后都回到邮局（C点）。如果 要选择最短的线路，谁先回到邮局？
观察下面的图形，哪些图形可以一笔画完，你能画出来吗？
连通图：任意两点间都有道路的就是连通图。
非连通图：非连通图看起来直接是断开的。
非连通图一定不能一笔画成，连通图有可能 一笔画成。
哥尼斯堡七桥问题
现今的加里宁格勒，旧称哥尼斯堡，是一座历史名城。 在十八、十九世纪，那里是东普鲁士的首府，曾经诞生和培育 过许多伟大的人物。著名的哲学家，古典唯心主义的创始人康 德，终生没有离开过哥尼斯堡一步!二十世纪最伟大的数学家 之一，德国的希尔伯特也出生于此地。
问题分析
问题的答案如何呢？让我们先来了解三个新概念。
①有奇数条边相连的点叫奇点。如：
●
●
●
②有偶数条边相连的点叫偶点。如：
●
●
●
③一笔画指：1、下笔后笔尖不能离开纸。 2、每条线都只能画一次而不能重复。
总结规律
①可以一笔画成的图形，与偶点个数无关， 与奇点个数有关。也就是说，凡是图形中没 有奇点的（奇点个数为0），可选任一个点做 起点，且一笔画后可以回到出发点。
哥城景致迷人，碧波荡漾的普累格河，横贯
其境。在河的中心有一座美丽的小岛。普河的两 条支流，环绕其旁汇成大河，把全城分为下图所 示的四个区域：岛区(A)，东区(B)，南区(C)和北 区(D)。
著名的哥尼斯堡大学，傍倚于两条支流 的河旁，使这一秀色怡人的区域，又增添了 几分庄重的韵味!有七座桥横跨普累格河及 其支流，其中五座把河岸和河心岛连接起来 。这一别致的桥群，古往今来，吸引了众多 的游人来此散步。
1、下图是国际奥委会的会标，你能一笔把它画出 来吗？
2、 一辆洒水车要给某城市的街道洒水，街 道地图如下：你能否设计一条洒水车洒水的 路线，使洒水车不重复地走过所有的街道， 再回到出发点？
小广场
超市 菜市场
文具店 电器城
服装城
3、 下图是一个公园的平面图，能不能使游 人走遍每一条路不重复？入口和出口又应设 在哪儿？
②若奇点个数为2，可选其中一个奇点做起点， 而终点一定是另一个奇点，即一笔画后不可以 回到出发点。
③凡是图形中有2个以上奇点的，不能完成一 笔画。
用你发现的规律，说一说七桥问题的答案？
由于七桥问题中的四个点都是奇点，因此可 以判断它是无法一笔画出来的 ，也就是说 根本不存在能不重复走遍七座桥的路线！
不难发现：右图中的点A、B、C、D，相当于 七桥问题中的四块区域；而图中的弧线，则相当于 连接各区域的桥。
想不到轰动一时的哥尼斯堡七桥 问题，竟然与孩子们的游戏，想用一 笔画画出“串”字和“田”字这类问 题一样。
聪明的欧拉，正是在此基础上， 经过悉心研究，确立了著名的“一笔 画原理”，从而成功地解决了哥尼斯 堡七桥问题。
的事！
问题的魔力，
竟然吸引了天才的 欧拉(Euler。1707--1783)。这位年轻 的瑞士数学家，以 其独具的慧眼，看 出了这个似乎是趣 味几何问题的潜在 意义。
欧拉运用他那娴熟的变换技巧，如同下图，把
哥尼斯堡七桥问题变为读者所熟悉的，简单的几何 图形的“一笔画”问题：即能否笔不离纸，一笔画 但又不重复地画完以下的图形？
早在十八世纪以前，当地的居民便热衷
于以下有趣的问题：能不能设计一次散步， 使得七座桥中的每一座都走过一次，而且只 走过一次?
这便是著名的哥尼斯堡七桥问题。
如果有兴趣，完全可以照样子画一张地图
，亲自尝试尝试。不过，要告诉大家的是,想把 所有的可能线路都试过一遍是极为困难的！因 为各种可能的线路有 P77=5040种。要想一一试 过，真是谈何容易。正因为如此，七桥问题的 解答便众说纷纭：有人在屡遭失败之后，倾向 于否定满足条件的解答的存在；另一些人则认 为，巧妙的答案是存在的，只是人们尚未发现 而已，这在人类智慧所未及的领域，是很常见