下载文档原格式
高等数学中微分方程的解析解求取思路微分方程是数学中一类重要的方程，它描述了变量之间的关系以及这些变量的变化规律。
微分方程的解析解是指能够用已知的数学函数表示的解，相较于数值解具有明确性和简洁性。
对于给定的微分方程，我们可以通过一定的方法和技巧来求取解析解。
1. 分离变量法分离变量法是求取微分方程解析解的常用方法。
该方法适用于可以将微分方程表达式中的未知函数和自变量分离成两个方程的情况。
首先，将方程中的未知函数和自变量分别放在等号两边，并将所有包含未知函数的项放在一边，包含自变量的项放在另一边。
接下来，对方程两边同时进行积分操作。
对包含未知函数的一边进行不定积分，对包含自变量的一边进行定积分。
最后，将两边的积分常数合并，并解出未知函数，得到微分方程的解析解。
2. 变量代换法变量代换法是求解微分方程的另一种常用方法。
通过选择适当的变量替换，可以将原方程转化为更简单的形式，进而求得解析解。
例如，可以通过引入新的变量替换原方程中的未知函数，或者将原方程中的未知函数表示为其他函数的导数形式来进行变量代换。
经过变量代换后，原方程可以转化为更简单的形式，使得求解更加容易。
3. 齐次方程的解法对于齐次微分方程，可以通过齐次方程的解法来求得解析解。
齐次方程指的是微分方程中，未知函数和自变量的项都是同次数的情况。
对于齐次方程，可以引入新的变量替换，将其转化为分离变量的形式，然后利用分离变量法进行求解。
在齐次方程的解法中，可以使用如分离变量法、变量代换法等的一些常用技巧来求得解析解。
4. 常数变易法常数变易法也是一种常用的求解微分方程的方法。
该方法适用于非齐次线性微分方程的情况。
常数变易法将微分方程的未知函数表示为特解与齐次方程的通解之和的形式。
首先，求得齐次方程的通解。
然后，假设非齐次方程的解为一个特解。
通过代入原方程，将特解代入通解中，并求得特解的具体形式。
最后，将特解和齐次方程的通解相加，得到非齐次方程的通解。
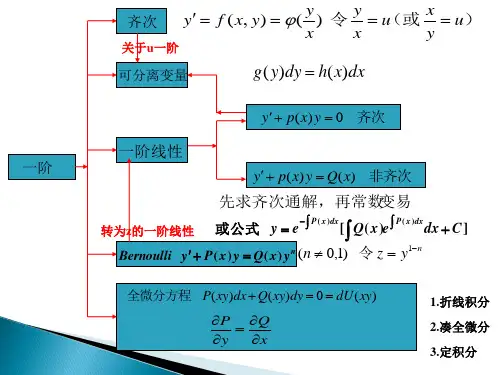
微分 方 程的相关 概 念 ：一阶微分方程： y f (x, y) 或 P( x, y)dx Q(x, y)dy 0 可分别变量的微分方程 ：一阶微分方程能够化 为 g ( y)dy 的形式，解法：f (x)dxg ( y) dy f ( x)dx 得： G( y) F (x) C 称为隐式通解。
齐次方程：一阶微分方 程能够写成 dyf ( x, y)，即写成 y的函数，解法：dx(x, y) x设 u y ，则 dy u x du ， udu (u) ， dxdu 分别变量，积分后将 y取代 ，x dx dx dx x (u) ux即得齐次方程通解。
一阶线性微分方程：1、一阶线性微分方程：dyP( x) y Q ( x)dx当 Q( x) 0时, 为齐次方程， yCe P( x) dx当 Q( x) 0时，为非齐次方程，yP( x) dxdxP ( x) dx( Q (x)e C )e、贝努力方程： dyP( x) y Q (x) y n ， 0,1)2 dx (n全微分方程：假如 P(x, y)dx Q ( x, y)dy 0中左端是某函数的全微分方程，即：du (x, y)P(x, y) dx Q( x, y) dy 0，此中：uP( x, y)，uQ ( x, y)xyu( x, y) C 应当是该全微分方程的通解。
二阶微分方程：2ydy， f ( x)时为齐次ddx 2P(x) dxQ( x) y f ( x)f ( x) 时为非齐次二阶常系数齐次线性微分方程及其解法：(*) y py qy 0，此中 p, q 为常数；求解步骤：、写出特点方程：)r 2pr q ，此中 2， 的系数及常数项恰巧是(*)式中的系数；1(rry , y , y2、求出 ( )式的两个根 r 1 ,r 23、依据 r 1 ,r 2的不一样状况，按下表写 出(*) 式的通解： r 1， r 2的形式(*) 式的通解两个不相等实根 ( p 24q 0)yc 1e r 1 x c 2 e r 2 x两个相等实根 ( p 24q0)y(c1 c2 x)e r1x一对共轭复根 ( p 24q0)y e x (c1 cos x c2 sin x) r1i ，r2ip ，4q p 222二阶常系数非齐次线性微分方程y py qy f ( x)， p,q为常数f ( x) e x P m ( x)型，为常数；f ( x) e x [ P l ( x) cos x P n ( x)sin x]型。
第十二章 微分方程§ 1 微分方程的基本概念1、由方程x 2-xy+y 2=C 所确定的函数是方程（ ）的解。
A. (x-2y)y '=2-xy '=2x-y C.(x-2)dx=(2-xy)dy D.(x-2y)dx=(2x-y)dy2、曲线族y=Cx+C 2 (C 为任意常数) 所满足的微分方程 （ ） 4.微分方程y '=yx 21-写成以y 为自变量，x 为函数的形式为（ ）A.yx 21dxdy -=B.yx 21dydx -='=2x-y D. y '=2x-y §2 可分离变量的微分方程1.方程P(x,y)dx+Q(x,y)dy=0是（ ）A.可分离变量的微分方程 一阶微分方程的对称形式， C.不是微分方程 D.不能变成)y ,x (P )y ,x (Q dy dx -= 2、方程xy '-ylny=0的通解为（ ）A y=e x B. y=Ce x cx D.y=e x +C 3、方程满足初始条件：y '=e 2x-y , y|x=0=0的特解为（ ）A. e y=e 2x+1 21e ln x 2+= C. y=lne 2x +1-ln2 D. e y =21e 2x +C4、已知y=y(x)在任一点x 处的增量α+∆+=∆x x1yy 2，且当∆x →0时，α是∆x 高阶无穷小，y(0)=π,则y(1)=( )A. 2πB. πC. 4e π 4eππ5、求特解 cosx sinydy=cosy sinxdx ， y|x=0=4π解：分离变量为tanydy=tanxdx ，即-ln(cosy)=-ln(cosx)-lnC ，cosy=ccosx 代入初始条件：y|x=0=4π得：22C =特解为：2cosy=cosx 6、求微分方程()2y x cos y x 21cos dxdy +=-+满足y(0)=π的特解。
解：由02y x cos 2y x cos dxdy =+--+得：2x sin 2y sin2dy-=，积分得：C 2x cos 2x y cot 2y csc ln +=- 代入初始条件：y(0)=π，得C= -2 7、求微分方程022/=++y x eyy 满足y(0)=0的特解解: 分离变量得dx e dy ye x y 22=--两边积分)2(21)(21222⎰⎰=--x d e y d e x y ，得C e e x y +=-22，将y (0)=0代入得C =0特解：x y 22-=§3 齐次方程1 .(x 2+y 2)dx-xydy=0，其通解为（ ）2=x 2(2ln|x|+C) B. y=x(2ln|x|+C) C. y 2=2x 2ln|x|+C D. y=2xln|x|+C 2.xy yx y +=', y|x=1=2，则特解为（ ）A. y 2=2x 2(lnx+C)2=2x 2(lnx+2) C .y=2xlnx+C D.y=2xlnx+23.0dy y x 1e 2dx e 21y xy x =⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛+的通解为（ ）A. x=2y+CB. 2xye yx=C ye 2yx =+ D.以上都不对 4、求y 'x 2+xy=y 2满足y|x=1=1的特解。
解：u xy ,xy x y y 2=-⎪⎭⎫ ⎝⎛='令，则x dx )2u (u du =-解得：2x 1x 2y += 5、求微分方程(x 2+2xy-y 2)dx-(y 2+2xy-x 2)dy=0满足初始条件y|x=1=1的特解解：xy u ,xx y 2y y x y 2x dx dy 2222=-+-+=令，可得1u 2u 1u u u dx du x 223------= 解得：lnx+lnC=ln(u+1)-ln(1+u 2)，即x(1+u 2）=C(1+u),代入初始条件y|x=1=1得特解x 2+y 2=x+y7、求曲线，使其上任一点到原点的距离等于该点的切线在x 轴上的截距 解：设曲线上任一点P(x,y)，曲线：y=y(x)，则由题意知：Y-y=y '(X-x)又y y x y x 22'-=+，得yxu ,dy dxy x 1y x 2=-=+⎪⎪⎭⎫ ⎝⎛令整理得：2u 1dyduy+=-，解得：()C y ln u 1u ln 2=+++，得通解C y x x 22=++§4 一阶线性微分方程1、微分方程(y 2+1)dx=y(y-2x)dy 的通解是（ ） A.⎪⎭⎫⎝⎛++=C y 311y 1y 32⎪⎭⎫ ⎝⎛++=C y 311y 1x 32；C. ⎪⎭⎫⎝⎛++=C y 311x 1y 32D.⎪⎭⎫ ⎝⎛+=32y 311y 1x2、微分方程xy '+2y=xlnx 满足y(1)=91-的解为（ ） A. x 91x ln x 31y+=， x 91x ln x 31y -=， C. x ln x 31C y x 32+=，. x 91x ln 31y -=3、y '+y=y 2(cosx-sinx)的通解为（ ） A .y=Ce x -sinx x -sinx C. Cye x -ysinx=C D.y=e x -sinx+C4、求 通解 32.23y x y dx dy x =+ 解：23231x y 23dx dy x y=+-，令32y z =得2x z 23dx dz 23x=+，2x 32z x 1dx dz =+ ⎪⎪⎭⎫ ⎝⎛⎰+⎰=⎰-dx x 12dx x 1e x 32C e z ，⎪⎭⎫ ⎝⎛+⋅=C x 4132x 1y 332，即x C x 61y 232+=，5、求 通解 xdy-ydx=y 2e y dy解：整理得yye x y 1dy dx -=-，C ye dy e ye C e x y dy y 1y dy y 1+-=⎪⎪⎭⎫ ⎝⎛⎰-+⎰=⎰---9、已知连续函数f(x)满足方程x 2x 30e dt 3tf )x (f +⎪⎭⎫⎝⎛=⎰，求f(x)解：原方程两边对x 求导数f '(x)=3f(x)+2e 2xf '(x)-3f(x)=2e 2x 解得：f(x)=Ce 3x -2e 2x 又f(0)=1，所以C=3，f(x)=3e 3x -2e 2x2、数ϕ(x)具有二阶连续导数，且ϕ(0)=ϕ'(0)=0，并已知y ϕ(x)dx+(sinx-ϕ'(x))dy=0是一个全微分方程，则ϕ(x)=( ) x B.2x x 23- C.x 2e x D.x sin C x cos C x sin 2x 21++3、别下列方程的类型并求其通解 （1）(a 2-2xy-y 2)dx-(x+y)2dy=0解：是全微分方程3222y 0x 0y 31xy y x x a dy )y ,x (Q dx )0,x (P )y ,x (u ---=+=⎰⎰，通解为: C y xy y x x a =---322231（2）(1+e 2θ)d ρ+2ρe 2θd θ=0解：是全微分方程d(ρ+ρe 2θ)=0，通解为ρ+ρe 2θ=C4、f(x)可导，f(0)=1，对任意简单闭曲线L,0))(()(2=-+⎰Ldy x x f dx x yf ， 求⎰10dx )x (x f解：对任意闭曲线L 有0dx )x )x (f (dx )x (yf L2=-+⎰，知yP x Q ∂∂=∂∂，由此得f '(x)-2x=f(x)解得：f(x)=Ce x -2x-2,再代入初始条件可得C=3。
于是f(x)=3e x -2x-2，34dx )x (xf 1=⎰ §6 可降阶的高阶微分方程1、yy "+y '2=0满足初始条件y|x=0=1，y '|x=0=21的特解为（ ）A. y 2=x+C 1x y += C. C 1x y ++= D. y 2=C 1x+C 2 2、方程xy "=y 'lny '的通解为（ ）2x C 1C e C 1y 1+= B.2x c 1C e C y 1+= ， C.x C e C y 2x C 11+= D.以上都不对3、 (1) 求y "=y '+x 的通解解：令y '=p 得p '-p=x p=-x-1+C 1e x22x1C x 2x e C y +--=(2) 求xy "+y '=0的通解解：令y '=p ，则xp '+p=0，xdx pdp -= 得 xC p 1= y=C 1lnx+C 2§7 高阶线性微分方程1、证明：x5x 22x 1e 121e C e C y ++=是方程y "-3y '+2y=e 5x 的通解 2、已知二阶线性非齐次方程y "+p(x)y '+q(x)y=f(x)的特解为y 1=x,y 2=e x ,y 3=e 2x ,试求 方程满足初始条件y(0)=1,y '(0)=3的特解。
解：由线性微分方程解的理论，非齐次微分方程y "+p(x)y '+q(x)y=f(x)任两解之差是对应齐次方程y "+p(x)y '+q(x)y=0的解。
得齐次方程的两个解：e x -x,e 2x -x ，且线性无关。
于是齐次方程的通解Y=C 1(e x -x)+C 2(e 2x -x).非齐次方程的通解是y=x+C 1(e x -x)+C 2(e 2x -x).由y(0)=1，y '(0)=3代入得：C 1= -1, C 2=2，所以特解为y=2e 2x -e x§8 常系数齐次线性微分方程1、设y=e x (C 1sinx+C 2cosx) (C 1,C 2 为任意常数)为某二阶常系数齐次线性微分方程 的通解，则该方程为（ ）A.y "+2y '+y=0 "-2y '+2y=0 C.y "-2y '=0 D.y "+y=0 2、设y 1=e x cos2x,y 2=e x sin2x 都是方程y "+py '+qy=0的解，则（ ）A. p=2,q=5, C.p=-3,q=2 D.p=2,q=2 3、设常系数线性齐次方程特征方程根r 1,2= -1,r 3,4=±i ，则此方程通解为 （ ）1+C 2x)e -x +C 3cosx+C 4sinx B.y=C 1e -x +C 2cosx+C 3sinx C. y=C 1e -x +C 2cosx+C 3xsinx D.C 1e -x +(C 2+x)cosx+C 3sinx 4、求下列微分方程的通解(1) y "-4y '+13y=0。
