2018版高考物理一轮复习热点专题突破系列2滑块_滑板模型课件
- 格式:ppt
- 大小:12.93 MB
- 文档页数:24


修养提高微打破02动力学中的“滑块-滑板”模型——建立模型,培育抽象思想意识“滑块 -滑板”模型“滑块 -滑板”模型波及两个物体,而且物体间存在相对滑动。
叠放在一同的滑块和木板,它们之间存在着互相作使劲,在其余外力作用下它们或加快度同样,或加快度不一样,不论哪一种状况受力剖析和运动过程剖析都是重点,特别是对相对运动条件的剖析。
本模型深刻表现了物理运动观点、互相作用观点的核心修养。
如图( a),物块和木板叠放在实验台上,物块用一不行伸长的细绳与固定在实验台上的力传感器相连,细绳水平。
t=0 时,木板开始遇到水平外力 F 的作用,在 t=4 s 时撤去外力。
细绳对物块的拉力 f 随时间 t 变化的关系如图( b)所示,木板的速度 v 与时间 t 的关系如图( c)所示。
木板与实验台之间的摩擦能够忽视。
重力加快度取 g=10 m/s2。
由题给数据能够得出A .木板的质量为 1 kgB .2 s~4 s 内,力 F 的大小为0.4 NC.0~2 s 内,力 F 的大小保持不变D.物块与木板之间的动摩擦因数为一、水平面上的滑块—滑板模型水平面上的滑块—滑板模型是高中参照题型,一般采纳三步解题法:如下图,质量m= 1 kg 的物块 A 放在质量M= 4 kg 的木板 B 的左端,开初A、 B 静止在水平川面上。
现用一水平向左的力 F 作用在 B 上,已知 A、 B 之间的动摩擦因数为μ=,地面与 B 之间的动摩擦因1数为μ2=。
假定最大静摩擦力等于滑动摩擦力,g=10 m/s2。
求:(1)能使 A、 B 发生相对滑动的力 F 的最小值;(2)若力 F = 30 N,作用 1 s 后撤去,要想 A 不从 B 上滑落,则 B 起码多长;从开始到A、 B 均静止, A 的总位移是多少。
二、斜面上的滑块—滑板模型1、抓住重点:一个转折和两个关系一个转折两个关系滑块与滑板达到同样速度转折前、后受力状况之间的关系和滑块、滑板位移与板长之间或许滑块从滑板上滑下是的关系。
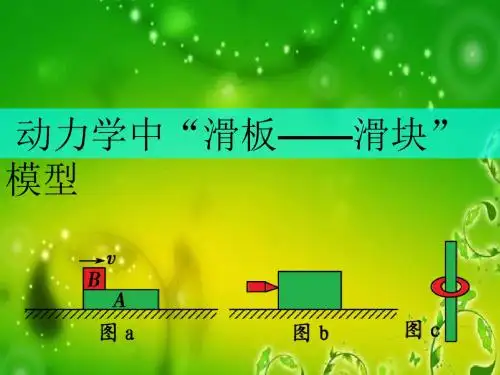


高中物理三种模型带你解决“滑块滑板”问题
滑块滑板问题是高考的热点,也是高一上的一个重难点,在高一上的滑块滑板中它主要涉及到受力分析,运动状况分析,以及牛顿运动定律,综合性较强,所以也成为学生学习感到困难的一部分,滑块滑板看似复杂,掌握好受力分析与运动的分析结合牛顿运动定律,再进行分析就比较轻松了。
类型一.“板—块”模型
1.模型特点
上、下叠放两个物体,在摩擦力的相互作用下两物体发生相对滑动.
2.两种位移关系
滑块由滑板的一端运动到另一端的过程中,若滑块和滑板同向运动,位移之差等于板长;反向运动时,位移之和等于板长.3.解题方法
整体法、隔离法.
4.解题思路
(1)分析滑块和滑板的受力情况,根据牛顿第二定律分别求出滑块和滑板的加速度.
(2)对滑块和滑板进行运动情况分析,找出滑块和滑板之间的位移关系或速度关系,建立方程.特别注意滑块和滑板的位移都是相对地的位移.
类型二.水平传送带问题
滑块在水平传送带上运动常见的三个情景
类型三.倾斜传送带问题
滑块在倾斜传送带上运动常见的四个情景
总结:处理滑块与滑板类问题的基本思路
判断滑块与滑板间是否存在相对滑动是思考问题的着眼点.方法有整体法隔离法、假设法等.即先假设滑块与滑板相对静止,然后根据牛顿第二定律求出滑块与滑板之间的摩擦力,再讨论滑块与滑板之间的
摩擦力是不是大于最大静摩擦力.。

第四讲滑块和滑板一、滑块—滑板类问题分析1.高考分析:滑块一滑板模型题是动力学中比较常见的问题,也是综合性很强的难题,由于从中能很好地考核和反映学生运用动力学规律解决问题的多种能力,具有很好的区分度,因此在历年的高考压轴题中频频出现2.滑块—滑板类问题的特点(1)涉及两个物体,并且物体间存在相对滑动.(2).滑块和滑板常见的两种位移关系滑块由滑板的一端运动到另一端的过程中,若滑块和滑板同向运动,位移之差等于板长;反向运动时,位移之和等于板长.3.滑块—滑板类问题的解题方法(1)此类问题涉及两个物体、多个运动过程,并且物体间还存在相对运动,所以应准确求出各物体在各运动过程的加速度(注意两过程的连接处加速度可能突变),找出物体之间的位移(路程)关系或速度关系是解题的突破口.求解中更应注意联系两个过程的纽带,每一个过程的末速度是下一个过程的初速度.(2).板块模型类问题中,滑动摩擦力的分析方法与传送带类似,但这类问题比传送带类问题更复杂,因为木板往往受到摩擦力的影响也做匀变速直线运动,处理此类问题,要注意从速度、位移、时间等角度寻找各物理量之间的联系。
4.物块不从木板的末端掉下来的临界条件是:物块到达木板末端时的速度与木板的速度恰好相等。
阅卷教师提醒易失分点1.不清楚滑块、滑板的受力情况,求不出各自的加速度.2.画不好运动草图,找不出位移、速度、时间等物理量间的关系.3.不清楚每一个过程的末速度是下一个过程的初速度.4.不清楚物体间发生相对滑动的条件.二、滑块—滑板选择题部分例题1.(多选)如图所示,一只猫在桌边猛地将桌布从鱼缸下拉出,鱼缸最终没有滑出桌面,若鱼缸、桌布、桌面两两之间的动摩擦因数均相等,则在上述过程中()A.桌布对鱼缸摩擦力的方向向左B.鱼缸在桌布上的滑动时间和在桌面上的相等C.若猫增大拉力,鱼缸受到的摩擦力将增大D.若猫减小拉力,鱼缸有可能滑出桌面例题2.如图所示,一足够长的木板静止在光滑水平面上,一物块静止在木板上,木板和物块间有摩擦.现用水平力向右拉木板,当物块相对木板滑动了一段距离但仍有相对运动时,撤掉拉力,此后木板和物块相对于水平面的运动情况为 ( ).A.物块先向左运动,再向右运动B .物块向右运动,速度逐渐增大,直到做匀速运动C .木板向右运动,速度逐渐变小,直到做匀速运动D .木板和物块的速度都逐渐变小,直到为零例题3.放在足够长的木板上的物体A 和B 由同种材料制成,且表面粗糙程度一样,现随长木板以速度v 向右做匀速直线运动,如图所示。

文档来源为 :从网络收集整理 .word 版本可编辑 .欢迎下载支持 .专题 :动力学中的滑块 —滑板模型1、模型特点:上、下叠放两个物体,并且两物体在摩擦力的相互作用下发生相对滑动.2、考点:“滑块 - 木板”类问题,具有涉及考点多(运动学公式、牛顿运动定律、功能关系等) ,情境丰富,设问灵活,解法多样,思维量高等特点,是一类选拔功能极强的试题,也是新课标力学常考的试题。
3、解题思路:( 1)动力学关系 : 受力分析注意摩擦的作用是相互的,灵活运用整体法和隔离法分析,根据牛顿第二定律分别求出滑块和木板的加速度;而出现最大加速度时往往是运动过程出现 临界转折的关键点。
( 2)运动关系:恰好“滑落”或“不滑落”常为找时间关系列位移方程,一般为同向运动位移差为板长,反向运动位移之和为板长。
( 3)能量关系:相互摩擦机械能损失转化为内能,常用能量守恒△ E=f 滑 X 相对。
( 4)区分选修 3-5 动量守恒中的滑块滑板: 要满足动量守恒必不受外力,一般无外界拉力和地面摩擦力。
【典例 1】【临界问题】木板 M 静止在光滑水平面上,木板上放着一个小滑块 m ,与木板之间的动摩擦因数 μ,为了使得 m能从 M 上滑落下来,求下列两种情况下力F 的大小范围。
Fm m F方法归纳:是否滑动的关键在于是否达到最大静摩擦,MM关键在最大静摩擦及最大加速度判断比较【变式一】图所示,在光滑的水平地面上有一个长为L ,质量为 M=4kg 的木板 A ,在木板的左端有一个质量为m=2kg 的小物体 B ,A 、B 之间的动摩擦因数为 μ=0.2 ,当对 B 施加水平向右的力 F 作用时 ( 设 A 、B 间的最大静摩擦力大小与滑动摩擦力大小相等 ) ,( 1)若 F=5N ,则 A 、B 加速度分别为多大?( 2)若 F=10N ,则 A 、B 加速度分别为多大?( 3)在( 2)的条件下,若力 F 作用时间 t =3s , B 刚好到达木板 A 的右端,则木板长 L 应为多少? 【变式二】【 2011·理综课标 I 第 21 题】 如图, 在光滑水平面上有一质量为m 的足够长的木板,其上叠放1一质量为 m 的木块。

第10讲滑板-滑块模型11.模型特点上、下叠放的两个物体,并且两物体在摩擦力的相互作用下发生相对滑动。
2.解题指导(1)分析滑块和木板的受力情况,根据牛顿第二定律分别求出滑块和木板的加速度;(2)对滑块和木板进行运动情况分析,找出滑块和木板之间位移关系或速度关系,建立方程。
(3)通常所说物体运动的位移、速度、加速度都是对地而言的。
在相对运动的过程中相互作用的物体之间位移、速度、加速度、时间一定存在关联。
它就是解决问题的突破口。
(4)求时间通常会用到牛顿第二定律加运动学公式或动量定理:应用动量定理时特别要注意条件和方向,最好是对单个物体应用动量定理求解。
(5)求位移通常会用到牛顿第二定律加运动学公式或动能定理,应用动能定理时研究对象为单个物体或可以看成单个物体的整体。
另外求相对位移时,通常会用到系统能量守恒定律。
(6)求速度通常会用到牛顿第二定律加运动学公式或动能定理或动量守恒定律:应用动量守恒定律时要特别注意系统的条件和方向。
3.两种位移关系滑块由滑板的一端运动到另一端的过程中,若滑块和滑板同向运动,二者位移之差等于滑板长度;反向运动时,二者位移之和等于滑板长。
4.易错点(1)不清楚滑块、滑板的受力情况,求不出各自的加速度;(2)不清楚物体间发生相对滑动的条件。
说明:两者发生相对滑动的条件:(1)摩擦力为滑动摩擦力(动力学条件);(2)二者速度或加速度不相等(运动学条件)。
(其中动力学条件是判断的主要依据)5.分析“滑块—滑板模型”问题时应掌握的技巧(1)分析题中滑块、滑板的受力情况,求出各自的加速度;(2)画好运动草图,找出位移、速度、时间等物理量间的关系;(3)明确每一过程的末速度是下一过程的初速度。
2一、单选题1.(2020·四川省高三三模)如图所示,质量均为M 的物块A 、B 叠放在光滑水平桌面上,质量为m 的物块C 用跨过轻质光滑定滑轮的轻绳与B 连接,且轻绳与桌面平行,A 、B 之间的动摩擦因数为μ,设最大静摩擦力等于滑动摩擦力,重力加速度大小为g ,下列说法正确的是( )A.若物块A 、B 未发生相对滑动,物块A 受到的摩擦力为2f MmgF M m=+B.要使物块A 、B 发生相对滑动,应满足关系1Mm μμ>- C.若物块A 、B 未发生相对滑动,轻绳拉力的大小为mgD.若物块A 、B 未发生相对滑动时,轻绳对定滑轮的作用力为22MmgF M m=+【答案】A【解析】A .若物块A 、B 未发生相对滑动,A 、B 、C 三者加速的大小相等,由牛顿第二定律得()2mg M m a =+对A ,由牛顿第二定律得f F Ma =解得2f MmgF M m=+,故A 正确;B .当A 、B 发生相对滑动时,A 所受的静摩擦力达到最大,根据牛顿第二定律有Mg Ma μ=解得a g μ=以A 、B 、C 系统为研究对象,由牛顿第二定律得()2mg M m a =+解得21Mm μμ=- 故要使物块A 、B 之间发生相对滑动,则21Mm μμ>-,故B 错误; C .若物块A 、B 未发生相对滑动,设轻绳拉力的大小为F ,对C 受力分析,根据牛顿第二定律有mg F ma -=解得F mg ma mg =-<,故C 错误;D .若物块A 、B 未发生相对滑动时,由A 可知,此时的加速度为2f mgMmF a M ==+对C 受力分析,根据牛顿第二定律有mg F ma -=解得22MmgF M m=+根据力的合成法则,可得轻绳对定滑轮的作用力2222+=2MmgN F F M m=+故D 错误。

热点2 滑块—木板模型[热点跟踪专练]1.(多选)如图所示,A 、B 两物块的质量分别为2m 和m ,静止叠放在水平地面上.A 、B间的动摩擦因数为μ,B 与地面间的动摩擦因数为12μ.最大静摩擦力等于滑动摩擦力,重力加速度为g .现对A 施加一水平拉力F ,则( )A .当F <2μmg 时,A 、B 都相对地面静止B .当F =52μmg 时,A 的加速度为13μg C .当F >3μmg 时,A 相对B 滑动D .无论F 为何值,B 的加速度不会超过12μg [解析] 当0<F ≤32μmg 时,A 、B 皆静止;当32μmg <F ≤3μmg 时,A 、B 相对静止,但两者相对地面一起向右做匀加速直线运动;当F >3μmg 时,A 相对B 向右做加速运动,B 相对地面也向右加速,选项A 错误,选项C 正确.当F =52μmg 时,A 与B 共同的加速度a =F -32μmg 3m=13μg ,选项B 正确.F 较大时,取物块B 为研究对象,物块B 的加速度最大为a 2=2μmg -32μmg m=12μg ,选项D 正确. [答案] BCD2.(2017·江西模拟)如图所示,在水平地面上叠放着质量均为M 的A 、B 两块木板,在木板A 的上方放着一个质量为m 的物块C ,木板和物块均处于静止状态.A 、B 、C 之间以及B 与地面之间的动摩擦因数都为μ.若用水平恒力F 向右拉动木板A ,使之从B 、C 之间抽出来,已知重力加速度为g ,最大静摩擦力等于滑动摩擦力.则拉力F 的大小应该满足的条件是( )A .F >μ(2m +M )gB .F >μ(m +2M )gC .F >2μmgD .F >2μ(m +M )g[解析] 要使A 能从B 、C 间抽出来,则A 要相对于B 、C 都滑动,所以A 、C 间与A 、B 间都是滑动摩擦力,对A 有a A =F -μmg -μM +m g M ,对C 有a C =μmg m,B 受到A 对B 的水平向右的滑动摩擦力μ(M +m )g 和地面对B 的摩擦力f ,由于f ≤μ(2M +m )g ,所以A 刚要从B 、C 间抽出时,B 静止不动,即a A >a C 时,A 能从B 、C 间抽出,得F >2μ(M +m )g ,D 对.[答案] D3.(2017·广州模拟)如图所示,光滑水平面上放置质量分别为m 、2m 和3m 的三个木块,其中质量为2m 和3m 的木块间用一根不可伸长的轻绳相连,轻绳能承受的最大拉力为F 0;质量为m 和2m 的木块间的最大静摩擦力为12F 0.现用水平拉力F 拉质量为3m 的木块,使三个木块一起加速运动,下列说法正确的是( )A .质量为2m 的木块受到四个力的作用B .当F 逐渐增大到F 0时,轻绳刚好被拉断C .在轻绳未被拉断前,当F 逐渐增大时,轻绳上的拉力也随之增大,并且大小总等于F 大小的一半D .在轻绳被拉断之前,质量为m 和2m 的木块间已经发生相对滑动[解析] 质量为2m 的木块受到5个力的作用,重力、拉力、压力、支持力和摩擦力,则选项A 错误;对三者整体,应用牛顿第二定律有F =6ma ,对质量为m 和2m 的木块整体,同理有,轻绳拉力T =3ma =F 2,隔离质量为m 的木块,有f =ma =F 6,可知在轻绳未被拉断前,当F 逐渐增大时,轻绳上的拉力也随之增大,并且大小总等于F 大小的一半,则选项C 正确;当F 逐渐增大到F 0时,轻绳拉力T =F 02,轻绳没有达到最大拉力不会被拉断,则选项B 错误;当T逐渐增大到F 0时,f =F 03,质量为m 和2m 的木块间的摩擦力没有达到最大静摩擦力12F 0,故在轻绳被拉断之前,质量为m 和2m 的木块间不会发生相对滑动,选项D 错误.[答案] C4.(多选)(2017·云南昆明质检)如图甲所示,质量m A =1 kg ,m B =2 kg 的A 、B 两物块叠放在一起静止于粗糙水平地面上.t =0时刻,一水平恒力F 作用在物块B 上,t =1 s 时刻,撤去F ,B 物块运动的速度—时间图象如图乙所示,若整个过程中A 、B 始终保持相对静止,则( )A .物块B 与地面间的动摩擦因数为0.2B .1~3 s 内物块A 不受摩擦力作用C .0~1 s 内物块B 对A 的摩擦力大小为4 ND .水平恒力的大小为12 N[解析] 在v -t 图象中图线的斜率大小等于物块运动的加速度大小,则a 1=4 m/s 2,a 2=2 m/s 2,对两物块受力分析,由牛顿第二定律可得:F -μ(m A +m B )g =(m A +m B )a 1,μ(m A +m B )g =(m A +m B )a 2,解得:μ=a 2g=0.2,F =18 N ,选项A 正确,选项D 错误;1~3 s 内两物块一起运动,物块A 也具有水平向左的加速度,对其受力分析,可知:B 对A 施加了水平向左的静摩擦力,选项B 错误;同理在0~1 s 内物块A 也具有水平向右的加速度,对其受力分析,可知:B 对A 施加了水平向右的静摩擦力,由牛顿第二定律可得:f =m A a 1=4 N ,选项C 正确.[答案] AC5.(多选)(2017·云南昆明质检)将A 、B 两物块叠放在一起放到固定斜面上,物块B 与斜面之间的动摩擦因数为μ1,物块A 、B 之间的动摩擦因数为μ2,设最大静摩擦力等于滑动摩擦力,下列说法正确的是( )A.若μ1=0,则物体A、B一定不会发生相对滑动B.若μ1=0,则物体A、B一定会发生相对滑动C.若μ1=μ2,则物体A、B一定会发生相对滑动D.若μ1=μ2,则物体A、B一定不会发生相对滑动[解析] 若物块B与斜面之间的动摩擦因数μ1=0,则A、B一起沿斜面以共同的加速度下滑,一定不会发生相对滑动,选项A正确,B错误;若μ1=μ2,A、B一起沿斜面以共同的加速度下滑,一定不会发生相对滑动,选项C错误,D正确.[答案] AD6.(多选)(2017·河南开封一模)如图所示,质量为M、长为L的木板置于光滑的水平面上,一质量为m的滑块放置在木板左端,滑块与木板间滑动摩擦力大小为f.现用一水平恒力F 作用在滑块上,当滑块运动到木板右端时,木板在地面上移动的距离为s.下列说法正确的是( )A.上述过程中,滑块克服摩擦力做的功为f(L+s)B.其他条件不变的情况下,M越大,s越小C.其他条件不变的情况下,F越大,滑块到达木板右端所用时间越长D.其他条件不变的情况下,F越大,滑块与木板间产生的热量越多[解析] 由功的定义式可知,滑动摩擦力对滑块做功W=-f(L+s),所以滑块克服摩擦力做功为f (L +s ),A 项正确;分别对滑块和木板受力分析,由牛顿第二定律,有F -f =ma 1,f =Ma 2,两物体均做初速度为零的匀加速直线运动,且a 1>a 2,速度图象如图所示.阴影面积表示滑块相对木板的最大位移,即木板的长度.M 越大,木板的速度图线斜率越小,滑块速度图线斜率不变,相对位移一定,故滑块到达木板右端所用时间越短,木板的位移s 越小,B 项正确;F 越大,滑块的速度图线斜率越大,木板的速度图线斜率不变,相对位移一定,由图可知滑块到达木板右端时间越短,C 项错误;滑块与木板之间因摩擦产生的热量Q =fL ,与其他因素无关,D 项错误.[答案] AB7.(2017·郑州质检(二))如图所示,长木板B 的质量为m 2=1.0 kg ,静止放在粗糙的水平地面上,质量为m 3=1.0 kg 的物块C (可视为质点)放在长木板的最右端.一个质量为m 1=0.5 kg 的物块A 从距离长木板B 左侧l =9.5 m 处,以速度v 0=10 m/s 向着长木板运动.一段时间后物块A 与长木板B 发生弹性正碰(时间极短),之后三者发生相对运动,整个过程物块C 始终在长木板上.已知物块A 及长木板与地面间的动摩擦因数均为μ1=0.1,物块C 与长木板间的动摩擦因数为μ2=0.2,物块C 与长木板间的最大静摩擦力等于滑动摩擦力,g 取10 m/s 2,求:(1)碰后瞬间物块A 和长木板B 的速度;(2)长木板B 的最小长度和物块A 与长木板左侧的最终距离.[解析] (1)设物块A 与木板B 碰前的速度为v由动能定理得-μ1m 1gl =12m 1v 2-12m 1v 20 解得v =v 20-2μ1gl =9 m/s A 与B 发生完全弹性碰撞,假设碰撞后瞬间的速度分别为v 1、v 2,由动量守恒定律得m 1v =m 1v 1+m 2v 2由机械能守恒定律得12m 1v 2=12m 1v 21+12m 2v 22 联立解得v 1=m 1-m 2m 1+m 2v =-3 m/s ,v 2=2m 1m 1+m 2v =6 m/s (2)之后B 做减速运动,C 做加速运动,B 、C 达到共同速度之前,由牛顿运动定律 对木板B 有-μ1(m 2+m 3)g -μ2m 3g =m 2a 1对物块C 有μ2m 3g =m 3a 2设从碰撞后到两者达到共同速度经历的时间为t ,v 2+a 1t =a 2t木板B 的最小长度d =v 2t +12a 1t 2-12a 2t 2=3 m B 、C 达到共同速度之后,因μ1<μ2,二者一起减速至停下,由牛顿运动定律得-μ1(m 2+m 3)g =(m 2+m 3)a 3整个过程B 运动的位移为x B =v 2t +12a 1t 2+0-a 2t 22a 3=6 mA 与B 碰撞后,A 做减速运动的加速度也为a 3,位移为x A =0-v 212a 3=4.5 m 物块A 与长木板B 左侧的最终距离为x A +x B =10.5 m[答案] (1)-3 m/s 6 m (2)3 m 10.5 m8.如图所示,在光滑水平地面上放置一质量M =2 kg 的长木板,木板上表面与固定的竖直弧形轨道相切.一质量m =1 kg 的小滑块自A 点沿弧面由静止滑下,A 点距离长木板上表面的高度h =0.6 m ,滑块在木板上滑行t =1 s 后,和木板以共同速度v =1 m/s 匀速运动,取g =10 m/s 2.求:(1)滑块与木板间的摩擦力大小;(2)滑块沿弧面下滑过程中克服摩擦力做的功;(3)滑块自A 点沿弧面由静止滑下到与木板共同运动过程中产生的内能.[解析] (1)滑块在木板上滑行时,对木板,根据牛顿第二定律有F f =Ma 1由运动学公式得v =a 1t代入数据解得F f =2 N.(2)滑块在木板上滑行时,对滑块,根据牛顿第二定律有-F f =ma 2设滑块滑上木板时的初速度为v 0,则有v -v 0=a 2t代入数据解得v 0=3 m/s滑块沿弧面下滑的过程,由动能定理得mgh +W f =12mv 2解得摩擦力做功W f 为-1.5 J ,所以克服摩擦力做功为1.5 J ,此过程中产生的内能Q 1=1.5 J.(3)滑块在木板上滑行,t =1 s 时木板的位移为s 1=12a 1t 2 此过程中滑块的位移为s 2=v 0t +12a 2t 2 故滑块相对木板滑行的距离为L =s 2-s 1=1.5 m所以Q 2=F f ·L =3 J ,则Q =Q 1+Q 2=4.5 J.[答案] (1)2 N (2)1.5 J (3)4.5 J9.如图所示,光滑水平面上有一质量为M =2 kg 的足够长木板,木板上最右端有一可视为质点的小物块,其质量为m =3 kg ,小物块与木板间的动摩擦因数为μ=0.4,且最大静摩擦力等于滑动摩擦力.开始时小物块与木板均静止,距木板左端L =2.4 m 处有一固定在水平面上的竖直弹性挡板P .现对小物块施加一水平向左的拉力F =6 N ,使小物块和木板向左运动.若不考虑木板与挡板P 发生碰撞时的能量损失,整个运动过程中小物块始终没有与挡板发生碰撞,重力加速度g 取10 m/s 2.(1)求木板第一次与挡板P 碰撞前瞬间的速度大小;(2)求木板从第一次撞击挡板P 到运动至距挡板最远处所需的时间及此时小物块距木板右端的距离;(3)若木板每次与挡板P 碰撞前小物块均已与木板保持相对静止,试求当木板与小物块均静止时,小物块距木板最右端的距离为多少?[解析] (1)设木板靠最大静摩擦力或滑动摩擦力产生的加速度大小为a 1,则有a 1=μmg M=6 m/s 2若木板与小物块间不发生相对滑动,设其共同加速度大小为a 2,则有a 2=F M +m =1.2 m/s 2因a 1>a 2,故小物块将与木板一起以共同的加速度a 2向左做加速运动设木板与挡板P 碰撞前瞬间木板与小物块的共同速度大小为v ,则有:v 2=2a 2L代入数据可解得v =2.4 m/s.(2)设木板第一次撞击挡板P 后向右运动时,小物块的加速度大小为a 3,则由牛顿第二定律可得μmg -F =ma 3代入数据解得a 3=2 m/s 2,故小物块将以a 3=2 m/s 2的加速度向左做匀减速直线运动 由于木板撞击挡板P 时无能量损失,故木板向右运动的初速度大小为v 1=2.4 m/s.由题意可知,此时木板将向右做匀减速直线运动,减速运动的加速度大小为a 1=6 m/s 2.由于a 1>a 3,所以当木板的速度减为零时,小物块仍在向左运动设木板第一次撞击挡板P 到运动至距挡板最远处所需要的时间为t ,小物块距木板右端的距离为Δx ,则有t =v 1a 1=0.4 s 设此段时间内木板向右运动的距离为x 1,则有x 1=v 212a 1=0.48 m 设此段时间内小物块向左运动的距离为x 2,则有x 2=vt -12a 3t 2=0.8 m Δx =x 1+x 2=1.28 m.(3)由题意可知,木板最终静止在挡板P 处,小物块最终静止在木板上,设此时小物块距木板最右端的距离为Δx ′,由功能关系可得F (Δx ′+L )-μmg Δx ′=0代入数据可解得Δx ′=2.4 m.[答案] (1)2.4 m/s (2)0.4 s 1.28 m (3)2.4 m。