答案 控制系统的状态空间描述 习题解答
- 格式:doc
- 大小:842.00 KB
- 文档页数:6
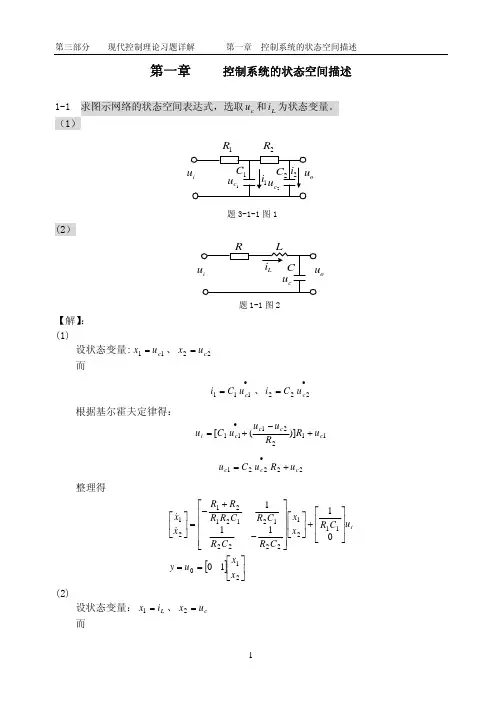



第八章 线性系统的状态空间分析与综合习题及解答8-1 已知电枢控制的直流伺服电机的微分方程组及传递函数 b aaa a a E dtdi L i R U ++=+ ⑴设状态变量m m x θ=1,m x θ =2,θ =3x 及输出量m y θ=,试建立其动态方程; ⑵设状态变量m m a x x i x θθ ===321,,及 my θ=,试建立其动态方程。
解:(1)由题意可知: ⎪⎪⎩⎪⎪⎨⎧=======123121xy xx x x x m m mmθθθθ ,由已知 ⎪⎪⎩⎪⎪⎨⎧+===++=m m m m m a m mmb ba a a a a f J M i C M K E E i L i R U θθθ可推导出 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=++-+-===12333221x y U J L C x J L C K f R x J L R J L f x x x x x a ma mm a m b m a m a a m a m 由上式,可列动态方程如下=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+-+-m a a m m a m a m b m a J L R J f L J L C K f R 0100010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x +⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡m a m J L C 00a U y =[]001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡321x x x(2)由题意可知:,1a i x =mm m y x x θθθ===,,32可推导出 ⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==-=-====+--=+--==23133231111x y x J f x J C J f i J C x x x U L x L K x L R U L L K i L R i x m m m m m m m m a m m m m a aa b a a a a m a b a a a aθθθθθ可列动态方程如下由 ⎪⎩⎪⎨⎧===mm m x x x θθθ 321和 ⎪⎩⎪⎨⎧===mm a x x i x θθ 321得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=-======3133221x J f x J C J f i J C x x x x x m m m m m m m a m m m m m θθθθ 由上式可得变换矩阵为 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=m m mm J f J C T 0100018-2 设系统微分方程为 u y y yy 66116=+++ 。
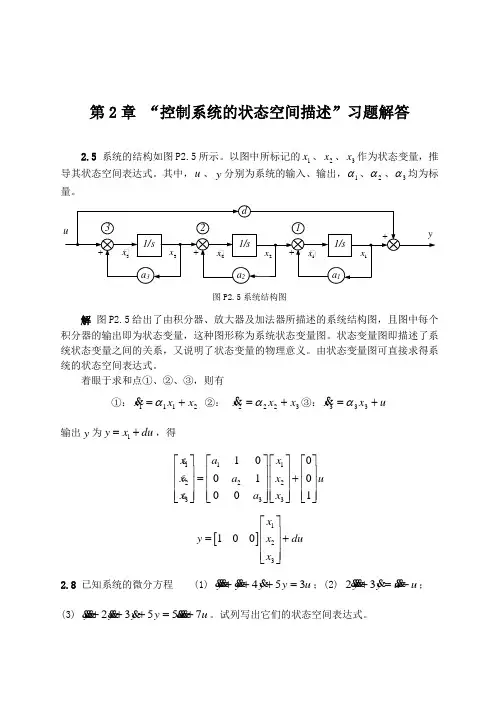
第2章 “控制系统的状态空间描述”习题解答2.5 系统的结构如图P2.5所示。
以图中所标记的1x 、2x 、3x 作为状态变量,推导其状态空间表达式。
其中,u 、y 分别为系统的输入、输出,1α、2α、3α均为标量。
3x 2x 图P2.5系统结构图解 图P2.5给出了由积分器、放大器及加法器所描述的系统结构图,且图中每个积分器的输出即为状态变量,这种图形称为系统状态变量图。
状态变量图即描述了系统状态变量之间的关系,又说明了状态变量的物理意义。
由状态变量图可直接求得系统的状态空间表达式。
着眼于求和点①、②、③,则有①:2111x x x +=α& ②: 3222x x x +=α&③:u x x +=333α&输出y 为1y x du =+,得11122233310001001x a x x a x u x a x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦&&& []123100x y x du x ⎡⎤⎢⎥=+⎢⎥⎢⎥⎣⎦2.8 已知系统的微分方程 (1) u y y y y 354=+++&&&&&&;(2) u u y y -=+&&&&&&32; (3) u u y y y y 75532+=+++&&&&&&&&&。
试列写出它们的状态空间表达式。
(1) 解 选择状态变量1y x =,2yx =&,3y x =&&,则有:122331231543x x x x x x x x u y x =⎧⎪=⎪⎨=---+⎪⎪=⎩&&& 状态空间表达式为:[]112233123010000105413100x x x x u x x x y x x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦&&&(2) 解 采用拉氏变换法求取状态空间表达式。

《现代控制理论》第一章习题解答1.1线性定常系统和线性时变系统的区别何在?答:线性系统的状态空间模型为:x = AxBu+y CxDu= +线性定常系统和线性时变系统的区别在于:对于线性定常系统,上述状态空间模型中的系数矩阵A,B,C和中的各分量均为常数,而对线性时变系统,其系数矩阵D A,B,C和D中有时变的元素。
线性定常系统在物理上代表结构和参数都不随时间变化的一类系统,而线性时变系统的参数则随时间的变化而变化。
1.2 现代控制理论中的状态空间模型与经典控制理论中的传递函数有什么区别?答: 传递函数模型与状态空间模型的主要区别如下:1.3 线性系统的状态空间模型有哪几种标准形式?它们分别具有什么特点?答: 线性系统的状态空间模型标准形式有能控标准型、能观标准型和对角线标准型。
对于n 阶传递函数G s( )= b s n−s1nn+−1a s+n−b s1n−n2−1n+−2 + +as a+1 bs b+1 +0 0+d ,分别有⎧⎡0 1 0 0 ⎤⎡⎤0⎪⎢0 0 1 0 ⎥⎥⎢⎥⎢⎥0⎪⎢⎪⎪x =⎢ ⎥x+⎢⎥ u ⑴能控标准型:⎨⎢0 0 0 1 ⎥⎥⎢⎥⎢⎥0⎪⎢⎪⎣⎢−a0 −a1 −a2 −a n−1⎥⎦⎢⎥⎣⎦1⎪⎪⎩y=[b0 b1 b n−2 b n−1]x du+⎧⎡0 0 0 −a0 ⎤⎡b0 ⎤⎪⎪⎢⎢1 0 0 −a1 ⎥⎥⎢⎢b1 ⎥⎥⎪⎪x =⎢0 1 0 −a2 ⎥⎥x+⎢⎢ ⎥⎥u⑵能观标准型:⎨⎢b n−2⎥⎪⎢ ⎥⎢⎪⎣⎢0 0 1 −a n−1⎦⎥⎢⎣b n−1⎥⎦⎪⎪⎩y=[0 0 0 1]x du+⎧⎡p1⎪⎢0⎪x =⎢⎢ 0 p20 0 ⎤⎡1⎤0 ⎥⎢1⎥⎥x+⎢⎥u ⎥⎢ ⎥⎪⑶对角线标准型:⎨⎪⎢⎣0⎪p n⎥⎦⎢⎣1⎥⎦⎪⎩y=[c1 c2 c x du n] + 式中的pp1, 2,, p n和c c1, 2,, c n可由下式给出,G s( )= b s n−s1nn−1a s+n−b s1n−n2−1n+−2 + +as a+1 bs b+1 +0 0 + =d s p−c1 1 + s p−c2 2 + + s p−c n n +d+能控标准型的特点:状态矩阵的最后一行由传递函数的分母多项式系数确定,其余部分具有特定结构,输出矩阵依赖于分子多项式系数,输入矩阵中的元素除了最后一个元素是1 外,其余全为0。
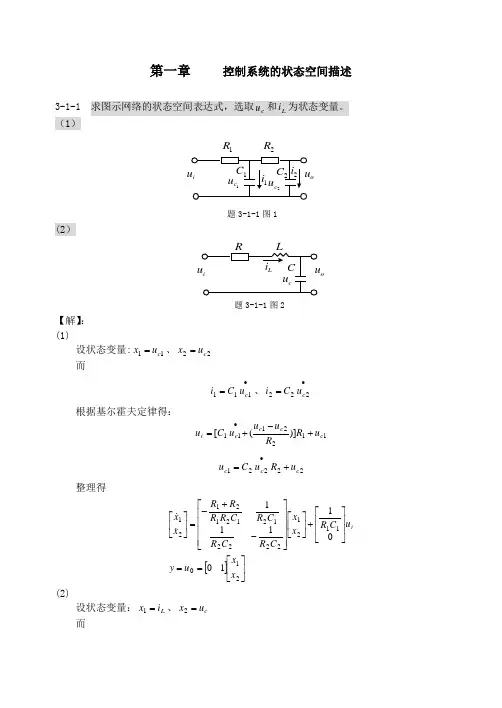
第一章 控制系统的状态空间描述3-1-1 求图示网络的状态空间表达式,选取c u 和L i 为状态变量。
(1)1R 2Ro题3-1-1图1(2)o题3-1-1图2【解】: (1)设状态变量:11c u x =、22c u x =而•=111c u C i 、•=222c u C i根据基尔霍夫定律得:1122111)]([c c c c i u R R u u u C u +-+=•22221c c c u R u C u +=•整理得[]⎥⎦⎤⎢⎣⎡==⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+-=⎥⎦⎤⎢⎣⎡210112122221212121211001111x x u y u C R x x C R C R C R C R R R R x x i(2)设状态变量:L i x =1、c u x =2 而•=c L u C i根据基尔霍夫定律得:c L L i u i L i R u ++⋅=•整理得[]⎥⎦⎤⎢⎣⎡==⎥⎥⎦⎤⎢⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎦⎤⎢⎣⎡21021211001011x x u y u L x x CL L R x x i【解】:此题多解,一般可以写成能控标准型、能观标准型或对角标准型,以下解法供参考。
(1)[]xy u x x 1111006116100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=结构图如图题3-1-5图1所示题3-1-5图1(2)655216552656513)(22222+++-=++--++=++++=s s s s s s s s s s s s s G uy u x x +--=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=]25[105610 结构图如图题3-1-5图2(a )所示题3-1-5图2(a)或有312116513)(22+-+-=++++=s s s s s s s G []ux y u x x +--=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=11113002 结构图如图题3-1-5图2(b )所示y题3-1-5图2(b)(3))3()1(4)(2++=s s s s G)1(1)1(2)3(3134)(2+-++-++-+=s s s s s G xy u x x⎥⎦⎤⎢⎣⎡---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=12313410111000110000300000 结构图如图题3-1-5图3所示题3-1-5图3(4)13332)(232+++++=s s s s s s G []xy u x x 123100331100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=结构图如图题3-1-5图4所示y题3-1-5图43-1-6 将下列状态方程化成对角标准型。

§3.3 Matlab 实验
1. 状态空间模型脉冲响应、阶跃响应和任意输入响
应
(1) [y,x,t]=impulse(a,b,c,d)
(2) [y,x,t]=step(a,b,c,d),其中y、x 和t 是输出、
状态向量和仿真时间。
(3) [y,x]=lsim(a,b,c,d,u,t,x0)。
例求管亠[0* x c£,为
u(t) =sint的状态输出值。
解程序和结果如下
-0.2
-0.4
2. 离散系统的脉冲响应、阶跃响应、任意输入响应
⑴[y, x]=dimpulse(sys);
(2) [y, x] = dstep( nu m,de n);
(3) [y, x]=dlsim(sys,u); 47y、x 和u 分别为输出、
状态和输入,sys可以是num,den或a,b,c,d,不绘图,当无y, x时直接绘图。
3 •连续和离散状态模型的零输入响应(只对初态x0 响应)
(1) [y,x,t]=i nitial(a,b,c,d,xO)
⑵[y,x,t]=dinitial(a,b,c,d,x0) ,y 为输出,x 为状态,
t为指定输出时间。
当不带y、x和t时,直接绘图。
4 •连续系统离散化
(1) [da,db,dc,dd]=c2dm(a,b,c,d,Ts)
⑵[dnum,dden]=c2d(num,den,Ts) , Ts 是采样周期。
5.矩阵指数
expm(a*t),其中t可为符号变量,也可为实值。
0 1
例如设A = 0',则求e At的命令和结果如下:
||-4 -4。

第五章 状态反馈和状态观测器3-5-1 已知系统结构图如图题3-5-1图所示。
(1)写出系统状态空间表达式;(2)试设计一个状态反馈矩阵,将闭环极点特征值配置在j 53±-上。
)(t y题3-5-1图【解】:方法一:根据系统结构直接设状态变量如题3-5-1图所示,写状态空间表达式:[]x y u x x10112101=⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--=23111=⎥⎦⎤⎢⎣⎡--=cc Urank U系统能控,可以设计状态反馈阵。
设状态反馈阵为][21k k K = 状态反馈控制规律为:Kxr u -=求希望特征多项式:34625)3()(*22++=++=s s s s f求加入反馈后的系统特征多项式:)22()3()(1212k s k k sbK A sI s f ++-++=+-=依据极点配置的定义求反馈矩阵:]1316[131634)22(6)3(21112=⎩⎨⎧==⇒⎩⎨⎧=+=+-K k k k k k方法二:[][][]1316)346(311110)(*10211=++⎥⎦⎤⎢⎣⎡--==--I A AA f U K c方法三:(若不考虑原受控对象的结构,仅从配置极点位置的角度出发) 求系统传递函数写出能控标准型:2321)111()()(2++-=+-+=s sss s s U s Y[]xy u x x10103210-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=求系统希望特征多项式:34625)3()(*22++=++=s s s s f求状态反馈矩阵K ~:[][][]33236234~21=--==k k K[][][][]5.05.031111010111=⎥⎦⎤⎢⎣⎡--==--Ab b P⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=105.05.011A P P P[]1316~==P K K【解】:依据系统传递函数写出能控标准型sss s s s s U s Y 2310)2)(1(10)()(23++=++=[]xy u x x0010100320100010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=求系统希望特征多项式:464]1)1)[(2()(*232+++=+++=s s s s s s f求状态反馈矩阵:[][][]144342604321=---==k k k K 。
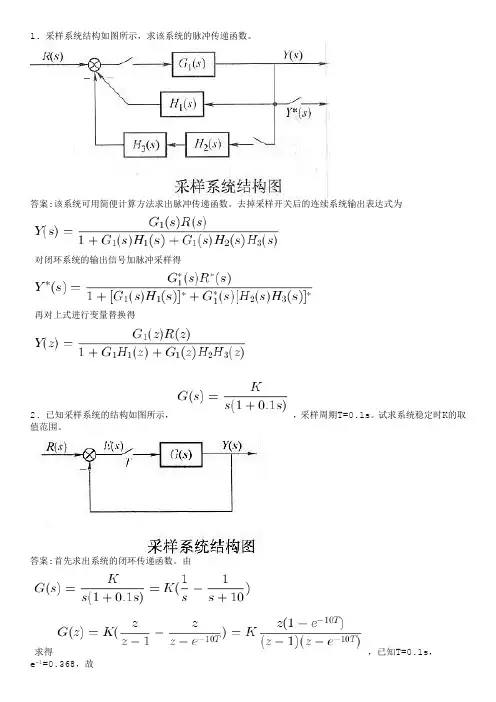
1. 采样系统结构如图所示,求该系统的脉冲传递函数。
答案:该系统可用简便计算方法求出脉冲传递函数。
去掉采样开关后的连续系统输出表达式为对闭环系统的输出信号加脉冲采样得再对上式进行变量替换得2. 已知采样系统的结构如图所示,,采样周期=0.1s。
试求系统稳定时K的取值范围。
答案:首先求出系统的闭环传递函数。
由求得,已知T=0.1s,e-1=0.368,故系统闭环传递函数为,特征方程为D(z)=1+G(z)=z2+(0.632K-1.368)z+0.368=0将双线性变换代入上式得+1 4 +( 7 -0.632K)=0要使二阶系统稳定,则有K>0,2.736-0.632K>0故得到K的取值范围为0<K<4.32。
3. 求下列函数的z变换。
(1). e(t)=te-at答案:e(t)=te-at该函数采样后所得的脉冲序列为e(nT)=nTe-anT n=0,1,2,…代入z变换的定义式可得E(z)=e(0)+P(T)z-1+e(2T)z-2+…+e(n )z-n+…= + e-aT z-1+2Te-2aT z-2+…+n e-naT z-n+…= (e-aT z-1+2e -2aT z-2+…+ne-naT z-n+…)两边同时乘以e-aT z-1,得e-aT z-1E(z)=T(e-2aT z-2+2e-3aT z-3+…+ne-a(n+1)T z-(n+1)+…)两式相减,若|e-aT z-1|<1,该级数收敛,同样利用等比级数求和公式,可得最后该z变换的闭合形式为(2). e( )=答案 e( )=对e( )= 取拉普拉斯变换.得展开为部分分式,即可以得到化简后得(3).答案:将上式展开为部分分式,得查表可得(4).答案:对上式两边进行z变换可得得4. 求下列函数的z反变换(1).答案:由于所以得所以可得(z)的z反变换为e(nT)=10(2n-1)(2).答案:由于所以得所以E(z)的z反变换为e(nT)=-n-1n+2n=2n-n-1(3).答案:由长除法可得E(z)=2z-1-6z-3+10z-5-14z-7+…所以其反变换为e*( )= δ( -T)- δ( - )+1 δ( -5T)-14δ( -7 )+18δ( -9 )+…(4).答案:解法1:由反演积分法,得解法2:由于所以得最后可得z 反变换为5. 分析下列两种推导过程:(1). 令x(k)=k1(k),其中1(k)为单位阶跃响应,有答案:(2). 对于和(1)中相同的(k),有x(k)-x(k-1)=k-(k-1)=1试找出(2)与(1)中的结果为何不同,找出(1)或(2)推导错误的地方。
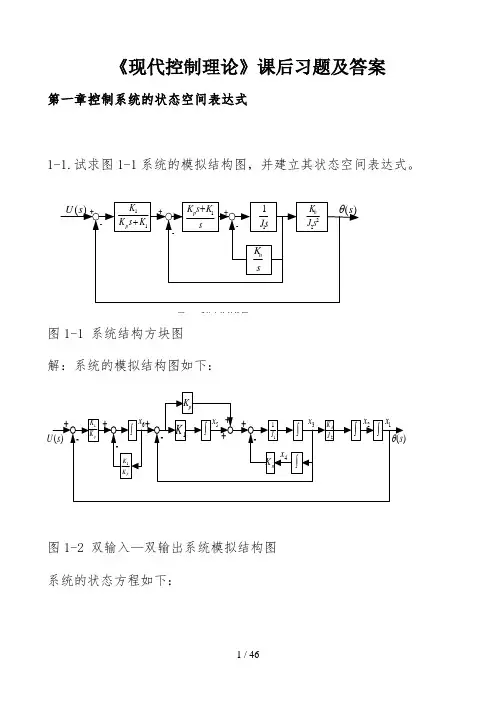
《现代控制理论》课后习题及答案第一章控制系统的状态空间表达式1-1.试求图1-1系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图图1-1 系统结构方块图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图图1-2 双输入—双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••6543211654321111111126543210000010000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2.有电路如图1-3所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图图1-3 电路图解:由图,令32211,,x u x i x i c===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
第1章 作业:34P 习题1.1,1.2,1.3,1.4,1.5,1.7,1.13,1.16,1.171.1 线性定常系统和线性时变系统的区别何在?答:线性定常系统的系统矩阵A 、输入矩阵B 、输出矩阵C 、直接传递矩阵D 都不与时间有t 关,而线性时变系统D C B A 、、、中至少有一个与时间有关。
1.2 现代控制理论中的“状态空间模型”与经典控制理论中的“传递函数”有什么区别?答:“传递函数”只描述系统的外部特性,并不能完全反映系统内部的动态特征,传递函数只考虑0初始条件,难以反映系统非0初始条件对系统性能的影响。
“状态空间模型”用状态变量来刻画系统内部特征,系统的动态特性用状态变量的一阶微分方程来描述,“状态空间模型”描述了系统的输入、输出与内部状态之间的关系,揭示了系统内部状态的运动规律,反映了控制系统动态特性的全部信息。
1.3 线性系统的状态空间模型有哪几种标准形式,他们分别具什么特点? 答:能控标准型18P (1.2.10),能观标准型26P 第1行、第2行,约当标准型23P (1.2.13),对角型21P 倒数第8行、第9行。
1.4 对于同一个系统,状态变量的选择是否唯一?答:状态变量的选择不唯一,状态空间模型也不唯一。
1.5 单输入单输出系统的传递函数在什么情况下,其状态空间实现中的直接转移项D 不等于0,其参数如何确定?答:当传递函数为假分式,即分子多项式最高次方大于分母多项式最高次方时,直接转移项D 不等于0,并且可以用长除法确定直接转移项D 。
1.7 已知系统的传递函数656)()()(2+++==s s s s U s Y s G ,求其状态空间实现的能控标准型和能观标准型。
解:能控标准型u x x ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛--=105610 ,⎪⎪⎭⎫ ⎝⎛=21)16(x x y 能控标准型u x x ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛--=165610 ,⎪⎪⎭⎫ ⎝⎛=21)10(x x y 1.13 一个传递函数的状态空间实现是否唯一?由状态空间模型导出的传递函数是否唯一?答:一个传递函数的状态空间有多种“实现”,由状态空间模型只能导出唯一的传递函数。
第二章 状态空间表达式的解3-2-1 试求下列矩阵A 对应的状态转移矩阵φ(t )。
(1) ⎥⎦⎤⎢⎣⎡-=2010A(2) ⎥⎦⎤⎢⎣⎡-=0410A(3)⎥⎦⎤⎢⎣⎡--=2110A (4)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=452100010A(5)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=00100001000010A (6)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=λλλλ0100010000A【解】: (1)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+-=-=Φ-----)2(10)2(11}201{])[()(11111s s s s L s sL A sI L t⎥⎥⎦⎤⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-=---ttees s s s L 22105.05.01)2(10)2(5.05.01(2)⎥⎦⎤⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+=⎥⎦⎤⎢⎣⎡-=-=Φ-----t tt ts s s s s s L s sL A sI L t 2cos 2sin 22sin 5.02cos 444414}41{])[()(222211111(3)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++-+++=⎥⎦⎤⎢⎣⎡+-=-=Φ-----222211111)1()1(1)1(1)1(2}211{])[()(s s s s s s L s s L A sI L t⎥⎥⎦⎤⎢⎢⎣⎡--+=Φ------tttttt teetete e te t )((4)特征值为:2,1321===λλλ。
由习题3-1-7(3)得将A 阵化成约当标准型的变换阵P 为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=421211101P ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=-1211321201P线性变换后的系统矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==-20010011~1AP P A⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=t tt ttA e ete e e2~0000⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡===Φ-121132120000421211101)(21~t t tttA Ate te eePPeet⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--++-----++-----++--=Φt t ttt tt t t t t t t tt tt t ttt t tt t t e te eete ee te e e te e e te e ete e ete e e te e tee t 34838424225342222322)(222222222(5)为结构四重根的约旦标准型。
习题7-1下面的微分方程代表了线性定常系统,请写出它们对应的状态空间表达(a ))(5)()(4)(22t r t c dtt dc dt t c d =++(b ))()()()(4)(5)(02233t r d c t c dtt dc dt t c d dt t c d t =++++⎰ττ (c )dtt dr t r t c dt t c d dt t c d )(4)()()(2)(2233+=++ 7-2 已知线性定常系统的状态方程为:Ax x =.,其中(1)⎥⎦⎤⎢⎣⎡-=2010A (2) ⎥⎦⎤⎢⎣⎡-=0110A (3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=010100010A 试求系统统的状态转移矩阵At e答案:(1)⎥⎦⎤⎢⎣⎡-=--tt Ate e e2205.05.01 (2)⎥⎦⎤⎢⎣⎡-=t t t t e Atcos sin sin cos (3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+-+-=------)(5.0)(5.00)(5.0)(5.001)(5.0)(5.01t t t t t t t t t t t t Ate e e e e e e e e e e e e 7-3 已知系统的状态方程为:u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=103210.,初始条件为⎥⎦⎤⎢⎣⎡=10)0(x ,试求单位阶跃收入时系统的时间响应x(t)答案:(1)求状态转移矩阵 先求出预解矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+++-+-+++-++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++-+++++=⎥⎦⎤⎢⎣⎡+-=---)2(2)1(1)2(2)1(2)2(1)1(1)2(1)1(2)2)(1()2)(1(2)2)(1(1)2)(1()3(321)(11s s s s s s s s s s s s s s s s s s s s A sI对上式进行拉式反变换,即可定出:⎥⎦⎤⎢⎣⎡+-+---=--------t t t t t t t t At2222e 2e e 2e 2e e e e 2e(2)求系统的时间响应()0022()2()()2()22()2()()2()022()e e ()d 002e e e e 2e e e e d 112e 2e e 2e 2e 2e e 2e 0.50.5tAt A t t t t t t t t t t t t t t t t t t t tx t x Bu e e ττττττττττττ---------------------------=+⎡⎤⎡⎤----⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥-+-+-+-+⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤-=⎢⎥⎣⎦⎰⎰7-4 已知矩阵:(1)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=t t t t t sin cos 0cos sin 0001)(ϕ (2)⎥⎦⎤⎢⎣⎡--+=-t t t t t t t e e e e e e e t 222222)(ϕ 试问:它们可能是某个系统的状态转移矩阵吗?为什么?答案:I =)0(ϕ时才是状态转移矩阵,所以上述两个矩阵均不是某个系统的状态转移矩阵。
第一章 控制系统的状态空间描述1-1 求图示网络的状态空间表达式,选取C u 和i 为状态变量。
RL +1-2 已知系统微分方程,试将其变换为状态空间表达式。
(1)u y y y y 2642=+++(2)u u y yy 237+=++(3)u u u y y yy 23745++=+++(4)u u u u y y y y 81786116+++=+++1-3试画出如图所示系统的状态变量图,并建立其状态空间表达式。
1-4 已知系统的传递函数,试建立其状态空间表达式,并画出状态变量图。
(1)61161)(232+++++=s s s s s s G (2)6513)(22++++=s s s s s G(3))3()1(4)(2++=s s s s G (4)13332)(232+++++=s s s s s s G1-5 已知系统233)()(2+++=s s s s U s Y ,试求其能控标准型和对角标准型。
1-6 已知系统传递函数,试用并联法求其状态空间表达式。
(1)61161)(23+++=s s s s G (2)2545)(23+++=s s s s G1-7 试求下列状态方程所定义系统的传递函数。
⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡21212121211001101142510x x y y u u x x x x1-8 试将下列状态方程化为对角标准型。
(1)u(t)x(t)(t)x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=106510(2)u(t)x(t)(t)x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=1751326712203010(3)u(t)x(t)(t)x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=01161161000101-9 试将下列状态方程化为约当标准型。
(1)u(t)x(t)(t)x⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=102112(2)u(t)x(t)(t)x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=357213*********(3)u(t)x(t)(t)x ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=100452100010第二章 线性控制系统状态空间表达式的解2-1 试求下列系统矩阵A 对应的状态转移矩阵。
第2章 “控制系统的状态空间描述”习题解答
系统的结构如图所示。
以图中所标记的1x 、2x 、3x 作为状态变量,推导其状态空间表达式。
其中,u 、y 分别为系统的输入、输出,1α、2α、3α均为标量。
3
x 2
x 图系统结构图
解 图给出了由积分器、放大器及加法器所描述的系统结构图,且图中每个积分器的输出即为状态变量,这种图形称为系统状态变量图。
状态变量图即描述了系统状态变量之间的关系,又说明了状态变量的物理意义。
由状态变量图可直接求得系统的状态空间表达式。
着眼于求和点①、②、③,则有
①:2111x x x +=α& ②: 3222x x x +=α&③:u x x +=333α&
输出y 为1y x du =+,得
1112223331000100
1x a x x a x u x a x ⎡⎤
⎡⎤⎡⎤⎡⎤
⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦
&&& []123100x y x du x ⎡⎤
⎢⎥=+⎢⎥
⎢⎥⎣⎦
已知系统的微分方程 (1) u y y y y 354=+++&&&&&&
;(2) u u y y -=+&&&&&&32; (3) u u y y y y 75532+=+++&&&&&&&&&。
试列写出它们的状态空间表达式。
(1) 解 选择状态变量1y x =,2y
x =&,3y x =&&,则有:
1223
31231
543x x x x x x x x u y x =⎧⎪=⎪⎨
=---+⎪⎪=⎩&&& 状态空间表达式为:[]112233123010000105413100x x x x u x x x y x x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦
⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦
&&&
(2) 解 采用拉氏变换法求取状态空间表达式。
对微分方程(2)在零初试条件
下取拉氏变换得:
3222332()3()()()
11()12
23()232
s Y s sY s s U s U s s Y s s U s s s s s
+=---==++ 由公式、可直接求得系统状态空间表达式为
1122330100001031002x x x x u x x ⎡⎤
⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢
⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦-⎢⎥
⎣⎦
&&& 123110
2
2x y x x ⎡⎤⎡⎤⎢⎥
=-
⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦
(3) 解 采用拉氏变换法求取状态空间表达式。
对微分方程(3)在零初试条件
下取拉氏变换得:
323()2()3()5()5()7()s Y s s Y s sY s Y s s U s U s +++=+
332
()57
()235
Y s s U s s s s +=+++ 在用传递函数求系统的状态空间表达式时,一定要注意传递函数是否为严格真有理分式,即m 是否小于n ,若m n =需作如下处理
323232()57101518
5()235235
Y s s s s U s s s s s s s +---==+++++++ 再由公式、可直接求得系统状态空间表达式为
112233010000105321x x x x u x x ⎡⎤
⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦&&& []1231005x y x u x ⎡⎤
⎢⎥=+⎢⎥⎢⎥⎣⎦
已知下列传递函数,试用直接分解法建立其状态空间表达式,并画出状态变量
图。
(1)3321()6116s s g s s s s ++=+++ (2)23223
()231
s s g s s s s ++=+++
(1) 解
首先将传函(1)化为严格真有理式即:
232
()6105()11()()6116
Y s s s g s g s U s s s s ---'==+=++++ 令()
()()
Y s g s U s ''=
',则有 123
123
6105()()16116s s s Y s U s s s s
---------''=+++, 123
1
()()
16116E s U s s s s ---''=+++,
即:
1231
2
3
()()6()11()6()()6()10()5()
E s U s s E s s E s s E s Y s s E s s E s s E s ------'=---'=---
由上式可得状态变量图如下:
由状态变量图或公式、直接求得能控标准型状态空间表达式
1122330100001061161x x x x u x x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦
&&& []123x y x u x ⎡⎤
⎢⎥+⎢⎥
⎢⎥⎣⎦
=-6-11-6
(2) 解 由已知得:
123
123
23()()123s s s Y s U s s s s
------++=+++, 令: 123
1
()()
123E s U s s s s ---=+++,
得: 1231
2
3
()()2()3()()()()2()3()
E s U s s E s s E s s E s Y s s E s s E s s E s ------=---=++
状态变量图如下:
状态表达式如下:
112233010000101321x x x x u x x ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦
⎣⎦⎣⎦⎣⎦
&&& []123321x y x x ⎡⎤
⎢⎥=⎢⎥
⎢⎥⎣⎦
列写图所示系统的状态空间表达式。
图
解 设 11()()x s y s = (7) ; 22()()x s y s = (8) 则由系统方框图 2.10P 可得:[]
112()()()c
x s u s x s s a
=-+ (9) []221()()()d
x s u s x s s b
=-+ (10)
对式()()710-进行拉氏反变换得
112121221122()()()()()()()()()()()()
x t ax t cx t cu t x t dx t bx t du t y t x t y t x t =--+=--+==&&
则系统状态空间表达式为
1112221122001001x x u a c c x x u d b d y x y x --⎡⎤⎡⎤⎡⎤
⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦
⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣
⎦⎣⎦⎣⎦
&&
已知系统的状态空间表达式为
[]512315124u y u
--⎡⎤⎡⎤
=+⎢⎥⎢⎥-⎣⎦⎣⎦=+&x x x 求其对应的传递函数。
解
5131--⎡⎤=⎢⎥-⎣⎦A ,25⎡⎤
=⎢⎥
⎣⎦
B ,[]12=
C ,4d = 1()()g s sI d -=-+C A B
1
5131111
()35(5)(1)3s s s s s s s s -+⎡⎤-=⎢⎥
-+⎣⎦
+-⎡⎤-=
⎢⎥++++⎣⎦
I A I A
[]122
()()1121
124355(2)(4)4369168
g s s d
s s s s s s s s -=-++-⎡⎤⎡⎤=+⎢⎥⎢⎥+++⎣⎦⎣⎦
++=++C I A B。