机械设计(经典)计算公式

机械设计计算公式机械设计是指利用机械原理和机械工程学知识设计制造各种机械装置、机械零部件以及机械系统，以满足工程技术要求和使用要求的工程领域。

在机械设计中，经典的计算公式是非常重要的工具，用于解决各种设计问题和计算设计参数。

本文将介绍几个经典的机械设计计算公式，并给出详细的说明。

1.扭矩和功率计算公式扭矩和功率是机械运动过程中常用的两个参数，它们之间存在一定的关系。

对于旋转运动的机械系统，扭矩和功率的计算公式如下：扭矩T=P/(ω×n)功率P=T×ω×n其中，T表示扭矩，P表示功率，ω表示角速度，n表示转速。

根据这两个公式，我们可以根据已知条件计算扭矩和功率，或者通过已知扭矩和功率计算转速和角速度。

2.强度和刚度计算公式在机械设计中，强度和刚度是两个重要的设计参数。

强度是指机械零部件在工作过程中能够承受的最大应力，而刚度是指机械零部件在受力情况下的变形程度。

对于常见的机械零部件，强度和刚度的计算公式如下：强度S=F/A刚度K=F/Δl其中，S表示强度，F表示受力，A表示受力面积，K表示刚度，Δl 表示变形量。

根据这两个公式，我们可以根据已知条件计算出零件的强度和刚度，以确保零件在工作过程中的可靠性和稳定性。

3.速度和加速度计算公式在机械运动的设计中，速度和加速度是两个重要的参数，它们与机械系统的动态性能密切相关。

对于直线运动的机械系统，速度和加速度的计算公式如下：速度v=s/t加速度a=(v-u)/t其中，v表示速度，s表示位移，t表示时间，u表示初速度。

根据这两个公式，我们可以根据已知条件计算出机械系统的速度和加速度，从而优化机械系统的动态性能。

总结起来，机械设计中经典的计算公式涵盖了扭矩和功率、强度和刚度、速度和加速度等多个方面。

这些计算公式为机械工程师提供了有效的工具和方法，用于解决各种设计问题和计算设计参数，在机械设计过程中起到了重要的作用。

运动学篇一、直线运动：基本公式：（距离、速度、加速度和时间之间的关系）1）路程=初速度x时间+加速度x时间^2/22）平均速度=路程/时间；3）末速度-初速度=2x加速度x路程；4）加速度=（末速度-初速度）/时间5）中间时刻速度=（初速度+末速度）/26）力与运动之间的联系：牛顿第二定律：F=ma，[合外力（N）=物体质量（kg）x加速度（m/s^2）] （注：重力加速度g=9.8m/s^2或g=9.8N/kg）二、旋转运动：（旋转运动与直线运动类似，注：弧度是没有单位的）单位对比：圆的弧长计算公式：弧长s=rθ=圆弧的半径x圆弧角度（角位移）周长=C=2πr=πd，即：圆的周长=2x3.14x圆弧的半径=3.14x圆弧的直径旋转运动中角位移、弧度（rad）和公转（r）之间的关系。

1）1r（公转）=2π（弧度）=360°（角位移）2）1rad=360°/（2π）=57.3°3）1°=2π/360°=0.01745rad4）1rad=0.16r5）1°=0.003r6）1r/min=1x2x3.14=6.28rad/min7)1r/min=1x360°=360°/min三、旋转运动与直线运动的联系：1）弧长计算公式（s=rθ）：弧长=圆弧的半径x圆心角（圆弧角度或角位移）2）角速度（角速度是角度（角位移）的时间变化率）（ω=θ/t）：角速度=圆弧角度/时间注：结合上式可推倒出角速度与圆周速度（即：s/t也称切线速度）之间的关系。

S3）圆周速度=角速度x半径，（即：v=ωr）注：角度度ω的单位一般为rad/s，实际应用中，旋转速度的单位大多表示为r/min （每分钟多少转）。

可通过下式换算:1rad/s=1x60/(2x3.14)r/min例如：电机的转速为100rad/s的速度运行，我们将角速度ω=100rad/s换算成r/min 单位，则为：ω=100rad/s=100x60/(2π)=955r/min4）rad/s和r/min的联系公式：转速n(r/min)= ω（rad/s）x60/（2π），即：转速（r/min）=角速度（rad/s）x60/（2π）；5）角速度ω与转速n之间的关系（使用时须注意单位统一）：ω=2πn，（即：带单位时为角速度（rad/s）=2x3.14x转速（r/min）/60）6)直线（切线）速度、转速和2πr（圆的周长）之间的关系（使用时需注意单位）：圆周速度v=2πrn=（πd）n注：线速度=圆周速度=切线速度四、转矩计算公式：（1）普通转矩：T=Fr即：普通转矩（N*m）=力（N）x半径（m）；（2）加速转矩：T=Jα即：加速转矩（N*m）=角加速度α（rad/s^2）x转动惯量J（kg*m^2）单位换算：转动惯量J（kg*cm^2）:1kg*cm^2=10^-6kg*m^2；角加速度α（rad/s^2）：1r/s^2=1x2xπrad/s^2；单位转换过程推导：（注：kgf*m（千克力*米），1kgf*m=9.8N*m，g=9.8N/kg=9.8m/s^2）假设转动惯量J =10kg*m^2，角加速度α=10rad/s^2，推导出转矩T的单位过程如下：T=J x α=10x（kg*m^2）x10（rad/s^2）=100（kgf*m/s^2）=（）（）（）=100N*m两个简化单位换算公式：（注：单位换算其物理含义也不同，下式仅用于单位换算过程中应用。

机械设计计算公式汇总
机械设计是工程设计中的重要组成部分之一，需要掌握一定的设计知识和计算方法。

本文将介绍常见的机械设计计算公式汇总，希望能够为机械设计工作者提供一些参考。

1. 齿轮传动计算公式：
- 齿轮的基本公式：〖(tan⁡α=n₂u₂/n₁u₁)〗^2+1=〖(d₁/d₂)〗^2 - 齿轮轮廓线齿数：Z=(2d₀/∏)tanα
- 齿轮模数： m=d₀/Z
- 齿轮载荷：Ft=2T/d₀，Fr=Ft/tan⁡α
2. 轴承选型计算公式：
- 基本动负荷额定值：P=Fr
- 动荷重系数：f₂=C₂/P
- 等效动荷重：P_1=(X_Fr+Y_Fa)_e
- 等效动荷重系数：f_1=C_1/P_1
3. 机床切削力计算公式：
- 切削力公式：Fc=kC （k为切削力系数，C为切削力矢量和）
- 切削力系数的计算方法：k=αT^b+c
4. 泵的性能计算公式：
- 扬程公式：H=(p_2-p_1)/ρg+H_s
- 流量公式：Q=3600VA/N
- 效率计算公式：η_m=H_p/H_f
以上是机械设计中常见的计算公式，实际设计过程中需要根据具体情况进行合理的使用和调整，以确保设计方案能够达到预期效果。

机械设计常用公式集锦一、直线运动基本公式：（距离、速度、加速度和时间之间的关系）1）路程=初速度x 时间+2）平均速度=路程/时间；3）末速度-初速度=2x 加速度x 路程；4）加速度=（末速度-初速度）/时间5）中间时刻速度=（初速度+末速度）6）力与运动之间的联系：牛顿第二定律：F=ma，[合外力（N）=物体质量（kg）x 加速度（）] （注：重力加速度g=9.8或g=9.8N/kg）二、旋转运动单位对比：圆的弧长计算公式：弧长s=rθ=圆弧的半径x 圆弧角度（角位移）周长=C=2πr=πd，即：圆的周长=2x3.14x 圆弧的半径=3.14x 圆弧的直径旋转运动中角位移、弧度（rad）和公转（r）之间的关系。

1）1r（公转）=2π（弧度）=360°（角位移）2）1rad==57.3°3）1°==0.01745rad4）1rad=0.16r5）1°=0.003r6）1r/min=1x2x3.14=6.28rad/min7)1r/min=1x360°=360°/min三、旋转运动与直线运动的联系：1）弧长计算公式（s=rθ）：弧长=圆弧的半径x 圆心角（圆弧角度或角位移）2）角速度（角速度是角度（角位移）的时间变化率）（ω=θ/t）：角速度=圆弧角度/时间注：结合上式可推倒出角速度与圆周速度（即：s/t 也称切线速度）之间的关系。

3）圆周速度=角速度x 半径，（即：v=ωr）注：角度度ω的单位一般为rad/s，实际应用中，旋转速度的单位大多表示为r/min（每分钟多少转）。

可通过下式换算:1rad/s=1x60/(2x3.14)r/min例如：电机的转速为100rad/s 的速度运行，我们将角速度ω=100rad/s 换算成r/min单位，则为：ω=100rad/s==955r/min4）rad/s 和r/min 的联系公式：转速n(r/min)=，即：转速（r/min）=；5）角速度ω与转速n 之间的关系（使用时须注意单位统一）：ω=2πn，（即：带单位时为角速度（rad/s）=2x3.14x 转速（r/min）/60）6)直线（切线）速度、转速和2πr（圆的周长）之间的关系（使用时需注意单位）：圆周速度v=2πrn=（πd）n注：线速度=圆周速度=切线速度四、转矩计算公式：（1）普通转矩：T=Fr即：普通转矩（N*m）=力（N）x 半径（m）；（2）加速转矩：T=Jα即：加速转矩（N*m）=角加速度α（）x 转动惯量J（）单位换算：转动惯量J（）:1=；角加速度α（）：1=1x2xπ；单位转换过程推导：（注：kgf*m（千克力*米），1kgf*m=9.8N*m，g=9.8N/kg=9.8）假设转动惯量J =10kg*，角加速度α=10rad/，推导出转矩T 的单位过程如下：T=J x α=10x（kg*）x10（rad/）=100（kgf*m/）=100N*m两个简化单位换算公式：（注：单位换算其物理含义也不同，下式仅用于单位换算过程中应用。

机械设计基础尺寸计算公式在机械设计中，尺寸计算是非常重要的一部分，它直接影响着机械零件的设计和制造质量。

正确的尺寸计算可以保证机械零件的功能和性能，同时也可以减少制造成本和提高生产效率。

本文将介绍一些机械设计中常用的基础尺寸计算公式，希望能对机械设计工程师有所帮助。

1. 直径计算公式。

在机械设计中，经常需要计算零件的直径，比如轴承、轴等零件的直径计算。

一般来说，直径计算公式可以按照零件的受力情况和使用要求来确定。

常用的直径计算公式有以下几种：（1）轴的直径计算公式。

轴的直径计算公式一般可以按照轴的受力情况和转速来确定。

一般情况下，轴的直径计算公式可以用以下公式表示：d = c (T / (K σ))^(1/3)。

其中，d为轴的直径，c为系数（通常取1.5-2），T为轴的扭矩，K为转矩系数，σ为轴材料的抗拉强度。

（2）轴承的直径计算公式。

轴承的直径计算公式一般可以按照轴承的受力情况和使用要求来确定。

一般情况下，轴承的直径计算公式可以用以下公式表示：d = (Fr / (3.14 p L))^(1/3)。

其中，d为轴承的直径，Fr为轴承的额定动载荷，p为轴承的等效动载荷系数，L为轴承的额定寿命。

2. 长度计算公式。

在机械设计中，经常需要计算零件的长度，比如轴、销等零件的长度计算。

一般来说，长度计算公式可以按照零件的受力情况和使用要求来确定。

常用的长度计算公式有以下几种：（1）轴的长度计算公式。

轴的长度计算公式一般可以按照轴的受力情况和使用要求来确定。

一般情况下，轴的长度计算公式可以用以下公式表示：L = (T K) / (π d τ)。

其中，L为轴的长度，T为轴的扭矩，K为转矩系数，d为轴的直径，τ为轴的允许剪切应力。

（2）销的长度计算公式。

销的长度计算公式一般可以按照销的受力情况和使用要求来确定。

一般情况下，销的长度计算公式可以用以下公式表示：L = (2 F l) / (π d τ)。

其中，L为销的长度，F为销的受力，l为销的长度，d为销的直径，τ为销的允许剪切应力。

机械设计考试重点公式
机械设计考试重点公式包括以下几类：
1.直线运动基本公式：
•路程=初速度×时间
•平均速度=路程/时间
•末速度-初速度=2×加速度×路程
•加速度=(末速度-初速度)/时间
•中间时刻速度=(初速度+末速度)/2
1.牛顿第二定律：F=ma（合外力=物体质量×加速度）
2.电机选型计算通用公式：
•P功率=T转矩×N转速/9550
•T转矩=P功率×9550/N转速
•P功率=F力×V线速度（直线运动）
•P功率=T转矩×ω角速度（圆周运动）
•N转速=V线速度×1000×60/（2πR）（物体速度和滚轮转速的关系）
此外，在齿轮设计中，还有一些重要的公式和概念：
•齿轮的模数公式：D=mz（齿数×模数）
•分度圆和压力角：分度圆是具有标准模数和标准压力角（通常为20°）的圆。

模数越大，分度圆的半径越大，齿轮的尺寸也就越大。

•渐开线齿轮的正确啮合条件：两轮的模数和压力角分别相等。

•标准齿轮：分度圆上齿厚和齿槽宽相等，且齿顶高和齿根高均为标准值的齿轮称为标准齿轮。

以上公式和概念是机械设计考试中需要重点掌握的内容。

请注意，具体的考试要求和重点可能因学校、专业和考试级别而有所不同，建议参考相关教材和考试大纲进行复习。

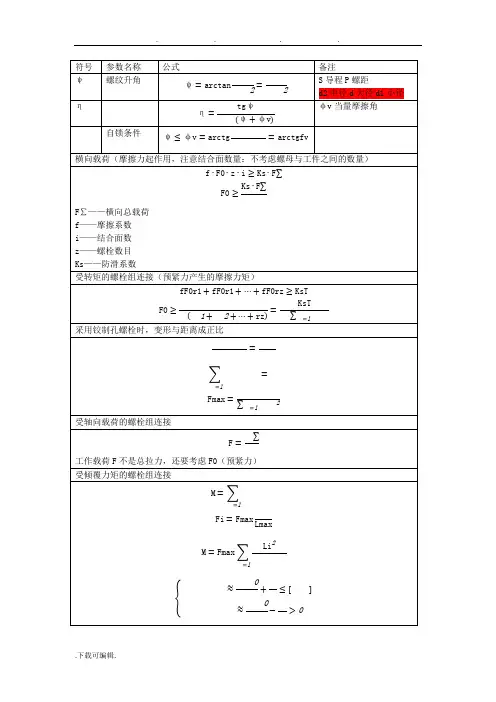
符号参数名称公式备注ψ螺纹升角S导程P螺距d2中径d大径d1小径ηφv当量摩擦角自锁条件横向载荷（摩擦力起作用，注意结合面数量：不考虑螺母与工件之间的数量）F∑——横向总载荷f—-摩擦系数i—-结合面数z--螺栓数目Ks——防滑系数受转矩的螺栓组连接（预紧力产生的摩擦力矩)采用铰制孔螺栓时，变形与距离成正比受轴向载荷的螺栓组连接工作载荷F不是总拉力，还要考虑F0（预紧力)受倾覆力矩的螺栓组连接b是倾覆力矩方向松螺栓连接紧螺栓连接（1.3倍）预紧力+工作拉力F2总拉力F0预紧力F1残余预紧力（1、余谐音）F工作拉力承受工作剪力的紧螺栓连接(挤压+剪切）挤压强度条件剪切强度条件键连接符号参数名称公式1备注普通平键连接的强度条件T——N∙mk=0。

5hl——键的工作长度，A圆B平C半圆d——轴的直径［σp］——许用挤压应力,多用于校核静连接导向平键连接和滑键连接［p］——许用应力，多用于校核动连接半圆键k——查表l=L花键静连接动连接ψ--载荷分配不均系数，与齿数多少有关，一般取ψ=0。

7~0。

8,齿数多取小h--花键齿侧面的工作高度，矩形花键渐开线花键α=30°：h=mα=45°：h=0。

8m dm——矩形花键渐开线花键dm=di带传动符号参数名称公式1公式2备注F1紧边拉力F2松边拉力F0初拉力Fe有效拉力可以用来校核是否打滑f应用fvα用弧度f与α同向，都是大好α1包角α2包角σ1紧边拉应力σ1=F1/Aσ2紧边拉应力σ2=F2/Aσb1弯曲应力σb2弯曲应力σc离心拉应力全长都有，一致σmax瞬时最大应力处Ld0带长a0初选中心距链传动符号参数名称公式1备注链速平均传动比分度圆直径链节数标准直齿轮符号参数名称公式1公式2备注圆周力Ft⊥过点半径径向力Fr Fr=Ft×tanα沿半径方向rt 法向载Fn Fn=Ft/cosα⊥齿面nc荷弯曲疲劳强度根据这个公式可见跟直径没关系，跟齿数也没关系左边主从都一样，右边有区别。

运动学篇一、直线运动：基本公式：（距离、速度、加速度和时间之间的关系）1）路程=初速度x时间+加速度x时间^2/22）平均速度=路程/时间；3）末速度-初速度=2x加速度x路程；4）加速度=（末速度-初速度）/时间5）中间时刻速度=（初速度+末速度）/26）力与运动之间的联系：牛顿第二定律：F=ma，[合外力（N）=物体质量（kg）x加速度（m/s^2）] （注：重力加速度g=9.8m/s^2或g=9.8N/kg）二、旋转运动：（旋转运动与直线运动类似，注：弧度是没有单位的）单位对比：圆的弧长计算公式：弧长s=rθ=圆弧的半径x圆弧角度（角位移）周长=C=2πr=πd，即：圆的周长=2x3.14x圆弧的半径=3.14x圆弧的直径旋转运动中角位移、弧度（rad）和公转（r）之间的关系。

1）1r（公转）=2π（弧度）=360°（角位移）2）1rad=360°/（2π）=57.3°3）1°=2π/360°=0.01745rad4）1rad=0.16r5）1°=0.003r6）1r/min=1x2x3.14=6.28rad/min7)1r/min=1x360°=360°/min三、旋转运动与直线运动的联系：1）弧长计算公式（s=rθ）：弧长=圆弧的半径x圆心角（圆弧角度或角位移）2）角速度（角速度是角度（角位移）的时间变化率）（ω=θ/t）：角速度=圆弧角度/时间注：结合上式可推倒出角速度与圆周速度（即：s/t也称切线速度）之间的关系。

S3）圆周速度=角速度x半径，（即：v=ωr）注：角度度ω的单位一般为rad/s，实际应用中，旋转速度的单位大多表示为r/min （每分钟多少转）。

可通过下式换算:1rad/s=1x60/(2x3.14)r/min例如：电机的转速为100rad/s的速度运行，我们将角速度ω=100rad/s换算成r/min 单位，则为：ω=100rad/s=100x60/(2π)=955r/min4）rad/s和r/min的联系公式：转速n(r/min)= ω（rad/s）x60/（2π），即：转速（r/min）=角速度（rad/s）x60/（2π）；5）角速度ω与转速n之间的关系（使用时须注意单位统一）：ω=2πn，（即：带单位时为角速度（rad/s）=2x3.14x转速（r/min）/60）6)直线（切线）速度、转速和2πr（圆的周长）之间的关系（使用时需注意单位）：圆周速度v=2πrn=（πd）n注：线速度=圆周速度=切线速度四、转矩计算公式：（1）普通转矩：T=Fr即：普通转矩（N*m）=力（N）x半径（m）；（2）加速转矩：T=Jα即：加速转矩（N*m）=角加速度α（rad/s^2）x转动惯量J（kg*m^2）单位换算：转动惯量J（kg*cm^2）:1kg*cm^2=10^-6kg*m^2；角加速度α（rad/s^2）：1r/s^2=1x2xπrad/s^2；单位转换过程推导：（注：kgf*m（千克力*米），1kgf*m=9.8N*m，g=9.8N/kg=9.8m/s^2）假设转动惯量J =10kg*m^2，角加速度α=10rad/s^2，推导出转矩T的单位过程如下：T=J x α=10x（kg*m^2）x10（rad/s^2）=100（kgf*m/s^2）=（）（）（）=100N*m两个简化单位换算公式：（注：单位换算其物理含义也不同，下式仅用于单位换算过程中应用。

常用机械设计公式及应用实例
常用机械设计公式及应用实例有：
1. 扭矩公式：T = F * r，应用于计算扭矩传递和转矩台计算。

2. 力的平衡公式：ΣF = 0，应用于平衡力的分析，例如平衡杆、平衡机构等设计。

3. 力的传递公式：F1 = F2 * (r2 / r1)，应用于齿轮传动、皮带
传动等设计。

4. 力矩公式：M = F * d，应用于杠杆、滑轮等设计，例如计
算需要的杠杆长度。

5. 加速度公式：a = (v2 - v1) / t，应用于动力装置的加速度计算，例如机械传动系统中的加速段计算。

6. 线速度公式：v = ω * r，应用于旋转装置的线速度计算，例
如风力发电机的叶片线速度计算。

7. 压力公式：P = F / A，应用于液压传动系统的压力计算，例
如液压缸的压力计算。

8. 流量公式：Q = A * v，应用于流体传动系统的流量计算，
例如水泵的流量计算。

9. 速度比公式：v2 / v1 = n2 / n1，应用于齿轮传动、带传动等
设计，例如计算两个齿轮的速度比。

10. 能量公式：E = m * g * h，应用于重力能、动能、势能等的计算，例如电梯的重力能计算。

以上是常用的机械设计公式及应用实例，根据具体的设计需求，还可以继续深化公式和应用领域。

机械设计常用公式一、名词定义零件：独立的制造单元构件：独立的运动单元体机构：用来传递运动和力的、有一个构件为机架的、用构件间能够相对运动的连接方式组成的构件系统机器：是执行机械运动的装置，用来变换或传递能量、物料、信息机械：机器和机构的总称机构运动简图：用简单的线条和符号来代表构件和运动副，并按一定比例确定各运动副的相对位置，这种表示机构中各构件间相对运动关系的简单图形称为机构运动简图运动副：由两个构件直接接触而组成的可动的连接运动副元素：把两构件上能够参加接触而构成的运动副表面运动副的自由度和约束数的关系f=6-s运动链：构件通过运动副的连接而构成的可相对运动系统高副：两构件通过点线接触而构成的运动副低副：两构件通过面接触而构成的运动副平面运动副的最大约束数为2，最小约束数为1；引入一个约束的运动副为高副，引入两个约束的运动副为平面低副平面自由度计算公式：F=3n-2PL-PH机构可动的条件：机构的自由度大于零机构具有确定运动的条件：机构的原动件的数目应等于机构的自由度数目局部自由度：与输出机构运动无关的自由度复合铰链：两个以上构件同时在一处用转动副相连接速度瞬心：互作平面相对运动的两构件上瞬时速度相等的重合点。

若绝对速度为零，则该瞬心称为绝对瞬心相对速度瞬心与绝对速度瞬心的相同点：互作平面相对运动的两构件上瞬时相对速度为零的点；不同点：后者绝对速度为零，前者不是三心定理：三个彼此作平面运动的构件的三个瞬心必位于同一直线上机构的瞬心数：N=K(K-1)/2机械自锁：有些机械中，有些机械按其结构情况分析是可以运动的，但由于摩擦的存在却会出现无论如何增大驱动力也无法使其运动曲柄：作整周定轴回转的构件；连杆：作平面运动的构件；摇杆：作定轴摆动的构件；连架杆：与机架相联的构件；周转副：能作360?相对回转的运动副摆转副：只能作有限角度摆动的运动副。

二、铰链四杆机构有曲柄的条件：1.最长杆与最短杆的长度之和应≤其他两杆长度之和，称为杆长条件。