极大似然估计的题库

机器学习题库一、 极大似然1、 ML estimation of exponential model (10)A Gaussian distribution is often used to model data on the real line, but is sometimesinappropriate when the data are often close to zero but constrained to be nonnegative. In such cases one can fit an exponential distribution, whose probability density function is given by()1xb p x e b-=Given N observations x i drawn from such a distribution:(a) Write down the likelihood as a function of the scale parameter b.(b) Write down the derivative of the log likelihood.(c) Give a simple expression for the ML estimate for b.2、换成Poisson 分布：()|,0,1,2,...!x e p x y x θθθ-==()()()()()1111log |log log !log log !N Ni i i i N N i i i i l p x x x x N x θθθθθθ======--⎡⎤=--⎢⎥⎣⎦∑∑∑∑3、二、 贝叶斯假设在考试的多项选择中，考生知道正确答案的概率为p ，猜测答案的概率为1-p ，并且假设考生知道正确答案答对题的概率为1，猜中正确答案的概率为1，其中m 为多选项的数目。

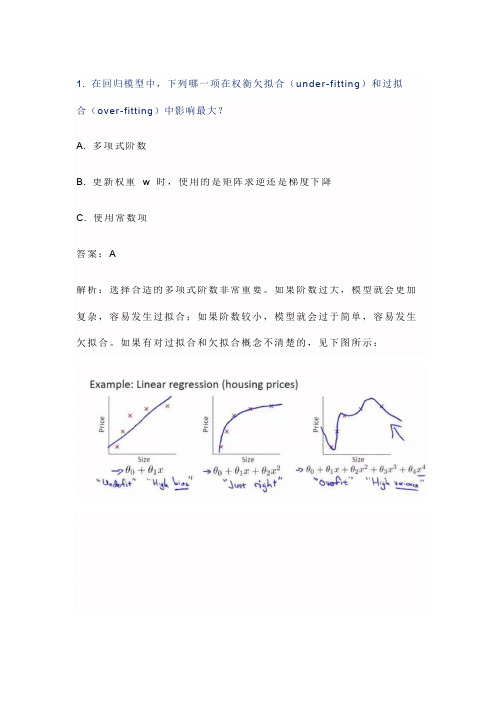
1. 在回归模型中，下列哪一项在权衡欠拟合（under-fitting）和过拟合（over-fitting）中影响最大？A. 多项式阶数B. 更新权重w 时，使用的是矩阵求逆还是梯度下降C. 使用常数项答案：A解析：选择合适的多项式阶数非常重要。

如果阶数过大，模型就会更加复杂，容易发生过拟合；如果阶数较小，模型就会过于简单，容易发生欠拟合。

如果有对过拟合和欠拟合概念不清楚的，见下图所示：2. 假设你有以下数据：输入和输出都只有一个变量。

使用线性回归模型（y=wx+b）来拟合数据。

那么使用留一法（Leave-One Out）交叉验证得到的均方误差是多少？A. 10/27B. 39/27C. 49/27D. 55/27答案：C解析：留一法，简单来说就是假设有N 个样本，将每一个样本作为测试样本，其它N-1 个样本作为训练样本。

这样得到N 个分类器，N个测试结果。

用这N 个结果的平均值来衡量模型的性能。

对于该题，我们先画出 3 个样本点的坐标：使用两个点进行线性拟合，分成三种情况，如下图所示：第一种情况下，回归模型是y = 2，误差E1 = 1。

第二种情况下，回归模型是y = -x + 4，误差E2 = 2。

第三种情况下，回归模型是y = -1/3x + 2,误差E3 = 2/3。

则总的均方误差为：3. 下列关于极大似然估计（Maximum Likelihood Estimate，MLE），说法正确的是（多选）？A. MLE 可能并不存在B. MLE 总是存在C. 如果MLE 存在，那么它的解可能不是唯一的D. 如果MLE 存在，那么它的解一定是唯一的答案：AC解析：如果极大似然函数L(θ)在极大值处不连续，一阶导数不存在，则MLE 不存在，如下图所示：另一种情况是MLE 并不唯一，极大值对应两个θ。

如下图所示：4. 如果我们说“线性回归”模型完美地拟合了训练样本（训练样本误差为零），则下面哪个说法是正确的？A. 测试样本误差始终为零B. 测试样本误差不可能为零C. 以上答案都不对答案：C解析：根据训练样本误差为零，无法推断测试样本误差是否为零。

《概率论与数理统计》试题(1)判断题(本题共15分，每小题3分。

正确打“V” ，错误打“X” )⑴对任意事件A和B ,必有P(AB)=P(A)P(B) ()⑵ 设A、B是Q中的随机事件,则(A U B)-B=A ()⑶ 若X服从参数为入的普哇松分布，则EX=DX⑷假设检验基本思想的依据是小概率事件原理1 n _⑸ 样本方差S：= —(X i X )2是母体方差DX的无偏估计(n i i、(20分)设A、B、C是Q中的随机事件，将下列事件用A、B、C表示出来(1) 仅A发生，B、C都不发生;(2) 代B,C中至少有两个发生；(3) 代B,C中不多于两个发生;(4) 代B,C中恰有两个发生；(5) 代B,C中至多有一个发生。

三、(15分)把长为a的棒任意折成三段，求它们可以构成三角形的概率四、(10分)已知离散型随机变量X的分布列为X 2 1 0 1 31 1 1 1 11P5 6 5 15 302 求Y X的分布列.1五、(10分)设随机变量X具有密度函数f(x) -e|x|, V x V2求X的数学期望和方差•六、(15分)某保险公司多年的资料表明，在索赔户中，被盗索赔户占20%，以随机抽查100个索赔户中因被盗而向保险公司索赔的户数，求P(14 X 30).七、(15分)设X1 ,X2,L ,X n是来自几何分布k 1P(X k) p(1 p) , k 1,2,L , 0 p 1 ,的样本，试求未知参数p的极大似然估计•X表示在x 0 0.5 1 1.5 2①(x ) 0.500 0.691 0.841 0.933 0.9772.5 30.994 0.999《概率论与数理统计》试题（1）评分标准⑴ X;（2） X;⑶“；⑷"；（5） X o 解(1) ABC(2)ABU AC U BC 或 ABC U ABC U ABC U ABC ；(3) AUBUC 或 ABC U ABC U ABC U ABC U ABC U ABC U ABC ； (4) ABC U ABC U ABC ；(5) AB U AC U BC 或 ABC U ABC U ABC U ABC六解X “ P(14 ^b(k;100,0.20), EX=100 X 0.2=20, DX=100 X 0.2 X 0.8=16.-- --5分 分 30 20 14 20、 X 30) ( --------- )( --------------- ) ------------------ V16 J16 ------10(2.5) ( 1.5)=0.994+0.933—10.927. -------------------------------------n——15分七解n x nL(X 1, L ,x n ；p)p(1 p)x i1 p n(1 p)i1---------5分 -------------------------------------- 10 分每小题4分；解 设A '三段可构成三角形'又三段的长分别为x,y,a x y ,Oxa, 0 ya, Oxy a ，不等式构成平面域S .Aa A 发生 0 x —, 02不等式确定S 的子域A , 所以a a y , x y a2 2------------------------------------ 10A 的面积 1S 的面积 4---------------------------------------- 15则 分分分四 解Y 的分布列为Y 0 1 4 91 7 1 11P — ----- — —5 30 5 30Y 的取值正确得2分， 分布列对一组得 2分； 五 解 EXx 2 凶 dx 0, （因为被积函数为奇函数）2D X EX 22 x 1 |x| 1 —e dx x 2e x dx22 xx e0 2 xe x dx 0------------------------- 4 分 2[ xe x 0e x dx] 2.In L n In p d In L n dp p (X i n )l n(1 p),i 1 X i n @0, --------------------------- 10 分 解似然方程 n n X in i 1 得p 的极大似然估计 ------------------------------------------------------------------- 15 分 《概率论与数理统计》期末试题(2) 与解答一、填空题(每小题 3分，共15分) 1. 设事件 代B 仅发生一个的概率为 0.3，且P(A) P(B) 0.5，则 代B 至少有一个不发 生的概率为 ___________ . 2. __________________________________________________________________________ 设随机变量X 服从泊松分布，且P(X 1) 4P(X 2)，则P(X 3) _______________________ . 23. _______________________ 设随机变量X 在区间(0,2)上服从均匀分布，则随机变量Y X 在区间(0,4)内的概率 密度为f Y (y) . 的指数分布，P(X 1) e 2，则4. 设随机变量 X,Y 相互独立，且均服从参数为5._______ , P{min( X ,Y) 1} = ____ 设总体X 的概率密度为 (1)x , 0 x 1, f (x)0, 其它 1.X 1 ,X 2, ,X n 是来自X 的样本，则未知参数 的极大似然估计量为 ___________解：1. P(AB AB) 0.3即 0.3 P(AB) P(AB) P(A) P(AB) P(B) P(AB) 0.5 2P(AB)2所以 P(AB) 0.1P(A B) P(AB) 1 P(AB) 092.P(X 1) P(X 0) P(X 1) e e , P(X 2) e由 P(X 1) 4P(X 2)知e e2 2e即2 21 0解得1，故P(X3)1 1 e . 63•设丫的分布函数为F Y (y), X 的分布函数为F x (x)，密度为f x (x)则F Y (V ) P(Y y) P(X 2 y) P( ...y X ,y) FxG.y) F x ( ,y) 因为 X ~U (0, 2)，所以 F X ( ,y) 0,即 F Y (y) F X G. y)1.ln x in i 1二、单项选择题(每小题 3分，共15分)1 .设A, B,C 为三个事件，且 A, B 相互独立，则以下结论中不正确的是(A) 若P(C) 1,则AC 与BC 也独立. (B) 若P(C) 1,则AUC 与B 也独立. (C) 若P(C) 0,则AUC 与B 也独立.J(y) F Y (y)1 _2丁x(J)0 y 4, 另解 在(0,2)上函数y 所以 2x 严格单调，反函数为h(y)其它..5f Y (y) Afx(7?)诙4孑 0 ,其它.y 4,4. P(X 1) 1 P(X P{min( X ,Y) 1} 111) eP{min( X,Y) 4 e ・ 1} P(X 1)P(Y 1)5.似然函数为L(X 1 ,L ,X n ；n(i 1n1)Xi(1叽1_ X )解似然方程得 ln L n ln(1)ln x i ln x i i 1@0的极大似然估计为EX X(D )若C B ，则A 与C 也独立• ()2•设随机变量 X~N(0,1), X 的分布函数为(x)，贝U P(|X| 2)的值为(A )2[1 (2)] . ( B )2 (2)1 .(C ) 2(2).( D )1 2 (2).()3•设随机变量 X 和Y 不相关，则下列结论中正确的是(A ) X 与 Y 独立. (B ) D(X Y) DX DY .(C ) D(X Y) DX DY .(D ) D(XY) DXDY .()4•设离散型随机变量 X 和Y 的联合概率分布为(X,Y) (1,1) (1,2) (1,3) (2,1) (2,2) (2,3) P1 1 1 1 691832. X ~ N(0,1)所以 P(| X | 2) 1 P(| X | 2)1 P(2 X1 (2) ( 2) 1 [2 (2) 1] 2[1 (2)]若X,Y 独立，则 7的值为2 112(A ) -, —(A ) J—99991 15 1 (C ), — (D ) — , . ()6618185 •设总体X 的数学期望为,X 1,X 2丄,X n为来自X 的样本，则下列结论中正确的是(A ) X i 是的无偏估计量 (B ) X i 是 的极大似然估计量(C ) X 1是 的相合(一致)估计量(D ) X i 不是 的估计量.() 解：1.因为概率为1的事件和概率为 0的事件与任何事件独立，所以( A ), (B ), (C )可见A 与C 不独立.2)应选(A )都是正确的，只能选(事实上由图EX X12 3 P(X 2, Y 2)1 1 1 11— — ■ 1 、69183(- )(-391 1 23321 1丄92 918故应(A).3•由不相关的等价条件知应选(B ) 4•若X,Y 独立则有)P(X 2)P(Y 2)f(o三、(7分)已知一批产品中90%是合格品，检查时，一个合格品被误认为是次品的概率为0.05，一个次品被误认为是合格品的概率为0.02，求(1) 一个产品经检查后被认为是合格品的概率；(2) 一个经检查后被认为是合格品的产品确是合格品的概率解：设A ‘任取一产品，经检验认为是合格品’B ‘任取一产品确是合格品’则(1) P(A) P(B)P(A|B) P(B)P(A|B)0.9 0.95 0.1 0.02 0.857.P(AB) 0.9 0.95 (2) P(B| A) 0.9977 .P(A) 0.857四、(12分)从学校乘汽车到火车站的途中有3个交通岗，假设在各个交通岗遇到红灯的事件是相互独立的，并且概率都是2/5.设X为途中遇到红灯的次数，求X的分布列、分布函数、数学期望和方差.解：X的概率分布为k2 k3 3 kP(X k) cf(5)k(5)3kX 0 1 2即P27 54 36 125 125 12X的分布函数为0 , x 0,27125 ,0 x 1,F(x )81 1 x 2, 125117 2 x3, 1251 , x 3.2 6 EX3 --5 5DX c 2 3 183 --5 5 25五、(10分)设二维随机变量(X,Y)在区域 D匀分布.求(1)(X,Y)关于X的边缘概率密度;38125{(x,y)|x 0, y 0, x y 1}上服从均(2)Z X Y的分布函数与概率密(1) (X ,Y)的概率密度为f(x, y) 2, (x, y) D 0,其它.k 0,1,2,3.2 2x, 0 x 1f(x，y)dy0 ,其它(2)利用公式f Z(z) f (x, z x)dx其中f(x,z x) 2, 0 x 1,0 z x 1 x0,其它2, 0 x 1, x z 1.0,其它.当z 0 或z 1 时f z (z) 0z的分布函数为z z0 z 1 时f z(z) 2 q dx 2x02z 故Z的概率密度为f z(z)2z, 0 z 1,0,其它.0, z 0 0, z 0,fZ⑵z zf Z(y)dy 02ydy,0 z 1 2z , 0 z 1,1,1 z 1.z 1或利用分布函数法0 , z 0,F Z(Z) P(Z z) P(X Y z) 2dxdy, 0 z 1D11 , z 1.0 , z 0,2z , 0 z 1,1 , z 1.f z (z) F z⑵2z,0 ,0 z 1,其它.六、（10分）向一目标射击，目标中心为坐标原点，已知命中点的横坐标X和纵坐标Y相互独立，且均服从N（0,22）分布.求（1）命中环形区域D ｛（ x, y） |1 x2 y2 2｝的概率；（2）命中点到目标中心距离Z X Y2的数学期望.D (1)P{X,Y) D} f(x,y)dxdyDx28dxdy 8rdrdf x(X)4 41 2 -8re 8 rdrd1 e 8 r 2dr 8 04 0r2re 丁r 2e T dr 02冷dr阪七、（11分）设某机器生产的零件长度（单位： cm ） X 〜N （ , 2），今抽取容量为样本，测得样本均值 X 10,样本方差s 2 0.16. （ 1）求的置信度为0.952区间；（2）检验假设H 。

深度学习之最⼤似然估计⼀、定义⼆、知识解读 极⼤似然估计，通俗理解来说，就是利⽤已知的样本结果信息，反推最具有可能（最⼤概率）导致这些样本结果出现的模型参数值！ 换句话说，极⼤似然估计提供了⼀种给定观察数据来评估模型参数的⽅法，即：“模型已定，参数未知”。

可能有⼩伙伴就要说了，还是有点抽象呀。

我们这样想，⼀当模型满⾜某个分布，它的参数值我通过极⼤似然估计法求出来的话。

⽐如正态分布中公式如下： 如果我通过极⼤似然估计，得到模型中参数和的值，那么这个模型的均值和⽅差以及其它所有的信息我们是不是就知道了呢。

确实是这样的。

极⼤似然估计中采样需满⾜⼀个重要的假设，就是所有的采样都是独⽴同分布的。

下⾯我通过俩个例⼦来帮助理解⼀下最⼤似然估计 但是⾸先看⼀下似然函数的理解： 对于这个函数：输⼊有两个：x表⽰某⼀个具体的数据；表⽰模型的参数 如果是已知确定的，是变量，这个函数叫做概率函数(probability function)，它描述对于不同的样本点，其出现概率是多少。

如果是已知确定的，是变量，这个函数叫做似然函数(likelihood function), 它描述对于不同的模型参数，出现这个样本点的概率是多少。

这有点像“⼀菜两吃”的意思。

其实这样的形式我们以前也不是没遇到过。

例如， , 即x的y次⽅。

如果x是已知确定的(例如x=2)，这就是 , 这是指数函数。

如果y是已知确定的(例如y=2)，这就是，这是⼆次函数。

同⼀个数学形式，从不同的变量⾓度观察，可以有不同的名字。

这么说应该清楚了吧？如果还没讲清楚，别急，下⽂会有具体例⼦。

现在真要先讲讲MLE了。

例⼦⼀ 别⼈博客的⼀个例⼦。

假如有⼀个罐⼦，⾥⾯有⿊⽩两种颜⾊的球，数⽬多少不知，两种颜⾊的⽐例也不知。

我们想知道罐中⽩球和⿊球的⽐例，但我们不能把罐中的球全部拿出来数。

现在我们可以每次任意从已经摇匀的罐中拿⼀个球出来，记录球的颜⾊，然后把拿出来的球再放回罐中。

一、单项选择题（每小题3分，共15分）1．设,A B 为两个随机事件，且B A ⊂，则下列式子正确的是A ．)()(A PB A P =⋃ B ．()()P AB P A =C ．()()|P B A P B =D ．()()()P B A P B P A -=-2. 设),(~2σμN X ,那么当σ增大时，{}-P X μσ<=A ．增大B ．不变C ．减少D ．增减不定 3．设()()()()~,E X-1X 21,X P poission λλ-==⎡⎤⎣⎦分布且则 Ａ．1 B. 2 C ．3 D ．04．设),(~2σμN X ，其中μ已知,2σ未知,123X , X ,X ,为其样本， 下列各项不是统计量的是 Ａ. 321X X X ++ Ｂ. {}123min X ,X ,X Ｃ. 23i 2i 1X σ=∑Ｄ．1X μ-5．在0H 为原假设，1H 为备择假设的假设检验中，显著性水平为α是A.}{00成立接受H H PB.}{11成立接受H H PC.}{10成立接受H H PD.}{01成立接受H H P1．A 2.B 3.A 4.C 5.D一、单项选择题（每小题3分，共15分）1．设,A B 为两个随机事件，且A B ⊂，则下面正确的等式是：(A))()()(A P B P A B P -=-； (B))(1)(A P AB P -=； (C))()|(B P A B P =； (D))()|(A P B A P =。

2. 设X ~2(,)N μσ,那么概率{2}P X μ<+(A) 随μ增加而变大; (B) 随μ增加而减小； (C) 随σ增加而不变; (D) 随σ增加而减小3. 设1{0,0}5P X Y ≥≥=,2{0}{0}5P X P Y ≥=≥=,则{max{,}0}P X Y ≥=(A) 15; (B) 25; (C) 35; (D) 454. 设总体X ,12,,,n X X X ⋅⋅⋅是取自总体X 的一个样本, X 为样本均值，则不是总体期望μ的无偏估计量的是 (A) X ; (B) 1ni i X =∑; (C) 1230.20.30.5X X X ++; (D) 123X X X +-5. 设总体X ~()2,N μσ，其中2σ已知, μ未知,123, ,X X X 为其样本， 下列各项中不是统计量的是(A) 123X X X ++; (B) {}123min ,,X X X ; (C) 2321i i X σ=∑; (D) 1X μ-1. (A) 2．(D) 3．(C) 4. (B) 5. (D)一、单项选择题（每小题3分，共15分）1．在一个确定的假设检验的问题中，与判断结果无关的因素有（ ）(A) 检验统计量 (B)显著性水平 (C) 样本值 (D)样本容量2. 设X ~2(,)N μσ,那么概率{2}P X μ<+(A) 随μ增大而变大; (B) 随μ增大而减小； (C) 随μ增大而不变; (D) 随σ增大而不变3．对于任意随机变量Y X ,，若)()()(Y E X E XY E =，则（ ）。

《概率论与数理统计》试题库陇南师范⾼等专科学校数信学院《概率论与数理统计》试题库⼆〇⼀四年⼋⽉⼗⼆⽇整理题库⽬录《概率论与数理统计》题库（⼀） (3)《概率论与数理统计》题库（⼆） (5)《概率论与数理统计》题库（三） (6)《概率论与数理统计》题库（四） (8)《概率论与数理统计》题库（五） (10)《概率论与数理统计》题库（六） (11)《概率论与数理统计》题库（七） (13)《概率论与数理统计》题库（⼋） (15)《概率论与数理统计》题库（九） (17)《概率论与数理统计》题库（⼗） (19)《概率论与数理统计》题库（⼗⼀） (21)《概率论与数理统计》题库（⼗⼆） (23)《概率论与数理统计》题库（⼗三） (25)《概率论与数理统计》题库（⼗四） (27)概率论与数理统计模拟试题1 (29)概率论与数理统计模拟试题2 (31)《概率论与数理统计》题库（⼀）⼀、填空题（10×3＝30分）1、随机变量相互独⽴，且～P(2.3)，～P(2.7)，，则，。

2、随机变量ξ～N(0,4)，则ξ的密度函数f(x)＝，D(2ξ＋1)= 。

3、随机变量～N(0,4;2,9;0),则，。

4、随机变量ξ～b(10,0.5)，则E(ξ)= ，D(ξ)= 。

5、随机变量ξ的密度函数是，则C= ，。

⼆、设事件，P(A)=0.5,P(B)=0.3,P(AB)=0.2,试计算的值。

三、已知离散型随机变量的分布列为：求的分布列。

四、设随机变量相互独⽴，且～U[0,2],～，求的联合密度函数五、掷20个骰⼦，求这20个骰⼦出现的点数之和的数学期望。

六、设相互独⽴，且，，试求:的数学期望和⽅差。

七、两名⼤学⽣约定在时间12时和13时之间于预定地点见⾯，先到者等⼀刻钟后离去，假定每个⼤学⽣可以在12时到13时之间的任意时刻到达，求他们相遇的概率。

⼋、设与的分布列为试问：为何值时，与相互独⽴？《概率论与数理统计》题库（⼆）⼀、填空题1、随机变量相互独⽴，且～P(0.27)，～P(1.73)，，则，。

1.设总体X 的概率密度函数是1, 01(;)0, x x f x a αα-⎧<<=⎨⎩其它 其中0α>为未知参数。

12, , , n x x x K 是一组样本值，求参数α的最大似然估计。

解：似然函数1111nnn ii i i L x x αααα--===∏=∏1ln ln (1)ln nii L n x αα==+-∑1ln ln 0ni i d L n x d αα==+=∑ 1ˆln nii nxα==-∑2、设总体X 的概率密度函数是1 01(;)0 x x f x a αα⎧+<<=⎨⎩（）其它123,,,,n x x x x K 是一组样本值，求参数α的最大似然估计。

解：似然函数11(1)(1)nnni i i i L x x αααα===∏+=+∏1ln ln(1)ln ni i L n x αα==++∑ 1ln ln 01ni i d L nx d αα==+=+∑ 1ˆ1ln nii nxα==--∑3、设总体X 的概率密度函数是22exp{}, 0()0, x x x f x λλ⎧->=⎨⎩其它λ>0为未知参数，123,,,,n x x x x K 是一组样本值，求参数λ的最大似然估计。

解：似然函数22111(2exp{})(2exp{})nnnnn i i i ii i i L x x x xλλλλ====∏-=∏-∑211ln ln(2)ln nniii i L n x xλλ===+-∑∑21ln 0n i i d L n x d αλ==-=∑21ˆnii nxα==∑4、设总体的概率密度函数是233exp{}, 0()0, x x x f x λλ⎧->=⎨⎩其它其中λ>0是未知参数，123,,,,n x x x x K 是一组样本值，求参数λ的最大似然估计。

解：似然函数2323111(3exp{})(3exp{})nnnnn ii i ii i i L x x x xλλλλ====∏-=∏-∑2311ln ln(3)ln nnii i i L n xx λλ===+-∑∑31ln 0n i i d L n x d αλ==-=∑ 31ˆnii nxλ==∑5、设总体X 服从参数为1θ的指数分布，123,,,,n x x x x K 是一组样本值，求参数θ的最大似然估计。