当前位置：文档之家 › 常用数制和码制

常用数制和码制

  • 格式：ppt
  • 大小：854.00 KB
  • 文档页数：1

下载文档原格式

  / 1

合集下载

绪论数制和码制-数字电子技术

绪论数制和码制-数字电子技术


十进制数制具有“逢十进一”的规则 ，即每数到十位时，就向高位进位。
二进制数制
定义
二进制数制，也称为二进位数制 或简称为二进制，是一种基数为2 的数制。它采用0和1这两个数字
符号进行计数。
特点
二进制数制具有“逢二进一”的规 则，即每数到二位时，就向高位进 位。
应用
二进制数制广泛应用于计算机科学、 电子工程和通信等领域，是计算机 内部信息处理的基础。
状态机是数字控制系统中的一种描述系统行为的方式，通过有限个 状态和状态之间的转换来描述系统的动态特性。
05 数字电路的发展趋势与展 望
集成电路技术
01
集成电路技术是数字电路发展的越高 ，功能越来越强大。
02
集成电路的发展趋势是向着更小 尺寸、更高性能、更低功耗的方 向发展，这为数字电路的发展提 供了更广阔的空间和可能性。
寄存器
移位寄存器
可以存储二进制数据，并可以将数据向左或向右移动。
计数寄存器
可以存储计数值，并可以递增或递减。
计数器
二进制计数器
可以计数从0到最大值（2^n-1）的二进制数。
十进制计数器
可以计数从0到最大值（10^n-1）的十进制数。
04 数字电路的应用
时钟与定时器
时钟信号
在数字电路中，时钟信号 是一种周期性信号，用于 同步电路中的各个操作。
02
03
ASCII码
ASCII码是用于表示英文 字符的一套码制，通过7 位二进制数表示128个字 符。
Unicode码
Unicode码是用于表示世 界各地文字字符的一套码 制，通过16位二进制数表 示65536个字符。
GB2312码
GB2312码是中国国家强 制标准，包含了常用汉字 及符号，主要用于简体中 文的处理。
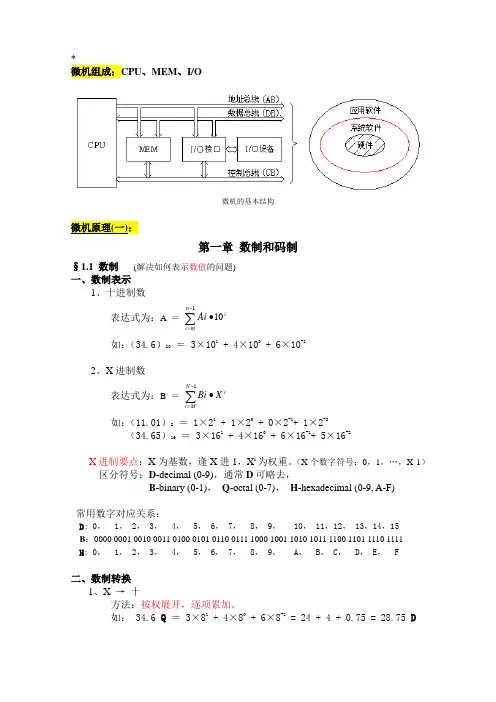
第1章 数和码制

第1章 数和码制

*微机组成：CPU、MEM、I/O微机的基本结构微机原理(一)：第一章数制和码制§1.1 数制(解决如何表示数值的问题)一、数制表示1、十进制数表达式为：A ＝∑-=•110 nmi iAi如：（34.6）10＝ 3×101 + 4×100 + 6×10-1 2、X进制数表达式为：B ＝∑-=•1 NM iiX Bi如：（11.01）2＝ 1×21 + 1×20 + 0×2-1+ 1×2-2（34.65）16＝ 3×161 + 4×160 + 6×16-1+ 5×16-2X进制要点：X为基数，逢X进1，X i为权重。

（X个数字符号：0，1，…，X-1）区分符号：D-decimal (0-9)，通常D可略去，B-binary (0-1)，Q-octal (0-7)，H-hexadecimal (0-9, A-F)常用数字对应关系：D: 0， 1， 2， 3， 4， 5， 6， 7， 8， 9， 10， 11，12， 13，14，15B：0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111H: 0， 1， 2， 3， 4， 5， 6， 7， 8， 9， A， B， C， D， E， F二、数制转换1、X →十方法：按权展开，逐项累加。

如： 34.6 Q＝ 3×81 + 4×80 + 6×8-1 = 24 + 4 + 0.75 = 28.75 D2、十→X即：A十进制＝B X进制令整数相等，即得：A整数＝（B N-1·X N-1 + … + B1·X1）+ B0·X0此式一次除以X可得余数B0，再次除以X可得B1，…，如此直至得到B N-1令小数相等，即得：A小数＝B-1·X-1 +（B-2·X-2 + … + B-M·X-M）此式一次乘X可得整数B-1，再次乘X可得B-2，…，如此直至得到B-M.归纳即得转换方法：除X取余，乘X取整。

数制和编码

数制和编码

34
补码[X]补
定义： 若X>0， 则[X]补= [X]反= [X]原 若X<0， 则[X]补= [X]反+1 正式定义为：
[ X ]补 2n＋X - 2n1 ≤ X＜2n1
35
例
X= –52= – 0110100 [X]原=10110100 [X]反=11001011 [X]补= [X]反+1=11001100
Y3 Y4 Y5 Y6 Y7 11111 11111 11111 11111 11111 11111 11111 01111 10111 11011 11101 11110
25
§2.3 符号数的表示及运算
计算机中的符号数的表示方法：
把二进制数的最高位定义为符号位。
符号位：“0”
表示正，

“1”
表示负。
38
8/16位符号数的表示范围
对8位二进制数： 原码： -127 ~ +127 反码： -127 ~ +127 补码： -128 ~ +127 对16位二进制数： 原码： -32767 ~ +32767 反码： -32767 ~ +32767 补码： -32768 ~ +32767
39
A
&
C
B
A∧B=C
A
≥1
C
B
A∨B=C
21
“非”、“异或”运算
“非”运算即按位求反
两个二进制数相“异或”： 相同则为0，相异则为1
A
1
B
A
⊕
C
B
B=A
A B=C
22
“与非”、“或非”运算
A∧B=C
A
&
数字电路-数制与编码

数字电路-数制与编码

常用进位制：二进制、八进制、十六 进制、十进制等。
数码的个 数和计数 规律是进 位计数制 的两个决 定因素
一、 十进制数的表示 数码个数10： ⒈ 数码个数 ：
0,1,2,3,4,5,6,7,8,9
计数规律: 计数规律
逢十进 1,借一当10
2.基与基数 2.基与基数
用来表示数的数码的集合称为基 用来表示数的数码的集合称为基（0—9）, ） 称为基数 十进制为10)。 称为基数(十进制为 。 基数 十进制为 集合的大小
lg α j≥i lg β
取满足不等式的最小整数
)16 ，已知精度为±(0.1)410
例: (0.3021)10→(
解： α＝10，β＝16，i＝4
lg10 j≥ 4 = 3.32 取 j=4 lg16
⑵按题意要求
例: (0.3021)10→( 解:
)2 ，要求精度 0.1% ∴取 j=10
1 1 0.1% = ≥ 10 1000 2
X ;0 ≤ X < 2n [ X ]补＝ 2n +1 + X ;-2n ≤ X < 0
例 2：
(321.4)8 = ( )10 =3×82+2×81+1×80 +4×8-1 =(209.5)10 192 16 1 0.5
基数乘除法（ 10 → R ）
分整数部分和小数部分分别转换。 ⒈整数的转换——基数除法 规则：除基取余， 规则：除基取余，商零为止 例1：(25) 10 = ( ) 2
例：已知 X1＝1100 X2＝1010 求 Y1＝ X1－ X2 ； Y2＝ X2－ X1
01100 +10101 100001 + 1 00010 01010 +10011 11101
计算机常用数制及编码

计算机常用数制及编码

计算机常用数制及编码1.二进制数制：二进制是计算机中最基本的数制，只包含两个数字0和1、它是一种逢二进一的计数法，每位上的数值以2为底数的幂来表示。

例如，二进制数1101表示1*2^3+1*2^2+0*2^1+1*2^0=13、在计算机中，二进制数被广泛应用于存储和运算等操作。

2.八进制数制：八进制使用8个数字0-7来表示。

它是二进制数制的一种压缩表示方法，每3位二进制数可以表示为一位八进制数。

例如，二进制数1101可以表示为八进制数15、八进制数在计算机界并不常见，但在一些特定场景下仍然有一定的应用。

3.十进制数制：十进制是我们常用的数制，使用10个数字0-9来表示数值，每位上的数值以10为底数的幂来表示。

例如，十进制数123表示1*10^2+2*10^1+3*10^0=123、十进制数制通常用于人类的日常计算中，但在计算机中也会涉及到十进制的处理，例如在涉及到金额、日期和时间等数字的场景中。

4.十六进制数制：十六进制使用16个数字0-9和A-F来表示，其中A-F分别表示十进制数10-15、它是二进制数制的另一种压缩表示方法，每4位二进制数可以表示为一位十六进制数。

十六进制数常用于计算机领域，因为它们可以更紧凑地表示二进制数。

例如，二进制数1101可以表示为十六进制数D。

编码系统是为了实现计算机和人类之间的信息交流而发展的。

下面介绍几种常见的编码系统：1.ASCII码：ASCII（American Standard Code for Information Interchange）是最早和最广泛使用的字符编码系统之一、它使用7位二进制数（扩展ASCII使用8位二进制数）来表示128（或256）个字符，包括英文字母、数字、符号等。

ASCII码可以用于存储和表示文本文件中的字符。

2. Unicode编码：3.UTF-8编码：UTF-8（Unicode Transformation Format - 8-bit）是一种对Unicode进行可变长度编码的字符编码系统。

数制与码制

数制与码制

4 3 2 1 0
1 816 =1⋅163 +12⋅162 +14⋅161 +8⋅160= 740010 CE 436.58= 4⋅82 +3⋅81 + 6⋅80 +5⋅8−1= 286.62510
Digital Electronics Technology 2011-11-2
= 5.12510
1.3 不同数制间的转换
1.3 不同数制间的转换
则其商整数部分为Q，而其余数为第1位系数 则其商整数部分为 ， 而其余数为第 位系数 k0 ； 按照同样方法 ， 以其商 除以 得到第 位系 按照同样方法， 以其商Q除以 得到第2位系 除以r得到第 如此重复进行， 直至其商小于基数r为止 为止， 数 k1 ； 如此重复进行 ， 直至其商小于基数 为止 ， 得到所转换进制的所有系数。 得到所转换进制的所有系数。
Digital Electronics Technology 2011-11-2
1.4 二进制算术运算
2. 减法运算 二进制减法运算法则（ 条 二进制减法运算法则（3条）： ① 0－0＝1－1＝0 － ＝ － ＝ ② 0－1＝1（借一当二） － ＝ （借一当二） ③ 1－0＝1 － ＝ 例：求(1010110)2－(1101.11)2＝? 1010110 1101.11 －) 1001000.01 则(1010110)2－(1101.11)2＝(1001000.01)2
5) 6) 3) 5) 5) 4)
0.726×8 0.808×8 0.464×8 0.712×8 0.696×8 0.568×8 0.544
2011-11-2
0.72610 ≈ 0.1011102
0.72610 ≈ 0.5635548
常用数制

常用数制


8421BCD码用0000H~1001H代表十进制数0~9，运算 法则是逢十进一。8421BCD码每位的权分别是8，4， 2，1，故得此名。 例如，1 649 的BCD码为0001 0110 0100 1001。
2.ASCII(American Standard Code for Information Interchange)码 ASCII码是一种字符编码，是美国信息交换标准代码的 简称，见表1-3.它由7位二进制数码构成，共有128个 字符。 ASCII主要用于微机与外设通信。当微机与ASCII码制 的键盘、打印机及CRT等连用时，均以ASCII码形式进 行数据传输。例如，当按微机的某一建时。键盘中的 单片机便将所按的键码转换成ASCII码传入微机进行相 应处理。
8+0+2+0=1010
（2）十进制
二进制
把一个十进制的整数一次除以所需要的底数，就能够转换 成不同底数的数。例如，为了把十进制的数转换成相应的 二进制数，只要把十进制数一次除以2并记下每次所得的余 数（余数总是1或0），所得的余数倒相排列即为相应的二 进制数。这种方法称为“除2取余”法。
（例1-1）把十进制数25转换成二进制数。 …… 余数 2 解 25 …… 1 2 12 …… 0 2 6 …… 0 2 3 …… 1 2 1 …… 1 0 所以，25D=11001B。
1.4
计算机中常用编码
由于计算机只能识别0和1两种状态，因而计算机 处理的任何信息必须以二进制形式表示。这些二进制 形式的代码即为二进制编码（Encode)。计算机中常用 的二进制编码有BCD码和ASCⅡ码等。 1.BCD（Binary Coded Decimal)码----二-十进制码 BCD码是一种二进制形式的十进制码，也称二-十进制 码。它用4位二进制数表示1位十进制数，最常用的是 8421BCD码，见表1-2。
数制与码制

数制与码制

0 0 0 1 1 1 0 1 0 1 0 0 . 0 1 1 0 ＝ (1D4.6)16 (AF4.76)16 = 1010 1111 0100 . 0111 0110
(3)、十进制数转换为二进制数
采用的方法 — 基数连除、连乘法 原理：将整数部分和小数部分分别进行转换。
整数部分采用基数连除法，小数部分 采用基数连乘法。转换后再合并。
0 0 1 1 0 1 0 1 0 . 0 1 0 ＝ (152.2)8
（2）八进制数转换为二进制数：将每位八进制数用3位二进
制数表示。
(374.26)8 = 011 111 100 . 010 110
(2)、二进制数与十六进制数的相互转换
二进制数与十六进制数的相互转换，按照每4位二进制数对应于一位十六进制 数进行转换。
用一定位数的二进制数来表示十进制数码、字母、符 号等信息称为编码。
用以表示十进制数码、字母、符号等信息的一定位数的 二进制数称为代码。
二-十进制代码：用4位二进制数b3b2b1b0来表示十进 制数中的 0 ~ 9 十个数码。简称BCD码。
用四位自然二进制码中的前十个码字来表示十进制数码， 因各位的权值依次为8、4、2、1，故称8421 BCD码。
×2 1.500 ……… 1=K－2 0.500 ×2
0 ……… 1=K5
高位
1.000 ……… 1=K－3
所以：(44.375)10＝(101100.011)2
采用基数连除、连乘法，可将十进制数转换为任意的N进制数。
高位 低位
2、编码
数字系统只能识别0和1，怎样才能表示更多的数码、符号 、字母呢？用编码可以解决此问题。
＋a－1 ×N-1＋a－2 ×N-2＋… ＋a－m×N-m ③由权展开式很容易将一个N进制数转换为十进制数。
预备知识(数制与码制)

预备知识(数制与码制)


码制间转换方法
二进制与十进制转换
通过权值相加法或除2取余法实现二进制数与十进制数之 间的转换。
二进制与十六进制转换
每4位二进制数对应1位十六进制数，通过分组转换法实现 二者之间的转换。
十进制与十六进制转换
先将十进制数转换为二进制数，再将二进制数转换为十六 进制数，或者通过直接计算法实现十进制数与十六进制数 之间的转换。
码制与数制转换密切相关
在进行数据传输、存储和处理时，经常需要在不同数制之间进行转换。这种转换依赖于特定的编码方式，如ASCII码 、Unicode码等。
码制设计需考虑数制特性
在设计编码方式时，需要充分考虑所采用数制的特性，如数值范围、精度、运算规则等，以确保编码的 有效性和可靠性。
两者在信息技术领域应用举例
04
典型数制与码制详解
典型数制与码制详解
• 请输入您的内容
05
数制与码制在编程中应用实践
编程语言中数制和码制表示方法
二进制表示
在编程语言中，二进制数通常以0b或0B开头பைடு நூலகம்，后面跟随0和1组成的数字序列。例如，二
进制数1010在Python中表示为0b1010。
十进制表示
十六进制数以0x或0X开头，后面跟随0-9和AF（或a-f）组成的数字序列。例如，十六进制 数A3F在C语言中表示为0xA3F。
03
数制与码制关系剖析
数制对码制影响分析
01
02
不同数制表示方法导 致码制差异
二进制、十进制、十六进制等数制在表 示数据时，对应的编码方式会有所不同， 如二进制编码（Binary Code）、十进 制编码（Decimal Code）等。
数制运算规则影响码 制设计
计算机中的数制和码制

计算机中的数制和码制

0-9，A-F，其中A表示10，B表示11，以此类推，F表示15。
运算规则
遵循四则运算规则，但需要注意进位和借位的情况。
八进制数制
定义
八进制数制是一种基数为8的数系统，使用0-7的数字 来表示数值。
数字符号
0-7。
运算规则
遵循四则运算规则，但需要注意进位和借位的情况。
02
不同数制间的转换
十进制转二进制
表格法
将十进制数转换为十六进制数的表格， 通过查表得到对应的十六进制数。
二进制转十进制
累加权重法
将二进制数从右往左依次乘以2的幂次方，并将结果相加得到十进制数。
表格法
将二进制数转换为十进制数的表格，通过查表得到对应的十进制数。
十六进制转十进制
累加权重法
将十六进制数从右往左依次乘以16的幂次方，并将结果相加得到十进制数。
误。
哈希码
MD5
一种常用的哈希算法，将任意长度的数 据映射为固定长度的哈希值，用于验证 数据的完整性和身份识别。
6等，也是常用的 哈希算法，具有更高的安全性和更难碰撞 的特点。
THANKS
感谢观看
GB2312和GBK
中国的字符编码标准，支持简体中文和部分 繁体中文。
校验码
奇偶校验码
通过在数据中添加一个校验位，使得整个数据（包括校验位）中1的个数为偶数（偶校 验）或奇数（奇校验）。用于检测数据传输过程中的错误。
CRC校验码
循环冗余校验码，通过将数据视为二进制数，并计算出一个余数，附加在数据后面，接 收方通过同样的算法计算校验，并与发送方的校验进行比较，检测数据传输过程中的错
二进制数制
定义
01
二进制数制是一种基数为2的数系统，仅使用0和1两个数字符号。
数制与码制

数制与码制


692 6102 9101+2100
对于任意一个n位十进制的正整数，都可用下式表示：
N 10 an1 10n1 an2 10n2 … a1 101 a0 100
即
n1
N 10
ai 10i
i0
式中： ai 为第i位的系数，为0～9十个数码中的一个；10i 为第i位的权；N 10 中
N R an1 Rn1 an2 Rn2 … a1 R1 a0 R0
n1
即
N R
ai Ri
i0
式中： 表示各个数字符号为0～(R-1)数码中的任意一个；R为进位制的基数（第i位
的权），计数规则是从低位到高位“逢R进一”；N R 中的下标表示N是R进制数。
下表为几种常见的数制对照表。 几种常见的数制对照表
除了前述二进制数与十进制数转换方法外，可用四位二进制数码对一位十进制 数进行编码。此方法称为二进制编码的十进制数，简称二－十进制代码，或BCD码 （Binary Coded Decimal）。
四位二进制码有16种组合，而每位十进制数只需用10种组合，另6种组合未用。 用四位二进制码来表示十进制数时，可以编制出多种BCD码。
(11110100101)2=(0111 1010 0101)2=(7A5)16 反之，十六进制数6ED转换成二进制数时，只要把每位十六进制数字写成对 应的四位二进制数即可，例如：
(6ED)16=(0110 1110 1101)2=(11011101101)2
二进制数在数字系统中得到广泛应用。但人们习惯使用十进制数，且为了便于 操作人员使用，常用十进制输入和输出。这就需要将二进制数与十进制数进行转换。
对于任意一个n位十六进制的正整数，都可用下式表示：

数制和码制


十进制转换为R进制: 需要将整数部分和小数部 分分别进行转换，然后再将它们合并起来。
整数依次除以R，用余数构成各位。 小数依次乘以R，用积的整数部分构成各位。 小数部分的转换有一个精度问题，不可能都十分准确 只要满足所提要求即可。 例如要求精度为 0.1% ，二进制数的小数点后第九位为 1 / 512，第十位为 1/ 1024。所以要保留到小数点后第 十位，第九位达不到要求，第十一位太多了。
结论： 1）减法运算=两数的补码相加 例如：13－10 这样的减法运算等价于13的补码与－10 的补码相加 2）两个加数的符号位、最高有效数字位的进位 这三 个数相加，得到的结果就是和的符号位。
1.5 几种常用的编码
一、十进制代码 我们常用的数字1、2、3……9、0 通常有两大用途： 表示大小： 10000（一万）， 8848米。 表示编码：000213班， 8341部队。 我们习惯使用十进制，计算机硬件却是基于二进制的 ，所以我们需要考虑： 如何用二进制编码来表示十进制的十个码元0 ~ 9？
低位
所以：(44.375)10＝(101100.011)2
采用基数连除、连乘法，可将十进制数转换为任意的N进制数。
二、二进制数与八进制数的相互转换
（1）二进制数转换为八进制数： 将二进制数由小数点开始， 整数部分向左，小数部分向右，每3位分成一组，不够3位补 零，则每组二进制数便是一位八进制数。
0 0 1 1 0 1 0 1 0. 0 1 0
0.375 × 2 整数 0.750 „„„ 0=K－1 0.750 × 2 1.500 „„„ 1=K－2 0.500 × 2 1.000 „„„ 1=K－3 高位
22 „„„ 0=K0 11 „„„ 0=K1 5 „„„ 1=K2 2 „„„ 1=K3 1 „„„ 0=K4 0 „„„ 5 1=K 高位

【数电】（一）数制和码制

【数电】（⼀）数制和码制⼀、数制常⽤的数制有⼆进制(Binary)、⼗进制(Decimal)、⼗六进制(Hexdecimal)和⼋进制(Octal)。

感觉⼋进制不常⽤啊。

1.1 ⼗进制→⼆进制 (64.03)10=(?)2整数部分：64/2=32——余032/2=16——余016/2 = 8——余08/2 = 4——余04/2 = 2——余02/2 = 1——余01/2 = 0——余1从下往上为整数部分⼆进制结果1000000⼩数部分：0.03x2=0.06——整数部分00.06x2=0.12——00.12x2=0.24——00.24x2=0.48——00.48x2=0.96——00.96x2=1.92——10.92x2=1.84——10.84x2=1.68——10.68x2=1.36——10.36x2=0.72——0从上到下为⼩数部分0.0000011110（精确到了⼩数点后10位有效数字）因此(64.03)10=(1000000.0000011110)21.2 ⼆进制→⼗进制 (101.011)2=(?)10 =22+0x21+20+0x2-1+2-2+2-3 =5.375⼆、编码与码制2.1 原码、反码和补码在数字电路中，⼗进制数字⼀般⽤⼆进制来表⽰，原因就是逻辑电路的输出⾼低电平刚好可以表⽰⼆进制数的1和0。

在⼆进制数前增加⼀位符号位即可区分数字的正负，正数符号位为0，负数符号位为1，这种形式称之为原码。

正数的原码、反码和补码都是⾃⼰。

负数的反、补码规则如下:原码：1 1001（⼆进制增加符号位后的形式）反码：1 0110（符号位对应取反）补码：1 0111（反码+1） //“+1”这⼀操作使得正负相加刚好溢出正数+对应负数的补码=0 ！2.2 常⽤编码8421码、余3码、2421码、5211码和余3循环码都属于⼗进制代码。

8421码（BCD码）：BCD码的每⼀位上的1都代表⼀个固定的⼗进制数，分别为8、4、2、1，将其代表的数值相加就是8421码对应的⼗进制数，属于恒权代码。

计算机中的数制及其编码

计算机中的数制及其编码1.数制的定义：数制是用来表示和运算数字的一种符号系统。

常见的数制包括二进制、八进制、十进制和十六进制。

2.二进制：二进制是数字系统的一种数制，只包含两个数字0和1、在计算机中，所有的信息都被转换为二进制形式进行存储和处理。

3.八进制：八进制是一种数制，基数为8、它使用了8个数字0-7，通过每一位上的数来表示数值。

4.十进制：十进制是我们日常生活中最常用的数制，基数为10。

它使用了10个数字0-9来表示数值。

5.十六进制：十六进制也是一种常见的数制，基数为16、它使用了16个数字0-9和字母A-F来表示数值。

十六进制常用于计算机科学和工程领域，特别是在内存地址和颜色编码中。

6.数制之间的转换：在计算机中，不同的数制之间可以进行相互转换。

例如，将十进制数转换为二进制数可以使用除2取余的方法，将十进制数一直除以2，直到商为0，然后将每次的余数倒序排列即可得到二进制数。

而将二进制数转换为十进制数，则可以通过每一位数乘以2的幂次方后相加得到结果。

7.数制的编码：在计算机中，数制的编码主要指对不同的字符和数字进行表示和存储的方式。

常见的编码方式包括ASCII码、Unicode、UTF-8等。

-ASCII码：ASCII码是一种基于拉丁字母的字符编码标准，使用7位或8位二进制（0-127或0-255）表示128个不同的字符。

它包括英文字母、数字、标点符号和控制字符等。

- Unicode：-UTF-8：UTF-8是一种可变长度的Unicode编码，使用8位二进制（0-255）表示字符。

它通过对不同的字符使用不同长度的编码，实现了用较少的存储空间表示更多的字符。

总结：数制是用来表示和运算数字的一种符号系统，常见的数制包括二进制、八进制、十进制和十六进制。

数制之间可以进行相互转换，常见的编码方式包括ASCII码、Unicode和UTF-8、这些数制和编码在计算机中起着重要的作用，帮助实现了数字的存储、处理和通信。

计算机常用数制及编码

28
（3）汉字编码 • 汉字也是字符，而且数量大，字形复杂，同音字
多，编码比拼音文字困难，因此在不同的场合要 使用不同的编码。通常有4种类型的编码，即输入 码、国标码、机内码、字形码。
29
① 输入码 输入码所解决的问题是如何使用西文标准键盘把汉字输入到 计算机内。有各种不同的输入码，主要可以分为三类：数字 编码、拼音编码和字型编码。 ● 数字编码：就是用数字串代表一个汉字，常用的是国标区 位码。 ● 拼音编码：是以汉字读音为基础的输入方法。由于汉字同 音字太多，输入后一般要进行选择，影响了输入速度。 ● 字形编码：是以汉字的形状确定的编码。如五笔字型、表 形码，便属此类编码，其难点在于如何拆分一个汉字。
--------将数的符号数值化！
2、小数点如何处理？
----------引入定点和浮点表示法。
22
二进制数在计算机内的表示
计算机内，数据是以二进制的形式存储和运算的。数的正负用 高位字节的最高位来表示，定义为符号位，用“0”表示正数， “1”表示负数。
1、定点数的表示：定点整数
定点数：小数点在数中有固定的位置。整数用定点数表示。
在于求出xn的值 （523）10=（Xxnn=x(n-01, …1 )… x2 x1 x0)2
= xn*2n + xn-1*2 n-1+……+ x 2*22 +
x1*21 + x0*20
两边同除 2；对应整数、小数应相等：
523/2 = 261+1/2 = xn*2 n-1 +xn- 1* 2n-2 +……+x2*21+x1+x0/2
17
例如:
将(0.8125)10 转换成二进制小数. 整数部分
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
[138]10=110 2+310 1+810 0
式中的1、3、8等数字符号是十进制的数码，十进制共有 十个数码0、1、2、3、4、5、6、7、8、9，所谓数码就是 一种数制中可能出现的数字符号。
十进制编码遵循是“逢十进一”的规则，即个位的数 码就由该数码本身的数值所代表；处于十位上的数码，它 的份量要重一些，应乘以“10”，这个“10”称为“权”， 在式中以101的形式出现；处于百位上的数码的权是“100” ，以102的形式出现。所以在十进制码中一个数码左移一位 相当乘以10。十进制的“10”称为基数。
13.1 常用数制和码制 13.2 加法电路 13.3 译码器和编码器 13.4 数据选择器 13.5 数码比较器 13.6 组合逻辑电路的设计 13.7 用VHDL语言描述组合逻
13.1 常用数制和码制
13.1.1 常用数制 13.1.2 常用编码
第13章 组合逻辑电路
第13章 组合逻辑电路
内容提要：组合逻辑电路是通用数字集成电路 的重要品种，它用途 广泛。本章讨论了与组 合逻辑电路密切相关的数制和码制的问题，介 绍了组合逻辑电路的分析和设计方法，译码器、 编码器、数据选择器、比较器等常用组合逻辑 电路的工作原理和应用。
第13章 组合逻辑电路
2010.03
第13章 组合逻辑电路
第13章 组合逻辑电路
2010.03
二进制 8421 5421 2421
0000 0000 0000 0000
第13章 组合逻辑电路
2010.03
13.1.2 常用编码
13.1.2.1 二进制码
二进制码的英文是Binary Code，常用B来表示。二进 制码遵循“逢二进一”的规则。最低位的二进制码是“0” 、“1”交替变化的，比最低位高一位的二进制码是“两个 0”、 “两个1”交替变化的，再高一位是“四个0”、“四个1”交 替变化的，…，最高位的“0”和“1”各占二分之一。
13.1.1.2 任意进制数的通式
什么是编码？按某种编排方式组成的N位数码，用它来 表示某种信息，称为编码，这些信息包括数值、语言、操 作命令、状态等。本节介绍数值的编码方式。
第13章 组合逻辑电路
2010.03
常用的数码有十进制、二进制和十六进制数，现以十 进制和二进制数为例加以说明。有一个十进制数138，它 可以写成如下形式
……
Pm f m (X1, X 2 , , X n1, X n )
X1 X2
X n-1 Xn
组合数字 电路
P1 P2
Pm -1 Pm
图13.0.1 组合逻辑电路框图
第13章 组合逻辑电路
2010.03
本章要讨论四个问题：
1. 组合数字电路的分析； 2. 组合数字电路的设计； 3. 电路逻辑功能的描述方法问题； 4. 通用组合数字电路的应用。
S = [1ABE]H =116 3+1016 2+112 1+1416 0 = 4096+2560+22+14 = [6692]10
第13章 组合逻辑电路
2010.03
13.1.2.3 BCD码(二-十进制编码)
BCD码的英文是Binary Code Decimal的缩写，即二-十 进制编码，是用二进制码表示十进制码的意思。若用二进制 码表示十进制码，如果用三位二进制码只有八个状态，是不 够表示十个数码的。至少需要四位，四位二进制码有十六个 状态，但要舍去其中的六个，即可构成许多种BCD码。只有 有特色的几种得到了应用，具体见下表。
2010.03
逻辑电路通常分为组合逻辑电路和时序逻辑电路两大 类。组合逻辑电路的定义是，有一个逻辑电路，在某一时 刻，它的输出仅仅由该时刻的输入所决定。
组合逻辑电路的框图如图13.0.1所示，每一个输出都是 一个组合逻辑函数。
P1 f1(X1, X 2 , , X n1, X n ) P2 f 2 (X1, X 2 , , X n1, X n )
组合数字电路的分析是指，已知逻辑图，求 解电路的逻辑功能。
组合数字电路的设计是指，已知对电路逻辑 功能的要求，将逻辑电路设计出来。
第13章 组合逻辑电路
2010.03
13.1.1 常用数制
13.1.1.1 概述
组合数字电路中往往与各种数码打交道，例如译码器 就是一种典型的组合数字电路，译码器是将一种编码转换 为另一种编码的逻辑电路。为此先对各种编码方式进行介 绍。数制是指计数的制式，如二进制码、十进制码和十六 进制码等等，码制是指不同的编码方式，如各种BCD码、 循环码等。
所以，二进制数可以写成一个通式
S
m
Si
2i
n
第13章 组合逻辑电路
m i n 二进制，Binary Code
2010.03
对于任意进制数，通式的形式
m
S Ki N i in
式中N为基数，也就是几进制的几；Ki是N进制编码中N 个数码中的任何一个，i为数所在数位的十进制的编号，从 -n到m，代表数位的高低；N i为所在数位的权（Weight）， 在一种固定的进制中，某一位的权就是以这种进制的基数为 底，以代表该数位高低的位置编号为幂的指数值的大小。
从最低位算起，二进制码权的规律符合1、2、4、8、 16…（20、21、22、23、24…）。二进制码某一位的“1”向 高位移一位，等于乘以2；向低位移一位，等于除以2。
第13章 组合逻辑电路
2010.03
13.1.2.2 十六进制编码
十六进制编码的英文是Hexadecimal，常用H表示。十 六进制数有十六个数码0、1、2、3、4、5、6、7、8、9、 A、B、C、D、E、F。其中A相当十，B相当十一，C相当 十二，D相当十三，E相当十四，F相当十五。十六进制码 在计算机设备中普遍采用。下面以通式形式为例，说明十 六进制数[1ABE]H对应的十进制数
第13章 组合逻辑电路
2010.03
对于二进制码，有两个数码0和1，遵循“逢二进一”的
规则，对于整数二进制码它的权应为…23、22、21、20，于是
有
8
4
2
1
权代表数码
1101 1 23 1 22 0 21 1 20 在不同数位
份量的大小
1代表数位的高低
2二进制的2，逢二进一的二。
二进制的数码 0、1